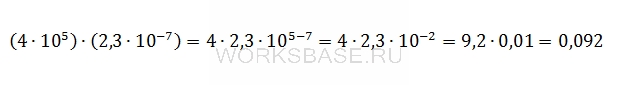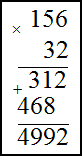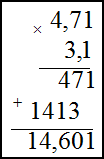Задачи повышенной сложности
Числовые множества
1. Натуральные числа – числа, которые мы используем для счета предметов, счёт начинается с единицы, поэтому ноль не является натуральным числом. Множество натуральных чисел обозначается $N$.
2. Целые числа – это ноль и «плюс – минус натуральные числа». Множество целых чисел обозначается $Z$.
3. Рациональные числа – это всевозможные дроби ${m}/{n}$, где $m$ – целое число, а $n$ – натуральное число, т.е. $n≠0$. Множество рациональных чисел обозначается $Q$.
Делимость
Число $а$ делится на число $с≠0$, если найдется такое число $b$, что $a=c·b$.
Если число $а$ делится на $с$, то число с называется делителем числа $а$.
Если числа $а$ и $b$ делятся на $с$, то их сумма $а + b$ тоже делится на $с$.
Признаки делимости:
Признак делимости на $2$
Число делится на $2$ тогда и только тогда, когда его последняя цифра ноль или делится на $2$, то есть является чётной.
Признак делимости на $3$
Число делится на $3$ тогда и только тогда, когда сумма его цифр делится на 3.
Признак делимости на $4$
Число делится на $4$ тогда и только тогда, когда число из двух последних его цифр нули или делится на $4$.
Признак делимости на $5$
Число делится на $5$ тогда и только тогда, когда последняя цифра делится на $5$ (то есть равна $0$ или $5$).
Признак делимости на $6$
Число делится на $6$ тогда и только тогда, когда оно делится на $2$ и на $3$.
Признак делимости на $7$
Число делится на $7$ тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на $7$ (например, $217$ делится на $7$, так как $21 — (2 · 7) = 7$ делится на $7$).
Признак делимости на $8$
Число делится на $8$ тогда и только тогда, когда три его последние цифры – нули или образуют число, которое делится на $8$.
Признак делимости на $9$
Число делится на $9$ тогда и только тогда, когда сумма его цифр делится на $9$.
Признак делимости на $10$
Число делится на $10$ тогда и только тогда, когда оно оканчивается на ноль.
Признак делимости на $11$
Число делится на $11$ тогда и только тогда, когда сумма цифр с чередующимися знаками делится на $11$ (то есть $182919$ делится на $11$, так как $1 – 8 + 2 – 9 + 1 – 9 = -22$ делится на $11$). Следствие факта, что все числа вида $10^n$ при делении на $11$ дают в остатке $(-1)^n$.
Признак делимости на $12$
Число делится на $12$ тогда и только тогда, когда оно делится на $3$ и на $4$.
Признак делимости на $13$
Число делится на $13$ тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно $13$ (например, $949$ делится на $13$, так как $94 + (4 · 9) = 130$ делится на $13$).
Признак делимости на $14$
Число делится на $14$ тогда и только тогда, когда оно делится на $2$ и на $7$.
Признак делимости на $15$
Число делится на $15$ тогда и только тогда, когда оно делится на $3$ и на $5.$
Признак делимости на $17$
Число делится на $17$ тогда и только тогда, когда разность между числом его десятков и упятеренным числом единиц, кратно $17.$
Признак делимости на $19$
Число делится на $19$ тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно $19$ (например, $646$ делится на $19$, так как $64 + (6 · 2) = 76$ делится на $19$).
Четность и нечетность чисел
- Число называется четным, если оно делится нацело на $2$. Если $а$ четное число, то его вид можно записать $a=2n$.
- Число называется нечетным, если оно не делится нацело на $2$. Если $а$ нечетное число, то его вид можно записать $a=2n+1$.
- Сумма любого количества четных слагаемых четна.
- Сумма четного количества нечетных слагаемых – четное число.
- Сумма нечетного количества нечетных слагаемых – нечетное число.
- Если в произведении все множители нечетные числа, то произведение – нечетное число.
- Если в произведении попадется хотя бы одно четное число, то в результате умножения получится четное число.
Простые и взаимно простые числа
Простые числа – это целые числа, большие единицы, которые имеют только два положительных делителя, а именно самих себя и $1$.
Взаимно простые числа – это числа, которые не имеют общих делителей, кроме единицы. Например, числа $15$ и $4$ взаимно просты, так как их общий делитель равен $1$.
Свойства взаимно простых чисел.
Пусть $а$ и $b$ – взаимно простые числа, тогда для них справедливы следующие высказывания.
- Если некоторое число делится на $а$ и $b$, то оно делится и на их произведение $аb$.
- Если произведение $ас$ делится на $b$, то с делится на $b$.
- Если целые числа $а$ и $b$ взаимно просты, то их сумма $(а + b)$ и произведение $(а·b)$ так же являются взаимно простыми числами.
- Если целые числа $а$ и $b$ взаимно просты, то НОД (наименьший общий делитель) из суммы $(а + b)$ или разности ($а – b$) равен $1$ или $2$.
- Любые два последовательных натуральных числа взаимно просты.
- Если целые числа $а$ и $b$ взаимно просты, то НОД $(а + b$ или $a^2-ab+b^2)$ равен $1$ или $3$.
Числовые свойства степеней
- Точный квадрат целого числа не может оканчиваться цифрами $2, 3, 7, 8,$ а также нечётным количеством нулей.
- Квадрат натурального числа либо делится на $4$, либо при делении на $8$ даёт остаток $1$.
- Квадрат натурального числа либо делится на $9$, либо при делении на $3$ даёт остаток $1$.
- Разность квадратов двух целых чисел одинаковой четности делится на $4$.
- При делении на $3$ куб целого числа и само число дают одинаковые остатки $(0,1,2)$.
- При делении на $9$ куб целого числа дает в остатке $0,1$ или $8$.
- При делении на $4$ куб целого числа дает в остатке $0,1$ или $3$.
- Число $m^5$ оканчивается на ту же цифру, что и число $m$.
Среднее арифметическое чисел
Среднее арифметическое нескольких величин — это отношение суммы величин к их количеству.
Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.
Среднее геометрическое чисел
Чтобы найти среднее геометрическое чисел надо:
- Перемножить все числа
- Из полученного выражения в п.1 надо извлечь корень, степени, равной количеству элементов ряда.
Пример:
Найдите среднее геометрическое чисел $3,9,8$
Решение:
1. Найдем произведение чисел $3·9·8=216$
2. Извлечем корень третьей степени из полученного произведения
$√^3{216}=6$ – полученный результат и есть среднее геометрическое.
Ответ: $6$
Факториал
Факториал числа — это произведение натуральных чисел от $1$ до самого числа (включая данное число). Обозначается знаком (!).
$n!=1·2·3·….·n$
Факториал нуля равен единице $0!=1$
Пример:
Вычислите $7!$
Решение:
7!=1·2·3·4·5·6·7=5040
Ответ: 5040
Последовательности
Последовательность чисел – это набор чисел, в котором каждому числу можно присвоить некоторый номер, причем каждому номеру соответствует единственное число данного набора. Номер числа – это всегда натуральное число, нумерация номеров начинается с единицы. Число с номером $n$ (то есть $n$ – ый член последовательности) обычно обозначается $a_n$.
Большинство последовательностей можно задать аналитическим способом.
Последовательность задана аналитически, если указана формула ее $n$ – го члена. Например, $a_n=4n+3$. В данной формуле указав конкретное число $n$, нетрудно найти член последовательности с соответствующим номером. Если номер $n=5$, то подставим $5$ в формулу последовательности, получим числовое выражение, вычислив которое получим член последовательности с соответствующим номером. $a_5=4·5+3=23$
Прогрессии
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
$а_1$ – первый член арифметической прогрессии
$d$ – разность между последующим и предыдущим членом прогрессии
$d=a_(n+1)-a_n$
$a_n$ – член арифметической прогрессии, стоящий на $n$-ом месте
$n$ – номер места для членов арифметической прогрессии
$S_n$ – сумма первых n членов арифметической прогрессии
Формула, для нахождения n-ого члена прогрессии:
$a_n=a_1+d(n-1)$
Формула суммы первых n членов арифметической прогрессии:
$S_n={(a_1+a_n)·n}/{2}$
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.
$b_1$ – первый член геометрической прогрессии
$q$ – знаменатель геометрической прогрессии, показывает во сколько раз последующее число больше предыдущего.
$q={b_{n+1}}/{b_n}$
$b_n$ – $n$-ый член геометрической прогрессии
$S_n$ – сумма первых $n$ членов геометрической прогрессии
Формула, для нахождения $n$-ого члена прогрессии:
$b_n=b_1·q^{n-1}$
Формула суммы первых n членов арифметической прогрессии:
$S_n={b_1·(q^n-1)}/{q-1},q≠1$
Формулировка задачи: Найдите произведение чисел (степени).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 2 (Действия со степенями).
Рассмотрим, как решаются подобные задачи на примере.
Пример задачи:
Найдите произведение чисел 4 ∙ 105 и 2,3 ∙ 10–7.
Решение:
Найдем произведение чисел. Для этого выполним умножение чисел в степенях с одинаковыми основаниями, после чего перемножим все, что останется:
Ответ: 0,092
Поделитесь статьей с одноклассниками «Найдите произведение чисел (степени) – как решать».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
1 мая
Бесплатные курсы подготовки к ЕГЭ и ОГЭ
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Варианты заданий
Версия для печати и копирования в MS Word
1
Тип 16 № 506485
i
Найдите произведение чисел и
Аналоги к заданию № 506465: 506485 506588 506628 … Все
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166213
Решение
·
Помощь
2
Тип 16 № 506588
i
Найдите произведение чисел и
Аналоги к заданию № 506465: 506485 506588 506628 … Все
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 137753
Решение
·
Помощь
3
Тип 16 № 506628
i
Найдите произведение чисел и
Аналоги к заданию № 506465: 506485 506588 506628 … Все
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 152741
Решение
·
Помощь
4
Тип 16 № 506710
i
Найдите произведение чисел и
Аналоги к заданию № 506465: 506485 506588 506628 … Все
Источник: Копия Апробация базового ЕГЭ по математике, 13—17 октября: вариант 153691
Решение
·
Помощь
5
Тип 16 № 506997
i
Найдите значение произведения чисел и
Аналоги к заданию № 506465: 506485 506588 506628 … Все
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.
Решение
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Содержание:
- Определение произведения чисел
- Свойства произведения чисел
Определение произведения чисел
Произведение $p$ чисел
$a_{1}, a_{2}, dots, a_{n}$ есть результат умножения этих чисел: $p=a_{1} cdot a_{2} cdot ldots cdot a_{n}$ .
В частности, если умножаются два числа $a$ и $b$, то
Пример
Задание. Найти произведение чисел:
1) 1.2$cdot 3$ ; 2) 4$cdot 5 cdot 13$
Ответ.
$1,2 cdot 3=3,6$
$4 cdot 5 cdot 13=260$
Свойства произведения чисел
- Коммутативность: $n cdot m=m cdot n$
-
Ассоциативность: $(n cdot m) cdot k=n cdot(m cdot k)$
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
- Дистрибутивность: $(n+m) cdot k=n cdot k+m cdot k$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти произведение чисел удобным способом:
1) 5$cdot 17 cdot 2$ ; 2) 7$cdot 2 cdot 15 cdot 5$
Решение. По свойства умножения имеем:
$$5 cdot 17 cdot 2=(5 cdot 2) cdot 17=10 cdot 17=170$$
$$7 cdot 2 cdot 15 cdot 5=(7 cdot(2 cdot 15)) cdot 5=(7 cdot 30) cdot 5=210 cdot 5=1050$$
Ответ.
$5 cdot 17 cdot 2=170$
$7 cdot 2 cdot 15 cdot 5=1050$
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие
натуральные числа или
десятичные дроби.
Пример
Задание. Найти произведение чисел
1) 156$cdot 32$ ; 2) $4,71 cdot 3,1$
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое,
полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем
под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в
столбик
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби
перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после
запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором – один, значит, в ответе
нужно отделить справа три знака:
Ответ.
$156 cdot 32=4992$
$4,71 cdot 3,1=14,601$
Читать дальше: что такое простое число.
Определение
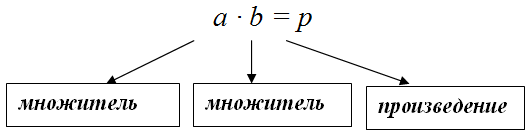
Произведением чисел в математике называется результат их умножения.
Пример: Найдите произведение чисел.
14×15=210
Здесь 14 и 15 называются — множители.
Свойства
1. Коммутативность.
Пример: Вычислить произведение чисел.
17×12=204 и 12×17=204
Переместительный закон: При перестановке множителей результат не меняется.
2. Ассоциативность.
Пример:
11×19×32=6688
(11×19)×32=6688
11×(19×32)=6688
Сочетательный закон: Если группу множителей заменить их произведением, результат не изменится.
3. Дистрибутивность.
Пример:
(15+12)×9=243 и 15×9+12×9=243
Распределительный закон: Умножая сумму на число, можно на это число каждое слагаемое умножить и результаты сложить.
Большие числа, а также десятичные дроби умножают в столбик.
Нет времени решать самому?
Наши эксперты помогут!
Произведение цифр числа
Пример: найти произведение цифр числа 428
4×2×8=64
Произведение суммы и разности чисел
(23+14)×(23-14)=37×9=333
Наименьшее произведение чисел
При умножении любого числа на 0, получится ноль. Наименьшее произведение чисел равно нулю.
Сумма двух произведений чисел
(7×8)+(9×3)=56+27=83
Ответ: 83
Пример: Найди сумму и произведение чисел 14 и 72
Решение:
14+72=86 — сумма
14×72=1008 — произведение