Как найти произведение чисел если известна сумма

Как найти произведение чисел если известна сумма

DrSMERTb

64 / 40 / 10

Регистрация: 12.11.2010

Сообщений: 841

09.03.2014, 16:42

 [ТС]

3

Лучший ответ Сообщение было отмечено Taatshi как решение

Решение

rrrFer, вот так переделал,

Prolog 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

predicates
        start
        summ(integer,integer,integer) /*A=B*N (A,B,N)*/
clauses      
    summ(A,B,N):-
        NN=N-1,
        NN>=0,
        AA=B+B,
        summ(AA,B,NN). 
    start:-
        write("A=B*N"),nl,
        write("B: "),readint(B),
        write("N: "),readint(N),
        summ(A,B,N),
        write(A),nl.
goal
    start

Только чот не пойму как описать остановку итераций, т.е. когда N приравняется к 0. Может можете поправить код?)

Добавлено через 1 час 26 минут
Добавил правило для умножения на ноль. Но не получается установить правило при умножении на 1.

Prolog 
1
2
3

Clauses
           sum(0,_,0).   %Работает
           sum(B,B,1).   %не робит

Как прописать второе правило?

Добавлено через 23 минуты
Всё доделал, конечный вариант

Prolog 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

        Domains
           A,B,N=real
        Predicates
           sum(A,B,N)
           start
        Clauses
           sum(0,_,0).
           sum(A,B,N):-N>0,N1=N-1,sum(A1,B,N1),A=A1+B.
start:-
        write("A=B*N"),nl,
        write("Введите первое число: "),readint(B),
        write("Введите втрое число: "),readint(N),
        sum(A,B,N),
        write("Ответ: ",B," * ",N," = ",A),nl.
goal
    start



0
Источник

Приветствую читателей и подписчиков канала Тесты_математика!

Легко ли найти два числа по их сумме и произведению? Кто-то скажет – элементарно, а кому-то это подумать нужно.

Проверьте свои вычислительные способности.

Вопросы теста.

1. Найти два числа, если сумма чисел равна 18, а произведение равно 17. Какому уравнению соответствую эти числа?

1. x^2 – 18 * х + 17 = 0;

2. x^2 + 17 * х – 18 = 0;

3. x^2 – 18 * х – 17 = 0;

сумма произв чисел..png
сумма произв чисел..png

2. Найти два числа, сумма чисел равна 20,5 , произведение равно 10. Какому уравнению соответствуют эти числа?

1. x^2 – 20,5 + 10 = 0.

2. x^2 + 20,5 * x + 10 = 0.

3. x^2 + 10 * x – 20,5 = 0.

сумма произв чисел1..png
сумма произв чисел1..png

3. Найти два числа, если сумма чисел равна 1000, произведение 999. Какому уравнению соответствуют эти числа?

1. x^2 – 1000 * x + 999 = 0.

2. x^2 + 1000 * x + 999 = 0.

3. x^2 + 999 * x – 1000 = 0.

сумма произв чисел2..png
сумма произв чисел2..png

4. Найдите два числа, если сумма чисел равна 33, а произведение равно 90. Какое уравнение соответствует этим числам?

1. x^2 – 33 * x + 90 = 0.

2. x^2 – 33 * x – 90 = 0.

3. x^2 – 90 * x + 33 = 0.

сумма произв чисел3.png
сумма произв чисел3.png

Все ответы на заданные вопросы можно найти и проверить в данном тесте.

В тесте, ответив на первый вопрос, нажав на кнопку “Далее” переходите ко второму вопросу, и так до пятого вопроса, ответив на который можно получить результат, нажав на кнопку “Отправить”.

Тест.

Спасибо за прочтение статьи и прохождение теста!

Подпишитесь на канал, Тесты_математика!

чтобы не пропустить новые публикации!

Пробуйте найти два числа по их сумме и произведению. Определите соответствующее уравнение

#тесты , #математика , #задачи на логику , #задания на логику

Источник

Содержание материала

  1. Определение произведения чисел
  2. Видео
  3. Что такое множитель по математике?
  4. Основное свойство произведения
  5. Как называются числа при умножении?
  6. Переместительный закон умножения
  7. Умножение многозначного числа на однозначное
  8. Изменение произведения чисел при изменении его сомножителей
  9. Умножение любого натурального числа на нуль

Определение произведения чисел

Произведение двух чисел это есть не что иное, как взятое одно из чисел в количестве другого числа.

Еще раз! Если произведение будет С, то номинальное значение одного из чисел пусть а, взятое в количестве b раз и будет этим произведением. Можно записать скажем так

С=а1+а2+а3+а4…+аb  где 1,2,3,4…b будут индексом указывающим на то, какое это число а по порядку и не более того!

 

Пример  Найти произведение чисел:

1) 1.2⋅3 ;

Ответ.1,2⋅3=3,6

2) 4⋅5⋅13

Ответ: 4⋅5⋅13=260

Видео

Что такое множитель по математике?

Компоненты умножения называются множители. Первый множитель показывает, какое число прибавляют, второй множитель показывает – сколько раз прибавляют это число. Результат умножения называется произведение.

Основное свойство произведения

Произведение не изменяется от перемены порядка производителей.

Доказательство. Умножить 7 на 3 значит 7 повторить три раза. Заменив 7 суммою 7 единиц и вложив их в вертикальном порядке, имеем:

Таким образом, при умножении двух чисел мы можем с

Таким образом, при умножении двух чисел мы можем считать множителем любой из двух производителей. На этом основании производители называются сомножителями или просто множителями.

Самый общий прием умножения состоит в сложении равных слагаемых; но, если производители велики, этот прием приводит к длинным вычислениям, поэтому самое вычисление располагают иначе.

Как называются числа при умножении?

Так же, как и при сложении и вычитании, числа при умножении тоже имеют свое название. Первое число при умножении называется первый множитель. Второе число при умножении называется второй множитель. Результат умножения называют произведение.

Переместительный закон умножения

Рассмотрим задачу:

Мы отдали по два яблока 5 своим друзьям. Математически запись будет выглядеть так: 2⋅5. Или мы отдали по 5 яблок двум своим друзьям. Математически запись будет выглядеть так: 5⋅2. В первом и втором случаем мы раздадим одинаковое количество яблок равное 10 штукам.

Если мы умножим  2⋅5=10 и 5⋅2=10, то результат не поменяется.

2⋅5=5⋅2

Свойство переместительного закона умножения: От перемены мест множителей произведение не меняется. m⋅n=n⋅m

Умножение многозначного числа на однозначное

Умножение числа 8094 на 3 обозначают тем, что подписывают множитель под множимым, ставят слева знак умножения и проводят черту с тем, чтобы отделить произведение.

Умножить многозначное число 8094 на 3 значит найти

Умножить многозначное число 8094 на 3 значит найти сумму трех равных слагаемых

следовательно, для умножения нужно все порядки мно

следовательно, для умножения нужно все порядки многозначного числа повторить три раза, то есть умножить на 3 единицы, десятки, сотни, и т. п. Сложение начинают с единицы, следовательно, и умножение нужно начинать с единицы, а затем переходят от правой руки к левой к единицам высшего порядка.

При этом ход вычислений выражают словесно:

  1. Начинаем умножение с единиц: 3 × 4 составляют 12, подписываем под единицами 2, а единицу (1 десяток) прикладываем к произведению следующего порядка на множитель (или запоминаем ее в уме).

  2. Умножаем десятки: 3 × 9 составляет 27, да 1 в уме составят 28; подписываем под десятками 8 и 2 в уме.

  3. Умножаем сотни: Нуль, умноженный на 3, дает нуль, да 2 в уме составит 2, подписываем под сотнями 2.

  4. Умножаем тысячи: 3 × 8 = 24, подписываем вполне 24, ибо не имеем следующих порядков.

Это действие выразится письменно:

Из предыдущего примера выводим следующее правило.

Из предыдущего примера выводим следующее правило. Чтобы умножить многозначное число на однозначное, нужно:

  1. Подписать множитель под единицами множимого, поставить слева знак умножения и провести черту.

  2. Умножение начинать с простых единиц, затем, переходя от правой руки к левой, последовательно умножают десятки, сотни, тысячи и т. д.

  3. Если при умножении произведение выражается однозначным числом, то его подписывают под умножаемой цифрой множимого.

  4. Если же произведение выражается двухзначным числом, то цифру единиц подписывают под тем же столбцом, а цифру десятков прибавляют к произведению следующего порядка на множитель.

  5. Умножение продолжается до тех пор, пока не получат полного произведения.

Изменение произведения чисел при изменении его сомножителей

Чтобы понять, что происходит с произведением чисел при изменении одного или нескольких сомножителей, нужно вспомнить, что действие умножения – это частный случай действия сложения, а также переместительный и сочетательный законы сложения.

Если увеличить один из сомножителей в несколько раз, произведение также увеличится в это же число раз.

Рассмотрим пример 18 ∙2. Увеличив второй сомножитель, к примеру, в 3 раза, мы получим другое выражение: 18 ∙6.

Умножение любого натурального числа на нуль

6⋅0=0 или  0⋅6=0 a⋅0=0 или 0⋅a=0 При умножении любого натурального числа на нуль произведение будет равно нулю.

Вопросы к теме “Умножение”:

Что такое произведение чисел? Ответ: произведением чисел или умножение чисел называется выражение m⋅n, где m – слагаемое, а n – число повторений этого слагаемого.

Для чего нужно умножение? Ответ: чтобы не писать длинное сложение чисел, а писать сокращенно. Например, 3+3+3+3+3+3=3⋅6=18

Что является результатом умножения? Ответ: значение произведения.

Что означает запись умножения  3⋅5? Ответ: 3⋅5=5+5+5=3+3+3+3+3=15

Если умножить миллион на нуль, чему будет равно произведение? Ответ: 0

Пример №1: Замените сумму произведением: а) 12+12+12+12+12  б)3+3+3+3+3+3+3+3+3 Ответ: а)12⋅5=60 б) 3⋅9=27

Пример №2: Запишите в виде произведения: а) а+а+а+а б) с+с+с+с+с+с+с Решение: а)а+а+а+а=4⋅а б) с+с+с+с+с+с+с=7⋅с

Задача №1: Мама купила 3 коробки конфет. В каждой коробке по 8 конфет. Сколько конфет купила мама? Решение: В одной коробке 8 конфет, а у нас таких коробок 3 штуки. 8+8+8=8⋅3=24 конфеты Ответ: 24 конфеты.

Задача №2: Учительница рисования сказала приготовить своим восемью ученикам по семь карандашей на урок. Сколько всего карандашей вместе было у детей? Решение: Можно посчитать суммой задачу. У первого ученика было 7 карандашей, у второго ученика было 7 карандашей и т.д. 7+7+7+7+7+7+7+7=56 Запись получилась неудобная и длинная, заменим сумму на произведение. 7⋅8=56 Ответ 56 карандашей.

Теги

Источник

Как найти произведение суммы

Сложение и умножение – базовые математические операции, стоящие в одном ряду с вычитанием, делением, возведением в степень, и другими. Комбинируя эти операции между собой, можно получить новые, более сложные операции.

Как найти произведение суммы

Инструкция

Чтобы умножить сумму на число, перемножьте каждое слагаемое с этим числом, полученные числа сложите между собой.Пример. (a+b+c)*p=a*p+b*p+c*p.Обратная операция – вынесение общего множителя за скобку: a*p+b*p+c*p=p(a+b+c).

Для перемножения двух скобок, содержащих в себе суммы каких-то переменных, существует определенная схема. Надо умножить сначала слагаемое первой скобки на каждое из слагаемых второй скобки, сложить полученные результаты, затем ту же операцию проделать со вторым и последующими слагаемыми первой скобки. Осталось сложить полученные числа между собой.Пример.(a+b)*(c+d)=a*c+a*d+b*c+b*d.Помните, что перемножаются также и знаки перед числами. Произведение одинаковых знаков дает плюс, разных знаков – минус. Например, (a-b)(c+d)=a*c+a*d-b*c-b*d; (a-b)(c-d)=a*c-a*d-b*c+b*d.Обратная операция – разложение суммы на множители.

Чтобы перемножить три скобки, являющиеся суммами некоторых переменных, надо перемножить сначала любые две скобки, затем полученный результат умножить на третью скобку. Умножение четырех и большего числа скобок происходит аналогично. Группируйте скобки так, чтобы считать было удобнее и проще.

Частный случай произведения сумм – возведение суммы в степень. Например, (a+b)^2, (c-d)^3, (p-k)^6. Можно представить возведение в степень в виде произведения нескольких одинаковых скобок и перемножать их по правилам, изложенным выше. А можно воспользоваться формулами сокращенного умножения, которые всегда полезно помнить.

Видео по теме

Полезный совет

Выведите самостоятельно формулы сокращенного умножения, последовательно перемножая скобки. Это позволит лучше понять суть происходящего, а заодно потренироваться в умножении сумм.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Содержание:

  • Определение произведения чисел
  • Свойства произведения чисел

Определение произведения чисел

Произведение $p$ чисел
$a_{1}, a_{2}, dots, a_{n}$ есть результат умножения этих чисел: $p=a_{1} cdot a_{2} cdot ldots cdot a_{n}$ .
В частности, если умножаются два числа $a$ и $b$, то

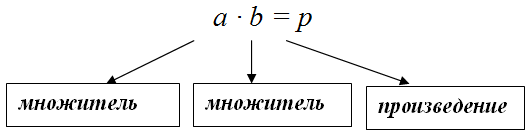
Пример

Задание. Найти произведение чисел:

1)  1.2$cdot 3$   ;   2)  4$cdot 5 cdot 13$ 

Ответ.  

$1,2 cdot 3=3,6$

$4 cdot 5 cdot 13=260$

Свойства произведения чисел

  1. Коммутативность: $n cdot m=m cdot n$

  2. Ассоциативность: $(n cdot m) cdot k=n cdot(m cdot k)$

    На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.

  3. Дистрибутивность: $(n+m) cdot k=n cdot k+m cdot k$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти произведение чисел удобным способом:

1)  5$cdot 17 cdot 2$   ;   2)  7$cdot 2 cdot 15 cdot 5$ 

Решение. По свойства умножения имеем:

$$5 cdot 17 cdot 2=(5 cdot 2) cdot 17=10 cdot 17=170$$

$$7 cdot 2 cdot 15 cdot 5=(7 cdot(2 cdot 15)) cdot 5=(7 cdot 30) cdot 5=210 cdot 5=1050$$

Ответ.  

$5 cdot 17 cdot 2=170$

$7 cdot 2 cdot 15 cdot 5=1050$

Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие
натуральные числа или
десятичные дроби.

Пример

Задание. Найти произведение чисел

1)  156$cdot 32$   ;   2)  $4,71 cdot 3,1$ 

Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое,
полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем
под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в
столбик

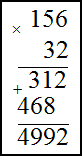
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби
перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после
запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором – один, значит, в ответе
нужно отделить справа три знака:

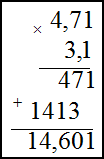
Ответ.  

$156 cdot 32=4992$

$4,71 cdot 3,1=14,601$

Читать дальше: что такое простое число.

Источник

Добавить комментарий