Как найти произведение чисел с погрешностью

Погрешность произведения

Пусть в результате измерений получено:

$$ x = x_0 pm Delta x, quad y = y_0 pm Delta y, quad x, y gt 0 $$

Найдём границы для произведения этих величин: z = xy

$$ {left{ begin{array}{c} x_0- Delta x le x le x_0+ Delta x \ y_0- Delta y le y le y_0+ Delta y end{array} right.} Rightarrow (x_0- Delta x)(y_0-Delta y) le xy le (x_0+ Delta x)(y_0+ Delta y) Rightarrow $$

$$ Rightarrow x_0 y_0-( Delta xy_0+x_0 Delta y- Delta x Delta y) le xy le x_0 y_0-( Delta xy_0+x_0 Delta y+ Delta x Delta y) $$

(О правилах умножения двух неравенств, см. §36 данного справочника).

Абсолютные погрешности $Delta x ≪ x_0, Delta y≪y_0$ заметно меньше $x_0$ и $ y_0$, поэтому будем считать, что произведение $Delta x Delta y approx 0$, и им можно пренебречь. Получаем:

$$ x_0 y_0-( Delta xy_0+x_0 Delta y) le xy le x_0 y_0-( Delta xy_0+x_0 Delta y) $$

$$ z = z_0 pm Delta z: z_0 = x_0 y_0, quad Delta z = Delta xy_0+x_0 Delta y $$

$$ δ_z = frac{Delta z}{z_0} = frac{Delta xy_0+x_0 Delta y}{x_0 y_0} = frac{Delta x}{x_0} + frac{Delta y}{y_0} = δ_x+δ_y $$

$$ δ_{xy} = δ_x+δ_y $$

При умножении приближенных величин их относительные погрешности складываются.

Погрешность степени

Пусть в результате измерений получено: $x = x_0 pm Delta x, x gt 0$

Тогда, для квадрата x из выражения для относительной погрешности произведения получаем: $δ_{x^2} = δ_x+δ_x = 2δ_x$.

Для куба: $δ_{x^3 } = δ_{x^2}+δ_x = 2δ_x+δ_x = 3δ_x$.

Для произвольной степени n:

$$ δ_{x^n} = n δ_x $$

При возведении приближенной величины в натуральную степень n, её относительная погрешность увеличивается в n раз.

Погрешность частного

Пусть в результате измерений получено:

$$x = x_0 pm Delta x, quad y = y_0 pm Delta y, quad x,y gt 0 $$

Найдём границы для частного этих величин: $z = frac{x}{y}$

$$ {left{ begin{array}{c} x_0- Delta x le x le x_0 + Delta x \ y_0- Delta y le y le y_0+ Delta y end{array} right.} Rightarrow {left{ begin{array}{c}x_0- Delta x le x le x_0+ Delta x \ frac{1}{y_0-Delta y} ge frac{1}{y} ge frac{1}{y_0+ Delta y} end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} x_0- Delta x le x le x_0+ Delta x \ frac{1}{y_0+ Delta y} le frac{1}{y} le frac{1}{y_0- Delta y} end{array} right.} Rightarrow frac{x_0- Delta x}{y_0+ Delta y} le frac{x}{y} le frac{x_0+ Delta x}{y_0- Delta y} Rightarrow $$

$$ Rightarrow frac{ (x_0- Delta x)(y_0- Delta y)}{(y_0+ Delta y)(y_0- Delta y)} le frac{x}{y} le frac{(x_0+ Delta x)(y_0+ Delta y)}{(y_0- Delta y)(y_0+ Delta y)} Rightarrow $$

$$ Rightarrow frac{x_0 y_0-( Delta xy_0+x_0 Delta y- Delta x Delta y)}{y_0^2- Delta y^2} le frac{x}{y} le frac{x_0 y_0+( Delta xy_0+x_0 Delta y+ Delta x Delta y)}{y_0^2- Delta y^2} $$

О правилах умножения двух неравенств и обращения положительных сторон, см. §36 данного справочника.

Считаем произведения и квадраты абсолютных погрешностей малыми величинами $Delta x Delta y approx 0, quad Delta y^2 approx 0$, которыми можно пренебречь. Получаем:

$$ frac{x_0 y_0-( Delta xy_0+x_0 Delta y)}{y_0^2} le frac{x}{y} le frac{x_0 y_0+( Delta xy_0+x_0 Delta y)}{y_0^2} $$

$$frac{x_0}{y_0} – left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2} right) le frac{x}{y} le frac{x_0}{y_0} + left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2} right) $$

$$ z = z_0 pm Delta z: z_0 = frac{x_0}{y_0}, Delta z = frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2}$$

$$ δ_z = frac{Delta z}{z_0} = left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2}right) : frac{x_0}{y_0} = left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2}right) cdot frac{y_0}{x_0} = frac{Delta x}{x_0} + frac{Delta y}{y_0} = δ_x+δ_y $$

$$ δ_{frac{x}{y}} = δ_x+δ_y $$

При делении приближенных величин их относительные погрешности складываются.

Примеры

Пример 1. Точное значение выражения:

$$5,31 cdot 4,16+2,19 cdot 1,51 = 22,0896+3,3069 = 25,3965 $$

Считая все величины, входящие в выражение, приближёнными с абсолютной погрешностью $Delta$ x = 0,01, выясните, нужно ли округлять ответ.

Во сколько раз абсолютная погрешность результата больше абсолютной погрешности исходных данных? Во сколько раз относительная погрешность результата больше относительной погрешности сомножителя 5,31?

Обозначим a = 5,31, b = 4,16, c = 2,19, d = 1,51.

Относительные погрешности (округление с избытком):

$$δ_a = frac{0,01}{5,31} cdot 100 text{%} = 0,19 text{%}, quad δ_b = frac{0,01}{4,16} cdot 100 text{%} = 0,25 text{%} $$

$$δ_c = frac{0,01}{2,19} cdot 100 text{%} = 0,46 text{%}, quad δ_d = frac{0,01}{1,51} cdot 100 text{%} = 0,67 text{%} $$

Относительные погрешности произведений:

$$ δ_{ab} = δ_a+δ_b = 0,19 text{%} + 0,25 text{%} = 0,44 text{%} $$

$$ δ_{cd} = δ_c+δ_d = 0,46 text{%} +0,67 text{%} = 1,13 text{%} approx ↑ 1,2 text{%} $$

Абсолютные погрешности произведений:

$$ Delta_{ab} = δ_{ab} cdot ab = 0,0044 cdot 22,0896 approx 0,09719 approx ↑ 0,098 $$

$$ Delta_{cd} = δ_{cd} cdot cd = 0,012 cdot 3,3069 approx 0,03968 approx 0,040 $$

Оставляем в промежуточных оценках 2 значащие цифры для последующего округления. Абсолютная погрешность выражения:

$$ Delta_{ab+cd} = Delta_{ab} + Delta_{cd} = 0,098+0,040 = 0,138 approx ↑ 0,2 $$

Таким образом, ответ нужно округлить до десятых:

$$ 5,31 cdot 4,16+2,19 cdot 1,51 approx 25,4 ± 0,2 $$

Отношение абсолютной погрешности результата к погрешности исходных данных:

$ frac{0,2}{0,01} = 20$ – абсолютная погрешность увеличилась в 20 раз.

Относительная погрешность результата: $δ = frac{0,2}{25,4} cdot 100 text{%} approx 0,79 text{%} $

По отношению к $δ_a: frac{δ}{δ_a} = frac{0,79}{0,19} approx 4,2$ – относительная погрешность результата в 4,2 раза больше.

Пример 2. а) Границы приближенных величин $5 le x le 6,6 le y le 7$. Оцените сумму, разность, произведение и частное этих величин.

б) Считая x и y точными величинами, принимающими значения на заданных отрезках, найдите границы суммы, разности и произведения этих величин.

а) По условию:

$$ {left{ begin{array}{c} x_0-Delta x = 5 \ x_0+Delta x = 6 end{array} right.} Rightarrow {left{ begin{array}{c} 2x_0 = 5+6 = 11 \ 2 Delta x = 6-5 = 1 end{array} right.} Rightarrow {left{ begin{array}{c} x_0 = 5,5 \ Delta x = 0,5 end{array} right.} Rightarrow δ_x = frac{0,5}{5,5} cdot 100 text{%} approx 9,1 text{%} $$

$$ {left{ begin{array}{c} y_0- Delta y = 6 \ y_0+ Delta y = 7 end{array} right.} Rightarrow {left{ begin{array}{c} 2y_0 = 6+7 = 13 \ 2 Delta y = 7-6 = 1 end{array} right.} Rightarrow {left{ begin{array}{c} y_0 = 6,5 \ Delta y = 0,5 end{array} right.} Rightarrow δ_y = frac{0,5}{6,5} cdot 100 text{%} approx 7,7 text{%} $$

Абсолютная погрешность суммы: $Delta_{x+y} = Delta_x+Delta_y = 0,5+0,5 = 1$

$$ x+y = (5,5+6,5) pm 1 = 12 pm 1 $$

Границы суммы: $ 11 le x+y le 13$

Абсолютная погрешность разности: $Delta _{x-y} = Delta _x + Delta _y = 0,5+0,5 = 1$

$$ x-y = (5,5-6,5) pm 1 = -1 pm 1 $$

Границы разности: $-2 le x-y le 0$

Относительная погрешность произведения:

$$δ_{xy} = δ_x+δ_y = 9,1 text{%} +7,7 text{%} = 16,8 text{%} approx 17 text{%}$$

Абсолютная погрешность произведения:

$$ Delta_{xy} = δ_{xy} cdot x_0 y_0 = 0,17 cdot 5,5 cdot 6,5 = 6,0775 approx ↑ 7 $$

$$ xy = (5,5 cdot 6,5) pm 7 approx 36 pm 7 $$

Границы произведения: $29 le xy le 43$

Относительная погрешность частного:

$$ δ_{x/y} = δ_x+δ_y = 9,1 text{%} +7,7 text{%} = 16,8 text{%} approx 17 text{%} $$

Абсолютная погрешность частного:

$$ Delta_{frac{x}{y}} = δ_{frac{x}{y}} cdot frac{x_0}{y_0} = 0,17 cdot frac{5,5}{6,5} approx 0,14 approx ↑ 0,2 $$

$$ frac{x}{y} = left( frac{5,5}{6,5} right) pm 0,2 approx 0,8 pm 0,2 $$

Границы частного: $0,6 le frac{x}{y} le 1,0$

б) Для точных величин получаем следующие границы:

Границы суммы:

$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow 5+6 le x+y le 6+7 Rightarrow 11 le x+y le 13 $$

Границы разности:

$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow {left{ begin{array}{c} 5 le x le 6 \ -7 le -y le -6 end{array} right.} Rightarrow 5-7 le x-y le 6-6 Rightarrow -2 le x-y le 0 $$

Границы произведения:

$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow 5 cdot 6 le xy le 6 cdot 7 Rightarrow 30 le xy le 42 $$

Границы частного:

$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow {left{ begin{array}{c} 5 le x le 6 \ frac{1}{7} le frac{1}{y} le frac{1}{6} end{array} right.} Rightarrow frac{5}{7} le frac{x}{y} le 1 $$

Пример 3. В эксперименте по определению плотности вещества получен объём V = 9, 7 $pm$ 0,05 мл и масса m = 107 $pm$ 2 г. Найдите плотность.

Это свинец или железо?

Плотность:

$$ ρ = frac{m}{V}, ρ_0 = frac{m_0}{V_0} = frac{107 cdot 10^{-3} кг}{9,7 cdot 10^{-6} м^3} approx 11031 frac{кг}{м^3} $$

Относительные погрешности (округление с избытком):

$$ δ_V = frac{0,05}{9,7} cdot 100 text{%} approx 5,2 text{%}, δ_m = frac{2}{107} cdot 100 text{%} approx 1,9 text{%} $$

$$ δ_ρ = δ_V+δ_m = 5,2 text{%} +1,9 text{%} = 7,1 text{%} $$

Абсолютная погрешность для плотности (округление с избытком):

$$ Δ_ρ = δ_ρ cdot ρ_0 = 0,071 cdot 11031 approx 800 frac{кг}{м^3} $$

$$ ρ = 11000 pm 800 frac{кг}{м^3} $$

Это – свинец (табличное значение $ρ_{таб} = 11340 frac{кг}{м^3}$ ).

1. Действия над приближенными числами

При
сложении или вычитании чисел их абсолютные
погрешности складываются. Относительная
погрешность суммы заключена между
наибольшим и наименьшим значениями
относительных погрешностей слагаемых;
на практике принимается наибольшее
значение.

(a

b) = a
+ b
.

При
умножении или делении чисел друг на
друга их относительные погрешности
складываются.

;

При
возведении в степень приближенного
числа его относительная погрешность
умножается на показатель степени.

Погрешность
суммы:
на
практике при сложении приближенных
чисел поступают следующим образом:

– выделяют числа,
десятичная запись которых обрывается
ранее других и оставляют их без изменения;

– остальные
числа округляют по образцу выделенных,
сохраняя один или два запасных десятичных
знака;

– производят
сложение данных чисел, учитывая все
сохраненные знаки;

– полученный
результат округляют на один знак.

Пример.
найти
сумму приближенных чисел 0.348
0.1834 345.4 235.2 11.75 9.27 0.0849 0.0214 0.000354
.

Решение.

0.35 + 0.18 + 345.4 + 235.2 +
11.75 + 9.27 + 0.08 + 0.02 + 0.00 = 602.25 . После
округления получаем 602.2 .

Полная
погрешность результата 
складывается
из трех слагаемых:

– суммы предельных
погрешностей исходных данных:

₁=10^-3+10^-4+10^-1+10^-1+10^-2
+10^-2+10^-4+10^-4+10^-6

= 0.221301 <
0.222

.-
абсолютной величины суммы ошибок (с
учетом их знаков) округления слагаемых:

₂
=-0.002+0.0034+0.0049+0.0014+0.000354=
0.008054 
0.009

– заключительной
погрешности округления результатов:

₃ =
0.050 .

Следовательно,

= ₁
+ ₂
+ ₃

0.222+0.009+0.050 = 0.281 <
0.3 и,
таким образом, искомая сумма равна 602.2

0.3 .

Погрешность
разности:
предельная
абсолютная погрешность разности (u
= x₁
– x₂)
равна
сумме предельных абсолютных погрешностей
уменьшаемого и вычитаемого:

_u =
_x1
+ _x2

Отсюда предельная
относительная погрешность разности

где А
–
точное значение абсолютной величины
разности чисел х₁
и
х₂
.

Если
приближенные числа х₁

и
х₂
достаточно
близки друг к другу и имеют малые
абсолютные погрешности, то число А
–
мало. В этом случае из этой же формулы
следует, что предельная относительная
погрешность может быть весьма большой,
т.е. происходит потеря точности.

Пример.
Найти
разность двух чисел х₁
= 47.132 и х₂
= 47.111 .

Решение.
Разность
u = 47.132 –
47.111 = 0.021 . Предельная
абсолютная погрешность разности равна
_u
=
0.0005+0.0005=0.001 .

Предельные
абсолютные погрешности вычитаемого,
уменьшаемого и разности равны:

_x1
= 0.0005/47.132 = 0.00001

_x2
= 0.0005/47.111 = 0.00001

_u
= 0.001/0.021 = 0.05

Поэтому при
приближенных вычислениях полезно
преобразовывать выражения, вычисления
числовых значений которых приводит к
вычитанию близких чисел.

Погрешность
произведения:
относительная погрешность произведения
нескольких приближенных чисел, отличных
от нуля, не превышает суммы относительных
погрешностей этих чисел:

  ₁
+
₂
+ … + _n
.

Поэтому
при вычислении произведения нескольких
приближенных чисел применяют следующие
правила:

– округляют
эти числа так, чтобы каждое из них
содержало на одну (или две) значащие
цифры больше, чем число верных значащих
цифр в наименее точном из сомножителей;

– в результате
умножения сохраняют столько значащих
цифр, сколько верных цифр имеется в
наименее точном из сомножителей.

Пример.
Найти
произведение х₁
= 2.5 и х₂
= 72.397 .

Решение.
После
округления имеем х₁=2.5
и х₂=72.4
.Т.е. u=x₁x₂=
2.572.4
= 181 .

Погрешность
частного:
относительная погрешность частного не
превышает суммы относительных погрешностей
делимого и делителя.

Пример.
Найти частное u
= 25.7 / 3.6,
если все написанные знаки делимого и
делителя верны.

Решение.
u = 25.7 /
3.6 = 7.14 . _u
= _x1
+ _x2
= 0.05/25.7 + 0.05/3.6 = 0.002 + 0.014 = 0.016 . Так
как u = 7.14,
то
u
= 0.016 
7.14 = 0.11 . Поэтому
u = 7.14 
0.11 .

Пример.
Найти
относительную погрешность функции:

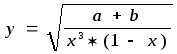
Решение.
Используя
формулы оценки погрешностей получаем

Из этой
формулы следует, что при х 
1 может получиться очень большая
погрешность.

Соседние файлы в папке 2

• #
• #
• #
• #
• #
• #
• #
• #

Действия с приближенными числами.

На практике пользуются более простыми правилами, которые называются

Правила подсчета цифр:

Задача:

Решение:

Задача:

Решение:

Задача:

Найдите произведение двух приближенных чисел: 0,3862 * 0,85

Решение:

Задача:

Решение:

Задача:

Решение:

Задача:

Решение:

(Лисичкин В.Т., Соловейчик И.Л. Сборник задач по математике с решениями для техникумов (учебное пособие))

При решении некоторых задач возникает необходимость указать верные цифры результата,

т.е. найти границу абсолютной погрешности результата вычислений.

На практике сначала находят относительную погрешность результата, а затем, используют формулу:

Формулы для вычисления границ абсолютной и относительной погрешностей некоторых функций приведены в таблице.

Задача:

 

Решение:

Так как a=0,3862 то ∆a=0,00005  , b = 0,8 значит ∆b=0,05

​​​​​​​

Находим границу абсолютной погрешности произведения по формуле

(Н.В. Богомолов Практические занятия по математике)

ПрактическАЯ РАБОТА

Тема: Умножение и деление приближенных значений чисел.

Цели:

 – закрепление навыков работы с приближенными числами, умения вычислять абсолютной и относительной погрешностей

Оснащение занятия:   конспект лекций.

Порядок выполнения работы

 Задание 1.

1.  Ознакомиться с лекцией 3.

2. Выписать в тетрадь виды и свойства операций над множествами. Ответить на вопросы:

     – В чем заключается правило умножения приближенных значений чисел?

     – В чем заключается правило деления приближенных значений чисел?

3. Выпишите в тетрадь рассмотренные в лекции примеры

Задание 2. Решите задачи для самостоятельного решения из лекции

Лекция 3. 

Умножение приближенных значений чисел.

         Формулы для оценки границ абсолютной погрешности произведения (частного) сложны, поэтому на практике сначала находят относительную погрешность произведения (частного), а затем границу абсолютной погрешности произведения (частного).

Формулы для границ абсолютной и относительной погрешностей некоторых функций приведены в таблице (см. лекцию 4).

Пример 1. Найти верные цифры произведения приближенных значений чисел a = 0,3862;  b = 0,8

Имеем 0,3862 ∙0,8 = 0,30896. Границы абсолютной погрешности сомножителей равны 0,00005 и 0,05. Находим относительную погрешность произведения
εab= 0,000050,3862+ 0,050,8
 = 0,063

Находим границу абсолютной погрешности произведения:

∆(a b)= 0,30896 ∙0,063 = 0,0195; 0,005<0,0195<0,05.

Полученный результат означает, что в произведении одна верная цифра (в разряде десятых): 0,30896≈0,3

Пример 2. Вычислить объем цилиндра V = πR2H, если R = 45,8 см,

H = 78, 6 см. Указать верные цифры ответа.

Имеем V = π∙ 45,82 ∙78,6 = 517000 см3. Используя формулу для нахождения относительной погрешности и π=3,14, находим:

εV= ∆ππ+ 2∆RR+ ∆HH = 0,0053,14+ 2∙0,0545,8+ 0,0578,6=0,0044

Находим границу абс

Просмотр содержимого документа

«Умножение и деление приближенных значений чисел»