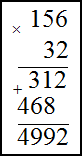Содержание:
- Определение произведения чисел
- Свойства произведения чисел
Определение произведения чисел
Произведение $p$ чисел
$a_{1}, a_{2}, dots, a_{n}$ есть результат умножения этих чисел: $p=a_{1} cdot a_{2} cdot ldots cdot a_{n}$ .
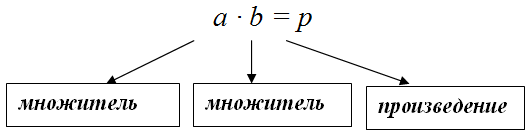
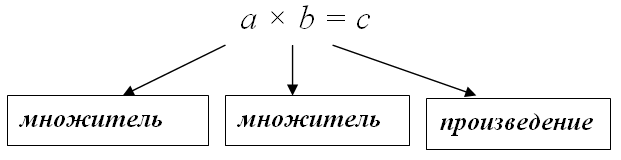
В частности, если умножаются два числа $a$ и $b$, то
Пример
Задание. Найти произведение чисел:
1) 1.2$cdot 3$ ; 2) 4$cdot 5 cdot 13$
Ответ.
$1,2 cdot 3=3,6$
$4 cdot 5 cdot 13=260$
Свойства произведения чисел
- Коммутативность: $n cdot m=m cdot n$
-
Ассоциативность: $(n cdot m) cdot k=n cdot(m cdot k)$
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
- Дистрибутивность: $(n+m) cdot k=n cdot k+m cdot k$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти произведение чисел удобным способом:
1) 5$cdot 17 cdot 2$ ; 2) 7$cdot 2 cdot 15 cdot 5$
Решение. По свойства умножения имеем:
$$5 cdot 17 cdot 2=(5 cdot 2) cdot 17=10 cdot 17=170$$
$$7 cdot 2 cdot 15 cdot 5=(7 cdot(2 cdot 15)) cdot 5=(7 cdot 30) cdot 5=210 cdot 5=1050$$
Ответ.
$5 cdot 17 cdot 2=170$
$7 cdot 2 cdot 15 cdot 5=1050$
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие
натуральные числа или
десятичные дроби.
Пример
Задание. Найти произведение чисел
1) 156$cdot 32$ ; 2) $4,71 cdot 3,1$
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое,
полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем
под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в
столбик
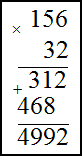
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби
перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после
запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором – один, значит, в ответе
нужно отделить справа три знака:
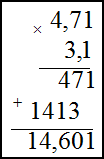
Ответ.
$156 cdot 32=4992$
$4,71 cdot 3,1=14,601$
Читать дальше: что такое простое число.
Определение
Произведением чисел в математике называется результат их умножения.
Пример: Найдите произведение чисел.
14×15=210
Здесь 14 и 15 называются — множители.
Свойства
1. Коммутативность.
Пример: Вычислить произведение чисел.
17×12=204 и 12×17=204
Переместительный закон: При перестановке множителей результат не меняется.
2. Ассоциативность.
Пример:
11×19×32=6688
(11×19)×32=6688
11×(19×32)=6688
Сочетательный закон: Если группу множителей заменить их произведением, результат не изменится.
3. Дистрибутивность.
Пример:
(15+12)×9=243 и 15×9+12×9=243
Распределительный закон: Умножая сумму на число, можно на это число каждое слагаемое умножить и результаты сложить.
Большие числа, а также десятичные дроби умножают в столбик.
Нет времени решать самому?
Наши эксперты помогут!
Произведение цифр числа
Пример: найти произведение цифр числа 428
4×2×8=64
Произведение суммы и разности чисел
(23+14)×(23-14)=37×9=333
Наименьшее произведение чисел
При умножении любого числа на 0, получится ноль. Наименьшее произведение чисел равно нулю.
Сумма двух произведений чисел
(7×8)+(9×3)=56+27=83
Ответ: 83
Пример: Найди сумму и произведение чисел 14 и 72
Решение:
14+72=86 — сумма
14×72=1008 — произведение
Математика
6 класс
Урок № 26
Произведение целых чисел. Часть 2
Перечень рассматриваемых вопросов:
- На уроке мы научимся формулировать и узнавать свойства умножения.
- Находить квадраты и кубы целых чисел.
- Вычислять значения числовых выражений, содержащих разные действия.
- Выполнять числовые подстановки в буквенные выражения и находить соответствующие им значения.
Тезаурус
Произведение любого целого числа a и нуля равно нулю.
Чтобы найти произведение нескольких чисел, нужно найти произведение двух первых чисел, умножить на третье число и так далее.
Степенью целого числа a с натуральным показателем n (n > 1) называется произведение n множителей, каждый из которых равен a.
Список литературы
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Мы уже изучали правила умножения целых чисел.
Сегодня рассмотрим свойства произведения целых чисел.
Умножение целых чисел на 0.
Произведение любого целого числа a и нуля равно нулю.
a ∙ 0 = 0
Рассмотрим примеры.
Найдите произведение целого положительного числа 209 и нуля.
Решение:
203 ∙ 0 = 0
Найдите произведение нуля и целого отрицательного числа (– 29).
Решение:
0 ∙ (– 29) = 0
Умножение целого числа на 1
Произведение целого числа и 1 равно cамому числу.
a ∙ 1 = a
Рассмотрим примеры.
Вычислите произведение положительного целого числа 64 и единицы.
Решение:
64 ∙ 1 = 64
Вычислите произведение единицы и отрицательного целого числа (– 475).
Решение:
1 ∙ (– 475) = – 475
Найдите произведение нуля и единицы.
Решение:
0 ∙ 1 = 0
Умножение на (– 1)
При умножении числа на (– 1) меняется только знак, то есть получается число, противоположное a.
a ∙ (– 1) = – a
Законы умножения
Переместительный и сочетательный законы умножения верны для любых целых чисел, и их можно применять для упрощения числовых выражений.
Переместительный закон умножения:
a ∙ b = b ∙ a
Сочетательный закон умножения:
a ∙ (b ∙ c) = (a ∙ b) ∙ c
Умножение или произведение нескольких целых чисел
Чтобы найти произведение нескольких чисел, нужно найти произведение двух первых чисел, умножить на третье число и так далее.
Вычислим произведение нескольких целых чисел:
9 ∙ (– 14) ∙ 5 ∙ (– 1)
Решение:
9 ∙ (– 14) ∙ 5 ∙ (– 1) = (9 ∙ (– 14)) ∙ 5 ∙ (– 1) = (– 126) ∙ 5 ∙ (– 1) = ((– 126) ∙ 5) ∙ (– 1) = (– 630) ∙ (– 1) = 630
Ответ: 630.
При перемножении целых чисел, результат всегда будет целым числом.
Выводы
1. Если в произведении нечётное количество отрицательных множителей, то произведение будет отрицательным.
2. Если в произведении чётное количество отрицательных множителей, то произведение будет положительным.
Степень целого числа a с натуральным показателем n
Определение: степенью целого числа a с натуральным показателем n (n > 1) называется произведение n множителей, каждый из которых равен a.
a ∙ a ∙ a ∙ a ·…∙ a = an
n множителей
Рассмотрим примеры.
1. Первая степень любого числа равна самому числу.
a1 = a
2. Вторая степень любого числа называется квадратом.
a2 = a ∙ a
3. Третья степень любого целого числа называется кубом.
a3 = a ∙ a ∙ a
Например,
24 = 2 ∙ 2 ∙ 2 ∙ 2 = 16
(– 5)3 = (– 5) ∙ (– 5) ∙ (– 5) = – 125
Итак, мы научились выполнять сложение, вычитание и умножение целых чисел. Рассмотрим, как найти значение выражения, которое содержит такие действия.
42 – 15 ∙ (– 6)
Решение
42 – 15 ∙ (– 6) = 42 – (15 ∙ (– 6)) = 42 – (– 90) = 42 + 90 = 132
Ответ: 132.
Дополнительный материал
Мы изучили правила и свойства умножения целых чисел.
Используя их, решим две задачи.
Задача №1
Чему равно произведение последовательных целых чисел, начинающихся числом (– 200) и оканчивающихся числом 200?
Решение
Между числами (– 200) и 200 находится 0, а любое число, умноженное на 0 равно 0. Поэтому произведение последовательных целых чисел от (– 200) до 200 равно 0.
Ответ: 0.
Задача №2
Чему равно произведение всех целых чисел?
Решение
Целые числа состоят из целых положительных, отрицательных чисел, а также нуля. При умножении любого числа на ноль будет 0. Поэтому произведение всех целых чисел равно 0.
Ответ: 0.
Разбор заданий тренировочного модуля
Тип 1. Разместите нужные подписи под изображениями.
Какие законы представлены в формулах?
Законы умножения
- a ∙ b = b ∙ а
- а ∙ (b ∙ с) = (а ∙ b) ∙ с
Варианты ответов:
Сочетательный закон умножения
Переместительный закон умножения
Свойство 0
Для ответа на вопрос задания обратимся к теоретическому материалу сегодняшнего урока.
Правильный ответ:
1. Переместительный закон умножения
2. Сочетательный закон умножения
Тип 2. Вставьте в текст нужные слова.
Чтобы найти … нескольких чисел, нужно найти произведение … чисел, … на третье число и так далее.
Варианты слов для вставки:
произведение
трёх
первого
двух первых
умножить
разделить
сложить
вычесть
Для ответа на вопрос задания обратимся к теоретическому материалу сегодняшнего урока.
Правильный ответ:
Чтобы найти произведение нескольких чисел, нужно найти произведение двух первых чисел, умножить на третье число и так далее.
 Одна из важных математических операций это произведение чисел. Что же скрыто за этими словами как произведение, умножение…? Именно об этом в нашей статье.
Одна из важных математических операций это произведение чисел. Что же скрыто за этими словами как произведение, умножение…? Именно об этом в нашей статье.
Давайте наверное начнем с банальных вещей. Когда у нас появляется много чего-то, то довольно сложно это хранить даже в виде информации. Нам каким-то образом это приходится компактно сокращать. Вот скажем у нас появилось более чем две пары носков в шкафу, а точнее пусть их будет 15… Как нам из записать на бумаге. Да, конечно, мы можем взять и записать 2+2+2… и так далее, пока не перечислим цифру два, с которой ассоциируется одна из пар носков на их количество, то есть на 15. Но это ведь право не удобно, особенно если представить, что речь идет не только о наших носках в шкафу, но и о случае их хранения в магазине! И здесь проще записать словами так. У нас две пары носков взято какое-то количество раз!
Вот, здесь где-то и образуется эта самая магия перехода от обычной суммы к произведению, когда мы подразумеваем, что берем какое-то число какое-то количество раз. Самое время дать определение.
Определение произведения чисел
Произведение двух чисел это есть не что иное, как взятое одно из чисел в количестве другого числа.
Еще раз! Если произведение будет С, то номинальное значение одного из чисел пусть а, взятое в количестве b раз и будет этим произведением. Можно записать скажем так
С=а1+а2+а3+а4…+аb где 1,2,3,4…b будут индексом указывающим на то, какое это число а по порядку и не более того!
Пример Найти произведение чисел:
1) 1.2⋅3 ;
Ответ.1,2⋅3=3,6
2) 4⋅5⋅13
Ответ: 4⋅5⋅13=260
Свойства произведения чисел
Коммутативность: n⋅m=m⋅n
Ассоциативность: (n⋅m)⋅k=n⋅(m⋅k)
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
Дистрибутивность: (n+m)⋅k=n⋅k+m⋅k
Пример Найти произведение чисел удобным способом:
1) 5⋅17⋅2 ; 2) 7⋅2⋅15⋅5
Решение. По свойства умножения имеем:
5⋅17⋅2=(5⋅2)⋅17=10⋅17=170
7⋅2⋅15⋅5=(7⋅(2⋅15))⋅5=(7⋅30)⋅5=210⋅5=1050
Ответ.5⋅17⋅2=170
7⋅2⋅15⋅5=1050
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.
Пример Найти произведение чисел
1) 156⋅32 ; 2) 4,71⋅3,1
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое, полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в столбик
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором – один, значит, в ответе нужно отделить справа три знака:
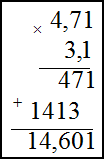
Ответ.
156⋅32=4992
4,71⋅3,1=14,601
Побалуемся с произведением!?
|
Вводим циферки Цифра которую будем брать N раз (множитель) |
|
А чему равно это самое N раз?(множитель) |
|
|
The product of number is the result you get when you multiply two or more numbers. A product is an expression that identifies factors to be multiplied. There are different types of products in maths they are products of natural numbers, decimals, fractions, integers, etc. Know more about the product of the number with solved problems from here. There are certain rules to find the product of the number. Let us discuss in detail the product of the number from this article.
Also, Refer:
- Estimating Products
- Multiplication
- Word Problems on Multiplication
Product Rules
- Any number multiplied by 0 will be always 0.
- Any number multiplied by 1 will be the same number.
- If the number is multiplied with the opposite sign then the product will be negative.
- If the number is multiplied with the same sign then the product will be positive.
Product of The Whole Numbers
The result of the multiplication of two or more numbers is called a product of the number. Let us see some examples on the product of 2-digit number, 3-digit number and 4-digit number
Product of 2-digit Number
The product of two numbers is the result you get when you multiply them together. For example, let us take two 2-digit numbers 20 and 12 you get the product as 240.
Example:
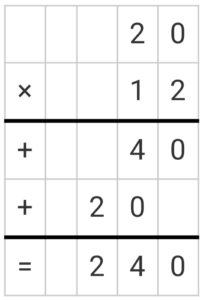
Product of 3-digit Number
The product of two 3-digit numbers is similar to the product of 2-digit number.
Example:
Product the number 365 and 123
Solution:
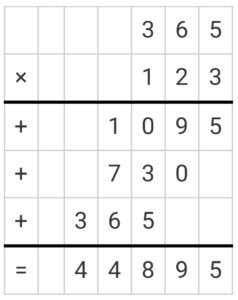
Product of 4-digit Number
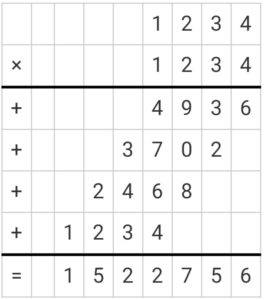
Example:
Product of two numbers 1234 and 1234 is
Solution:
The product of two 3-digit numbers is the result you get when you multiply them together.
Do Check:
- Expansion Method of Multiplication
- Column Method of Multiplication
Product of Decimal Number
Multiplying decimals is similar to that multiplying whole numbers except for the placement of the decimal point in the answer. When you multiply decimals, the decimal point is placed in the product so that the number of decimal places in the product is the sum of the decimal places in the factors.
Example:
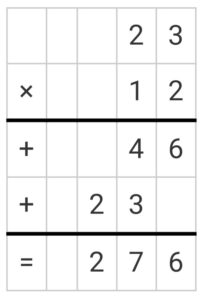
Product of two decimal numbers 0.23 and 0.12
Solution:
There are 4 total decimal places in both numbers.
Ignore the decimal places and complete the multiplication as if operating on two integers.
Rewrite the product with 4 total decimal places.
Therefore 0.23 × 0.12 = 0.0276
Solved Problems on Product of the Number
Example 1.
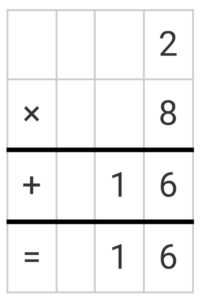
What is the product of 2 and 8?
Solution:
Example 2.
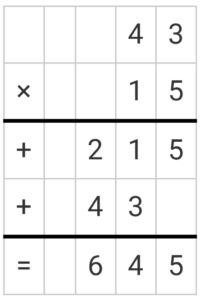
What is the product of 43 and 15?
Solution:
Example 3.
What is the product of 921 and 53?
Solution:

Example 4.
Find the product of 1265 and 0?
Solution:
Any number multiplied by 0 will be always 0.
So, the product of 1265 and 0 results in 0.
Therefore, 1265 × 0 = 0
Example 5.
Find the product of 0.15 and 1.23?
Solution:
There are 4 total decimal places in both numbers.
Ignore the decimal places and complete the multiplication as if operating on two integers.
Rewrite the product with 4 total decimal places.
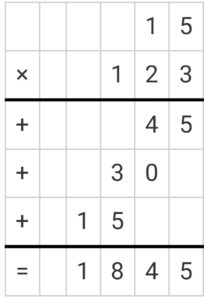
Therefore 0.15 × 1.23 = 0.1845
FAQs on Product of the Number
1. What is a product?
The product is the answer to a multiplication problem.
2. What is the product of any number and 1?
The product of any number and 1 is equal to that number. The number 1 is often called the multiplicative identity.
3. What is the product of any number and zero?
Any number multiplied by 0 will be always 0.