В данной публикации мы рассмотрим формулы, с помощью которых можно найти произведение двух комплексных чисел, представленных в алгебраической или тригонометрической форме. Также приведены примеры для лучшего понимания теоретического материала.
- Умножение в алгебраической форме
- Произведение в тригонометрической форме
Умножение в алгебраической форме
Произведением двух комплексных чисел x = a1 + b1i и y = a2 + b2i также является комплексное число z:
z = x ⋅ y = (a1a2 – b1b2) + (a1b2 + b1a2) ⋅ i
Формула получается путем перемножения двучленов (a1 + b1i)(a2 + b2i). При этом не забываем, что i2 = -1.
Пример 1
Найдем произведением комплексных чисел: x = 3 + 7i и y = 2 – i.
Решение:
x ⋅ y = (3 + 7i)(2 – i) = 3 ⋅ 2 – 3 ⋅ i + 7i ⋅ 2 – 7i ⋅ i = 6 – 3i + 14i – 7i2 = 6 + 11i – 7 ⋅ (-1) = 13 + 11i.
Произведение в тригонометрической форме
Комплексные числа могут быть заданы в тригонометрической форме, например x = |x| ⋅ (cos φ1 + i ⋅ sin φ1) и y = |y| ⋅ (cos φ2 + i ⋅ sin φ2).
В этом случае формула произведения выглядит следующим образом:
x ⋅ y = |x| ⋅ |y| ⋅ [cos(φ1 + φ2) + i ⋅ sin(φ1 + φ2)]
Пример 2
Выполним умножение двух комплексных чисел: x = 2 ⋅ (cos 15° + i ⋅ sin 15°) и y = 5 ⋅ (cos 30° + i ⋅ sin 30°).
Решение:
|x| ⋅ |y| = 2 ⋅ 5 = 10
φ1 + φ2 = 15° + 30° = 45°
x ⋅ y = 10 ⋅ (cos 45° + i ⋅ sin 45°)
Тригонометрическая форма комплексных чисел
29 ноября 2021
Второй урок по комплексным числам. Если вы только начинаете изучать эту тему (что такое комплексная единица, модуль, сопряжённые), см. первый урок: «Что такое комплексное число».
Сегодня мы узнаем:
- Что такое тригонометрическая форма
- Умножение и деление комплексных чисел в тригонометрической форме
- Формула Муавра (возведение в степень)
- Дополнение 1. Геометрический подход, чтобы не путать, где синус, а где косинус
- Дополнение 2. Как быстро и надёжно искать аргумент комплексного числа?
Начнём с ключевого определения.
1. Тригонометрическая форма
Определение. Тригонометрическая форма комплексного числа — это выражение вида
[z=left| z right|cdot left( cos text{ }!!varphi!!text{ }+isin text{ }!!varphi!!text{ } right)]
где $left| z right|$ — модуль комплексного числа, $text{ }!!varphi!!text{ }$ — некоторый угол, который называется аргумент комплексного числа (пишут $text{ }!!varphi!!text{ }=arg left( z right)$).
Любое число $z=a+bi$, отличное от нуля, можно записать с тригонометрической форме. Для этого нужно вычислить модуль и аргумент. Например:
Записать в тригонометрической форме число $z=sqrt{3}+i$.
Переписываем исходное число в виде $z=sqrt{3}+1cdot i$ и считаем модуль:
[left| z right|=sqrt{{{left( sqrt{3} right)}^{2}}+{{1}^{2}}}=2]
Выносим модуль за скобки:
[z=sqrt{3}+1cdot i=2cdot left( frac{sqrt{3}}{2}+frac{1}{2}cdot i right)]
Вспоминаем тригонометрию, 10-й класс:
[frac{sqrt{3}}{2}=cos frac{text{ }!!pi!!text{ }}{6};quad frac{1}{2}=sin frac{text{ }!!pi!!text{ }}{6}]
Окончательный ответ:
[z=2cdot left( cos frac{text{ }!!pi!!text{ }}{6}+icdot sin frac{text{ }!!pi!!text{ }}{6} right)]
Понятно, что вместо $frac{text{ }!!pi!!text{ }}{6}$ с тем же успехом можно взять аргумент $frac{13text{ }!!pi!!text{ }}{6}$. Синус и косинус не поменяется. Главное — выбрать такой аргумент, чтобы в тригонометрической форме не осталось никаких минусов. Все минусы должны уйти внутрь синуса и косинуса. Сравните:
Записать в тригонометрической форме число $z=-1-i$.
Правильно:
[z=sqrt{2}cdot left( cos frac{5text{ }!!pi!!text{ }}{4}+isin frac{5text{ }!!pi!!text{ }}{4} right)]
Неправильно:
[begin{align} & z=-sqrt{2}cdot left( cos frac{text{ }!!pi!!text{ }}{4}+isin frac{text{ }!!pi!!text{ }}{4} right) \ & z=sqrt{2}cdot left( -cos frac{text{ }!!pi!!text{ }}{4}-isin frac{text{ }!!pi!!text{ }}{4} right) \ & z=sqrt{2}cdot left( cos frac{3text{ }!!pi!!text{ }}{4}-isin frac{3text{ }!!pi!!text{ }}{4} right) \ end{align}]
2. Умножение и деление комплексных чисел
Комплексные числа, записанные в тригонометрической форме, очень удобно умножать и делить.
Теорема. Пусть даны два комплексных числа:
[begin{align} & {{z}_{1}}=left| {{z}_{1}} right|cdot left( cos alpha +isin alpha right) \ & {{z}_{2}}=left| {{z}_{2}} right|cdot left( cos beta +isin beta right) \ end{align}]
Тогда их произведение равно
[{{z}_{1}}cdot {{z}_{2}}=left| {{z}_{1}} right|cdot left| {{z}_{2}} right|cdot left( cos left( alpha +beta right)+isin left( alpha +beta right) right)]
А если ещё и $left| {{z}_{2}} right|ne 0$, то их частное равно
[frac{{{z}_{1}}}{{{z}_{2}}}=frac{left| {{z}_{1}} right|}{left| {{z}_{2}} right|}cdot left( cos left( alpha -beta right)+isin left( alpha -beta right) right)]
Получается, что при умножении комплексных чисел мы просто умножаем их модули, а аргументы складываем. При делении — делим модули и вычитаем аргументы. И всё!
Найти произведение и частное двух комплексных чисел:
[begin{align} & {{z}_{1}}=2cdot left( cos frac{pi }{3}+isin frac{pi }{3} right) \ & {{z}_{2}}=5cdot left( cos frac{pi }{6}+isin frac{pi }{6} right) \ end{align}]
Считаем произведение:
[begin{align} {{z}_{1}}cdot {{z}_{2}} & =2cdot 5cdot left( cos left( frac{pi }{3}+frac{pi }{6} right)+isin left( frac{pi }{3}+frac{pi }{6} right) right)= \ & =10cdot left( cos frac{pi }{2}+isin frac{pi }{2} right) \ end{align}]
Считаем частное:
[begin{align} frac{{{z}_{1}}}{{{z}_{2}}} & =frac{2}{5}cdot left( cos left( frac{pi }{3}-frac{pi }{6} right)+isin left( frac{pi }{3}-frac{pi }{6} right) right)= \ & =0,4cdot left( cos frac{pi }{6}+isin frac{pi }{6} right) \ end{align}]
По сравнению со стандартной (алгебраической) формой записи комплексных чисел экономия сил и времени налицо.:)
3. Формула Муавра
Пусть дано комплексное число в тригонометрической форме:
[z=left| z right|cdot left( cos text{ }!!varphi!!text{ }+isin text{ }!!varphi!!text{ } right)]
Возведём его в квадрат, умножив на само себя:
[begin{align} {{z}^{2}} & =zcdot z = \ & =left| z right|left| z right|cdot left( cos left( text{ }!!varphi!!text{ + }!!varphi!!text{ } right)+isin left( text{ }!!varphi!!text{ + }!!varphi!!text{ } right) right)= \ & ={{left| z right|}^{2}}cdot left( cos 2text{ }!!varphi!!text{ }+isin 2text{ }!!varphi!!text{ } right) \ end{align}]
Затем возведём в куб, умножив на себя ещё раз:
[{{z}^{3}}={{left| z right|}^{3}}cdot left( cos 3varphi +isin 3varphi right)]
Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.
Формула Муавра. При возведении всякого комплексного числа
[z=left| z right|cdot left( cos varphi +isin varphi right)]
в степень $nin mathbb{N}$ получим
[{{z}^{n}}={{left| z right|}^{n}}cdot left( cos left( nvarphi right)+isin left( nvarphi right) right)]
Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $nin mathbb{R}$, а не только натуральном. Но об этом позже. Сейчас примеры:
Вычислить:
[{{left( sqrt{3}-i right)}^{16}}]
Представим первое число в тригонометрической форме:
[begin{align} sqrt{3}-i & = 2cdot left( frac{sqrt{3}}{2}+icdot left( -frac{1}{2} right) right)= \ & =2cdot left( cos left( -frac{pi }{6} right)+isin left( -frac{pi }{6} right) right) \ end{align}]
По формуле Муавра:
[begin{align} & {{left( 2cdot left( cos frac{11pi }{6}+isin frac{11pi }{6} right) right)}^{16}}= \ & ={{2}^{16}}cdot left( cos frac{88pi }{3}+isin frac{88pi }{3} right)= \ & ={{2}^{16}}cdot left( cos frac{4pi }{3}+isin frac{4pi }{3} right) \ end{align}]
Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.
Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:
Вычислить:
[{{left( left( -frac{sqrt{2}}{2} right)+left( -frac{sqrt{2}}{2} right)i right)}^{2022}}]
Теперь второе число запишем в комплексной форме:
[begin{align} & left( -frac{sqrt{2}}{2} right)+left( -frac{sqrt{2}}{2} right)i= \ & =1cdot left( cos frac{5pi }{4}+isin frac{5pi }{4} right) \ end{align}]
По формуле Муавра:
[begin{align} & {{left( 1cdot left( cos frac{5pi }{4}+isin frac{5pi }{4} right) right)}^{2022}}= \ & ={{1}^{2022}}cdot left( cos frac{5055pi }{2}+isin frac{5055pi }{2} right)= \ & =1cdot left( cos frac{3pi }{2}+isin frac{3pi }{2} right)=-i \ end{align}]
Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.
4. Дополнение 1. Геометрический подход
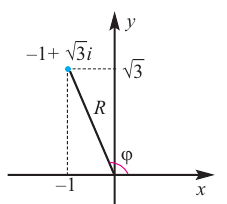
Многие путают местами косинус и синус. Почему комплексная единица стоит именно у синуса? Вспомним, что есть декартова система координат, где точки задаются отступами по осям $x$ и $y$:
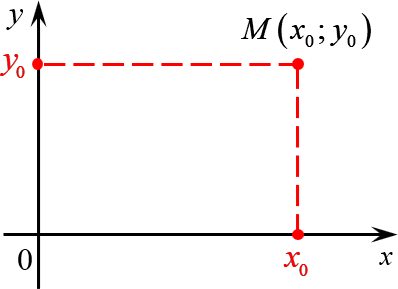
А есть полярная система координат, где точки задаются поворотом на угол $varphi $ и расстоянием до центра $r$:
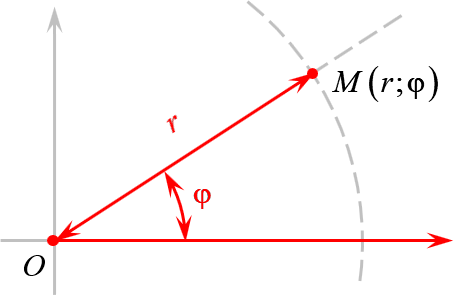
А теперь объединим эти картинки и попробуем перейти из декартовой системы координат в полярную:
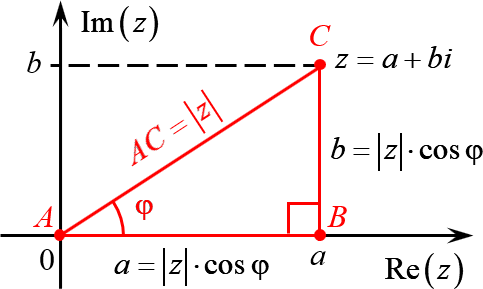
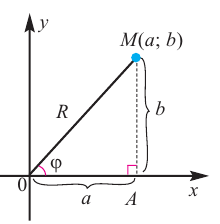
Комплексное число $z=a+bi$ задаёт на плоскости точку $C$, удалённую от начала координат на расстояние
[AC=sqrt{{{a}^{2}}+{{b}^{2}}}=left| z right|]
Треугольник $ABC$ — прямоугольный. Пусть $angle BAC=varphi $. Тогда:
[begin{align} & AB=ACcdot cos varphi =left| z right|cdot cos varphi \ & BC=ACcdot sin varphi =left| z right|cdot sin varphi \ end{align}]
С другой стороны, длины катетов $AB$ и $BC$ — это те самые отступы $a$ и $b$, с помощью которых мы задаём комплексное число. Поэтому:
[begin{align} a+bi & =left| z right|cos varphi +icdot left| z right|sin varphi = \ & =left| z right|left( cos varphi +isin varphi right) \ end{align}]
Итак, мы перешли от пары $left( a;b right)$ к паре $left( left| z right|;varphi right)$, где $left| z right|$ — модуль комплексного числа, $varphi $ — его аргумент (проще говоря, угол поворота).
Важное замечание. А кто сказал, что такой угол $varphi $ существует? Возьмём число $z=a+bi$ и вынесем модуль за скобку:
[begin{align} z & =a+bi= \ & =sqrt{{{a}^{2}}+{{b}^{2}}}cdot left( frac{a}{sqrt{{{a}^{2}}+{{b}^{2}}}}+icdot frac{b}{sqrt{{{a}^{2}}+{{b}^{2}}}} right)= \ & =left| z right|cdot left( cos text{ }!!varphi!!text{ }+isin text{ }!!varphi!!text{ } right) \ end{align}]
Осталось подобрать такой угол $varphi $, чтобы выполнялось два равенства:
[begin{align} & frac{a}{sqrt{{{a}^{2}}+{{b}^{2}}}}=cos text{ }!!varphi!!text{ } \ & frac{b}{sqrt{{{a}^{2}}+{{b}^{2}}}}=sin text{ }!!varphi!!text{ } \ end{align}]
Такой угол обязательно найдётся, поскольку выполняется основное тригонометрическое тождество:
[begin{align} {{sin }^{2}}text{ }!!varphi!!text{ } & +{{cos }^{2}}text{ }!!varphi!!text{ }= \ & ={{left( frac{a}{sqrt{{{a}^{2}}+{{b}^{2}}}} right)}^{2}}+{{left( frac{b}{sqrt{{{a}^{2}}+{{b}^{2}}}} right)}^{2}}= \ & =frac{{{a}^{2}}}{{{a}^{2}}+{{b}^{2}}}+frac{{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}=frac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}=1 \ end{align}]
На практике основная трудность заключается именно в поиске подходящего аргумента.
5. Дополнение 2. Как найти аргумент?
В учебниках пишут много разной дичи, типа вот этой:
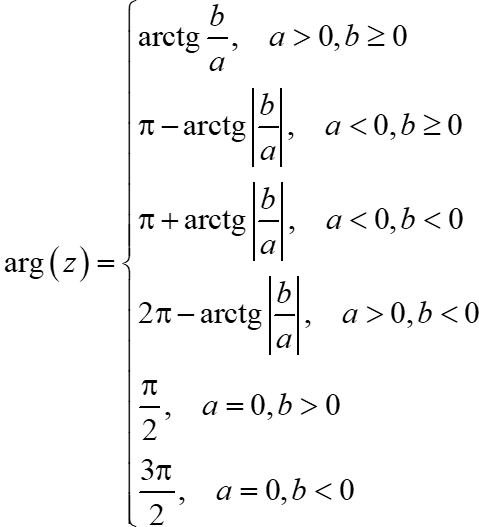
Формула правильная, но пользы от неё — ноль. Запомнить сложно, а применять и вовсе невозможно. Мы пойдём другим путём.
5.1. Точки на координатных осях
Для начала рассмотрим точки, лежащие осях координат.
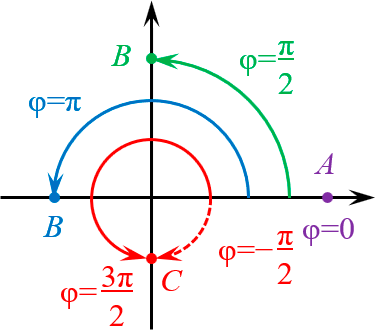
Тут всё очевидно:
- На положительной полуоси абсцисс $varphi =0$ (фиолетовая точка $A$).
- На отрицательной — $varphi =pi $ (синяя точка $B$).
- На положительной полуоси ординат $varphi =frac{pi }{2}$ (зелёная точка $B$).
- На отрицательной — $varphi =frac{3pi }{2}$ (красная точка $C$). Однако ничто не мешает рассмотреть $varphi =-frac{pi }{2}$ — результат будет тем же самым.:)
5.2. Точки с арктангенсом
А если точки не лежат на осях, то в записи комплексного числа $a+bi$ числа $ane 0$ и $bne 0$. Рассмотрим вспомогательный угол
[{{varphi }_{1}}=operatorname{arctg}left| frac{b}{a} right|]
Очевидно, это острый угол:
[0 lt operatorname{arctg}left| frac{a}{b} right| lt frac{pi }{2}]
Зная знаки чисел $a$ и $b$, мы немедленно определим координатную четверть, в которой располагается искомая точка. И нам останется лишь отложить вспомогательный угол ${{varphi }_{1}}$ от горизонтальной оси в эту четверть.
В правой полуплоскости мы откладываем от «нулевого» луча:
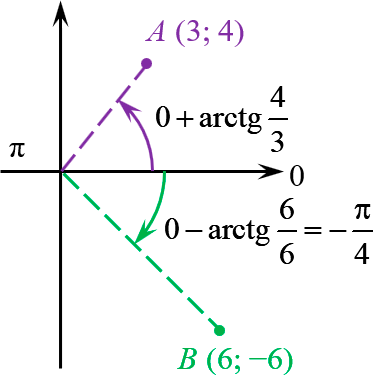
Точка $Aleft( 3;4 right)$ удалена от начала координат на расстояние 5:
[begin{align} 3+4i & =5cdot left( cos varphi +isin varphi right) \ varphi & =operatorname{arctg}frac{4}{3} end{align}]
Для точки $Bleft( 6;-6 right)$ арктангенс оказался табличным:
[6-6i=6sqrt{2}cdot left( cos left( -frac{pi }{4} right)+isin left( -frac{pi }{4} right) right)]
В левой полуплоскости откладываем от луча, соответствующего углу $pi $:
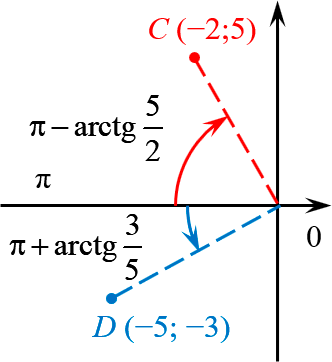
Итого для точки $Cleft( -2;5 right)$ имеем:
[begin{align} -2+5i & =sqrt{29}cdot left( cos varphi +isin varphi right) \ varphi & =pi -operatorname{arctg}frac{5}{2} end{align}]
И, наконец, для точки $Dleft( -5;-3 right)$:
[begin{align} -5-3i & =sqrt{34}cdot left( cos varphi +isin varphi right) \ varphi & =pi +operatorname{arctg}frac{3}{5} end{align}]
Звучит просто, выглядит красиво, работает идеально! Но требует небольшой практики. Пробуйте, тренируйтесь и берите на вооружение.
А в следующем уроке мы научимся извлекать корни из комплексных чисел.:)
Смотрите также:
- Как извлекать корни из комплексных чисел

- Комплексные числа — первый и самый важный уок

- Тест к параграфу «Что такое логарифм» (легкий)

- Тест к уроку «Площади многоугольников без координатной сетки» (средний)

- Четырехугольная пирамида: как найти координаты вершин

- Задача C1: тригонометрические уравнения и формула двойного угла

Содержание:
- Умножение комплексных чисел в алгебраической форме
- Умножение комплексных чисел в геометрической форме
Умножение комплексных чисел в алгебраической форме
Определение
Произведением двух комплексных чисел $z_{1}=a_{1}+b_{1} i$ и
$z_{2}=a_{2}+b_{2} i$$z_{2}=a_{2}+b_{2} i$ называется
комплексное число
$z$, равное
$z=z_{1} cdot z_{2}=left(a_{1} a_{2}-b_{1} b_{2}right)+left(a_{1} b_{2}+b_{1} a_{2}right) i$
На практике чаще всего комплексные числа перемножают как алгебраические двучлены
$left(a_{1}+b_{1} iright)left(a_{2}+b_{2} iright)$, просто раскрыв скобки, в
полученном результате надо учесть, что $i^{2}=-1$ .
Пример
Задание. Найти произведение комплексных чисел
$z_{1}=2+3 i$ и
$z_{2}=-1+i$ .
Решение. Перемножим заданные комплексные числа как два двучлена, то есть
$z_{1} cdot z_{2}=(2+3 i)(-1+i)=2 cdot(-1)+2 cdot i+3 i cdot(-1)+3 i cdot i=$
$=-2+2 i-3 i+3 i^{2}=-2-i+3 cdot(-1)=-5-i$
Ответ. $z_{1} cdot z_{2}=-5-i$
Умножение комплексных чисел в геометрической форме
Если комплексные числа $z_{1}$ и
$z_{2}$ заданы в
геометрической форме:
$z_{1}=left|z_{1}right|left(cos phi_{1}+i sin phi_{1}right)$,
$z_{2}=left|z_{2}right|left(cos phi_{2}+i sin phi_{2}right)$, то произведением этих чисел есть число
$z_{1} z_{2}=left|z_{1}right| cdotleft|z_{2}right|left[cos left(phi_{1}+phi_{2}right)+i sin left(phi_{1}+phi_{2}right)right]$
То есть модуль произведения двух комплексных чисел в тригонометрической форме равен произведению
модулей сомножителей, а аргумент равен сумме аргументов сомножителей.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти произведение чисел
$z_{1}=3 cdotleft(cos 10^{circ}+i sin 10^{circ}right)$,
$z_{2}=2 cdotleft(cos 50^{circ}+i sin 50^{circ}right)$ .
Решение. Модуль произведения равен
$|z|=3 cdot 2=6$, а аргумент
$phi=10^{circ}+50^{circ}=60^{circ}$, а тогда искомое число в
тригонометрической форме имеет вид:
$z=|z|(cos phi+i sin phi)=6 cdotleft(cos 60^{circ}+i sin 60^{circ}right)$
Запишем результат в
алгебраической форме, для этого вычислим значения соответствующих тригонометрических
функций, будем в результате иметь:
$z=6 cdotleft(frac{1}{2}+i cdot frac{sqrt{3}}{2}right)=3+3 sqrt{3} i$
Ответ. $z=6 cdotleft(cos 60^{circ}+i sin 60^{circ}right)=3+3 sqrt{3} i$
Читать дальше: деление комплексных чисел.
Содержание:
Хроника возникновения комплексных чисел:

Исследование.
1) Подтвердите примерами справедливость следующих высказываний. Если высказывание ложно, то сделайте так, чтобы оно стало истинным.
- а) Если а и b – натуральные числа, то корень уравнения х + а = b также является натуральным числом.
- б) Если а и b -целые числа, то корень уравнения ах = b также является целым числом
- в) Если а неотрицательное рациональное число, то корень уравнения х1 = а также является рациональным числом.
- г) Если а неотрицательное действительное число, то корень уравнения х2 = а также является действительным числом.
2) Существует ли действительное число квадрат которого равен -1?
3)
- а) Существуют ли действительные корни уравнения х2 = а при
- б) Можно ли решить эту задачу расширив множество действительных чисел?
4) Существует ли однозначное соответствие между множеством действительных чисел и множеством точек на числовой оси? А какие числа соответствуют точкам на координатной плоскости?
На множестве действительных чисел уравнение х2 = -1 не имеет решений. Значит, мы должны расширить множество действительных чисел так, чтобы корни этого уравнения входили в него. Для этого введём новое число и примем, что оно является корнем уравнения х2 + 1 = 0, т.е. 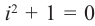 . Отсюда
. Отсюда 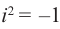 . После этого, корнями уравнения х2 + 1 = 0 являются числа
. После этого, корнями уравнения х2 + 1 = 0 являются числа 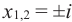 . Число
. Число 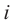 называется мнимой единицей.
называется мнимой единицей.
Расширим множество действительных чисел так, чтобы в него входили все действительные числа и число 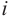 , и были справедливы все свойства сложения и умножения. Для произвольных действительных чисел а и b введём “произведение”
, и были справедливы все свойства сложения и умножения. Для произвольных действительных чисел а и b введём “произведение” 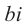 и “сумму”
и “сумму” 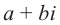 , и назовём комплексным числом следующее выражение
, и назовём комплексным числом следующее выражение 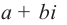 . Выражение вида
. Выражение вида 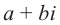 называется комплексным числом, где а и b – действительные числа,
называется комплексным числом, где а и b – действительные числа, 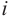 мнимая единица.Комплексные числа можно обозначать через
мнимая единица.Комплексные числа можно обозначать через  и т.д.Например,
и т.д.Например, 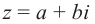 . Запись
. Запись 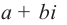 называется алгебраической формой комплексного числа, а является действительной частью, b – мнимой частью комплексного числа
называется алгебраической формой комплексного числа, а является действительной частью, b – мнимой частью комплексного числа 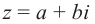 , и записывается так:
, и записывается так: 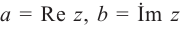 . При а = 0 получается число вида
. При а = 0 получается число вида  . Эти числа называются чисто мнимыми числами. При а = 0, b = 0 комплексное число равно нулю и наоборот, если а +
. Эти числа называются чисто мнимыми числами. При а = 0, b = 0 комплексное число равно нулю и наоборот, если а +  = 0, то а = 0 и b = 0.
= 0, то а = 0 и b = 0.
Следствие: для комплексных чисел а +  и с +
и с +  равенство
равенство
а +  = с +
= с +  справедливо тогда и только тогда, если а = с, b = d.
справедливо тогда и только тогда, если а = с, b = d.
Пример. Из равенства 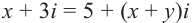 найдите х и у.
найдите х и у.
Решение: Из равенства действительных и мнимых частей получаем: х = 5
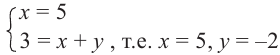 .
.
Суммой комплексных чисел 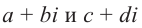 называется комплексное число
называется комплексное число 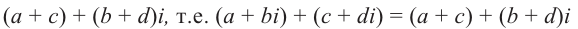
Действия над комплексными числами
Произведением комплексных чисел 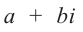 и
и 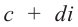 называется число
называется число 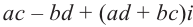 , т.е.
, т.е.
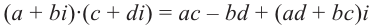
Значит, два комплексных числа умножаются по правилу умножения многочленов при условии, что 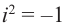 .
.
Пример №1
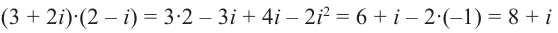
Рассмотрим частные случаи степеней мнимых единиц: 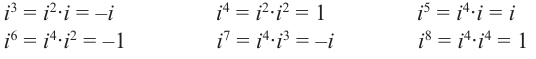
Как видно, натуральные степени мнимой единицы 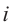 равны
равны 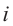 , -1, –
, -1, –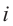 ‘, 1 и повторяются через каждые четыре шага, т.е.справедливо равенство
‘, 1 и повторяются через каждые четыре шага, т.е.справедливо равенство 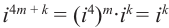
Пример №2
Вычислите: а) 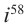 б)
б) 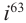
Решение: а) 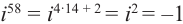 б)
б) 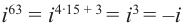
Число  называется сопряжённым для числа
называется сопряжённым для числа  и обозначается как :
и обозначается как : 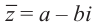 . Ясно, что если число
. Ясно, что если число  является сопряжённым для числа
является сопряжённым для числа  , то число
, то число  является сопряжённым для числа
является сопряжённым для числа  . Поэтому, числа
. Поэтому, числа 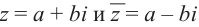 называются взаимно сопряжёнными комплексными числами. Действительные части взаимно сопряжённых чисел равны, а мнимые части являются противоположными числами.
называются взаимно сопряжёнными комплексными числами. Действительные части взаимно сопряжённых чисел равны, а мнимые части являются противоположными числами.
Произведение взаимно сопряжённых комплексных чисел является действительным числом: 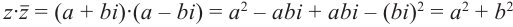 .
.
В частном случае, сопряжённым для действительного числа является само число, для мнимого – произведение числа и (-1).
Для каждого комплексного числа 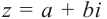 существует противоположное число
существует противоположное число 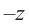 и
и 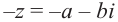 . Для каждого, отличного от нуля, комплексного числа
. Для каждого, отличного от нуля, комплексного числа 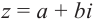 существует противоположное.
существует противоположное. 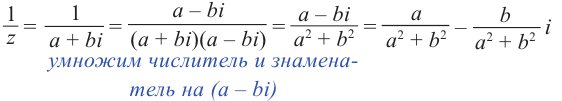
Вычитание и частное комплексных чисел определяется равенствами:
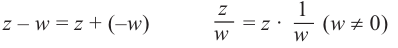
Для нахождения отношения комплексных чисел, удобнее числитель и знаменатель умножить на число, сопряжённое для знаменателя .
Пример №3
Найдём разность и отношение чисел 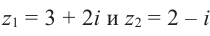 .
.
Решение: 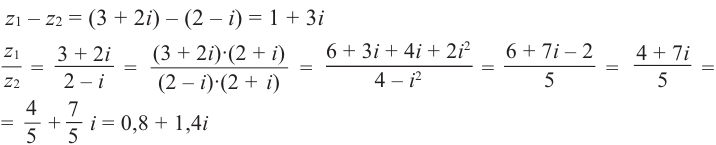
Все свойства арифметических операций для действительных чисел, справедливы для комплексных чисел. Как следствие, получаем, что любые алгебраические тождества справедливы для множества комплексных чисел. Например, для комплексных чисел 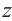 и
и 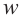 справедливы тождества
справедливы тождества
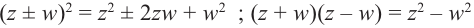
Квадратный корень комплексного числа
Число, квадрат которого равен 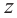 называется квадратным корнем комплексного числа
называется квадратным корнем комплексного числа 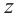 и обозначается как
и обозначается как 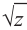 .
.
Пример №4
Найдём квадратный корень комплексного числа 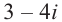
Решение: Пусть 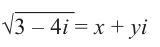 . Возведём обе части равенства в квадрат:
. Возведём обе части равенства в квадрат: 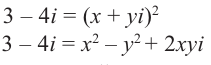
Из равенства действительных и мнимых частей имеем:
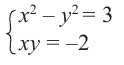
Отсюда получаем решение (2; -1) и (-2; 1). Значит, 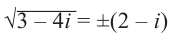
Примечание: В отличии от действительных чисел, говоря о квадратном корне комплексного числа, имеется в виду каждое из двух значений, различающихся знаками. Корни квадратного уравнения 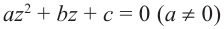 для множества комплексных чисел находится по тому же правилу, что и для действительных чисел.
для множества комплексных чисел находится по тому же правилу, что и для действительных чисел. 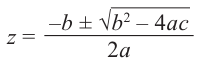
Пример №5
Решим уравнение 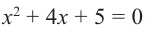 .
.
Решение:
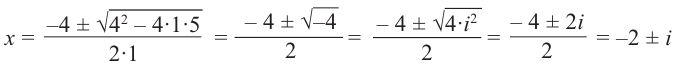 .
.

Легко можно проверить, что также в силе остаётся и теорема Виета. Для квадратного уравнения с действительными коэффициентами комплексные корни являются сопряжёнными числами. Комплексное число 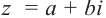 задаётся парой действительных чисел (а; b) и эта пара соответствует определённым точкам на координатной плоскости. Поставим в соответствие числу
задаётся парой действительных чисел (а; b) и эта пара соответствует определённым точкам на координатной плоскости. Поставим в соответствие числу 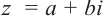 точку А (а; b) и обозначим её через
точку А (а; b) и обозначим её через  . Каждая точка на координатной плоскости изображает комплексное число и наоборот, каждое комплексное число на координатной плоскости, соответствует одной точке. Действительные числа располагаются на оси абсцисс, чисто мнимые числа на оси ординат. Поэтому ось абсцисс называется действительной осью, ось ординат – мнимой, а плоскость – комплексной плоскостью.
. Каждая точка на координатной плоскости изображает комплексное число и наоборот, каждое комплексное число на координатной плоскости, соответствует одной точке. Действительные числа располагаются на оси абсцисс, чисто мнимые числа на оси ординат. Поэтому ось абсцисс называется действительной осью, ось ординат – мнимой, а плоскость – комплексной плоскостью.
Пример:
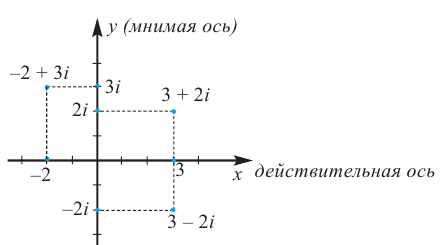
Точки, соответствующие комплексно сопряжённым числам располагаются симметрично оси абсцисс.
Модуль и аргумент комплексного числа
Тригонометрическая форма комплексного числа
Пусть на комплексной плоскости комплексному числу 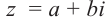 соответствует точка М(а; b). Обозначим расстояние ОМ через R, угол между лучом ОМ и положительным направлением оси абсцисс через
соответствует точка М(а; b). Обозначим расстояние ОМ через R, угол между лучом ОМ и положительным направлением оси абсцисс через  . Из
. Из  по теореме Пифагора имеем:
по теореме Пифагора имеем: 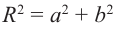
Отсюда: 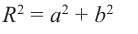
Расстояние, от начала координат до точки соответствующей комплексному числу, называется модулем комплексного числа и обозначается как:  .
.
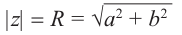
Угол, образованный конечной стороной угла поворота луча ОМ,
называется аргументом  комплексного числа
комплексного числа 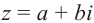 .
.
Из 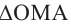 :
: 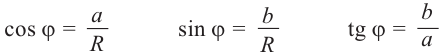
Модуль числа 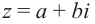 имеет единственное значение, а аргумент
имеет единственное значение, а аргумент  находится с точностью
находится с точностью 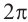 . То есть, если одно из значений аргумента равно
. То есть, если одно из значений аргумента равно  , то другое будет иметь вид
, то другое будет иметь вид 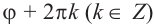 .
.
Для аргумента комплексного числа, обычно берётся угол принадлежащий промежутку [0;  ).
).
Пример №6
Найдём модуль и аргумент комплексного числа 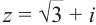
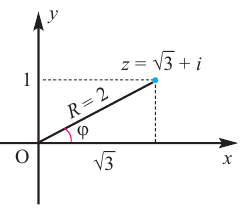
Решение: Из того, что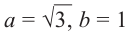 следует,что
следует,что 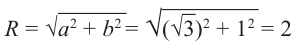
и принимая внимание, что угол 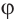 расположен в I четверти,
расположен в I четверти,
получим: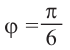
Из формул 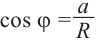 ,
, 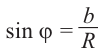 получаем:
получаем: 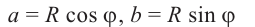
Тогда 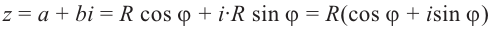
Для комплексного числа 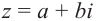 число
число 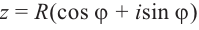 называется тригонометрической формой комплексного числа.
называется тригонометрической формой комплексного числа.
В частном случае для модуля и аргумента числа 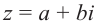 имеем:
имеем:
Пример №7
Запишем комплексное число 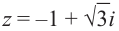
в тригонометрической форме.
Решение: 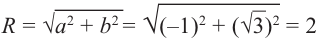
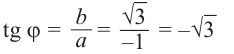
Так как угол 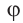 принадлежит II четверги, то
принадлежит II четверги, то
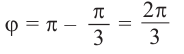
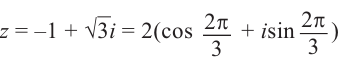
Действия над комплексными числами, заданными в тригонометрической форме
Найдём произведение комплексных чисел, заданных в тригонометрической форме 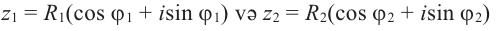 .
.
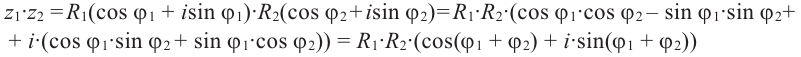
Чтобы найти произведение комплексных чисел, заданных в тригонометрической форме, надо перемножить их модули и сложить их аргументы.
Пример:
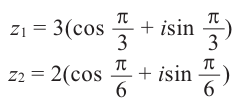
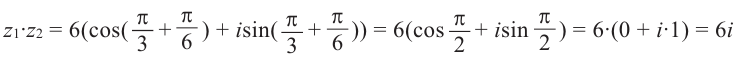
Теперь найдём отношение 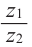
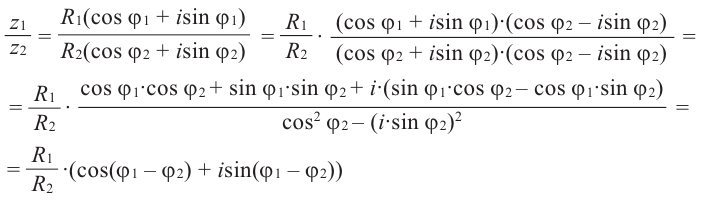
Модуль отношение равен отношению модулей делимого и делителя, а аргумент равен разности аргументов делимого и делителя.
Пример:
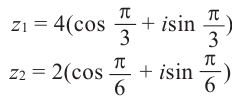
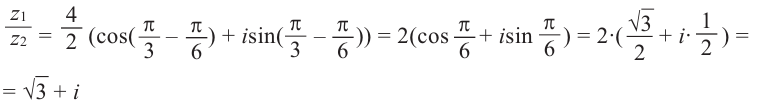
Возвести число 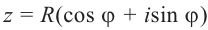 в степень с натуральным показателем n можно умножив n раз число
в степень с натуральным показателем n можно умножив n раз число 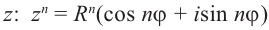
Модуль степени комплексного числа с натуральным показателем равен степени модуля основания, а аргумент равен аргументу основания умноженному на показатель степени n.
Пример:
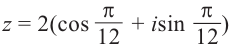
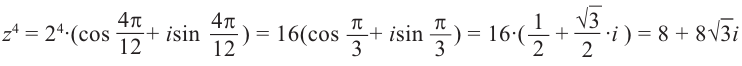
Формулу 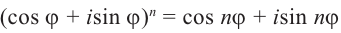 называют формулой Муавра. При помощи этой формулы можно найти синус и косинус n кратных углов через синус и косинус одинарных углов. Например, при n = 2 имеем:
называют формулой Муавра. При помощи этой формулы можно найти синус и косинус n кратных углов через синус и косинус одинарных углов. Например, при n = 2 имеем:
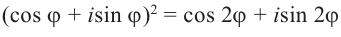
Отсюда
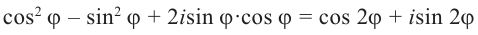
Из равенства двух комплексных чисел имеем:
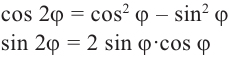
Аналогичным образом можно написать формулы для 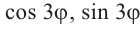 .
.
Корень n-ой степени комплексного числа
Найдём значение выражения 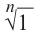 .
.
Запишем в виде 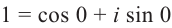 и найдём корень n – ой степени
и найдём корень n – ой степени
виде 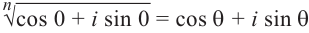 .
.
Возведём каждую из двух сторон в n-ую степень:
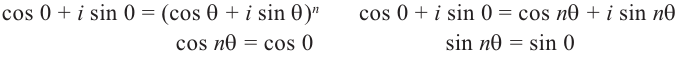
Если два комплексных числа, заданных в тригонометрической форме равны, то их модули равны, а аргументы отличаются на 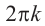 .
.
Это значит,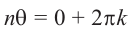
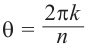
Таким образом, 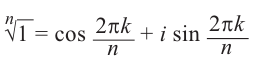
Отсюда при 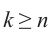 для первых
для первых 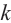 значений полученного числа равны значениям, полученным при
значений полученного числа равны значениям, полученным при  .
.
Обозначим корни  – ой степени единицы через
– ой степени единицы через 
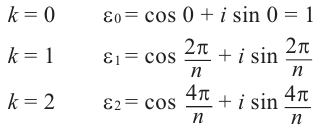
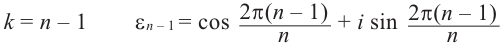
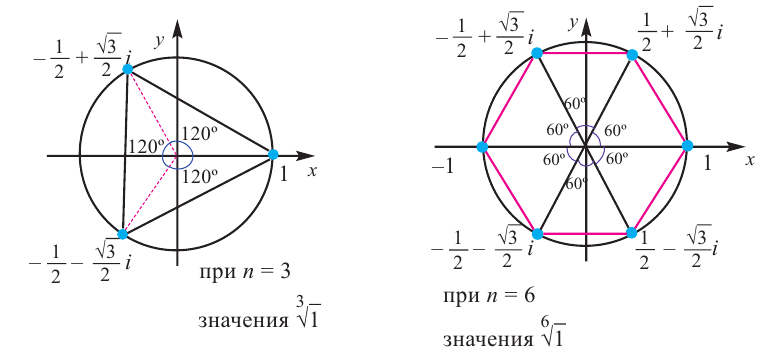
Как видно, модули корней  -ой степени равны 1, аргументы отличаются друг от друга в
-ой степени равны 1, аргументы отличаются друг от друга в 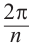 раз. То есть, эти числа расположены внутри единичной окружности, центр которой совпадает с началом координат, и соответствуют комплексным числам, являющимися вершинами правильного
раз. То есть, эти числа расположены внутри единичной окружности, центр которой совпадает с началом координат, и соответствуют комплексным числам, являющимися вершинами правильного  -угольника.
-угольника.
Корнем  -ой степени комплексного числа
-ой степени комплексного числа 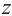 называется такое число
называется такое число 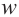 , что
, что 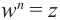 . Если
. Если 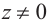 , то для корня
, то для корня  -ой степени существуют
-ой степени существуют  различных значений.
различных значений.
Запишем 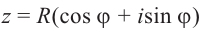 в виде
в виде
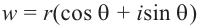 .
.
Для 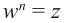 получим:
получим:
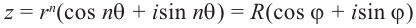
Из равенства двух комплексных чисел получим:
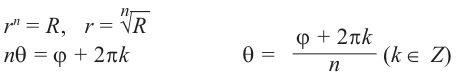
Значения при  отличаются от первых
отличаются от первых  значений на
значений на 
Поэтому, должно соблюдаться следующее: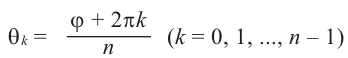
Формула корни n-ой степени комплексного числа
Если 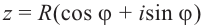 , то
, то
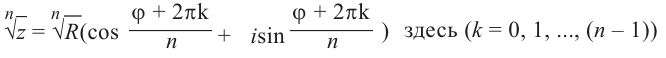
Пример №8
Найдём все значения 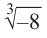
Решение: пусть 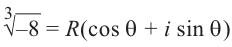
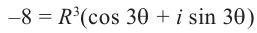
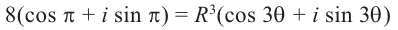
Отсюда 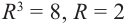
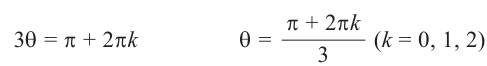
При 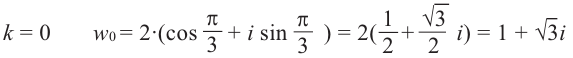
При 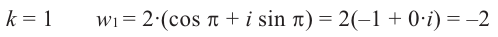
При 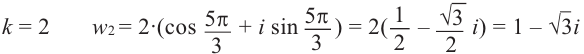
Для чего нужны комплексные числа
Комплексные числа возникают в связи с задачей решения квадратных уравнений. Так, оставаясь в множестве действительных чисел, невозможно решить квадратное уравнение, дискриминант которого меньше нуля.
Комплексные числа необходимы в различных приложениях математики. В частности, теория функций комплексной переменной является действенным инструментом при использовании математических методов в различных областях науки.
Арифметические операции над комплексными числами
Комплексным числом называется выражение вида 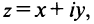 где
где 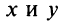 — действительные числа,
— действительные числа, 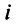 — мнимая единица.
— мнимая единица.
Число 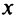 называется действительной частью числа
называется действительной частью числа 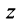 и обозначается
и обозначается 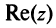 (от франц. reele — «действительный»), а число
(от франц. reele — «действительный»), а число 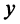 — мнимой частью числа
— мнимой частью числа 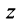 и обозначается
и обозначается 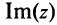 (от франц. imaginaire — «мнимый»), т.е.
(от франц. imaginaire — «мнимый»), т.е. 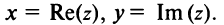
Действительное число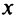 является частным случаем комплексного
является частным случаем комплексного 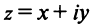 при
при 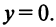 Комплексные числа вида
Комплексные числа вида 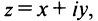 не являющиеся действительными, т.е. при
не являющиеся действительными, т.е. при 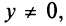 называются мнимыми, а при
называются мнимыми, а при 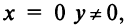 т.е. числа вида
т.е. числа вида 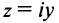 — чисто мнимыми.
— чисто мнимыми.
Числа 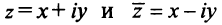 называются сопряженными.
называются сопряженными.
Два комплексных числа 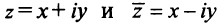 называются равными, если равны их действительные и мнимые части, т.е.
называются равными, если равны их действительные и мнимые части, т.е. 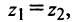 если
если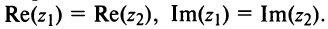 В частности,
В частности, 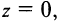 если
если 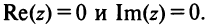
Арифметические операции на множестве комплексных чисел определяются следующим образом.
1.Сложение (вычитание) комплексных чисел
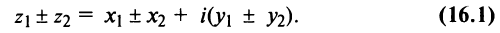
2. Умножение комплексных чисел
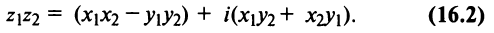
В частности,
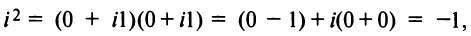
т.е. мнимая единица есть число, квадрат которого равен — 1.
3. Деление двух комплексных чисел
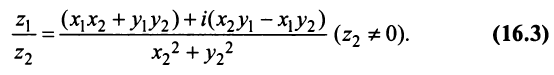
Нетрудно убедиться в том, что все арифметические операции (16.1)-(16.3) над комплексными числами определяются естественным образом из правил сложения и умножения многочленов 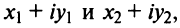 если считать
если считать 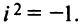 Например, произведение комплексных чисел (16.2) есть
Например, произведение комплексных чисел (16.2) есть
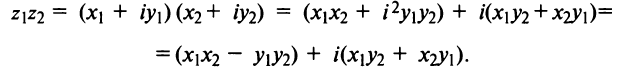
Пример №9
Даны комплексные числа 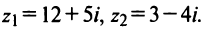
Найти 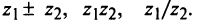
Решение:
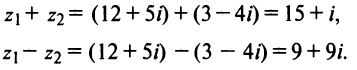
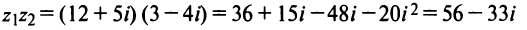 (учли, что
(учли, что 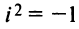 ).
).
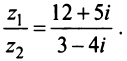 Умножая числитель и знаменатель на сопряженное делителю комплексное число
Умножая числитель и знаменатель на сопряженное делителю комплексное число 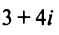 , получим
, получим
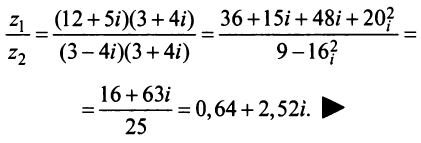
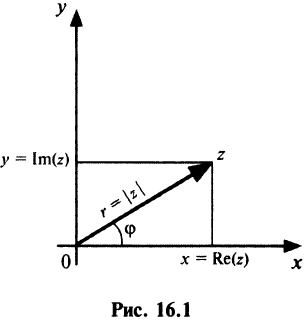
Если для геометрического изображения действительных чисел используются точки числовой прямой, то для изображения комплексных чисел служат точки координатной плоскости 
Плоскость называется комплексной, если каждому комплексному числу 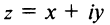 ставится в соответствие точка плоскости
ставится в соответствие точка плоскости 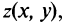 причем это соответствие взаимно однозначное (рис. 16.1).
причем это соответствие взаимно однозначное (рис. 16.1).
Оси  , на которых расположены действительные числа
, на которых расположены действительные числа и чисто мнимые числа
и чисто мнимые числа  называются соответственно действительной и мнимой осями.
называются соответственно действительной и мнимой осями.
Тригонометрическая и показательная формы комплексного числа
С каждой точкой 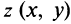 комплексной плоскости связан радиус-вектор этой точки
комплексной плоскости связан радиус-вектор этой точки 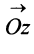 , длина которого
, длина которого 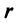 называется модулем комплексного числа
называется модулем комплексного числа 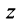 и обозначается
и обозначается 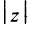 (см. рис. 16.1):
(см. рис. 16.1):

Угол 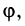 образованный радиусом-вектором
образованный радиусом-вектором 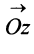 с осью
с осью 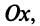 называется аргументом комплексного числа
называется аргументом комплексного числа 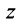 и обозначается
и обозначается 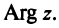 Из значений
Из значений 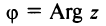 выделяется главное значение
выделяется главное значение 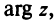 удовлетворяющее условию
удовлетворяющее условию 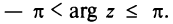 Например,
Например, 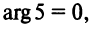
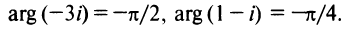
Очевидно (см. рис. 16.1), что
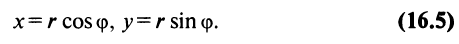
Следовательно, комплексное число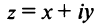 можно представить как
можно представить как

Представление комплексного числа в виде (16.6), где 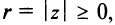
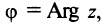 называется тригонометрической формой комплексного числа.
называется тригонометрической формой комплексного числа.
Сформулируем некоторые свойства арифметических операций над комплексными числами.
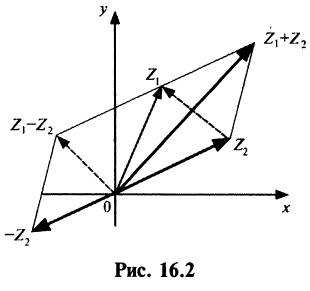
1. При сложении (вычитании) комплексных чисел их радиусы-векторы складываются (вычитаются) по правилу параллелограмма.
На рис. 16.2 показаны радиусы-векторы комплексных чисел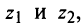 их суммы
их суммы 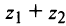 и разности
и разности 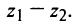
2. Модуль произведения (частного) двух комплексных чисел равен произ ведению (частному) модулей этих чисел, а его аргумент — сумме (разности) аргументов этих чисел, т.е.
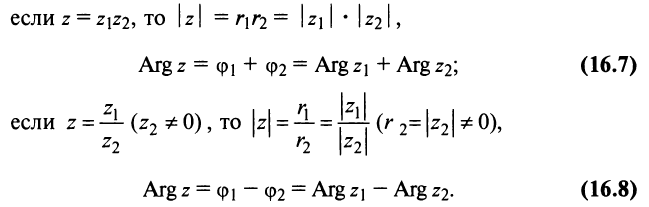
Геометрически умножение числа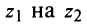 означает изменение длины радиуса-вектора
означает изменение длины радиуса-вектора 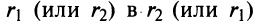 раз и его поворот вокруг точки
раз и его поворот вокруг точки 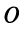 против часовой стрелки на угол
против часовой стрелки на угол 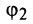
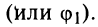
Пример №10
Комплексные числа 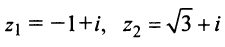 представить в тригонометрической форме и найти
представить в тригонометрической форме и найти 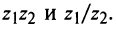
Решение:
По формуле (16.4) найдем модуль комплексного числа 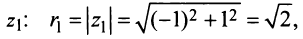 а из соотношений (16.5)
а из соотношений (16.5) 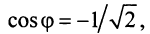
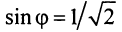 получим аргумент числа
получим аргумент числа 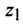 (берем его главное значение):
(берем его главное значение): 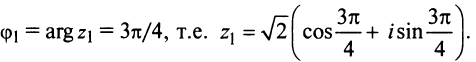
Аналогично 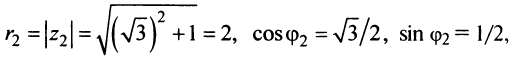 т.е.
т.е. 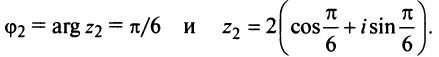
Теперь по формулам (16.7) и (16.8)
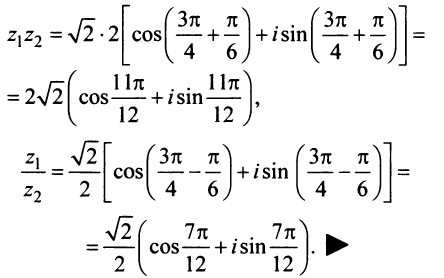
Так как в соответствии с формулами (16.7) и (16.8) при умножении комплексных чисел их модули перемножаются, а аргументы складываются, легко получить формулу возведения комплексного числа в натуральную степень 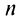 , известную как формула Муавра:
, известную как формула Муавра:
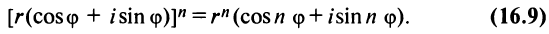
Пример №11
Найти 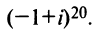
Решение:
По формуле Муавра (16.9)
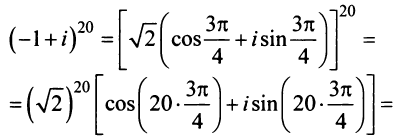
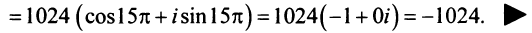 Обратимся к извлечению корня из комплексного числа.
Обратимся к извлечению корня из комплексного числа.
Пусть

Тогда, используя определение корня и формулу Муавра (16.9), получим
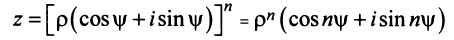
или
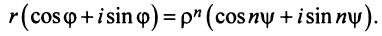
Отсюда следует, что
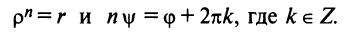
Итак,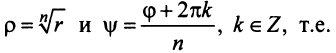
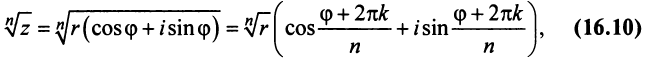
где 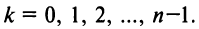
При 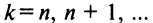 значения корня уже будут повторяться.
значения корня уже будут повторяться.
Таким образом, корень 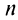 -й степени из комплексного числа (не равного нулю) имеет
-й степени из комплексного числа (не равного нулю) имеет 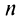 различных значений.
различных значений.
Пример №12
Найти 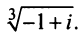
Решение:
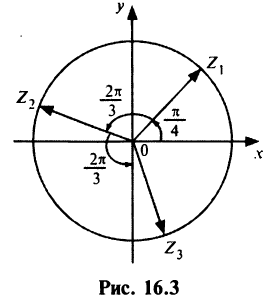
В примере 16.2 было получено
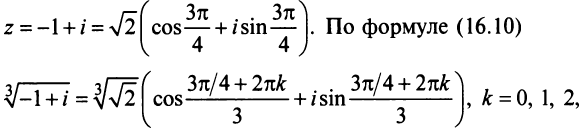
откуда получаем три значения корня
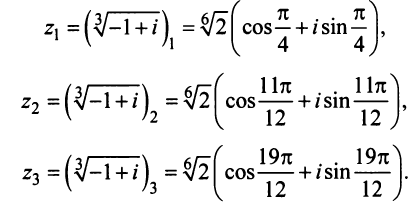
На комплексной плоскости найденные значения корня представляют равноотстоящие друг от друга точки 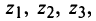 расположенные на окружности радиуса
расположенные на окружности радиуса 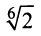 (рис. 16.3). ►
(рис. 16.3). ►
Связь между тригонометрическими и показательными функциями выражается формулой Эйлера.
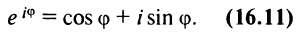
Отсюда следует показательная форма комплексного числа. 
где 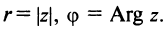
В заключение отметим, что в показательной форме, так же как и в тригонометрической, легко проводить операции умножения, деления, возведения в степень, извлечение корня из комплексных чисел.
Формы записи комплексного числа
Решение простейшего квадратного уравнения 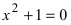 невозможно в области вещественных чисел. Однако, если выполнить решение формально, то получим
невозможно в области вещественных чисел. Однако, если выполнить решение формально, то получим 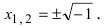
Определение: Выражение 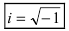 называется мнимой единицей.
называется мнимой единицей.
Определение: Комплексным числом называется выражение вида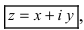 где х,у
где х,у
Определение: Приведенная форма записи комплексного числа называется алгебраической.
Определение: Два комплексных числа 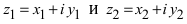 называются равными, если равны их вещественные и мнимые части, т.е.
называются равными, если равны их вещественные и мнимые части, т.е. 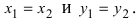
Определение: Комплексное число называется нулевым, если вещественная и мнимая части равны нулю.
Определение: Комплексно-сопряженным к комплексному числу 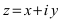 называется комплексное число
называется комплексное число 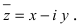
Пример №13
Записать комплексно-сопряженное число к комплексному числу 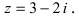
Решение:
Согласно определению комплексно-сопряженного числа получаем 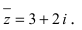
Замечание: Двойное комплексное сопряжение приводит к исходному комплекс- ному числу, т.е. 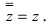
Решение квадратных уравнений с отрицательным дискриминантом невозможно в области вещественных чисел, так как нельзя извлекать корень четной степени из отрицательного числа на множестве действительных чисел. Однако это ограничение снимается в области комплексных чисел.
Пример №14
Решить квадратное уравнение 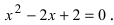
Решение:
Вычислим дискриминант уравнения 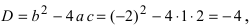 таким образом,
таким образом, 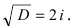 Следовательно,
Следовательно, 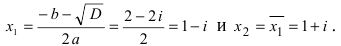
Замечание: Решение квадратного уравнения с отрицательным дискриминантом всегда состоит из комплексно-сопряженных корней.
Комплексное число 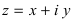 изобретается на комплексной плоскости
изобретается на комплексной плоскости  в виде вектора, соединяющего начало координат с точкой М(х; у) (Рис. 2):
в виде вектора, соединяющего начало координат с точкой М(х; у) (Рис. 2): 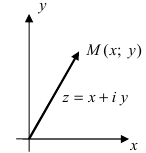
Рис. 2. Изображение комплексного числа на комплексной плоскости.
Пример №15
Изобразить на комплексной плоскости число z = 2-3i (Рис. 3). 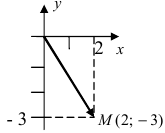
Решение:
Рис. 3. Изображение комплексного 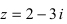 на комплексной плоскости. Если перейти от декартовой системы координат к полярной системе отсчета, т.е.
на комплексной плоскости. Если перейти от декартовой системы координат к полярной системе отсчета, т.е. 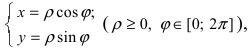 то комплексное число
то комплексное число 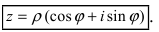
Определение: Полученная форма записи комплексного числа называется тригонометрической.
Обратный переход от полярной системы отсчета к декартовой системе координат осуществляется по формулам: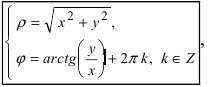 при этом
при этом 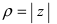 является модулем, а
является модулем, а 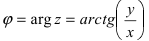 – аргументом комплексного числа z .
– аргументом комплексного числа z .
Замечание: Аргумент комплексного числа 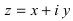 определяется в зависимости от знаков вещественной и мнимой частей:
определяется в зависимости от знаков вещественной и мнимой частей:
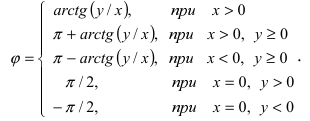
Действия с комплексными числами
1. Для того чтобы сложить (найти разность) два комплексных числа 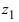
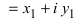 и
и 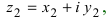 сложить (найти разность) отдельно действительные и мнимые части,
сложить (найти разность) отдельно действительные и мнимые части, 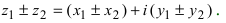
Пример №16
Найти сумму и разность чисел 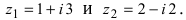 Изобразить все числа на комплексной плоскости.
Изобразить все числа на комплексной плоскости.
Решение:
Найдем сумму заданных комплексных чисел  Вычислим разность данных чисел
Вычислим разность данных чисел  Изобразим заданные и полученные числа на комплексной плоскости (Рис. 4):
Изобразим заданные и полученные числа на комплексной плоскости (Рис. 4):
Рис. 4. Изображение комплексных чисел на комплексной плоскости.
Замечание: Отметим, что 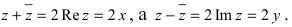
2. Для того чтобы найти произведение двух комплексных чисел 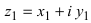 и
и 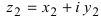 надо их перемножить, как два выражения с учетом того, что
надо их перемножить, как два выражения с учетом того, что 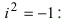
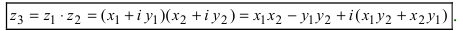
Замечание: Отметим, что 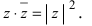
Замечание: Произведение комплексных чисел в тригонометрической форме записи имеет вид 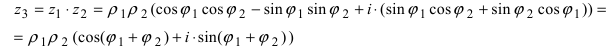 Из полученной формулы видно, что модули комплексных чисел перемножаются, а аргументы складываются. Следовательно, n-ая степень любого комплексного числа будет иметь вид
Из полученной формулы видно, что модули комплексных чисел перемножаются, а аргументы складываются. Следовательно, n-ая степень любого комплексного числа будет иметь вид 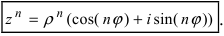 При извлечении корня п -ой степени применяют формулу Муавра
При извлечении корня п -ой степени применяют формулу Муавра 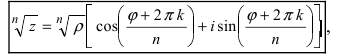 где величина
где величина 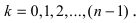
3. Деление комплексного числа 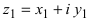 на комплексное число
на комплексное число 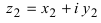 осуществляется так
осуществляется так 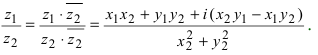
Замечание: Деление этих чисел в тригонометрической форме записи имеет вид: 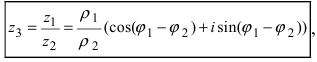 т.е. при делении комплексных чисел берут отношение модулей этих чисел, а из аргумента первого числа вычитают аргумент второго комплексного числа.
т.е. при делении комплексных чисел берут отношение модулей этих чисел, а из аргумента первого числа вычитают аргумент второго комплексного числа.
Показательная форма записи комплексного числа
Известно, что любую дифференцируемую функцию можно представить по формуле Тейлора-Маклорена (см. Лекцию № 22, Первый семестр), например, 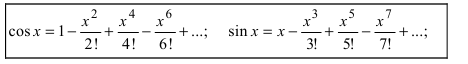
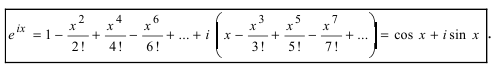
Последняя формула называется формулой Эйлера. Используя эту формулу,
запишем комплексное число 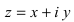 в показательной форме:
в показательной форме: 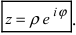 Отсюда видно, что при нахождении произведения и отношения комплексных чисел получаем
Отсюда видно, что при нахождении произведения и отношения комплексных чисел получаем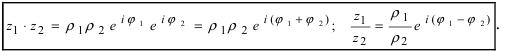
Комплексные числа и арифметические операции
Как известно, под комплексным числом понимается выражение вида
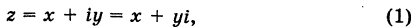
где х и у — действительные числа, a i — мнимая единица.
Числа вида 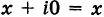 отождествляются с действительными числами; в частности,
отождествляются с действительными числами; в частности, 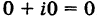 . Числа вида 0 + iy = iy называются чисто мнимыми.
. Числа вида 0 + iy = iy называются чисто мнимыми.
Действительные числа х и у называются соответственно действительной и мнимой частями числа z и обозначаются следующим образом:
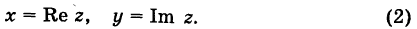
Под модулем комплексного числа z понимается неотрицательное число
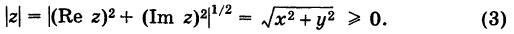
Сопряженным числом 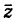 к числу (1) называется комплексное число
к числу (1) называется комплексное число
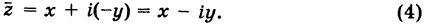
Таким образом,
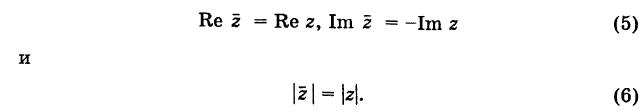
На множестве комплексных чисел следующим образом определено отношение равенства двух чисел, а также операции сложения, вычитания, умножения и деления.
I. Пусть z1=x1+iy1 и z2=x2+iy2.Тогда
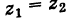
 Rez1 = Re z2, Im z1 = Im z2
Rez1 = Re z2, Im z1 = Im z2
В частности, z = 0 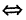 Re z = 0, Im z = 0.
Re z = 0, Im z = 0.
II. z1±z2= (x1± x2) + i(y1 ± y2)-
Отсюда следует, что
Re (z1 ± z2) – Re z1 ± Re z2,
Im (z1 ± z2) – Imz1 ± 1mz2
III. z1z2 = (x1x2 – y1y2) + i(x1y2+x2y1).
Отсюда, в частности, получаем важное соотношение
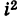 =
=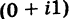
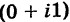 =
=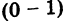 +
+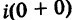 =-1
=-1
Заметим, что правило умножения III получается формально путем умножения двучленов 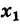 +
+ 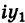 и
и 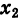 +
+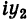 с учетом (7).
с учетом (7).
Очевидно также, что для 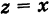
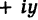
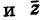
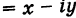 имеем
имеем
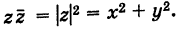
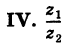 =
=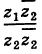 =
=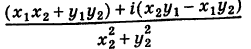
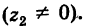
Легко проверить следующие свойства:
1)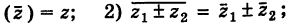
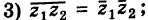
- Заказать решение задач по высшей математике
Комплексная плоскость
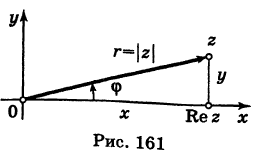
Рассмотрим плоскость с прямоугольной системой координат Оху. Каждому комплексному числу z = х + iy может быть поставлена в соответствие точка плоскости z(x, у) (рис. 161), причем это соответствие взаимно однозначно. Плоскость, на которой реализовано такое соответствие, называют комплексной плоскостью, и вместо комплексных чисел говорят о точках комплексной плоскости.
На оси Ох расположены действительные числа: z =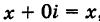 :, поэтому она называется действительной осью. На оси Оу расположены чисто мнимые числа z = 0 + iy = iy, она носит название мнимой оси.
:, поэтому она называется действительной осью. На оси Оу расположены чисто мнимые числа z = 0 + iy = iy, она носит название мнимой оси.
Заметим, что г = |z| представляет собой расстояние точки г от начала координат.
С каждой точкой z связан радиус-вектор этой точки Oz; угол, образованный радиусом-вектором точки z с осью Ох, называется аргументом ф = Arg z этой точки. Здесь 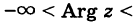
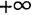 . Для нулевой точки z = 0 аргумент произволен. Наименьшее по модулю значение Arg z называется главным значением его и обозначается через arg z:
. Для нулевой точки z = 0 аргумент произволен. Наименьшее по модулю значение Arg z называется главным значением его и обозначается через arg z:

Для аргумента ср имеем (рис. 161)
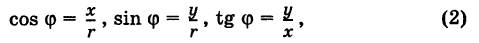
где 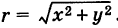
Примеры: 1) arg 2 = 0; 2) arg (-1) = 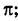 ; 3) arg i =
; 3) arg i = 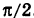 .
.
Модуль г и аргумент ф комплексного числа z можно рассматривать (рис. 161) как полярные координаты точки z. Отсюда получаем
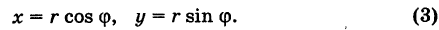
Таким образом, имеем тригонометрическую форму комплексного числа
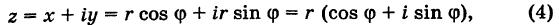
где 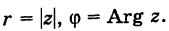
Теорема: При сложении комплексных чисел их радиусы-векторы складываются (по правилу параллелограмма).
Действительно, если число 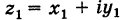 соответствует точке с координатами
соответствует точке с координатами 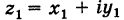 , а число
, а число 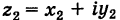 — точке с координатами
— точке с координатами 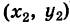 то числу
то числу 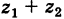 отвечает точка
отвечает точка 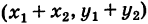 Так как (рис. 162) заштрихованные прямоугольные треугольники с катетами х2 и у2 равны между собой, то четырехугольник с вершинами 0,
Так как (рис. 162) заштрихованные прямоугольные треугольники с катетами х2 и у2 равны между собой, то четырехугольник с вершинами 0, 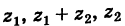 есть параллелограмм. Следовательно, радиус-вектор точки
есть параллелограмм. Следовательно, радиус-вектор точки 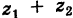 является суммой радиусов-векторов точек
является суммой радиусов-векторов точек 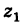 и
и 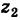 .
.
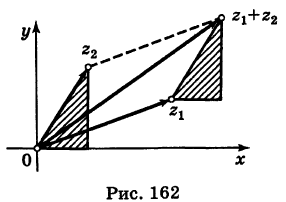
Следствие. Так как  есть длина вектора
есть длина вектора  , то
, то
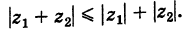
Теорема: При вычитании комплексных чисел их радиусы-векторы вычитаются. Так как 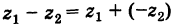 , то
, то  равен второй диагонали параллелограмма, построенного на векторах
равен второй диагонали параллелограмма, построенного на векторах 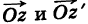 (рис. 163), т. е. равен разности радиусов-векторов точек
(рис. 163), т. е. равен разности радиусов-векторов точек 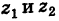 .
.
Следствие. Расстояние между двумя точками 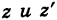 равно
равно
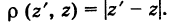
Теоремы о модуле и аргументе
Теорема: Модуль произведения комплексных чисел равен произведению модулей этих чисел, а аргумент произведения равен сумме аргументов сомножителей. Действительно, если
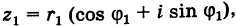
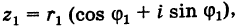
то имеем
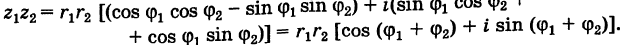
Отсюда
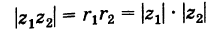
и
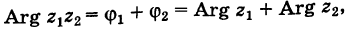
где значения многозначной функции Arg, стоящие в левой и правой частях равенства (1), следует подбирать соответствующим образом. Это замечание надо иметь в виду и для дальнейшего.
Следствие. Модуль целой положительной степени комплексного числа равен такой же степени модуля этого числа, а аргумент степени равен аргументу числа, умноженному на показатель степени, т. е.
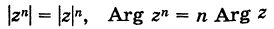
(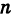 — целое положительное число).
— целое положительное число).
Доказательство непосредственно вытекает из рассмотрения произведения равных сомножителей.
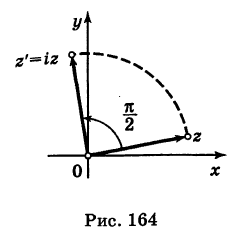
Пример №17
Построить точку 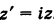 .
.
Решение:
Имеем
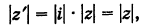
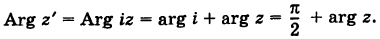
Следовательно, при умножении на i вектор  поворачивается на прямой угол против хода часовой стрелки (рис. 164).
поворачивается на прямой угол против хода часовой стрелки (рис. 164).
Теорема: Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя. Пусть
Так как
то на основании теоремы 1 имеем
Отсюда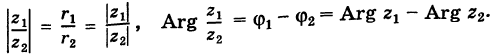
Извлечение корня из комплексного числа
Пусть
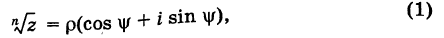
где 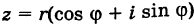 . Тогда на основании имеем
. Тогда на основании имеем
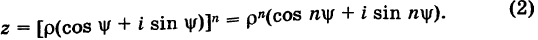
Отсюда получаем
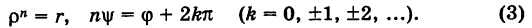
Таким образом,
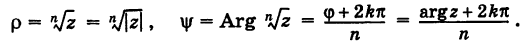
Заметим, что здесь под 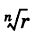 понимается арифметическое значение корня.
понимается арифметическое значение корня.
Здесь в качестве числа k достаточно брать лишь значения 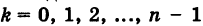 , так как при всех прочих значениях k получаются повторения уже найденных значений корня. Следовательно, окончательно имеем
, так как при всех прочих значениях k получаются повторения уже найденных значений корня. Следовательно, окончательно имеем
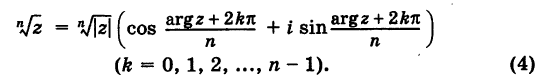
Из формулы (4) следует, что корень 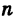 -й степени из любого комплексного числа
-й степени из любого комплексного числа 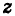 =0 имеет точно л значений.
=0 имеет точно л значений.
Пример №18
Найти 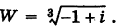
Решение:
Так как 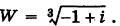 , то на основании формулы (4) имеем
, то на основании формулы (4) имеем
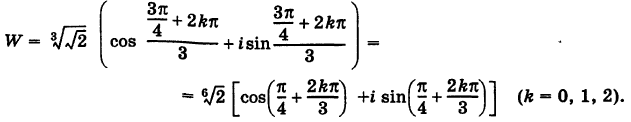
Отсюда
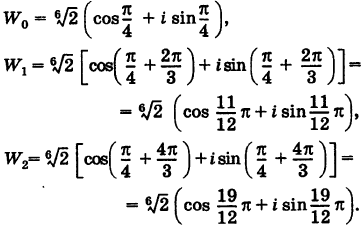
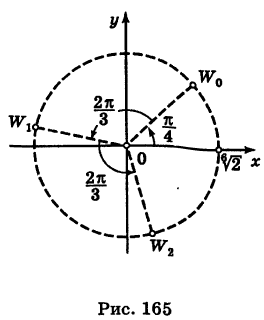
Точки 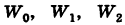 представляют собой равноотстоящие друг от друга точки, расположенные на окружности радиуса
представляют собой равноотстоящие друг от друга точки, расположенные на окружности радиуса 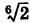 (рис. 165).
(рис. 165).
Понятие функции комплексной переменной
Пусть даны две комплексные плоскости Оху (плоскость г) и O’uv (плоскость w).
Определение: Если каждой точке z  Е (Е — множество точек плоскости z) по некоторому закону f ставится в соответствие единственная точка w
Е (Е — множество точек плоскости z) по некоторому закону f ставится в соответствие единственная точка w  Е’ (Е’ — множество точек плоскости w), то говорят, что w есть функция от z (однозначная)
Е’ (Е’ — множество точек плоскости w), то говорят, что w есть функция от z (однозначная)

с областью определения Е, значения которой принадлежат множеству Е’ (рис. 166). Если множество значений функции f(z) исчерпывает все множество Е то Е’ называется множеством значений (областью изменения) функции f(z). В этом случае пишут

Множества Е и Е’ можно изображать на одной комплексной плоскости.
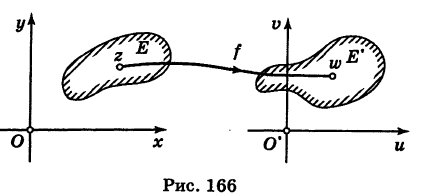
Таким образом, каждая комплексная функция реализует однозначное в одну сторону отображение одного множества на другое. Благодаря этому комплексные функции находят свое применение в таких науках, как гидродинамика и аэродинамика, так как с их помощью удобно описывать «историю» движения объема жидкости (или газа).
Раздел математики, изучающий свойства комплексных функций, носит название теории функций комплексной переменной.
Пример:
Во что переходит сектор Е
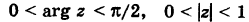
(рис. 167, а) при отображении 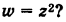
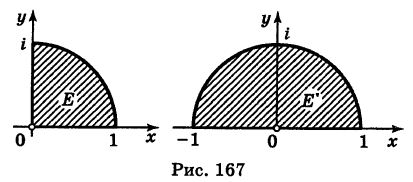
Решение:
Имеем
Поэтому отображенная область E’ представляет собой полукруг (рис. 167, б).
Определение комплексных чисел
Определение комплексного числа и основные функции комплексной переменной
Определение 7.1. Множеством комплексных чисел 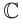 называется множество пар действительных чисел
называется множество пар действительных чисел 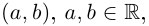 на котором введены операции сложения и умножения следующим образом. Если
на котором введены операции сложения и умножения следующим образом. Если 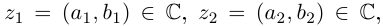 то
то 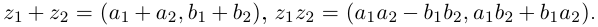 Элементы множества
Элементы множества 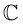 называются комплексными числами. Два комплексных числа
называются комплексными числами. Два комплексных числа 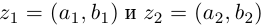 называются равными, если
называются равными, если 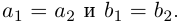
Операции сложения и умножения на множестве 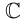 обладают привычными свойствами (коммутативность сложения и умножения, ассоциативность сложения и умножения, дистрибутивность умножения относительно сложения).
обладают привычными свойствами (коммутативность сложения и умножения, ассоциативность сложения и умножения, дистрибутивность умножения относительно сложения).
Лемма 7.1. Для любых комплексных чисел 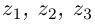 выполняются равенства
выполняются равенства
- 1)
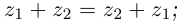
- 2)
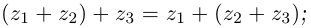
- 3)
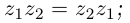
- 4)
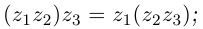
- 5)
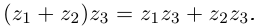
□ Докажем, например, свойство 4 (свойство 5 доказывается аналогично, свойства 1, 2, 3 очевидны).
Пусть 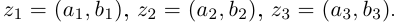 Тогда
Тогда
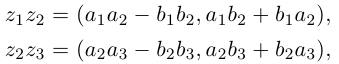
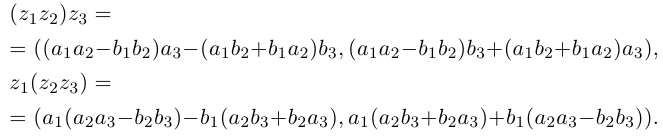
Два последних комплексных числа совпадают. После раскрытия скобок оказывается, что оба они равны
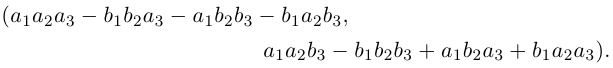 ■
■
Определение 7.2. Комплексное число 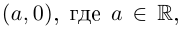 отождествляется с действительным числом а.
отождествляется с действительным числом а.
Это определение оправдывается тем, что установлено взаимно однозначное соответствие между множеством пар 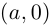 и множеством действительных чисел, сохраняющее операции сложения и умножения:
и множеством действительных чисел, сохраняющее операции сложения и умножения:
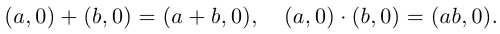
Такое соответствие в высшей алгебре называется изоморфизмом.
Определение 7.3. Комплексное число (0,1) обозначается буквой 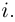
Легко видеть, что 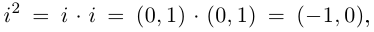 т.е.
т.е. 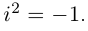
Далее, так как 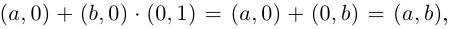 то пару
то пару  можно записать в виде
можно записать в виде 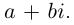 В дальнейшем комплексное число так и будем записывать:
В дальнейшем комплексное число так и будем записывать: 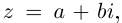 где
где 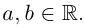 Определения операций при этом запишутся так:
Определения операций при этом запишутся так:
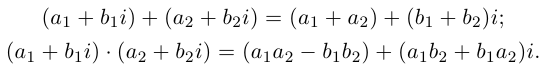
Иными словами, комплексные числа можно складывать и умножать, пользуясь известными законами сложения и умножения (лемма 7.1), имея в виду, что 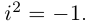
Определение 7.4. Разностью двух комплексных чисел 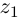 и
и 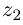 называется такое комплексное число
называется такое комплексное число 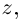 что
что 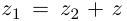 (обозначается
(обозначается 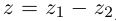 ). Частным двух комплексных чисел
). Частным двух комплексных чисел 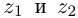 (
(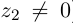 ) называется такое комплексное число z, что
) называется такое комплексное число z, что 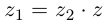 (обозначается
(обозначается 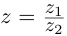 ).
).
Проверим, что эти операции однозначно определены.
□ Пусть 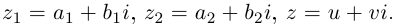 Для разности имеем:
Для разности имеем: 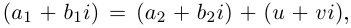 откуда
откуда 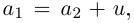
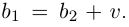 Тогда
Тогда 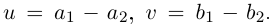 Разность двух комплексных чисел
Разность двух комплексных чисел 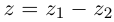 определяется однозначно:
определяется однозначно: 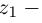
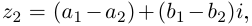 т.е. вычитание можно осуществлять непосредственно.
т.е. вычитание можно осуществлять непосредственно.
Для частного имеем: 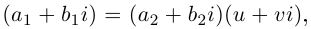 откуда
откуда 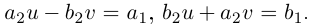 Так как
Так как 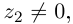 то определитель этой системы
то определитель этой системы 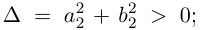 решая систему по правилу Крамера, получим:
решая систему по правилу Крамера, получим: 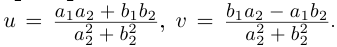 Частное двух комплексных чисел
Частное двух комплексных чисел 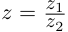 определено однозначно:
определено однозначно:
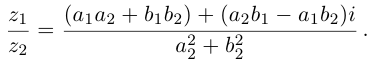
Такое деление можно осуществлять непосредственно:
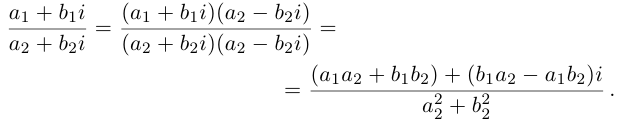
Комплексное число 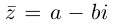 называется сопряжённым к числу
называется сопряжённым к числу  Мы воспользовались тем, что
Мы воспользовались тем, что 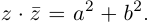 Произведённые действия аналогичны домножению числителя и знаменателя дроби со знаменателем вида
Произведённые действия аналогичны домножению числителя и знаменателя дроби со знаменателем вида 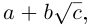 где
где 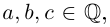
 на число
на число 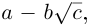 сопряжённое к знаменателю (такие действия применяются для избавления от иррациональности в знаменателе).
сопряжённое к знаменателю (такие действия применяются для избавления от иррациональности в знаменателе).
Определение 7.5. Пусть 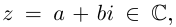 где
где 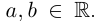 Тогда числа
Тогда числа  называются соответственно действительной и мнимой частью числа
называются соответственно действительной и мнимой частью числа 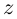 (
(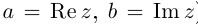 ). Комплексное число
). Комплексное число 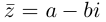 называется числом, сопряжённым к
называется числом, сопряжённым к 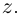 Действительное неотрицательное число
Действительное неотрицательное число 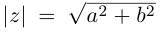 называется модулем числа
называется модулем числа 
Лемма 7.2. Для любых комплексных чисел 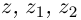 имеют место следующие соотношения:
имеют место следующие соотношения:
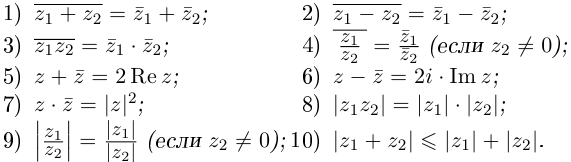
Доказать эти утверждения будет предложено самостоятельно в качестве упражнения.
Множество комплексных чисел  геометрически интерпретируется как множество точек плоскости (комплексная плоскость
геометрически интерпретируется как множество точек плоскости (комплексная плоскость  ). Если координаты точек заданы в прямоугольной системе координат 0,
). Если координаты точек заданы в прямоугольной системе координат 0, 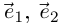 (кратчайший поворот от
(кратчайший поворот от 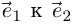 осуществляется против часовой стрелки), то комплексное число
осуществляется против часовой стрелки), то комплексное число 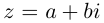 соответствует точке
соответствует точке 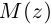 с координатами
с координатами 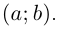 Такое соответствие является взаимно однозначным. Точка
Такое соответствие является взаимно однозначным. Точка 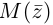 симметрична точке
симметрична точке 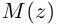 относительно оси абсцисс, которая называется действительной осью, ось ординат называется мнимой осью. Расстояние от точки
относительно оси абсцисс, которая называется действительной осью, ось ординат называется мнимой осью. Расстояние от точки 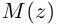 до начала координат равно
до начала координат равно 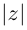 (см. рис. 7.1).
(см. рис. 7.1).
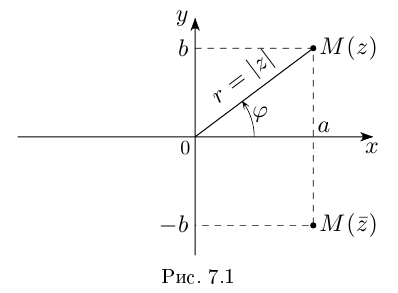
Аргументом числа 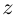 называется угол
называется угол 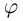 поворота от положительного луча действительной оси к лучу
поворота от положительного луча действительной оси к лучу 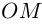 (против часовой стрелки). Этот угол определён с точностью до
(против часовой стрелки). Этот угол определён с точностью до 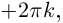
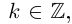 и обозначается
и обозначается 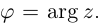 Аргумент нулевого комплексного числа не определён. Фактически мы ввели полярные координаты на комплексной плоскости:
Аргумент нулевого комплексного числа не определён. Фактически мы ввели полярные координаты на комплексной плоскости: 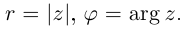 При этом
При этом 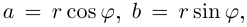 и комплексное число
и комплексное число 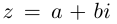 можно записать в тригонометрической форме:
можно записать в тригонометрической форме:
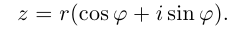
Пример:
Записать в тригонометрической форме числа 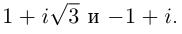
□ 1) 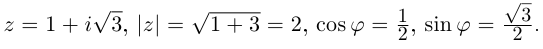
При записи комплексного числа в тригонометрической форме обычно берут одно фиксированное («наиболее простое») значение аргумента. Возьмём 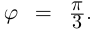 Тогда
Тогда 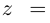
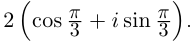
2) 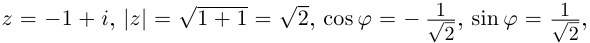
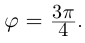 Тогда
Тогда 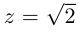 (
(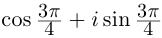 ).
).
Комплексные числа, записанные в тригонометрической форме, удобно умножать и делить. При умножении модули чисел перемножаются, аргументы складываются. При делении модули делятся, аргументы вычитаются.
Лемма 7.3. Пусть 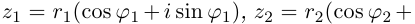
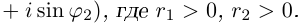 Тогда
Тогда
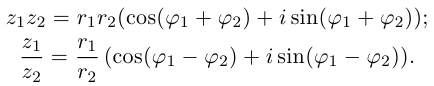
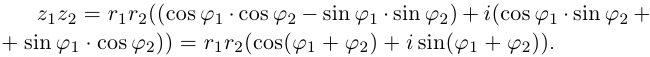
Если 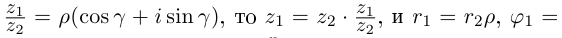
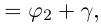 откуда следует, что
откуда следует, что 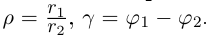
Степень с целым показателем для комплексных чисел определяется так же, как и для действительных. Поэтому мы можем сформулировать
Следствие (формула Муавра). Если 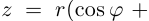
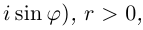 то при любом целом
то при любом целом 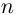 имеет место равенство
имеет место равенство
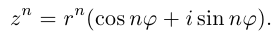
Иными словами, при возведении комплексного числа в целую степень модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Пример:
Применяя формулу Муавра, получить известные формулы тригонометрии для 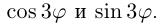
□ Имеем: 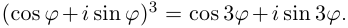 Возводя двучлен в куб, получим:
Возводя двучлен в куб, получим: 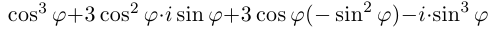 (мы воспользовались тем, что
(мы воспользовались тем, что 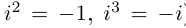 ). Приравнивая действительные и мнимые части двух равных выражений, имеем
). Приравнивая действительные и мнимые части двух равных выражений, имеем
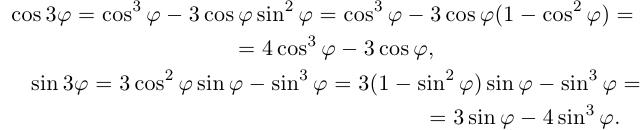
Определение 7.6. Пусть  — натуральное число,
— натуральное число,  Корнем
Корнем  степени из комплексного числа
степени из комплексного числа 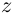 называется комплексное число
называется комплексное число 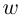 такое, что
такое, что 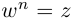 (обозначение:
(обозначение: 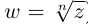 ).
).
Лемма 7.4. Если 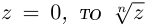 принимает единственное значение 0 при любом
принимает единственное значение 0 при любом 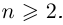 Если
Если 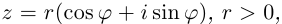 то
то 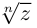 принимает ровно
принимает ровно 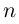 комплексных значений, имеющих одинаковый модуль
комплексных значений, имеющих одинаковый модуль 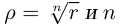 различных значений аргумента
различных значений аргумента 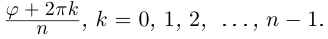
□ Правая часть леммы очевидна, так как 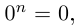 и если
и если 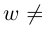
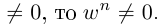 Пусть теперь
Пусть теперь 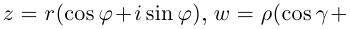
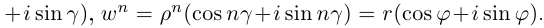 Комплексные числа, записанные в тригонометрической форме, равны тогда и только тогда, когда их модули равны, а аргументы отличаются на
Комплексные числа, записанные в тригонометрической форме, равны тогда и только тогда, когда их модули равны, а аргументы отличаются на 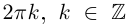 (пока значение
(пока значение 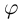 стояло только под знаком косинуса и синуса, неоднозначность определения
стояло только под знаком косинуса и синуса, неоднозначность определения 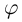 можно было не учитывать, если сравнивать сами углы — эту неоднозначность учитывать необходимо). Итак,
можно было не учитывать, если сравнивать сами углы — эту неоднозначность учитывать необходимо). Итак, 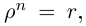
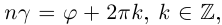 откуда
откуда 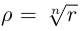 (арифметический корень
(арифметический корень 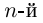 степени из положительного числа),
степени из положительного числа), 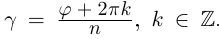
При замене 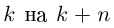 получим тот же угол, увеличенный на
получим тот же угол, увеличенный на 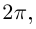 поэтому существенно различные значения
поэтому существенно различные значения 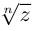 дают лишь
дают лишь 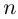 значений
значений 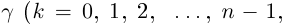 далее значения корня повторяются).
далее значения корня повторяются).
Замечание. 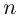 значений
значений 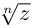 на комплексной плоскости соответствуют
на комплексной плоскости соответствуют 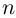 точкам, лежащим в вершинах правильного
точкам, лежащим в вершинах правильного 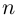 -угольника, вписанного в окружность радиуса
-угольника, вписанного в окружность радиуса 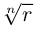 с центром в начале координат.
с центром в начале координат.
Пример №19
Найти все значения 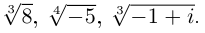
□ 1) 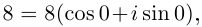 поэтому
поэтому 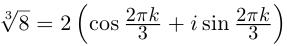
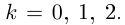 Получим 3 значения:
Получим 3 значения:  (см. рис. 7.2).
(см. рис. 7.2).
Первое из них — арифметическое значение кубического корня из положительного числа 8.
2) 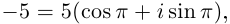 поэтому
поэтому
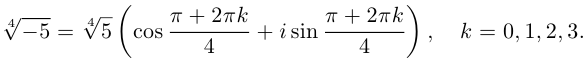
Получим 4 значения:
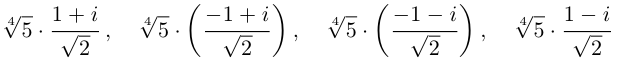
(см. рис. 7.3). 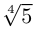 здесь — арифметическое значение корня 4-й степени из положительного числа 5.
здесь — арифметическое значение корня 4-й степени из положительного числа 5.
3) 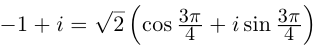 , поэтому
, поэтому
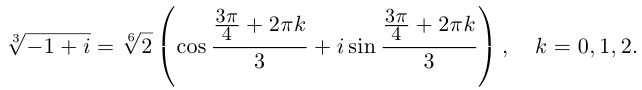
Получим 3 значения:
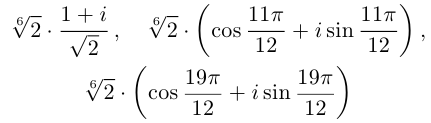
(см. рис. 7.4). ■
Определение 7.7. Пусть 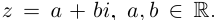 Тогда
Тогда 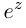 определяется как комплексное число
определяется как комплексное число 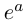
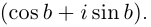
Если 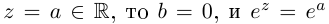 (при
(при 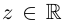 получаем обычное действительное значение
получаем обычное действительное значение 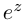 ). Отмстим, что
). Отмстим, что 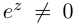 при любых
при любых 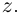
Лемма 7.5. Для любых 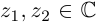 имеют место равенства
имеют место равенства 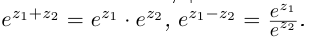
□ Пусть  Тогда
Тогда
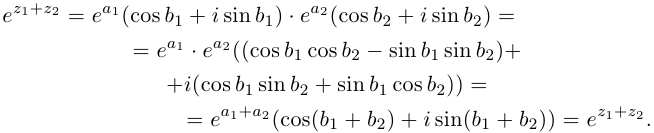
Далее, так как 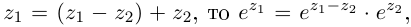 откуда следует второе утверждение леммы.
откуда следует второе утверждение леммы.
Пример №20
Вычислить 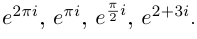
□ Имеем: 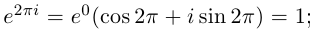
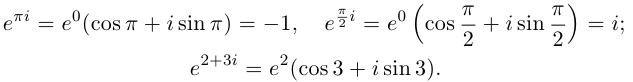
Так как при всех 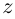 выполняются равенства
выполняются равенства 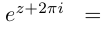
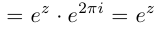 , то функция комплексной переменной
, то функция комплексной переменной 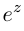 имеет мнимый период
имеет мнимый период 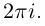 Привычной взаимной однозначности отображения при помощи функции
Привычной взаимной однозначности отображения при помощи функции 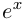 уже нет.
уже нет.
Определение 7.8. Логарифмом комплексного числа 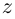 называется комплексное число
называется комплексное число 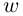 такое, что
такое, что 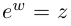 (обозначение:
(обозначение: 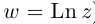 ).
).
Лемма 7.6. Если 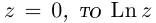 не определен. Если
не определен. Если 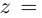
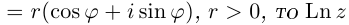 принимает бесконечно много значений, имеющих одинаковую действительную часть
принимает бесконечно много значений, имеющих одинаковую действительную часть 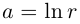 (обычный натуральный логарифм положительного числа) и бесконечное число значений мнимой части
(обычный натуральный логарифм положительного числа) и бесконечное число значений мнимой части 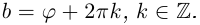
□ Первая часть леммы следует из того, что 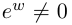 при любых
при любых 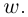 Пусть теперь
Пусть теперь 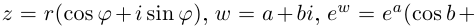
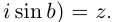 Тогда
Тогда 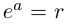 (откуда
(откуда 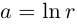 ),
), 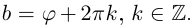
Таким образом, множество значений функции 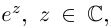 есть вся комплексная плоскость, кроме точки 0.
есть вся комплексная плоскость, кроме точки 0.
Пример №21
Найти все значения 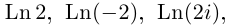
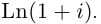
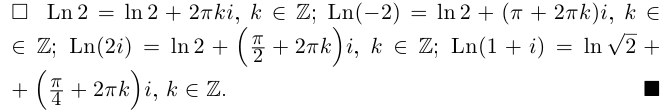
Определение 7.9. Для любых  определим
определим 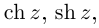
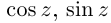 так:
так:
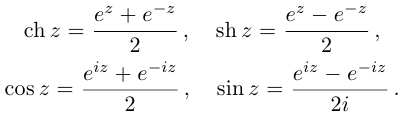
Если 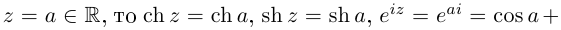
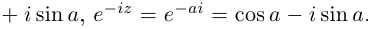 Поэтому
Поэтому
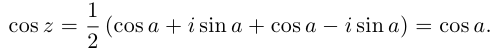
Аналогично, 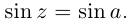
Отметим также, что все известные формулы тригонометрии сохраняются для комплексных значений аргументов (при этом 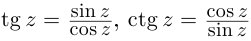 ). Например, для всех
). Например, для всех 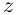
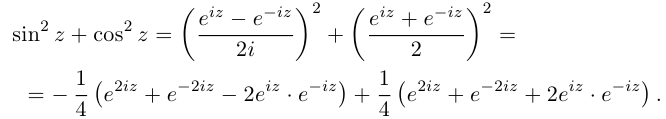
Так как 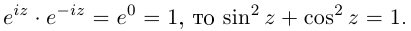
Легко видеть, что 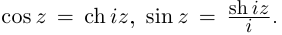 Косинус на действительной оси соответствует гиперболическому косинусу на мнимой оси и наоборот: аналогично для синусов. Поэтому формально все операции для тригонометрических и гиперболических функций проводятся одинаково с точностью до некоторых степеней числа
Косинус на действительной оси соответствует гиперболическому косинусу на мнимой оси и наоборот: аналогично для синусов. Поэтому формально все операции для тригонометрических и гиперболических функций проводятся одинаково с точностью до некоторых степеней числа 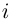 (если работать только с действительными числами, то всё будет происходить одинаково с точностью до степеней числа —1). Этим и объясняется сходство формул тригонометрии с соответствующими формулами для гиперболических функций, включая формулы для производных и разложения по формуле Тейлора.
(если работать только с действительными числами, то всё будет происходить одинаково с точностью до степеней числа —1). Этим и объясняется сходство формул тригонометрии с соответствующими формулами для гиперболических функций, включая формулы для производных и разложения по формуле Тейлора.
Комплекснозначные функции действительной переменной
Рассмотрим функцию 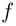 такую, что
такую, что 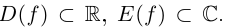 Тогда при всех
Тогда при всех 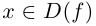 можно рассмотреть
можно рассмотреть 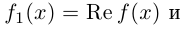
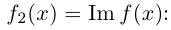
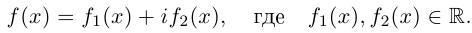
Так как 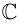 можно интерпретировать как плоскость
можно интерпретировать как плоскость 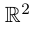 , то комплекснозначная функция действительной переменной фактически есть двумерная вектор-функция, значения которой записываются как комплексные числа.
, то комплекснозначная функция действительной переменной фактически есть двумерная вектор-функция, значения которой записываются как комплексные числа.
Определение 7.10. Комплекснозначная функция действительной переменной 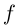 называется непрерывной (дифференцируемой, непрерывно дифференцируемой, дважды дифференцируемой и т.д.) в точке или на промежутке, если таковыми же являются обе функции
называется непрерывной (дифференцируемой, непрерывно дифференцируемой, дважды дифференцируемой и т.д.) в точке или на промежутке, если таковыми же являются обе функции 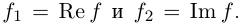 Для дифференцируемой функции по определению
Для дифференцируемой функции по определению 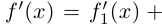
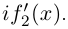
Для комплекснозначных функций сохраняются формулы производной суммы, произведения и частного.
Лемма 7.7. Если комплекснозначные функции действительной переменной 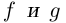 дифференцируемы в точке
дифференцируемы в точке 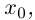 то функции
то функции 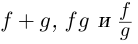 также дифференцируемы в этой точке, причем
также дифференцируемы в этой точке, причем
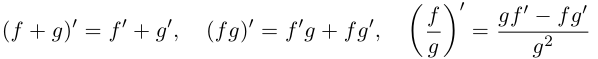
в точке 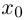 (в последнем случае нужно требовать, чтобы
(в последнем случае нужно требовать, чтобы 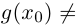
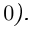
□ Докажем лемму для случая производной произведения. Утверждение для производной суммы доказывается проще, а для производной частного — несколько сложнее, но, по сути дела, аналогично.
Пусть 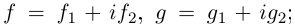 функции
функции 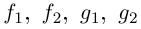 дифференцируемы в точке
дифференцируемы в точке 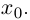 Тогда
Тогда
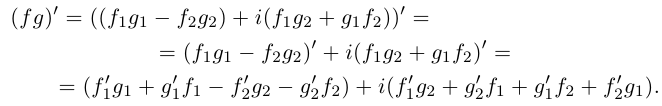
Функция 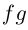 дифференцируема в точке
дифференцируема в точке 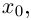 так как существуют и конечны все производные в последнем выражении. Далее,
так как существуют и конечны все производные в последнем выражении. Далее,
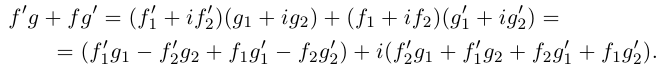
Легко видеть, что это выражение совпадает с 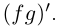
Пример №22
Доказать, что при любом 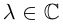 имеет место равенство
имеет место равенство
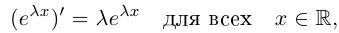
т.е. привычная для действительных 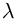 формула сохраняется и при комплексных
формула сохраняется и при комплексных 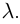
□ Пусть 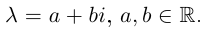
Тогда 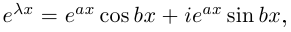
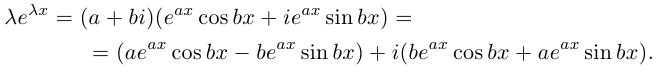
С другой стороны, 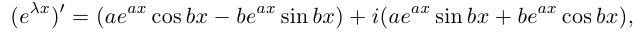
что совпадает с 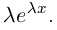
Отметим, что производная комплекснозначной функции берётся по действительной переменной. Принципиально иная ситуация возникает при рассмотрении комплекснозначных функций комплексной переменной и при дифференцировании их по комплексной переменной. Здесь имеют место совершенно неожиданные эффекты (например, если функция дифференцируема в окрестности точки, то она имеет производные всех порядков в этой окрестности), которые студенты обычно изучают на III курсе (курс ТФКП — теория функций комплексной переменной).
Многочлены
Функция комплексной переменной 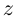
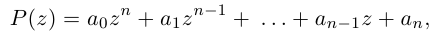
где 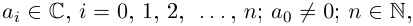 называется многочленом степени
называется многочленом степени 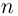 от переменной
от переменной 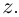 Многочлен степени 0 — это постоянная функция
Многочлен степени 0 — это постоянная функция 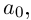 где
где 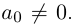 Нулевому многочлену не приписывается никакая степень (иногда удобно считать, что его степень равна
Нулевому многочлену не приписывается никакая степень (иногда удобно считать, что его степень равна 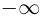 ). Если все
). Если все 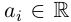 , то говорят о многочлене с действительными коэффициентами (
, то говорят о многочлене с действительными коэффициентами (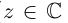 или
или 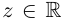 по смыслу задачи). Если все
по смыслу задачи). Если все 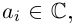 то говорят о многочлене с комплексными коэффициентами
то говорят о многочлене с комплексными коэффициентами 
Если 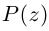 — многочлен степени
— многочлен степени 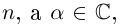 то многочлен
то многочлен  можно разделить с остатком на
можно разделить с остатком на 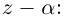
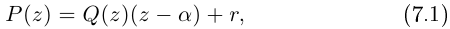
где 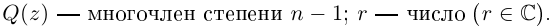
Теорема 7.1 (Безу). Остаток от деления многочлена 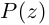 на двучлен
на двучлен 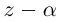 равен
равен 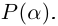
□ Из (7.1) имеем при 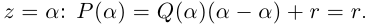
Следствие. Многочлен 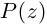 делится без остатка на
делится без остатка на  тогда и только тогда, когда число
тогда и только тогда, когда число 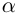 является корнем многочлена
является корнем многочлена 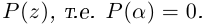
□ Утверждение немедленно следует из теоремы Безу.
Таким образом, число 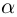 является корнем многочлена
является корнем многочлена 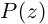 тогда и только тогда, когда
тогда и только тогда, когда 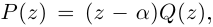 где степень многочлена
где степень многочлена 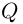 на единицу меньше степени Р.
на единицу меньше степени Р.
Теорема 7.2 (основная теорема алгебры). Любой многочлен степени 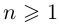 с комплексными коэффициентами имеет комплексный корень.
с комплексными коэффициентами имеет комплексный корень.
В настоящее время мы не располагаем математическим аппаратом для доказательства этой теоремы, поэтому примем её без доказательства. Доказана она будет очень просто в курсе ТФКП (и даже двумя способами — как простое следствие из теоремы Лиувилля или теоремы Руше).
Теорема 7.3. Многочлен с комплексными коэффициентами
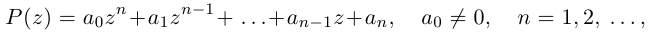
раскладывается в произведение линейных множителей
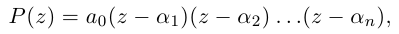
где 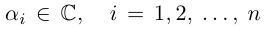 (среди чисел
(среди чисел 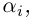 возможно, есть равные).
возможно, есть равные).
□ По основной теореме алгебры 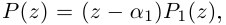 где
где 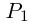 — многочлен степени
— многочлен степени 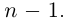 Применяя такую же процедуру к
Применяя такую же процедуру к 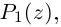 получим:
получим: 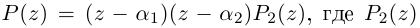 — многочлен степени
— многочлен степени 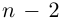 и т.д. В конце концов дойдём до многочлена степени 0.
и т.д. В конце концов дойдём до многочлена степени 0.
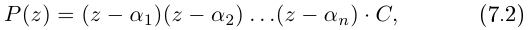
где 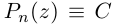 (комплексная постоянная). Здесь
(комплексная постоянная). Здесь 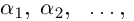
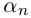 — комплексные числа, среди которых могут быть равные.
— комплексные числа, среди которых могут быть равные.
Если раскрыть скобки в правой части (7.2), то коэффициент при 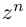 будет равен С, т.е.
будет равен С, т.е. 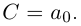
Определение 7.11. Комплексное число  называется корнем кратности
называется корнем кратности 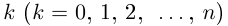 многочлена
многочлена 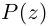 степени
степени 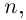 если
если 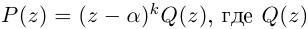 — многочлен такой, что
— многочлен такой, что 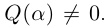 При
При 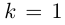 корень называется простым, при
корень называется простым, при 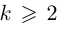 — кратным.
— кратным.
Если 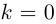 , то число
, то число 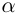 не является корнем многочлена
не является корнем многочлена 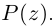
В общем случае, учитывая кратность корней, многочлен 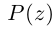 степени
степени 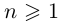 раскладывается на линейные множители:
раскладывается на линейные множители:
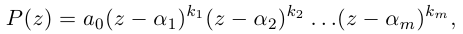
где все комплексные числа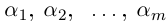 различны, корень
различны, корень 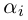 имеет кратность
имеет кратность 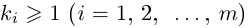 , при этом степень многочлена равна
, при этом степень многочлена равна 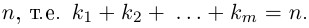
Лемма 7.8. Пусть 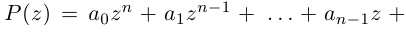
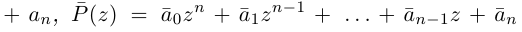 (многочлен, сопряжённый к P). Число
(многочлен, сопряжённый к P). Число  является корнем многочлена Р кратности
является корнем многочлена Р кратности 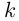 тогда и только тогда, когда число а является корнем многочлена
тогда и только тогда, когда число а является корнем многочлена 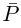 той же кратности
той же кратности 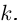
□ Так как 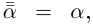 то утверждение достаточно доказать лишь в одну сторону. Пусть
то утверждение достаточно доказать лишь в одну сторону. Пусть 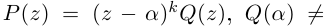
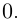 Тогда
Тогда 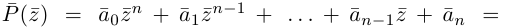
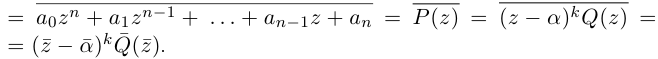
Так как 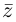 — любое комплексное число, то в последней записи можно заменить
— любое комплексное число, то в последней записи можно заменить 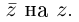 Получим
Получим
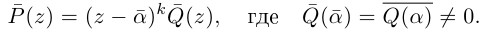
Это и означает, что 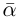 — корень многочлена
— корень многочлена 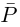 кратности
кратности 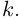
Следствие. Если 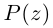 — многочлен с действительными коэффициентами, то числа
— многочлен с действительными коэффициентами, то числа 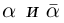 одновременно являются его корнями, причем кратности их совпадают (т.е. недействительные корни появляются «парочками» — взаимно сопряжённые корни одинаковой кратности).
одновременно являются его корнями, причем кратности их совпадают (т.е. недействительные корни появляются «парочками» — взаимно сопряжённые корни одинаковой кратности).
□ Это очевидно из леммы 7.8, так как 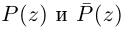 — один и тот же многочлен.
— один и тот же многочлен.
Теорема 7.4. Многочлен степени 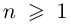 с действительными коэффициентами
с действительными коэффициентами 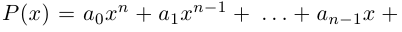
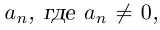 раскладывается в произведение линейных и неприводимых квадратичных множителей:
раскладывается в произведение линейных и неприводимых квадратичных множителей:
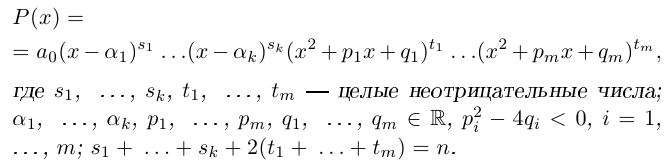
□ По теореме 7.3 и лемме 7.8
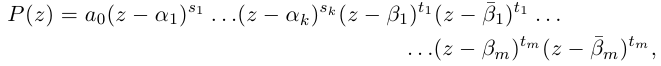
где  — действительные корни многочлена
— действительные корни многочлена  кратностей
кратностей  соответственно, a
соответственно, a  — оставшиеся корни (
— оставшиеся корни ( имеют одинаковую кратность
имеют одинаковую кратность 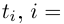
 ). Очевидно, что степень многочлена равна
). Очевидно, что степень многочлена равна 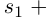
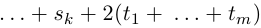 т.е. эта сумма равна
т.е. эта сумма равна 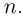
Пусть 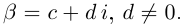 Тогда
Тогда 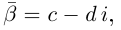
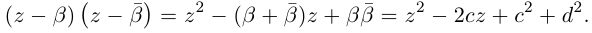
Получили квадратный трёхчлен с действительными коэффициентами 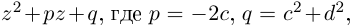 который имеет отрицательный дискриминант
который имеет отрицательный дискриминант 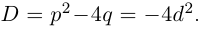 Остаётся символически заменить
Остаётся символически заменить 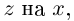 подчёркивая этим, что нас интересуют лишь действительные значения
подчёркивая этим, что нас интересуют лишь действительные значения 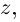 и мы получим нужное равенство.
и мы получим нужное равенство.
Теорема 7.4 является примером утверждения, в формулировке которого отсутствуют комплексные числа (чисто действительное утверждение), а естественное доказательство его получается с выходом во множество комплексных чисел. Таких утверждений можно встретить немало в различных математических курсах и прикладных науках.
Кстати, квадратный трехчлен с комплексными коэффициентами имеет такой же вид разложения на линейные множители, как и квадратный трёхчлен с действительными корнями в элементарной алгебре:
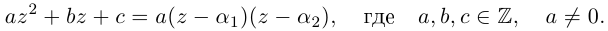
Корни 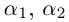 — комплексные, и они обязательно существуют. Роль дискриминанта
— комплексные, и они обязательно существуют. Роль дискриминанта 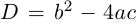 сводится только к определению того, различны ли корни
сводится только к определению того, различны ли корни 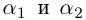 или они совпадают (т.е. квадратный трёхчлен имеет один корень
или они совпадают (т.е. квадратный трёхчлен имеет один корень 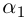 кратности 2). Если
кратности 2). Если 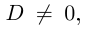 то квадратный трёхчлен имеет два различных простых корня, если
то квадратный трёхчлен имеет два различных простых корня, если 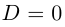 — один корень кратности 2. В самом деле, решая квадратное уравнение
— один корень кратности 2. В самом деле, решая квадратное уравнение 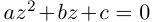 методом выделения полного квадрата, получим, как и в элементарной алгебре:
методом выделения полного квадрата, получим, как и в элементарной алгебре:
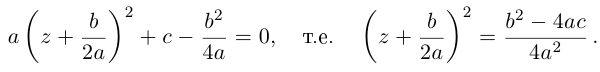
Если 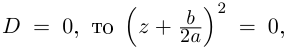 и уравнение имеет один корень
и уравнение имеет один корень 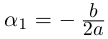 кратности 2
кратности 2 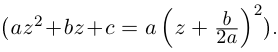 Если
Если 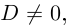 то
то 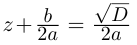 (писать ± не имеет смысла, так как
(писать ± не имеет смысла, так как 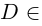
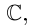 и под
и под 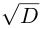 понимаются оба значения квадратного корня из ненулевого комплексного числа). Окончательно получим привычную формулу корней квадратного уравнения:
понимаются оба значения квадратного корня из ненулевого комплексного числа). Окончательно получим привычную формулу корней квадратного уравнения:
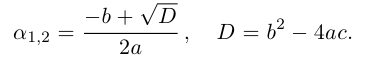
Пример №23
Решить уравнение 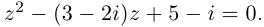
□ 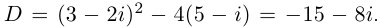 Найдём оба значения
Найдём оба значения 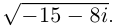 Пусть
Пусть 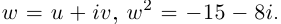 Тогда
Тогда 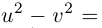
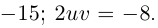 Решая эту систему, получим:
Решая эту систему, получим: 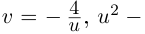
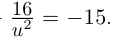 Полученное биквадратное уравнение
Полученное биквадратное уравнение 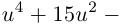
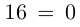 решается при помощи замены
решается при помощи замены 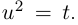 Квадратное уравнение
Квадратное уравнение 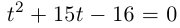 имеет корни
имеет корни 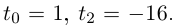 Так как
Так как 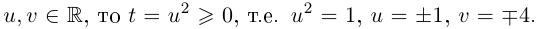 Получили два значения квадратного корня:
Получили два значения квадратного корня: 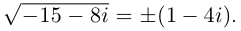 Тогда корни данного уравнения равны
Тогда корни данного уравнения равны
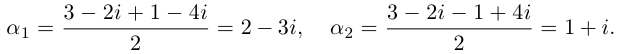
Пример №24
Найти все значения 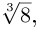 решая уравнение
решая уравнение 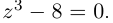
□ Левая часть раскладывается на множители:
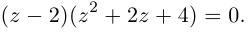
Поэтому один из корней равен 2. Квадратный трёхчлен 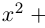
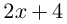 не имеет действительных корней
не имеет действительных корней 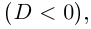 поэтому
поэтому 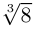 имеет всего одно действительное значение 2. Найдём оставшиеся два комплексно-сопряжённых значения. Решаем квадратное уравнение
имеет всего одно действительное значение 2. Найдём оставшиеся два комплексно-сопряжённых значения. Решаем квадратное уравнение 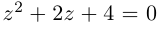 по формуле чётного коэффициента:
по формуле чётного коэффициента:
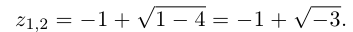
Во множестве комплексных чисел 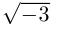 имеет два значения
имеет два значения 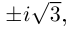 поэтому
поэтому 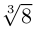 имеет 3 комплексных значения:
имеет 3 комплексных значения: 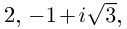
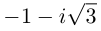 (такой же результат был получен в примере 7.3 другим способом). ■
(такой же результат был получен в примере 7.3 другим способом). ■
Разложение правильной дроби в сумму простейших дробей
Мы будем рассматривать действительные дробно-рациональные функции 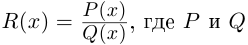 — многочлены степеней соответственно
— многочлены степеней соответственно 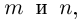 где
где 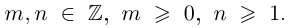 Дробь называется правильной, если
Дробь называется правильной, если 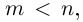 и неправильной, если
и неправильной, если 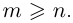
Лемма 7.9. Если 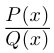 правильная дробь и
правильная дробь и 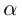 —действительный корень многочлена
—действительный корень многочлена  кратности
кратности  то
то
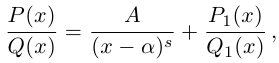
где 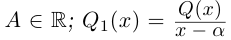 — многочлен, для которого
— многочлен, для которого 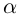 является корнем кратности
является корнем кратности 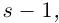 a
a 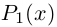 — такой многочлен, что дробь
— такой многочлен, что дробь 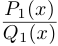 является правильной.
является правильной.
□ Так как 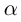 — корень
— корень 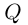 кратности
кратности 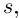 то
то 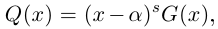 где
где 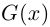 — многочлен такой, что
— многочлен такой, что 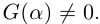 Рассмотрим число
Рассмотрим число 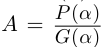 и многочлен
и многочлен 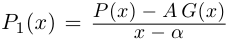 (это многочлен, так как
(это многочлен, так как 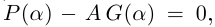 и числитель делится нацело на
и числитель делится нацело на 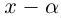 ).
).
Так как степень G меньше степени Q и степень Р меньше степени Q, то степень числителя последней дроби меньше степени Q; значит, степень 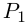 меньше степени
меньше степени 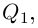 т.е. дробь
т.е. дробь 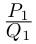 правильная. Далее,
правильная. Далее, 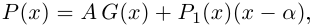 откуда
откуда 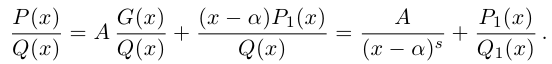
Утверждение леммы, очевидно, сохраняется, если все числа и многочлены считать комплексными.
Лемма 7.10. Пусть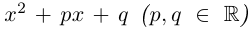 — неприводимый квадратный трёхчлен, входящий в разложение многочлена
— неприводимый квадратный трёхчлен, входящий в разложение многочлена  на множители в степени
на множители в степени  Тогда правильная дробь
Тогда правильная дробь 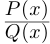 представляется в виде
представляется в виде
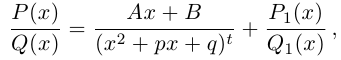
где 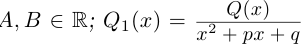 — многочлен, в разложение которого
— многочлен, в разложение которого 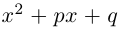 входит в степени
входит в степени 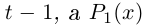 — такой многочлен, что дробь
— такой многочлен, что дробь 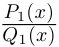 является правильной.
является правильной.
□ Пусть 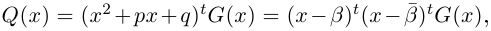 где
где 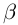 и
и 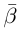 комплексно-сопряжённые корни квадратного трёхчлена
комплексно-сопряжённые корни квадратного трёхчлена 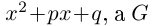 — действительный многочлен такой, что
— действительный многочлен такой, что 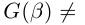
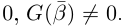 Рассмотрим действительные числа А и В такие, что
Рассмотрим действительные числа А и В такие, что
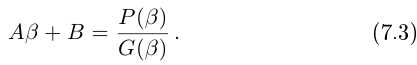
Такие числа А и В определены единственным образом, так как если 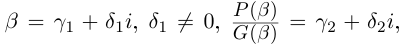 то равенство (7.3) перепишется так:
то равенство (7.3) перепишется так:
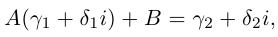
и числа А, В находятся из системы 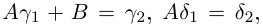 очевидно, имеющей единственное решение. Из (7.3) следует также, что
очевидно, имеющей единственное решение. Из (7.3) следует также, что 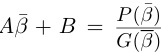 так как
так как  — многочлены с действительными коэффициентами.
— многочлены с действительными коэффициентами.
Рассмотрим многочлен 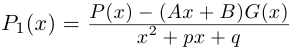 (это — многочлен, так как
(это — многочлен, так как 
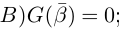 значит, числитель делится нацело на
значит, числитель делится нацело на 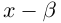 и на
и на 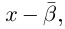 следовательно, делится на
следовательно, делится на 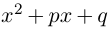 ). Пусть степень Q равна
). Пусть степень Q равна 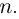 Так как степень G не превосходит
Так как степень G не превосходит 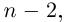 то степень многочлена
то степень многочлена 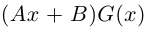 не превосходит
не превосходит 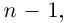 т.е. меньше степени Q. Степень Р также меньше степени Q, поэтому степень числителя последней дроби меньше степени Q.
т.е. меньше степени Q. Степень Р также меньше степени Q, поэтому степень числителя последней дроби меньше степени Q.
Значит, степень 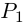 меньше, чем
меньше, чем  , т.е. меньше степени
, т.е. меньше степени 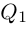 и дробь
и дробь 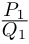 правильная. Далее,
правильная. Далее,
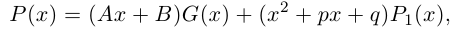
откуда
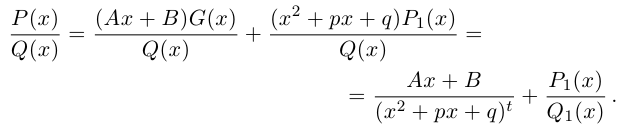
Последовательно выделяя из многочлена 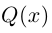 линейные, а затем неприводимые квадратичные множители, и применяя соответственно леммы 7.9 и 7.10, получим разложение
линейные, а затем неприводимые квадратичные множители, и применяя соответственно леммы 7.9 и 7.10, получим разложение 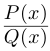 в сумму правильных дробей вида
в сумму правильных дробей вида

(здесь 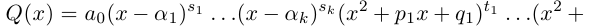
 — как разложение многочлена в теореме 7.4).
— как разложение многочлена в теореме 7.4).
Все слагаемые последней суммы называются простейшими дробями. Все коэффициенты, обозначенные символом  , являются действительными числами (вообще говоря, различными). Всего их
, являются действительными числами (вообще говоря, различными). Всего их 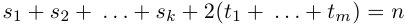 штук. Можно доказать, что они определены единственным образом. Процесс выделения слагаемых по леммам 7.9 и 7.10 прекратится, когда в знаменателе останется ровно один множитель вида
штук. Можно доказать, что они определены единственным образом. Процесс выделения слагаемых по леммам 7.9 и 7.10 прекратится, когда в знаменателе останется ровно один множитель вида  Но такая правильная дробь сама будет простейшей. Таким образом, доказана
Но такая правильная дробь сама будет простейшей. Таким образом, доказана
Теорема 7.5. Любая правильная рациональная дробь с действительными коэффициентами раскладывается в сумму простейших дробей.
Пример №25
Разложить в сумму простейших дробей:
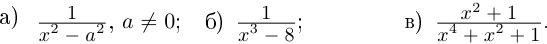
а) 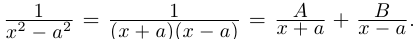 Приводя к общему знаменателю, имеем:
Приводя к общему знаменателю, имеем: 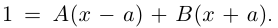 При
При 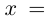
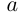 получим
получим 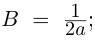 при
при 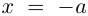 получим
получим 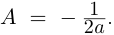 Окончательно имеем:
Окончательно имеем: 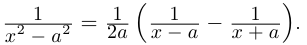
б)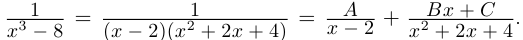 Приводя в общему знаменателю, имеем:
Приводя в общему знаменателю, имеем: 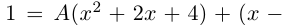
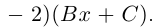 При
При 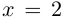 получим
получим 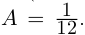 Приравнивая коэффициенты при
Приравнивая коэффициенты при 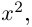 получим
получим 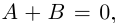 т.е.
т.е. 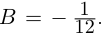 Приравнивая свободные члены, получим
Приравнивая свободные члены, получим 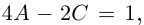 откуда
откуда 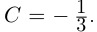 Окончательно имеем
Окончательно имеем
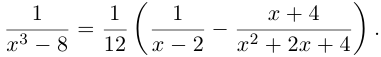
в) 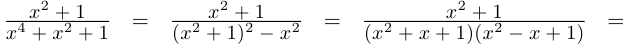
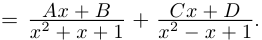 Приводя к общему знаменателю, имеем:
Приводя к общему знаменателю, имеем: 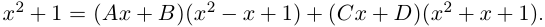 Приравнивая коэффициенты при
Приравнивая коэффициенты при  получим:
получим: 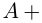
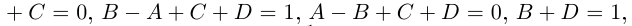 откуда
откуда 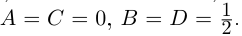 Окончательно имеем
Окончательно имеем
Вычисление комплексного числа
Определение 1.1. Многочленом (полиномом) степени n с действительными коэффициентами называется любое выражение вида
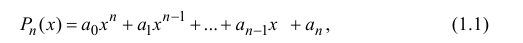
где 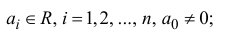
х – переменная.
Корнем многочлена (1.1) называется любое число 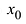 такое, что
такое, что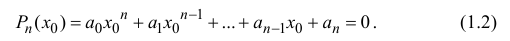
Нетрудно заметить, что некоторые многочлены вообще не имеют
действительных корней, например: 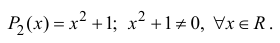
Расширим множество действительных чисел. Добавим к этому
множеству символ i , такой что 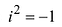 ( i называется мнимой единицей).
( i называется мнимой единицей).
Тогда ±i – два корня уравнения 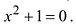
Определение 1.2. Множеством комплексных чисел называется множество
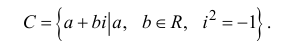
Суммой двух комплексных чисел 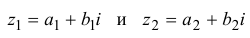 называется число
называется число
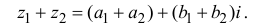 .
.
Произведением двух комплексных чисел 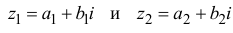 называется число
называется число
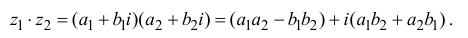
Для числа z= a +bi число а называется действительной частью,
число b – мнимой частью. Обозначения: 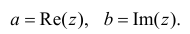
Относительно операций «+» и « · » комплексные числа С обладают
такими же свойствами, как и действительные числа. Эти операции
коммутативны и ассоциативны; для них существуют обратные операции:
вычитание и деление (кроме деления на 0).
Пример №26
Найти 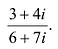
Решение:
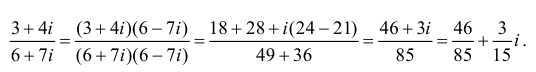
Теорема 1.1 (основная теорема алгебры). Любое уравнение вида (1.2)
имеет решение во множестве С.
Пример №27
Решить уравнение
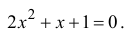
Решение:
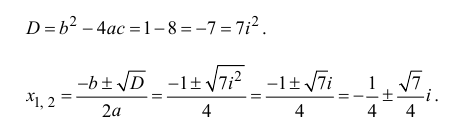
Определение 1.3. Для комплексного числа z =a +bi число z =a -bi называется комплексно-сопряженным, число 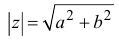 называется модулем z.
называется модулем z.
Если рассмотреть плоскость с декартовой системой координат ( O,x,y ) и на оси Ох отложить а – действительную часть z, а на оси Oy – b – мнимую часть z, то получим взаимно однозначное соответствие между множеством С всех
комплексных чисел и множеством точек плоскости.
Такая плоскость называется комплексной плоскостью, рис. 1.1.
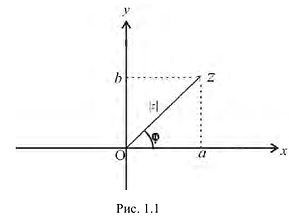
При этом 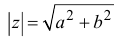 – длина радиуса-вектора точки z.
– длина радиуса-вектора точки z.
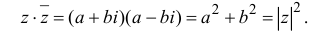
Определение 1.4. Аргументом комплексного числа z =a +bi называется
угол 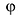 , который образует радиус-вектор точки z с положительным
, который образует радиус-вектор точки z с положительным
направлением оси Ох Аргумент будем обозначать Argz . Аргумент
определен с точностью до 2 πn. При этом значение 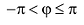 называется
называется
главным и обозначается argz.
Замечание. 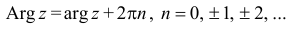
При этом
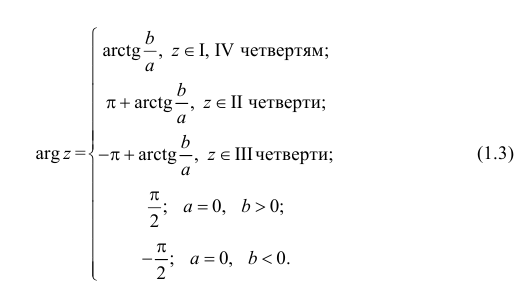
Если 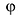 – аргумент z, то z представляется в виде
– аргумент z, то z представляется в виде 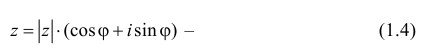
тригонометрическая форма комплексного числа.
Теорема 1.2. Пусть 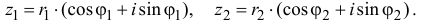
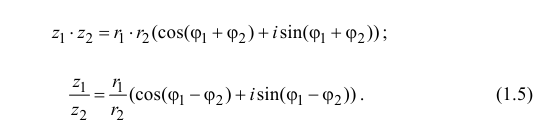
Доказательство
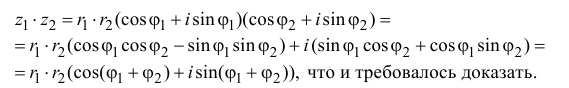
Из формул (1.5) следует, в частности, что 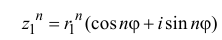 – формула Муавра. (1.6)
– формула Муавра. (1.6)
Пример №28
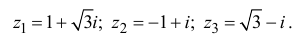 Представить числа
Представить числа  в тригонометрической форме.
в тригонометрической форме.
Решение:
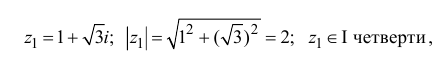
поэтому по формуле (1.3)
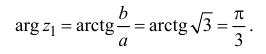
Тогда по формуле (1.4)
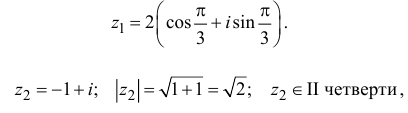
поэтому по формуле (1.3)
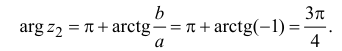
Тогда 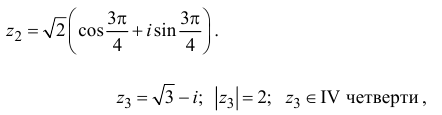
Из формул (1.5), (1.6) видно, что аргумент 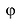 комплексного числа z при
комплексного числа z при
умножении, делении, возведении в степень ведет себя как показатель
степени. Обозначим 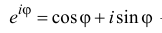 – формула Эйлера. (1.7)
– формула Эйлера. (1.7)
Тогда из теоремы 1.2 следует, что
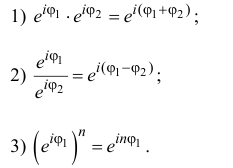
Учитывая (1.7), формулу (1.4) для z можно переписать в виде 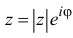 показательная форма комплексного числа.
показательная форма комплексного числа.
Пример №29
Вычислить 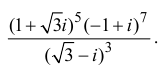
Решение:
Согласно примеру 1.3 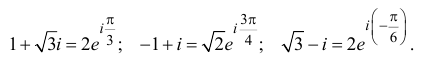
Поэтому
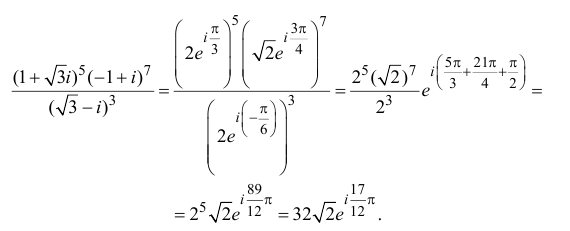
Определение 1.5. Корнем n-й степени из числа z  C называется такое
C называется такое
число  , что
, что 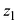 , при этом обозначается
, при этом обозначается 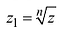 . Таким образом
. Таким образом

Из формулы (1.8) видно что 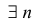 корней n-й степени из числа z, при этом,
корней n-й степени из числа z, при этом,
если 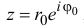 , то
, то

Пример №30
Найти 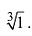
Решение:
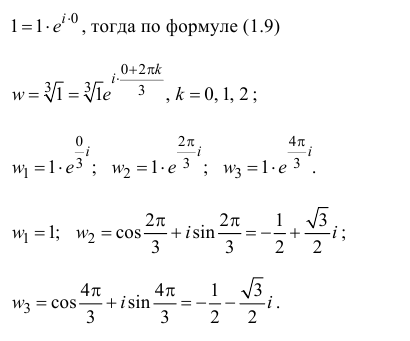
- Координаты на прямой
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Степенные ряды
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
Что такое комплексные числа и их умножение
В математических науках часто применяют при решении задач не только натуральные, рациональные и вещественные числа, но и комплексные.
Определение
Комплексное число — это отдельный вид чисел, который представлен множеством, обозначаемым с помощью символа (mathbb{C}).
Рассмотреть комплексное число можно на доказательстве примера. Если записать обычное множество в виде z = a + ib, то под мнимой единицей будет подразумеваться выражение (i = sqrt{-1}). Числа (a,b in mathbb{R}) являются вещественными числами.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В том случае, когда b = 0, комплексное число трансформируется в вещественное число. Исходя из этого, можно сделать вывод, что действительные числа являются частным случаем комплексных чисел. Запись данного заключения будет иметь следующий вид подмножества:
(mathbb{R} subset mathbb{C})
Следует отметить, что также допустимо равенство:
a = 0
Согласно принятым правилам, мнимая часть комплексного числа записывается в виде:
Im(z) = b
Действительная часть комплексного числа представляет собой выражение:
Re(z) = a
Рассмотрев множество на примере, можно представить формулировку комплексно-сопряженных чисел.
Определение
Каждое комплексное число z = a+ib предполагает наличие такого числа, называемого сопряженным, при котором (overline{z} = a-ib).
Разница между записанными числами заключается в неодинаковых знаках перед действительным и мнимым компонентом чисел.
В математической науке для данных чисел предусмотрено несколько форм. Таким образом, одинаковые числа достаточно просто записать разными методами:
- Алгебраическая форма: (z = a+ib).
- Показательная форма: (z = |z|e^{ivarphi}).
- Тригонометрическая форма: (z = |z|cdot(cos(varphi)+isin(varphi))).
С помощью несложных манипуляций одну форму числа можно перевести в другой вариант записи. Алгебраическая запись является более распространенной. Однако допустимо изображать комплексные числа на плоскости. В итоге получим числа (a,b in mathbb{R}) расположенные на соответствующих осях плоскости.
Комплексное число z = a+ib можно представить в качестве вектора (overline{z}). При этом для обозначения аргумента можно использовать запись (varphi). При определении модуля |z| используют длину вектора (overline{z}) и соответствующую формулу:
(|z| = sqrt{a^2+b^2})
С помощью различных уравнений, выбор которых определяется полуплоскостью, в котором расположено само число, определяют аргумент комплексного числа (varphi).
Справедливы следующие закономерности:
- a>0, то (varphi = arctgfrac{b}{a}).
- a<0, b>0, то (varphi = pi + arctgfrac{b}{a}).
- a<0, b<0, то (varphi = -pi + arctgfrac{b}{a}).
Умножить комплексные числа в алгебраической форме можно, таким образом:
(z_1 cdot z_2 = (a_1+ib_1) cdot (a_2+ib_2) = (a_1 a_2 – b_1 b_2)+i(a_1 b_2 + a_2 b_1))
Операция умножения комплексных чисел, записанных в показательном варианте, имеет следующий вид:
(z_1 cdot z_2 = |z_1|e^{ivarphi_1} cdot |z_2|e^{ivarphi_2} = |z_1|cdot|z_2|cdot e^{i(varphi_1 + varphi_2)})
Разновидности формул умножения в зависимости от формы записи
Благодаря наличию специальных формул, можно оперативно выполнять различные операции с комплексными числами, включая примеры из тригонометрии. Теоретический порядок действий при умножении зависит от того, в какой форме записано комплексное число.
Формула умножения в алгебраической форме
В данном случае для того чтобы умножить комплексные числа, необходимо перемножить их компоненты, поочередно раскрывая скобки, согласно формуле. При этом следует учитывать, что (i^2 = -1).
В итоге получим:
(z_1 cdot z_2 = (x_1+y_1i) cdot (x_2 + y_2i) = (x_1 cdot x_2 – y_1 cdot y_2) + (x_1 cdot y_2 + x_2 cdot y_1)i)
Формула умножения в показательной форме
Если требуется найти произведение комплексных чисел, которые записаны в показательной форме, то целесообразно воспользоваться способом прямого перемножения всех элементов:
(z_1 cdot z_2 = r_1e^{varphi_1 i} cdot r_2e^{varphi_2 i} = r_1cdot r_2 cdot e^{(varphi_1+varphi_2)i})
Формула умножения в тригонометрической форме
Найти произведение комплексных чисел, записанных с помощью тригонометрической формы, можно, таким образом:
(z_1 cdot z_2 = r_1 cdot r_2 cdot (cos(varphi_1+varphi_2) + isin(varphi_1+varphi_2)))
Примеры решения задач с комплексными числами
Задача 1
Необходимо представить алгебраическую форму комплексного числа в виде тригонометрической и показательной записи. Комплексное число:
z = 4-4i
Решение
В первую очередь следует определить модуль комплексного числа:
(|z| = sqrt{4^2 + (-4)^2} = sqrt{16 + 16} = sqrt{32} = 4sqrt{2})
Далее целесообразно найти аргумент:
(varphi = arctg frac{b}{a} = arctg frac{-4}{4} = arctg (-1) = -frac{pi}{4})
В результате можно составить тригонометрическую форму комплексного числа, которое дано в условии задачи:
(z = 4sqrt{2}bigg(sin(-frac{pi}{4}) + isin(-frac{pi}{4}) bigg))
Таким же способом можно представить комплексное число в показательной форме:
(z = 4sqrt{2} e^{-frac{pi}{4}i})
Ответ: (z = 4sqrt{2}bigg(sin(-frac{pi}{4}) + isin(-frac{pi}{4}) bigg)), (z = 4sqrt{2} e^{-frac{pi}{4}i})
Задача 2
Требуется найти произведение пары комплексных чисел:
(z_1 = 3+i)
(z_2 = 2-3i)
Решение
В первую очередь следует записать выражение:
(z_1 cdot z_2 = (3+i) cdot (2-3i))
Затем целесообразно приступить к раскрытию скобок и перемножить множители поэлементно:
(z_1 cdot z_2 = (3+i) cdot (2-3i)= (3 cdot 2 + 3 cdot (-3i) + i cdot 2 + i cdot (-3i))
Полученное равенство можно упростить. Для этого нужно учитывать, что:
(i^2 = -1)
Запишем готовое выражение:
(6 – 9i + 2i + 3 = 9 – 7i)
Ответ: (z_1 cdot z_2 = 9 – 7i)
Задача 3
Даны комплексные числа:
(z_1 = 3e^{frac{pi}{2}i})
(z_2 = 2e^{frac{pi}{3}i})
Необходимо найти произведение этих комплексных чисел.
Решение
Вначале требуется записать выражение:
(z_1 cdot z_2 = 3e^{frac{pi}{2}i} cdot 2e^{frac{pi}{3}i})
Путем перегруппировки множителей и применения свойства степени:
(e^x cdot e^y = e^{x+y})
Преобразуем выражение:
(3 cdot 2 cdot e^{(frac{pi}{2} + frac{pi}{3})i} = 6e^{frac{5pi}{6}i})
Ответ: (z_1 cdot z_2 = 6e^{frac{5pi}{6}i})
Задача 4
Даны комплексные числа:
(z_1 = 2bigg (cosfrac{pi}{3} + isin frac{pi}{3} bigg ))
(z_2 = 4 bigg (cosfrac{pi}{4} + isin frac{pi}{4} bigg ))
Требуется найти произведение этих комплексных чисел.
Решение
Если необходимо умножить комплексные числа, представленные в тригонометрической форме, то целесообразно сложить их аргументы и перемножить модули:
(z_1 cdot z_2 = 2 cdot 4 cdot bigg ( cos (frac{pi}{3} + frac{pi}{4}) + isin (frac{pi}{3} + frac{pi}{4}) bigg ) = 8 bigg (cos frac{7}{12} + isin frac{7}{12} bigg ))
Ответ: (z_1 cdot z_2 = 8 bigg (cos frac{7}{12} + isin frac{7}{12} bigg ))
Задача 5
Необходимо выполнить несколько действий с комплексными числами:
(z_1 = 3+i)
(z_2 = 5-2i)
Требуется найти их сумму и разность.
Решение
В первую очередь следует сложить комплексные числа. В этом случае нужно найти сумму соответствующих мнимых частей комплексных чисел:
(z_1 + z_2 = (3+i) + (5-2i) = (3+5)+(i-2i) = 8 – i)
Аналогичным способом можно найти разность комплексных чисел:
(z_1 – z_2 = (3+i) – (5-2i) = (3-5)+(i+2i) = -2 + 3i)
Ответ: (z_1 + z_2 = 8 – i; z_1 – z_2 = -2 + 3i)
Задача 6
Даны комплексные числа:
(z_1 = 3+i)
(z_2 = 5-2i)
Необходимо найти их произведение и выполнить деление комплексных чисел.
Решение
Вначале нужно записать выражение:
(z_1 cdot z_2 = (3+i) cdot (5-2i))
Далее требуется раскрыть скобки и выполнить приведение подобных слагаемых с учетом, что:
(i^2 = -1)
Таким образом, получим:
(15 – 6i + 5i -2i^2 = 15 – i – 2cdot(-1) = 15 – i + 2 = 17 – i)
Затем необходимо поделить первое число на второе:
(frac{z_1}{z_2} = frac{3+i}{5-2i})
Принцип деления заключается в исключении комплексного числа, которое расположено в знаменателе. Для того чтобы получить результат, необходимо домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю. По итогу следует раскрыть все скобки:
(=frac{(3+i)(5+2i)}{(5-2i)(5+2i)} = frac{15 + 6i + 5i + 2i^2}{25 + 10i – 10i -4i^2} =)
(= frac{15 + 11i -2}{25 + 4} = frac{13 + 11i}{29})
Поделив числитель на 29, можно записать дробь алгебраическим способом:
(frac{z_1}{z_2} = frac{13}{29} + frac{11}{29}i)
Ответ: (z_1 cdot z_2 = 17 – i; frac{z_1}{z_2} = frac{13}{29} + frac{11}{29}i)
Задача 7
Дано комплексное число:
z = 3+3i
Данное число требуется возвести в степени:
- n=2
- n=7
Решение
В первом варианте:
(n = 2)
Комплексное число достаточно просто возвести в квадрат, если умножить его само на себя:
(z^2 = (3+3i)^2 = (3+3i)cdot (3+3i) =)
Применяя формулу, справедливую для умножения, следует раскрыть скобки и привести подобные:
(=9 + 9i + 3icdot 3 + 9i^2 = 9 + 18i – 9 = 18i)
В итоге получим:
(z^2 = (3+i)^2 = 18i)
Во втором варианте:
n = 7
Данный пример отличается повышенной сложностью вычислений, по сравнению с первым примером, где потребовалось лишь возвести комплексное число в квадрат. Если пойти стандартным путем и умножать комплексное число само на себя 7 раз, то вычисления могут занять неопределенное время. Упростить задачу легко, если применить к решению формулу Муавра. Данная закономерность справедлива в случае операций с комплексными числами, которые записаны в тригонометрической форме. По условиям задачи число представлено в алгебраическом виде. Поэтому в первую очередь целесообразно перевести его в тригонометрическую форму.
Требуется найти модуль:
(|z| = sqrt{3^2 + 3^2} = sqrt{9 + 9} = sqrt{18} = 3sqrt{2})
Далее следует вычислить аргумент:
(varphi = arctg frac{3}{3} = arctg(1) = frac{pi}{4})
Можно записать комплексное число в тригонометрической форме:
(z = 3sqrt{2}(cos frac{pi}{4} + isin frac{pi}{4}))
Возведение в степень n = 7 будет выглядеть следующим образом:
(z^7 = (3sqrt{2})^7 (cos frac{7pi}{4} + isin frac{7pi}{4}) =)
Представить наглядный ответ лучше в алгебраической форме. Для этого необходимо выполнить ряд манипуляций:
(=(3sqrt{2})^7 (frac{1}{sqrt{2}}-ifrac{1}{sqrt{2}}) = 3^7 sqrt{2}^7 (frac{1}{sqrt{2}}-ifrac{1}{sqrt{2}}) = 3^7 sqrt{2}^6 (1-i) = 3^7 cdot 8(1-i) =)
(= 2187 cdot 8 (1-i) = 17496(1-i))
Ответ: (z^2 = (3+i)^2 = 18i; ) (z^7 = 17496(1-i)).
Задача 8
Необходимо извлечь корень (sqrt[3]{-1}) над множеством (mathbb{C}.)
Решение
Следует преобразовать комплексное число в тригонометрическую форму. Для этого необходимо найти значение модуля и аргумента:
(|z| = sqrt{(-1)^2 + 0^2} = sqrt{1+0} = sqrt{1}=1)
(varphi = arctg frac{0}{-1} +pi = arctg 0 + pi = pi)
В результате получим выражение:
(z = (cos pi + isin pi))
С помощью формулы Муавра представляется возможным найти значение корней какой-либо степени:
(z^frac{1}{n} = r^frac{1}{n}bigg(cos frac{varphi + 2pi k}{n}+isin frac{varphi + 2pi k}{n}bigg))
(k=0,1,…,n-1)
По условию степень соответствует n = 3. Таким образом, согласно формуле:
k = 0,1,2
В результате получим:
(z_0 = sqrt[3]{1} (cos frac{pi}{3}+isin frac{pi}{3}) = frac{1}{2}+ifrac{sqrt{3}}{2})
(z_1 = sqrt[3]{1} (cos frac{3pi}{3}+isin frac{3pi}{3}) = -1)
(z_2 = sqrt[3]{1} (cos frac{5pi}{3}+isin frac{5pi}{3}) = frac{1}{2} – ifrac{sqrt{3}}{2})
Ответ: (z_0 = frac{1}{2}+ifrac{sqrt{3}}{2};) (z_1 = -1); (z_2 = frac{1}{2} – ifrac{sqrt{3}}{2})
Задача 9
Необходимо найти решение для квадратного уравнения:
(x^2 + 2x + 2 = 0) над (mathbb{C})
Решение
Найти ответ на данную задачу следует, используя общую формулу. Для начала необходимо вычислить дискриминант:
(D = b^2 – 4ac = 2^2 – 4cdot 1 cdot 2 = 4-8 = -4)
В результате получим:
(D=-4<0)
Однако на этом решение задачи не заканчивается. По условию требуется определить уравнение над комплексным множеством. Получение в итоге отрицательного дискриминанта говорит только о том, что в выражении отсутствуют вещественные корни. Это утверждение не отменяет наличие комплексных корней. Таким образом, следует их найти:
(x_{1,2} = frac{-bpm sqrt{D}}{2a} = frac{-2pm sqrt{-4}}{2} =)
Можно отметить, что:
(sqrt{-4} = 2sqrt{-1} = 2i)
Далее следует продолжить вычисления:
(= frac{-2 pm 2i}{2} = -1 pm i)
В результате получаются комплексно-сопряженные корни:
(x_1 = -1 – i)
(x_2 = -1 – i)
Ответ: (x_1 = -1 – i;) (x_2 = -1 – i)
