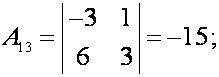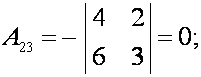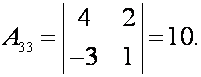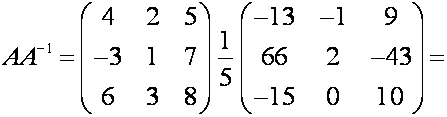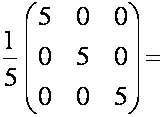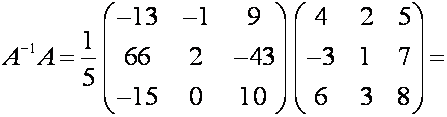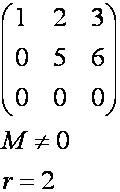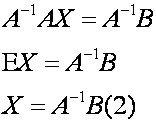Содержание:
- Матрицы – основные определения
- Действия над матрицами
- Транспонирование матриц
- Матрица и её определение
- Обратная матрица
- Ранг матрицы
- Матрицы и общие сведения о матрицах
- Перемножение матриц и его свойства
- Матрицы, действия над матрицами
- Определители
- Ранг матрицы и способы его вычисления
- Обратная матрица
- Линейная алгебра
- Числовые матрицы и действия над ними
- Определение матриц и некоторые их разновидности
- Действия над матрицами
- Системы линейных алгебраических уравнений. Основные определения
Матрицы – основные определения
Понятие матрицы впервые появилось в середине прошлого столетия в работах английских математиков У. Гамильтона (1805-1865) и А. Келли (1821-1895). В современной прикладной математике матрицы и связанные с ними понятия используются очень широко при решении самых разнообразных задач. В частности, использование матриц значительно упрощает решение сложных систем уравнений.
Матрицей называют прямоугольную таблицу с m строчек и n столбцов, составленную из чисел или любых объектов.
Ограничимся рассмотрением только действительных матриц, то есть матриц составленных из действительных чисел:
Числа 


Матрицы обозначают:
– круглыми скобками или двойными вертикальными черточками:
– большими буквами А, В, С:
– через сокращённую запись:
В зависимости от чисел 
– если 
– если 
– если 

– если n=1 (матрица типа 
– матрица типа 
(если рассмотреть следующие матрицы
то видим, что матрица А – квадратная, матрицы В, С – прямоугольные, матрица D – вектор-строчки, матрица М – вектор-столбец, матрица К – скаляр);
– если все элементы квадратной матрицы, кроме 

– если все ненулевые элементы диагональной матрицы равны 1, то её называют единичной матрицей и обозначают Е:
(если ввести символ Кронекера
тогда единичную матрицу можно записать в сокращённом виде 
– если все элементы матрицы – нули, то её называют нулевой матрицей
– матрицы вида:
называют треугольными (нижняя треугольная и верхняя треугольная).
Действия над матрицами
Над матрицами можно выполнять определённые действия, которые, по аналогии с числами, называют сложением, вычитанием, умножением. Также существуют действия, которые определены только для матриц. Введём правила действий над матрицами.
1. Матрицы считают равными, если они одного и того же типа, то есть имеют одинаковое количество строчек и столбцов, и соответствующие элементы равны, то есть матрицы 


2. Суммой двух матриц 


Свойства действий сложения матриц:
Пример.
а) Найти сумму матриц А и В.
Пусть
Тогда
б) Записать матрицу А как сумму матриц:
3. Аналогично вычисляют разность матриц:
4. Произведением матрицы 
Свойства действий умножения матрицы на число:
4. Матрица (-1)А=-А называется противоположной для А.
(Если матрицы отрицаются только знаками своих элементов, то их называют противоположными).
Пример.
5. Умножение матриц.
Если количество столбцов матрицы 


Элементы матрицы С находят по следующим правилам:
элемент 
Пример. Найти произведение матриц А и В, если
Решения. Согласно приведённого правила, что бы найти 
Свойства действий умножения матриц:
Внимание!
Если АВ=ВА, то матрицы называют коммутативными. Единичная матрица Е коммутативная с любой другой, то есть АЕ=ЕА=А и играет роль единицы при умножении.
Пример.
а) Найти произведение матриц АВ и ВА если:
Как видим,
б) Проверить существуют ли произведения АВ и ВА, если
Решение. Количество столбцов матрицы А совпадает с количеством строчек матрицы В, следовательно можно найти произведение матриц АВ:
Найти произведение матриц ВА невозможно, поскольку количество столбцов матрицы В не совпадает с количеством строчек матрицы А.
Транспонирование матриц
Если в матрице 



Пример.
Свойства действий транспонирования матриц:
– дважды транспонированная матрица равна начальной
– транспонированная матрица суммы равна сумме транспонированных матриц слагаемых
– транспонированная матрица произведения равна произведению транспонированных матриц сомножителей, взятому в обратном порядке
7. Матрица называется симметричной, если она совпадает со своей транспонированной матрицей, то есть если
Очевидно, что
– симметричная матрица обязательно квадратная;
– элементы, симметричные относительно основной диагонали равны;
– произведение 
Пример.
8. Две матрицы называют эквивалентными, если одна получена из другой с помощью элементарных преобразований.
Элементарными преобразованиями матриц называют следующие операции:
а) перестановка двух строк или столбцов матрицы;
б) умножение всех элементов любой строки (столбца) на одно и тоже число, отличное от нуля;
в) прибавление к элементам любой строки (столбца) соответствующих элементов другой строки (столбца), умножение на одно и тоже число.
Пример. Рассмотрим матрицы:
Матрицы А, В, С, D эквивалентны, поскольку: матрица В получена из матрицы А перестановкой первой и второй строки; матрица С получена из матрицы А через умножение всех элементов второй строки на число 5; матрица D получена из матрицы А с помощью замены третьей строки суммой удвоенных элементов первой строки с элементами третьей.
Матрица и её определение
Матрицей называется прямоугольная таблица из m × n чисел, содержащая m строк и n столбцов, взятая в квадратные или круглые скобки.
Или коротко [ аij ] (i = 1, 2, …, m; j = 1, 2, …, n).
В этом случае считают, что матрица имеет размерность m × n. Матрицы обозначают большими латинскими буквами А, В, С, Е, …
Числа aij называются элементами матрицы, где первый индекс i означает номер строки, а второй j — номер столбца. Если количество строк не равно количеству столбцов, то есть m ≠ n, то матрица называется прямоугольной, размерности m × n, а если m = n — квадратной. В этом случае число m = n называется порядком матрицы. Элементы квадратной матрицы, в которых i = j , образуют главную диагональ.
Квадратная матрица называется диагональной, если все ее элементы, кроме элементов главной диагонали, равны нулю, то есть
А =
Здесь отдельные элементы главной диагонали могут быть нулевыми.
Если в диагональной матрицы все элементы главной диагонали равны единице, то ее называют единичной матрицей. Она обозначается буквой Е и имеет вид:
Е =
Две матрицы А и В называются равными, если они имеют равное количество строк и столбцов и соответствующие элементы которых совпадают.
Матрица, в которой все элементы равны нулю, называется нуль-матрицей или нулевой. Ее обозначают буквой О.
Если матрица состоит только из одной строки, то она называется матрицей-строкой.
Матрица, состоящая из одного столбца, называется матрицей-столбцом.
Если в матрице А поменять строки на столбцы, а столбцы — на соответствующие строки, то полученную матрицу называют транспонированной и обозначают АT.
Если определитель квадратной матрицы равен нулю 

матрица вида
А =
а матрица
А =
Матрицу
A =
называют матрицей трапецеидального вида, если одновременно a11, a22, …, ajj отличные от нуля.
Пример 1. Заданs матрицы:
1) 

4) 

Здесь:
1) A — прямоугольная матрица размерности 2 × 3,
2) AT — транспонированная матрица к матрице A;
3) B — матрица-столбец;
4) C — матрица-строка;
5) D — диагональная матрица четвертого порядка;
6) О — нулевая матрица второго порядка.
Пример 2. Для изготовления пяти видов елочных украшений на фабрике тратится определенное количество материала. Конкретные цифровые данные указаны в таблице:

Решение. Указанные 15 чисел можно записать в виде прямоугольной матрицы размерности 3 × 5.
Каждые строка и столбец этой матрицы имеют определенный экономический смысл. Так, элементы первой строки указывают количество израсходованного стекла (в кг) на изготовление каждого из пяти видов елочных украшений. Числа второй строки указывают на потребности в количестве железных прищепок, необходимых для изготовления этих изделий. Элементы третьей строки характеризуют потребности в краске (в кг), которая используется при изготовлении соответствующего вида продукции.
Столбцы матрицы указывают на конкретное количество стекла, железных прищепок и краски, которые нужны на изготовление каждого из пяти видов елочных украшений. Так, например, элементы третьего столбца означают, что на изготовления украшений третьего вида нужно 2,8 кг стекла, 185 шт. железных прищепок и 1,4 кг краски.
Пример 3. Цены на некоторые виды товара характеризуются в гривнах, долларах США (USD), евро (EUR), английских фунтах (GBR) и рублях России (RUR).
Охарактеризовать содержание отдельных элементов таблицы.
Решение. Числовые данные этой таблицы можно записать в виде прямоугольной матрицы:
Каждый элемент имеет определенный экономический смысл. Например, элемент a21 значит, что женская кофта стоит 120 гр., элемент a32 означает, что спортивный костюм стоит 60,4 долларов США, а элемент a44 указывает на цену сапог в 52,4 английских фунтов. Элементы, например, первой строки определяют цены мужской куртки в различных денежных единицах: 1230 грн.; 232,1 долларов США; 238,8 евро; 155,3 английских фунтов; 7318,5 российских рублей.
Действия над матрицами
Пусть заданы две матрицы одной размерности m × n:
Определение. Суммой (разностью) двух матриц А и В называется такая матрица С размерности m × n, элементы которой сij равны алгебраической сумме (разности) соответствующих элементов aij и bij матриц А и В, то есть:
Из этого определения вытекают свойства:
1. A + B = B + A (коммутативность)
2. A + (B + C) = (A + B) + C (ассоциативность)
3. A ± 0 = 0 ± A = A (нейтральность)
4. (A ± B) T = AT ± BT (транспонированность).
Пример 1. Найти сумму и разность матриц.
Решение.
Пример 2. Три магазина “Продтовары” продают продукты в течение рабочего дня. Данные о торговле двух смен характеризуются таблицами:
I смена:
II смена
Найти данные о совокупной однодневной продаже товара каждым магазином.
Решение. Содержание этих таблиц можно записать в виде двух прямоугольных таблиц:
Сумма этих двух матриц характеризует данные о совокупную однодневную продажу каждого из видов продукции:
Определение. Произведением матрицы A на число k (или числa k на матрицу A) называется матрица, элементами которой являются произведения элементов матрицы A на число k:
A ⋅ k = k ⋅ A = k ⋅
Из определения произведения матрицы на число (или числа на матрицу) вытекает, что
1. k (mA) = (km) A;
2. (k + m) A = A (k + m) = kA + mA = Ak + Am;
3. λ (A + B) = λA + λB;
4. λA = 0, если λ = 0;
5. λA = 0, если A = 0.
Пример 3. Найти матрицу 4A, если матрица
A =
Решение. Согласно определению, получим:
4A =
Пример 4. Вычислить матрицу C = 2A – 4B, если
Решение. Использовав формулу умножения матрицы на число и формулу вычитания матриц, получим:
Пример 5. Предприятие производит три вида продукции А, В, С. Нормы затрат ресурсов на единицу продукции заданы в таблице:
Найти затраты ресурсов на изготовление 6 комплектов продукции.
Решение. Затраты ресурсов на производство единицы продукции можно представить в виде матрицы:
A =
Каждый элемент матрицы имеет определенный экономический смысл. Например, a21 = 2 означает, что на изготовление единицы вида продукции A расходуется 2 кг сырья Y; элемент a12 = 4 означает, что для изготовления единицы вида продукции B нужно потратить 4 шт. единиц сырья X.
Очевидно, что для нахождения затрат на изготовление 6 комплектов продукции, нужно вычислить матрицу 6 A, то есть
6A = 6
Замечание. Умножение матрицы на число отличается от умножения определителя на число. Матрицу умножают на число k, умножив все ее элементы на это число. Если определитель умножается на число k, то умножают на него все элементы одной какой-нибудь строки (или столбца).
Пусть матрица A содержит m строк и p столбцов, а матрица B имеет p строк и n столбцов.
Определение. Произведением матриц А и В называется матрица С, элементы сij которой равны сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B, то есть cij = ai1 b1j + ai2 b2j + … + aip bpj (i = 1, 2, …, m; j = 1, 2, …, n).
Произведение матрицы A на матрицу B обозначают АВ (A × B). Умножение матрицы A на матрицу B выполняется по следующей схеме:
Здесь элемент cij находят как скалярное произведение элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B.
Произведение матриц характеризуется свойствами:
1. AE = EA = A;
2. A⋅ 0 = 0 ⋅ A = 0;
3. AB ≠ BA (некоммутативность)
4. (AB) C = A (BC) (ассоциативность)
5. C (A+B) = CA + CB , (A+B) C= AC + BC (дистрибутивность)
6. (A ⋅ B)T = BT ⋅ AT.
Это свойство имеет место для произвольного числа множителей
7. Определитель произведения двух квадратных матриц равен произведению их определителей.
Пример 6. Найти произведения AB и BA, если
и убедиться, что AB ≠ BA.
Решение.
AB =
аналогично
BA =
Отсюда следует, что AB ≠ BA.
Пример 7. Найти произведение AB, если
Решение.
AB =
(Здесь произведение BA неопределенный, так как количество столбцов первой матрицы не равно количеству строк второй матрицы).
Пример 8. Найти произведение AE, если
A =
Решение.
AE =
(Легко убедиться, что имеет место и равенство EA = A).
Пример 9. Найти произведение AB, если
Решение. Произведение этих матриц возможен, поскольку количество столбцов матрицы A равно числу строк матрицы B.
Получим
AB =
Пример 10. Дана матрица:
A = 
Решение.
А2 = A ⋅ A =
=
Замечание 1. Произведение двух матриц может быть нулевой матрицей и тогда, когда каждая из матриц сомножителей не является нулевой.
Пример 11. Найти произведение матриц:
A ⋅ B =
=
Замечание 2. Произведением двух диагональных матриц одного и того же порядка является диагональная матрица того же порядка.
Пример 12. Найти произведение диагональных матриц:
Тогда
A⋅ B =
Для таких двух матриц произведение коммутативно:
A⋅ B = B⋅ A.
Пример 13. Торгово-строительная компания заключила договор на строительство 6 жилых домов, 3 офисных зданий и 4 домов отдыха. Цены на отдельные виды материалов следующие: кирпич — 32 у.е./тыс. шт., цемент — 300 у.е./т., лес круглый — 44 у.е./м3, оцинкованное железо — 6 у.е./м2, стекло — 5 у.е./м2.
Информация о количестве материалов на каждый вид строительства представлена в таблице:
Необходимо найти:
1) общее количество материалов;
2) цену материалов для каждого вида строения;
3) общую стоимость материалов.
Решение. 1) Запишем в виде матрицы А данные, которые характеризуют количество материалов на каждый вид строения, а данные об их ценах — в виде матрицы-столбца С.
Обозначим данные о договоре, заключенном на строительство сооружений через
Чтобы найти общее количество материалов для строительства, нужно перемножить матрицы В и А и найти произведение BA, то есть
BА =
Таким образом, для выполнения договора на строительство 6 жилых, 3 офисных и 4 домов отдыха компания должна приобрести 960 тыс. шт. кирпича; 116 т цемента; 506 м3 круглого леса; 2580 м2 оцинкованного железа и 1780 м2 стекла.
2) Чтобы найти общую стоимость материалов для каждого вида строительства, нужно перемножить матрицу А на матрицу-столбец С, составленную из чисел, характеризующих цены на соответствующие материалы:
Стоимость материалов для строительства жилого дома составляет 8860 у.е., для строительства офиса — 9348 у.е. и для строительства дома отдыха — 7740 у.е.
3) Для того, чтобы найти общую стоимость строительства согласно договора 6 жилых, 3 офисных и 4 домов отдыха нужно найти произведение матриц
Это же число можно получить еще так:
Таким образом, общая стоимость всего здания составляет 112 164 у.е.
Обратная матрица
Определение 1. Квадратная матрица А n-го порядка называется невырожденной (или неособенной), если ее определитель 
Определение 2. Квадратная матрица А n-го порядка называется вырожденной (или особенной), если ее определитель 
Определение 3. Матрица А-1 называется обратной матрицей для квадратной невырожденной матрицы А, если выполняются равенства AA-1 = A-1A = E.
ТЕОРЕМА. Если матрица А n-го порядка невырожденная, то для нее существует обратная матрица А-1.
Доказательство. Пусть задана квадратная невырожденная матрица А, то есть ее определитель 
A =
Рассмотрим другую матрицу
В =
где Aij — алгебраические дополнения элементов aij матрицы A.
Найдем произведение АВ:
АВ = 
Каждый элемент cij матрицы С равен
cij = ai1 Aj1 + ai2 Aj2 + … + ain Ajn.
Если i ≠ j, то есть выражение, которое является суммой произведений элементов i-й строки на алгебраические дополнения элементов другой строки определителя матрицы А. По теореме аннулирования эта сумма равна нулю.
Если i = j, то выражение cii = ai1Ai1 + ai2Ai2 + … + ainAin представляет собой сумму произведений элементов произвольной строки на соответствующие алгебраические дополнения этой строки определителя матрицы А. По теореме Лапласа такая величина равна определителю матрицы 
То есть матрица С имеет вид
С =
Если каждый элемент этой матрицы С разделить на 

Это доказывает теорему.
Итак, обратная матрица имеет вид:
Дадим схему нахождения обратной матрицы для заданной квадратной невырожденной матрицы.
1. Вычислим определитель матрицы 
2. Транспонирует матрицу A, то есть получаем матрицу:
3. Находим алгебраические дополнения каждого элемента транспонированной матрицы АТ и запишем их в виде матрицы АП:
4. Делим каждый элемент матрицы АП на определитель матрицы A, то есть умножим число

Матрица АП, которая составлена из алгебраических дополнений элементов транспонированной матрицы, называется присоединенной (или союзной) к матрице A.
Замечание 1. Присоединенная матрица будет иметь такой же вид AП, если транспонировать матрицу, составленную из алгебраических дополнений элементов матрицы A.
Пример 1. Найти обратную матрицу для матрицы
A =
и показать, что AA-1 = A-1A = E.
Решение. Определитель этой матрицы
Транспонированная матрица AТ имеет вид
Найдем алгебраические дополнения каждого элемента этой матрицы
Присоединена матрица будет такой:
Обратная матрица А-1 для заданной матрицы А имеет вид
Легко проверить, что
Пример 2. Найти обратную матрицу для матрицы
A =
Решение. Вычислим определитель этой матрицы:
Поскольку 
Замечание 2. Квадратная невырожденная матрица второго порядка 
Пример 3. Найти обратную матрицу к матрице
A =
Решение. Заданная квадратная матрица второго порядка невырожденная, поскольку ее определитель
поэтому обратная к матрице A существует, и ее можно найти по предыдущей формуле:
Ранг матрицы
Рассмотрим прямоугольную матрицу размерности m × n (1.2).
Определение. Рангом матрицы называется самый высокий порядок отличных от нуля миноров. Его обозначают через r (или rang (A)).
Из определения вытекают следующие свойства ранга матрицы.
1. Ранг матрицы равен нулю только тогда, когда матрица нулевая. В других случаях ранг матрицы равен некоторому положительному числу.
2. Ранг прямоугольной матрицы не превышает меньшего из двух чисел m и n, то есть 0 ≤ r ≤ min (m, n).
3. Для квадратной матрицы n-го порядка r = n только тогда, когда матрица невырожденная.
4. Если r <n то определитель матрицы равен нулю.
Рассмотрим два метода нахождения ранга матрицы.
Первый метод — метод окантовки — заключается в следующем. Если все миноры 1-го порядка, то есть элементы матрицы, равны нулю, то r = 0.
Если хотя бы один из миноров 1-го порядка не равен нулю, а все миноры 2-го порядка равны нулю, то r = 1. Аналогично, если минор 2-го порядка отличен от нуля, то исследуем миноры 3-го порядка. Таким способом находят минор k-го порядка и проверяют, не равны ли нулю миноры (k + 1)-го порядка. Если все миноры (k + 1)-го порядка равны нулю, то ранг матрицы A равен числу k. Такие миноры (k + 1)-го порядка, как правило, находят путем “окантовки” минора k-го порядка.
Пример 1. Найти ранг матрицы:
A = 
Решение. Все миноры 2-го порядка
равны нулю. Значит, ранг матрицы A равен единице: r (A) = 1.
Пример 2. Найти ранг матрицы:
A = 
Решение. Поскольку в матрице A есть миноры 1-го порядка, отличные от нуля, то ее ранг может быть равен единице. Минор 2-го порядка
но, например, минор
отличен от нуля. Окантовывая минор М2 , получим минор 3-го порядка (в матрице A показано пунктиром)
Рассмотрим миноры 4-го порядка, которые окантовывают данный минор М3
Все они равны нулю, потому, что первая и четвертая строки пропорциональны. Значит ранг матрицы A равен 3 (r = 3).
Рассмотрен способ нахождения ранга матрицы не всегда удобный, поскольку нужно вычислять большое количество миноров.
Второй метод определения ранга матрицы заключается в применении элементарных преобразований матрицы при сведении ее в диагональному виду.
Элементарными преобразованиями матрицы называются такие операции:
1) перестановка местами любых двух строк (или столбцов);
2) умножение каждого элемента произвольной строки (или столбца) на отличное от нуля число;
3) вычеркивания строки (или столбца), которая содержит все нулевые элементы;
4) прибавление к элементам произвольной строки (или столбца) соответствующих элементов другой строки (или столбца), умноженных на одно и тоже отличное от нуля число.
При таких элементарных преобразованиях ранг матрица не изменяется.
Две матрицы называются эквивалентными, если одна из них получается из второй с помощью конечного числа элементарных преобразований. Эквивалентные матрицы не равны между собой, зато они имеют одинаковые ранги.
Если матрицы A и B эквивалентны, то это записывают так: ⇔.
С помощью элементарных преобразований матрицу можно свести к диагональному виду. Ранг такой матрицы равен числу отличных от нуля диагональных элементов.
Пример 3. Найти ранг матрицы
A =
Решение.
1-й шаг. В заданной матрице переставим первую и вторую строки. На месте элемента а11 имеем элемент, равный 1.
2-й шаг. Добавим к элементам второй и третьей строк соответствующие элементы первой строки, умноженные на “–3”, а к элементам четвертой строки — соответствующие элементы первой, помноженные на “–5”.
3-й шаг. В первой строке можно автоматически записать все нули, кроме первого элемента “1”. Этого можно добиться, если к элементам 2-го, 3-го, 4-го и 5-го столбцов прибавить соответствующие элементы первого столбца, умноженные соответственно на числа: “–3”, “–3”, “–2”, “–5”.
4-й шаг. Добавим к элементам третьей и четвертой строк соответствующие элементы второй строки, умноженные на число “–2”.
5-й шаг. Во второй строке на месте элементов “–7”, “–3”, “–11” запишем нули (аналогично как на третьем шаге).
Рассмотренные шаги приведения матрицы A к диагональному виду покажем схематически так:
В последний матрице вычеркнем третью строчку и третий и четвертый столбцы, которые содержат все нулевые элементы:
A ⇔
Ранг этой матрицы равен трем, а значит и ранг матрицы A тоже равен 3, то есть r = 3.
Пример 4. Найти ранг матрицы:
A =
Решение.
1-й шаг. Из элементов второй строки вычтем соответствующие элементы первой и поменяем их местами.
2-й шаг. К элементам второй и третьей строк добавим соответствующие элементы первой, умноженные соответственно на “–3” и “–5”.
3-й шаг. Запишем в первой строке все нули, кроме первого элемента “1”.
4-й шаг. Вычтем соответствующие элементы второй и третьей строк.
5-й шаг. Подобно тому, как на 3-м шаге, получим во второй строке нули на месте элементов “9” и “–7”. Покажем рассмотрены шаги схематично.
Ранг последней матрицы равен двум, а значит и ранг матрицы A равен 2, то есть r = 2.
Матрицы и общие сведения о матрицах
Многие экономические задачи связаны с обработкой информации, которая представлена таблицами данных. Поэтому исключительно важную роль играет понятие матрицы.
Определение 1. Матрицей называется прямоугольная таблица, составленная из чисел. Размерностью (или размером) матрицы называется пара чисел 


Матрицы обозначают обычно большими латинскими буквами и записывают следующим образом:
Здесь 
Пример №22
Три завода выпускают пять различных видов продукции. Отчет о производстве за год в тыс. ед. представлен матрицей:
Где, например, 
Если число строк в матрице равно числу столбцов, т.е. размерность матрицы 








Если все элементы матрицы равны нулю, то матрица называется нулевой. Две матрицы одинаковой размерности равны, если равны их соответствующие элементы. Транспонированной матрицей к матрице А называют матрицу 
Размерность этой матрицы 5 x 3.
Над матрицами можно производить ряд операций. Матрицы одинаковой размерности можно складывать. Сложить две матрицы означает сложить их элементы, стоящие на одинаковых местах.
Матрицы можно умножать на число. Это означает, что все элементы матрицы надо умножить на данное число.
Пример №23
Если ассортимент продукции заводов из примера 1 не изменился в течение следующего года, то отчет о производстве за второй год тоже имеет вид матрицы:
Если же в течение третьего года производство каждого вида продукции на каждом заводе увеличилось на 20% по сравнению со вторым годом, то отчет за третий год будет таким:
Отчет же за три года будет выглядеть следующим образом:
Перемножение матриц и его свойства
Важнейшей операцией линейной алгебры является операция умножения матриц.
Пусть даны две матрицы: А – размерности 




Пример №24
Даны матрицы:

Произведение АВ оказалось возможным, т.к. число столбцов первой матрицы совпадает с числом строк второй и равно 3. В то же время, произведение ВА невозможно, т.к. теперь число столбцов первой матрицы равно 3, а число строк второй – 2 .
Приведем основные свойства умножения матриц.
1. Как известно, для любых чисел а и b выполняется свойство: ab = ba. Для матриц, в общем случае, АВ 

3. Произведение матриц подчиняется сочетательному закону: (АВ)С = А(ВС).
4. При перемножении матриц и транспонировании имеет место свойство: 
Пример №25
Предприятие выпускает три вида продукции 

Например, 


1) Требуется определить затраты сырья, необходимые для выполнения плана выпуска продукции: 




Решение:
1) Введем вектор-столбец плана выпуска продукции:
Рассчитаем затраты сырья, необходимые для выполнения этого плана:


Общие расходы на приобретения сырья, необходимые для выполнения плана:
Решая подобные задачи в дальнейшем, можно без рассуждений использовать формулу: 
Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:
Другие темы которые вам помогут понять высшую математику:
Матрицы, действия над матрицами
Матрицей 



Иногда матрица 


Матрица размерности 


Определитель, сложенный из элементов квадратной матрицы, называется определителем (детерминантом) матрицы и обозначают так:
Квадратная матрица, в которой на главной диагонали стоят единицы, а другие элементы равны нулю, называется единичной и обозначается
Если все элементы матрицы равны нулю, то такую матрицу называют нулевой и обозначают
Две матрицы 

Произведением числа 


Таким образом, чтобы умножить матрицу 

Суммой матриц 






Следует, складывание матриц приводится к складыванию соответственных элементов этих матриц.
Отнимание матриц обозначаются через действия, которые уже рассматривали:
то есть отнимание двух матриц приводится к отниманию их соответственных элементов. Очевидно, что отнимать можно только матрицы одинакового размера.
Произведением матрицы 







Для произведения матриц в общем случае справедливы соотношения:
(если же, обычно, существует каждый из слагаемых).
Операции складывания матриц имеют свойства:
4. Если 


Операции умножения матриц имеют такие свойства:
Квадратная матрица 


Если в матрице 

Решение примеров и задач:
Пример 1.1.
Для матриц:
найти матрицы
Решение.
Отметим, что
Матрицы дают возможность укоротить записи и использовать одинаковые соображения для разных объектов.
Задача 1.2
Предприятие выпускает продукцию двух видов, используя при этом сырье трех типов. Затраты сырья на производстве продукции задаются матрицей 





Решение . Запишем план выпуска продукции в виде матрицы 


Следует, для ежедневного выпуска продукции используется 930, 390 и 540 единиц сырья первого, второго и третьего типов соответственно.
Зададим стоимость единицы каждого типа сырья матрицы 
Заметим, что использование матриц а этой задаче привело к наглядности, упрощения и компактности вычислений.
Определители
Число 
Числа 




Аналогично, определителем третьего порядка называется число, что образуется из девяти чисел по такому правилу:
Эта сумма складывается из шести произведений. В каждое произведение входит по одному числу из каждого порядка и в то же время до одного элемента из каждого столбца. Знаки произведений легко запомнить воспользовавшись схемами:
Напомним основные свойства определителей третьего порядка
- Величина определителя не изменяется, если его ряды заменить столбцами, причем каждый ряд заменяют столбиком с тем же самым номером.
- Если в определителе поменять местами только два ряда (или два столбика), то определитель изменяет знак на противоположный, сохраняя абсолютное значение.
- Если определитель имеет два одинаковых столбца или два одинаковых ряда. то он равен нулю.
- Если определитель содержит два пропорциональных ряда (столбца), то значение его равно нулю. Если элементы некоторого ряда (столбца) равны нулю, то и сам определитель равен нулю.
- Если все элементы некоторого ряда (столбца) умножить на одно и то же число, то значение определителя так же умножиться на то же число. Это подразумевает, что общий множитель всех элементов ряда (столбца) можно вынести за знак определителя.
- Если каждый элемент некоторого ряда (столбца) является сумма двух слагаемых, то определитель можно предоставить в виде суммы двух определителей: в первом из них на месте каждой суммы остается только первое слагаемое, а во втором – только второе слагаемое (другие элементы определителя сохраняются).
- Значение определителя не изменяется, если к элементами некоторого ряда (столбца) прибавить соответственные элементы другого параллельного ряда (столбца), умножив их поочередно на одно и то же число.
Если в определителе 








Еще одно свойство определителя.
8. Определитель равен сумме произведений элементов некоторого ряда (столбца) на соответственные их алгебраические дополнения.
Если по этому правилу раскрыть определитель 
Решение примеров:
Пример 1.11.
Вычислить определитель
Решение. Сделаем этого двумя способами:
а) Вычислим определитель раскладывая его по элементам третьего порядка (используем свойство 8).
б) В этом случае, образуем нули во втором порядке (или в нем есть единица или же выбирается тот ряд ( или столбец), в котором пропорциональные элементы). Для этого к элементам второго столбца прибавим элементы первого, предварительно умножив их в уме на 2, потом к элементам третьего столбца прибавим элементы первого столбца, умноженные перед этим на – 3. Значение определителя при этом, согласно со свойствами 7, не измениться.
Пример 1.12
Вычислить определитель третьего порядка
Решение. Преобразуем определитель таким образом, чтобы ниже главной диагонали все элементы его стали нулями. Тогда из определитель равен произведению диагональных элементов.
Найдем разницу первого и второго рядов, а потом умножим первый порядок на 2 и отнимем от третьего порядка. Получим определитель
Отняв второй порядок от третьего, получим:
Пример 1.13
Вычислить определитель четвертого порядка
Решение. Сложим первый ряд к второму и четвертому, получим определитель
Переставим первый и третий столбцы:
Сложим второй порядок к третьему и четвертому ряду и вынесем общий множитель элементов третьего и четвертого ряда:
Отняв третий ряд от четвертого, получим:
Ранг матрицы и способы его вычисления
Матрица имеет ранг 


Пример 1.29
Найти ранг матрицы
Решение. Эта матрица третьего порядка, следует, ее ранг не может быть больше трех. Определитель третьего порядка равен нулю:
но существует минор второго порядка 

Пример 1.30
Найти ранг матрицы
Решение. Эта матрица имеет размер 

Элементарными преобразованиями матрицы называют такие ее преобразования:
- Транспортировка, то есть замена каждого ряда столбцом с тем же номером и наоборот.
- Перестановка двух рядов или двух столбиков.
- Умножение всех элементов ряда или столбца на любое число не равное нулю.
- Складывание всех элементов ряда или столбца соответственных элементов параллельного ряда, умножено на одно и то же число.
Матрицы полученные одна из другой элементарными преобразованиями, называются эквивалентными. Эквиваленты матрицы не равны одна другой, но при элементарных преобразований матриц ее ранг не изменяется.
Пример 1.31.
Найти ранг матрицы
Решение. Разделим элементы первого ряда на 2, получим эквивалентную матрицу ( ранг этой матрицы равен рангу исходной):
Отнимем от третьего ряда второй, умноженный на 3.
При нахождении ранга матрицы, как правило, нужно вычислить большое количество определителей. Чтобы облегчить этот процесс, используют специальные способы. Ранг можно вычислить, например, так: над матрицей последовательно выполняют элементарные преобразования до тех пор, пока в каждом ряде и каждом столбце стоит не более одного ненулевого элемента. Тогда ранг матрицы будет равен числу этих ненулевых элементов.
Пример 1.32
Найти ранг матрицы
Решение. Преобразуем в нули все элементы первого ряда, кроме первого элемента, для чего первый и второй столбец оставим без изменения, вместо третьего столбца запишем разницу между первым и третьим столбцом, а вместо четвертого – сумму четвертого и первого, умноженного на (-2).
Далее без изменения оставим первый и третий столбцы, вместо второго запишем разницу между третьим и вторым столбцами, а вместо четвертого – сумму четвертого столбца и третьего, умноженного на -4.
И наконец, остаточный столбик преобразуем на нули. Вместо него запишем разницу между вторым и четвертым столбцами.
Полученная матрица содержит три ненулевых элемента, то есть
Обратная матрица
Матрица 

Отсюда вытекает. что обратную матрицу могут иметь только квадратные матрицы.
То есть обратная матрица складывается из алгебраических дополнений к элементам рядов, которые записываются в столбцы с соответственными номерами, а потом каждое алгебраическое дополнение делится на детерминант матрицы.
Обратную матрицу можно использовать при решение системы линейных алгебраических уравнений матричным способом: матрицу – столбец 


Решение примеров:
Пример 1.45
Найти матрицу 
Решение. Вычислим определитель матрицы 
Обратная матрица имеет вид:
Матрица 
Пример 1.46
Найти матрицу 
Решение. Поскольку определитель матрицы
то для матрицы 


тогда
Легко можно определить, что 
Задача 1.47
В цеху предприятия изготовляют две модели женской одежды. На изготовление первой модели тратят 2 м ткани, для изготовления второй – 3 м. При этом на изготовление этих моделей тратится 4 и 5 часов соответственно. Известно, что месячный запас ткани 100 м, а рабочее время ограниченно – 190 часов. Сложить такой план месячного изготовления этих моделей одежды, при котором полностью используются ресурсы (ткань и время).
Решение. Обозначим через 

Решим эту систему матричным способом. Запишем ее в матричном виде:
где
Для матрицы 

Тогда
Решением системы является
Следует, для использования ресурсов еженедельно нужно изготовить 25 единиц первой и 10 единиц второй модели одежды.
Заметим, что при решении экономических задач удобно использовать матричный способ. Вычислив один раз обратную матрицу и изменив ограничения на ресурсы (ежедневные, ежемесячные, ежегодные и так далее), получим план для выпуска продукции.
Линейная алгебра
Линейная алгебра как самостоятельная математическая дисциплина начала формироваться в XVIII веке, когда в работах немецкого математика Г.Ф.Лейбница и швейцарского математика Г. Крамера впервые было введено понятие определителя (детерминанта) и приведены общие формулы для определения решений систем линейных уравнений. Позже английскими математиками А. Келли и Дж. Сильвестром было введено понятие матрицы и заложены основы матричного исчисления, что является аппаратом для компактной записи и анализа систем уравнений. Именно эти понятия линейной алгебры широко используются в прикладных задачах экономики. Так, для характеристики параметров производственных или бизнес-процессов выходные данные предоставляются в виде матрицы размером
Методы линейной алгебры также применяются для обоснования управленческих решений, при обработке результатов наблюдений и тому подобное. Например, решение задач оптимизации планов работы предприятия, изучение спроса, планирование транспортных артерий можно свести к решению систем 

После изучения данной темы вы сможете:
• использовать числовые матрицы для формирования и анализа таблиц исходных данных в экономике;
• использование систем линейных уравнений при разработке линейных экономико-математических моделей;
• применять понятие линейных векторных пространств с целью геометрической интерпретации экономических задач;
• иметь представление о собственных числа и собственные векторы квадратных матриц в аналитических задачах экономики;
• использовать собственные числа и собственные векторы квадратных матриц при разработке экономико-математических моделей;
• применять модель межотраслевого баланса (многоотраслевой экономики) для решения реальных задач экономики;
• строить линейную модель обмена (модель международной торговли) при решении конкретных задач.
Числовые матрицы и действия над ними
Для чего нужны матрицы? Например для решения задачи об использовании сырья:
Рассмотрим реальную задачу планирования выпуска промышленной продукции на примере отдельного предприятия, производящего электродвигатели как общего, так и специального назначения. Кроме электродвигателей, завод производит сложные изделия бытового и сельскохозяйственного назначения. Сформулируем задачу о распределении материальных ресурсов при изготовлении четырех основных видов продукции электродвигателей AИP 80, AИP 90, АИР 100 и электрических насосов БЦ 1,1-20.
Основными факторами производства являются сырье, полуфабрикаты, которые доставляются на предприятие, топливо и транспорт. Однако их объемы имеют определенные ограничения. Удельные затраты (затраты на изготовление единицы изделия каждого вида) и общие объемы имеющихся ресурсов (в соответствующих единицах) приведены в таблице 1.1.
Удельные затраты материальных ресурсов и объемы их имеющихся запасов Таблица 1.1
Задача состоит в построении такого плана производства основных видов продукции, который бы обеспечил полное использование материальных ресурсов, которые имеет в наличии предприятие. Составим математическую модель задачи, то есть опишем поставленную задачу с помощью математической символики. Введем обозначения величин, которые являются числовыми характеристиками плана производства. Пусть, 




Мы получили систему линейных уравнений – уравнений первой степени относительно неизвестных, – которая и является математической моделью задачи о полном использовании материальных ресурсов. Такие системы известны со школьного курса математики, но методы иx решения и, тем более, исследования для произвольного конечного числа уравнений и неизвестных в школьном курсе не изучаются (методы решения этой системы будут приведены позднее).
В общем случае задача о полном использовании ресурсов формулируется так: пусть предприятие выпускает продукцию 

Задача о полном использовании ресурсов Таблица 1.2
Необходимо определить количество продукции каждого из наименований, которое надо выработать предприятию, чтобы имеющиеся ресурсы были полностью использованы.
Составим математическую модель задачи. Пусть 
Таким образом, нахождение решения задачи о полном использовании сырья сведено к решению системы 

Определение матриц и некоторые их разновидности
Числовой матрицей размером 



Матрицы обозначают большими буквами латинского алфавита 




Каждый элемент 



В общем случае элементами матрицы могут быть другие объекты: векторы, функции, иx производные и т. д.
В теоретических исследованиях при ссылке на матрицу определенного размера обычно применяют обозначения
Матрица 





Матрицей-строкой называется матрица размера 
Матрицей-столбцом называется матрица размера 
Если рассматривается матрица-строка (или матрица-столбец), то для ее элементов номер строки (или, соответственно, номер столбца) указывать не надо.
Матрица может состоять даже из одного элемента.
Нулевой матрицей называют матрицу, все элементы которой равны нулю. Она обозначается буквой 
Главной диагональю квадратной матрицы 



Симметричной называется квадратная матрица, в которой все элементы, расположенные симметрично относительно главной диагонали, есть попарно равными между собой. То есть для произвольных ее элементов при 
Если элементы каждой строки матрицы 


а сама операция перехода от матрицы 


Верхней (нижней) треугольной матрицей называется ненулевая квадратная матрица, все элементы которой, расположенные ниже (выше) главной диагонали, равны нулю.
Диагональной матрицей называется квадратная матрица, в которой все элементы, кроме, возможно, элементов главной диагонали, равны нулю. Такую матрицу целесообразно задавать перечнем ее диагональных элементов, указывая только один индекс:
Единичной матрицей называется диагональная матрица, все элементы главной диагонали которой равны единице:
Обозначения единичной матрицы удобно сопровождать индексом, который указывает на ее порядок, следовательно, единичная матрица размера 

Символические определения основных типов матриц и их примеры приведены в таблице 1.3.
Основные разновидности матриц Таблица 1.3
Действия над матрицами
Элементы двух матриц одинакового размера, которые стоят на пересечении одних и тех же (по номеру) строк и столбцов называются соответствующими.
Матрицы 

Над матрицами определены следующие действия (операции): умножение матрицы на скаляр, добавление матриц, умножение матриц. Рассмотрим определение и свойства этих операций.
1. Произведением матрицы 




Если 

2. Суммой матриц 



Согласно с определением нулевой матрицы имеем:
Последствие: разницу двух матриц 


Найдем матрицу 
Поскольку заданные матрицы имеют одинаковый размер, то указанные действия можно выполнить. Следовательно,
Операции сложения матриц и умножения матрицы на скаляр называются линейными операциями над матрицами. Эти операции сводятся к соответствующим арифметических действий над числами и имеют те же свойства, что и операции над числами. Приведем эти свойства:



Произведением матрицы 






С (1.5) следует правило, называют правилом 

чтобы вычислить элемент 





Найдем за этим правилом произведение 
Количество столбцов матрицы 






Понятно, что для приведенных матриц не существует произведение матрицы 



Из определения произведения матриц вытекают следующие свойства операций умножения матриц.
1. Для того, чтобы две матрицы 








2. Если матрицы 






3. Для произведения матриц выполняется ассоциативный закон, а именно:
Приведем свойства, присущие действиям над матрицами, в виде таблицы:
Свойства операций над матрицами Таблица 1.4
Системы линейных алгебраических уравнений. Основные определения
Построение математических моделей процессов и явлений во всех сферах деятельности человека требует разработок соответствующего математичноrо аппарата, и системы линейных алгебраических уравнений является его важной составляющей. Эти уравнения играют важную роль и при построении математических моделей экономических процессов.
Системой линейных алгебраических уравнений (СЛАУ) называется совокупность 


где 




Краткая запись системы уравнений (1.6) можно получить с помощью символа 
Вернемся. к примеру, в котором рассматривалась математическая модель задачи об использовании. ресурсов. Если записать удельные затраты ресурсов как матрицу 


Приведем еще один способ представления системы уравнений с помощью матриц. Пусть матрица-столбец 





Расходы ресурсов на изготовление 




Матрицу 



Понятно, что операции над строками расширенно и матрицы являются операциями над соответствующими уравнениями системы.
Решением системы уравнений называется такой набор чисел 

Система линейных алгебраических уравнений называется совместной, если она имеет по крайней мере одно решение, и несовместимой, если она не имеет никакого решения. Совместимую систему уравнений называют определенной, если она имеет единственное решение, и неопределенной, если количество решений более одного.
Система линейных уравнений называется неоднородной, если хотя бы один элемент матрицы-столбца свободных членов отличается от нуля. Если все элементы 
где 


Лекции:
- Расстояние между скрещивающимися прямыми
- Нахождение промежутков возрастания и убывания функции
- Изменить порядок интегрирования
- Производная функции заданной неявно
- Методы определенного интегрирования
- Обыкновенные дифференциальные уравнения
- Частные производные. Частные дифференциалы
- Теорема об остатке
- Найти частные производные
- Уравнения с двумя переменными
Given an N * N matrix, the task is to find the product of the elements of left and right diagonal.
Examples:
Input: arr[] = 1 2 3 4
5 6 7 8
9 7 4 2
2 2 2 1
Output: 9408
Explanation:
Product of left diagonal = 1 * 4 * 6 * 1 = 24
Product of right diagonal = 4 * 7 * 7 * 2 = 392
Total product = 24 * 392 = 9408Input: arr[] = 2 1 2 1 2
1 2 1 2 1
2 1 2 1 2
1 2 1 2 1
2 1 2 1 2
Output : 512
Explanation:
Product of left diagonal = 2 * 2 * 2 * 2 * 2 = 32
Product of right diagonal = 2 * 2 * 2 * 2 * 2 = 32
But we have a common element in this case so
Total product = (32 * 32)/2 = 512
Approach:
- We need to find out the principal diagonal and secondary diagonal elements of the matrix. Please refer to this article for this [ Program to print the Diagonals of a Matrix ]
- In this method, we use one loop i.e. a loop for calculating product of both the principal and secondary diagonals
- Divide the answer by middle element for matrix of odd size
Below is the implementation of the above approach:
CPP
#include <bits/stdc++.h>
using namespace std;
int productDiagonals(int arr[][100], int n)
{
int product = 1;
for (int i = 0; i < n; i++) {
product = product * arr[i][i];
product = product * arr[i][n - i - 1];
}
if (n % 2 == 1) {
product = product / arr[n / 2][n / 2];
}
return product;
}
int main()
{
int arr1[100][100] = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 7, 4, 2 },
{ 2, 2, 2, 1 } };
cout << productDiagonals(arr1, 4) << endl;
int arr2[100][100] = { { 2, 1, 2, 1, 2 },
{ 1, 2, 1, 2, 1 },
{ 2, 1, 2, 1, 2 },
{ 1, 2, 1, 2, 1 },
{ 2, 1, 2, 1, 2 } };
cout << productDiagonals(arr2, 5) << endl;
return 0;
}
Java
import java.util.*;
class GFG
{
static int productDiagonals(int arr[][], int n)
{
int product = 1;
for (int i = 0; i < n; i++)
{
product = product * arr[i][i];
product = product * arr[i][n - i - 1];
}
if (n % 2 == 1)
{
product = product / arr[n / 2][n / 2];
}
return product;
}
public static void main(String[] args)
{
int arr1[][] = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 7, 4, 2 },
{ 2, 2, 2, 1 } };
System.out.print(productDiagonals(arr1, 4) + "n");
int arr2[][] = { { 2, 1, 2, 1, 2 },
{ 1, 2, 1, 2, 1 },
{ 2, 1, 2, 1, 2 },
{ 1, 2, 1, 2, 1 },
{ 2, 1, 2, 1, 2 } };
System.out.print(productDiagonals(arr2, 5) + "n");
}
}
Python3
def productDiagonals(arr, n):
product = 1;
for i in range(n):
product = product * arr[i][i];
product = product * arr[i][n - i - 1];
if (n % 2 == 1):
product = product // arr[n // 2][n // 2];
return product;
if __name__ == '__main__':
arr1 = [[ 1, 2, 3, 4 ],[ 5, 6, 7, 8 ],
[ 9, 7, 4, 2 ],[ 2, 2, 2, 1 ]];
print(productDiagonals(arr1, 4));
arr2 = [[ 2, 1, 2, 1, 2 ],[ 1, 2, 1, 2, 1 ],
[ 2, 1, 2, 1, 2 ],[ 1, 2, 1, 2, 1 ],
[ 2, 1, 2, 1, 2 ]];
print(productDiagonals(arr2, 5));
C#
using System;
class GFG
{
static int productDiagonals(int [,]arr, int n)
{
int product = 1;
for (int i = 0; i < n; i++)
{
product = product * arr[i,i];
product = product * arr[i,n - i - 1];
}
if (n % 2 == 1)
{
product = product / arr[n / 2,n / 2];
}
return product;
}
public static void Main(String[] args)
{
int [,]arr1 = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 7, 4, 2 },
{ 2, 2, 2, 1 } };
Console.Write(productDiagonals(arr1, 4) + "n");
int [,]arr2 = { { 2, 1, 2, 1, 2 },
{ 1, 2, 1, 2, 1 },
{ 2, 1, 2, 1, 2 },
{ 1, 2, 1, 2, 1 },
{ 2, 1, 2, 1, 2 } };
Console.Write(productDiagonals(arr2, 5) + "n");
}
}
Javascript
<script>
function productDiagonals(arr, n)
{
var product = 1;
for (var i = 0; i < n; i++) {
product = product * arr[i][i];
product = product * arr[i][n - i - 1];
}
if (n % 2 == 1) {
product =
product / arr[parseInt(n / 2)][parseInt(n / 2)];
}
return product;
}
var arr1 = [ [ 1, 2, 3, 4 ],
[ 5, 6, 7, 8 ],
[ 9, 7, 4, 2 ],
[ 2, 2, 2, 1 ] ];
document.write( productDiagonals(arr1, 4) + "<br>");
var arr2 = [ [ 2, 1, 2, 1, 2 ],
[ 1, 2, 1, 2, 1 ],
[ 2, 1, 2, 1, 2 ],
[ 1, 2, 1, 2, 1 ],
[ 2, 1, 2, 1, 2 ] ];
document.write( productDiagonals(arr2, 5));
</script>
Time Complexity: O(N), traversing a loop from 0 to N.
Auxiliary Space: O(1) because constant extra space is required.
Last Updated :
30 Aug, 2022
Like Article
Save Article
Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц. Элементы новой матрицы получаются из элементов старых матриц в соответствии с правилами, проиллюстрированными ниже.
Матрицы 



Матрицы обладают многими алгебраическими свойствами умножения, присущими обычным числам, за исключением коммутативности.
Для квадратных матриц, помимо умножения, может быть введена операция возведения матрицы в степень и обратная матрица
.
Тогда как матрицы используются для описания, в частности, преобразований математических пространств (поворот, отражение, растяжение и другие), произведение матриц будет описывать композицию преобразований.
Определение[править | править код]
Пусть даны две прямоугольные матрицы 



Тогда матрица 

в которой:
называется их произведением.
Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что матрицы согласованы. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.
Таким образом, из существования произведения 

Иллюстрация[править | править код]
Произведение матриц AB состоит из всех возможных комбинаций скалярных произведений вектор-строк матрицы A и вектор-столбцов матрицы B. Элемент матрицы AB с индексами i, j есть скалярное произведение i-ой вектор-строки матрицы A и j-го вектор-столбца матрицы B.
Иллюстрация справа демонстрирует вычисление произведения двух матриц A и B, она показывает как каждые пересечения в произведении матриц соответствуют строкам матрицы A и столбцам матрицы B. Размер результирующей матрицы всегда максимально возможный, то есть для каждой строки матрицы A и столбца матрицы B есть всегда соответствующее пересечение в произведении матрицы.
Значения на пересечениях, отмеченных кружочками, будут:

В общем случае, произведение матриц не является коммутативной операцией. К примеру:
Элемент 
Первая координата в обозначении матрицы обозначает строку, вторая координата — столбец; этот порядок используют как при индексации, так и при обозначении размера. Элемент 




Это объясняет почему ширина и высота умножаемых матриц должны совпадать: в противном случае скалярное произведение не определено.
Обсуждение[править | править код]
Увидеть причины описанного правила матричного умножения легче всего, рассмотрев умножение вектора на матрицу.
Последнее естественно вводится исходя из того, что при разложении векторов по базису действие (любого) линейного оператора A даёт выражение компонент вектора v’ = Av:
То есть линейный оператор оказывается представлен матрицей, векторы — векторами-столбцами, а действие оператора на вектор — матричным умножением вектора-столбца слева на матрицу оператора (это частный случай матричного умножения, когда одна из матриц — вектор-столбец — имеет размер 
(Равно переход к любому новому базису при смене координат представляется полностью аналогичным выражением, только 

Рассмотрев последовательное действие на вектор двух операторов: сначала A, а потом B (или преобразование базиса A, а затем преобразование базиса B), дважды применив нашу формулу, получим:
откуда видно, что композиции BA действия линейных операторов A и B (или аналогичной композиции преобразований базиса) соответствует матрица, вычисляемая по правилу произведения соответствующих матриц:
Определённое таким образом произведение матриц оказывается совершенно естественным и очевидно полезным (даёт простой и универсальный способ вычисления композиций произвольного количества линейных преобразований).
Свойства[править | править код]
Сочетательное свойство, ассоциативность:
Распределительное свойство, дистрибутивность относительно сложения:
.
Произведение матрицы на единичную матрицу 
Произведение матрицы на нулевую матрицу 
Если 

Умножение матриц в общем случае некоммутативно:
Если 


Простейшие примеры коммутирующих матриц:
- любая квадратная матрица — с самой собой:
(возведение матрицы в квадрат);
- любая квадратная матрица — с единичной матрицей того же порядка:
;
- любая квадратная матрица — с нулевой матрицей того же порядка:
;
- любая невырожденная квадратная матрица — со своей обратной матрицей:
.
Определитель и след произведения не зависят от порядка умножения матриц:
Обратная матрица[править | править код]
Квадратная матрица 

В противном случае матрица 
Матрица ![A=left[a_{ik}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a01bb07c21110e6da874868082f2529ab616d070)

![det A=det left[a_{ik}right]neq 0;](https://wikimedia.org/api/rest_v1/media/math/render/svg/94de2af97d80f9a3716cc7c115bfd303e550d869)


где 

![det left[a_{ik}right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ee0470c90d16ae67c8c58ae2f2854741f59b156)
Алгоритмы быстрого перемножения матриц[править | править код]
Сложность вычисления произведения матриц по определению составляет 
- Алгоритм Штрассена (1969)
- Первый алгоритм быстрого умножения больших матриц был разработан Фолькером Штрассеном[2] в 1969 году. В основе алгоритма лежит рекурсивное разбиение матриц на блоки 2Х2. Штрассен доказал, что матрицы 2Х2 можно некоммутативно перемножить с помощью семи умножений, поэтому на каждом этапе рекурсии выполняется семь умножений вместо восьми. В результате асимптотическая сложность этого алгоритма составляет
. Недостатком данного метода является бо́льшая сложность программирования по сравнению со стандартным алгоритмом, слабая численная устойчивость и больший объём используемой памяти. Разработан ряд алгоритмов на основе метода Штрассена, которые улучшают численную устойчивость, скорость по константе и другие его характеристики. Тем не менее, в силу простоты алгоритм Штрассена остаётся одним из практических алгоритмов умножения больших матриц. Штрассен также выдвинул следующую гипотезу Штрассена: для сколь угодно малого
существует алгоритм, при достаточно больших натуральных n гарантирующий перемножение двух матриц размера
за
операций.
- Дальнейшие улучшения показателя степени ω для скорости матричного умножения
Хронология улучшения оценок показателя степени ω для вычислительной сложности матричного умножения 
- В дальнейшем оценки скорости умножения больших матриц многократно улучшались. Однако эти алгоритмы носили теоретический, в основном приближённый характер. В силу неустойчивости алгоритмов приближённого умножения в настоящее время они не используются на практике.
- Алгоритм Пана (1978)
- В 1978 году Пан[3] предложил свой метод умножения матриц, сложность которого составила Θ(n2.78041).
- Алгоритм Бини (1979)
- В 1979 году группа итальянских учёных во главе с Бини[4] разработала алгоритм умножения матриц с использованием тензоров. Его сложность составляет Θ(n2.7799).
- Алгоритмы Шёнхаге (1981)
- В 1981 году Шёнхаге[5] представил метод, работающий со скоростью Θ(n2.695). Оценка получена с помощью подхода, названного частичным матричным умножением. Позже ему удалось получить оценку Θ(n2.6087).
- Затем Шёнхаге на базе метода прямых сумм получил оценку сложности Θ(n2.548). Романи сумел понизить оценку до Θ(n2.5166), а Пан — до Θ(n2.5161).
- Алгоритм Копперсмита — Винограда (1990)
- В 1990 году Копперсмит и Виноград[6] опубликовали алгоритм, асимптотическая сложность которого составляла O(n2.3755). Этот алгоритм использует идеи, схожие с алгоритмом Штрассена. На сегодняшний день модификации алгоритма Копперсмита-Винограда являются наиболее асимптотически быстрыми. В последней модификации Джоша Алмана и Вирджинии Вильямс (2020) алгоритм умножает матрицы со скоростью O(n2.3728596)[7]. Тот факт, что последние полученные улучшения ничтожны, позволяет говорить о существовании «барьера Копперсмита-Винограда» в асимптотических оценках скорости алгоритмов. Алгоритм Копперсмита-Винограда эффективен только на матрицах астрономического размера и на практике применяться не может.
- Связь с теорией групп (2003)
- В 2003 году Кох и др. рассмотрели в своих работах[8] алгоритмы Штрассена и Копперсмита-Винограда в контексте теории групп. Они показали, что гипотеза Штрассена справедлива (т.е. минимальная сложность ограничена
для любого
) , если выполняется одна из гипотез теории групп[9].
Степени матриц[править | править код]
Квадратные матрицы можно многократно умножать сами на себя так же, как обычные числа, так как у них одинаковое число строк и столбцов.
Такое последовательное умножение можно назвать возведением матрицы в степень — это будет частный случай обычного умножения нескольких матриц. У прямоугольных матриц число строк и столбцов разное, поэтому их никогда нельзя возводить в степень.
Матрица A размерности n × n, возведённая в степень, определяется формулой
и обладает следующими свойствами (λ — некоторый скаляр):
Нулевая степень:
где E – единичная матрица. Это аналог того факта, что нулевая степень любого числа равна единице.
Умножение на скаляр:
Определитель:
Наиболее простой способ вычисления степени матрицы — это умножать k раз матрицу A на результат предыдущего умножения, начиная с единичной матрицы, как это часто делают для скаляров.
Для диагонализируемых матриц существует лучший метод, основанный на использовании спектрального разложения матрицы A.
Ещё один метод, основанный на теореме Гамильтона — Кэли, строит более эффективное выражение для Ak, в котором в требуемую степень возводится скаляр, а не вся матрица.
Особый случай составляют диагональные матрицы.
Так как произведение диагональных матриц сводится к умножению соответствующих диагональных элементов, то k-ая степень диагональной матрицы A состоит из элементов, возведённых в требуемую степень:
Таким образом, возвести диагональную матрицу в степень несложно.
При возведении произвольной матрицы (не обязательно диагональной) в степень часто полезным оказывается использовать сначала свойства диагонализируемых матриц.
Используя умножение матриц и возведение матриц в степень, можно определить другие операции над матрицами. Например, матричная экспонента может быть определена через степенной ряд, матричный логарифм — как обратная к матричной экспоненте функция и так далее.
См. также[править | править код]
- Произведение Кронекера
- Произведение Адамара
Литература[править | править код]
- Корн Г., Корн Т. Алгебра матриц и матричное исчисление // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 392—394.
Примечания[править | править код]
- ↑ Кибернетический сборник. Новая серия. Вып. 25. Сб. статей 1983 — 1985 гг.: Пер. с англ. — М.: Мир, 1988 — В.Б. Алекссев. Сложность умножения матриц. Обзор.
- ↑ Strassen V. Gaussian Elimination is not Optimal (англ.) // Numerische Mathematik / F. Brezzi — Springer Science+Business Media, 1969. — Vol. 13, 13, Iss. 4. — P. 354—356, 354—356. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF02165411
- ↑ Pan V. Ya, Strassen’s algorithm is not optimal — trilinear technique of aggregating uniting and canceling for constructing fast algorithms for matrix operations. — Proc. 19th Annual Symposium on Foundations of Computer Science, Ann Arbor, Mich., 1978
- ↑ Bini D., Capovani M., Lotti G., Romani F. —
complexity for approximate matrix multiplication. — Inform. Process. Lett., 1979
- ↑ Schonhage A. Partial and total matrix multiplication. — SIAM J. Comput., 1981
- ↑ Don Coppersmith and Shmuel Winograd. Matrix multiplication via arithmetic progressions. Journal of Symbolic Computation, 9:251-280, 1990.
- ↑ Quanta Magazine
- ↑ Group-theoretic Algorithms for Matrix Multiplication. Дата обращения: 26 сентября 2009. Архивировано 6 августа 2011 года.
- ↑ Toward an Optimal Algorithm for Matrix Multiplication. Дата обращения: 26 сентября 2009. Архивировано из оригинала 31 марта 2010 года.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
matr = [[1,2,3,4,5,6,7,8,9,0], [1,0,3,4,5,6,7,8,9,1], [1,2,3,4,5,6,7,8,9,2], [1,2,3,0,5,6,0,8,9,3], [1,2,3,4,5,0,7,8,9,4], [1,2,3,4,0,6,7,8,9,5], [1,2,3,4,5,6,7,8,9,6], [1,2,3,4,5,6,7,0,9,7], [1,0,3,4,5,6,7,8,9,8], [1,2,3,4,5,6,7,8,9,9]] print reduce(lambda res, x: res*x, [el[i] for i, el in enumerate(matr) if el[i] > 0], 1) print reduce(lambda res, x: res*x, [el[i] for i, el in enumerate(matr[::-1]) if el[i] > 0], 1) >>51030 864 |
ЛЕКЦИЯ 3
2.
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
2.1. Понятие
матрицы
О п р е д е л е н и е. Матрицей называется прямоугольная таблица чисел,
состоящая из m строк и n столбцов. – порядок или размер матрицы. Например, матрица
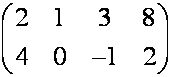
имеет
размер , так как в этой
матрице количество строк равно , а количество столбцов равно
. Числа, из которых состоит матрица, называются элементами. В
общем случае матрицы символически обозначаются следующим образом

Типы
матриц:
1.
Прямоугольные – .
2.
Квадратные – .
3.
Трапецеидальные –
прямоугольные матрицы, у которых при
или
.
4.
Треугольные –
квадратные матрицы, у которых при
или
.
5.
Диагональные –
квадратные матрицы, у которых при
.
6.
Единичная
матрица – диагональная
матрица, у которой .
7.
Траспонированная
матрица – это матрица, которая получается из матрицы
путём замены в ней строк столбцами.
П р и м е р ы
м а т р и ц.
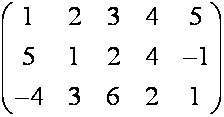
прямоугольная матрица,
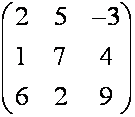
квадратная матрица,
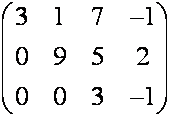
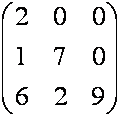
треугольная матрица,


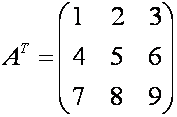
2.2. Действия с матрицами
С матрицами можно выполнять следующие операции:
1)
Сложение матриц. Матрица называется суммой
матриц , если
, Матрица А и В
должны быть одного и того же порядка, Матрица С получится того же порядка, что и матрицы А и В.
П р и м е р. Найдите сумму матриц 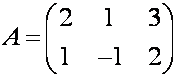
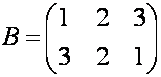
Р е ш е н и е. Элементы матрицы
получаем путём
суммирования соответствующих элементов матриц
А и В
2) Умножение
матрицы на число. Матрица называется
произведением матрицы на число
если
.
П р и м е р.
Найдите произведение матрицы 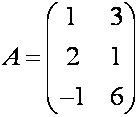
.
Р е ш е н и е. Элементы матрицы получаем путём
умножения элементов матрицы на число
3) Умножение
матриц. Матрица называется
произведением матрицы размером
и матрицы
размером
, если элементы матрицы
вычисляются по
формуле
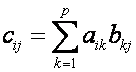
(1)
Перемножать
можно только матрицы, у которых количество столбцов первой равно количеству
строк второй. Произвольные матрицы перемножать нельзя.
П р и м е р. Найдите произведение матриц
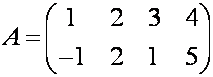
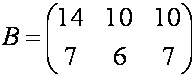
Р е ш е н и е. Согласно формуле
(1), имеем
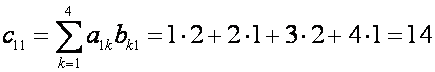
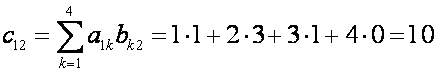
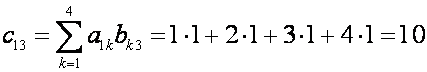
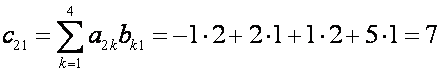


Значит,
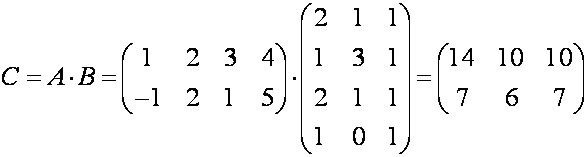
Рассмотренные
операции с матрицами обладают теми же свойствами, что и операции
сложения и умножения для вещественных чисел, за исключением произведения
матриц, которое не коммутативно, т.е. . В этом можно убедиться с помощью следующего примера для
матриц 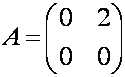
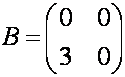
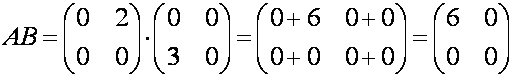

Как
видим, 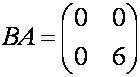
2.3. Определители
Каждой квадратной матрице по определённому правилу
можно поставить в соответствие единственное число. Это число называется определителем и
символически обозначается

Порядок определителя равен порядку квадратной матрицы.
Определитель
второго порядка вычисляется следующим образом
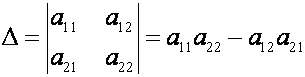
(2)
т.е. из произведения элементов, стоящих на так
называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний
угол), вычитается произведение элементов, находящихся на побочной диагонали (идущей из левого нижнего
в правый верхний угол).
П р и м е р. Вычислите определитель матрицы 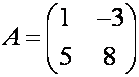
Р
е ш е н и е. Значения элементов
матрицы , т.е.
Подставляем
в формулу (2) и получаем
.
Определитель
третьего порядка вычисляется с помощью формулы
(3)
З а м е ч а н и е. Чтобы легче
запомнить эту формулу, можно использовать так называемое правило треугольников
(правило Саррюса). Оно заключается в следующем. Элементы, произведения которых входят
в определитель со знаком «+», располагаются на главной диагонали и в вершинах
треугольников, симметричных относительно
главной диагонали
Элементы,
произведения которых входят в определитель со знаком «–», располагаются
аналогичным образом относительно побочной диагонали

П р и м е р. Вычислите определитель матрицы
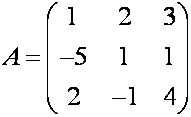
Р е ш е н и е. Подставляем значения элементов матрицы в формулу (3) и находим
величину заданного определителя
Для вычисления определителей третьего
порядка можно пользоваться ещё правилом «35». Согласно этому правилу к заданной матрице
добавляют
ещё первые два столбца

Элементы, произведения которых входят в определитель
со знаком «+», располагаются на главной диагонали и на отрезках, параллельных
главной диагонали

Элементы, произведения которых входят в определитель
со знаком «–», располагаются на побочной диагонали и на отрезках, параллельных
побочной диагонали

Определитель
равен сумме указанных
произведений элементов с учетом их
знаков.
Основные
свойства определителей
Рассмотрим основные свойства определителей 2-го и 3-го
порядка
С в о й с т в о
1. Определитель не
изменяется при транспонировании, т.е.
.
(4)
Действительно,
,
=,
Из чего следует
справедливость равенства (4).
Из свойства 1
следует, что свойствами определителей,
сформулированные для строк будут такими же как и для столбцов. Поэтому следующие свойства определителей будут формулироваться
только для строк.
С в о й с т в о 2. При умножении элементов строки определителя на
некоторое число определитель умножается
на это число, т.е.
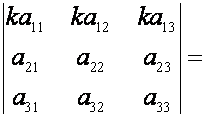
В справедливости этого свойства можно убедиться,
вычислив эти определители
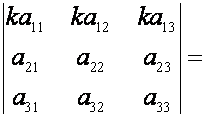
Свойство 3.
Определитель равен нулю в следующих
случаях:
a)
одна из строк
нулевая

б) две равные строки
в) элементы
двух строк пропорциональны
В
справедливости перечисленных свойств легко убедиться с помощью формулы (3).
С в о й с т в о 4. Если две какие-либо строки определителя поменять
местами, то знак определителя изменится на противоположный
Доказательство
этого свойства выполняется с помощью формулы (3).
С в о й с т в о
5. Если в
определителе некоторая строка, например, первая является линейной
комбинацией двух строк с коэффициентами и
,
то определитель будет
равен сумме двух определителей, определяемых формулой
Справедливость
этого свойства можно доказать, сравнив значения левой и правой частей
равенства, найденные с помощью формулы (3).
С в о й с т в о
6. Величина определителя
не изменится, если к элементам одной строки прибавить соответствующие элементы
другой строки, умноженные на одно и то же число
2.4. Обратная матрица
Минором к элементу
матрицы
-го порядка называется определитель
-го порядка той матрицы, которая получается из матрицы
в результате
вычёркивания -ой строки и
-го столбца.
О п р е д е л е н и е. Матрица В
называется обратной матрице А, если
АВ=ВА=Е.
Символически
обратная матрица обозначается . Вычисляется обратная матрица с помощью формулы
|
|
(5) |
где – алгебраическое
дополнение к элементу .
Вырожденной
матрицей называется матрица, у которой
определитель равен 0.
Обратные
матрицы могут иметь только невырожденные матрицы.
П р и м е р. Найти матрицу, обратную к
матрице 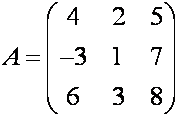
Р е ш е н и е. Вычисляем
определитель
.
Так
как определитель матрицы не равен нулю, то существует. Найдем
алгебраические дополнения:
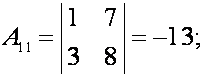
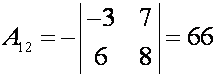
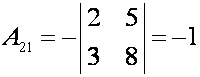
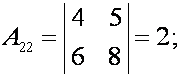
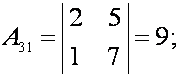
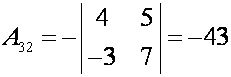
Подставляем
найденные значения определителя матрицы и алгебраических дополнений в формулу
(5) и получаем искомое значение обратной
матрицы
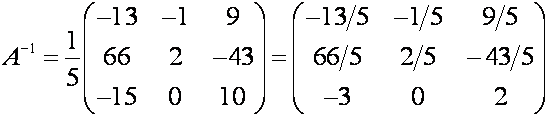
Выполним проверку, для чего вычислим
и
Как видим, оба произведения
равны единичной матрице. Значит, обратная матрица вычислена верно.
2.5 Ранг матрицы
Рангом
матрицы А называется число r,
удовлетворяющее следующим двум требованиям:
1.
Существует минор порядка r.
2.
Все миноры порядка
r+1 равны 0.
Наиболее
простой способ вычисления ранга матрицы сводится к приведению матрицы к
трапециидальному виду.
Пример:
Определить
ранг матрицы А.
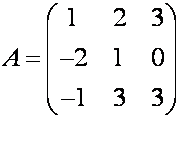
получились нули. В данном случае домножаем на 2 и 1

домножаем на (-1),чтобы в третьей
получились нули.
Теорема Кронекера-Капелли. Система линейных алгебраических уравнений имеет
решения (т.е. совместна)тогда и только тогда, когда ранг расширенной матрицы
равен рангу основной матрицы.
2.6. Матричный способ решения СЛАУ
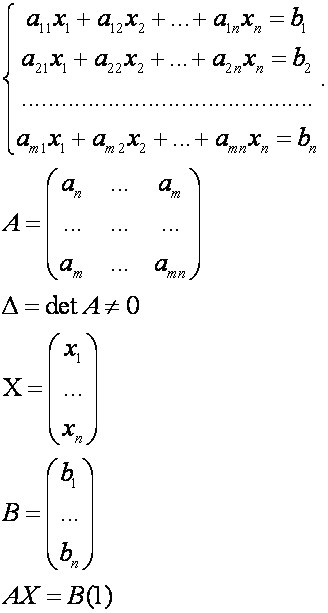
Выражение
(1)-матричная форма записи системы.
Так
как матрица А невырожденная, она имеет обратную матрицу . Умножим равенство
(1) слева на
Выражение
(2) представляет собой решение в матричной форме.
Пример: решить систему.
Замечание:
если главный определитель системы равен 0, то нужно выделить уравнения, для
которых определитель не равен 0, а свободные переменные переносятся в правую
часть.







































































































































































































































































![A^{-1}=left[a_{ik}right]^{-1}=left[{frac {A_{ki}}{det A}}right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/728e599f82952094ff4fd506edd088dac1f03ff3)












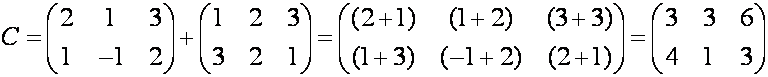
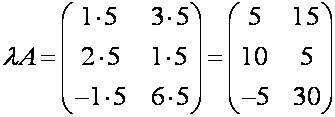
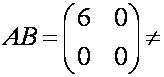







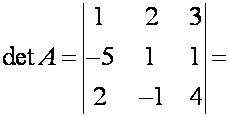












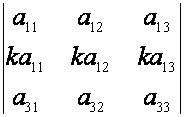

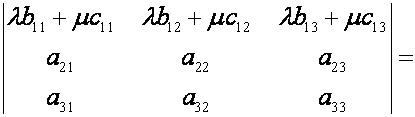
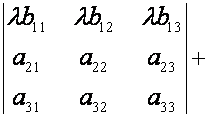
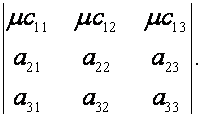
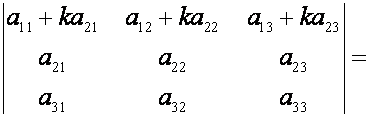
 ,
,