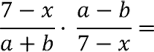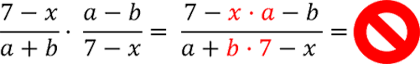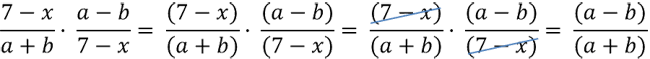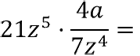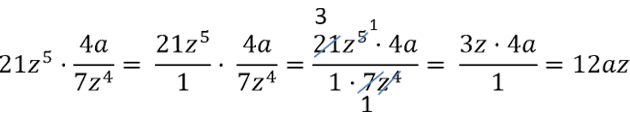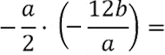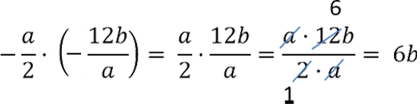Умножение и деление алгебраических дробей
- Умножение дробей
- Возведение алгебраических дробей в степень
- Деление дробей
Умножение дробей
Чтобы умножить одну алгебраическую дробь на другую, надо умножить числитель первой дроби на числитель второй дроби (полученное произведение будет числителем результата) и отдельно умножить знаменатель первой дроби на знаменатель второй (полученное произведение будет знаменателем результата).
Правило умножения алгебраических дробей в виде формулы:
| a | · | c | = | ac | , |
| b | d | bd |
где b≠0 и d≠0.
Пример. Выполнить умножение алгебраических дробей:
Решение: Перед тем, как приступать к умножению дробей, желательно разложить их числители и знаменатели на множители — это поможет сократить алгебраическую дробь, которая получится в результате:
| 2a2 | · | a + b | = | 2a2 | · | a + b | = |
| a2 – b2 | a | (a + b)(a – b) | a |
| = | 2a2(a + b) | . |
| (a + b)(a – b)a |
Теперь сокращаем полученную дробь:
| 2a2(a + b) | = | 2a | . |
| (a + b)(a – b)a | a – b |
Чтобы умножить многочлен на алгебраическую дробь или алгебраическую дробь на многочлен, надо умножить многочлен на числитель дроби, а знаменатель оставить без изменений.
Пример. Выполнить умножение многочлена на алгебраическую дробь:
Решение:
| (2x + 6) · | x – 2 | = | (2x + 6)(x – 2) | . |
| x + 3 | x + 3 |
Разложим числитель на множители и сократим дробь:
| (2x + 6)(x – 2) | = | 2(x + 3)(x – 2) | = |
| x + 3 | x + 3 |
= 2(x – 2) = 2x – 4.
Правило умножения алгебраической дроби на многочлен (или умножение многочлена на алгебраическую дробь) в виде формулы:
| a · | b | = | ab | или | b | · a | = | ab | , |
| c | c | c | c |
где c≠0.
Возведение алгебраических дробей в степень
Чтобы возвести в степень алгебраическую дробь, надо возвести в эту степень отдельно её числитель и отдельно знаменатель.
Правило возведения алгебраических дробей в степень в виде формулы:
| ( | a | )n = | an | . |
| b | bn |
Пример. Выполнить возведение в степень:
| а) ( | a2 | )3 ; б) (- | 2x3 | )2 | . |
| b | y2 |
Решение:
| а) ( | a2 | )3 = | (a2)3 | = | a6 | ; |
| b | (b)3 | b3 |
| б) (- | 2x3 | )2 = | (2x3)2 | = | 4x6 | . |
| y2 | (y2)2 | y4 |
Посмотреть правила возведения степени в степень вы можете на странице Свойства степени
.
Деление дробей
Чтобы разделить одну алгебраическую дробь на другую, надо дробь, выступающую в качестве делителя, заменить на обратную ей дробь и после этого умножить первую дробь на вторую.
Правило деления алгебраических дробей в виде формулы:
| a | : | c | = | a | · | d | = | ad | . |
| b | d | b | c | bc |
Следовательно, частное двух дробей равно произведению первой дроби и перевёрнутой второй дроби.
Пример. Выполнить деление алгебраических дробей:
Решение: Переворачиваем делитель и умножаем дроби по правилам умножения:
| ab + ac | : | ab – ac | = | ab + ac | · | bc | = |
| bc | bc | bc | ab – ac |
| = | (ab + ac)bc | . |
| bc(ab – ac) |
Теперь можно приступать к сокращению полученной дроби:
| (ab + ac)bc | = | ab + ac | = |
| bc(ab – ac) | ab – ac |
| = | a(b + c) | = | b + c | . |
| a(b – c) | b – c |
Чтобы разделить многочлен на алгебраическую дробь, надо перевернуть дробь и выполнить умножение многочлена на полученную дробь по правилам умножения.
Правило деления многочлена на алгебраическую дробь в виде формулы:
| a : | b | = a · | c | = | ac | . |
| c | b | b |
Пример. Выполнить деление:
Решение:
| 6xy2 : | x | = 6xy2 · | y | = 6y3. |
| y | x |
Чтобы разделить алгебраическую дробь на многочлен, надо представить многочлен в виде дроби и перевернуть её, затем выполнить умножение дробей по правилам умножения.
Правило деления алгебраической дроби на многочлен в виде формулы:
| a | : c = | a | : | c | = | a | · | 1 | = | a | . |
| b | b | 1 | b | c | bc |
Пример. Выполнить деление:
Решение:
| 2xy | : 6y = | 2xy | : | 6y | = | 2xy | · | 1 | = |
| 3 | 3 | 1 | 3 | 6y |
| = | 2xy | = | x | . |
| 18y | 9 |
Чтобы перемножить дроби, числители и знаменатели которых являются многочленами, необходимо:
-
эти многочлены разложить на множители (если это возможно);
-
умножить числитель на числитель и знаменатель на знаменатель;
-
произведение числителей разделить на произведение знаменателей.
Пример:
.
Нахождение значения степени
an
называется возведением в степень.
Степенью алгебраической дроби AB с натуральным показателем (n) называется произведение (n) множителей, каждый из которых равен
AB
:
Степень дроби тождественно равна дроби, у которой числитель есть степень числителя, а знаменатель — степень знаменателя.
Из закона умножения алгебраических дробей следует, что
ABn=AnBn(B≠0)
.
Пример:
1)
2a3b2=2a32b2=22⋅a3⋅2b2=4⋅a6b2=4a6b2¯¯
;
2)
−c3xy34=−c34xy34=c3⋅4×4⋅y3⋅4=c12x4⋅y12=c12x4y12¯¯
;
3)
x+y3x32=x+y23x32=x2+2xy+y232⋅x3⋅2=x2+2xy+y29x6¯¯
.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Умножение алгебраических дробей
Поддержать сайт
При умножении алгебраических дробей используют
правила умножения обыкновенных дробей.
Правило умножения алгебраических дробей
Запомните!
При умножении алгебраических дробей
числитель
умножается на числитель,
а знаменатель — на знаменатель.
Рассмотрим пример умножения алгебраических дробей.
При сокращении алгебраических дробей используют
правила сокращения алгебраических дробей.
Рассмотрим еще один пример умножения алгебраических дробей, которые содержат многочлены и в числителе, и в
знаменателе.
Важно!
При умножении алгебраических дробей, которые содержат многочлены и в числителе, и в
знаменателе, заключайте многочлены в скобки целиком.
Неправильно
Правильно
Как умножить алгебраическую дробь на одночлен (букву)
Рассмотрим пример умножения алгебраической дроби на одночлен.
Представим одночлен «21z5» как
алгебраическую дробь со знаменателем «1».
Это можно сделать, так как при делении на
«1» получается тот же самый одночлен.
Важно!
При умножении алгебраической дроби не забывайте использовать
правило знаков.
Рассмотрим пример умножения двух отрицательных алгебраических дробей.
Перед тем как перемножить алгебраические дроби, определим итоговый знак по
правилу знаков: «минус на
минус дает
плюс».
Значит, итоговым знаком произведения будет знак «+».
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
В этой статье мы продолжаем изучение основных действий, которые можно выполнять с алгебраическими дробями. Здесь мы рассмотрим умножение и деление: сначала выведем нужные правила, а затем проиллюстрируем их решениями задач.
Как правильно делить и умножать алгебраические дроби
Чтобы выполнить умножение алгебраических дробей или разделить одну дробь на другую, нам нужно использовать те же правила, что и для обыкновенных дробей. Вспомним их формулировки.
Когда нам надо умножить одну обыкновенную дробь на другую, мы выполняем отдельно умножение числителей и отдельно знаменателей, после чего записываем итоговую дробь, расставив по местам соответствующие произведения. Пример такого вычисления:
23·47=2·43·7=821
А когда нам надо разделить обыкновенные дроби, мы делаем это с помощью умножения на дробь, обратную делителю, например:
23:711=23·117=227=1121
Умножение и деление алгебраических дробей выполняется в соответствии с теми же принципами. Сформулируем правило:
Чтобы перемножить две и более алгебраические дроби, нужно перемножить отдельно числители и знаменатели. Результатом будет дробь, в числителе которой будет стоять произведение числителей, а в знаменателе – произведение знаменателей.
В буквенном виде правило можно записать как ab·cd=a·cb·d . Здесь a, b, c и d будут представлять из себя определенные многочлены, причем b и d не могут быть нулевыми.
Для того чтобы разделить одну алгебраическую дробь на другую, нужно выполнить умножение первой дроби на дробь, обратную второй.
Это правило можно также записать как ab:cd=ab·dc=a·db·c . Буквы a, b, c и d здесь означают многочлены, из которых a, b, c и d не могут быть нулевыми.
Отдельно остановимся на том, что такое обратная алгебраическая дробь. Она представляет из себя такую дробь, которая при умножении на исходную дает в итоге единицу. То есть такие дроби будут аналогичны взаимно обратным числам. Иначе можно сказать, что обратная алгебраическая дробь состоит из таких же значений, что и исходная, однако числитель и знаменатель у нее меняются местами. Так, по отношению к дроби a·b+1a3 дробь a3a·b+1 будет обратной.
Решение задач на умножение и деление алгебраических дробей
В этом пункте мы посмотрим, как правильно применять озвученные выше правила на практике. Начнем с простого и наглядного примера.
Условие: умножьте дробь 1x+y на 3·x·yx2+5 , а потом разделите одну дробь на другую.
Решение
Сначала выполним умножение. Согласно правилу, нужно отдельно перемножить числители и знаменатели:
1x+y·3·x·yx2+5=1·3·x·y(x+y)·(x2+5)
Мы получили новый многочлен, который нужно привести к стандартному виду. Заканчиваем вычисления:
1·3·x·y(x+y)·(x2+5)=3·x·yx3+5·x+x2·y+5·y
Теперь посмотрим, как правильно разделить одну дробь на другую. По правилу нам надо заменить это действие умножением на обратную дробь x2+53·x·y :
1x+y:3·x·yx2+5=1x+y·x2+53·x·y
Приведем полученную дробь к стандартному виду:
1x+y·x2+53·x·y=1·x2+5(x+y)·3·x·y=x2+53·x2·y+3·x·y2
Ответ: 1x+y·3·x·yx2+5=3·x·yx3+5·x+x2·y+5·y ; 1x+y:3·x·yx2+5=x2+53·x2·y+3·x·y2 .
Довольно часто в процессе деления и умножения обыкновенных дробей получаются результаты, которые можно сократить, например, 29·38=672=112 . Когда мы выполняем эти действия с алгебраическими дробями, мы также можем получить сократимые результаты. Для этого полезно предварительно разложить числитель и знаменатель исходного многочлена на отдельные множители. Если нужно, перечитайте статью о том, как правильно это делать. Разберем пример задачи, в которой нужно будет выполнить сокращение дробей.
Условие: перемножьте дроби x2+2·x+118·x3 и 6·xx2-1 .
Решение
Перед тем, как вычислять произведение, разложим на отдельные множители числитель первой исходной дроби и знаменатель второй. Для этого нам потребуются формулы сокращенного умножения. Вычисляем:
x2+2·x+118·x3·6·xx2-1=x+1218·x3·6·x(x-1)·(x+1)=x+12·6·x18·x3·x-1·x+1
У нас получилась дробь, которую можно сократить:
x+12·6·x18·x3·x-1·x+1=x+13·x2·(x-1)
О том, как это делается, мы писали в статье, посвященной сокращению алгебраических дробей.
Перемножив одночлен и многочлен в знаменателе, мы получим нужный нам результат:
x+13·x2·(x-1)=x+13·x3-3·x2
Вот запись всего решения без пояснений:
x2+2·x+118·x3·6·xx2-1=x+1218·x3·6·x(x-1)·(x+1)=x+12·6·x18·x3·x-1·x+1==x+13·x2·(x-1)=x+13·x3-3·x2
Ответ: x2+2·x+118·x3·6·xx2-1=x+13·x3-3·x2 .
В некоторых случаях исходные дроби перед умножением или делением удобно преобразовать, чтобы дальнейшие вычисления стали быстрее и проще.
Условие: разделите 217·x-1 на 12·x7-x .
Решение: начнем с упрощения алгебраической дроби 217·x-1 , чтобы избавиться от дробного коэффициента. Для этого умножим обе части дроби на семь (это действие возможно благодаря основному свойству алгебраической дроби). В итоге у нас получится следующее:
217·x-1=7·27·17·x-1=14x-7
Видим, что знаменатель дроби 12·x7-x , на которую нам нужно разделить первую дробь, и знаменатель получившейся дроби являются противоположными друг другу выражениями. Изменив знаки числителя и знаменателя 12·x7-x , получим 12·x7-x=-12·xx-7 .
После всех преобразований можем наконец перейти непосредственно к делению алгебраических дробей:
217·x-1:12·x7-x=14x-7:-12·xx-7=14x-7·x-7-12·x=14·x-7x-7·-12·x==14-12·x=2·7-2·2·3·x=7-6·x=-76·x
Ответ: 217·x-1:12·x7-x=-76·x .
Как умножить или разделить алгебраическую дробь на многочлен
Чтобы выполнить такое действие, мы можем воспользоваться теми же правилами, что мы приводили выше. Предварительно нужно представить многочлен в виде алгебраической дроби с единицей в знаменателе. Это действие аналогично преобразованию натурального числа в обыкновенную дробь. Например, можно заменить многочлен x2+x−4 на x2+x−41 . Полученные выражения будут тождественно равны.
Условие: разделите алгебраическую дробь на многочлен x+45·x·y:x2-16 .
Решение
Начнем с замены многочлена дробью, далее действуем согласно основному правилу.
x+45·x·y:x2-16=x+45·x·y:x2-161=x+45·x·y·1×2-16==x+45·x·y·1(x-4)·x+4=(x+4)·15·x·y·(x-4)·(x+4)=15·x·y·x-4==15·x2·y-20·x·y
Ответ: x+45·x·y:x2-16=15·x2·y-20·x·y.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
С алгебраическими дробями можно проводить любые математические операции, такие как сравнение, сложение, вычитание, умножение, деление и возведение в степень.
Умножение алгебраических дробей
Алгебраические дроби умножают по тому же правилу, что и обыкновенные дроби
т.е. при умножении алгебраических дробей необходимо умножить числители исходных дробей и знаменатели исходных дробей
Пример 1
Найти произведение $frac{17b^2}{a}cdot frac{2 d}{c}$
Для нахождения произведения воспользуемся правилом умножения дробей, тогда получим
[frac{17b^2}{a}cdot frac{2d}{c}=frac{17b^2cdot 2d}{acdot c}=frac{34b^2d}{ac}]
Пример 2
Найти произведение двух дробей $frac{4ab}{cx+dx}cdot frac{ax+bx}{2ab}$
Для нахождения произведения воспользуемся правилом умножения дробей, тогда получим
[frac{4ab}{cx+dx}cdot frac{ax+bx}{2ab}=frac{4abcdot (ax+bx)}{left(cx+dxright)cdot 2ab}]
Заметим, что многочлены, стоящие в скобках, можно разложить на множители путем вынесения общего множителя, который в данном случае будет являться переменной $x$.
[frac{4ab}{cx+dx}cdot frac{ax+bx}{2ab}=frac{4abcdot left(ax+bxright)}{left(cx+dxright)cdot 2ab}=frac{4abcdot xcdot (a+b)}{2abcdot xcdot (c+d)}]
После подобного преобразования можно отметить, что, воспользовавшись основным свойством дроби, полученную можно сократить на одинаковые множители, входящие в состав числителя и знаменателя: $ 2abx$.
[frac{4ab}{cx+dx}cdot frac{ax+bx}{2ab}=frac{4abcdot left(ax+bxright)}{left(cx+dxright)cdot 2ab}=frac{4abcdot xcdot left(a+bright)}{2abcdot xcdot left(c+dright)}=frac{2(a+b)}{c+d}]
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Деление алгебраических дробей
Алгебраические дроби делят по тому же правилу, что и обыкновенные дроби
т.е. при делении алгебраических дробей необходимо первую дробь оставить без изменений, деление заменить на умножение, а вторую дробь изменить на обратную, затем произвести умножение полученных дробей
Пример 3
Найти частное двух дробей $frac{16}{x-4}:frac{x^2}{x^2-16}$
Воспользуемся правилом, тогда получим
[frac{16}{x-4}:frac{x^2}{x^2-16}= frac{16}{x-4}cdot frac{x^2-16}{x^2}=frac{16cdot (x^2-16)}{x^2cdot x-4)}]
Далее заметим, что полученную дробь можно сократить, но для этого сначала необходимо разложить многочлен, стоящий в скобках в числителе, на множители. Для этого воспользуемся формулой разности квадратов, обратив внимание на то, что $16=4^2$, значит, указанную формулу сокращенного умножения можно применять для того, чтобы разложить выражение, стоящее в числителе на множители.
Применив данную формулу, получим:
[x^2-16=(x-4)(x+4).]
Тогда дробь примет вид
[frac{16}{x-4}:frac{x^2}{x^2-16}=frac{16cdot (x^2-16)}{x^2cdot (x-4)}=frac{16cdot (x-4)(x+4)}{x^2cdot (x-4)}]
Теперь заметим, что числитель и знаменатель дроби содержит одинаковое выражение х-4, на которое можно сократить дробь
[frac{16}{x-4}:frac{x^2}{x^2-16}=frac{16cdot (x^2-16)}{x^2cdot (x-4)}=frac{16cdot (x-4)(x+4)}{x^2cdot (x-4)}=frac{16cdot (x+4)}{x^2}]
«Умножение, деление и возведение дробей в степень » 👇
Возведение в степень алгебраических дробей
Алгебраические дроби возводят в степень по тому же правилу, что и обыкновенные дроби
т.е. при возведении алгебраических дробей в степень необходимо числитель возвести в указанную степень и знаменатель возвести в степень.
Пример 4
Выполнить действия $({frac{m^4}{n^{-1}a^{-2}})}^4$
Сначала воспользуемся правилом возведения дроби в степень, т.е. необходимо числитель возвести в указанную степень и знаменатель возвести в степень
[({frac{m^4}{n^{-1}a^{-2}})}^4=frac{{{(m}^4)}^4}{{left(n^{-1}a^{-2}right)}^4}]
Теперь воспользуемся правилом возведения степени в степень в числителе
[{{(m}^4)}^4=m^{16}]
В знаменателе воспользуемся правилом возведения в степень произведения
[{left(n^{-1}a^{-2}right)}^4=n^{-4}a^{-8}]
А теперь преобразуем по свойству возведения в отрицательный показатель степени:
[{ left(n^{-1}a^{-2}right)}^4=n^{-4}a^{-8}=frac{1}{n^4}cdot frac{1}{a^8}=frac{1}{n^4a^8}]
Тогда исходная дробь примет вид
[({frac{m^4}{n^{-1}a^{-2}})}^4=frac{m^{16}}{frac{1}{n^4a^8}}=m^{16}:frac{1}{n^4a^8}=m^{16}n^4a^8]
Пример 5
Выполнить действия $({frac{x+2}{3x-3})}^3:({frac{x+2}{x-1})}^2$
Сначала преобразуем знаменатель первой дроби посредством разложения на множители и вынесения общего множителя за скобки: $3x-3=3(x-1).$
Теперь воспользуемся правилом возведения в степень дроби, тогда получим:
[{frac{(x+2)}{{(3(x-1))}^3}}^3:{frac{(x+2)}{{(x-1)}^2}}^2]
Заметим, что в знаменателе первой дроби находится произведение, которое мы возводим в степень. Вспомним, что для этого необходимо каждый множитель возвести в степень: $ {(3(x-1))}^3=27{(x-1)}^3$
Теперь применим правило деления дробей:${frac{(x+2)}{{(3(x-1))}^3}}^3:{frac{(x+2)}{{(x-1)}^2}}^2=frac{{(x+2)}^3}{{27(x-1)}^3}cdot frac{{left(x-1right)}^2}{{left(x+2right)}^2}=frac{{(x+2)}^3cdot {left(x-1right)}^2}{{27(x-1)}^3cdot {left(x+2right)}^2}$
Заметим, что в числителе и знаменателе есть общие множители:$ {left(x+2right)}^2$ и ${left(x-1right)}^2$, воспользуемся основным свойством дроби и сократим на них:
[frac{{(x+2)}^3}{{27(x-1)}^3}cdot frac{{left(x-1right)}^2}{{left(x+2right)}^2}=frac{{left(x+2right)}^3cdot {left(x-1right)}^2}{{27left(x-1right)}^3cdot {left(x+2right)}^2}=frac{x+2}{27(x-1)}]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме