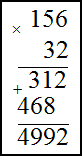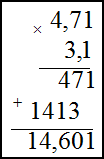Содержание:
- Определение произведения чисел
- Свойства произведения чисел
Определение произведения чисел
Произведение $p$ чисел
$a_{1}, a_{2}, dots, a_{n}$ есть результат умножения этих чисел: $p=a_{1} cdot a_{2} cdot ldots cdot a_{n}$ .
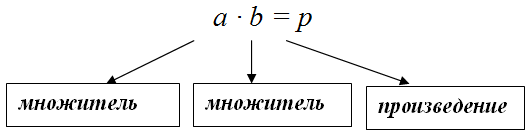
В частности, если умножаются два числа $a$ и $b$, то
Пример
Задание. Найти произведение чисел:
1) 1.2$cdot 3$ ; 2) 4$cdot 5 cdot 13$
Ответ.
$1,2 cdot 3=3,6$
$4 cdot 5 cdot 13=260$
Свойства произведения чисел
- Коммутативность: $n cdot m=m cdot n$
-
Ассоциативность: $(n cdot m) cdot k=n cdot(m cdot k)$
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
- Дистрибутивность: $(n+m) cdot k=n cdot k+m cdot k$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти произведение чисел удобным способом:
1) 5$cdot 17 cdot 2$ ; 2) 7$cdot 2 cdot 15 cdot 5$
Решение. По свойства умножения имеем:
$$5 cdot 17 cdot 2=(5 cdot 2) cdot 17=10 cdot 17=170$$
$$7 cdot 2 cdot 15 cdot 5=(7 cdot(2 cdot 15)) cdot 5=(7 cdot 30) cdot 5=210 cdot 5=1050$$
Ответ.
$5 cdot 17 cdot 2=170$
$7 cdot 2 cdot 15 cdot 5=1050$
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие
натуральные числа или
десятичные дроби.
Пример
Задание. Найти произведение чисел
1) 156$cdot 32$ ; 2) $4,71 cdot 3,1$
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое,
полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем
под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в
столбик
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби
перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после
запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором – один, значит, в ответе
нужно отделить справа три знака:
Ответ.
$156 cdot 32=4992$
$4,71 cdot 3,1=14,601$
Читать дальше: что такое простое число.
Содержание материала
- Определение произведения чисел
- Видео
- Что такое множитель по математике?
- Основное свойство произведения
- Как называются числа при умножении?
- Переместительный закон умножения
- Умножение многозначного числа на однозначное
- Изменение произведения чисел при изменении его сомножителей
- Умножение любого натурального числа на нуль
Определение произведения чисел
Произведение двух чисел это есть не что иное, как взятое одно из чисел в количестве другого числа.
Еще раз! Если произведение будет С, то номинальное значение одного из чисел пусть а, взятое в количестве b раз и будет этим произведением. Можно записать скажем так
С=а1+а2+а3+а4…+аb где 1,2,3,4…b будут индексом указывающим на то, какое это число а по порядку и не более того!
Пример Найти произведение чисел:
1) 1.2⋅3 ;
Ответ.1,2⋅3=3,6
2) 4⋅5⋅13
Ответ: 4⋅5⋅13=260
Видео
Что такое множитель по математике?
Компоненты умножения называются множители. Первый множитель показывает, какое число прибавляют, второй множитель показывает – сколько раз прибавляют это число. Результат умножения называется произведение.
Основное свойство произведения
Произведение не изменяется от перемены порядка производителей.
Доказательство. Умножить 7 на 3 значит 7 повторить три раза. Заменив 7 суммою 7 единиц и вложив их в вертикальном порядке, имеем:
Таким образом, при умножении двух чисел мы можем считать множителем любой из двух производителей. На этом основании производители называются сомножителями или просто множителями.
Самый общий прием умножения состоит в сложении равных слагаемых; но, если производители велики, этот прием приводит к длинным вычислениям, поэтому самое вычисление располагают иначе.
Как называются числа при умножении?
Так же, как и при сложении и вычитании, числа при умножении тоже имеют свое название. Первое число при умножении называется первый множитель. Второе число при умножении называется второй множитель. Результат умножения называют произведение.
Переместительный закон умножения
Рассмотрим задачу:
Мы отдали по два яблока 5 своим друзьям. Математически запись будет выглядеть так: 2⋅5. Или мы отдали по 5 яблок двум своим друзьям. Математически запись будет выглядеть так: 5⋅2. В первом и втором случаем мы раздадим одинаковое количество яблок равное 10 штукам.
Если мы умножим 2⋅5=10 и 5⋅2=10, то результат не поменяется.
2⋅5=5⋅2
Свойство переместительного закона умножения: От перемены мест множителей произведение не меняется. m⋅n=n⋅m
Умножение многозначного числа на однозначное
Умножение числа 8094 на 3 обозначают тем, что подписывают множитель под множимым, ставят слева знак умножения и проводят черту с тем, чтобы отделить произведение.
Умножить многозначное число 8094 на 3 значит найти сумму трех равных слагаемых
следовательно, для умножения нужно все порядки многозначного числа повторить три раза, то есть умножить на 3 единицы, десятки, сотни, и т. п. Сложение начинают с единицы, следовательно, и умножение нужно начинать с единицы, а затем переходят от правой руки к левой к единицам высшего порядка.
При этом ход вычислений выражают словесно:
-
Начинаем умножение с единиц: 3 × 4 составляют 12, подписываем под единицами 2, а единицу (1 десяток) прикладываем к произведению следующего порядка на множитель (или запоминаем ее в уме).
-
Умножаем десятки: 3 × 9 составляет 27, да 1 в уме составят 28; подписываем под десятками 8 и 2 в уме.
-
Умножаем сотни: Нуль, умноженный на 3, дает нуль, да 2 в уме составит 2, подписываем под сотнями 2.
-
Умножаем тысячи: 3 × 8 = 24, подписываем вполне 24, ибо не имеем следующих порядков.
Это действие выразится письменно:
Из предыдущего примера выводим следующее правило. Чтобы умножить многозначное число на однозначное, нужно:
-
Подписать множитель под единицами множимого, поставить слева знак умножения и провести черту.
-
Умножение начинать с простых единиц, затем, переходя от правой руки к левой, последовательно умножают десятки, сотни, тысячи и т. д.
-
Если при умножении произведение выражается однозначным числом, то его подписывают под умножаемой цифрой множимого.
-
Если же произведение выражается двухзначным числом, то цифру единиц подписывают под тем же столбцом, а цифру десятков прибавляют к произведению следующего порядка на множитель.
-
Умножение продолжается до тех пор, пока не получат полного произведения.
Изменение произведения чисел при изменении его сомножителей
Чтобы понять, что происходит с произведением чисел при изменении одного или нескольких сомножителей, нужно вспомнить, что действие умножения – это частный случай действия сложения, а также переместительный и сочетательный законы сложения.
Если увеличить один из сомножителей в несколько раз, произведение также увеличится в это же число раз.
Рассмотрим пример 18 ∙2. Увеличив второй сомножитель, к примеру, в 3 раза, мы получим другое выражение: 18 ∙6.
Умножение любого натурального числа на нуль
6⋅0=0 или 0⋅6=0 a⋅0=0 или 0⋅a=0 При умножении любого натурального числа на нуль произведение будет равно нулю.
Вопросы к теме “Умножение”:
Что такое произведение чисел? Ответ: произведением чисел или умножение чисел называется выражение m⋅n, где m – слагаемое, а n – число повторений этого слагаемого.
Для чего нужно умножение? Ответ: чтобы не писать длинное сложение чисел, а писать сокращенно. Например, 3+3+3+3+3+3=3⋅6=18
Что является результатом умножения? Ответ: значение произведения.
Что означает запись умножения 3⋅5? Ответ: 3⋅5=5+5+5=3+3+3+3+3=15
Если умножить миллион на нуль, чему будет равно произведение? Ответ: 0
Пример №1: Замените сумму произведением: а) 12+12+12+12+12 б)3+3+3+3+3+3+3+3+3 Ответ: а)12⋅5=60 б) 3⋅9=27
Пример №2: Запишите в виде произведения: а) а+а+а+а б) с+с+с+с+с+с+с Решение: а)а+а+а+а=4⋅а б) с+с+с+с+с+с+с=7⋅с
Задача №1: Мама купила 3 коробки конфет. В каждой коробке по 8 конфет. Сколько конфет купила мама? Решение: В одной коробке 8 конфет, а у нас таких коробок 3 штуки. 8+8+8=8⋅3=24 конфеты Ответ: 24 конфеты.
Задача №2: Учительница рисования сказала приготовить своим восемью ученикам по семь карандашей на урок. Сколько всего карандашей вместе было у детей? Решение: Можно посчитать суммой задачу. У первого ученика было 7 карандашей, у второго ученика было 7 карандашей и т.д. 7+7+7+7+7+7+7+7=56 Запись получилась неудобная и длинная, заменим сумму на произведение. 7⋅8=56 Ответ 56 карандашей.
Теги
- Главная
- Справочники
- Справочник по математике для начальной школы
- Умножение
В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.
В математике существует знак для умножения – это точка посередине строки между числами, которые нужно перемножить.
Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24
Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.
Первое число при умножении показывает, какое слагаемое повторяют несколько раз.
Второе число при умножении показывает, сколько раз повторяют это слагаемое.
Результат умножения показывает, какое число получается.
6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24
6 – первый множитель
4 – второй множитель
24 – произведение
Числа при умножении
Первый множитель
Второй множитель
Результат умножения, или Произведение
Чтение числовых выражений
6 • 4 = 24
Этот пример можно прочитать по-разному.
- 6 умножить на 4 равняется 24.
- 6 увеличить в 4 раза – получится 24.
- Первый множитель – 6, второй множитель – 4, произведение – 24.
- Произведение 6 и 4 равно 24.
Умножение на 1
4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.
23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.
Умножение на 0
8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.
26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.
Умножение на 10
8 • 10 = 80, потому что число 8 повторяют 10 раз.
15 • 10 = 150, потому что число 15 повторяют 10 раз.
Связь деления и умножения
8 • 3 = 24, потому что 8 повторяют 3 раза.
24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.
24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.
В несколько раз больше
Решим задачу:
В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?
Это значит, что котят было 4 раза по 2.
2 + 2 + 2 + 2 = 4 (к.)
Заменяем сложение умножением и получаем:
2 • 4 = 8 (к.)
Вывод: Если в задаче есть слова «в … раз больше», то задача решается умножением.
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
8 : 2 = 4 (раза)
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Советуем посмотреть:
Табличное умножение
Внетабличное умножение
Умножение суммы на число
Умножение на однозначное число в столбик
Умножение на числа, оканчивающиеся нулями
Свойства умножения
Правило встречается в следующих упражнениях:
2 класс
Страница 57. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 49,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 53,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 101,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 46,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 48,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 52,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 52. Урок 20,
Петерсон, Учебник, часть 2
Страница 71. Урок 26,
Петерсон, Учебник, часть 3
3 класс
Страница 33,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 41,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 45,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 86,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 21,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 9,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 27,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 4,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 12. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 41. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 12,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Номер 36,
Мерзляк, Полонский, Якир, Учебник
Математика, 2 класс
Урок № 51. Названия компонентов и результата действия умножения
Перечень вопросов, рассматриваемых в теме:
– Связь умножения со сложением, умение заменять сумму одинаковых слагаемых произведением и произведение – суммой одинаковых слагаемых
Глоссарий по теме:
Умножение – математическое действие, посредством которого из двух чисел получается новое число, которое содержит слагаемым первое число столько раз, сколько единиц во втором.
Произведение – это результат умножения.
Основная и дополнительная литература по теме урока:
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А. Бантова, Г.В. Бельтюкова и др. –
8-е изд. – М.: Просвещение, 2017. – с.54.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова –
7-е изд., дораб. – М.: Просвещение, 2016. – с.46.
Открытые электронные ресурсы по теме урока:
1.https://knowworld.ru/fakty/interesnyie-faktyi-o-matematike/
2. https://dic.academic.ru/
3. https://kopilkaurokov.ru/matematika/uroki/
Теоретический материал для самостоятельного изучения
Составьте выражения к рисункам:
2 

Учимся рассуждать. Числа разные: 2 и 3.
К данному рисунку можем составить выражение на сложение: 2 + 3 = 5
2
Числа одинаковые: 2, 2, 2. К данному рисунку можем составить выражение на умножение:
2 · 3 = 6
Компоненты каждого математического действия имеют название.
Компоненты сложения указывают на производимое действие – сложение: первое слагаемое, второе слагаемое, сумма.
Компоненты вычитания указывают на производимое действие – вычитание: уменьшаемое, вычитаемое, разность.
Компоненты умножения указывают на производимое действие – умножение.
Названия носят города и реки,
Вам от рождения фамилия дана.
И каждому числу при умножении
Особенные дали имена.
Так же, как и при сложении и вычитании, числа при умножении тоже имеют свое название.
Первое число при умножении называется первый множитель. Второе число при умножении называется второй множитель. Результат умножения называют произведение.
Зная, как называются числа при умножении, можно использовать эти термины при чтении выражений.
Равенство 5 · 2 = 10 можно прочитать несколькими способами:
– Первый множитель – пять, второй множитель – два, произведение – десять.
– Произведение пяти и двух равно десяти.
– Пять умножить на два, равняется десять.
Рассмотрим задание: слагаемое 12 повторяется 4 раза. Запишите такую сумму в виде произведения.
Назовите первый множитель этого произведения. Что он обозначает?
Первый множитель этого произведения обозначает слагаемое.
Слагаемое 12 повторяется 4 раза.
Назовите второй множитель этого произведения. Что он обозначает? Второй множитель этого произведения обозначает количество слагаемых.
Слагаемое 12 повторяется 4 раза.
Получилась запись: 12+12+12+12=12·4
Помните, что заменить сложение умножением можно там, где находятся суммы одинаковых слагаемых.
Тренировочные задания.
1. Запишите пример на умножение там, где это возможно:
8 + 8 + 8 + 8 + 8 + 8 =
4 + 4 + 3 + 4 + 4 + 4 =
Правильные ответы:
8 + 8 + 8 + 8 + 8 + 8 = 8 · 6
2. Соедините сумму и произведение:
2 + 2 + 2 5 · 2
1 + 1 + 1 + 1 6 · 4
3 + 3 + 3 + 3 + 3 1 · 4
5 + 5 3 · 5
6 + 6 + 6 + 6 2 · 3
Правильный вариант:
2 + 2 + 2 = 2 · 3
1 + 1 + 1 + 1 = 1 · 4
3 + 3 + 3 + 3 + 3 = 3 · 5
5 + 5 = 5 · 2
6 + 6 + 6 + 6 = 6 · 4
Цели:
- Продолжить работу с понятием «произведение»;
- Расширить терминологическую базу с помощью
введения терминов «первый множитель», «второй
множитель». - Развивать познавательный интерес и умение
использовать в работе ранее полученные знания.
Оборудование: персональный компьютер;
мультимедиа-проектор; презентация к уроку (Приложение 1), карточки
«Солнышкино задание» для индивидуальной работы;
учебник А.Л.Чекин «Математика» 1 часть, 2 класс,
издательство «Академкнига/Учебник» 2007г.;
тетрадь на печатной основе Е.П.Юдина,
О.А.Захарова издательство «Академкнига/
Учебник», 2007 г.
ХОД УРОКА
I. Организационный момент
На экране высвечивается 1 слайд.
– Здравствуйте, ребята. В каждом из нас есть
маленькое солнце – доброта. Добрый человек – это
тот, кто любит людей и помогает им. Добрый человек
любит природу и охраняет её, а любовь и помощь
согревают, как солнце. Я очень хочу, чтобы урок
был для вас действительно добрым и тёплым, принёс
много нового и интересного. А вы хотите? Тогда
вперёд.
II. Актуализация опорных знаний
На экране высвечивается 2 слайд.
– Откройте тетради и запишите число и название
работы.
На экране высвечивается 3 слайд.
– Посмотрите на запись. Что вы можете сказать?
25 –
5
40 – 18
82 +
10
64 + 12
2 ·
9
3 · 5
(На экране написаны выражения.)
– Запишите в тетради выражения, распределив
на группы.
– На сколько групп вы распределили эти
выражения? (Эти выражения мы распределили на
три группы.)
Проверка: на экране высвечивается 4 слайд.
– Прочитайте выражения 1 группы. (Мы
выписали выражения 25 – 5, 40 – 18)
– Что общего у данных выражений? (Это
разности.)
– Прочитайте выражения 2 группы. (Мы выписали
выражения 82 + 10, 64 + 12)
– Что общего у данных выражений? (Это суммы.)
– Прочитайте выражения 3группы. (Мы
выписали выражения 2 · 9, 3 · 5)
– Что общего у данных выражений? (Это
произведения)
– Проверьте. Поднимите руки те, у кого не было
ошибок, кто распределил выражения на такие
группы. Молодцы!
Продолжение работы по 4 слайду.
– Прочитайте выражения другого цвета разными
способами.
– С помощью какого знака обозначено
произведение? (Знак в виде точки. По данной
программе действие умножения даётся на
следующем уроке)
– Можем ли прочитать выражения 3 группы так же
как предыдущие? (Нет, ещё не умеем.)
– А хочется ли вам научиться читать эти
выражения несколькими способами? (Да)
III. Самоопределение к деятельности.
Постановка учебной задачи.
– Прежде чем рассматривать данное выражение,
откройте содержание учебника на стр. 5.
– Найдите тему, над которой работали на
предыдущем уроке.
– Прочитайте название темы следующей за ней. («Произведение
и множители».)
На экране высвечивается пятый слайд с
темой урока: «Произведение и множители».
– Поделитесь, над чем, будем работать на уроке? (Будем
работать над произведениями, узнаем, что такое
множители)
– Какие задачи ставим перед собой? (Проверить
свои знания. Посмотреть чему научились. Открыть
что-то новое.)
IV. Открытие нового знания
На экране шестой слайд.
– Из всех данных выражений выбери и запиши
только произведения.
2 +
3 7
– 5
3 ·
4
10 + 1
12 –
2
8 · 12
– Какие выражения выписали? (Мы выписали
произведения 3 · 4; 8 ·12)
На этом же слайде проявляются эти выражения
– Какой знак есть в этих выражениях? (Знак в
виде точки.)
– Кто догадался, как называются числа, которые
образуют произведение? (Множители)
– Прочитайте тему нашего урока ещё раз.
На экране седьмой слайд.
– Как можно прочитать компоненты в
выражениях, которые выписали? (Множители 3 и 4,
множители 8 и 12.)
– Подтвердим своё предположение с выводом
учебника на стр. 93. (Числа, из которых
состоит произведение, называются множители.
Первое число в произведении это первый
множитель, второе число – второй множитель)
– Наше предположение совпало, мы сделали
открытие.
На экране восьмой слайд.
– Вернёмся к началу урока. Прочитайте
выражение разными способами. (Произведение
чисел двух и девяти; первый множитель – 2, второй
множитель – 9)
V. Первичное закрепление
Учебник стр. 93 №2 (1 ученик у доски, остальные
в тетради).
(Составь и запиши произведение, в котором
первый множитель равен 2, второй – 4. Замени это
произведение суммой)
– Прочитайте, какое произведение вы записали. (Мы
записали 2·4; произведение чисел 2 и 4; первый
множитель – 2, второй множитель – 4)
Учебник стр. 93, № 3.
(Запиши сумму в виде произведения. 3+ 3 +3 +3+3+3+3)
– Как вы записали эту сумму в виде
произведения. (Мы записали 3 · 7)
Проверка, девятый слайд
– Что обозначает первый множитель этого
произведения? (Берём число 3)
– Что показывает второй множитель этого
произведения? (Сколько раз берём число 3)
На экране десятый слайд.
Физминутка
Под мелодию песни «Вместе весело шагать…»
шагаем, считая в прямом порядке по 2. Прыгаем,
считая в обратном порядке по 2. Шагаем, считая в
прямом порядке по 3. Прыгаем, считая в обратном
порядке по 3.
VI. Самостоятельная работа с самопроверкой
по эталону
– Дальше вы будете работать самостоятельно.
Учебник стр. 94 № 4 (Слагаемое 12
повторяется 4 раза. Запиши такую сумму в виде
произведения.)
– Прочитайте внимательно задание,
постарайтесь выполнить самостоятельно, а на
закрытой доске работает 2 ученика.
– Что нужно было выполнить? Проверим работу у
доски.
– Кто сомневался? Поставьте знак «?».
– Кто не допустил ошибок? Поставьте «+».
– Назовите первый множитель этого произведения.
Что он обозначает?
– Назовите второй множитель этого произведения.
Что он обозначает?
VII. Включение в систему знаний и повторение
Тетрадь на печатной основе. Стр. 40, № 1.
- 1 ряд – 1 задача. На столе 4 стопки по 3 тетради
в каждой. Сколько тетрадей на столе? - 2 ряд – 2 задача. В классе 4 ряда столов по 3
стола в каждом. Сколько всего столов в классе? - 3 ряд – 3 задача. Одна ручка стоит 3 рубля. Сколько
нужно заплатить за 4 таких ручки?
Проверяем с экрана. Слайды 11, 12, 13.
– Прочитайте 1 ряд задачу, которую было
предложено решить.
– Какое решение задачи вы записали?
– Что обозначает первое число в записи
произведения? (По 3 тетради). Второе число? (взяли 4
стопки, 4 раза)
Аналогично проверяется 2 и 3 задачи.
– Как называются компоненты в произведении?
(Множители)
«Солнышкино задание» по карточкам.
У каждого из вас лежит на парте карточка, это
«Солнышкино задание». Прочитайте задание и
выполните самостоятельно.
(На карточке задание: запиши суммы, состоящие
из одинаковых слагаемых в виде произведения
2+2+3
5+6+5+6
6+6+6+6
4+4+4
11+11+1+11 13+13+13+13)
Проверка «Солнышкино задание» слайд 14.
– Проверьте, так ли у вас получилось?
– У кого всё верно, поставьте «+».
– У кого есть ошибки, поставьте «–».
– У кого были трудности, сомнения?
VIII. Рефлексия деятельности
– Какое открытие для себя вы сегодня сделали? (Узнали,
как называются компоненты в произведении,
учились читать выражения разными
способами. Слайд 15.)
– Какую ставили учебную задачу?
– Удалось её решить?
– Каким способом? (Работой в паре, с помощью
учителя, ранее изученного, дружной работой и т.д.)
– Где можно применить эти знания?
– Давайте оценим свою работу. Определите
качество успеха. (Слайд 16. Обучающиеся выбирают
солнышко по своему настроению от урока: смеётся
солнышко – всё было понятно на уроке, всё
получилось; грустит солнышко – всё понравилось,
но были трудности, надо ещё поработать; грозное
солнышко – ничего непонятно, всё было трудно)
– Кто выбрал первое солнышко? Поднимите руки.
– Кто выбрал второе солнышко? Поднимите руки.
– Кто выбрал третье солнышко? Поднимите руки.
IX. Домашнее задание
Высвечивается 17 слайд с домашним
заданием.
– Вы подарили мне тепло и радость хорошей
работой. Всем за урок спасибо.