Правило
умножения десятичных дробей
Чтобы
найти произведение двух десятичных дробей, надо:
1)перемножить
десятичные дроби как натуральные числа, не обращая внимания на запятую;
2)посчитать
количество цифр после запятой в первом и во втором множителях;
3) в
произведении отделить справа столько цифр, сколько их стоит в первом и во
втором множителях, поставить запятую.
Например:
2,31 х 0,2 =
1) Умножаем
231 на 2, не обращая внимания на запятую, получаем 462.
2) Считаем
количество цифр после запятой: в первом множителе 2 цифры и во втором
множителе 1 цифра, всего 3.
3) В
произведении справа отделяем три цифры и ставим запятую: 0,462.
Умножение десятичных
дробей на 10,100,1000 и т.д.
1)
Чтобы
десятичную дробь умножить на 10, надо в этой десятичной дроби запятую
перенести на одну цифру вправо.
Например:
3,547х10=35,47
2)
Чтобы
десятичную дробь умножить на 100, надо в этой десятичной дроби запятую
перенести на две цифры вправо.
Например: 0,759х100=75,9
3)
Чтобы
десятичную дробь умножить на 1000, надо в этой десятичной дроби запятую
перенести на три цифры вправо.
Например:
42,53 х1000 = 42530
В этой статье мы рассмотрим такое действие, как умножение десятичных дробей. Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100, 10 и др.)
В рамках этого материала мы коснемся только правил умножения положительных дробей. Случаи с отрицательными разобраны отдельно в статьях об умножении рациональных и действительных чисел.
Умножение десятичных дробей: общие принципы
Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.
Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.
Посмотрим, как решаются такие задачи.
Вычислите произведение 1,5 и 0,75.
Решение: для начала заменим десятичные дроби на обыкновенные. Мы знаем, что 0,75 – это 75/100, а 1,5 – это 1510. Мы можем сократить дробь и произвести выделение целой части. Полученный результат 1251000 мы запишем как 1,125.
Ответ: 1,125.
Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.
Умножьте одну периодическую дробь 0,(3) на другую 2,(36).
Решение
Для начала приведем исходные дроби к обыкновенным. У нас получится:
0,(3)=0,3+0,03+0,003+0,003+…=0,31-0,1=0,39=39=132,(36)=2+0,36+0,0036+…=2+0,361-0,01=2+3699=2+411=2411=2611
Следовательно, 0,(3)·2,(36)=13·2611=2633.
Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:
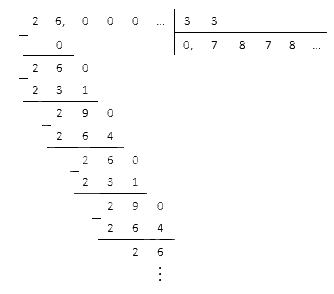
Ответ: 0,(3)·2,(36)=0,(78).
Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см. статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.
Вычислите произведение 5,382… и 0,2.
Решение
У нас в задаче есть бесконечная дробь, которую нужно предварительно округлить до сотых. Получится, что 5,382…≈5,38. Второй множитель округлять до сотых смысла не имеет. Теперь можно подсчитать нужное произведение и записать ответ: 5,38·0,2=538100·210=1 0761000=1,076.
Ответ: 5,382…·0,2≈1,076.
Как умножать десятичные дроби столбиком
Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:
Умножение десятичных дробей столбиком выполняется в 2 шага:
1. Выполняем умножение столбиком, не обращая внимание на запятые.
2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе. Если в результате не хватает для этого цифр, дописываем слева нули.
Разберем примеры таких расчетов на практике.
Умножьте десятичные дроби 63,37 и 0,12 столбиком.
Решение
Первым делом выполним умножение чисел, игнорируя десятичные запятые.
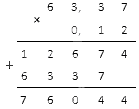
Теперь нам надо поставить запятую на нужное место. Она будет отделять четыре цифры с правой стороны, поскольку сумма десятичных знаков в обоих множителях равна 4. Дописывать нули не придется, т.к. знаков достаточно:
Ответ: 3,37·0,12=7,6044.
Подсчитайте, сколько будет 3,2601 умножить на 0,0254.
Решение
Считаем без учета запятых. Получаем следующее число:
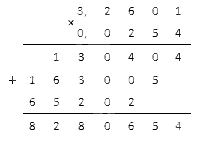
Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:
Ответ: 3,2601·0,0254=0,08280654.
Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д
Умножать десятичные дроби на такие числа приходится часто, поэтому важно уметь делать это быстро и точно. Запишем особое правило, которым мы будем пользоваться при таком умножении:
Если мы умножим десятичную дробь на 0,1, 0,01 и т.д., в итоге получится число, похожее на исходную дробь, запятая которого перенесена влево на нужное количество знаков. При нехватке цифр для переноса нужно дописывать нули слева.
Так, для умножения 45,34 на 0,1 надо перенести в исходной десятичной дроби запятую на один знак. У нас получится в итоге 4,534.
Умножьте 9,4 на 0,0001.
Решение
Нам придется переносить запятую на четыре знака по количеству нулей во втором множителе, но цифр в первом для этого не хватит. Приписываем необходимые нули и получаем, что 9,4·0,0001=0,00094.
Ответ: 0,00094.
Для бесконечных десятичных дробей мы пользуемся тем же правилом. Так, к примеру, 0,(18)·0,01=0,00(18) или 94,938…·0,1=9,4938…. и др.
Как перемножить десятичную дробь с натуральным числом
Процесс такого умножения ничем не отличается то действия умножения двух десятичных дробей. Удобно пользоваться методом умножения в столбик, если в условии задачи стоит конечная десятичная дробь. При этом надо учитывать все те правила, о которых мы рассказывали в предыдущем пункте.
Подсчитайте, сколько будет 15·2,27.
Решение
Умножим столбиком исходные числа и отделим два знака запятой.
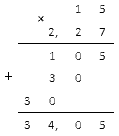
Ответ: 15·2,27=34,05.
Если мы выполняем умножение периодической десятичной дроби на натуральное число, надо сначала поменять десятичную дробь на обыкновенную.
Вычислите произведение 0,(42) и 22.
Решение
Приведем периодическую дробь к виду обыкновенной.
0,(42)=0,42+0,0042+0,000042+…=0,421-0,01=0,420,99=4299=1433
Далее умножаем:
0,42·22=1433·22=14·223=283=913
Итоговый результат можем записать в виде периодической десятичной дроби как 9,(3).
Ответ: 0,(42)·22=9,(3).
Бесконечные дроби перед подсчетами надо предварительно округлить.
Вычислите, сколько будет 4·2,145….
Решение
Округлим до сотых исходную бесконечную десятичную дробь. После этого мы придем к умножению натурального числа и конечной десятичной дроби:
4·2,145…≈4·2,15=8,60.
Ответ: 4·2,145…≈8,60.
Как умножить десятичную дробь на 1000, 100, 10 и др
Умножение десятичной дроби на 10, 100 и др. часто встречается в задачах, поэтому мы разберем этот случай отдельно. Основное правило умножения звучит так:
Чтобы умножить десятичную дробь на 1000, 100, 10 и др., нужно перенести ее запятую на 3, 2,1 цифры в зависимости от множителя и отбросить слева лишние нули. Если цифр для переноса запятой недостаточно, дописываем справа столько нулей, сколько нам нужно.
Покажем на примере, как именно это делать.
Выполните умножение 100 и 0,0783.
Решение
Для этого нам надо перенести в десятичной дроби запятую на 2 цифры в правую сторону. Мы получим в итоге 007,83Нули, стоящие слева, можно отбросить и записать результат как 7,38.
Ответ: 0,0783·100=7,83.
Умножьте 0,02 на 10 тысяч.
Решение: мы будем переносить запятую на четыре цифры вправо. В исходной десятичной дроби нам не хватит для этого знаков, поэтому придется дописывать нули. В этом случае будет достаточно трех 0. В итоге получилось 0,02000,перенесем запятую и получим 00200,0. Игнорируя нули слева, можем записать ответ как 200.
Ответ: 0,02·10 000=200.
Приведенное нами правило будет работать так же и в случае с бесконечными десятичными дробями, но здесь следует быть очень внимательным к периоду итоговой дроби, так как в нем легко допустить ошибку.
Вычислите произведение 5,32(672) на 1 000.
Решение: первым делом мы запишем периодическую дробь как 5,32672672672…, так вероятность ошибиться будет меньше. После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326,726726… Заключим период в скобки и запишем ответ как 5 326,(726).
Ответ: 5,32(672)·1 000=5 326,(726).
Если в условиях задачи стоят бесконечные непериодические дроби, которые надо умножать на десять, сто, тысячу и др., не забываем округлить их перед умножением.
Как перемножить десятичную дробь с обыкновенной или со смешанным числом
Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.
Умножьте 0,4 на 356
Решение
Cначала переведем десятичную дробь в обыкновенную. Имеем: 0,4=410=25.
Далее считаем: 0,4·356=25·236=2315=1815.
Мы получили ответ в виде смешанного числа. Можно записать его как периодическую дробь 1,5(3).
Ответ: 1,5(3).
Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.
Вычислите произведение 3,5678…·23
Решение
Второй множитель мы можем представить как 23=0,6666…. Далее округлим до тысячного разряда оба множителя. После этого нам будет нужно вычислить произведение двух конечных десятичных дробей 3,568 и 0,667. Посчитаем столбиком и получим ответ:
Итоговый результат нужно округлить до тысячных долей, так как именно до этого разряда мы округляли исходные числа. У нас получается, что 2,379856≈2,380.
Ответ: 3,5678…·23≈2,380
На этом уроке мы продолжим работу с десятичными
дробями. Узнаем правило умножения десятичных дробей.
Эта тема очень важна, т.к. она в дальнейшем
используется при изучении математики в старших классах и даже в курсе высшей
математики.
Задача
Школьный участок имеет длину 8,7 м и ширину 5,3 м.
Найдите площадь школьного участка.
Решение
Мы справились с заданием, нашли площадь школьного
участка. Для решения задачи мы перевели одни величины в другие и с лёгкостью
нашли произведение двух натуральных чисел. А если бы в условии задачи, не было
ни каких величин и переводить было бы не чего, как тогда бы мы справились?
В таких случаях используют правило умножения
десятичных дробей.
Для того чтобы найти произведение двух
десятичных дробей, надо:
1) умножить
их столбиком как целые числа, не обращая внимания на запятые.
2) После
этого, в каждом множителе нужно посчитать количество знаков после запятой и сложить
эти значения.
3) В
полученном результате отделить запятой справа столько цифр, сколько их стоит в
обоих множителях вместе.
Задание
Найти произведение чисел 3,143
и 1,5.
Как видите, в этом нет ничего сложного, если
соблюдать правило умножения десятичных дробей.
Если в произведении получается меньше
цифр, чем надо отделить запятой, то впереди дописывают нуль или несколько нулей.
Например
Найти произведение чисел 2,85
и 0,31.
Задание
Найти произведение чисел 8,5
и 0,1; и 3,4
и 0,01.
Запомним ещё одно правило:
Чтобы умножить десятичную дробь на 0,1; 0,01;
0,001; и т.д., надо в этой дроби перенести запятую влево на столько знаков,
сколько нулей стоит перед единицей в множителе.
Не забудьте, что считаем и нуль целых!
Если десятичную дробь умножить на неправильную
десятичную дробь, то она либо увеличится, либо не изменится.
Например
А если десятичную дробь умножить на правильную
десятичную дробь, то она уменьшится.
Например
Итоги
Для того чтобы найти произведение двух
десятичных дробей, надо
1) Умножить их столбиком как целые
числа, не обращая внимания на запятые.
2) После этого, в каждом множителе нужно
посчитать количество знаков после запятой и сложить эти значения.
3) В полученном результате отделить
запятой справа столько цифр, сколько их стоит в обоих множителях вместе.
Если в произведении получается меньше
цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей.
Чтобы умножить десятичную дробь на 0,1;
0,01; 0,001; и т.д., надо в этой дроби перенести запятую влево на столько
знаков, сколько нулей стоит перед единицей в множителе.
Математика
6 класс
Урок № 60
Умножение положительных десятичных дробей. Часть 1
Перечень рассматриваемых вопросов:
- десятичная запись дробей;
- десятичная дробь;
- умножение десятичной дроби на десятичную;
- умножение десятичной дроби на натуральное число.
Тезаурус
Десятичная дробь – это дробь, у которой знаменатель является степенью числа 10.
Десятичные дроби записывают без знаменателей, выделяя целую часть (целая часть правильной дроби считается равной 0) и отделяя её запятой от числителя дробной части.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
- Кордина Н. Е. Виват, математика! Занимательные задания и упражнения 5 кл. // Кордина Н. Е. — издательство «Учитель», 2009. — 112 с.
- Гельфман Э. Г., Демидова Л. Н., Зильберберг Н. И., Просвирова И. Г. Десятичные дроби: рабочая тетрадь по математике. 5 класс. // Томск: Изд-во Томского государственного педагогического университета, 2007. — 76 с.
Теоретический материал для самостоятельного изучения
Умножая натуральные числа, мы действуем по алгоритму.
Десятичная форма записи дробей позволяет умножать их практически по тем же правилам, что и натуральные числа. Отличие лишь в том, что в ответе следует правильно определять место запятой.
Рассмотрим произведение дробей 2,5 и 1,02. Переведём их в неправильные обыкновенные дроби и выполним умножение.
Выполним умножение другим способом. Переведём дроби в натуральные числа. Для этого перенесём запятую на один знак вправо в числе 2,5 и на два знака вправо в числе 1,02. Таким образом, произведение натуральных чисел 25 и 102 будет в 1000 раз больше произведения 2,5 на 1,02. Выполним умножение.
25·102=2550
Чтобы получить из него произведение дробей 2,5 на 1,02, нужно разделить 2550 на 1000. Для этого передвинем запятую на три знака влево. Получим 2,55.
Таким образом, чтобы перемножить две десятичные дроби, достаточно перемножить их, не обращая внимания на запятые, как обычные натуральные числа, а потом в полученном произведении отделить запятой справа столько цифр, сколько их было после запятой в обоих множителях вместе.
Для десятичных дробей справедливы те же законы, что и для натуральных чисел.
Разбор заданий
1. Найдите произведение.
6,5 · 0,014 = 0,091
Выполняем умножение, не обращая внимания на запятые. В результате получилось число 910. Теперь определим место запятой. В дроби 6,5 – одна цифра после запятой, в дроби 0,014 – три цифры. Значит, всего мы должны отсчитать справа четыре цифры. Отсчитаем и припишем недостающий ноль. Получилось 0,091.
16 ·0,08 = 1,28
Умножив 8 на 16, получили 128. В числе 16 нет цифр после запятой, в числе 0,08 – две цифры. Значит, отсчитаем справа две цифры и поставим запятую. Получилось число 1,28.
2. Найдите произведение, применяя законы умножения.
0,25·0,3·0,4
Удобнее сначала 0,25 · 0,4, получим 0,1. Умножим 0,1 на 0,3 получим 0,03.
2,4 · 4,8 + 2,6 · 4,8
Вынесем за скобку общий множитель 4,8. Получим
4,8 · (2,4+2,6) = 4,8 · 5 = 24,0 = 24
3. Вычислите площадь прямоугольника со сторонами 3,12 дм и 3,5 дм.
Чтобы найти площадь прямоугольника, нужно длину умножить на ширину. Получаем 3,12 дм·3,5 дм = 10,92 дм2
4. Вычислите объём прямоугольного параллелепипеда, длина, ширина и высота которого соответственно равны 4,5 см, 2,3 см, 10 см.
Вспомним формулу объёма прямоугольного параллелепипеда.
V = a·b·c
Получаем
V = 4,5 см · 2,3 см · 10см = 103,5 см3.
Разбор заданий тренировочного модуля
№ 1. Собственная скорость моторной лодки 11,5 км/ч, а скорость течения реки 1,6 км/ч. Какой путь пройдёт моторная лодка по течению за 3 часа?
Чтобы найти скорость движениялодки по течению, нужно к собственной скорости лодки прибавить скорость течения.
11,5 км/ч + 1,6 км/ч = 13,1 (км/ч) – скорость по течению.
Чтобы найти расстояние, нужно скорость умножить на время.
13,1 км/ч·3ч = 39,3 (км).
Ответ: 39,3 км пройдёт лодка по течению за 3 часа.
№ 2. Из двух населённых пунктов вышли навстречу друг другу два пешехода. Скорость первого пешехода 4,9 км/ч, скорость второго на 1,5 км/ч меньше. Пешеходы встретились через 2,5 часа. Найдите расстояние между пунктами.
Решение
Найдём сначала скорость второго пешехода.
4,9 км/ч– 1,5 км/ч = 3,4 (км/ч) – скорость второго пешехода.
Когда объекты движутся навстречу другу друг, мы можем найти скорость сближения, сложив их скорости.
4,9 км/ч + 3,4 км/ч = 8,3 (км/ч) – скорость сближения.
Чтобы найти расстояние между пунктами, нужно скорость сближения умножить на время до встречи.
S = vсближ. · t
Получаем: 8,3 км/ч ∙ 2,5 ч = 20,75 (км) – расстояние между пунктами.
Ответ: расстояние между пунктами равно 20,75 км.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Десятичные дроби
- Умножение десятичных дробей
Умножение и деление отличается от сложения и вычитание десятичных дробей.
Умножение десятичной дроби на натуральное число
Чтобы умножить десятичную дробь на натуральное число, надо:
1) умножить их как натуральные числа, не обращая внимание на запятую;
2) в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятой у умножаемой дроби.
Примеры:
1) 2,8
5 = 14,0 = 14.
| × | 2 | 8 | |
| 5 | |||
| 1 | 4 | 0 | |
| 1 | 4 | 0 |
2) 0,463 = 1,38.
| × | 0 | 4 | 6 | |
| 3 | ||||
| 1 | 3 | 8 | ||
| 1 | 3 | 8 |
3) 110,005 = 0,055.
| × | 1 | 1 | |||
| 0 | 0 | 0 | 5 | ||
| 5 | 5 | ||||
| 0 | 0 | 5 | 5 |
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
1) записать дроби в столбик, как два натуральных числа не обращая внимание на запятые;
2) умножить их как натуральные числа, не обращая внимание на запятые;
3) в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Примеры:
1) 2,351,2 = 2,820 = 2,82.
| × | 2 | 3 | 5 | |
| 1 | 2 | |||
| 4 | 7 | 0 | ||
| 2 | 3 | 5 | ||
| 2 | 8 | 2 | 0 |
2) 67,34,6 = 309,58
| × | 6 | 7 | 3 | ||
| 4 | 6 | ||||
| 4 | 0 | 3 | 8 | ||
| 2 | 6 | 9 | 2 | ||
| 3 | 0 | 9 | 5 | 8 |
3) 0,00840,31 = 0,002604.
| × | 0 | 0 | 0 | 8 | 4 | ||
| 0 | 3 | 1 | |||||
| 8 | 4 | ||||||
| 2 | 5 | 2 | |||||
| 0 | 0 | 0 | 2 | 6 | 0 | 4 |
4) 1,040,005 = 0,00520 = 0,0052.
| × | 1 | 0 | 4 | |||
| 0 | 0 | 0 | 5 | |||
| 5 | 2 | 0 | ||||
| 0 | 0 | 0 | 5 | 2 | 0 |
Умножение десятичных дробей на 10, 100, 1 000 и т.д.
Чтобы умножить десятичную дробь на 10, 100, 1 000 и т. д., надо в этой дроби перенести запятую вправо соответственно на 1, 2, 3 и т. д. цифры.
Примеры:
1) 3,5610 = 35,6;
2) 45,678100 = 4 567,8;
3) 3,561 000 = 3 560;
4) 0,4567810 000 = 4567,8;
5) 0,041 000 = 40;
6) 0,00065100 = 0,065.
Обратите внимание:
1) если цифр после запятой меньше, чем цифр, на которые нужно перенести запятую, справа у дроби добавляем нули (в итоге получится натуральное число);
2) если слева у десятичной дроби были нули и мы перенесли запятую вправо, то нули, стоящие слева, не пишем.
Умножение десятичных дробей на 0,1, 0,01, 0,001 и т.д.
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.
Примеры:
1) 56,80,1 = 5,68;
2) 678,30,01 = 6,783;
3) 4832,60,001 = 4,8326;
4) 56,40,0001 = 0,00564.
Обратите внимание: если цифр до запятой меньше, чем цифр, на которые нужно перенести запятую, слева у дроби добавляем нули.
Свойства умножения десятичных дробей
1) 
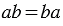– переместительное свойство умножения,
2) 
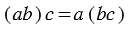– сочетательное свойство умножения,
3) 
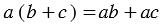– распределительное свойство умножения относительно сложения.
4) 
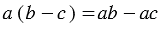– распределительное свойство умножения относительно вычитания.
Советуем посмотреть:
Десятичная запись дробных чисел
Сравнение десятичных дробей
Сложение и вычитание десятичных дробей
Приближенные значения чисел. Округление чисел
Деление десятичных дробей
Среднее арифметическое
Десятичные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 1392,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1488,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1541,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1593,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1597,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 919,
Мерзляк, Полонский, Якир, Учебник
Номер 940,
Мерзляк, Полонский, Якир, Учебник
Номер 1071,
Мерзляк, Полонский, Якир, Учебник
Номер 1089,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 596,
Мерзляк, Полонский, Якир, Учебник
Номер 653,
Мерзляк, Полонский, Якир, Учебник
Задание 546,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 595,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 762,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 766,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1121,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1141,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1341,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1440,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 5,
Мерзляк, Полонский, Якир, Учебник
Номер 28,
Мерзляк, Полонский, Якир, Учебник
Номер 126,
Мерзляк, Полонский, Якир, Учебник
Номер 352,
Мерзляк, Полонский, Якир, Учебник
Номер 430,
Мерзляк, Полонский, Якир, Учебник
Номер 494,
Мерзляк, Полонский, Якир, Учебник
Номер 579,
Мерзляк, Полонский, Якир, Учебник
Номер 580,
Мерзляк, Полонский, Якир, Учебник
Номер 1035,
Мерзляк, Полонский, Якир, Учебник
Номер 1229,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 201,
Мерзляк, Полонский, Якир, Учебник
Номер 278,
Мерзляк, Полонский, Якир, Учебник
Номер 279,
Мерзляк, Полонский, Якир, Учебник
Номер 294,
Мерзляк, Полонский, Якир, Учебник
Номер 296,
Мерзляк, Полонский, Якир, Учебник
Номер 313,
Мерзляк, Полонский, Якир, Учебник
Номер 329,
Мерзляк, Полонский, Якир, Учебник
Номер 356,
Мерзляк, Полонский, Якир, Учебник
Номер 499,
Мерзляк, Полонский, Якир, Учебник
Номер 506,
Мерзляк, Полонский, Якир, Учебник
