Умножение дробей онлайн
Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели, первое произведение записать числителем, а второе знаменателем.
Правила умножения дробей
Произведение двух дробей равно дроби. В числителе которой произведение числителей, а в знаменателе произведение знаменателей.
Как умножать обыкновенные дроби
Для умножения обыкновенных дробей нужно найти произведение числителей и произведение знаменателей. Первое произведение записать числителей а второе знаменателем.
Разберём пример: умножим дроби 1/4 × 1/3. Для этого перемножим числители 1 × 1 = 1 и знаменатели 4 × 3 = 12 в итоге у нас получится дробь 1/12
Как умножать натуральное число на дробь
Чтобы умножить дробь на натуральное число нужно числитель умножить на это число а знаменитель оставить без изменения.
Как умножать 3 и более дробей
При умножении 3 и более дробей мы пользумеся теми же правилами что и при умножении двух дробей.
Разберём пример: умножим правильную дробь 1/4 на натуральное число 5 и на смешанную дробь 3 целые 1/8.
Перед умножением нужно смешанную дробь перевести в неправильную 3 целые 1/8 = 25/8. Затем перемножить числители 1*5*25 = 125 и знаменатели 4*8 = 32. Полученное записать в виде дроби 125/32. При необходимости сократить и перевести в смешанную дробь.
Как умножить смешанную дробь на целое число
Чтобы умножить смешанную дробь на целое число нужно смешанную дробь перевести в неправильную. Затем числитель неправильной дроби умножить на целое число. Знаменатель оставить без изменения.
Разберём пример: умножим смешанную дробь 2 целые 1/4 на целое число 6.
Перед умножением нужно смешанную дробь перевести в неправильную 2 целые 1/4 = 9/4. Затем умножить числитель неправильной дроби на целое число 9*6 = 54 а знаменатель останется без изменения 4. При необходимости сократить и перевести в смешанную дробь.
Как перемножить смешанные дроби
Чтобы перемножить смешанные дроби, нужно их перевести в неправильные. Затем перемножить числители и знаменатели.
Разберём пример: умножим смешанную дробь 1 целая 2/5 на смешанную дробь 2 целые 1/3.
Переведём смешанные дроби в нерпавильные 1 целая 2/5 = 7/5 и 2 целые 1/3 = 7/3. Затем перемножим числители 7*7 = 49 и знаменатели 5*3 = 15. Получится дробь 49/15. При необходимости сократить и перевести в смешанную дробь.
Похожие калькуляторы
Умножение смешанных дробей
Чтобы умножить смешанные дроби, надо записать их в виде неправильных дробей, а затем умножить их числители, а затем их знаменатели.
Пример Умножить смешанные дроби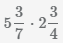 
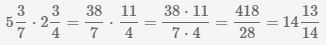
Сократим дробь 
с помощью нахождения наибольшего общего делителя числителя и знаменателя и деления полученного числа на числитель и знаменатель, НОД(418,28)=2.
Пример Умножить смешанное число на дробь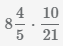 
.
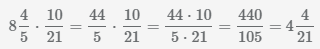В результате умножения получили смешанную дробь.
Примеры умножения нескольких дробей
Пример Умножить 3 дроби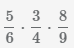 
.
Пример Найти произведение дробей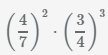 
Первая дробь во 2 степени, вторая дробь в 3 степени, чтобы найти произведение дробей, возведем первую дробь в квадрат, потом возведем вторую дробь в куб и перемножим дроби между собой.
.
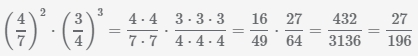Сократим дробь 
с помощью нахождения наибольшего общего делителя числителя и знаменателя и деления полученного числа на числитель и знаменатель, НОД(432,3136)=16.
Математика
5 класс
Урок № 75
Умножение смешанных дробей
Перечень рассматриваемых вопросов:
– умножение смешанной дроби на натуральное число;
– возведение смешанной дроби в степень;
– умножение смешанных дробей.
Тезаурус
Распределительный закон умножения – чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Переместительный закон умножения – от перестановки множителей произведение не меняется.
Площадь прямоугольника – произведение длины на ширину.
Порядок убывания – расположение элементов от большего к меньшему.
Порядок возрастания – расположение элементов от меньшего к большему.
Обязательная литература
- Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
На предыдущих уроках вы научились умножать обыкновенные дроби и записывать смешанные дроби в виде неправильных.
Произведение двух дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Чтобы записать смешанную дробь неправильной дробью, надо знаменатель дробной части умножить на целую часть, прибавить числитель дробной части и полученное число записать в числитель, а знаменатель оставить прежним.
Этих умений достаточно, чтобы сегодня научиться умножать смешанные дроби.
Правило умножения смешанных дробей звучит так: чтобы умножить смешанные дроби, нужно записать их в виде неправильных дробей и выполнить умножение с обыкновенными дробями.
Результат получился тот же, что и при умножении.
Рассмотрим ещё один случай применения распределительного закона умножения для упрощения вычислений.
Найдём сумму произведения трёх целых четырёх пятых и пяти восьмых с произведением четырёх целых одной пятой и пяти восьмых.
В этих произведениях есть одинаковый множитель – пять восьмых. Его по распределительному закону вынесем за скобки, в которых останется сумма трёх целых четырёх пятых и четырёх целых одной пятой. Найдём значение суммы в скобках. Складываем отдельно целые части – три и четыре – это будет семь, и дробные части – четыре пятых и одну пятую – это будет пять пятых.
Сумму целой и дробной части записываем смешанной дробью – семь целых пять пятых и умножаем на пять восьмых. Так как дробная часть получившейся смешанной дроби – неправильная дробь, равная одному, то смешанную дробь заменяем на восемь целых. Умножаем восемь на пять восьмых – это пять.
Расставим порядок действий. Сначала выполняются действия в скобках. В скобках есть умножение и сложение. Умножение выполняется в первую очередь, затем сложение. Четвёртым действием будет вычитание из числа суммы в скобках. Пятое действие – нахождение частного в знаменателе. Шестое действие – деление числителя исходной дроби на знаменатель. Деление заменяется умножением, а умножать мы научились:
Итак, чтобы умножить смешанные дроби необходимо:
• представить эти смешанные дроби неправильными дробями;
• выполнить умножение неправильных дробей;
• сократить, если возможно;
• представить неправильную дробь, полученную в результате умножения, смешанной дробью.
При возведении смешанной дроби в степень нужно:
• представить эту смешанную дробь неправильной дробью;
• возвести полученную неправильную дробь в нужную степень.
Тренировочные задания
№ 1. Поставьте на места пропусков числа так, чтобы вычисления были верными.
Перед тем как перейти к умножению дробей, вспомним теоретические основы. Итак, дробь — это форма записи числа:
где a — числитель, b — знаменатель.
Дробь называется правильной — если числитель меньше знаменателя (к примеру, 4/5), неправильной — если числитель больше знаменателя (например, 8/7).
Как умножать обыкновенные дроби?
Умножение дробей — это арифметическое действие, в результате которого получается новое число, содержащее произведение заданных чисел. Разберем на конкретных примерах: как находить произведение дробей, как натуральное число умножить на дробь, познакомимся с умножением смешанных дробей.
Многие по аналогии со сложением и вычитанием, считают, что существует какая-то разница между умножением дробей в зависимости от их знаменателей. На самом деле её нет. Сейчас на примерах мы в этом убедимся.
Как умножать дроби с одинаковым знаменателем?
Умножение дробей с одинаковыми знаменателями сводится к умножению и числителей и знаменателей и в общем виде выглядит следующим образом:
Пример 1:
2 5
×
3 5
Решение:
2 5
×
3 5
=
2 ∙ 3 5 ∙ 5
=
6 25
Как умножать дроби с разными знаменателями?
Умножение дробей с разными знаменателями заключается в умножении и числителей и знаменателей. В общем виде выглядит следующим образом:
Пример 2:
5 6
×
4 5
Решение:
5 6
×
4 5
=
5 ∙ 4 6 ∙ 5
=
20 30
=
2 3
Как вы могли заметить, разницы между умножением дробей с разными и одинаковыми знаменателями — нет, а сам алгоритм сводится к умножению обоих компонентов.
Как умножить дробь на целое число?
Чтобы умножить дробь на число необходимо числитель умножить число, а знаменатель оставить без изменения. Т.е.:
Пример 3:
5 ×
3 4
Решение:
5
×
3 4
=
5 ∙ 3 4
=
15 4
=
3
3 4
Таким образом, умножение дроби на целое число, сводится к умножению числителей.
Как умножать смешанные дроби?
Умножение смешанных дробей сводится к переводу их к неправильному виду и дальнейшим действиям согласно вышеописанным алгоритмам. Перевод смешанного числа в неправильную дробь, в общем виде, выглядит следующим образом:
Пример 4:
6
3 5
×
6 4
Решение:
6
3 5
×
6 4
=
6 ∙ 5 + 3 5
×
6 4
=
33 5
×
6 4
=
33 ∙ 6 5 ∙ 4
=
198 20
=
99 10
=
9
9 10
Правила умножения дробей
Резюмируя вышесказанное, выведем общий алгоритм умножения дробей:
- Если дробь смешанная — приводим её к неправильному виду;
- Неважно одинаковые или разные знаменатели у дробей — перемножаем и числители и знаменатели;
- При необходимости сокращаем и приводим к неправильному виду.
Смотрите также:
- Смотрите также
- Калькуляторы
- Последние примеры
Калькулятор умножения дробей
Оцените материал:
Загрузка…
Умножение дробей
Как перемножить две обыкновенные дроби:
Определение: Произведением дробей называется дробь, числитель которой равен произведению числителей исходных дробей, со знаменателем равным произведению знаменателей исходных дробей.
Решим дробь: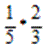 
По определению: 1 умножаем на 2 и 5 умножаем на 3 и получаем выражение: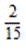 
Важно: При умножении дробей с разными знаменателями не нужно приводить их к общему знаменателю.
Умножение дроби на натуральное число:
Правило: Чтобы умножить дробь на натуральное число нужно числитель умножить на это число, а знаменатель оставить исходный.
Решим выражение: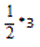 
Находим ответ: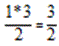 
Из дроби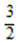 
вычисляем целую часть и получаем ответ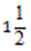 
Умножение смешанных чисел:
Правило: Чтобы найти произведение смешанных чисел, необходимо:
– преобразовывать смешанные дроби в неправильные;
– перемножить числители и знаменатели дробей;
– сократить дробь;
– если получилась неправильная дробь, то преобразовываем ее в смешанную.
Произведем умножение смешанных дробей:
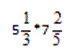
Алгоритм решения:
Онлайн калькулятор умножения дробей:
Помимо всего вышеперечисленного калькулятор выполняет следующие операции:
-Умножение целого числа на дробь
-Умножение дробей на целое число
-Умножение натуральных дробей
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»
