Как найти произведение графов пример - Сайт, где вы сможете решить свои вопросы

Произведение графов — это бинарная операция на графах. Конкретнее, это операция, которая двум графам G₁ и G₂ сопоставляет граф H со следующими свойствами:

Множество вершин графа H — это прямое произведение V(G₁) × V(G₂), где V(G₁) и V(G₂) являются множествами вершин G₁ и G₂ соответственно.
Две вершины (u₁, u₂) и (v₁, v₂) графа H соединены ребром тогда и только тогда, когда вершины u₁, u₂, v₁, v₂ удовлетворяют определённым условиям, соответствующим типу произведения (смотрите ниже).

Виды произведений[править | править код]

Следующая таблица показывает наиболее употребительные произведения графов. В таблице sim означает «соединены ребром» и означает «не соединены ребром». Символы операций, приведённые ниже, не всегда означают стандарт, особенно в ранних работах.

Название	Условие для ( $u_{1}$ , ${displaystyle u_{2}}$ ) ∼ ( $v_{1}$ , $v_{2}$ ).	Размеры	Пример
Декартово произведение	( $u_{1}$ = $v_{1}$ и ${displaystyle u_{2}}$ $v_{2}$ ) или ( $u_{1}$ $v_{1}$ и ${displaystyle u_{2}}$ = $v_{2}$ )	${displaystyle G_{V_{1},E_{1}}square H_{V_{2},E_{2}}rightarrow J_{(V_{1}V_{2}),(E_{2}V_{1}+E_{1}V_{2})}}$
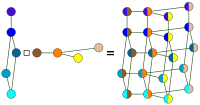
Тензорное произведение (Категорийное произведение)	$u_{1}$ $v_{1}$ и ${displaystyle u_{2}}$ $v_{2}$	${displaystyle G_{V_{1},E_{1}}times H_{V_{2},E_{2}}rightarrow J_{(V_{1}V_{2}),(2E_{1}E_{2})}}$
Лексикографическое произведение или	u₁ ∼ v₁ или ( u₁ = v₁ и u₂ ∼ v₂ )	${displaystyle G_{V_{1},E_{1}}cdot H_{V_{2},E_{2}}rightarrow J_{(V_{1}V_{2}),(E_{2}V_{1}+E_{1}V_{2}^{2})}}$
Сильное произведение (Нормальное произведение)	( u₁ = v₁ и u₂ ∼ v₂ ) или ( u₁ ∼ v₁ и u₂ = v₂ ) или ( u₁ ∼ v₁ и u₂ ∼ v₂ )	${displaystyle G_{V_{1},E_{1}}boxtimes H_{V_{2},E_{2}}rightarrow J_{(V_{1}V_{2}),(V_{1}E_{2}+V_{2}E_{1}+2E_{1}E_{2})}}$
Конормальное произведение графов (Дизъюнктное произведение)	u₁ ∼ v₁ или u₂ ∼ v₂
Модулярное произведение^[en]	${displaystyle (u_{1}sim v_{1}}$ и ${displaystyle u_{2}sim v_{2})}$ или ${displaystyle (u_{1}not sim v_{1}}$ и ${displaystyle u_{2}not sim v_{2})}$
Корневое произведение	см. статью	${displaystyle G_{V_{1},E_{1}}cdot H_{V_{2},E_{2}}rightarrow J_{(V_{1}V_{2}),(E_{2}V_{1}+E_{1})}}$
Произведение Кронекера	см. статью	см. статью	см. статью
Зигзаг-произведение	см. статью	см. статью	см. статью
Заменяющее произведение^[en]
Гомоморфное произведение^[1]^[2]^[1]	${displaystyle (u_{1}=v_{1})}$ или ${displaystyle (u_{1}sim v_{1}}$ и ${displaystyle u_{2}not sim v_{2})}$

В общем случае произведение графов определяется любым условием для (u₁, u₂) ∼ (v₁, v₂), которое может быть выражено в терминах утверждений u₁ ∼ v₁, u₂ ∼ v₂, u₁ = v₁ и u₂ = v₂.

Мнемоника[править | править код]

Пусть $K_{2}$ — полный граф с двумя вершинами (т.е. единственное ребро). Произведения графов ${displaystyle K_{2}square K_{2}}$ , ${displaystyle K_{2}times K_{2}}$ , и ${displaystyle K_{2}boxtimes K_{2}}$ выглядят в точности как знак операции умножения. Например, ${displaystyle K_{2}square K_{2}}$ является циклом длины 4 (квадрат), а ${displaystyle K_{2}boxtimes K_{2}}$ является полным графом с четырьмя вершинами. Нотация для лексикографического произведения напоминает, что произведение не коммутативно.

См. также[править | править код]

Операции над графами

Примечания[править | править код]

↑ ¹ ² David E. Roberson, Laura Mancinska. Graph Homomorphisms for Quantum Players. — 2012.
↑ R. Bačík, S. Mahajan. Computing and Combinatorics. — 1995. — Т. 959. — С. 566, Semidefinite programming and its applications to NP problems. — (Lecture Notes in Computer Science). — ISBN 3-540-60216-X. — doi:10.1007/BFb0030878.

Литература[править | править код]

Imrich, Wilfried; Klavžar, Sandi. Product Graphs: Structure and Recognition (англ.). — Wiley, 2000. — ISBN 0-471-37039-8..

Источник

n1=3 m1=3

G1 n1=4 m1=5

G=G1+G2

n=n1+n2=4+3=7 m=m1+m2+n1n2=5+3+4·3=20

Рис. 6.12

Пусть даны два графа G1= (V(G1), U(G1)), G2 = (V(G2), U(G2)),

причем множества V(G1), V(G2) не пересекаются. Тогда произведение графов G1, G2, обозначаемой G1·G2, называется граф, множество вершин которого образовано как декартово произведение множеств вершин исходных графов V1·V2, а множество ребер как декартово произведение окрестностей соответствующих исходных вершин (рис. 6.13).

V = V1·V2 = {1,2,3}·{a,b,c} = {(1,a), (1,b), (1,c), (2,a), (2,b), (2,c), (3,a), (3,b), (3,c)},

Г1 = {2}, Г2 = {1},

Г3 = , Гa = {b,c}, Гb = {a,c},

Гc = {a,b},

Г1,a = Г1·Гa={2}·{b,c}={(2,b),(2,c)}, Г1,b = Г1·Гb={2}·{a,c}={(2,a),(2,c)},

…

Г3,c=Г3·Гc= ·{a,b}= .

Источник

Декартово произведение графов.

Декартово произведение или прямое произведение ^[1] G square H графов G и H — это граф, такой, что

Декартово произведение может быть распознано эффективно за линейное время^[2]. Операция является коммутативной как операция на классах изоморфизмов графов, и более строго, графы G square H и H square G естественно изоморфны, но операция не является коммутативной как операция на помеченных графах. Операция является также ассоциативной, так как графы (F square G) square H и F square (G square H) естественно изоморфны.

Обозначение G × H порой используется и для декартова произведения графов, но чаще оно используется для другой конструкции, известной как тензорное произведение графов^[en]. Символ квадратика чаще используется и является недвусмысленным для декартова произведения графов. Он показывает визуально четыре ребра, получающиеся в результате декартова произведения двух рёбер^[3]

Примеры

Декартово произведение двух рёбер является циклом с четырьмя вершинами: K₂ K₂=C₄.
Декартово произведение K₂ и пути является лестницей.
Декартово произведение двух путей является решёткой.
Декартово произведение n рёбер является гиперкубом:

${displaystyle (K_{2})^{square n}=Q_{n}.}$

Таким образом, декартово произведение двух графов гиперкубов является другим гиперкубом — Q_i square

Q_j=Q_i+j.

Декартово произведение двух медианных графов является другим медианным графом.
Граф вершин и рёбер n-угольной призмы является декартовым произведением K₂ C_n.
Ладейный граф является декартовым произведением двух полных графов.

Свойства

Если связный граф является декартовым произведением, его можно разложить единственным образом на произведение простых множителей, графов, которые нельзя разложить на произведение графов ^[4]^[5]. Однако, Имрих и Клавжар^[6] описали несвязный граф, который можно представить двумя различными путями как декартово произведение простых графов:

(K₁ + K₂ + K₂²) square

(K₁ + K₂³)=(K₁ + K₂² + K₂⁴) square

(K₁ + K₂),

где знак плюс означает несвязное объединение, а верхний индекс означает кратное декартово произведение.

Декартово произведение является вершинно-транзитивным графом тогда и только тогда, когда каждое из его множителей является вершинно-транзитивным^[7].

Декартово произведение является двудольным тогда и только тогда, когда каждый из его множителей является двудольным. Более обще, хроматическое число декартова произведения удовлетворяет уравнению

χ(G

H)=max {χ(G), χ(H)}^[8].

Гипотеза Хедетними^[en] утверждает связанное равенство для тензорного произведения графов^[en]. Число независимости декартовых произведений непросто вычислить, но, как показал Визинг^[5], число независимости удовлетворяет неравенствам

α(G)α(H) + min{|V(G)|-α(G),|V(H)|-α(H)} ≤ α(G square

H) ≤ min{α(G) |V(H)|, α(H) |V(G)|}.

Гипотеза Визинга утверждает, что число доминирования декартова произведения удовлетворяет неравенству

γ(G

H) ≥ γ(G)γ(H).

Алгебраическая теория графов

Алгебраическую теорию графов можно использовать для анализа декартова произведения графов.
Если граф $G_{1}$ имеет $n_{1}$ вершин и ${displaystyle n_{1}times n_{1}}$ матрицу смежности ${displaystyle mathbf {A} _{1}}$ , а граф $G_{2}$ имеет $n_{2}$ вершин и ${displaystyle n_{2}times n_{2}}$ матрицу смежности ${displaystyle mathbf {A} _{2}}$ , то матрица смежности декартова произведения двух графов задаётся формулой

${displaystyle mathbf {A} _{1square 2}=mathbf {A} _{1}otimes mathbf {E} _{n_{2}}+mathbf {E} _{n_{1}}otimes mathbf {A} _{2}}$

где otimes означает произведение Кронекера матриц, а ${displaystyle mathbf {E} _{n}}$ означает единичную матрицу^[9].

История

Согласно Имриху и Клавжару^[6] декартовы произведения графов определили в 1912 Уайтхед и Рассел. Произведение графов неоднократно переоткрывалось позже, в частности, Гертом Сабидусси^[4].

Примечания

↑ Визинг использовал термин «декартово произведение», в статье «Прямое произведение» то же произведение называется прямым.
↑ (Imrich, Peterin 2007). Для более ранних алгоритмов полиномиального времени см. статью Фейгенбаума, Хершбергерга и Шеффера (Feigenbaum, Hershberger, Schäffer 1985), а также статью Ауренхаммера, Хагауэра и Имриха(Aurenhammer, Hagauer, Imrich 1992).
↑ Hahn, Sabidussi, 1997.
↑ ¹ ² Sabidussi, 1960.
↑ ¹ ² Визинг, 1963.
↑ ¹ ² Imrich, Klavžar, 2000.
↑ Imrich, Klavžar, 2000, с. Theorem 4.19.
↑ Sabidussi, 1957.
↑ Kaveh, Rahami, 2005.

Литература

F. Aurenhammer, J. Hagauer, W. Imrich. Cartesian graph factorization at logarithmic cost per edge // Computational Complexity. — 1992. — Т. 2, вып. 4. — С. 331–349. — DOI:10.1007/BF01200428.
Joan Feigenbaum, John Hershberger, Alejandro A. Schäffer. A polynomial time algorithm for finding the prime factors of Cartesian-product graphs // Discrete Applied Mathematics. — 1985. — Т. 12, вып. 2. — С. 123–138. — DOI:10.1016/0166-218X(85)90066-6.
Geňa Hahn, Gert Sabidussi. Graph symmetry: algebraic methods and applications. — Springer, 1997. — Т. 497. — С. 116. — ISBN 978-0-7923-4668-5.
Wilfried Imrich, Sandi Klavžar. Product Graphs: Structure and Recognition. — Wiley, 2000. — ISBN 0-471-37039-8.
Wilfried Imrich, Sandi Klavžar, Douglas F. Rall. Graphs and their Cartesian Products. — A. K. Peters, 2008. — ISBN 1-56881-429-1.
Wilfried Imrich, Iztok Peterin. Recognizing Cartesian products in linear time // Discrete Mathematics. — 2007. — Т. 307, вып. 3-5. — С. 472–483. — DOI:10.1016/j.disc.2005.09.038.
A. Kaveh, H. Rahami. A unified method for eigendecomposition of graph products // Communications in Numerical Methods in Engineering with Biomedical Applications. — 2005. — Т. 21, вып. 7. — С. 377–388. — DOI:10.1002/cnm.753.
G. Sabidussi. Graphs with given group and given graph-theoretical properties // Canadian Journal of Mathematics. — 1957. — Т. 9. — С. 515–525. — DOI:10.4153/CJM-1957-060-7.
G. Sabidussi. Graph multiplication // Mathematische Zeitschrift. — 1960. — Т. 72. — С. 446–457. — DOI:10.1007/BF01162967.
В. Г. Визинг. Декартово произведение графов // Вычислительные системы. — 1963. — Т. 9. — С. 30–43.

Ссылки

Weisstein, Eric W. Graph Cartesian Product (англ.) на сайте Wolfram MathWorld.

Источник

Например: Найти декартово произведение графов Γ1 и Γ2

РЕШЕНИЕ.

Если даны два ориентированных графа Γ1 и Γ2, то их декартово произведение строится так. В качестве множества вершин берётся декартово произведение множеств вершин, то есть вершинами нового графа будут все пары вида (v1,v2), где vi — вершина графа Γi (i=1,2). Далее проводим ориентированные рёбра, делая это для каждой из пар ориентированных рёбер из Γ1 и Γ2. Например, если e1 и e2 — два таких ребра, где первое идёт из a в b, а второе из c в d, то проводим стрелочку из вершины (a,c) в вершину (b,d).

В Вашем примере получится ориентированный граф с четырьмя вершинами и одной стрелочкой.

Источник

Сообщение от 25th_July

Перелопатил инет, расходятся определения везде.

Сообщение от 25th_July

Везде говорится про декартово произведения в множествах, то есть просто про набор пар элементов.

Как к вам относиться ввиду следующих фактов?

1) Сначала вы говорите, что определения расходятся, что подразумевает, что вы все-таки нашли определения требуемого понятия, то есть декартова произведения орграфов.

2) Потом вы говорите, что вы нашли только определение декартова произведения множеств.

А если вы нашли только определения произведения множеств, значит, определение в сообщении №1 вы придумали? И где вы нашли различные определения произведения множеств?

Сообщение от 25th_July

Что значит статус матрицы смежности?

В сообщении №1 вы привели матрицу 9×9, но не сказали, откуда ее взяли. Насколько я знаю, вы могли заполнить ее случайными числами.

В общем, возьмите уважаемый учебник по теории графов и изучите определение там. Можете взять следующие учебники.

Харари Ф. Теория графов. – М.: Мир, 1973.

Уилсон Р. Введение в теорию графов. – М.: Мир, 1977.

Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. – М.: Наука, 1990.

Берж К. Теория графов и ее применения. – М.: Изд. иностр. лит., 1962.

Новиков Ф.А. Дискретная математика для программистов. СПб: Питер, 2001.

Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженеров. М.: Энергоатомиздат, 1988. 2-е изд., переработанное и дополненное.

Нефедов В.Н., Осипова В.А. Курс дискретной математики: Учеб. пособие. – М.: Изд-во МАИ, 1992.

Источник

Виды произведений[править | править код]

Мнемоника[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Примеры

Свойства

Алгебраическая теория графов

История

Примечания

Литература

Ссылки

Вам также может понравиться

Как найти мужа негра

Как найти сумму делителей нескольких чисел

Как играть небо тебя найдет

Добавить комментарий Отменить ответ