Как найти произведение логарифмов - Сайт, где вы сможете решить свои вопросы

Умножение логарифмов

Содержание:

Понятие логарифма. Примеры с решением
Свойства логарифмов
Возможно вам будут полезны данные страницы:
Логарифм степени и произведение числа и логарифма

1 случай. Доказательство. Используя частный случай формулы перехода к новому основанию (свойство 11), будем иметь: Что и требовалось доказать. например.

2 случай. При умножении нескольких логарифмов с разными основаниями выражение также можно в некоторых случаях упростить, перейдя к логарифмам с одним основанием по формуле перехода

Логарифмом положительного числа по основанию называется показатель степени, в которую надо возвести , чтобы получить : Например, т.е т. е. т. е. Логарифм единицы по любому основанию равен нулю.

Понятие логарифма. Примеры с решением

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Пример 1:

Найдите число a) б) Решение: а) Поскольку то

б) Поскольку то тогда

Пример 2:

Вычислите: а) б) Решение: а) б)

Свойства логарифмов

Логарифм произведения и сумма логарифмов Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел. Сумма логарифмов положительных чисел равна логарифму произведения этих чисел.

Пример 3:

Вычислите: a) б) в) Решение: а) б) в)

Возможно вам будут полезны данные страницы:

Пример 4:

Найдите значение выражения: Решение:

Логарифм частного двух положительных чисел равен разности логарифмов этих чисел.

Разность логарифмов двух чисел равен логарифму частного.

Пример 5:

Вычислите: Решение:

Пример 6:

Вычислите: Решение:

Логарифм степени и произведение числа и логарифма

Логарифм степени положительного числа равен произведению показателя степени и логарифма этого числа.

Пример 7:

Вычислите: а) б) в) г) д)

Решение: а) б) в) г) д)

Пример 8:

Упростите: a) б) Решение: а) б)

Пример 9:

Вычислите: а) б) в) Решение: а) б) в)

Лекции:

Вычислить определитель матрицы
Геометрический и физический смысл производной
Найти фундаментальную систему решений
Квадратичные формы
Преобразование выражений, содержащих переменную под знаком логарифма
Среднее квадратическое отклонение
Численные методы решения слау
Уравнение нормали: пример решения
Метод множителей Лагранжа
Интегралы, зависящие от параметра

Источник

Умножение логарифмов

Умножение логарифмов может быть выполнено в отдельных случаях с привлечением тех или иных свойств логарифмов. Готовой формулы для умножения логарифмов нет.

Например, два логарифма, у которых основание и выражение под знаком логарифма меняются местами — взаимно обратные числа:

$[{log _a}b cdot {log _b}a = {log _a}b cdot frac{1}{{{{log }_a}b}} = 1]$

Примеры.

$[1){log _2}3 cdot {log _3}2 = {log _2}3 cdot frac{1}{{{{log }_2}3}} = 1;]$

$[2)lg 7 cdot {log _7}10 = lg 7 cdot frac{1}{{lg 7}} = 1;]$

$[3)ln 5 cdot {log _5}e = ln 5 cdot frac{1}{{ln 5}} = 1.]$

При умножении нескольких логарифмов с разными основаниями можно попытаться перейти к логарифмам с одинаковым основанием по формуле

$[{log _a}b = frac{{{{log }_c}b}}{{{{log }_c}a}}]$

Пример.

Найти значение выражения:

$[{log _{16}}3 cdot {log _3}7 cdot {log _7}41 cdot {log _{41}}128]$

Решение:

Приведём все логарифмы к одинаковому основанию. Удобнее всего перейти к основанию 10 (короче запись)

$[{log _{16}}3 = frac{{lg 3}}{{lg 16}},{log _3}7 = frac{{lg 7}}{{lg 3}},]$

$[{log _7}41 = frac{{lg 41}}{{lg 7}},{log _{41}}128 = frac{{lg 128}}{{lg 41}}]$

$[{log _{16}}3 cdot {log _3}7 cdot {log _7}41 cdot {log _{41}}128 = ]$

$[ = frac{{lg 3 cdot lg 7 cdot lg 41 cdot lg 128}}{{lg 16 cdot lg 3 cdot lg 7 cdot lg 41}} = ]$

Сократив дробь, приходим к частному двух логарифмов по одинаковому основанию и переходим от частного логарифмов к одному логарифму

$[ = frac{{lg 128}}{{lg 16}} = {log _{16}}128 = ]$

По формуле

$[{log _{{a^n}}}{a^m} = frac{m}{n}{log _a}a = frac{m}{n}]$

$[ = {log _{{2^4}}}{2^7} = frac{7}{4} = 1,75.]$

(Вариант — сразу же во всех логарифмах перейти к основанию 2).

Умножение логарифмов с одинаковыми основаниями также можно попытаться изменить, используя свойства логарифмов.

Примеры.

Вычислить:

$[log _{21}^23 + {log _{21}}7 cdot {log _{21}}63 = ]$

$[ = log _{21}^23 + {log _{21}}7 cdot ({log _{21}}7 + 2{log _{21}}3) = ]$

$[ = log _{21}^23 + log _{21}^27 + 2{log _{21}}3 cdot {log _{21}}7 = ]$

По формуле квадрата суммы

$[ = {({log _{21}}3 + {log _{21}}7)^2} = {({log _{21}}(3 cdot 7))^2} = ]$

$[ = {({log _{21}}21)^2} = {1^2} = 1.]$

Источник

Данная статья содержит сводку разнообразных алгебраических и аналитических тождеств, связанных с логарифмами. Эти тождества особенно полезны при решении алгебраических и дифференциальных уравнений, содержащих логарифмы.

Далее все переменные подразумеваются вещественными, основания логарифма и логарифмируемые выражения положительны, причём основание логарифма не равно 1. Обобщение на комплексные числа см. в статье Комплексный логарифм.

Алгебраические тождества[править | править код]

Из определения логарифма следует основное логарифмическое тождество^[1]:

$a^{log _{a}b}=b$

Ещё несколько равенств, очевидных из определения логарифма:

${displaystyle log _{a}1=0}$

${displaystyle log _{a}a=1}$

${displaystyle log _{a}a^{b}=b}$

Логарифм произведения, частного от деления, степени и корня[править | править код]

Сводка тождеств^[2]:

	Формула	Пример	Доказательство
Произведение	${displaystyle log _{a}(xy)=log _{a}(x)+log _{a}(y)}$	${displaystyle log _{3}(243)=log _{3}(9cdot 27)=log _{3}(9)+log _{3}(27)=2+3=5}$
Частное от деления	${displaystyle log _{a}!left({frac {x}{y}}right)=log _{a}(x)-log _{a}(y)}$	$lg left({frac {1}{1000}}right)=lg(1)-lg(1000)=0-3=-3$
Степень	${displaystyle log _{a}(x^{p})=plog _{a}(x)}$	${displaystyle log _{2}(64)=log _{2}(2^{6})=6log _{2}(2)=6}$	Доказательство ${displaystyle log _{a}{x^{p}}=y}$ ${displaystyle a^{y}=x^{p}}$ ${displaystyle a^{frac {y}{p}}=x}$ ${displaystyle log_{a}{x}={frac {y}{p}}}$ ${displaystyle pcdot log_{a}{x}=y}$
Степень в основании	${displaystyle log _{(a^{p})}(x)={frac {1}{p}}log _{a}(x)={frac {log _{a}(x)}{p}}}$	${displaystyle log _{2^{10}}{sin {({frac {pi }{6}})}}={frac {log _{2}{frac {1}{2}}}{10}}=-{frac {1}{10}}=-0.1}$	Доказательство ${displaystyle log _{a^{p}}{x}=y}$ ${displaystyle a^{ycdot p}=x}$ ${displaystyle log_{a}{x}=pcdot y}$ ${displaystyle {frac {log_{a}{x}}{p}}=y}$
Корень	${displaystyle log _{a}{sqrt[{p}]{(x)}}={frac {1}{p}}log _{a}(x)={frac {log _{a}(x)}{p}}}$	$lg {sqrt {1000}}={frac {1}{2}}lg 1000={frac {3}{2}}=1.5$	Доказательство ${displaystyle log _{a}{sqrt[{p}]{x}}=y}$ ${displaystyle a^{y}={sqrt[{p}]{x}}}$ ${displaystyle a^{pcdot y}=x}$ ${displaystyle log_{a}{x}=pcdot y}$ ${displaystyle {frac {log_{a}{x}}{p}}=y}$
Корень в основании	${displaystyle log _{sqrt[{p}]{a}}(x)=plog _{a}(x)}$	${displaystyle log _{sqrt {pi }}{(4cdot arctan {1})}=2cdot log _{pi }{(4cdot {frac {pi }{4}})}=2cdot log _{pi }{(pi )}=2}$	Доказательство ${displaystyle log _{sqrt[{p}]{a}}{x}=y}$ ${displaystyle a^{frac {y}{p}}=x}$ ${displaystyle a^{y}=x^{p}}$ ${displaystyle a^{frac {y}{p}}=x}$ ${displaystyle log_{a}{x}={frac {y}{p}}}$ ${displaystyle pcdot log_{a}{x}=y}$

Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные значения переменных, например:

$log _{a}|xy|=log _{a}|x|+log _{a}|y|$

$log _{a}!left|{frac {x}{y}}right|=log _{a}|x|-log _{a}|y|$

Формулы для логарифма произведения без труда обобщаются на произвольное количество сомножителей:

$log _{a}(x_{1}x_{2}dots x_{n})=log _{a}(x_{1})+log _{a}(x_{2})+dots +log _{a}(x_{n})$

$log _{a}|x_{1}x_{2}dots x_{n}|=log _{a}|x_{1}|+log _{a}|x_{2}|+dots +log _{a}|x_{n}|$

Логарифм суммы и разности[править | править код]

Хотя логарифм суммы (или разности) не выражается через логарифмы слагаемых, приведенные ниже формулы могут оказаться полезными.

${displaystyle log _{a}(b+c)=log _{a}b+log _{a}left(1+{frac {c}{b}}right)}$

${displaystyle log _{a}(b-c)=log _{a}b+log _{a}left(1-{frac {c}{b}}right),quad }$

здесь

Обобщение:

${displaystyle log _{a}sum limits _{k=1}^{N}b_{k}=log _{a}b_{1}+log _{a}left(1+sum limits _{k=2}^{N}{frac {b_{k}}{b_{1}}}right)=log _{a}b_{1}+log _{a}left(1+sum limits _{k=2}^{N}a^{left(log _{a}b_{k}-log _{a}b_{1}right)}right)}$

Замена основания логарифма[править | править код]

Логарифм $log _{a}b$ по основанию можно преобразовать^[3] в логарифм по другому основанию :

$log _{a}b={frac {log _{c}b}{log _{c}a}}$

Следствие (при b=c ) — перестановка основания и логарифмируемого выражения:

$log _{a}b={frac {1}{log _{b}a}}$

Другие тождества[править | править код]

Если выражения для основания логарифма и для логарифмируемого выражения содержат возведение в степень, для упрощения можно применить следующее тождество:

${log _{a^{q}}{b}}^{p}={frac {p}{q}}log _{a}{b}$

Это тождество сразу получается, если в логарифме слева заменить основание $a^{q}$ на по вышеприведённой формуле замены основания. Следствия:

$log _{a^{k}}b={frac {1}{k}}log _{a}b;quad log _{sqrt[{n}]{a}}b=nlog _{a}b;quad log _{a^{k}}b^{k}=log _{a}b$

Ещё одно полезное тождество:

$c^{log _{a}b}=b^{log _{a}c}$

Для его доказательства заметим, что логарифмы левой и правой частей по основанию совпадают (равны ${displaystyle log _{a}bcdot log _{a}c}$ ), а тогда левая и правая части тождественно равны. Прологарифмировав предыдущее тождество по произвольному основанию получаем ещё одно тождество «обмена основаниями»:

${displaystyle log _{a}bcdot log _{d}c=log _{d}bcdot log _{a}c}$

Это тождество легко распространить на любое число сомножителей, например:

${displaystyle log _{a}xcdot log _{b}ycdot log _{c}zcdot log _{d}w=log _{b}xcdot log _{d}ycdot log _{c}zcdot log _{a}w}$

Другими словами, в произведении такого вида можно делать произвольную перестановку оснований логарифмов.

${displaystyle x^{frac {log _{a}b}{log _{a}x}}=b}$

Это тождество также просто доказать, прологарифмировав обе части по основанию

${displaystyle log _{xy}a={frac {1}{{frac {1}{log _{x}a}}+{frac {1}{log _{y}a}}}}}$

Для доказательства этого тождества надо дважды применить приведенное выше правило перестановки:

${displaystyle {frac {1}{log _{x}a}}=log _{a}x;quad {frac {1}{log _{y}a}}=log _{a}y;quad {frac {1}{log _{a}(xy)}}=log _{xy}a}$

Аналитические тождества[править | править код]

Предельные соотношения[править | править код]

Приведём несколько полезных пределов, связанных с логарифмами^[4]:

$lim _{xto 0}{frac {log _{a}(1+x)}{x}}=log _{a}e={frac {1}{ln a}}$

$lim _{xto 0^{+}}x^{b}log _{a}x=0quad (b>0)$

$lim _{xto infty }{frac {log _{a}x}{x^{b}}}=0quad (b>0)$

$ln x=lim _{nto infty }nleft({sqrt[{n}]{x}}-1right)=lim _{nto infty }nleft(1-{frac {1}{sqrt[{n}]{x}}}right)$

$ln x=lim _{hto 0}{frac {x^{h}-1}{h}}$

Производная и интеграл[править | править код]

Производная для логарифмической функции вычисляется по формуле:

{displaystyle {d over dx}ln x={1 over x},}

${displaystyle {d over dx}log _{a}x={1 over xln a}={log _{a}e over x}}$

Определение логарифма через определённый интеграл:

${displaystyle ln x=int _{1}^{x}{frac {1}{t}}dt}$

Первообразная для логарифма:

${displaystyle int log _{a}x,dx=x(log _{a}x-log _{a}e)+C}$

Чтобы привести формулы для интегралов высоких порядков, обозначим ${displaystyle H_{n} n-}$ е по порядку гармоническое число:

${displaystyle H_{n}={frac {1}{1}}+{frac {1}{2}}+{frac {1}{3}}+dots +{frac {1}{n}}}$

Далее обозначим:

${displaystyle x^{left[0right]}=ln x}$

${displaystyle x^{left[nright]}=x^{n}(ln x-H_{n});quad }$

(

)

Мы получаем последовательность функций:

${displaystyle x^{left[1right]}=xln x-x}$

${displaystyle x^{left[2right]}=x^{2}ln x-{begin{matrix}{frac {3}{2}}end{matrix}},x^{2}}$

${displaystyle x^{left[3right]}=x^{3}ln x-{begin{matrix}{frac {11}{6}}end{matrix}},x^{3}}$

и т. д. Тогда имеют место тождества:

${displaystyle {frac {d}{dx}},x^{left[nright]}=n,x^{left[n-1right]};quad }$

(

)

${displaystyle int x^{left[nright]},dx={frac {x^{left[n+1right]}}{n+1}}+C;quad }$

(

)

Примечания[править | править код]

↑ Алгебра и начала анализа. Учебник для 10—11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 233.
↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187.
↑ Корн Г., Корн Т. Справочник по математике, 1973, с. 34.
↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 164.

Литература[править | править код]

Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: АСТ, 2003, ISBN 5-17-009554-6.
Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.
Шахмейстер А. Х. Логарифмы. Пособие для школьников, абитуриентов и преподавателей. — изд. 5-е. — СПб.: МЦНМО, 2016. — 288 с. — ISBN 978-5-4439-0648-5.

Ссылки[править | править код]

Weisstein, Eric W. Logarithm (англ.) на сайте Wolfram MathWorld.

Источник

Наталья Игоревна Восковская

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Логарифм произведения двух чисел $x$ и $y$ равен сумме логарифмов этих чисел при условии, что $x, y, a$ – положительные числа и $a ne 1$:

$log_{a}⁡(x cdot y)=log_{a}⁡x+log_{a}⁡y$.

Докажем данную теорему:

Возьмем два положительных числа $х$ и $у$. Примем $log_{a}⁡x=k$, $log_{a}⁡y=l$. Тогда $x=a^k$ и $y=a^l$. Найдем их произведение:

$x cdot y=a^k cdot a^l=a^{k+l}$.

Из выражения $x cdot y=a^{k+l}$ получим $k+l=log_{a}⁡(x cdot y)$.

Т.к. $k=log_{a}⁡x$, $l=log_{a}⁡y$, тогда $log_{a}⁡(x cdot y)=log_{a}⁡x+log_{a}⁡y$.

Формула логарифма произведения применяется для упрощения вычисления логарифмов.

Пример 1

$log_{11}⁡21=log_{11}⁡(3 cdot 7)=log_{11}⁡3+log_{11}⁡7$;

$log_{1,8}1,8 sqrt{11}=log_{1,8}⁡1,8+log_{1,8} sqrt{11}=1+log_{1,8} sqrt{11}$.

Формула логарифма произведения

Теорема 2

Формула логарифма произведения распространяется не только на произведение двух чисел, но и на произведение конечного количества чисел:

$log_{a}⁡(x_1 cdot x_2 cdot cdots cdot x_n )=log_{a}x_1+log_{a}x_2+ cdots +log_{a}x_n$

при $a, x_1, x_2, cdots, x_n > 0$ , $a ne 1$.

Пример 2

$lg⁡(12sqrt{3} y)=lg⁡12+lgsqrt{3}+lg⁡y$.

Замечание 1

Логарифм произведения применяется в тех случаях, когда необходимо упростить выражение или выражение данного логарифма через другой необходимо для его вычисления при известном значении другого логарифма.

Пример 3

Вычислить $log_{13}⁡2197$.

Решение.

Применим свойство логарифма произведения:

$log_{13}⁡2197=log_{13}⁡(13 cdot 13 cdot 13)=log_{13}⁡13+log_{13}⁡13+log_{13}⁡13=3 log_{13}13=3 cdot 1=3$.

Ответ: $log_{13}⁡2197=3$.

«Логарифм произведения» 👇

Данный пример демонстрирует применение формулы логарифма числа, которое раскладывается на три множителя.

Пример 4

Вычислить $log_{7}49 sqrt[3]{49}$.

Решение.

Применим теорему о логарифме произведения:

$log_{7}49 sqrt[3]{49}=log_{7}⁡49+log_{7} sqrt[3]{49}=$

подлогарифмические выражения обоих логарифмов запишем как основание логарифма в степени, а затем применим формулу логарифма степени:

$=log_{7}7^2+log_{7}7^{frac{2}{3}}=$

показатели степени вынесем из-под знака логарифма и запишем перед ним:

$=2 log_{7}⁡7+frac{2}{3} log_{7}⁡7=2+frac{2}{3}=2 frac{2}{3}$.

Ответ: $log_{7}49 sqrt[3]{49}=2 frac{2}{3}$.

Сумма логарифмов

Верным будет и обратное определение:

Теорема 3

Сумму логарифмов с одинаковыми основаниями можно представить в виде логарифма произведения подлогарифмических выражений:

$log_{a}⁡x+log_{a}⁡y=log_{a}⁡(x cdot y)$

при $x, y, a > 0$, $a ne 1$.

Пример 5

Упростить выражение $log_{11}⁡8+log_{11}⁡20$.

Решение.

Применим формулу суммы логарифмов:

$log_{11}⁡8+log_{11}⁡20=log_{11}⁡(8 cdot 20)=log_{11}⁡160$.

Ответ: $log_{11}⁡8+log_{11}⁡20=log_{11}⁡160$.

Пример 6

Упростить выражение $log_{39}3+log_{39}13$.

Решение.

Применив формулу суммы логарифмов и воспользовавшись свойством $log_{a}⁡a=1$, получим:

$log_{39}⁡3+log_{39}⁡13=log_{39}⁡(3 cdot 13)=log_{39}⁡39=1$.

Ответ: $log_{39}⁡3+log_{39}⁡13=1$.

Пример 7

Упростить выражение $log_{12}⁡2+log_{12}⁡72$.

Решение.

По формуле суммы логарифмов:

$log_{12}⁡2+log_{12}⁡72=log_{12}⁡(2 cdot 72)=log_{12}⁡144=$

запишем подлогарифмическое выражение как основание логарифма $12$ в определенной степени:

$=log_{12}12^2=$

теперь можем применить свойство логарифма степени:

$=2 log_{12}⁡12=$

воспользуемся свойством $log_{a}⁡a=1$ и получим:

$=2 cdot 1=2$.

Ответ: $log_{12}⁡2+log_{12}⁡72=2$.

Пример 8

Упростить выражение $log_{4}⁡32+log_{4}⁡128$.

Решение.

Согласно сумме логарифмов:

$log_{4}⁡32+log_{4}⁡128=log_{4}⁡(32 cdot 128)=log_{4}⁡4096=$

запишем подлогарифмическое выражение как основание логарифма $4$ в определенной степени:

$=log_{4}4^6=$

теперь можем применить свойство логарифма степени:

$=6 log_{4}⁡4=$

воспользуемся свойством $log_{a}⁡a=1$ и получим:

$=6 cdot 1=6$.

Ответ: $log_{4}⁡32+log_{4}⁡128=6$.

Пример 9

Упростить выражение $log_{7}⁡98+log_{7}frac{1}{2}$.

Решение.

Используем формулу суммы логарифмов:

$log_{7}⁡98+log_{7}frac{1}{2}=log_{7}⁡(98 cdot frac{1}{2})=log_{7}⁡49=$

запишем подлогарифмическое выражение как основание логарифма $7$ в определенной степени:

$=log_{7}7^2=$

теперь можем применить свойство логарифма степени:

$=2 log_{7}⁡7=$

воспользуемся свойством $log_{a}⁡a=1$ и получим:

$=2 cdot 1=2$.

Ответ: $log_{7}⁡98+log_{7}frac{1}{2}=2$.

Пример 10

Упростить выражение $frac{log_{8}⁡4+log_{8}⁡16}{log_{6}⁡16+log_{6}⁡81}$.

Решение.

Применим к числителю и знаменателю формулу суммы логарифмов:

$frac{log_{8}⁡4+log_{8}⁡16}{log_{6}⁡16+log_{6}⁡81}=frac{log_{8}⁡(4 cdot 6)}{log_{6}⁡(16 cdot 81)} =frac{log_{8}⁡64}{log_{6}⁡1296} =$

запишем подлогарифмическое выражение в числителе как основание логарифма $8$ в определенной степени, а в знаменателе – как основание логарифма 6 в определенной степени:

$=frac{log_{8}8^2}{log_{6}6^4} =$

теперь можем применить свойство логарифма степени:

$=frac{2 log_{8}⁡8}{4 log_{6}⁡6}=$

воспользуемся свойством $log_{a}⁡a=1$ и получим:

$=frac{2}{4}=frac{1}{2}$.

Ответ: $frac{log_{8}⁡4+log_{8}⁡16}{log_{6}⁡16+log_{6}⁡81}=frac{1}{2}$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Умножение логарифмов

$log _{a} bcdot log _{b} a=1,; a,, b>0,; a,, bne 1$

1 случай. .

Доказательство. Используя частный случай формулы перехода к новому основанию (свойство 11), будем иметь:

$[log _{a} bcdot log _{b} a=log _{a} bcdot frac{1}{log _{a} b} =1]$

Что и требовалось доказать.

$log _{2} 5cdot log _{5} 2=log _{2} 5cdot frac{1}{log _{2} 5} =1$

Например. .

2 случай. При умножении нескольких логарифмов с разными основаниями выражение также можно в некоторых случаях упростить, перейдя к логарифмам с одним основанием по формуле перехода

$[log _{a} b=frac{log _{c} b}{log _{c} a} ,; a,, b,, c>0;; a,, cne 1]$

Примеры решения задач

Задание	Найти значение выражения $log _{3} 5cdot log _{5} 7cdot log _{7} 8cdot log _{8} 9$ .
Решение	Приведем все логарифмы к одному основанию, например, 3:

$[log _{3} 5cdot log _{5} 7cdot log _{7} 8cdot log _{8} 9=log _{3} 5cdot frac{log _{3} 7}{log _{3} 5} cdot frac{log _{3} 8}{log _{3} 7} cdot frac{log _{3} 9}{log _{3} 8} ]$

После сокращения будем иметь:

$[log _{3} 5cdot log _{5} 7cdot log _{7} 8cdot log _{8} 9=log _{3} 9=2]$

3 случай. Произведение логарифмов с одинаковыми основаниями также можно иногда преобразовать, основываясь на свойствах логарифма.

Основные свойства логарифмов

Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.

Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.

Сложение и вычитание логарифмов

Рассмотрим два логарифма с одинаковыми основаниями: log _a x и log _a y . Тогда их можно складывать и вычитать, причем:

log _a x + log _a y = log _a ( x · y );
log _a x − log _a y = log _a ( x : y ).

Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают!

Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры — и убедитесь:

Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log₆ 4 + log₆ 9 = log₆ (4 · 9) = log₆ 36 = 2.

Основания одинаковые, используем формулу разности:
log₂ 48 − log₂ 3 = log₂ (48 : 3) = log₂ 16 = 4.

Задача. Найдите значение выражения: log₃ 135 − log₃ 5.

Снова основания одинаковые, поэтому имеем:
log₃ 135 − log₃ 5 = log₃ (135 : 5) = log₃ 27 = 3.

Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.

Вынесение показателя степени из логарифма

Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:

log _a x n = n · log _a x ;

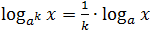
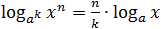
Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.

Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.

Задача. Найдите значение выражения: log₇ 49 6 .

Избавимся от степени в аргументе по первой формуле:
log₇ 49 6 = 6 · log₇ 49 = 6 · 2 = 12

Задача. Найдите значение выражения:

[Подпись к рисунку]

Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 16 = 2 4 ; 49 = 7 2 . Имеем:

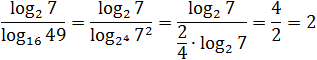
[Подпись к рисунку]

Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели — получили «трехэтажную» дробь.

Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log₂ 7. Поскольку log₂ 7 ≠ 0, можем сократить дробь — в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.

Переход к новому основанию

Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?

На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:

Пусть дан логарифм log _a x . Тогда для любого числа c такого, что c > 0 и c ≠ 1, верно равенство:

[Подпись к рисунку]

В частности, если положить c = x , получим:

[Подпись к рисунку]

Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.

Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.

Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:

Задача. Найдите значение выражения: log₅ 16 · log₂ 25.

Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log₅ 16 = log₅ 2 4 = 4log₅ 2; log₂ 25 = log₂ 5 2 = 2log₂ 5;

А теперь «перевернем» второй логарифм:

[Подпись к рисунку]

Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.

Задача. Найдите значение выражения: log₉ 100 · lg 3.

Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:

[Подпись к рисунку]

Теперь избавимся от десятичного логарифма, перейдя к новому основанию:

[Подпись к рисунку]

Основное логарифмическое тождество

Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:

n = log _a a n

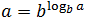
В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.

Вторая формула — это фактически перефразированное определение. Она так и называется: .

В самом деле, что будет, если число b возвести в такую степень, что число b в этой степени дает число a ? Правильно: получится это самое число a . Внимательно прочитайте этот абзац еще раз — многие на нем «зависают».

Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.

Задача. Найдите значение выражения:

[Подпись к рисунку]

Заметим, что log₂₅ 64 = log₅ 8 — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:

[Подпись к рисунку]

Если кто-то не в курсе, это была настоящая задача из ЕГЭ 🙂

Логарифмическая единица и логарифмический ноль

В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.

log _a a = 1 — это . Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице.
log _a 1 = 0 — это . Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a 0 = 1 — это прямое следствие из определения.

Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.

Умножение логарифмов

Логарифмом положительного числа по основанию называется показатель степени, в которую надо возвести , чтобы получить : Например, т.е т. е. т. е. Логарифм единицы по любому основанию равен нулю.

Понятие логарифма. Примеры с решением

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Пример 1:

Найдите число a) б) Решение: а) Поскольку то

б) Поскольку то тогда

Пример 2:

Вычислите: а) б) Решение: а) б)

Свойства логарифмов

Пример 3:

Вычислите: a) б) в) Решение: а) б) в)

Возможно вам будут полезны данные страницы:

Пример 4:

Найдите значение выражения: Решение:

Логарифм частного двух положительных чисел равен разности логарифмов этих чисел.

Разность логарифмов двух чисел равен логарифму частного.

Пример 5:

Вычислите: Решение:

Пример 6:

Вычислите: Решение:

Логарифм степени и произведение числа и логарифма

Логарифм степени положительного числа равен произведению показателя степени и логарифма этого числа.

Пример 7:

Вычислите: а) б) в) г) д)

Решение: а) б) в) г) д)

Пример 8:

Упростите: a) б) Решение: а) б)

Пример 9:

Вычислите: а) б) в) Решение: а) б) в)

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник

Умножение логарифмов

Понятие логарифма. Примеры с решением

Пример 1:

Пример 2:

Свойства логарифмов

Пример 3:

Возможно вам будут полезны данные страницы:

Пример 4:

Пример 5:

Пример 6:

Логарифм степени и произведение числа и логарифма

Пример 7:

Пример 8:

Пример 9:

Алгебраические тождества[править | править код]

Логарифм произведения, частного от деления, степени и корня[править | править код]

Логарифм суммы и разности[править | править код]

Замена основания логарифма[править | править код]

Другие тождества[править | править код]

Аналитические тождества[править | править код]

Предельные соотношения[править | править код]

Производная и интеграл[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Формула логарифма произведения

Сумма логарифмов

Умножение логарифмов

Примеры решения задач

Основные свойства логарифмов

Сложение и вычитание логарифмов

Вынесение показателя степени из логарифма

Переход к новому основанию

Основное логарифмическое тождество

Логарифмическая единица и логарифмический ноль

Умножение логарифмов

Понятие логарифма. Примеры с решением

Пример 1:

Пример 2:

Свойства логарифмов

Пример 3:

Возможно вам будут полезны данные страницы:

Пример 4:

Пример 5:

Пример 6:

Логарифм степени и произведение числа и логарифма

Пример 7:

Пример 8:

Пример 9:

Вам также может понравиться

Как можно найди фильм по сюжету

Как найти айфон с приложением локатор

Как найти кратчайший путь между точками

Добавить комментарий Отменить ответ