Как найти произведение вектора на скаляр

Скаля́рное произведе́ние (иногда называемое внутренним произведением) — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат.
Используется в определении длины векторов и угла между ними.

Обычно для скалярного произведения векторов и используется одно из следующих обозначений.

или просто

и второе обозначение применяется в квантовой механике для векторов состояния^[1].

В простейшем случае, а именно в случае конечномерного вещественного евклидового пространства, иногда используют «геометрическое» определение скалярного произведения ненулевых векторов и как произведения длин этих векторов на косинус угла между ними^[2]:

Равносильное определение: скалярное произведение есть произведение длины проекции первого вектора на второй и длины второго вектора (см. рисунок). Если хотя бы один из векторов нулевой, то произведение считается равным нулю^[3].

У понятия скалярного произведения существует также большое количество обобщений для различных векторных пространств, то есть для множеств векторов с операциями сложения и умножения на скаляры^[⇨]. Данное выше геометрическое определение скалярного произведения предполагает предварительное определение понятий длины вектора и угла между ними. В современной математике используется обратный подход: аксиоматически определяется скалярное произведение, а уже через него — длины и углы^[4]. В частности, скалярное произведение определяется для комплексных векторов, многомерных и бесконечномерных пространств, в тензорной алгебре.

Скалярное произведение и его обобщения играют чрезвычайно большую роль в векторной алгебре, теории многообразий, механике и физике. Например, работа силы при механическом перемещении равна скалярному произведению вектора силы на вектор перемещения^[5].

Определение и свойства[править | править код]

Будем говорить, что в вещественном или комплексном векторном пространстве определено скалярное произведение, если каждой паре векторов из поставлено в соответствие число из того числового поля, над которым задано удовлетворяющее следующим аксиомам.

1. Для любых трёх элементов пространства и любых чисел справедливо равенство: (линейность скалярного произведения по первому аргументу).
2. Для любых справедливо равенство , где черта означает комплексное сопряжение.
3. Для любого имеем: , причём только при (положительная определённость и невырожденность скалярного произведения соответственно).

Заметим, что из аксиомы 2 следует, что — вещественное число. Поэтому аксиома 3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения. Если аксиома 3 не выполняется, то произведение называется индефинитным или неопределённым.

Если не только при , то произведение называется квазискалярным^[6].

Из данных аксиом получаются следующие свойства:

1. коммутативность для вещественных векторов:

   

   Дистрибутивность скалярного произведения в случае вещественного евклидового пространства

2. дистрибутивность относительно сложения: и
3. инволюционная линейность относительно второго аргумента: (в случае вещественного — просто линейность по второму аргументу).
4. (что совпадает с для вещественного ).

Также есть свойства, связанные не с данными аксиомами:

1. неассоциативность относительно умножения на вектор^[7]‘: ;
2. ортогональность: два ненулевых вектора a и b ортогональны тогда и только тогда, когда (a, b) = 0 (определения ниже).

Замечание. В квантовой физике скалярное произведение (волновых функций, которые комплекснозначны) принято определять как линейное по второму аргументу (а не по первому), соответственно, по первому аргументу оно будет инволюционо линейным. Путаницы обычно не возникает, поскольку традиционное обозначение для скалярного произведения в квантовой физике также отличается: , т.е. аргументы отделяются вертикальной чертой, а не запятой, и скобки всегда угловые.

Определение и свойства в евклидовом пространстве[править | править код]

Вещественные векторы[править | править код]

В -мерном вещественном евклидовом пространстве векторы определяются своими координатами — наборами вещественных чисел в ортонормированном базисе. Определить скалярное произведение векторов можно так^[4]:

Проверка показывает, что все три аксиомы выполнены.

Например, скалярное произведение векторов и будет вычислено так:

Можно доказать^[8], что эта формула равносильна определению через проекции или через косинус:

Комплексные векторы[править | править код]

Для комплексных векторов определим аналогично^[9]:

Пример (для ):

Свойства[править | править код]

Помимо общих свойств скалярного произведения, для многомерных евклидовых векторов верно следующее:

1. в отличие от обычного умножения скаляров, где если ab = ac и a ≠ 0, то b равняется c, для скалярного умножения векторов это неверно: если a · b = a · c, то есть a · (b − c) = 0, то в общем случае a и b − c лишь ортогональны; но вектор b − c в общем случае не равен 0, то есть b ≠ c;
2. правило произведения: для дифференцируемых вектор-функций a(t) и b(t) верно соотношение (a(t), b(t))′ = a′(t) ⋅ b(t) + a(t) ⋅ b′(t)^[10];
3. оценка угла между векторами:

   в формуле знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение больше 0, если угол между векторами острый, и меньше 0, если угол между векторами тупой;

4. проекция вектора на направление, определяемое единичным вектором :

   , так как

5. площадь параллелограмма, натянутого на два вектора и , равна

Теорема косинусов в вещественном пространстве[править | править код]

Теорема косинусов легко выводится с использованием скалярного произведения. Пусть на сторонах треугольника находятся векторы a, b и c, первые два из которых образуют угол θ, как показано в изображении справа. Тогда, следуя свойствам и определению скалярного произведения через косинус:

Связанные определения[править | править код]

В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия^[11]:

Длина вектора, под которой обычно понимается его евклидова норма:

(термин «длина» обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).

Углом между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):

Данные определения позволяют сохранить формулу: и в общем случае. Корректность формулы для косинуса гарантирует неравенство Коши — Буняковского^[12]:

В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):

• Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например, ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.
• Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называется предгильбертовым пространством.
  • При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.
• Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.

История[править | править код]

Скалярное произведение было введено У. Гамильтоном в 1846 году^[13] одновременно с векторным произведением в связи с кватернионами — соответственно, как скалярная и векторная часть произведения двух кватернионов, скалярная часть которых равна нулю^[14].

Вариации и обобщения[править | править код]

В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных или комплексных функций можно ввести положительно определённое скалярное произведение:

При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора^[15] :

При этом сама метрика (говоря точнее, её представление в данном базисе) так связана со скалярными произведениями базисных векторов :

Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:

где К — положительно определённая, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определённое скалярное произведение).

Простейшим обобщением конечномерного скалярного произведения в тензорной алгебре является свёртка по повторяющимся индексам.

См. также[править | править код]

• Гильбертово пространство
• Векторное произведение
• Внешнее произведение
• Псевдоскалярное произведение
• Смешанное произведение

Примечания[править | править код]

Литература[править | править код]

• Гельфанд И. М. Лекции по линейной алгебре. — 4-е изд. — М.: Наука, 1971. — 272 с.

Ссылки[править | править код]

• Емелин А. Скалярное произведение векторов. Дата обращения: 14 ноября 2019.

Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.

Скалярное произведение векторов

Формула

Пусть даны векторы $ overline{a} = (a_x; a_y) $ и $ overline{b} = (b_x; b_y) $. Как найти скалярное произведение векторов? Для того, чтобы найти скалярное произведение векторов необходимо воспользоваться формулой: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y $$ Стоит заметить, что скалярное произведение записывается в скобках, в которых векторы записываются через запятую. Данное обозначение широко применяется в математике и его нужно запомнить.

Если в задаче векторы заданы тремя координатами (в пространстве), то найти скалярное произведение векторов нужно по другой формуле, основанной на предыдущей. Но с тем же смыслом: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y + a_z cdot b_z $$

По сути скалярное произведение – это сумма произведений соответствующих координат данных векторов. Первая координата умножается на первую, вторая на вторую и затем произведения суммируются.

Примеры решений

Пример 1

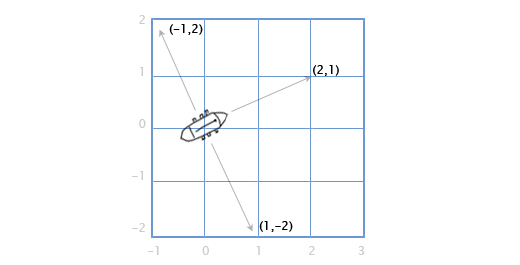
Найти скалярное произведение векторов $ overline{a} = (-1;2) $ и $ overline{b} = (2;1) $

Решение

В данном примере векторы заданы двумя координатами, поэтому применяем первую формулу для плоской задачи. Умножаем соответствующие координаты, а потом складываем их: $$ (overline{a},overline{b}) = -1 cdot 2 + 2 cdot 1 = -2 + 2 = 0 $$ Произведение получилось равным нулю, а это кстати означает, что векторы оказались ортогональными (перпендикулярными) друг к другу. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ (overline{a},overline{b}) = 0 $$

Пример 2

В пространстве заданы начала и концы векторов: $$ A = (1;3;-2), B = (-1;4;1), C = (2; 1; -2) $$ Требуется найти скалярное произведение векторов $ overline{AB} $ и $ overline{AC} $.

Решение

В примеры решения данной задачи даны только точки и сразу вычислить произведение векторов не представляется возможным. Сначала нужно найти сами векторы $ overline{AB} $ и $ overline{AC} $. Вычисляются они с помощью разности соответствующих координат точек (из конца вычитается начало вектора): $$ overline{AB} = (-1 – 1; 4-3; 1-(-2)) = (-2; 1; 3) $$ $$ overline{AC} = (2 – 1; 1 – 3; -2 – (-2)) = (1; -2; 0) $$ Теперь, когда необходимые векторы найдены, то вычисляем их произведение: $$ (overline{AB},overline{AC}) = -2 cdot 1 + 1 cdot (-2) + 3 cdot 0 = -2-2+0 = -4 $$

Ответ

$$ (overline{AB},overline{AC}) = -4 $$

В статье мы ответили на вопрос: «Как найти скалярное произведение векторов?», а так же привели формулы и примеры решений задач.

Определение.
Произведением вектора

на скаляр

называется вектор, модуль которого
равен произведению модулей сомножителей,
а направление совпадает с направлением
вектора
,
если число

положительно, и противоположно направлению
вектора
,
если число

отрицательно.

Произведение
вектора

на скаляр

обозначается

или
.
По определению:

1. ;

2. ,
   если
   , ,
   если
   ;

3. если
   ,
   то
   ;

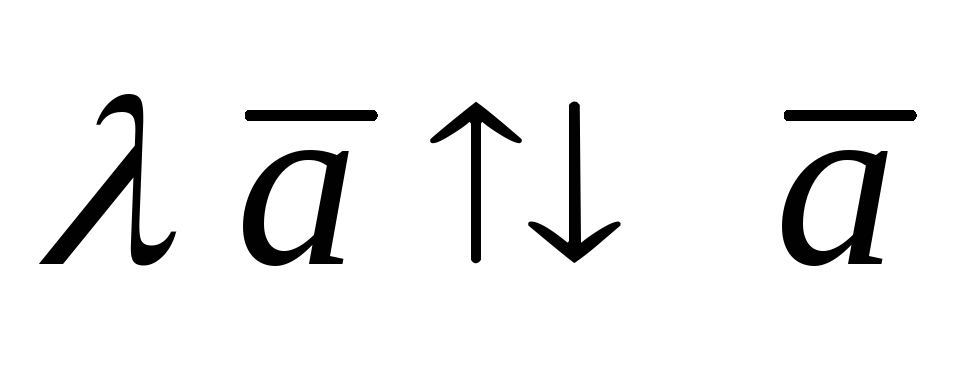4. если
   ,
   то
   .

Согласно
определению, произведение вектора

на скаляр

есть вектор, коллинеарный вектору
.

Теорема
(о проекции на ось произведения вектора
на скаляр). Проекция на ось произведения
вектора на скаляр равна произведению
этого скаляра на проекцию рассматриваемого
вектора на ту же ось, т.е.

,

где

– любая ось.

Доказательство.
По теореме о проекции вектора на ось

,

где

– орт оси
.
Если в правой части этого равенства
воспользоваться определением понятия
модуля произведения вектора на скаляр,
то получим

(*)

При
этом возможны следующие случаи:

1. 
   .

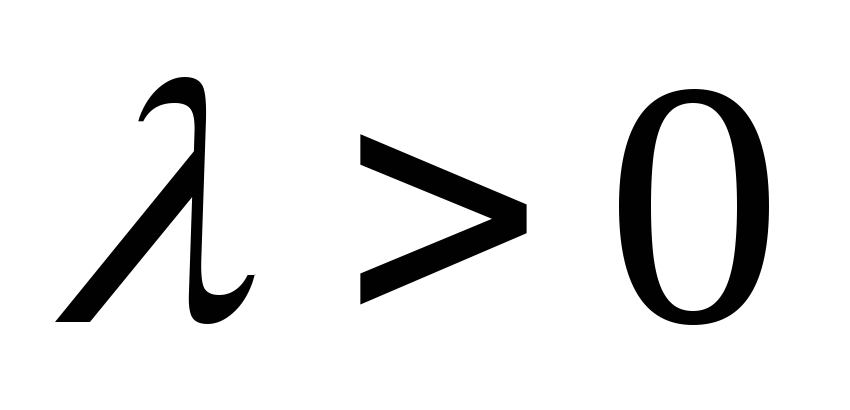
В
этом случае по определению модуля числа
.
Кроме того, при

,
и поэтому
.
Следовательно, в силу равенства (*) имеем

.

Если
теперь в правой части последнего
равенства воспользоваться свойством
сочетательности умножения чисел и
применить теорему о проекции вектора
на ось, то получим

.

1. 

В
этом случае по определению модуля числа
.
Кроме того, при

,
т.е.

и потому
.

Исходя
из равенства (*), приходим к выводу, что
в рассматриваемом случае

,

и
потому, как и при
,
имеем

.

В
справедливости утверждения при

предлагаем убедиться самостоятельно.

Основные
свойства операции умножения вектора
на скаляр

1. Умножение
вектора на скаляр обладает свойством
сочетательности, т.е.

.

Доказательство.
Для того, чтобы доказать, что векторы

и

равны, достаточно доказать, что равны
их проекции на любую ось. Пусть

– произвольная ось. Найдем проекции
векторов

и

на ось
.
Применяя теорему о проекции на ось
произведения вектора на скаляр, имеем
соответственно

и

В
силу свойства сочетательности умножения
чисел правые части двух последних
равенств совпадают, и потому

,

где

– любая ось. Следовательно, по критерию
равенства векторов,

.

2. Умножение
вектора на скаляр обладает свойством
распределительности по отношению к
сумме скаляров, т.е.

.

Доказательство.
Для того, чтобы доказать, что векторы

и

равны, достаточно доказать, что равны
их проекции на любую ось. Пусть

-произвольная ось. Согласно теореме о
проекции на ось произведения вектора
на скаляр, имеем

,

или,
учитывая свойство распределительности
действий над числами,

.

Если
же теперь в каждом слагаемом в правой
части применить теорему о проекции на
ось произведения вектора на скаляр, а
затем воспользоваться теоремой о
проекции суммы двух векторов на ось, то
придем к выводу, что

,

где

– любая ось. Следовательно, на основании
критерия равенства векторов,

.

3.
Умножение вектора на скаляр обладает
свойством распределительности по
отношению к сумме векторов, т.е.

Доказательство.
Для того, чтобы доказать, что векторы

и

равны, достаточно доказать, что равны
их проекции на любую ось. Пусть

– произвольная ось. По теореме о проекции
на ось произведения вектора на скаляр

.

Если
в правой части применить теорему о
проекции суммы векторов на ось, то
получим

,

или,
в силу свойства распределительности
действий над числами,

.

Если
же в каждом слагаемом правой части ещё
раз воспользоваться теоремой о проекции
на ось произведения вектора на скаляр,
а затем теоремой о проекции суммы
векторов на ось, то придем к выводу, что

,

где

– любая ось. Следовательно, по критерию
равенства векторов,

,

что
и требовалось доказать.

Теорема
о противоположных векторах

Произведение
вектора

на

есть вектор, противоположный вектору
.

Доказательство.
Действительно,
,

т.е.

и, кроме того,

Утверждение
доказано.

Вектор

обозначают
.
Введем теперь понятие разности двух
векторов.

Определение.
Разностью векторов

и

называется вектор, равный сумме вектора

и вектора, противоположного вектору
.

Разность
векторов

и

обозначается
.По
определению

.

Имеет
место равенство
,
где

– любая ось.

Если
воспользоваться этой формулой, то
нетрудно привести ещё одно доказательство,
наряду с рассмотренным ранее, критерия
равенства двух векторов. Рекомендуем
проделать это самостоятельно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Скалярное произведение в координатах

Вычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве.

Скаларное произведение двух векторов на плоскости, в трехмерном простарнстве называют сумму координат заданных векторов a→ и b→.

При вычислении на плоскости скаларного произведения заданных векторов a→=(ax,ay), b→=(bx,by) в декартовой системе используют:

a→,b→=ax·bx+ay·by,

для трехмерного пространства применимо выражение:

a→,b→=ax·bx+ay·by+az·bz.

Фактически это является третьим определением скалярного произведения.

Докажем это.

Скалярное произведение и его свойства

Существуют свойства скалярного произведения, которые применимы для a→,b→ и c→:

1. коммутативность (a→,b→)=(b→,a→);
2. дистрибутивность(a→+b→,c→)=(a→,c→)+(b→,c→), (a→+b→,c→)=(a→,b→)+(a→,c→);
3. сочетательное свойство (λ·a→,b→)=λ·(a→,b→),(a→,λ·b→)=λ·(a→,b→), λ – любое число;
4. скалярный квадрат всегда больше нуля (a→,a→)≥0, где (a→,a→)=0 в том случае, когда a→ нулевой.

Скалярное произведение с примерами и решениями

Любая задача такого плана решается с применением свойств и формул, касающихся скалярного произведения:

1. (a→,b→)=a→·b→·cos(a→,b→^);
2. (a→,b→)=a→·npa→b→=b→·npb→a→;
3. (a→,b→)=ax·bx+ay·by или (a→,b→)=ax·bx+ay·by+az·bz;
4. (a→,a→)=a→2.

Рассмотрим некоторые примеры решения.

Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию.

Физический смысл скалярного произведения

Механика рассматривает приложение скалярного произведения.

При работе А с постоянной силой F→ перемещаемое тело из точки M в N можно найти произведение длин векторов F→ и MN→ с косинусом угла между ними, значит работа равна произведению векторов силы и перемещения:

A=(F→,MN→).

Эта статья является переводом цикла из четырёх статей «Linear algebra for game developers», написанных David Rosen и посвящённых линейной алгебре и её применению в разработке игр. С оригинальными статьями можно ознакомиться тут: часть 1, часть 2, часть 3 и часть 4. Я не стал публиковать переводы отдельными топиками, а объединил все статьи в одну. Думаю, что так будет удобнее воспринимать материал и работать с ним. Итак приступим.

Зачем нам линейная алгебра?

Одним из направлений в линейной алгебре является изучение векторов. Если в вашей игре применяется позиционирование экранных кнопок, работа с камерой и её направлением, скоростями объектов, то вам придётся иметь дело с векторами. Чем лучше вы понимаете линейную алгебру, тем больший контроль вы получаете над поведением векторов и, следовательно, над вашей игрой.

Что такое вектор?

В играх вектора используются для хранения местоположений, направлений и скоростей. Ниже приведён пример двухмерного вектора:

Вектор местоположения (также называемый «радиус-вектором») показывает, что человек стоит в двух метрах восточнее и в одном метре к северу от исходной точки. Вектор скорости показывает, что за единицу времени самолёт перемещается на три километра вверх и на два — влево. Вектор направления говорит нам о том, что пистолет направлен вправо.

Как вы можете заметить, вектор сам по себе всего лишь набор цифр, который обретает тот или иной смысл в зависимости от контекста. К примеру, вектор (1, 0) может быть как направлением для оружия, как показано на картинке, так и координатами строения в одну милю к востоку от вашей текущей позиции. Или скоростью улитки, которая двигается вправо со скоростью в 1 милю в час (прим. переводчика: довольно быстро для улитки, 44 сантиметра в секунду).

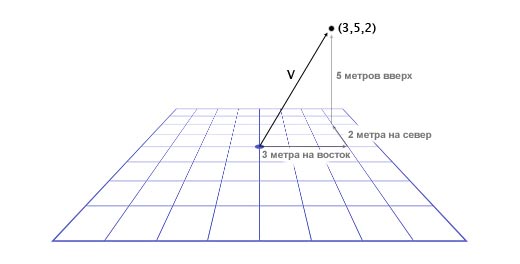
Важно отслеживать единицы измерения. Допустим у нас есть вектор V (3,5,2). Это мало что говорит нам. Три чего, пять чего? В нашей игре Overgrowth расстояния указываются в метрах, а скорости в метрах в секунду. Первое число в этом векторе — это направление на восток, второе — направление вверх, третье — направление на север. Отрицательные числа обозначают противоположные направления, на запад, вниз и на юг. Местоположение, определяемое вектором V (3,5,2), находится в трёх метрах к востоку, в пяти метрах вверху и в двух метрах к северу, как показано на картинке ниже.

Итак, мы изучили основы работы с векторами. Теперь узнаем как вектора использовать.

Сложение векторов

Чтобы сложить вектора, нам надо просто сложить каждую их составляющую друг с другом. Например:

(0, 1, 4) + (3, -2, 5) = (0+3, 1-2, 4+5) = (3, -1, 9)

Зачем нам нужно складывать вектора? Наиболее часто сложение векторов в играх применяется для физического интегрирования. Любой физический объект будет иметь вектора для местоположения, скорости и ускорения. Для каждого кадра (обычно это одна шестидесятая часть секунды), мы должны интегрировать два вектора: добавить скорость к местоположению и ускорение к скорости.

Давайте рассмотрим пример с прыжками Марио. Он начинает с позиции (0, 0). В момент начала прыжка его скорость (1, 3), он быстро двигается вверх и вправо. Его ускорение равно (0, -1), так как гравитация тянет его вниз. На картинке показано, как выглядит его прыжок, разбитый на семь кадров. Чёрным текстом показана его скорость в каждом фрейме.

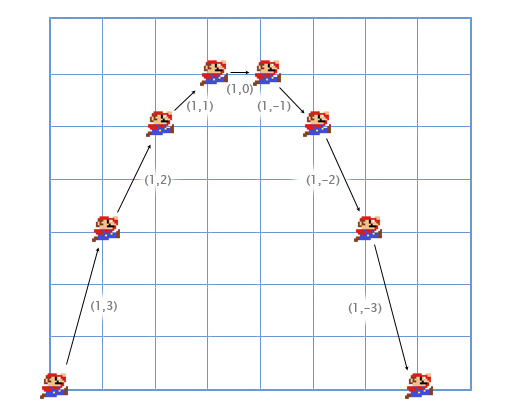
Давайте рассмотрим первые кадры поподробнее, чтобы понять как всё происходит.

Для первого кадра, мы добавляем скорость Марио (1, 3) к его местоположению (0, 0) и получаем его новые координаты (1, 3). Затем мы складываем ускорение (0, -1) с его скоростью (1, 3) и получаем новое значение скорости Марио (1, 2).

Делаем то-же самое для второго кадра. Добавляем скорость (1, 2) к местоположению (1, 3) и получаем координаты (2, 5). Затем добавляем ускорение (0, -1) к его скорости (1, 2) и получаем новую скорость (1, 1).

Обычно игрок контролирует ускорение игрового персонажа с помощью клавиатуры или геймпада, а игра, в свою очередь, рассчитывает новые значения для скоростей и местоположения, используя физическое сложение (через сложение векторов). Это та-же задача, которая решается в интегральном исчислении, просто мы его сильно упрощаем для нашей игры. Я заметил, что мне намного проще внимательно слушать лекции по интегральному исчислению, думая о практическом его применении, которое мы только что описали.

Вычитание векторов

Вычитание рассчитывается по тому-же принципу что и сложение — вычитаем соответствующие компоненты векторов. Вычитание векторов удобно для получения вектора, который показывает из одного местоположения на другое. Например, пусть игрок находится по координатам (1, 2) с лазерным ружьём, а вражеский робот находится по координатам (4, 3). Чтобы определить вектор движения лазерного луча, который поразит робота, нам надо вычесть местоположение игрока из местоположения робота. Получаем:

(4, 3) — (1, 2) = (4-1, 3-2) = (3, 1).

Умножение вектора на скаляр

Когда мы говорим о векторах, мы называем отдельные числа скалярами. Например (3, 4) — вектор, а 5 — это скаляр. В играх, часто бывает нужно умножить вектор на число (скаляр). Например, моделируя простое сопротивление воздуха путём умножения скорости игрока на 0.9 в каждом кадре. Чтобы сделать это, нам надо умножить каждый компонент вектора на скаляр. Если скорость игрока (10, 20), то новая скорость будет:

0.9*(10, 20) = (0.9 * 10, 0.9 * 20) = (9, 18).

Длина вектора

Если у нас есть корабль с вектором скорости V (4, 3), нам также понадобится узнать как быстро он двигается, чтобы посчитать потребность в экранном пространстве или сколько потребуется топлива. Чтобы сделать это, нам понадобится найти длину (модуль) вектора V. Длина вектора обозначается вертикальными линиями, в нашем случае длина вектора V будет обозначаться как |V|.

Мы можем представить V как прямоугольный треугольник со сторонами 4 и 3 и, применяя теорему Пифагора, получить гипотенузу из выражения: x² + y² = h²

В нашем случае — длину вектора H с компонентами (x, y) мы получаем из квадратного корня: sqrt(x² + y²).

Итак, скорость нашего корабля равна:

|V| = sqrt(4² + 3²) = sqrt(25) = 5

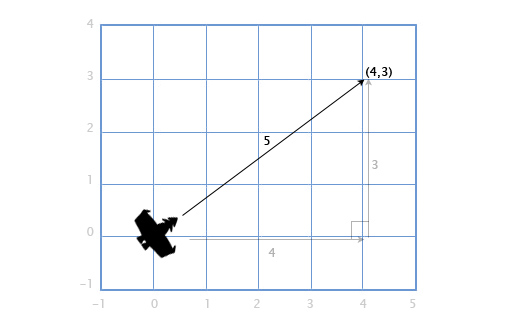
Этот подход используется и для трёхмерных векторов. Длина вектора с компонентами (x, y, z) рассчитывается как sqrt(x² + y² + z²)

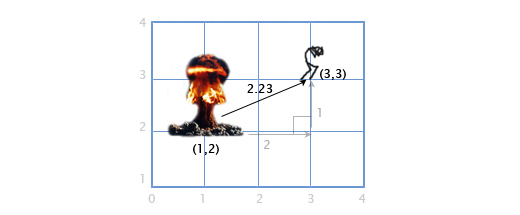
Расстояние

Если игрок P находится в точке (3, 3), а взрыв произошёл в точке E по координатам (1, 2), нам надо определить расстояние между игроком и взрывом, чтобы рассчитать степень ущерба, нанесённого игроку. Это легко сделать, комбинируя две вышеописанных операции: вычитание векторов и их длину.
Мы вычитаем P — E, чтобы получить вектор между ними. А затем определяем длину этого вектора, что и даёт нам искомое расстояние. Порядок следования операндов тут не имеет значения, |E — P| даст тот-же самый результат.

Расстояние = |P — E| = |(3, 3) — (1, 2)| = |(2, 1)| = sqrt(2²+1²) = sqrt(5) = 2.23

Нормализация

Когда мы имеем дело с направлениями (в отличие от местоположений и скоростей), важно, чтобы вектор направления имел длину, равную единице. Это сильно упрощает нам жизнь. Например, допустим орудие развёрнуто в направлении (1, 0) и выстреливает снаряд со скоростью 20 метров в секунду. Каков в данном случае вектор скорости для выпущенного снаряда?

Так как вектор направления имеет длину равную единице, мы умножаем направление на скорость снаряда и получаем вектор скорости (20, 0). Если-же вектор направления имеет отличную от единицы длину, мы не сможем сделать этого. Снаряд будет либо слишком быстрым, либо слишком медленным.

Вектор с длиной равной единице называется «нормализованным». Как сделать вектор нормализованным? Довольно просто. Мы делим каждый компонент вектора на его длину. Если, к примеру, мы хотим нормализовать вектор V с компонентами (3, 4), мы просто делим каждый компонент на его длину, то есть на 5, и получаем (3/5, 4/5). Теперь, с помощью теоремы Пифагора, мы убедимся в том, что его длина равна единице:

(3/5)² + (4/5)² = 9/25 + 16/25 = 25/25 = 1

Скалярное произведение векторов

Что такое скалярное произведение (записывается как •)? Чтобы рассчитать скалярное произведение двух векторов, мы должны умножить их компоненты, а затем сложить полученные результаты вместе

(a1, a2) • (b1, b2) = a1b1 + a2b2

Например: (3, 2) • (1, 4) = 3*1 + 2*4 = 11. На первый взгляд это кажется бесполезным, но посмотрим внимательнее на это:

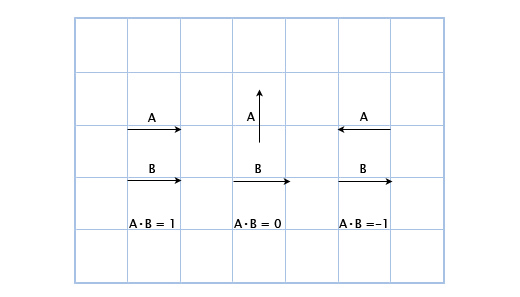
Здесь мы можем увидеть, что если вектора указывают в одном направлении, то их скалярное произведение больше нуля. Когда они перпендикулярны друг другу, то скалярное произведение равно нулю. И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля.
В основном, с помощью скалярного произведения векторов можно рассчитать, сколько их указывает в одном направлении. И хоть это лишь малая часть возможностей скалярного произведения, но уже очень для нас полезная.

Допустим у нас есть стражник, расположенный в G(1, 3) смотрящий в направлении D(1,1), с углом обзора 180 градусов. Главный герой игры подсматривает за ним с позиции H(3, 2). Как определить, находится-ли главный герой в поле зрения стражника или нет? Сделаем это путём скалярного произведения векторов D и V (вектора, направленного от стражника к главному герою). Мы получим следующее:

V = H — G = (3, 2) — (1, 3) = (3-1, 2-3) = (2, -1)
D•V = (1, 1) • (2, -1) = 1*2 + 1*-1 = 2-1 = 1

Так как единица больше нуля, то главный герой находится в поле зрения стражника.

Мы уже знаем, что скалярное произведение имеет отношение к определению направления векторов. А каково его более точное определение? Математическое выражение скалярного произведения векторов выглядит так:

A•B = |A||B|cosΘ

Где Θ (произносится как «theta») — угол между векторами A и B.

Это позволяет нам найти Θ (угол) с помощью выражения:

Θ = acos([AB] / [|A||B|])

Как я говорил ранее, нормализация векторов упрощает нашу жизнь. И если A и B нормализованы, то выражение упрощается следующим образом:

Θ = acos(AB)

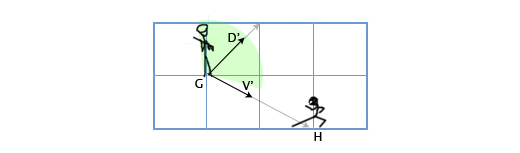
Давайте опять рассмотрим сценарий со стражником. Пусть теперь угол обзора стражника будет равен 120 градусам. Получим нормализованные вектора для направления взгляда стражника (D’) и для направления от стражника к главному герою (V’). Затем определим угол между ними. Если угол более 60 градусов (половина от угла обзора), то главный герой находится вне поля зрения стражника.

D’ = D / |D| = (1, 1) / sqrt(1² + 1²) = (1, 1) / sqrt(2) = (0.71, 0.71)
V’ = V / |V| = (2, -1) / sqrt(2² + (-1)²) = (2,-1) / sqrt(5) = (0.89, -0.45)

Θ = acos(D’V’) = acos(0.71*0.89 + 0.71*(-0.45)) = acos(0.31) = 72

Угол между центром поля зрения стражника и местоположением главного героя составляет 72 градуса, следовательно стражник его не видит.

Понимаю, что это выглядит довольно сложно, но это потому, что мы всё делаем вручную. В программе это всё довольно просто. Ниже показано как я сделал это в нашей игре Overgrowth с помощью написанных мной С++ библиотек для работы с векторами:

//Инициализируем вектора
vec2 guard_pos = vec2(1,3);
vec2 guard_facing = vec2(1,1);
vec2 hero_pos = vec2(3,2);

//Рассчитываем нормализованные вектора
vec2 guard_facing_n = normalize(guard_facing);
vec2 guard_to_hero = normalize(hero_pos - guard_pos);

//Рассчитываем угол
float angle = acos(dot(guard_facing_n, guard_to_hero));

Векторное произведение

Допустим у нас есть корабль с пушками, которые стреляют в правую и в левую стороны по курсу. Допустим, что лодка расположена вдоль вектора направления (2, 1). В каких направлениях теперь стреляют пушки?

Это довольно просто в двухмерной графике. Чтобы повернуть направление на 90 градусов по часовой стрелке, достаточно поменять местами компоненты вектора, а затем поменять знак второму компоненту.
(a, b) превращается в (b, -a). Следовательно у корабля, расположенного вдоль вектора (2, 1), пушки справа по борту будут стрелять в направлении (1, -2), а пушки с левого борта, будут стрелять в противоположном направлении. Меняем знаки у компонент вектора и получаем (-1, 2).

А что если мы хотим рассчитать это всё для трехмерной графики? Рассмотрим пример с кораблём.
У нас есть вектор мачты M, направленной прямо вверх (0, 1, 0) и направление ветра: север-северо-восток W (1, 0, 2). И мы хотим вычислить вектор направления паруса S, чтобы наилучшим образом «поймать ветер».

Для решения этой задачи мы используем векторное произведение: S = M x W.

Векторное произведение A(a₁,a₂,a₃) и B(b₁,b₂,b₃) будет равно:

(a₂b₃-a₃b₂, a₃b₁-a₁b₃, a₁b₂-a₂b₁)

Подставим теперь нужные нам значения:

S = MxW = (0, 1, 0) x (1, 0, 2) = ([1*2 — 0*0], [0*1 — 0*2], [0*0 — 1*1]) = (2, 0, -1)

Для расчётов вручную довольно сложно, но для графических и игровых приложений я рекомендую написать функцию, подобную той, что указана ниже и не вдаваться более в детали подобных расчётов.

vec3 cross(vec3 a, vec3 b) {
    vec3 result;
    result[0] = a[1] * b[2] - a[2] * b[1];
    result[1] = a[2] * b[0] - a[0] * b[2];
    result[2] = a[0] * b[1] - a[1] * b[0];
    return result;
}

Векторное произведение часто используется в играх, чтобы рассчитать нормали к поверхностям. Направления, в которых «смотрит» та или иная поверхность. Например, рассмотрим треугольник с векторами вершин A, B и С. Как мы найдем направление в котором «смотрит» треугольник, то есть направление перпендикулярное его плоскости? Это кажется сложным, но у нас есть инструмент для решения этой задачи.

Используем вычитание, для определения направления из A в С (C — A), пусть это будет «грань 1» (Edge 1) и направление из A в B (B — A), пусть это будет «грань 2» (Edge 2). А затем применим векторное произведение, чтобы найти вектор, перпендикулярный им обоим, то есть перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».

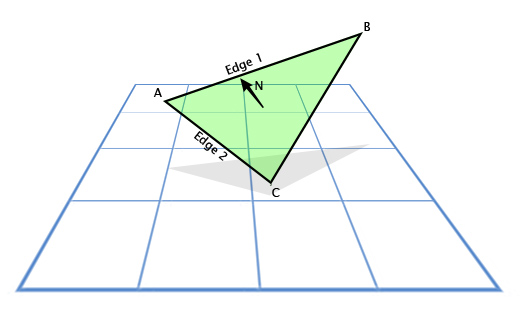
Вот так это выглядит в коде:

vec3 GetTriangleNormal(vec3 a, vec3 b, vec3 c) {
    vec3 edge1 = b-a;
    vec3 edge2 = c-a;
    vec3 normal = cross(edge1,edge2);
    return normal;
}

В играх основное выражение освещённости записывается как N • L, где N — это нормаль к освещаемой поверхности, а L — это нормализованный вектор направления света. В результате поверхность выглядит яркой, когда на неё прямо падает свет, и тёмной, когда этого не происходит.

Теперь перейдем к рассмотрению такого важного для разработчиков игр понятия, как «матрица преобразований» (transformation matrix).

Для начала изучим «строительные блоки» матрицы преобразований.

Базисный вектор

Допустим мы пишем игру Asteroids на очень старом «железе» и нам нужен простой двухмерный космический корабль, который может свободно вращаться в своей плоскости. Модель корабля выглядит так:

Как нам рисовать корабль, когда игрок поворачивает его на произвольный градус, скажем 49 градусов против часовой стрелки. Используя тригонометрию, мы можем написать функцию двухмерного поворота, которая принимает координаты точки и угол поворота, и возвращает координаты смещённой точки:

vec2 rotate(vec2 point, float angle){
           vec2 rotated_point;
           rotated_point.x = point.x * cos(angle) - point.y * sin(angle);
           rotated_point.y = point.x * sin(angle) + point.y * cos(angle);
           return rotated_point;
}

Применяя эту функцию ко всем трём точкам, мы получим следующую картину:

Операции с синусами и косинусами работают довольно медленно, но так как мы делаем расчёты лишь для трёх точек, это будет нормально работать даже на старом «железе» (прим. переводчика: в случаях, когда предполагается интенсивное использование тригонометрических функций, для ускорения вычислений, в памяти организуют таблицы значений для каждой функции и рассчитывают их во время запуска приложения. Затем при вычислении той или иной тригонометрической функции просто производится обращение к таблице).

Пусть теперь наш корабль выглядит вот так:

Теперь старый подход будет слишком медленным, так как надо будет поворачивать довольно большое количество точек. Одно из элегантных решений данной проблемы будет звучать так — «Что если вместо поворота каждой точки модели корабля, мы повернём координатную решётку нашей модели?»

Как это работает? Давайте посмотрим внимательнее, что собой представляют координаты.
Когда мы говорим о точке с координатами (3, 2), мы говорим, что её местоположение находится в трех шагах от точки отсчёта по координатной оси X, и двух шагах от точки отсчёта по координатной оси Y.

По-умолчанию координатные оси расположены так: вектор координатной оси X (1, 0), вектор координатной оси Y (0, 1). И мы получим расположение: 3(1, 0) + 2(0, 1). Но координатные оси не обязательно должны быть в таком положении. Если мы повернём координатные оси, в это-же время мы повернём все точки в координатной решётке.

Чтобы получить повернутые оси X и Y мы применим тригонометрические функции, о которых говорили выше. Если мы поворачиваем на 49 градусов, то новая координатная ось X будет получена путём поворота вектора (0, 1) на 49 градусов, а новая координатная ось Y будет получена путём поворота вектора (0, 1) на 49 градусов. Итак вектор новой оси X у нас будет равен (0.66, 0.75), а вектор новой оси Y будет (-0.75, 0.66). Сделаем это вручную для нашей простой модели из трёх точек, чтобы убедиться, что это работает так, как нужно:

Координаты верхней точки (0, 2), что означает, что её новое местоположение находится в 0 на новой (повёрнутой) оси X и 2 на новой оси Y:

0*(0.66,0.75) + 2*(-0.75, 0.66) = (-1.5, 1.3)

Нижняя левая точка (-1, -1), что означает, что её новое местоположение находится в -1 на повернутой оси X, и -1 на повернутой оси Y:

-1*(0.66,0.75) + -1*(-0.75, 0.66) = (0.1, -1.4)

Нижняя правая точка (1, -1), что означает её новое местоположение находится в 1 на повернутой оси X, и -1 на повернутой оси Y

1*(0.66,0.75) + -1*(-0.75, 0.66) = (1.4, 0.1)

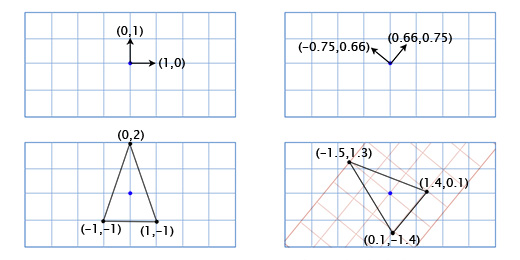
Мы показали, как координаты корабля отображаются в другой координатной сетке с повернутыми осями (или «базисными векторами»). Это удобно в нашем случае, так как избавляет нас от необходимости применять тригонометрические преобразования к каждой из точек модели корабля.

Каждый раз, когда мы изменяем базисные вектора (1, 0) и (0, 1) на (a, b) и (c, d), то новая координата точки (x, y) может быть найдена с помощью выражения:

x(a,b) + y(c,d)

Обычно базисные вектора равны (1, 0) и (0, 1) и мы просто получаем x(1, 0) + y(0, 1) = (x, y), и нет необходимости заботиться об этом дальше. Однако, важно помнить, что мы можем использовать и другие базисные вектора, когда нам это нужно.

Матрицы

Матрицы похожи на двухмерные вектора. Например, типичная 2×2 матрица, может выглядеть так:

   [a c 
    b d]

Когда вы умножаете матрицу на вектор, вы суммируете скалярное произведение каждой строки с вектором, на который происходит умножение. Например, если мы умножаем вышеприведённую матрицу на вектор (x, y), то мы получаем:

(a,c)•(x,y) + (b,d)•(x,y)

Будучи записанным по-другому, это выражение выглядит так:

x(a,b) + y(c,d)

Выглядит знакомо, не так-ли? Это в точности такое-же выражение, которые мы использовали для смены базисных векторов. Это означает, что умножая 2×2 матрицу на двухмерный вектор, мы тем самым меняем базисные вектора. Например, если мы вставим стандартные базисные вектора в (1, 0) и (0, 1) в колонки матрицы, то мы получим:

[1 0 
 0 1]

Это единичная матрица, которая не даёт эффекта, который мы можем ожидать от нейтральных базисных векторов, которые мы указали. Если-же мы повернём базисные вектора на 49-градусов, то мы получим:

[0.66 -0.75 
 0.75  0.66]

Эта матрица будет поворачивать двухмерный вектор на 49 градусов против часовой стрелки. Мы можем сделать код нашей игры Asteriods более элегантным, используя матрицы вроде этой. Например, функция поворота нашего корабля может выглядеть так:

void RotateShip(float degrees){
        Matrix2x2 R = GetRotationMatrix(degrees);
        for(int i=0; i<num_points; ++i){
                rotated_point[i] = R * point[i];
        }
}

Однако, наш код будет ещё более элегантным, если мы сможем также включить в эту матрицу перемещение корабля в пространстве. Тогда у нас будет единая структура данных, которая будет заключать в себе и применять информацию об ориентации объекта и его местоположении в пространстве.

К счастью есть способ добиться этого, хоть это и выглядит не очень элегантно. Если мы хотим переместиться с помощью вектора (e, f), мы лишь включаем его в нашу матрицу преобразования:

[a c e 
 b d f 
 0 0 1]

И добавляем дополнительную единицу в конец каждого вектора, определяющего местоположение объекта, например так:

[x y 1]

Теперь, когда мы перемножаем их, мы получаем:

(a, c, e) • (x, y, 1) + (b, d, f) • (x, y, 1) + (0, 0, 1) • (x, y, 1)

Что, в свою очередь, может быть записано как:

x(a, b) + y(c, d) + (e, f)

Теперь у нас есть полный механизм трансформации, заключённый в одной матрице. Это важно, если не принимать в расчёт элегантность кода, так как с ней мы теперь можем использовать все стандартные манипуляции с матрицами. Например перемножить матрицы, чтобы добавить нужный эффект, или мы можем инвертировать матрицу, чтобы получить прямо противоположное положение объекта.

Трехмерные матрицы

Матрицы в трехмерном пространстве работают так-же как и в двухмерном. Я приводил примеры с двухмерными векторами и матрицами, так как их просто отобразить с помощью дисплея, показывающего двухмерную картинку. Нам просто надо определить три колонки для базисных векторов, вместо двух. Если базисные вектора это (a,b,c), (d,e,f) and (g,h,i) то наша матрица будет выглядеть так:

[a d g 
 b e h 
 c f i]

Если нам нужно перемещение (j,k,l), то мы добавляем дополнительную колонку и строку, как говорили раньше:

[a d g j 
 b e h k 
 c f i l 
 0 0 0 1]
 

И добавляем единицу [1] в вектор, как здесь:

[x y z 1]

Вращение в двухмерном пространстве

Так как в нашем случае у нас только одна ось вращения (расположенная на дисплее), единственное, что нам надо знать, это угол. Я говорил об этом ранее, упоминая, что мы можем применять тригонометрические функции для реализации функции двухмерного вращения наподобие этой:

vec2 rotate(vec2 point, float angle){
        vec2 rotated_point;
        rotated_point.x = point.x * cos(angle) - point.y * sin(angle);
        rotated_point.y = point.x * sin(angle) + point.y * cos(angle);
        return rotated_point;
}

Более элегантно это можно выразить в матричной форме. Чтобы определить матрицу, мы можем применить эту функцию к осям (1, 0) и (0, 1) для угла Θ, а затем включить полученные оси в колонки нашей матрицы. Итак, начнём с координатной оси X (1, 0). Если мы применим к ней нашу функцию, мы получим:

(1*cos(Θ) — 0*sin(Θ), 1*sin(Θ) + 0*cos(Θ)) = (cos(Θ), sin(Θ))

Затем, мы включаем координатную ось Y (0, 1). Получим:

(0*cos(Θ) — 1*sin(Θ), 0*sin(Θ) + 1*cos(Θ)) = (-sin(Θ), cos(Θ))

Включаем полученные координатные оси в матрицу, и получаем двухмерную матрицу вращения:

[cos(Θ) -sin(Θ) 
 sin(Θ)  cos(Θ)]

Применим эту матрицу к Сюзанне, мартышке из графического пакета Blender. Угол поворота Θ равен 45 градусов по часовой стрелке.

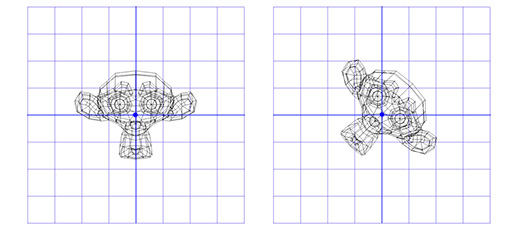
Как видите — это работает. Но что если нам надо осуществить вращение вокруг точки, отличной от (0, 0)?
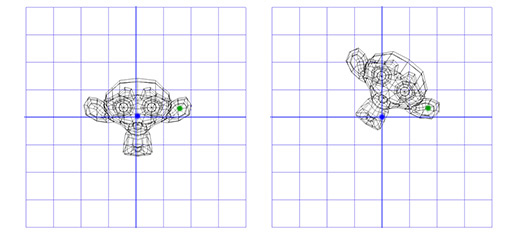
Например, мы хотим вращать голову мартышки вокруг точки, расположенной в её ухе:

Чтобы сделать это, мы можем начать с создания матрицы перемещения (translation matrix) T, которая перемещает объект из начальной точки в точку вращения в ухе мартышки, и матрицу вращения R, для вращения объекта вокруг начальной точки. Теперь для вращения вокруг точки, расположенной в ухе, мы можем сперва переместить точку в ухе на место начальной точки, с помощью инвертирования матрицы T, записанной как T^-1. Затем, мы вращаем объект вокруг начальной точки, с помощью матрицы R, а затем применяем матрицу T для перемещения точки вращения назад, к своему исходному положению.
Ниже дана иллюстрация к каждому из описанных шагов:

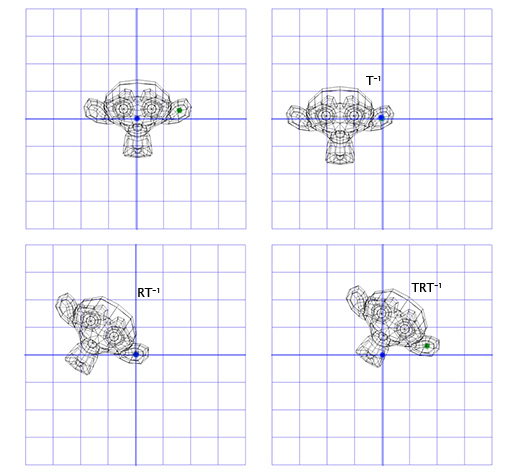
Это важный шаблон, который мы будем применять позднее — применение вращения для двух противоположных трансформаций позволяет нам вращать объект в другом «пространстве». Что очень удобно и полезно.

Теперь рассмотрим трёхмерное вращение.

Трёхмерное вращение

Вращение вокруг оси Z работает по тому-же принципу, что и вращение в двухмерном пространстве. Нам лишь нужно изменить нашу старую матрицу, добавив к ней дополнительную колонку и строку:

[cos(Θ) -sin(Θ) 0 
 sin(Θ)  cos(Θ) 0 
 0       0      1]

Применим эту матрицу к трехмерной версии Сюзанны, мартышки из пакета Blender. Угол поворота Θ пусть будет равен 45 градусов по часовой стрелке.

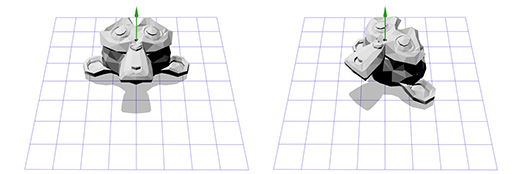
То-же самое. Вращение только вокруг оси Z ограничивает нас, как насчёт вращения вокруг произвольной оси?

Вращение, определяемое осью и углом (Axis-angle rotation)

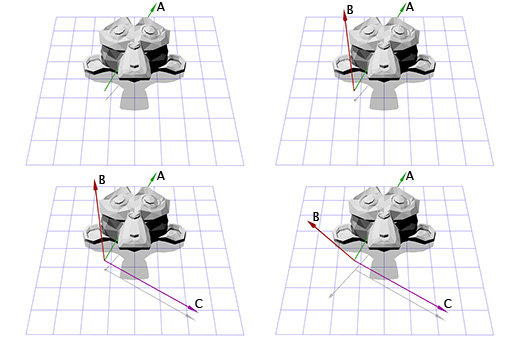
Представление вращения, определяемого осью и углом, также известно как вращение в экспоненциальных координатах, параметризованное вращением двух величин. Вектора, определяющего вращение направляющей оси (прямая линия) и угла, описывающего величину поворота вокруг этой оси. Вращение осуществляется согласно правилу правой руки.

Итак, вращение задаётся двумя параметрами (axis, angle), где axis — вектор оси вращения, а angle — угол вращения. Этот приём довольно прост и являет собой отправную точку для множества других операций вращения, с которыми я работаю. Как практически применить вращение, определяемое осью и углом?

Допустим мы имеем дело с осью вращения, показанной на рисунке ниже:

Мы знаем как вращать объект вокруг оси Z, и мы знаем как вращать объект в других пространствах. Итак, нам лишь надо создать пространство, где наша ось вращения будет являться осью Z. И если эта ось будет осью Z, то что будет являться осями X и Y? Займемся вычислениями сейчас.

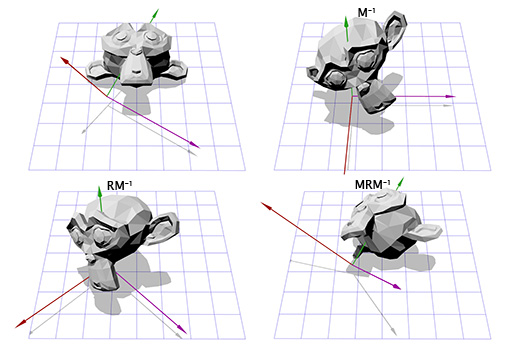
Чтобы создать новые оси X и Y нам нужно лишь выбрать два вектора, которые перпендикулярны новой оси Z и перпендикулярны друг другу. Мы уже говорили ранее о векторном умножении, которое берёт два вектора и даёт в итоге перпендикулярный им вектор.

У нас есть один вектор сейчас, это ось вращения, назовём его A. Возьмём теперь случайный другой вектор B, который находится не в том-же направлении, что и вектор A. Пусть это будет (0, 0, 1) к примеру.

Теперь мы имеем ось вращения A и случайный вектор B, мы можем получить нормаль C, через векторное произведение A и B. С перпендикулярен векторам A и B. Теперь мы делаем вектор B перпендикулярным векторам A и C через их векторное произведение. И всё, у нас есть все нужные нам оси координат.

На словах это звучит сложно, но довольно просто выглядит в коде или будучи показанным в картинках.
Ниже показано, как это выглядит в коде:

B = (0,0,1); 
C = cross(A,B); 
B = cross(C,A);

Тут показана иллюстрация для каждого шага:

Теперь, имея информацию о новых координатных осях, мы можем составить матрицу M, включив каждую ось как колонку в эту матрицу. Нам надо убедиться, что вектор A является третьей колонкой, чтобы он был нашей новой осью координат Z.

[B0 C0 A0 
 B1 C1 A1 
 B2 C2 A2]

Теперь это похоже на то, что мы делали для поворота в двухмерном пространстве. Мы можем применить инвертированную матрицу M, чтобы переместиться в новую систему координат, затем произвести вращение, согласно матрице R, чтобы повернуть объект вокруг оси Z, затем применить матрицу M, чтобы вернуться в исходное координатное пространство.

Теперь мы можем вращать объект вокруг произвольной оси. В конце концов мы можем просто создать матрицу T = T = M^-1RM и использовать её много раз, без дополнительных усилий с нашей стороны. Есть более эффективные способы конвертирования вращений, определяемых осью и углом во вращения, определяемые матрицами. Просто описанный нами подход показывает многое из того, о чём мы говорили ранее.

Вращение, определяемое осью и углом, возможно, самый интуитивно понятный способ. Применяя его, очень легко инвертировать поворот, поменяв знак у угла, и легко интерполировать, путём интерполяции угла. Однако тут есть серьёзное ограничение, и заключается оно в том, что такое вращение не является суммирующим. То есть вы не можете комбинировать два вращения, определяемых осью и углом в третье.
Вращение, определяемое осью и углом — хороший способ для начала, но оно должно быть преобразовано во что-то другое, чтобы использоваться в более сложных случаях.

Эйлеровские углы

Эйлеровские углы представляют собой другой способ вращения, заключающийся в трёх вложенных вращениях относительно осей X, Y и Z. Вы, возможно, сталкивались с их применением в играх, где камера показывает действие от первого лица, либо от третьего лица.

Допустим вы играете в шутер от первого лица и вы повернулись на 30 градусов влево, а затем посмотрели на 40 градусов вверх. В конце-концов в вас стреляют, попадают, и, в результате удара, камера поворачивается вокруг своей оси на 45 градусов. Ниже показано вращение с помощью углов Эйлера (30, 40, 45).

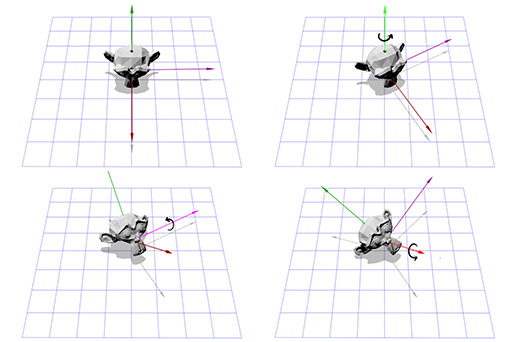
Углы Эйлера — удобное и простое в управлении средство. Но у этого способа есть два недостатка.

Первый, это вероятность возникновения ситуации под названием «блокировка оси» или «шарнирный замок» (gimbal lock). Представьте, что вы играете в шутер от первого лица, где вы можете посмотреть влево, вправо, вверх и вниз или повернуть камеру вокруг зрительной оси. Теперь представьте, что вы смотрите прямо вверх. В этой ситуации попытка взглянуть налево или направо будет аналогична попытке вращения камеры. Всё что мы можем вы этом случае, это вращать камеру вокруг своей оси, либо посмотреть вниз. Как вы можете представить, это ограничение делает непрактичным применение углов Эйлера в лётных симуляторах.

Второе — интерполяция между двумя эйлеровскими углами вращения не даёт кратчайшего пути между ними.
Например, у вас две интерполяции между двумя одинаковыми вращениями. Первая использует интерполяцию эйлеровского угла, вторая использует сферическую линейную интерполяцию (spherical linear interpolation (SLERP)), чтобы найти кратчайший путь.

Итак, что-же больше подойдет для интерполяции вращений? Может быть матрицы?

Вращение с помощью матриц

Как мы уже говорили ранее, матрицы вращения хранят в себе информацию о трёх осях. Это означает, что интерполяция между двумя матрицами лишь линейно интерполирует каждую ось. В результате это даёт нам эффективный путь, то так-же привносит новые проблемы. Например, тут показаны два вращения и одно интерполированное полу-вращение:

Как вы можете заметить, интерполированное вращение значительно меньше, чем любое из исходных вращений, и две оси более не перпендикулярны друг другу. Это логично, если вдуматься — середина отрезка, соединяющего любые две точки на сфере будет расположена ближе к центру сферы.

Это в свою очередь порождает известный «эффект фантика» (candy wrapper effect), при применении скелетной анимации. Ниже показана демонстрация этого эффекта на примере кролика из нашей игры Overgrowth (прим. переводчика: обратите внимание на середину туловища кролика).

Вращение, основанное на матричных операциях, очень полезно, так как они могут аккумулировать вращения без всяких проблем, вроде блокировки оси (gimbal lock), и может очень эффективно применяться к точкам сцены. Вот почему поддержка вращения на матрицах встроена в графические карты. Для любого типа трёхмерной графики матричный формат вращения — это всегда итоговый применяемый способ.

Однако, как мы уже знаем, матрицы не очень хорошо интерполируются, и они не столь интуитивно понятны.

Итак, остался только один главный формат вращения. Последний, но тем не менее, важный.

Кватернионы

Что-же такое кватернионы? Если очень кратко, то это альтернативный вариант вращения, основанный на оси и угле (axis-angle rotation), который существует в пространстве.

Подобно матрицам они могут аккумулировать вращения, то есть вы можете составлять из них цепочку вращений, без опаски получить блокировку оси (gimbal lock). И в то-же время, в отличие от матриц, они могут хорошо интерполироваться из одного положения в другое.

Являются-ли кватернионы лучшим решением, нежели остальные способы вращений (rotation formats)?
На сегодняшний день они комбинируют все сильные стороны других способов вращений. Но у них есть два слабых места, рассмотрев которые, мы придём к выводу, что кватернионы лучше использовать для промежуточных вращений. Итак, каковы недостатки кватернионов.

Во-первых кватернионы непросто отобразить на трёхмерном пространстве. И мы вынуждены всегда реализовывать вращение более простым способом, а затем конвертировать его. Во-вторых, кватернионы не могут эффективно вращать точки, и мы вынуждены конвертировать их в матрицы, чтобы повернуть значительное количество точек.

Это означает, что вы скорее всего не начнете или не закончите серию вращений с помощью кватернионов. Но с их помощью можно реализовать промежуточные вращения более эффективно, нежели при применении любого другого подхода.

«Внутренняя кухня» механизма кватернионов не очень понятна и не интересна мне. И, возможно, не будет интересна и вам, если только вы не математик. И я советую вам найти библиотеки, которые работают с кватернионами, чтобы облегчить вам решение ваших задач с их помощью.

Математические библиотеки «Bullet» или «Blender» будут хорошим вариантом для начала.