Как найти произведение векторов без косинуса

Векторное произведение векторов

Определение

Определение

Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $.

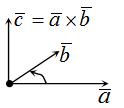
Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.

Формула

Формула 1

Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле: $$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$

Формула 2

В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$ где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $.

Определитель во второй формуле можно раскрыть по первой строке:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 – a_3 b_2) – overline{j} (a_1 b_3 – a_3 b_1) + overline{k} (a_1 b_2 – a_2 b_1) $$

Итого вторая формула приобретает окончательный короткий вид:

$$ overline{a} times overline{b} = (a_2 b_3 – a_3 b_2; a_3 b_1 – a_1 b_3; a_1 b_2 – a_2 b_1) $$

Свойства

1. При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
2. Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
3. $$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$

Примеры решений

Пример 1

Найти векторное произведение векторов, заданных координатами $$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$

Решение

Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) – overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} – overline{j} + 3overline{k} $$ Полученный ответ можно записать в удобном виде: $$ overline{a} times overline{b} = (5, -1, 3) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ overline{a} times overline{b} = (5, -1, 3) $$

Геометрический смысл

• Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
• Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
• Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.

 

Пример 2

Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$

Решение

Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов. Находим определитель: $$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) – overline{j}(2+3) + overline{k}(4+1) = -5overline{i} – 5overline{j} + 5overline{k} $$ Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора: $$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$ По формуле нахождения площади треугольника имеем: $$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$

Ответ

$$ S_Delta = 4.33 $$

Скалярное произведение

Скалярное произведение — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат. Используется в определении длины векторов и угла между ними.
$$ c = |overline a||overline b|cos(theta )$$

Обычно для скалярного произведения векторов $overline a$ и $overline b$ используется одно из следующих обозначений:

$$ c= (overline a,overline b) = overline acdotoverline b$$

Скалярным произведением двух векторов $overline a$ и $overline b$ будет скалярная величина, равная сумме попарного произведения координат векторов $overline a$ и $overline b$.

Для плоскости:
Скалярное произведение векторов $overline a = (a_x, a_y)$ и $overline b = (b_x, b_y)$ можно найти воспользовавшись следующей формулой:
$$ overline acdotoverline b = a_x b_x + a_y b_y $$

Для пространства:
Скалярное произведение двух векторов в пространстве $overline a = (a_x, a_y, a_z)$ и $overline b = (b_x, b_y, b_z)$ можно найти воспользовавшись следующей формулой:
$$ overline acdotoverline b = a_x b_x + a_y b_y + a_z b_z $$

Векторное произведение

Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого численно равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой. Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.

Определение:
Векторным произведением вектора $overline a$ на вектор $overline b$ в трёхмерном евклидовом пространстве называется вектор $overline c$, удовлетворяющий следующим требованиям:

• длина вектора $overline c$ равна произведению длин векторов $overline a$ и $overline c$ на синус угла между ними (т. е. площади параллелограмма, образованного векторами $overline a$ и $overline b$
  $$ | overline c| = | overline a| cdot | overline b|cdot sin (theta ),$$
• вектор $overline c$ ортогонален каждому из векторов $overline a$ и $overline b$;
• вектор $overline c$ направлен так, что тройка векторов $(overline a,overline b,overline c)$ является правой.

Понятие правой и левой тройки векторов:
Совместим начала векторов в одной точке. Упорядоченная тройка некомпланарных векторов $(overline a,overline b,overline c)$ в трёхмерном пространстве называется правой, если с конца вектора $overline c$ кратчайший поворот от вектора $overline a$ к вектору $overline b$ виден наблюдателю против часовой стрелки. И наоборот, если кратчайший поворот виден по часовой стрелке, то тройка называется левой.

Название правой и левой тройки пошло от определения направления тройки с помощью руки человека:

Правая тройка. Указательный палец к среднему пальцу двигается против часовой стрелки.

Векторное произведение обозначают:

$$overline c = overline a times overline b = [overline a, overline b]$$

Получение координат вектора $overline c$:
Если два вектора $overline a$ и $overline {b}$ представлены в правом ортонормированном базисе координатами $ overline a=(a_x,a_y,a_z), overline b=(b_x,b_y,b_z)$, то их векторное произведение имеет координаты:

$$ overline a timesoverline b = (a_yb_z – a_zb_y,a_zb_x-a_xb_z,a_xb_y-a_yb_x).$$

Для запоминания этой формулы удобно использовать мнемонический определитель:
$$overline a timesoverline b = begin{vmatrix}
i & j & k \
a_x & a_y & a_z \
b_x & b_y & b_z \
end{vmatrix}, $$

где $i=(1,0,0), j=(0,1,0), k=(0,0,1)$.

Псевдоскалярное произведение двух векторов

Псевдоскалярным (или косым) произведением векторов $overline{a}$ и $overline{b}$ на плоскости называют число

$$c = | overline a| cdot | overline b|cdot sin (theta ),$$

где $theta$ – угол вращения (против часовой стрелки) от $overline{a}$ к $overline{b}$. Приставка “псевдо” означает, что объект может менять или не менять знак при отражениях пространства.

Псевдоскалярное произведение обозначают так:
$$c = overline a wedge overline b.$$

Если хотя бы один из векторов нулевой, то полагают $overline a wedge overline b = 0$.

Геометрически псевдоскалярное произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.

С его помощью удобно работать с площадями многоугольников, выражать условия коллинеарности векторов и находить углы между ними.

Псевдоскалярное произведение существует только для 2-мерных векторов, его аналогом в трехмерном пространстве является смешанное произведение.

Основные свойства:

1. Линейность: $overline a wedge (lambda overline b + muoverline c ) = lambdaoverline awedgeoverline b + muoverline a wedge overline c$. Где $lambda, mu$ – произвольные вещественные числа.
2. Антикоммутативность: $overline a wedgeoverline b = -overline bwedgeoverline a$.
3. Ориентированная площадь треугольника ABC выражается формулой $S = (overline{AB}wedgeoverline{AC}) / 2$, а его площадь равна модулю этой величины.
4. $overline a wedge overline b = 0$ – необходимое и достаточное условие коллинеарности ненулевых векторов на плоскости.
5. Пусть заданы вектора $overline a = (a_1, a_2), overline b = (b_1, b_2)$. Тогда их псевдоскалярное произведение равно $overline a wedgeoverline b = a_1b_2 – a_2b_1$.

Использование в геометрических задачах

Пример 1. Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому достаточно посчитать косое произведение векторов $overline{P_1P_2}$ и $overline{P_1M}$ и по его знаку сделать вывод.

Пример 2. Определить, принадлежит ли точка отрезку.

Пусть точки $P_1(x_1, y_1), P_2(x_2, y_2)$ – концы заданного отрезка. Необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через $P_1, P_2$. Далее нужно определить лежит ли точка между точками $P_1$ и $P_2$. Для этого используем скалярное произведение векторов $overline{MP_1}, overline{MP_2}$. Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. $overline{P_1P_2} wedge overline{P_1M} = 0$ – косое произведение (точка лежит на прямой);
2. $(overline{MP_1}, overline{MP_2}) ≤ 0$ – скалярное произведение (точка лежит между $P_1$ и $P_2$).

Пример 3. Определить, пересекаются ли две прямые (прямые не совпадают).

Если прямые заданы точками $P_1(x_1, y_1), P_2(x_2, y_2), M_1(x_3, y_3), M_2(x_4, y_4)$, то условие их параллельности заключается в проверки косого произведения векторов $overline{P_1P_2}$ и $overline{M_1M_2}$: если оно равно нулю, то прямые параллельны, иначе – пересекаются.

Пример 4. Определить, пересекаются ли два отрезка.

Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Необходимо проверить, лежат ли концы каждого из отрезков по разные стороны относительного концов другого отрезка. Применим косое произведение векторов. Посмотрим на первый рисунок: $overline{P_1P_2}wedge overline{P_1M_2} * overline{P_1P_2}wedge overline{P_1M_1} < 0$ и $overline{M_1M_2}wedge overline{M_1P_1} * overline{M_1M_2}wedge overline{M_1P_2} < 0$. Важно обратить внимание на строгое неравенство, потому что возможен случай, при котором произведение равно нулю, но отрезки не пересекаются (отрезки лежат на одной прямой, но не имеют общих точек). Поэтому необходимо проверить, принадлежит ли хотя бы один конец каждого отрезка другому.

Еще примеры:

• https://foxford.ru/wiki/informatika/primenenie-skalyarnogo-i-vektornogo-proizvedeniya
• https://habr.com/en/post/147691/

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве.

Векторное Произведение Векторов. Свойства, определение

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.

Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.

Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.

Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.

Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.

Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.

В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.

И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.

Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:

Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.

Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:

Векторное произведение векторов →a и →b обозначается как [→a • →b].

Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.

Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.

Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:

• Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
• Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
• Если определитель равен нулю, то векторы компланарны (линейно зависимы).

Координаты векторного произведения

• Рассмотрим векторное произведение векторов в координатах.
• Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
• В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор

1. , где
2. →i, →j, →k — координатные векторы.
3. Это определение показывает нам векторное произведение в координатной форме.
4. Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
5. Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:

Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.

Свойства векторного произведения

Векторное произведение в координатах представляется в виде определителя матрицы:

На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:

1. Антикоммутативность
2. Свойство дистрибутивностиили
3. Сочетательное свойствоили, где λ произвольное действительное число.

• Для большей ясности докажем свойство антикоммутативности векторного произведения.
• По определению
• и
• Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
• что доказывает свойство антикоммутативности векторного произведения.
• Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
• Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).

Геометрический смысл векторного произведения

По определению длина векторного произведения векторов равна. А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.

Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.

Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F]. Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до векторов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Приходите на бесплатный вводный урок и попробуйте сами!

Смешанное произведение векторов: свойства примеры и решения, геометрический смысл смешанного произведения векторов

Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение.

В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.

Термин

Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.

Определение 1

Смешанным произведением a→, b→ и d→ является та величина, которая равняется скалярному произведению a→×b→ и d→ , где a→×b→ — умножение a→ и b→ . Операцию умножения a→, b→ и d→ зачастую обозначают a→·b→·d→ . Можно преобразовать формулу так:a→·b→·d→=(a→×b→,d→) .

Умножение в системе координат

• Мы можем умножить вектора, если они указаны на координатной плоскости.
• Возьмем i→, j→, k→
• Произведение векторов в данном конкретном случае будет иметь следующий вид:a→×b→=(ay·bz-az·by)·i→+(az·bx+ax·bz)·j→+(ax·by+ay·bx)·k→=ayazbybz·i→-axazbxbz·j→+axaybxby·k→

Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.

1. Из этого следует:
2. a→×b→=(ay·bz-az·by)·i→+(az·bx+ax·bz)·j→+(ax·by+ay·bx)·k→=ayazbybz·i→-axazbxbz·j→+axaybxby·k→
3. Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.
4. a→×b→=( ayazbybz·i→-axazbxbz·j→+axaybxby·k→, dx·i→+dy·j→+dz·k→)==ayazbybz·dx-axazbxbz·dy+axaybxby·dz=axayazbxbybzdxdydz
5. Таким образом, можно сделать вывод, что:
6. a→·b→·d=a→×b→, d→=axayazbxbybzdxdydz

Определение 3

Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: a→·b→·d=a→×b→, d→=axayazbxbybzdxdydz .

Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства.

1. (λ·a→)·b→·d→=a→·(λ·b→)·d→=a→·b→·(λ·d→)=λ·a→·b→·d→    λ∈R ;
2. a→·b→·d→=d→·a→·b→=b→·d→·a→;   a→·d→·b→=b→·a→·d→=d→·b→·a→ ;
3. (a(1)→+a(2)→)·b→·d→=a(1)→·b→·d→+a(2)→·b→·d→a→·(b(1)→+b(2)→)·d→=a→·b(1)→·d→+a→·b(2)→·d→a→·b→·(d(1)→+d(2)→)=a→·b→·d(2)→+a→·b→·d(2)→

Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль. Результатом умножения также будет нуль в том случае, если два или больше множителей равны.

Действительно, если a→=b→ , то, следуя определению векторного произведения [a→×b→]=a→·b→·sin 0 =0 , следовательно, смешанное произведение равно нулю, так как ([a→×b→], d→)=(0→, d→)=0 .

Если же a→=b→ или b→=d→ , то угол между векторами [a→×b→] и d→ равен π2 . По определению скалярного произведения векторов ([a→×b→], d→)=[a→×b→]·d→·cosπ2=0 .

Свойства операции умножения чаще всего требуются во время решения задач. Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.

Пример 1

Докажите равенство ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→) , где λ — некоторое действительное число.

Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:

• ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→)+([a→×b→], λ·a→)+([a→×b→], b→) Мы разобрали, что (([a→×b→], b→)=0. Из этого следует, что ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→)+([a→×b→], λ·a→)+([a→×b→], b→)==([a→×b→], d→)+([a→×b→], λ·a→)+0=([a→×b→], d→)+([a→×b→], λ·a→)

Согласно первому свойству ([a⇀×b⇀], λ·a→)=λ·([a⇀×b⇀],a→) , а ([a⇀×b⇀], a→)=0 . Таким образом, ([a⇀×b⇀], λ·a→) . Поэтому,
([a⇀×b⇀], d→+λ·a→+b→)=([a⇀×b⇀], d→)+([a⇀×b⇀], λ·a→)==([a⇀×b⇀], d→)+0=([a⇀×b⇀], d→)

Равенство доказано.

Пример 2

Необходимо доказать, что модуль смешанного произведения трех векторов не больше, чем произведения их длин.

Решение

Исходя из условия, можно представить пример в виде неравенства a→×b→, d→≤a→·b→·d→ .

По определению, преобразуем неравенство a→×b→, d→=a→×b→·d→·cos(a→×b→^, d→)==a→·b→·sin(a→, b→^)·d→·cos([a→×b→^], d)

Используя элементарные функции, можно сделать вывод, что 0≤sin(a→, b→^)≤1,  0≤cos([a→×b→^], d→)≤1 .

Из этого можно сделать вывод, что
(a→×b→, d→)=a→·b→·sin(a→, b→)^·d→·cos(a→×b→^, d→)≤≤a→·b→·1·d→·1=a→·b→·d→

Неравенство доказано.

Разбор типовых задач

Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz .

Пример 3

В прямоугольной системе координат представлены 3 вектора с такими координатами: a→=(1, -2, 3),  b→(-2, 2, 1),  d→=(3,-2, 5) . Необходимо определить, чему равно произведение указанных векторов a→·b→·d→ .

Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz=1-23-2213-25==1·2·5+(-1)·1·3+3·(-2)·(-2)-3·2·3-(-1)·(-2)·5-1·1·(-2)=-7

Пример 4

Необходимо найти произведение векторовi→+j→, i→+j→-k→, i→+j→+2·k→ , где i→,j→, k→ — орты прямоугольной декартовой системы координат.

Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: i→+j→=(1, 1, 0)i→+j→-k→=(1, 1, -1)i→+j→+2·k→=(1, 1, 2)

Используем формулу, которая использовалась выше
i→+j→×(i→+j→-k→, (i→+j→+2·k→)=11011-1112=0i→+j→×(i→+j→-k→, (i→+j→+2·k→)=0

Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.

Пример 5

В прямоугольной системе координат расположены три вектора a→,b→ и d→ , которые перпендикулярны между собой. Они представляют собой правую тройку, их длины составляют 4, 2 и 3. Необходимо умножить вектора.

Обозначим c→=a→×b→ .

Согласно правилу, результатом умножения скалярных векторов является число, которое равно результату умножения длин используемых векторов на косинус угла между ними. Делаем вывод, что a→·b→·d→=([a→×b→], d→)=c→,d→=c→·d→·cos(c→, d→^) .

Используем длину вектора d→ , указанную в условии примера: a→·b→·d→=c→·d→·cos(c→, d→^)=3·c→·cos(c→, d→^) . Необходимо определить с→и с→, d→^ . По условию a→,b→^=π2, a→=4, b→=2 .

Вектор c→ найдем с помощью формулы: c→=[a→×b→]=a→·b→·sina→, b→^=4·2·sinπ2=8 Можно сделать вывод, что c→ перпендикулярен a→ и b→ . Вектора a→, b→, c→ будут являться правой тройкой, так использована декартовая система координат.

Векторы c→ и d→ будут однонаправленными, то есть, c→,d→^=0 . Используя выведенные результаты, решаем пример a→·b→·d→=3·c→·cos(c→, d→^)=3·8·cos 0=24 .

a→·b→·d→=24 .

Геометрический смысл

Используем множители a→, b→ и d→ .

Вектора a→, b→ и d→ исходят от одной точки. Используем их как стороны для построения фигуры.

Обозначим, что c→=[a→×b→]. Для данного случая можно определить произведение векторов как a→·b→·d→=c→·d→·cos(c→, d→^)=c→·npc→d→ , где npc→d→ — числовая проекция вектора d→ на направление вектора c→=[a→×b→] .

Абсолютная величина npc→d→ равняется числу, которое также является равно высоте фигуры, для которого использованы вектора a→, b→ и d→ в качестве сторон. Исходя из этого, следует уточнить, что c→=[a→×b→] перпендикулярен a→ и вектору и вектору согласно определению умножения векторов. Величина c→=a→xb→ равняется площади параллелепипеда, построенного на векторах a→ и b→ .

Делаем вывод, что модуль произведения a→·b→·d→=c→·npc→d→ равен результату умножения площади основания на высоту фигуры, которая построена на векторах a→, b→ и d→ .

Определение 4

Абсолютная величина векторного произведения является объемом параллелепипеда: Vпараллелепипида=a→·b→·d→ .

Данная формула и является геометрическим смыслом.

Определение 5

Объем тетраэдра, который построен на a→,b→ и d→ , равняется 1/6 объема параллелепипеда Получаем, Vтэтраэда=16·Vпараллелепипида=16·a→·b→·d→ .

Содержание:

1. Переходим к понятию векторного произведения
2. Некоторые приложения к механике векторов

В векторной алгебре наряду с умножением вектора на скаляр и скалярным произведением двух векторов определяется также векторное произведение двух векторов, к описанию которого мы переходим.

Напомним что поверхность в пространстве ориентирована, если указано, какая ее сторона считается внешней, а какая — внутренней. Принято считать, что если эта поверхность незамкнутая (т.е. с краем), то ориентация поверхности порождает также ориентацпю ее контура, т.е.

направление его обхода. Обратно, если указывается направление обхода контура, это приводит к ориентации самой поверхности. Связь между ориентацией поверхности и ориентацией ее контура указана па рис. 134; если за основу системы координат взята правая тройка векторов (т. е. такая тройка, что, смотря с конца третьего вектора, мы видим кратчайший поворот от первого ко второму против часовой стрелки), то применяется правило правого винта, в противном случае — правило левого винта.

Например, правило правого винта можно сформулировать так: если правый винт (который обычно применяется в технике и обыденной жизни) вращать в направлении обхода контура, то винт должен пойти от внутренней стороны поверхности к наружной. Или, другими словами: если маленький человечек обходит по наружной стороне поверхности ее контур по указанному направлению обхода, то сама поверхность должна быть у него но левую руку*).

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Переходим к понятию векторного произведения

Векторное произведение двух векторов и определению, представляет собой вектор площадки (см. § Х.4), которая получится, если и отнести к одному началу, затем построить на этих векторах параллелограмм и обходить его контур, начиная с первого вектора (т. е. см. рис. 135,

Где принято правило правого винта, которым мы всегда будем пользоваться, если не оговорено противное).

Таким образом, векторное произведение двух векторов и — это вектор, направленный перпендикулярно обоим векторам, по модулю равный построенного на и и образующий с этими векторами тройку такого же смысла (т. е. правую пли левую), как векторы Обозначается векторное произведение косым крестом или квадратными скобками Отметим наиболее важные свойства векторного произведения. Так, векторное произведение двух ненулевых векторов равно нуль-вектору в том и только том случае, если векторы параллельны: равносильно так как параллельность векторов означает вырождение параллелограмма в отрезок, площадь которого равна нулю. В частности, всегда

Векторное произведение «аитикоммутативно» **)

Действительно, при перемене порядка множителей параллелограмм не изменится, но контур его будет проходиться в противоположном направлении и потому вектор площадки заменится на противоположный.

Можно проверить, что скалярный множитель можно выносить за знак векторного произведения:

на что справедлив распределительный закон:

Раскрывая скобки в выражениях, включающих векторное произведение, надо тщательно следить за порядком множителей. Приведем пример:

Пусть векторы и даны своими разложениями в декартовых проекциях

Тогда, если воспользоваться равенствами (проверьте их!)

получим

(продумайте структуру последнего выражения!).

Этот результат очень просто запомнить, если записать его в виде определителя (см. формулу

Пусть, например, надо вычислить площадь параллелограмма, построенного на векторах Так как то вычисляем

Так как в этом примере векторы безразмерные, то и площадь получается, соответственно, безразмерной.

Иногда применяется также векторно-скалярное или, иначе, смешанное произведение трех векторов которое, по определению, равно скалярной величине Ее геометрический смысл виден из рис. 136:

т. е. смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах. На рис. 138 векторы

образуют правую тройку, и получился объем со знаком плюс. Для левой тройки угол между и был бы тупой; в этом случае (Предполагается, что за основу принято правило правого винта.) Векторно-скалярное произведение равно пулю тогда и только тогда, когда все три вектора параллельны одной плоскости, так как такая параллельность означает, что параллелограмм вырождается в часть плоскости, т. е. имеет нулевой объем.

Легко получить выражение для смешанного иризведенпя в случае, с ели даны разложения сомножителей в декартовой системе координат. Для этого нужно правую часть (2) помножить обычным способом скалярнп (по формуле (IX,5)) на вектор Это даст после перегруппировки слагаемых

Нам понадобится еще формула для векторно-векторного произведения трех векторов. Для ее вывода представим себе, что мы выбрали оси координат так, что ось пошла по вектору а ось лежит в плоскости векторов Тогда вектор будет иметь проекцию только на ось т.е. аналогично Пользуясь формулой (3), получаем

Этот результат неудобен тем, что «привязан» к специальному выбору осей координат. Поэтому преобразуем его (проверьте)):

Эта формула уже не содержит координатных проекций, а потому не зависит от специального выбора системы координат.

Возможно вам будут полезны данные страницы:

Примеры с решением

Пример 1.

Определим векторное произведение векторов и из примера 48.

Векторное произведение векторов равно

Пример 2.

Даны точки Определим площадь треугольника

Из геометрического смысла векторного произведения векторов следует, что площадь треугольника равна Найдем координаты векторов

Тогда векторное произведение векторов и равно Отсюда Поэтому площадь треугольника равна

Пример 3.

Вектор перпендикулярный векторам и образует с осью тупой угол. Модуль вектора равен Определим координаты вектора

Из свойств векторного произведения векторов получаем что векторное произведение перпендикулярно векторам Поэтому векторы и коллинеарны.

Тогда модуль векторного произведения равен

Так как векторы коллинеарны, то соответствующие координаты этих векторов пропорциональны.

Пусть коэффициент пропорциональности. Тогда координаты вектора

Так как вектор образует с осью тупой угол, то соответствующий направляющий косинус меньше нуля:

Тогда Модуль вектора равен Отсюда Поэтому

Тогда вектор

Некоторые приложения к механике векторов

Векторное произведение особенно удобно при описании вращательного движения и связанных с ним понятий. Рассмотрим вращение твердого тела вокруг некоторой оси (рис. 137) с угловой скоростью Такое вращение принято изображать вектором угловой скорости который расположен но оси вращения и направлен в соответствии с направлением вращения согласно выбранному правилу винта; например, на рис. 137 направление выбрано по правилу правого винта, как мы всегда будем делать. Где именно на оси берется вектор

— безразлично; такой вектор, который можно произвольно перемещать вдоль некоторой оси, но не в сторону от этой оси, называется скользящим*).

Будем ‘ считать, что начало координа выбрано в любой точке оси вращения, и найдем линейную скорость произвольной точки с радиусом-вектором (рис. 137). Очевидно, что вектор перпендикулярен обоим векторам и а потому перпендикулярен и всему параллелограмму построенному на последних векторах. Численное значение равно произведению на кратчайшее расстояние точки оси вращения, т. е. как раз площади указанного параллелограмма. Но этим условиям, сформулированным для вектора удовлетворяет векторное произведение Таким образом,

(проверьте, что векторное произведение надо брать именно в выписанном порядке п что правая часть (5) не зависит от конкретного выбора точки на оси вращения).

Удобство вектора угловой скорости видно, в частности, из следующего. Допустим, что тело испытывает одновременно два вращения с (вообще говоря, непараллельными) векторами угловой скорости и причем оси вращения пересекаются в точке Тогда в силу формулы (5) линейная скорость любой точки равна где обозначено Значит, тело вращается с угловой скоростью и мы приходим к выводу, что при сложении вращений векторы угловой скорости складываются по правилу параллелограмма. Именно поэтому и можно называть угловую скорость вектором!

С помощью векторного произведения вводится такое важное понятие, как момент произвольного вектора с началом в точке относительно любой точки по определению, этот момент равен где В механике наиболее часто рассматривают момент силы т. е. величину и момент количества движения

При вычислении момента вектора этот вектор можно считать скользящим. В самом деле, если вектор скользит сам по себе, то это значит, что к прибавляется где — какой-то скаляр. Однако т. е. от такого скольжения момент вектора не меняется (рис. 138).

Если же вектор относить в сторону относительно его направления, то момент изменяется.

Рассмотрим систему как-то связанных между собой материальных частиц, каждая из которых имеет постоянную массу и (вообще говоря, переменный) радиус-вектор Пусть на каждую из этих точек действуют различные силы; обозначим равнодействующую всех «внутренних» сил (т. е. сил взаимодействия между точками системы), приложенных к точке, через а равнодействующую всех «внешних» сил — через ). Характерная особенность внутренних сил состоит в том, что на основе третьего закона Ньютона («действие рагсно противодействию») для каждой внутренней силы имеется противоположная ей внутренняя сила, причем, что очень важно, расположенная на продолжении первой.

Поэтому сумма всех внутренних сил, а также сумма их моментов относительно любой точки равны нулю.

Основные уравнения движения системы частиц получаются, если записать второй закон Ньютона («сила равна произведению массы на ускорение

Если просуммировать эти равенства по всем частицам, получим

гак как сумма всех внутренних сил, как было сказано выше, равна пулю. Удобно ввести точку с радиусом-вектором

— общая масса системы; эта точка называется «центром масс» рассматриваемой системы. При таком обозначении уравнение (7) можно переписать в виде

Итак, центр масс движется гак, как будто он обладает полной массой системы и на него действует сила, равная сумме всех внешних сил. В частности, если внешние силы отсутствуют, то центр масс системы движется прямолинейно и равномерно,

Перейдем к моментам. Если обе части равенства (6) умножить слева векторпо на мы получим

Воспользуемся равенством

которое вытекает из общей формулы производной векторного произведения

эта формула выводится совершенно так же, как аналогичная формула для скалярного произведения. Отсюда равенство (8) можно переписать так

Суммируя эти равенства по всем получим

так как сумма моментов всех внутренних сил равна нулю. Сумма

моментов количества движения всех частиц, составляющих систему, называется кинетическим моментом (моментом вращения) этой системы относительно той же точки по отношению к которой берутся все .моменты. Сумма моментов всех внешних сил, действующих на систему, называется полным (главным) моментом внешних сил. Таким образом, формулу (9) можно переписать

т. е. скорость изменения кинетического момента системы равна полному моменту внешних сил, действующих на эту систему. В частном случае, если внешние силы отсутствуют или если их полный момент равен нулю, получаем, что кинетический момент системы остается постоянным.

Скалярное произведение векторов (далее в тексте СП). Дорогие друзья! В состав экзамена по математике входит группа задач на решение векторов. Некоторые задачи мы уже рассмотрели. Можете посмотреть их в категории «Векторы».  В целом, теория векторов несложная, главное последовательно её изучить. Вычисления и действия с векторами в школьном курсе математики просты, формулы не сложные.  Загляните в справочник. В этой статье мы разберём задачи на СП векторов (входят в ЕГЭ). Теперь «погружение» в теорию:

Чтобы найти координаты вектора, нужно из координат его конца вычесть соответствующие координаты его начала

И ещё:

*Длина вектора (модуль) определяется следующим образом:

Данные  формулы необходимо запомнить!!!

Покажем угол между векторами:

Понятно, что он может изменяться в пределах от 0 до 180⁰ (или в радианах от 0 до Пи).

Можем сделать некоторые выводы о знаке скалярного произведения. Длины векторов имеют положительное значение, это очевидно. Значит знак скалярного произведения зависит от значения косинуса угла между векторами.

Возможны случаи:

1. Если угол между векторами острый (от 0⁰ до 90⁰), то косинус угла будет иметь положительное значение.

2. Если угол между векторами тупой (от 90⁰ до 180⁰), то косинус угла будет иметь отрицательное  значение.

*При нуле градусов, то есть когда векторы имеют одинаковое направление, косинус равен единице и соответственно результат будет положительным.

При  180^о, то есть когда векторы имеют противоположные направления, косинус равен минус единице,  и соответственно результат будет отрицательным.

Теперь ВАЖНЫЙ МОМЕНТ!

При 90^о, то есть когда векторы перпендикулярны друг другу, косинус равен нулю, а значит и СП равно нулю. Этот факт (следствие, вывод) используется при решение многих задач, где речь идёт о взаимном расположении векторов, в том числе и в задачах входящих в открытый банк заданий по математике.

Сформулируем утверждение:  скалярное произведение равно нулю тогда и только тогда, когда данные векторы лежат на перпендикулярных прямых.

Итак, формулы СП векторов:

Если известны координаты векторов или координаты точек их начал и концов, то всегда сможем найти угол между векторами:

Рассмотрим задачи:

27724 Найдите скалярное произведение векторов a и b.

Скалярное произведение векторов мы можем найти по одной из двух формул:

Угол между векторами неизвестен, но мы без труда можем найти координаты векторов и далее воспользоваться первой формулой. Так как начала обоих векторов совпадают с началом координат, то координаты данных векторов равны координатам их концов, то есть

Как найти координаты вектора изложено в этой статье.

Вычисляем:

Ответ: 40

Найдём координаты векторов и воспользуемся формулой:

Чтобы найти координаты вектора необходимо из координат конца вектора вычесть соответствующие координаты его начала, значит

Вычисляем скалярное произведение:

Ответ: 40

Найдите угол между векторами a и b. Ответ дайте в градусах.

Пусть координаты векторов имеют вид:

Для нахождения угла между векторами используем формулу скалярного произведения векторов:

Косинус угла между векторами:

Следовательно:

Координаты данных векторов равны:

Подставим их в формулу:

Угол между векторами равен 45 градусам.

Ответ: 45

Посмотреть решение

Посмотреть решение

27710. Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов АВ и AD.

Посмотреть решение

27719. Диагонали ромба ABCD пересекаются в точке О и равны 12 и 16. Найдите скалярное произведение векторов AB и BO.

Посмотреть решение

27719. Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов AB и АС.

Посмотреть решение

На этом  всё! Успехов вам! 

С уважением, Александр Крутицких.

На уроке физкультуры: — Так, парни, кто из вас курит? Честно! Не врать! Так. … значит, ты… и ты. … Понятно… Значит, так: мы с вами покурим, остальным — пять кругов по стадиону.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.