Применение векторов к решению задач

Данная разработка – подробный разбор нескольких обучающих задач на применение векторов к задачам на доказательство, содержит доказательство теоремы о средней линии трапеции. Презентация может быть использована на уроках геометрии в 8 классе, либо в 9 классе в зависимости от календарно-тематического планирования (учебник Геометрия 7-9, автор Л.С.Атанасян)
Просмотр содержимого документа
«Применение векторов к решению задач»

Применение векторов к решению задач
К учебнику Геометрия 7-9,
автор Л.С.Атанасян и др.
Автор: Софронова Наталия Андреевна,
учитель математики высшей категории
МОУ «Упшинская основная общеобразовательная школа»
Оршанского района Республики Марий Эл
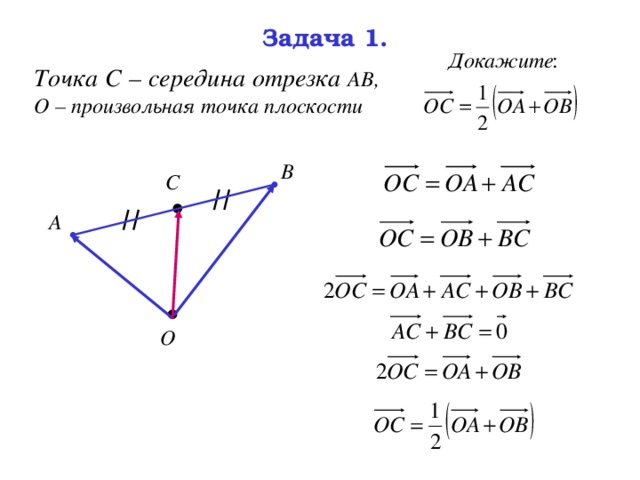
Точка С – середина отрезка АВ, О – произвольная точка плоскости

Доказать, что прямая, проведенная через середины оснований трапеции проходит через точку пересечения продолжений боковых сторон.

В треугольнике АВС В 1 – середина стороны АС, точка А 1 лежит на стороне ВС так, что ВА 1 : А 1 С = 1 : 2. Используя векторы, докажите, что середина ВВ 1 лежит на прямой АА 1.
Доказать: О є АА 1
О – середина ВВ 1

Задача 3 (продолжение).
О – середина ВВ 1
Доказать: О є АА 1
лежат на одной прямой,
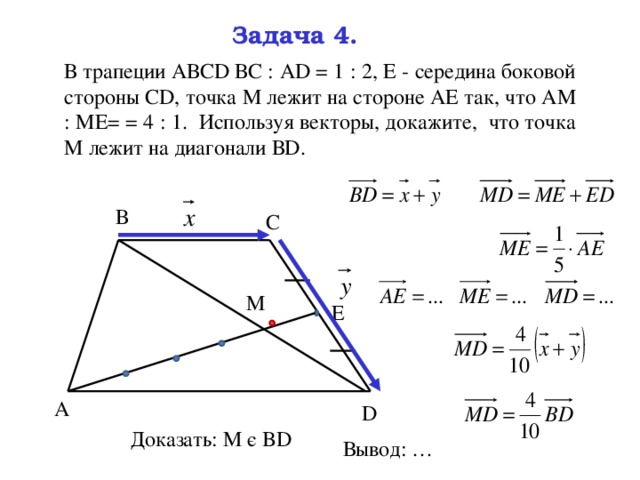
В трапеции АВСD ВС : АD = 1 : 2, Е – середина боковой стороны СD, точка М лежит на стороне АЕ так, что АМ : МЕ= = 4 : 1. Используя векторы, докажите, что точка М лежит на диагонали ВD.
Доказать: М є BD
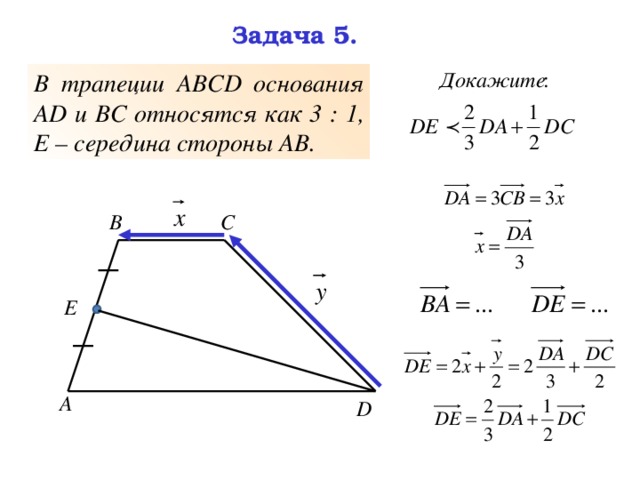
В трапеции АВСD основания АD и ВС относятся как 3 : 1, Е – середина стороны АВ.

Задача 5 (продолжение).
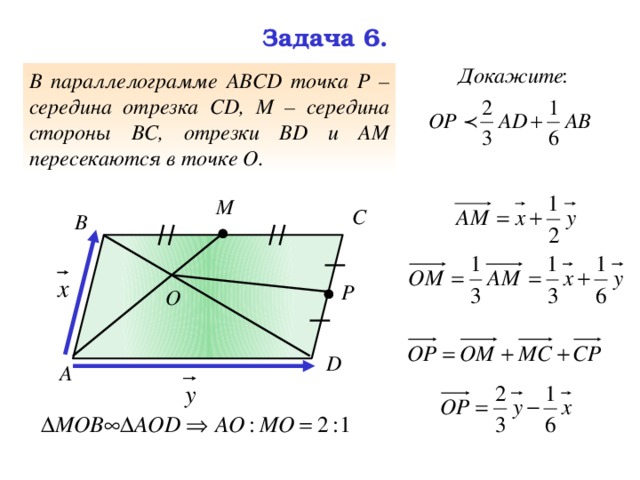
В параллелограмме АВСD точка Р – середина отрезка СD, М – середина стороны ВС, отрезки ВD и АМ пересекаются в точке О.

Задача 6 (продолжение).
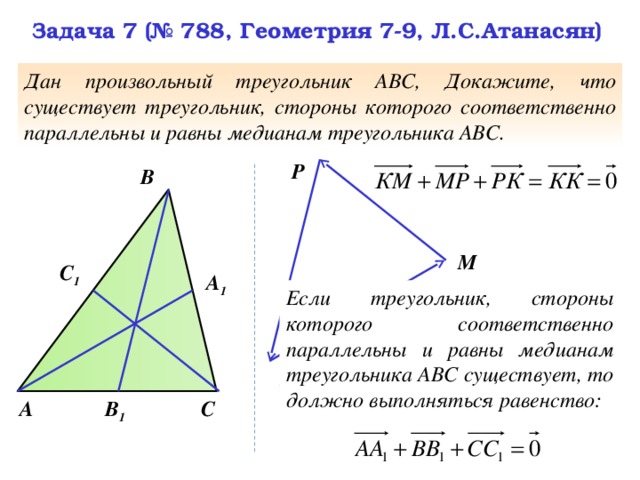
Задача 7 (№ 788, Геометрия 7-9, Л.С.Атанасян)
Дан произвольный треугольник АВС, Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС.
Если треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС существует, то должно выполняться равенство:
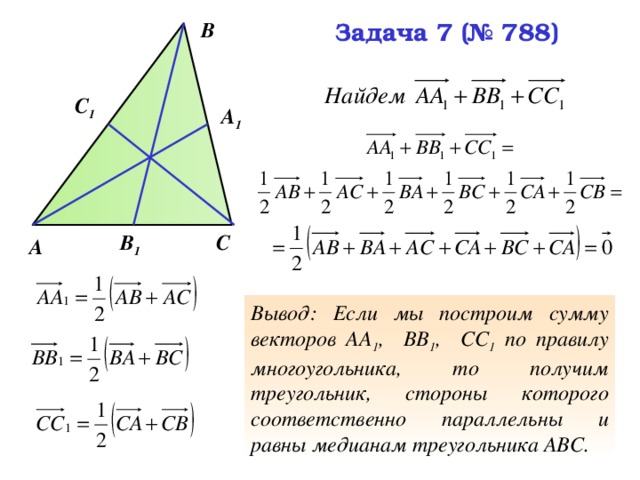
Вывод: Если мы построим сумму векторов АА 1 , ВВ 1 , СС 1 по правилу многоугольника, то получим треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС.
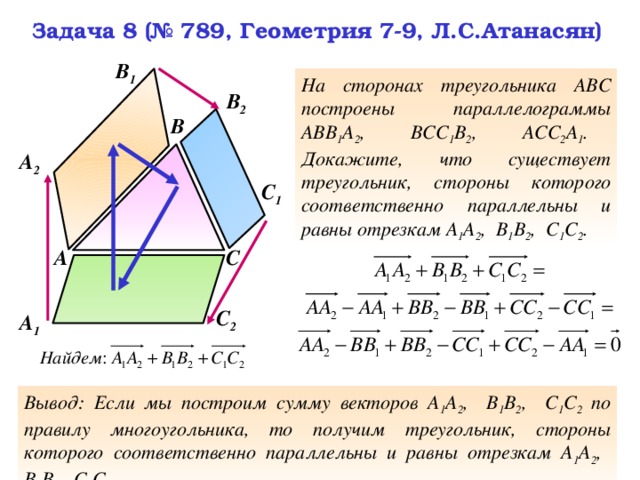
Задача 8 (№ 789, Геометрия 7-9, Л.С.Атанасян)
На сторонах треугольника АВС построены параллелограммы АВВ 1 А 2 , ВСС 1 В 2 , АСС 2 А 1 . Докажите, что существует треугольник, стороны которого соответственно параллельны и равны отрезкам А 1 А 2 , В 1 В 2 , С 1 С 2 .
Вывод: Если мы построим сумму векторов А 1 А 2 , В 1 В 2 , С 1 С 2 по правилу многоугольника, то получим треугольник, стороны которого соответственно параллельны и равны отрезкам А 1 А 2 , В 1 В 2 , С 1 С 2 .
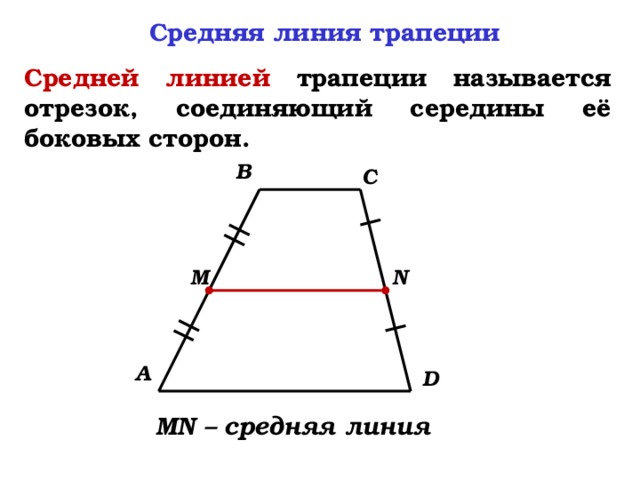
Средняя линия трапеции
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
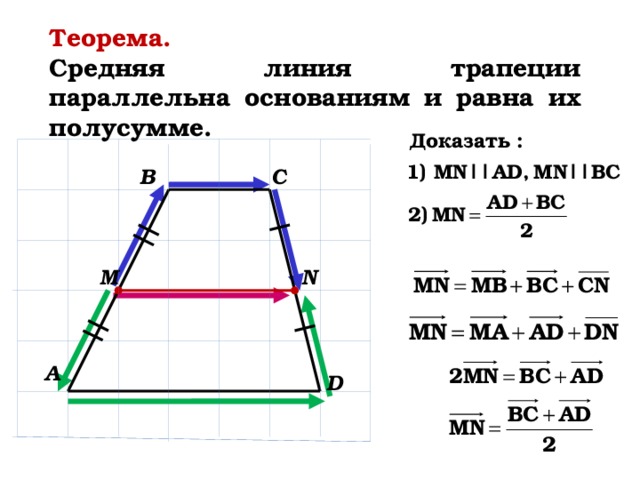
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Разработка урока по теме “Применение векторов к решению задач. Средняя линия трапеции”.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Г – 9 класс Урок № 7
Тема: «Применение векторов к решению задач. Средняя линия трапеции».
Дидактическая: на конкретных примерах показать применение векторов при решении геометрических задач; ввести понятия средней линии трапеции; доказать теорему о средней линии трапеции с помощью векторов.
Развивающая: развивать логическое мышление учащихся, учить решать задачи; развивать воображение – репродуктивное, творческое, образное; абстрактное мышление, умение обобщать.
Воспитательная: нравственное воздействие, воспитание культуры умственного труда, культуры общения.
Знать, действия производимые с векторами, понятие средней линии трапеции, теорему о средней линии трапеции.
Уметь вычислять среднюю линию трапеции, решать задачи с помощью векторов.
Сообщение темы и целей урока.
Актуализация знаний и умений обучающихся.
Проверка выполнения домашнего задания. Разбор нерешенных заданий.
Повторение изученного материала.
1. Ответить на вопросы на с. 213–214.
2. Проверка усвоения учащимися материала.
1. Устно ответить на вопросы:
1) Какие векторы называются коллинеарными? Изобразите на рисунке сонаправленные векторы  и
и  и противоположно направленные векторы
и противоположно направленные векторы 
 и .
и .
2) Какой вектор называется произведением данного вектора на данное число?
3) Могут ли векторы  и
и  быть неколлинеарными?
быть неколлинеарными?
4) Сформулируйте основные свойства умножения вектора на число.
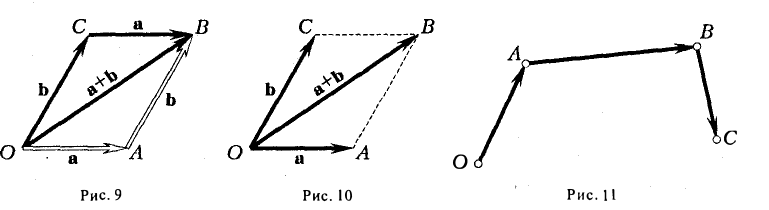
2. Решить задачу на доске и в тетрадях по готовому чертежу:

Точки M и N лежат соответственно на сторонах AD и BC четырехугольника ABCD, причем AM : MD = BN : NC = 3 : 4.
Докажите, что середины отрезков AB, MN и CD лежат на одной прямой.
Пусть K1 – середина AB, K2 – середина MN, K3 – середина CD. Согласно задаче 2 из п. 84 имеем  . Из условия следует, что
. Из условия следует, что  , поэтому
, поэтому  .
.
Таким образом, векторы  и
и  коллинеарные, и, значит, точки K1, K2 и K3 лежат на одной прямой.
коллинеарные, и, значит, точки K1, K2 и K3 лежат на одной прямой.
Изучение нового материала.
1. Определение трапеции. Виды трапеций.
2. Определение средней линии трапеции.
3. Доказательство теоремы о средней линии трапеции.
Доказательство оформить на доске и в тетрадях в виде следующей краткой записи:
Дано: ABCD – трапеция, AD || BC, M – середина стороны AB; N – середина стороны CD (рис. 266 учебника).
Доказать: MN || AD, MN =  .
.
1) Согласно рассмотренной в классе задаче 1  .
.
2) Так как  , то
, то  и, значит, MN || AD.
и, значит, MN || AD.
3) Так как  , то
, то  = AD + BC, поэтому MN =
= AD + BC, поэтому MN =  (AD + BC).
(AD + BC).
Формирование умений и навыков.
Работа по учебнику.
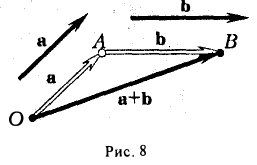
1. Векторы могут использоваться для решения геометрических задач. Рассмотрим вспомогательную задачу.
2. Разобрать решение задачи 1 на с. 208 учебника по рис. 264.
3. Решить задачу 2. Точки M и N – середины сторон AB и CD четырехугольника ABCD. Докажите, что 
Пусть О – произвольная точка. Согласно задаче 1 из п. 84 имеем 
 поэтому
поэтому 
 .
.
Примечание. Результат задачи 2 можно использовать при доказательстве теоремы о средней линии трапеции на следующем уроке.
4. 1. Решить на доске и в тетрадях задачу № 793.
Пусть a и b – основания трапеции, тогда а + b = 48 – (13 + 15) = 20 (см); средняя линия MN =  = 10 (см).
= 10 (см).
2. Решить задачу № 795.
3. Решить задачу № 799 на доске и в тетрадях.

Пусть BK – перпендикуляр, проведенный к основанию AD данной трапеции.
Тогда KD = AD – AK.
Но AK =  , поэтому KD = AD –
, поэтому KD = AD –  , то есть отрезок KD равен средней линии трапеции. Значит, средняя линия трапеции равна 7 см.
, то есть отрезок KD равен средней линии трапеции. Значит, средняя линия трапеции равна 7 см.
5. Решить задачу 3. Точка С лежит на отрезке AB, причем АС : СВ = 2 : 3. Докажите, что для любой точки О справедливо равенство 
По условию AC:CB=2 : 3,поэтому  Но
Но  Следовательно,
Следовательно,  откуда получается
откуда получается 
Примечание. Задача 3 является частным случаем более общей задачи 806.
6. Решить задачу № 786 на доске и в тетрадях.
Так как точка А1 – середина стороны ВС, то 
 .
.
Далее 
7. При наличии времени решить задачу 4.
Точки K, L, M, N – середины сторон AB, BC, CD, DE пятиугольника ABCDE, а точки P и Q – середины отрезков KM и LN. Докажите, что PQ || AE и PQ = 1/4 AE.

Пусть О – произвольная точка. Согласно задаче 1 из п. 84  . Аналогично,
. Аналогично,  .
.
Из этих равенств следует, что  Отсюда следует, что PQ || AE и PQ =
Отсюда следует, что PQ || AE и PQ =  AE.
AE.
Подвести итоги урока, выставить отметки обучающимся за урок.
В результате изучения параграфа обучающиеся должны знать, какой вектор называется произведением вектора на число; уметь формулировать свойства умножения вектора на число; знать, какой отрезок называется средней линией трапеции; уметь формулировать и доказывать теорему о средней линии трапеции; уметь решать задачи типа №№ 782–787; 793–799.
Домашнее задание: изучить материал п. 87, 88; ответить на вопросы 18–20, с. 214 учебника; решить задачи №№ 787, 794, 796.
Применение векторов к решению задач (продолжение)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

На данном уроке мы рассмотрим применение векторов для решения различных геометрических задач, вспомним и докажем некоторые геометрические факты.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»
[spoiler title=”источники:”]
http://infourok.ru/razrabotka-uroka-po-teme-primenenie-vektorov-k-resheniyu-zadach-srednyaya-liniya-trapecii-1442001.html
http://interneturok.ru/lesson/geometry/8-klass/vektory/primenenie-vektorov-k-resheniyu-zadach-prodolzhenie
[/spoiler]
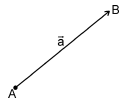
Вектором называется направленный отрезок. Вектор обозначается либо символом 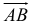 (
(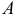 — точка начала,
— точка начала, 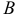 — точка конца вектора), либо
— точка конца вектора), либо  . В математике обычно рассматриваются свободные векторы, то есть векторы, точка приложения которых может быть выбрана произвольно.
. В математике обычно рассматриваются свободные векторы, то есть векторы, точка приложения которых может быть выбрана произвольно.
2. Длиной (модулем) вектора 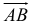 называется длина отрезка
называется длина отрезка 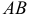 . Модуль вектора обозначается
. Модуль вектора обозначается 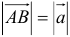 .
.
3.Вектор называется единичным, если его длина равна «1»; единичный вектор 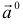 направления вектора
направления вектора  называется ортом вектора
называется ортом вектора  и определяется по формуле
и определяется по формуле 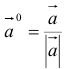 .
.
4. Вектор называется нулевым, если его начало и конец совпадают 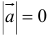 ; любое направление можно считать направлением нулевого вектора.
; любое направление можно считать направлением нулевого вектора.
5. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарность векторов обозначается: 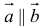 . Необходимым и достаточным условием коллинеарности векторов
. Необходимым и достаточным условием коллинеарности векторов  и
и 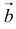 является существование такого числа
является существование такого числа 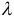 , что
, что 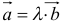 .
.
6. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление.
7. Вектор 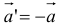 называется противоположным вектору
называется противоположным вектору  , если модули их равны, а направления противоположны.
, если модули их равны, а направления противоположны.
8. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Для решения задач необходимо уметь выполнять линейные операции над вектором в геометрической форме, то есть над вектором, как над
направленным отрезком: сложение, вычитание векторов и умножение вектора на число.
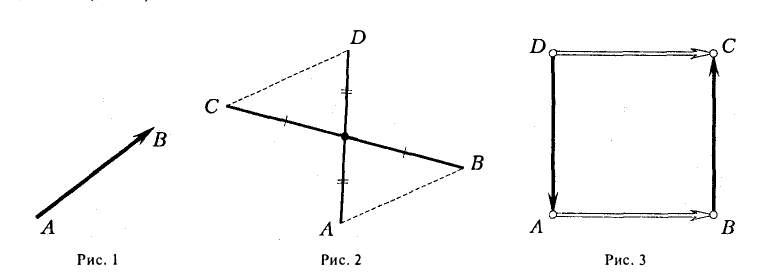
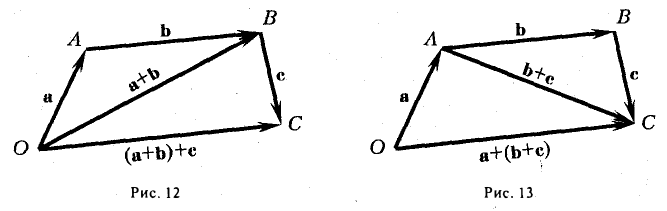
9. Сложение двух векторов можно выполнить по правилу параллелограмма (рис. 1) или по правилу треугольника (рис. 2).
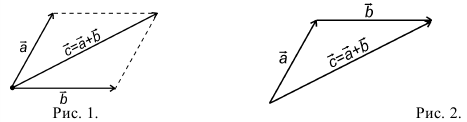
При сложении более двух векторов, лежащих в одной плоскости, используется правило «замыкающей линии многоугольника» (рис. 3).
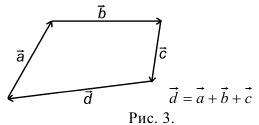
При сложении трех некомпланарных векторов удобно пользоваться правилом «параллелепипеда» (рис. 4).
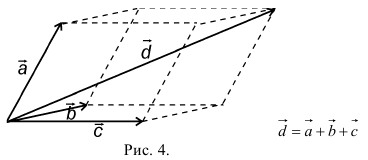
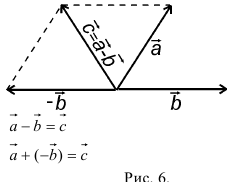
10. Действие вычитания двух векторов связано с действием сложения (рис.5).
Разностью двух векторов называется вектор, проведенный из конца вычитаемого в конец уменьшаемого. Заметим, что разностью является вектор, служащий второй диагональю параллелограмма.
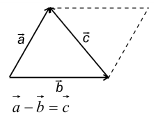
Разность можно также представить в виде сложения с противоположным вектором (рис. 6).
11. Произведением вектора  на число
на число 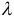 называется вектор
называется вектор 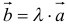 , который имеет :
, который имеет :
12. Для решения задач полезно знать также следующие законы и свойства:
- переместительный:
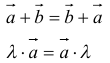
- сочетательный:
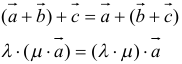
- распределительный:
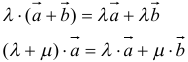

Примеры задач решаемых с применением векторной алгебры
Задача:
Пусть даны точки 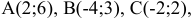
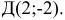
1) Найти координаты векторов
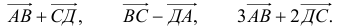
2) Написать разложение этих векторов по базису 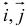
3) Найти длины этих векторов
4) Найти скалярное произведение 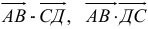
5) Найти угол между векторами  и
и  .
.
6) Найти разложение вектора  по базису
по базису  и
и 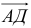
Решение:
1) Вычислим координаты векторов  и
и 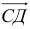 (нужно из координат точки его конца вычесть координаты его начала):
(нужно из координат точки его конца вычесть координаты его начала):
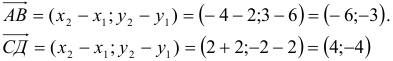
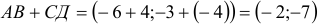 , аналогично,
, аналогично, 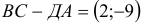
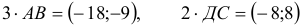 и
и 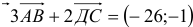
2) 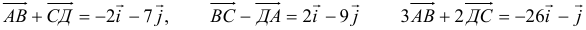
3)
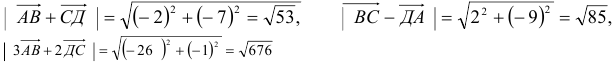
4) Для вычисления угла между векторами воспользуемся формулой:
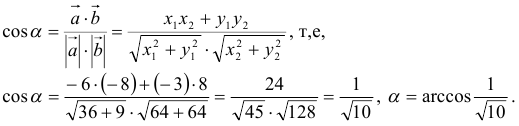
5) Разложить вектор  по векторам
по векторам  и
и 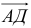 — это значит представить вектор
— это значит представить вектор  в виде линейной комбинации векторов
в виде линейной комбинации векторов  и
и 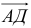 , т. е.
, т. е.
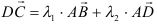 , где
, где 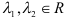 . Имеем
. Имеем 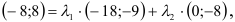
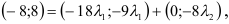
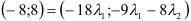 , но у равных векторов соответственно равны координаты, следовательно, получим систему, из которой найдем
, но у равных векторов соответственно равны координаты, следовательно, получим систему, из которой найдем 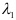 и
и 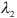 .
.
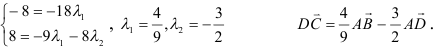
Задача:
а). Даны векторы 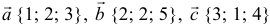 и
и 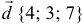 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы 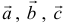 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 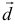 в этом базисе.
в этом базисе.
Решение:
Три вектора образуют базис, если 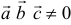 .
.
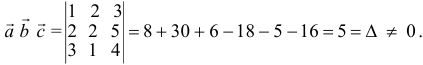
Найдем координаты вектора 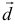 в базисе
в базисе 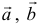 и
и 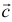 .
.
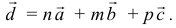
Два вектора равны, если их соответствующие координаты равны.
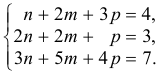
Решим систему методом Крамера:
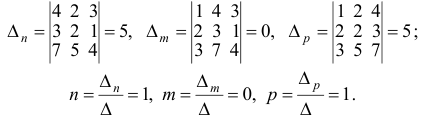
Ответ: 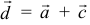 .
.
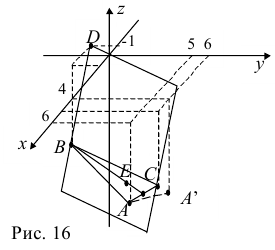
Задача:
Даны координаты вершин тетраэдра 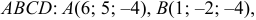
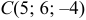 и
и 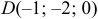 . Найти: 1) координаты точки пересечения медиан треугольника
. Найти: 1) координаты точки пересечения медиан треугольника 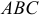 ; 2) уравнение прямой, проходящей через вершину
; 2) уравнение прямой, проходящей через вершину  параллельно медиане, проведенной из вершины
параллельно медиане, проведенной из вершины 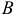 треугольника
треугольника 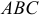 ; 3) координаты точки, симметричной точке
; 3) координаты точки, симметричной точке  относительно плоскости
относительно плоскости  . Сделать чертёж.
. Сделать чертёж.
Решение:
1) Найдем координаты т. 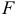 середины отрезка
середины отрезка 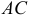 (рис. 16):
(рис. 16): 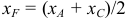
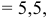
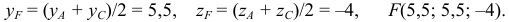
Точка 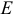 пересечения медиан треугольника делит медиану
пересечения медиан треугольника делит медиану 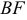 в отношении
в отношении 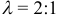 , считая от вершины
, считая от вершины 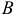 . Найдем координаты точки
. Найдем координаты точки  :
:
2) Найдем направляющий вектор прямой 
 . Уравнение прямой, проходящей через вершину
. Уравнение прямой, проходящей через вершину  параллельно прямой
параллельно прямой 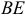 :
:
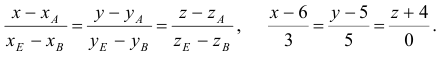
3) Найдем уравнение плоскости  :
:
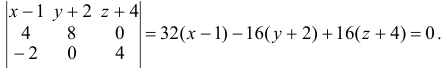
Найдем каноническое уравнение прямой, перпендикулярной плоскости  и проходящей через т.
и проходящей через т.  :
: 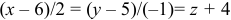 . Запишем каноническое уравнение прямой в параметрическом виде:
. Запишем каноническое уравнение прямой в параметрическом виде: 
 .
.
Найдем координаты точки  пересечения плоскости
пересечения плоскости  и найденной прямой:
и найденной прямой: 
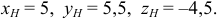
Координаты точки 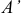 симметричной точке
симметричной точке  относительно плоскости
относительно плоскости  —
— 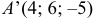 .
.
Ответ: 1) координаты точки пересечения медиан 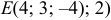 уравнение прямой
уравнение прямой 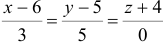 ; 3) координаты симметричном точки
; 3) координаты симметричном точки 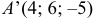 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
Векторная алгебра — решение заданий и задач по всем темам с вычислением
Понятие вектора. Линейные операции над векторами
1°. Любые две точки 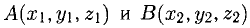 пространства, если они упорядочены (например, А является первой, а В — второй точкой), определяют отрезок вместе с выбранным направлением (а именно, от A к В). Направленный отрезок называется вектором. Вектор с началом в A и концом в В обозначается
пространства, если они упорядочены (например, А является первой, а В — второй точкой), определяют отрезок вместе с выбранным направлением (а именно, от A к В). Направленный отрезок называется вектором. Вектор с началом в A и концом в В обозначается 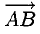 или
или 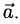 Длина вектора, обозначаемая
Длина вектора, обозначаемая 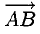 , АВ или
, АВ или 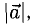 а, называется также модулем вектора. Чтобы найти координаты вектора, нужно из координат конца вектора вычесть одноименные координаты начала:
а, называется также модулем вектора. Чтобы найти координаты вектора, нужно из координат конца вектора вычесть одноименные координаты начала: 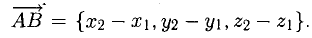 Тогда длина вектора найдется так:
Тогда длина вектора найдется так:
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.
Два вектора  называются равными, если они коллинеарны, имеют одинаковые модули и направления. В этом случае пишут
называются равными, если они коллинеарны, имеют одинаковые модули и направления. В этом случае пишут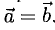 Равные векторы имеют равные координаты.
Равные векторы имеют равные координаты.
Векторы  называются противоположными, если они коллинеарны, имеют одинаковые длины и противоположные направления:
называются противоположными, если они коллинеарны, имеют одинаковые длины и противоположные направления: 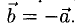
Вектор называется нулевым, если его модуль равен нулю, и обозначается 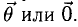
2°. Линейными называются действия сложения, вычитания векторов и умножения вектора на число.
1.Если начало  совмещено с концом
совмещено с концом  то начало
то начало  совпадает с началом
совпадает с началом  а конец — с концом
а конец — с концом  (рис. 3.1).
(рис. 3.1).
2.Если начала векторов  совмещены, то начало
совмещены, то начало  совпадает с концом
совпадает с концом  , а конец
, а конец  совпадает с концом
совпадает с концом  (рис. 3.2).
(рис. 3.2).
3.При умножении вектора на число (скаляр)
на число (скаляр) 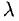 длина вектора умножается на
длина вектора умножается на 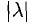 , а направление сохраняется, если
, а направление сохраняется, если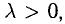 и изменяется на противоположное, если
и изменяется на противоположное, если 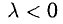 (рис. 3.3).
(рис. 3.3).
Вектор 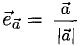 называется ортом, или единичным вектором вектора
называется ортом, или единичным вектором вектора  его длина равна единице:
его длина равна единице: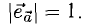
3°. Запись ci — 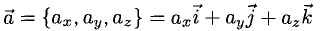 означает, что вектор
означает, что вектор  имеет координаты
имеет координаты или
или  разложен по базису
разложен по базису 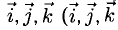 — орты осей Ох, Оу и Oz пространственной системы координат Oxyz). При этом
— орты осей Ох, Оу и Oz пространственной системы координат Oxyz). При этом
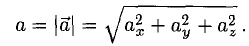
4°. Числа 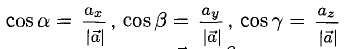 называются направляющими косинусами вектора
называются направляющими косинусами вектора 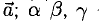 — углы между вектором
— углы между вектором  и координатными осями Ох, Оу, Oz соответственно. Единичный вектор
и координатными осями Ох, Оу, Oz соответственно. Единичный вектор 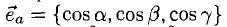 — орт вектора
— орт вектора  . Для любого вектора справедливо:
. Для любого вектора справедливо: 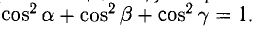
5°. Линейные операции над векторами, которые заданы своими координатами, определяются так: пусть 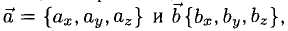 тогда
тогда
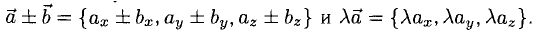
Следовательно, при сложении векторов складываются их соответствующие координаты, а при умножении вектора на число умножаются на число все координаты вектора.
6°. Необходимое и достаточное условие коллинеарности векторов  , устанавливаемое равенством
, устанавливаемое равенством 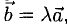 может быть записано соотношениями
может быть записано соотношениями 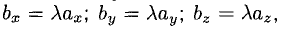 из которых следует пропорциональность их координат:
из которых следует пропорциональность их координат: 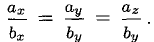
Если один из членов какого-нибудь из этих отношений равен нулю, то и второй член того же отношения должен быть нулем. Геометрически это значит, что в этом случае оба вектора перпендикулярны соответствующей координатной оси (например, если 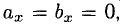 то векторы
то векторы 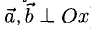 ).
).
7°. Система векторов 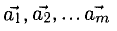 называется линейно независимой, если равенство
называется линейно независимой, если равенство
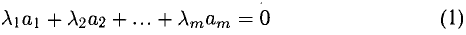
(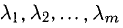 — действительные числа) возможно только при
— действительные числа) возможно только при  Если же равенство (1) возможно при некотором нетривиальном наборе
Если же равенство (1) возможно при некотором нетривиальном наборе 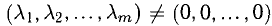 то система этих векторов называется линейно зависимой. Любой вектор линейно зависимой системы линейно выражается через остальные.
то система этих векторов называется линейно зависимой. Любой вектор линейно зависимой системы линейно выражается через остальные.
Примеры с решениями
Пример:
Доказать, что треугольник с вершинами в точках A(1,2), B(2,5), С(3,4) прямоугольный.
Решение:
Построим векторы, совпадающие со сторонами треугольника (см. п. 1°): 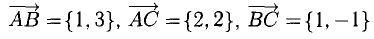 (рис. 3.4).
(рис. 3.4).
Найдем длины сторон: 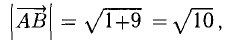
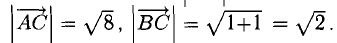
Нетрудно видеть, что 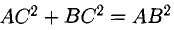 Следовательно, треугольник ABC прямоугольный с гипотенузой
Следовательно, треугольник ABC прямоугольный с гипотенузой 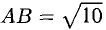 и катетами
и катетами 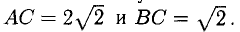
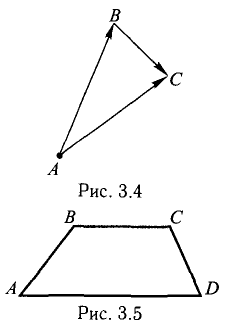
Пример:
Проверить, что точки А( 2,-4,3), В(5, —2,9), С( 7,4,6) и D(6,8, -3) являются вершинами трапеции.
Решение:
Составим векторы-стороны с целью обнаружения коллинеарности векторов (в трапеции ВС || AD) (рис. 3.5):
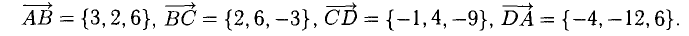
Имеем 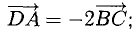 значит, ABCD — трапеция.
значит, ABCD — трапеция.
Пример:
Найти орт и направляющие косинусы вектора 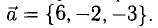
Решение:
Имеем 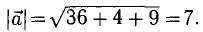 В соответствии с п. 3°, 4°
В соответствии с п. 3°, 4°
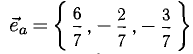 и направляющие косинусы вектора
и направляющие косинусы вектора 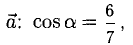
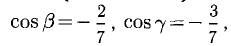 причем
причем 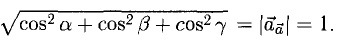
Пример:
Определить точку В, которая является концом вектора 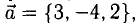 , если его начало совпадает с точкой
, если его начало совпадает с точкой
Решение:
Пусть точка В имеет координаты B(x,y,z) (рис. 3.6). Тогда координа- ^ ты вектора (п. 1°)
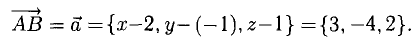
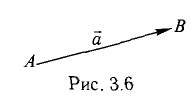
Следовательно, 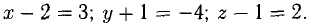 Ответ. В(5, -5,3).
Ответ. В(5, -5,3).
Пример:
Вектор 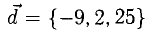 разложить по векторам
разложить по векторам
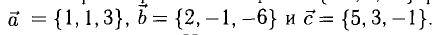
Решение:
Необходимо найти такие числа х, у, z, что 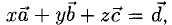 т.е.
т.е.
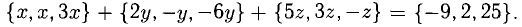
Имея в виду, что при сложении векторов складываются их координаты и равные векторы имеют равные координаты, приходим к системе уравнений
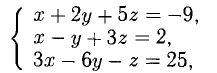
из которой
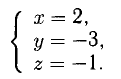
Ответ. 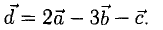
Пример:
Показать, что система векторов 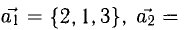
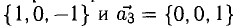 линейно независима.
линейно независима.
Решение:
В данном случае равенство (1) имеет вид 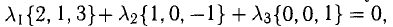 , или
, или 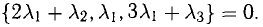 Отсюда получаем систему уравнений
Отсюда получаем систему уравнений
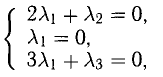
из которой следует, что 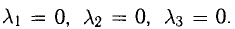 Это подтверждает линейную независимость данных векторов.
Это подтверждает линейную независимость данных векторов.
Пример:
Показать, что система векторов 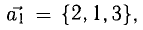
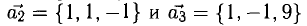 линейно зависима.
линейно зависима.
Решение:
Равенство (1) равносильно системе уравнений
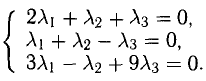
Она имеет ненулевое решение, например,  Таким образом,
Таким образом,  Отсюда видно, что
Отсюда видно, что  т.е. вектор
т.е. вектор  линейно выражается через
линейно выражается через 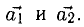 Очевидно, что
Очевидно, что 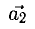 можно выразить через
можно выразить через 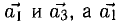 — через
— через 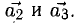
Скалярное произведение векторов
1°. Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению их длин на косинус угла 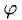 между ними:
между ними:
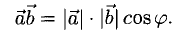
Из 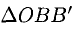 (рис. 3.7) имеем
(рис. 3.7) имеем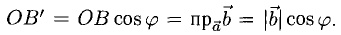 (
(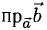 — проекция вектора
— проекция вектора на направление вектора
на направление вектора  ).
).
Итак, 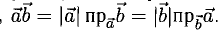
2°. Если
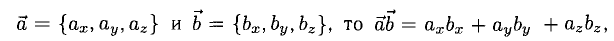
т.е. скалярное произведение векторов равно сумме произведений одноименных координат этих векторов.
При этом  если же
если же  , т. е.
, т. е. 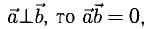 поскольку cos 90° = 0 (условие перпендикулярности двух векторов).
поскольку cos 90° = 0 (условие перпендикулярности двух векторов).
3°. Из определения скалярного произведения следует формула для вычисления угла между двумя векторами:
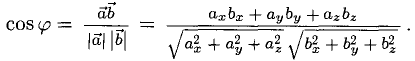
Примеры с решениями
Пример:
Перпендикулярны ли векторы  если
если 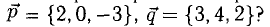
Решение:
Условие перпендикулярности векторов (п. 2°) 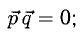 в нашем случае
в нашем случае
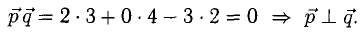
Ответ. Да.
Пример:
Найти проекцию вектора 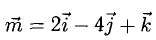 на направление вектора
на направление вектора 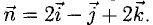
Решение:
Имеем 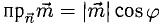 (п. 1°). Подставив сюда выражение для
(п. 1°). Подставив сюда выражение для 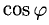 из п. 3°, получим
из п. 3°, получим
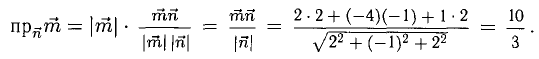
Ответ 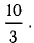
Пример:
Зная векторы, совпадающие с двумя сторонами: 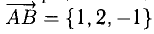 и
и 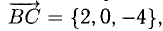 найти внутренние углы треугольника ABC.
найти внутренние углы треугольника ABC.
Решение:
Имеем (рис. 3.8)
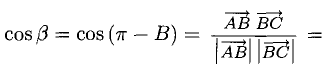
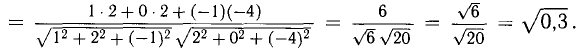
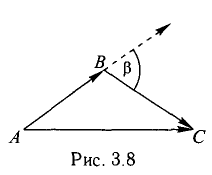
При помощи таблиц находим  Для нахождения других углов нам понадобится вектор
Для нахождения других углов нам понадобится вектор  который является суммой
который является суммой  :
:  поэтому
поэтому 
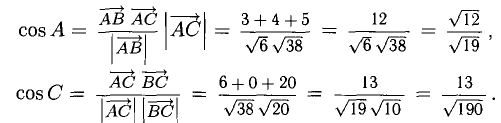
Ответ. 123° 10′, 19°29′, 37°21′.
Пример:
Найти координаты вектора 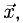 если
если 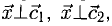 где
где 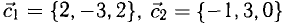 и
и 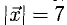
Решение:
На рис. 3.9 имеем 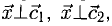 Из условий перпендикулярности векторов (п. 2°) имеем
Из условий перпендикулярности векторов (п. 2°) имеем 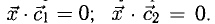 Положим
Положим 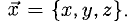 Условие задачи перепишем в виде Рис. 3.9 системы
Условие задачи перепишем в виде Рис. 3.9 системы
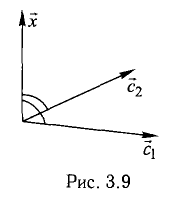
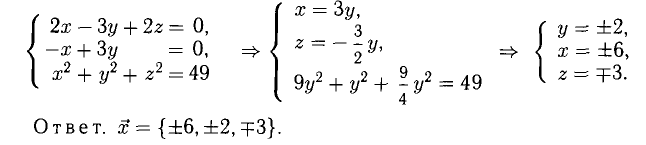
Векторное произведение векторов
1°. Векторы 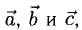 приведенные к одному началу, образуют правую (левую) тройку при условии: если смотреть из конца вектора
приведенные к одному началу, образуют правую (левую) тройку при условии: если смотреть из конца вектора  на плоскость векторов
на плоскость векторов 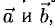 то кратчайший поворот от
то кратчайший поворот от  совершается против (по) часовой стрелки (рис. 3.10).
совершается против (по) часовой стрелки (рис. 3.10).
2°. Векторным произведением ненулевых векторов 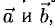 называется вектор
называется вектор  , обозначаемый
, обозначаемый 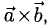 удовлетворяющий следующим трем условиям.
удовлетворяющий следующим трем условиям.
1)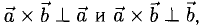 вектор
вектор 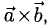 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 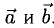
2) Вектор  направлен так, что векторы
направлен так, что векторы 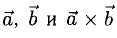 образуют правую тройку.
образуют правую тройку.
3) 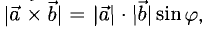 т.е. его длина численно равна площади параллелограмма, построенного на векторах
т.е. его длина численно равна площади параллелограмма, построенного на векторах 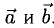 (рис. 3.11), таким образом,
(рис. 3.11), таким образом, 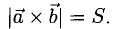
Если векторы 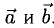 коллинеарны, то под
коллинеарны, то под  понимается нулевой вектор:
понимается нулевой вектор: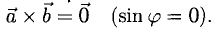
3°. Если известны координаты векторов-сомножителей 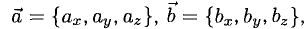 то для отыскания координат векторного произведения служит формула
то для отыскания координат векторного произведения служит формула
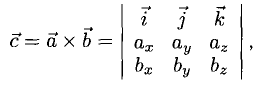
в которой определитель следует разложить по элементам первой строки.
Примеры с решениями
Пример:
Найти площадь треугольника, вершины которого находятся в точках А(1,2,3), В{3,2,1), С(1,0,1).
Решение:
Найдем координаты векторов 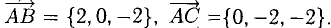 Определим координаты векторного произведения
Определим координаты векторного произведения 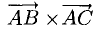 (рис. 3.12):
(рис. 3.12):
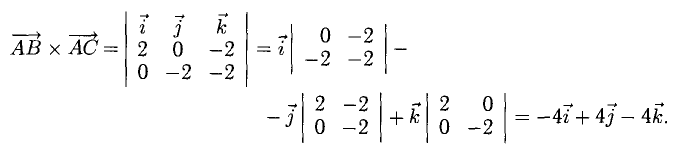
Найдем длину этого вектора, которая равна численно площади параллелограмма S (п. 2°): 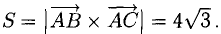 Площадь треугольника
Площадь треугольника 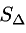 равна
равна 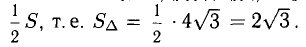
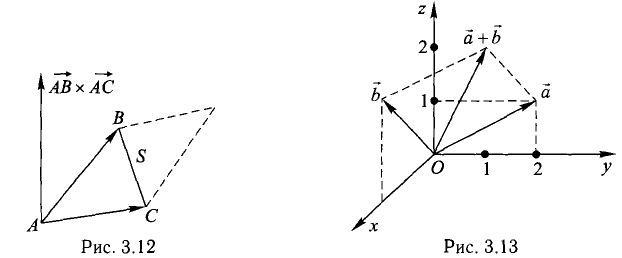
Пример:
Построить параллелограмм на векторах 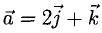 и
и 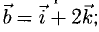 вычислить его площадь и высоту, опущенную на
вычислить его площадь и высоту, опущенную на  .
.
Сделаем чертеж (рис. 3.13). Имеем 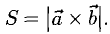 Отдельно вычисляем векторное произведение:
Отдельно вычисляем векторное произведение:
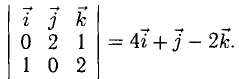
Следовательно,
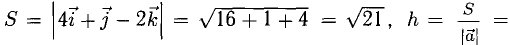
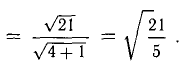
Смешанное произведение векторов
1°. Смешанным произведением трех ненулевых векторов  называется число, равное скалярному произведению двух векторов, один из которых — векторное произведение
называется число, равное скалярному произведению двух векторов, один из которых — векторное произведение  , а другой — вектор
, а другой — вектор  . Обозначение:
. Обозначение: 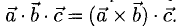 Если
Если  образуют правую тройку, то
образуют правую тройку, то 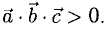 Если
Если образуют левую тройку, то
образуют левую тройку, то 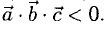
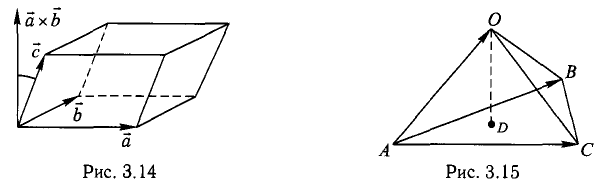
Модуль смешанного произведения векторов равен объему параллелепипеда (рис. 3.14), построенного на этих векторах,
равен объему параллелепипеда (рис. 3.14), построенного на этих векторах,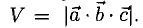 Условие
Условие 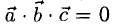 равносильно тому, что векторы
равносильно тому, что векторы  расположены в одной плоскости, т.е. компланарны. Имеет место равенство
расположены в одной плоскости, т.е. компланарны. Имеет место равенство
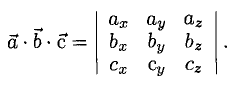
Объем тетраэдра с вершинами в точках 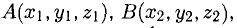
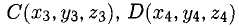 можно вычислить по формуле
можно вычислить по формуле 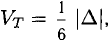 где
где
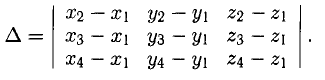
2°. Условие 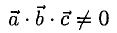 равносильно условию линейной независимости
равносильно условию линейной независимости  , а тогда любой вектор
, а тогда любой вектор 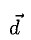 линейно выражается через них, т. е.
линейно выражается через них, т. е. 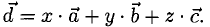 Для определения х, у, z следует решить соответствующую систему линейных уравнений
Для определения х, у, z следует решить соответствующую систему линейных уравнений
Примеры с решениями
Пример:
Найти объем параллелепипеда, построенного на векторах 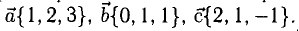
Решение:
Искомый объем 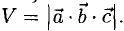 Поскольку
Поскольку
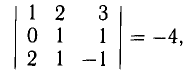
Пример:
В точках 0(0,0,0), А(5,2,0), В(2,5,0) и С(1,2,4) находятся вершины пирамиды. Вычислить ее объем, площадь грани ABC и высоту пирамиды, опущенную на эту грань.
Решение:
1) Сделаем схематический чертеж (рис. 3.15).
2) Введем векторы 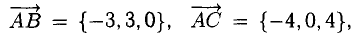
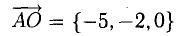 .Объем пирамиды ОАВС (тетраэда) равен
.Объем пирамиды ОАВС (тетраэда) равен
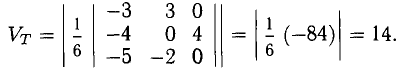
3) Площадь грани ABC
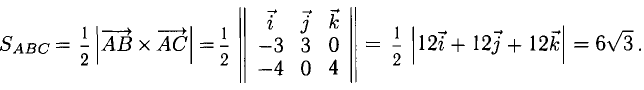
4) Объем пирамиды 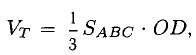 отсюда
отсюда 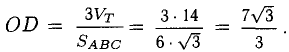
Ответ. 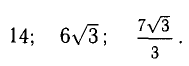
Основные понятия векторной алгебры




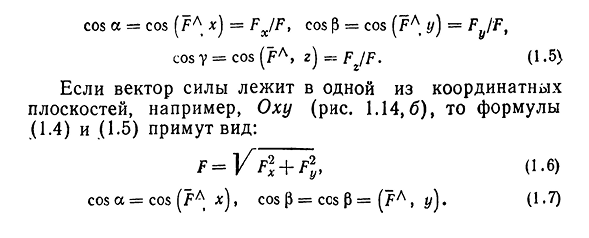
Прямоугольные декартовы координаты
Координатная ось
Пусть на плоскости или в пространстве задана произвольная прямая L: Ясно, что по этой прямой L сы можем перемещаться в oднoм из двух противоположных направлений. Выбор любого (одного) из этих направлений будем называть ориентацией прямой L.
Оnределение:
Прямая с заданной на ней ориентацией называется осью. На чертеже ориентация оси указывается стрелкой (рис. 1 ) . Фиксируем на оси  некоторую точку О и выберем какой-нибудь отрезок а, доложив по определению его длину равной единице (рис. 2).
некоторую точку О и выберем какой-нибудь отрезок а, доложив по определению его длину равной единице (рис. 2).
Пусть М — произвольная точка оси  . Поставим этой точке в соответствие число х по следующему прав илу: х равно расстоюiию между точками О и М, взятому со знаком плюс или со знаком минус н зависимости от того, совпадает ли направление движения от точки О к точке М с заданным направлением или противоположно ему (рис. 3).
. Поставим этой точке в соответствие число х по следующему прав илу: х равно расстоюiию между точками О и М, взятому со знаком плюс или со знаком минус н зависимости от того, совпадает ли направление движения от точки О к точке М с заданным направлением или противоположно ему (рис. 3).

Оnределение:
Ось  с точкой начала отсчета О и масштабными отрезками а называется координатной осью, а число х, вычисляемое по указанному правилу, называется координатой точки М. Обозначение: М (х).
с точкой начала отсчета О и масштабными отрезками а называется координатной осью, а число х, вычисляемое по указанному правилу, называется координатой точки М. Обозначение: М (х).
Прямоугольные декартовы координаты на плоскости
Пусть П — произвольная плоскость. Возьмем на ней некоторую точку О и проведем через эту точку взаимно перпендикулярные прямые L 1 и L 2. Зададим на каждой из nрямых L 1 и L 2 ориентацию и выберем единый масштабный отрезок а. Тогда эти прямые nревратятся в координатные оси с общей точкой отсчета О (рис. 4).
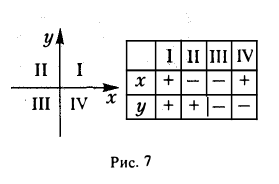
Назовем одну из координатных осей осью абсцисс (осью Ох), друrую —осью ординат (осью Оу) (рис. 5). Точка О называется началом координат. Пусть М — произвольная точка плоскости П (рис. 6). Проведем через точку М прямые, перпендикулярные координатным осям, и поставим ей в соответствие упорядоченную пару чисел (х, у) по следующему nравилу:
Числа х и у называются прямоугольными декартовыми при этом х называется ее абсциссой, а у — ординатой. координатами точки М; Обозначение: М(х, у). Чтобы кратко охарактеризовать описанную конструкцию, говорят, что на плоскости П задана прямоугольная декартова система координат Ох у. Координатные оси разбивают плоскость на четыре части, называемые четвертями или квадрантами. На рисунке и в таблице показано, как эти квадранты нумеруются (рис. 7).
Замечание:
Масштабные от резки на координатных осях могут быть и разной длины. В этом случае координатная система называется просто прямоугольной.
Прямоугольные декартовы координаты в пространстве
Возьмем в пространстве некоторую точку О и проведем через нее три взаимно перпендикулярные прямые L 1 , L 2 и L 3 . Выберем на каждой из nрямых ориентацию и единый масштаб. Прямые L 1 , L 2 и L 3 превратятся в координатные оси с общей точкой отсчета О (рис. 8).
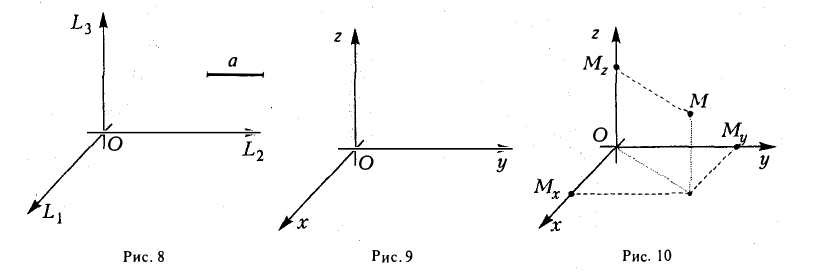
Назовем одну из этих осей осью абсцисс (осью Ох), вторую — осью ординат (осью Оу) и третью — осью аппликат (осью Oz) (рис. 9). Точка О называется началом координат. Пусть М — nроизвольная точка (рис. 10). Проведем через точку М nлоскости, перпендикулярные координатным осям, и поставим ей в соответстnие упорядоченную тройку чисел (х, у, z) по следующему правилу:

Числа х, у и z называются прямоугольными декартовыми координатами точки М; при этом х называется абсциссой точки М, у — ее ординатой, а z —аппликатой. Обозначение: М(х, у, z). Таким образом, в пространстве введена прямоугольная декартова система координат.
Оnределение:
Плоскость, проходящая через любую пару координатных осей, называется координатной плоскостью.
Координатных плоскостей три: Оху, Oyz и Oxz. Эти плоскости разбивают пространство на восемь частей — октантов. 1 .4. Простейшие задачи аналитической геометрии А. Расстояние между точками Пусть М 1 (х 1 ) и М 2 (х 2 )- две точки на координатной оси. Тогда расстояние d между ними вычисляется по формуле
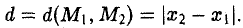
Если на плоскости задана прямоугольная декартова система координат Оху, то расстояние d между любыми двумя точками М 1 (х 1 , у1 и М2 (х2 , y2) вычисляется по следующей формуле
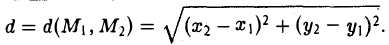
Рассмотрим прямоугольный треугольник ∆MM1M2 (pиc. l l). По теореме Пифагора
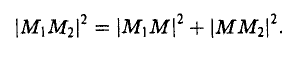
Так как расстояние d между точками M 1 и M 2 равно длине отрезка M1M2 а |M1M| = |x 2 — x 1|, |MM2| = |y 2 — y 1|, то отсюда получаем, что
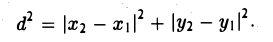
Замечая, что
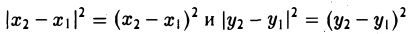
,и извлекая из обеих частей равенства квадратный корень, приходим к требуемой формуле .
Замечание:
Расстояние между точками 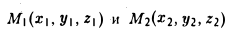 в пространстве вычисляется по следующей формуле
в пространстве вычисляется по следующей формуле
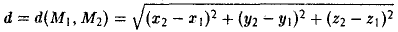
Задача:
Написать уравнение окружности радиуса т с центром в точке Р(а, b).
Пусть М(х, у) — точка окружности (рис. 12). Это означает, что |M P| = r. Заменим |M P|его выражением
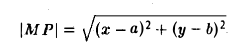
и возведем обе части полученного равенства в квадрат:
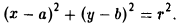
Это есть каноническое уравнение окружности радиуса r с центром в точке Р(а, b) .
Задача:
Пусть F л (-с, 0) и F n (c, 0) -фиксированные точки плоскости, а -заданное число (а > с ≥ 0). Найти условие, которому удовлетворяют координаты х и у точки М, обладающей следующим свойством: сумма расстояний от точки М до Fл и до F n равна 2а.
Вычислим расстояния между точками М и F л и между точками М и F n . Имеем
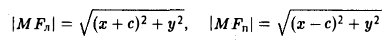
(рис. 13). Отсюда
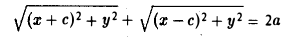
Перенесем второй корень в правую часть
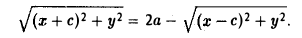
Возводя обе части в квадрат, после простых преобразований получим
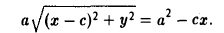
С целью дальнейших упрощений вновь возводим обе части в квадрат. В результате nриходим к равенству
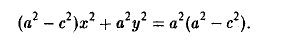
Полагая b 2 = а 2 — с 2 и деля обе части nоследнего соотноwения на а 2 b2 , nолучаем уравнение эллипса
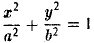
(см. главу 111) .
Деление отрезка в данном отношении:
Пусть М1 (х1 , y1) и М2 (х2 , y2) — различные точки плоскости. Пусть, далее, точка М(х, у) лежит на отрезке М1М2 и делит его в отношении λ 1 : λ 2 , т. е.
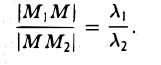
Требуется выразить координаты х и у этой точки через координаты концов отрезка М1М2 и числа λ 1 и λ 2 . Предположим сначала, что отрезок М1М2 не параллелен оси ординат Оу (рис. 14). Тогда
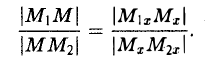
Так как
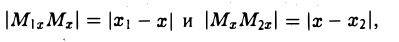
то из последних двух соотношений получаем, что
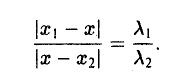
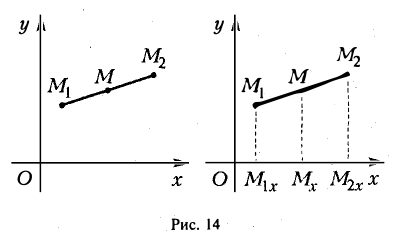
Точка М лежит между точками М1 и М2 , поэтому либо х 1 < х < х 2 , либо х 1 > х > х 2 . В любом из этих случаев разности х1 — х и х — х 2 имеют одинаковые знаки. Это позволяет переписать последнее равенство в следующей форме
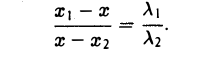
Отсюда

В случае, когда отрезок М1М2 параллелен оси Оу, х 1 = х 2 = х. Заметим, что тот же результат дает формула (*), если nоложить в ней х 1 = х 2 . Справедливость формулы
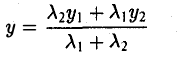
доказывается аналогичным рассуждением .
Задача:
Найти координаты центра тяжести М треугольника с вершинами в точках . М1 ( х 1 , у 1 ), М2 ( х 2 , у 2 ) и М3 ( х 3 , у 3 ). Восnользуемся тем, что центр тяжести треугольника совпадает с точкой пересечения его медиан. Точка М делит каждую медиану в отношении 2 : 1, считая от вершины (рис. 15). Тем самым, ее координаты х и у можно найти по формулам
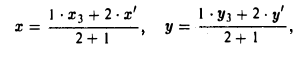
где х’ и у’ — координаты второго конца М’ медианы М3 М’. Так как М’ — середина отрезка М1М2, то
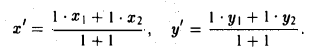
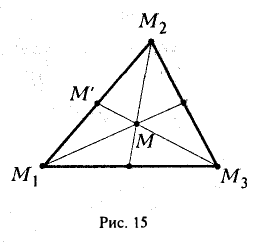
Полученные соотношения позволяют выразить координаты z и у центра тяжести М треугольника ∆М1М2М3 через координаты его вершин:
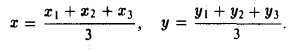
Замечание:
Если точка М(х,у,z ) делит отрезок с концами М1( х1, у1, z1) и М2( х2, у2, z2) в отношении λ1 : λ2, то ее координаты вычисляются по формулам
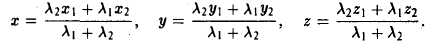
Полярные координаты
Предположим, что задана точка О, ось  .содержащая точку О, и масштабный отрезок (эталон длины) (рис. 16).
.содержащая точку О, и масштабный отрезок (эталон длины) (рис. 16).
Пусть М — произвольная точка плоскости, отличная от точки О (рис.17). Ее положение на плоскости однозначно определяется двумя числами: расстоянием г между точками О и М и отсчитываемым против часовой стрелки углом φ между положительным лучом оси  и лучом ОМ с началом в точке О. Пару (г, φ) называют полярными координатами точки М; г — полярный радиус точки М , φ — полярный угол.
и лучом ОМ с началом в точке О. Пару (г, φ) называют полярными координатами точки М; г — полярный радиус точки М , φ — полярный угол.
Точка О называется полюсом,  — полярной осью.
— полярной осью.
Ясно, что Если точка М совпадаете полюсом, то считаем г = 0; полярный угол φ в этом случае не определен.
Если точка М совпадаете полюсом, то считаем г = 0; полярный угол φ в этом случае не определен.
Таким образом, на плоскости можно задать еще одну координатную систему — полярную.
Прямоугольную декартову систему координат Оху будем называть согласованной с заданной полярной, если начало координат 0(0, 0) — полюс, ось Ох — полярная ось, а ось Оу составляете осью Ох угол, равный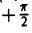 . Тогда
. Тогда
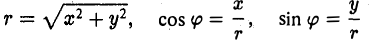
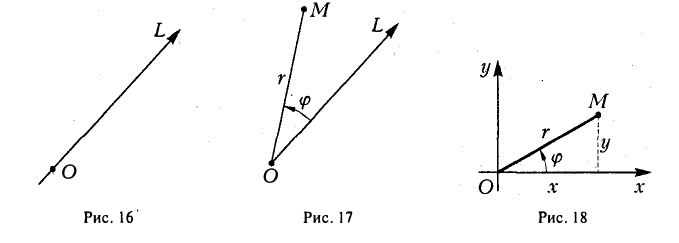
(рис.18). В свою очередь 
Пример:
Пусть R > О — заданное число. Множество точек плоскости, полярные координаты (г, <р) которых удовлетворяют равенству
r = R,
является окружностью радиуса R с центром в полюсе (рис. 19)
Определители 2-го и 3-го порядков
Пусть имеем четыре числа а11, а12, а21, а22 (читается — «а-один-один», «а-один-два», «а-два-один», «а-два-два»).
Определителем второго порядка называется число
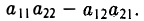
Обозначение:
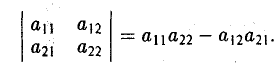
Числа а11, а12, а21, а22 называются элементами определителя; пары элементов а11, а12 и а21, а22 образуют строки определителя, а пары элементов а11, а21 и а12, а22 — его столбцы; пара элементов а11, а22 образует главную диагональ определителя, а пара а12, а21 — побочную диагональ.
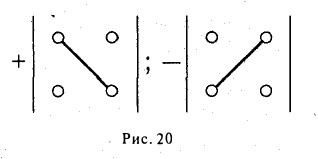
Тем самым, для вычисления определителя второго порядка нужно из произведения а11, а22 элементов главной диагонали вычесть произведение а12, а21 элементов его побочной диагонали (рис. 20).
Пример:
Вычислить определитель
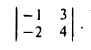
По правилу (1) имеем
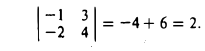
С определителями второго порядка мы встречаемся уже при отыскании решения системы двух линейных алгебраических уравнений с двумя неизвестными
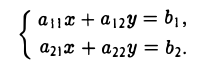
Решая эту систему методом исключения неизвестных при условии, что
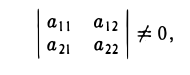
находим
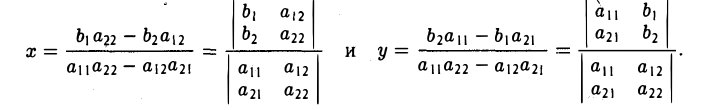
Пусгь теперь даны девять чисел aij (i = I, 2, 3; j = I, 2, 3).
Определителем третьего порядка называется число, обозначаемое символом

и вычисляемое по следующему правилу:
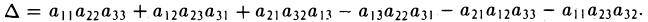
Первый индекс i элемента aij указывает номер строки, в которой он расположен, а второй индекс j — номер столбца.
Элементы а11, а22, а33 образуют главную диагональ определителя ∆, элементы а13, а22, а31 — побочную диагональ, элементы а13, а22, а31 — побочную диагональ.
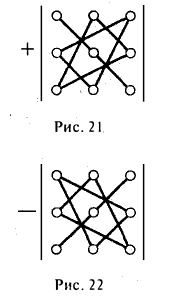
Чтобы разобраться с распределением знаков в правой части формулы (2), обратим внимание на следующее: произведение элементов а11, а22, а33 главной диагонали входит в формулу со своим знаком, также как и произведение а11, а22, а33 и а11, а22, а33 элементов, расположенных в вершинах треугольников, основания которых параллельны главной диагонали (рис. 21); с другой стороны, произведение а13, а22, а31 элементов побочной диагонали, а также произведения а12, а21, а33 и а11, а23, а32 — с противоположным знаком (рис.22). Такой подход к вычислению определителя третьего порядка называется правилом треугольника.
Пример:
Вычислить определитель

Применяя правило треугольника, находим
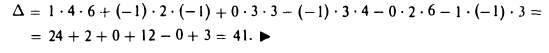
Установим некоторые свойства определителей 3-го порядка, легко проверяемые при помощи разложений (1) и (2).
Свойство:
Величина определителя не изменится, если все его строки заменить его столбцами с теми же номерами
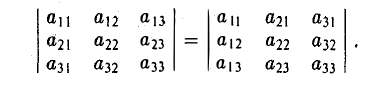
Свойство:
При перестановке любых двух строк (или любых двух столбцов) определителя он изменяет свой знак на противоположный.
Свойство:
Общий множитель всех элементов одной строки (или одного столбца) определителя можно вынести за знак определителя
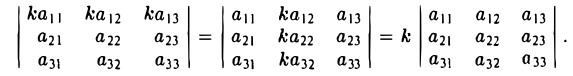
Следующие три свойства определителя вытекают из свойств 1-3. Впрочем, в их справедливости можно убедиться и непосредственно, пользуясь формулами (1) и (2).
Свойство:
Если определитель имеет две равные строки (или дна равных столбца), то он равен нулю.
Свойство:
Если все элементы некоторой строки (или некоторого столбца) равны нулю, то и сам определитель равен нулю.
Свойство:
Если соответствующие элементы двух строк (или двух столбцов) пропорциональны, то определитель равен нулю.
Укажем еще один способ вычисления определителя 3-го порядка

Минором Mij элемента aij определителя ∆ называется определитель, получаемый изданного путем вычеркивания элементов i-й строки и j-ro столбца, на пересечении которых находится этот элемент. Например, минором элемента a23 будет определитель
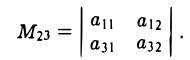
Алгебраическим дополнением элемента Aij называется минор Mij — этого элемента, взятый со своим знаком, если сумма i + j номеров строки и столбца, на пересечении которых расположен элемент aij, есть число четное, и с противоположным знаком, если это число нечетное:
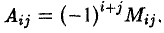
Теорема:
Определитель равен сумме произведений элементов любой его строки (любого его столбца) на их алгебраические дополнения, так что имеют место следующие равенства
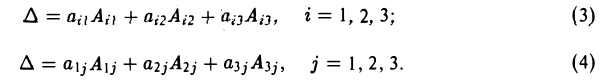
Покажем, например, что
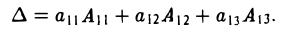
Пользуясь формулой (2), получаем, что
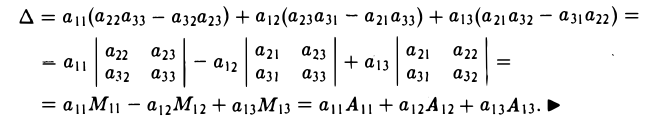
Правило (3) называется разложением определителя по элементам i-й строки, а правило (4) — разложением определителя по элементам j -го столбца.
Пример:
Вычислить определитель
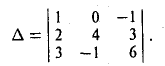
Раскладывая определитель по элементам 1-ой строки, получим
Понятия связанного и свободного векторов
Рассмотрим две точки А и В. По соединяющему их отрезку можно перемещаться в любом из двух противоположных направлений. Если считать, например, точку А начальной, а точку В конечной, то тогда получаем направленный отрезок АВ, в другом случае — направленный отрезок В А. Направленные отрезки часто называют связанными или закрепленными векторами. На чертеже заданное направление указывается стрелкой (рис. 1).
В случае, когда начальная и конечная точки совпадают, А = В, связанный вектор называется нулевым.
Определение:
Будем говорить, что связанные векторы АВ и CD равны, если середины отрезков AD и ВС совпадают (рис. 2).
Обозначение:
А В = CD.
Заметим, что в случае, когда точки А, В, С и D не лежат на одной прямой, это равносильно тому, что четырехугольник ABCD — параллелограмм. Ясно, что равные связанные векторы имеют равные длины.
Пример:
Рассмотрим квадрат и выберем векторы, как указано на рис.3. Векторы АВ и DC равны, а векторы ВС и DA не равны.
Укажем некоторые свойства равных связанных векторов:
- Каждый связанный вектор равен самому себе: АВ = АВ.
- Если АВ = CD, той CD = АВ.
- Если АВ = CD и CD = EF,то АВ = EF (рис.4).
Пусть АВ — заданный связанный вектор и С — произвольная точка. Ясно, что, опираясь на определение, всегда можно построить точку D так, чтобы
CD = АВ.
Тем самым, от каждой точки можно отложить связанный вектор, равный исходному (рис. 5).
Мы будем рассматривать свободные векторы, т. е. такие векторы, начальную точку которых можно выбирать произвольно, или, что то же самое, которые можно произвольно переносить параллельно самим себе. Ясно, что свободный вектор  однозначно определяется заданием связанного вектора АВ.
однозначно определяется заданием связанного вектора АВ.
Если в качестве начальных выбирать лишь те точки, которые лежат на прямой, определяемой заданным (ненулевым) связанным вектором, то мы приходим к понятию скользящего вектора (рис. 6).
Связанные и скользящие векторы широко используются в теоретической механике.
Для обозначен ия свободных векторов будем пользоваться полужирными строчными латинскими буквами — а, b, с,… ; нулевой вектор обозначается через 0.
Пусть заданы вектор а и точка А. Существует ровно одна точка В, для которой
 = а
= а
(рис.7). Операция построения связанного вектора АВ, для которого выполняется это равенство, называется откладыванием свободного вектора а от точки А.
Заметим, что связанные векторы, получаемые в результате описанной операции откладывания, равны между собой и, значит, имеют одинаковую дли ну. Это позволяет ввести длину свободного вектора а, которую мы будем обозначать символом |а. Длина нулевого вектора равна нулю. Если а = b, то |а| = |b; обратное неверно.
Линейные операции над векторами
Сложение векторов
Пусть заданы два вектора а и b. Возьмем какую-нибудь точку О и отложим от нее вектор a:  = а. От полученной точки А отложим вектор b:
= а. От полученной точки А отложим вектор b:  = b. Полученный в результате вектор
= b. Полученный в результате вектор называется суммой векторов а и b и обозначается через a + b (рис. 8). Этот способ построения суммы векторов называется правилом треугольника.
называется суммой векторов а и b и обозначается через a + b (рис. 8). Этот способ построения суммы векторов называется правилом треугольника.
Нетрудно заметить, что сложение векторов коммутативно, т. е. для любых векторов а и b справедливо равенство
Если отложить векторы а и 1» от обшей точки О и построить на них как на сторонах параллелограмм, то вектор  , идущий из общего начала О в противоположную вершину параллелограмма, будет их суммой а + b (или b +а) (рис. 10). Этот способ построения суммы векторов называется правилом параллелограмма.
, идущий из общего начала О в противоположную вершину параллелограмма, будет их суммой а + b (или b +а) (рис. 10). Этот способ построения суммы векторов называется правилом параллелограмма.
Пусть заданы три вектора, например, a, b и с. Отложим от произвольной точки О вектор a:  = а; от полученной точки А отложим вектор b:
= а; от полученной точки А отложим вектор b:  = b; отточки В — вектор с:
= b; отточки В — вектор с:  = с (рис. 11). По определению суммы
= с (рис. 11). По определению суммы  — а + b и
— а + b и  = (а + b) + с (рис. 12). С другой стороны, АС = b + с и, значит, ОС = а + (Ь + с) (рис. 13). Тем самым, для любых векторов a, b и с выполняется равенство
= (а + b) + с (рис. 12). С другой стороны, АС = b + с и, значит, ОС = а + (Ь + с) (рис. 13). Тем самым, для любых векторов a, b и с выполняется равенство
(а +b) + с = а + (b + с),
т. е. сложение векторов ассоциативно. Опуская скобки, можно говорить о сумме трех векторов и записывать ее так:
а + b + с.
Аналогично определяется сумма любого числа векторов: это есть вектор, который замыкает ломаную, построенную из заданных векторов. На рис. 14 показан», как построить сумму семи векторов:
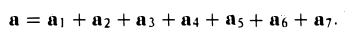
Приведенный способ сложения произвольного числа векторов называется правилом замыкающего ломаную.
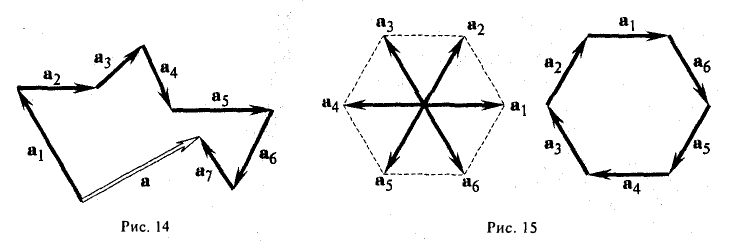
Пример:
Найти сумму векторов, идущих из центра правильного шестиугольника в его вершины.
По правилу замыкающего ломаную получаем
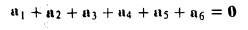
(рис. 15).
Умножение вектора на число
Определение:
Свободные векторы а и b называются коллинеарными, если определяющие их связанные векторы лежат на параллельных или на совпадающих прямых (рис. 16).
Обозначение: а||b.
Замечание:
Из определения следует, что если хотя бы один из векторов a и b нулевой, то они коллинеарны.
Если отложить коллинеарные векторы а и b от обшей точки О,  = n,
= n,  = Ь, то точки О, А н В будут лежать на одной прямой. При этом возможны два случая: точки А и В располагаются на этой прямой: 1) по одну сторону от точки О, 2) по разные стороны (рис. 17). В первом случае векторы а и b называются одинаково направленными, а во втором — противоположно направленными.
= Ь, то точки О, А н В будут лежать на одной прямой. При этом возможны два случая: точки А и В располагаются на этой прямой: 1) по одну сторону от точки О, 2) по разные стороны (рис. 17). В первом случае векторы а и b называются одинаково направленными, а во втором — противоположно направленными.
Если векторы имеют равные длины и одинаково направлены, то они равны. Пусть а — вектор, λ — вещественное число.
Определение:
Произведением вектора а на число λ называется вектор b такой, что
- |Ь| = |λ| • |а|;
2) векторы а и b одинаково (соответственно, противоположно) направлены, если λ > 0 (соответственно, λ < 0).
Обозначение: b = λа.
При λ = 0 положим λа = 0.
Таким образом, векторы а и Ь = λа коллинеарны по определению. Верной обратное: если векторы а(а ≠ 0) и Ь коллинеарны, то можно найти число А такое, что h = λа.
Укажем основные свойства этой операции умножения вектора на число:
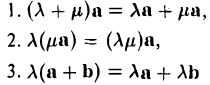
(здесь λ и μ — любые действительные числа, а и Ь — произвольные векторы).
Определение:
Вектор, длина которого равна единице, называется единичным вектором, или ортом, и обозначается а° (читается: а с нуликом), |а°| = 1.
Если а ≠ 0, то вектор
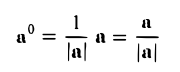
есть единичный вектор (орт) направления вектора а (рис. 18).
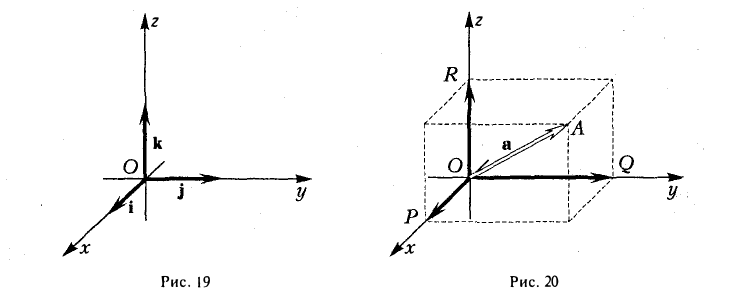
Координаты и компоненты вектора
Выберем в пространстве прямоугольную декартову систему координат. Обозначим через i, j, к единичные векторы (орты) положительных направлений осей Ox, Оу, Oz (рис. 19). Рассмотрим произвольный вектор п, начало которого лежит в начале координат О, а конец — в точке А. Проведем через точку А плоскости, перпендикулярные осям Ох, Оу и Oz. Эти плоскости пересекут координатные оси в точках Р, Q и R соответственно. Из рис. 20 видно, что

Векторы  коллинеарны соответственно единичным векторам i, j, k,
коллинеарны соответственно единичным векторам i, j, k,
поэтому найдутся числа х, у, z такие, что
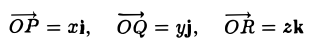
и, следовательно,
а = xi + yj + zk. (2)
Формула (2) называется разложением вектора а по векторам i, j, к. Указанным способом всякий вектор может быть разложен по векторам i, j, k.
Векторы i, j, к попарно ортогональны, и их длины равны единице. Тройку i, j, k называют ортонормированным (координатным) базисом (ортобазисом).
Можно показать, что для каждого вектора а разложение (2) по базису i, j, к единственно, т. е. коэффициенты х, у, z в разложении вектора а по векторам i, j, к определены однозначно. Эти коэффициенты называются координатами вектора а. Они совпадают с координатами х, у, z точки А — конца вектора а. Мы пишем в этом случае
а = {х, y,z}.
Эта запись означает, что свободный вектор а однозначно задастся упорядоченной тройкой своих координат. Векторы xi, yj, zk, сумма которых равна вектору а, называются компонентами вектора а.
Из вышеизложенного следует, что два вектора а = { х1, у1, z1 } и b = {х2, у2, z2} равны тогда и только тогда, когда соответственно равны их координаты, т. е.
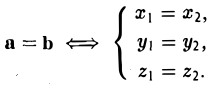
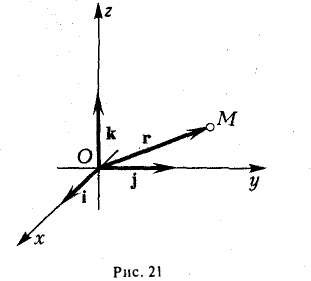
Радиус-вектором точки М(х,у, z) называется вектор г = xi + yj + zk, идущий из начала координат О в точку М (рис. 21).
Линейные операции над векторами в координатах
Пусть имеем два вектора а = { х1, у1, z1} и b = { х2, у2, z2 },так что а = х1i, у1j+ z1k. b = х2i+ у2j+z2k. На основании правила сложения векторов имеем
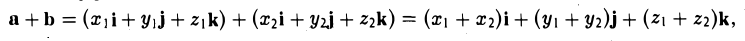
или, что то же,
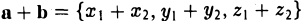
— при сложении векторов их координаты попарно складываются. Аналогично получаем
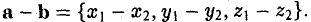
Далее,
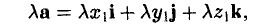
или, что то же,
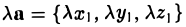
— при умножении вектора на число все его координаты умножаются на это число.
Пусть а = { х1, у1, z1}, b = { х2, у2, z2 } — коллинеарные векторы, причем b ≠ 0. Тогда а = μb, т.е.
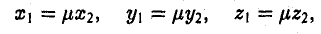
или (3)
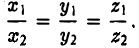
Обратно, если выполняются соотношения (3), то а = μb, т. е. векторы a и b коллинеарны.
Таким образом, векторы а и b коллинеарны тогда и только тогда, когда их координаты пропорциональны.
Пример:
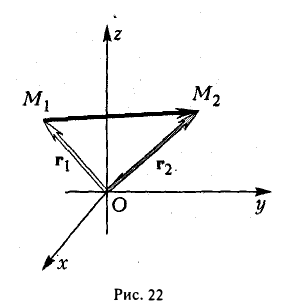
Найти координаты вектора 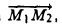 начало которого находится в точке М1 ( х1, у1, z1 ). а конец — в точке M2 (х2, у2, z2).
начало которого находится в точке М1 ( х1, у1, z1 ). а конец — в точке M2 (х2, у2, z2).
Из рис. 22 видно, что 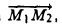 = r2 — r1 , где r2, r1 — радиус-векторы точек М1 и M2 соответственно. Поэтому
= r2 — r1 , где r2, r1 — радиус-векторы точек М1 и M2 соответственно. Поэтому
— координаты вектора ММг равны разностям одноименных координат конечной М2 и начальной М точек этого вектора.
Проекция вектора на ось
Рассмотрим на оси l ненулевой направленный отрезок АВ (рис.23). Величиной направленного отрезка АВ на оси l называется число, равное длине отрезка АВ, взятой со знаком «+», если направление отрезка АВ совпадаете направлением оси l, и со знаком «-», если эти направления противоположны.
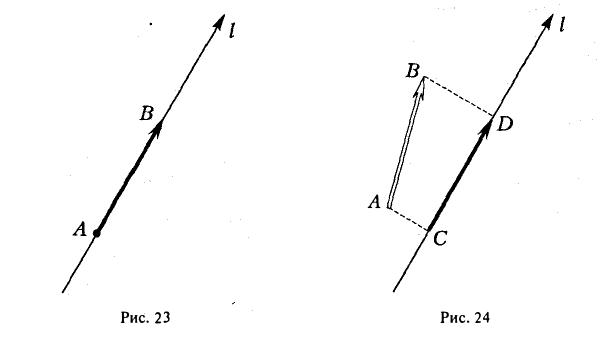
Рассмотрим теперь произвольный вектор  , определяемый связанным вектором АВ. Опуская из его начала и конца перпендикуляры на заданную ось l, построим на ней направленный отрезок CD (рис. 24).
, определяемый связанным вектором АВ. Опуская из его начала и конца перпендикуляры на заданную ось l, построим на ней направленный отрезок CD (рис. 24).
Определение:
Проекцией вектора  на ось l называется величина направленного отрезка CD, построенного указанным выше способом.
на ось l называется величина направленного отрезка CD, построенного указанным выше способом.
Обозначение: 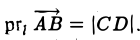
Основные свойства проекций
- Проекция вектора АВ на какую-либо ось l равна произведению длины вектора на косинус угла между осью и этим вектором (рис. 25)
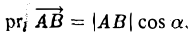
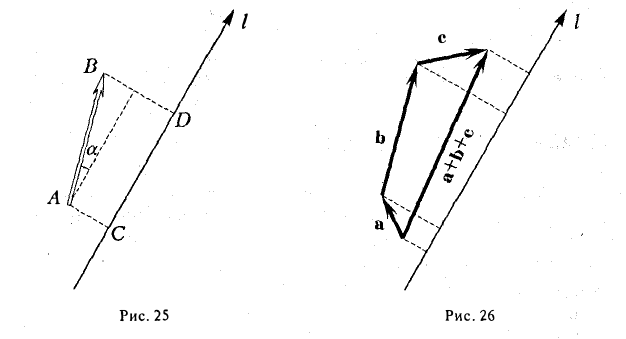
- Проекция суммы векторов на какую-либо ось l равна сумме проекций векторов на ту же ось.
Например,
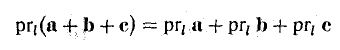
(рис. 26).
Скалярное произведение векторов
Пусть имеем два вектора a и b.
Определение:
Скалярным произведением вектора а на вектор b называется число, обозначаемое символом (а, b) и определяемое равенством
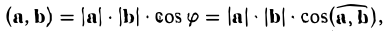
(1)
где φ, или в иной записи ( ), есть угол между векторами а и b (рис. 27 а).
), есть угол между векторами а и b (рис. 27 а).
Заметив, что |b| cos φ есть проекция вектора b на направление вектора а, можем написать
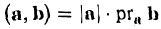
(рис. 27 б) и, аналогично,’ (2)
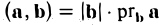
(рис. 27 в), т.е. скалярное произведение двух векторов равно длине одного из них, помноженной на проекцию на него другого вектора. В случае, если один из векторов а или b — нулевой, будем считать, что
(a, b) = 0.
Свойства скалярного произведения
- Скалярное произведение обращается в нуль в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда векторы а и b ортогональны, a ⊥ b.
Это следует из формулы (1), определяющей скалярное произведение.
Поскольку направление нулевого вектора не определено, мы можем его считать ортогональным любому вектору. Поэтому указанное свойство скалярного произведения можно сформулировать так:
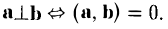
2. Скалярное произведение коммутативно:
(а, b) = (b, а).
Справедливость утверждения вытекает из формулы (I), если учесть четность функции cos φ: cos(- φ) = cos φ.
3. Скалярное произведение обладает распределительным свойством относительно сложения:
(а + b, с) = (а, с) + (b, c).
Действительно,
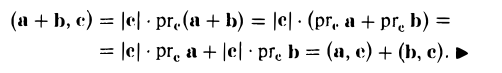
4. Числовой множитель А можно выносить за знак скалярного произведения
(λа, b) = (а, λb) = λ (а, b).
- Действительно, пусть λ > 0. Тогда
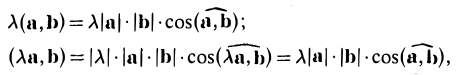
поскольку при λ > 0 углы ( ) и (λ
) и (λ ) равны (рис.28).
) равны (рис.28).
Аналогично рассматривается случай λ < 0. При λ = 0 свойство 4 очевидно.
Замечание:
В общeм случае (а, b)c ≠ a(b, c).
Скалярное произведение векторов, заданных координатами
Пусть векторы а и b заданы своими координатами в ортонормированном базисе i, j, k:
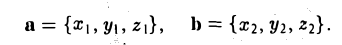
Рассмотрим скалярное произведение векторов а и b:
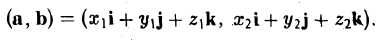
Пользуясь распределительным свойством скалярного произведения, находим
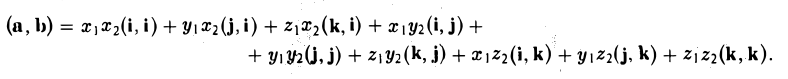
Учитывая, что
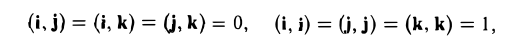
получаем (4)
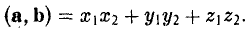
То есть, если векторы а и b заданы своими координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений одноименных координат.
Пример:
Найти скалярное произведение векторов n = 4i — 2j + k и b = 6i + 3j + 2k.
(a, b) = 4 • 6 + (-2) • 3 + 1 • 2 = 20.
Скалярное произведение вектора на себя называется скалярным квадратом:
(а, а) = а2.
Применяя формулу (4) при b = а, найдем (5)
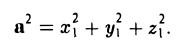
С другой стороны,
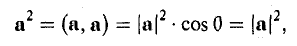
так что из (5) следует, что (6)
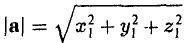
— в ортонормированном базисе длина вектора равна квадратному корню из суммы квадратов его координат.
Косинус угла между векторами. Направляющие косинусы
Согласно определению
(а, b) = |а| • |b| • cos φ,
где φ — у гол между векторами а и b. Из этой формулы получаем
(7)
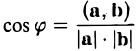
(предполагается, что векторы а и b — ненулевые).
Пусть а = { х1, у1, z1}, b = { х2, у2, z2 }. Тогда формула (7) примет следующий вид
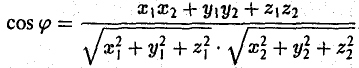
Пример:
Найти угол между векторами a = {2, -4,4,} и d = {-3,2,6}. Пользуясь формулой (8), находим
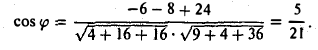
Пусть b = i, T.e. b = {1,0,0}. Тогда для всякого вектора а = { х1, у1, z1} ≠ 0 имеем
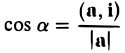
или, в координатной записи, (9)
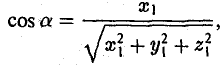
где а есть угол, образованный вектором я с осью Ох. Аналогично получаем формулы
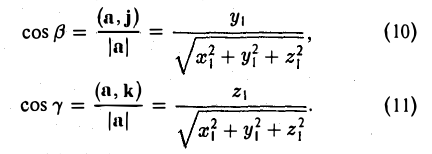
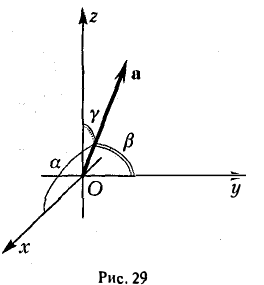
Формулы (9)-(11) определяют направляющие косинусы вектора а, т. е. косинусы углов, образуемых вектором n с осями координат (рис. 29).
Пример:
Найти координаты единичного вектора n°. По условию | n°| = 1. Пусть n° = zi+ yj+ zk. Тогда
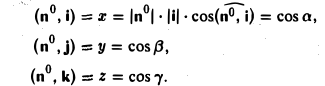
Таким образом, координатами единичного вектора являются косинусы углов, образованных этим вектором с осями координат:
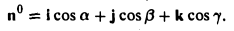
Отсюда получаем
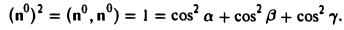
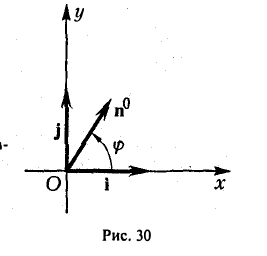
Пример:
Пусть единичный вектор n° ортогонален оси z:
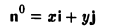
(рис. 30). Тогда его координаты г и у соответственно равны
x=cos φ, y = sin φ.
Тем самым,
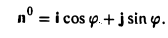
Векторное произведение векторов
Определение:
Векторным произведением вектора а на вектор b называется вектор, обозначаемый символом [a, b] (или a х b), такой, что
1) длина вектора [а, b] равна |а| • |Ь| • sin φ, где φ — угол между векторами а и b (рис.31);
2) вектор [а, b] перпендикулярен векторам а и b, т.е. перпендикулярен плоскости этих векторов;
3) вектор [а, Ь] направлен так, что из конца этого вектора кратчайший поворот от л к Ь виден происходящим против часовой стрелки (рис. 32).
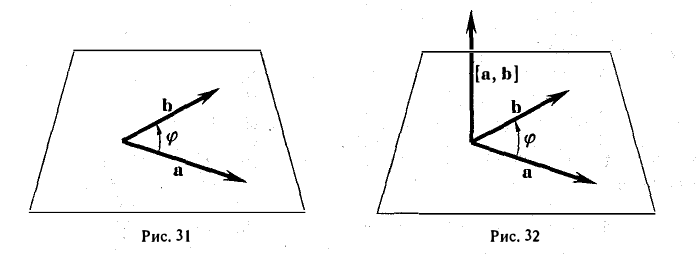
Иными словами, векторы я, b и [a, b] образуют правую тройку векторов, т.е. расположены так, как большой, указательный и средний пальцы правой руки. В случае, если векторы a и b коллинеарны, будем считать, что [a, b] = 0.
По определению длина векторного произведения (1)
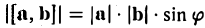
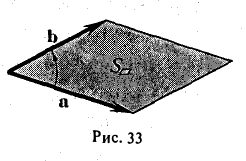
численно равна площади  параллелограмма (рис.33), построенного на перемножаемых векторах a и b как на сторонах:
параллелограмма (рис.33), построенного на перемножаемых векторах a и b как на сторонах:
|[a, b]| =  .
.
Свойства векторного произведения
- Векторное произведение равно нулевому вектору тогда и только тогда, когда по крайней мере один из перемножаемых векторов является нулевым или когда эти векторы коллинеарны (если векторы я и b коллинеарны, то угол между ними равен либо 0, либо тг).
Это легко получить из того, что |[a, b]| = |a| • |b| • sin φ.
Если считать нулевой вектор коллинеарным любому вектору, то условие коллинеарности векторов a и b можно выразить так
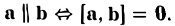
2. Векторное произведение антикоммутативно, т. е. всегда (2)
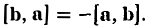
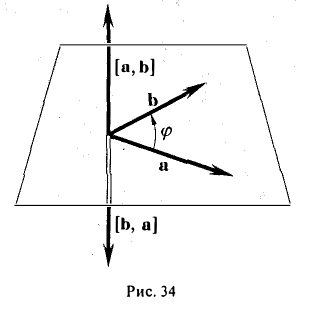
В самом деле, векторы [а, b] и [b, а] имеют одинаковую длину и коллинеарны. Направления же этих векторов противоположны, так как из конца вектора [a, b] кратчайший поворот от a к b будет виден происходящим против часовой стрелки, а из конца вектора [b, a] — почасовой стрелке (рис. 34).
3. Векторное произведение обладает распределительным свойством по отношению к сложению
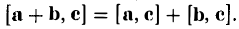
4. Числовой множитель λ можно выносить за знак векторного произведения
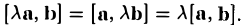
Векторное произведение векторов, заданных координатами
Пусть векторы a и b заданы своими координатами в базисе i,j, k: а = { х1, у1, z1}, b = { х2, у2, z2 }. Пользуясь распределительным свойством векторного произведения, находим (3)
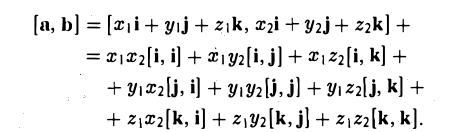
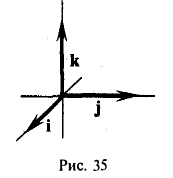
Выпишем векторные произведения координатных ортов (рис. 35):
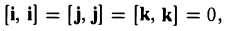
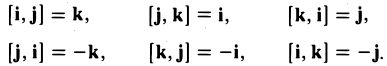
Поэтому для векторного произведения векторов a и b получаем из формулы (3) следующее выражение (4)
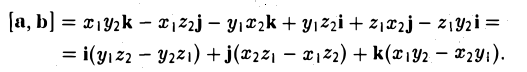
Формулу (4) можно записать в символической, легко запоминающейся форме, если воспользоваться определителем 3-го порядка: (5)
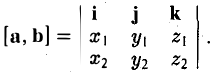
Разлагая этот определитель по элементам 1-й строки, получим (4). Примеры:
- Найти площадь параллелограмма, построенного на векторах а = i + j- k, b = 2i + j- k.
Искомая площадь  = |[а, b]. Поэтому находим
= |[а, b]. Поэтому находим
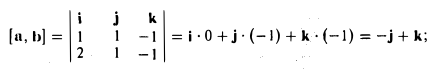
откуда
2. Найти площадь треугольника ОАВ (рис.36).
Ясно, что площадь S∆ треугольника ОАВ равна половине площади S параллелограмма О АС В. Вычисляя векторное произведение [a, b] векторов a= и b =
и b =  , получаем
, получаем
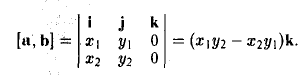
Отсюда
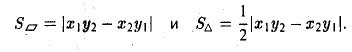
Замечание:
Векторное произведение не ассоциативно, т.е. равенство [[а, b], с] = [а, b,с]] в общем случае неверно. Например, при а = i, b = j. c= j имеем
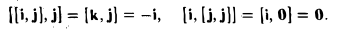
Смешанное произведение векторов
Пусть имеем три вектора а, b и с. Перемножим векторы а и b векторно. В результате получим вектор [а, b). Умножим его скалярно на вектор с:
([a, b], с).
Число ([а, b], с) называется смешанным произведением векторов а, b, с и обозначается символом (а, b, с).
Геометрический смысл смешанного произведения
Отложим векторы а, b и с от общей точки О (рис. 37). Если все четыре точки О, А, В, С лежат в одной плоскости (векторы a, b и с называются в этом случае компланарными), то смешанное произведение ([а, b], с) = 0. Это следует из того, что вектор [а, b] перпендикулярен плоскости, в которой лежат векторы а и b, а значит, и вектору с.
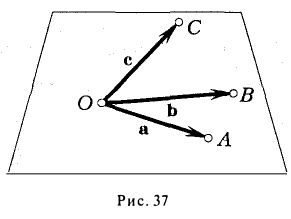
Если же точки О, А, В, С не лежат в одной плоскости (векторы a, b и с некомпланарны), построим на ребрах OA, OB и ОС параллелепипед (рис. 38 а). По определению векторного произведения имеем
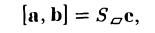
где  — площадь параллелограмма OADB, а с — единичный вектор, перпендикулярный векторам а и b и такой, что тройка а, b, с — правая, т. е. векторы a, b и с расположены соответственно как большой, указательный и средний пальцы правой руки (рис. 38 6).
— площадь параллелограмма OADB, а с — единичный вектор, перпендикулярный векторам а и b и такой, что тройка а, b, с — правая, т. е. векторы a, b и с расположены соответственно как большой, указательный и средний пальцы правой руки (рис. 38 6).
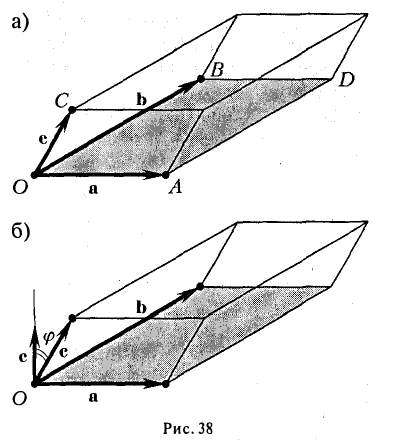
Умножая обе части последнего равенства справа скалярно на вектор с, получаем, что
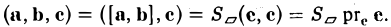
Число ргe с равно высоте h построенного параллелепипеда, взятого со знаком « + », если угол ip между векторами с и с острый (тройка а, b, с — правая), и со знаком «-», если угол — тупой (тройка а, b, с — левая), так что
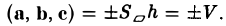
Тем самым, смешанное произведение векторов a, b и с равно объему V параллелепипеда, построенного на этих векторах как на ребрах, если тройка а, b, с — правая, и -V, если тройка а, b, с — левая.
Исходя из геометрического смысла смешанного произведения, можно заключить, что, перемножая те же векторы a, b и с в любом другом порядке, мы всегда будем О получать либо +V, либо -V. Знак произведения будет зависеть лишь от того, какую тройку образуют перемножаемые векторы — правую или левую. Если векторы а, b, с образуют правую тройку, то правыми будут также тройки b, с, а и с, а, b. В то же время все три тройки b, а, с; а, с, b и с, b, а — левые. Тем самым,
(а, b, с) = (b, с, а) = (с, a,b) = -(b, а, с) = -(а, с, b) = -(с, b, а).
Еще раз подчеркнем, что смешанное произведение векторов равно нулю тогда и только тогда, когда перемножаемые векторы а, b, с компланарны:
{а, b, с компланарны} <=> (а, b, с) = 0.
Смешанное произведение в координатах
Пусть векторы а, b, с заданы своими координатами в базисе i, j, k:
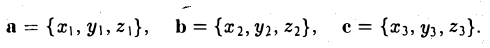
Найдем выражение для их смешанного произведения (а, b, с). Имеем
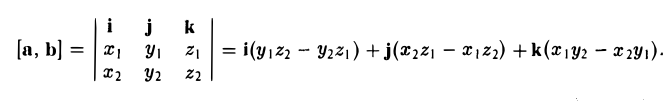
Откуда
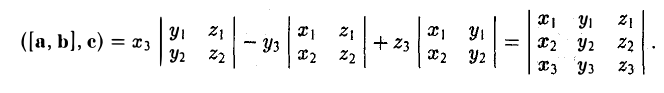
Итак,
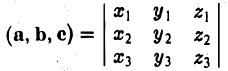
— смешанное произведение векторов, заданных своими координатами в базисе i, j, k, равно определителю третьего порядка, строки которого составлены соответственно из координат первого, второго и третьего из перемножаемых векторов.
Необходимое и достаточное условие компланарности векторов а = { х1, у1, z1}, b = { х2, у2, z2 }, c = { х3, у3, z3} запишется в следующем виде
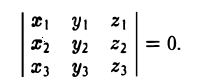
Пример:
Проверить, компланарны ли векторы
a = {7, 4,-6}, b = {2, 1,1}, с ={19, 11,17}.
Рассматриваемые векторы будут компланарны или некомпланарны в зависимости от того, будет равен нулю или нет определитель
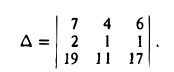
Разлагая его по элементам первой строки, получим
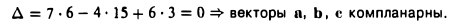
Двойное векторное произведение
Двойное векторное произведение [а, [b, с]] представляет собой вектор, перпендикулярный к векторам а и [b, с]. Поэтому он лежит в плоскости векторов b и с и может быть разложен по этим векторам. Можно показать, что справедлива формула
[а, [b, с]] = b(а, с) — с(а, b).
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

Конспект урока: Умножение вектора на число
Векторы на плоскости и в пространстве
Умножение вектора на число. Применение векторов к решению задач
План урока
- Произведение вектора на число.
- Применение векторов к решению задач
- Средняя линия трапеции
Цели урока
- Знать определение произведения вектора на число, свойства умножения вектора на число, правила действий с векторами, определение и свойство средней линии трапеции
- Уметь применять свойства умножения вектора на число, применять векторы при доказательстве теорем и решении геометрических задач.
Разминка
- В чём заключается правило многоугольника сложения нескольких векторов?
- Какой вектор называется разностью двух векторов?
- Какой вектор называется противоположным данному?
- Что утверждает теорема о разности двух векторов?
Произведение вектора на число
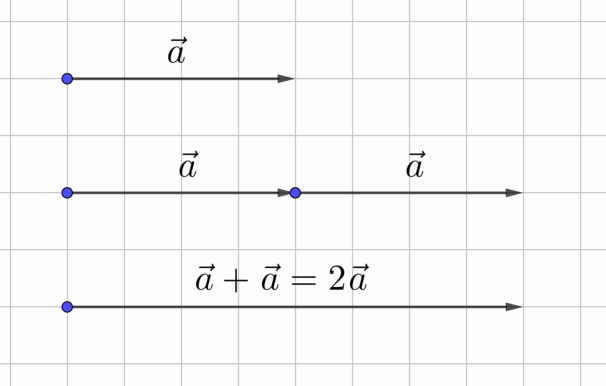
Рис. 1.
Предположим, что нам надо сложить два равных вектора. В результате мы получим новый вектор, который будет сонаправлен с исходным, но его длина будет вдвое больше. Логично считать, что получившийся вектор вдвое больше исходного, то есть он получился при умножении вектора на число 2 (рис. 1).
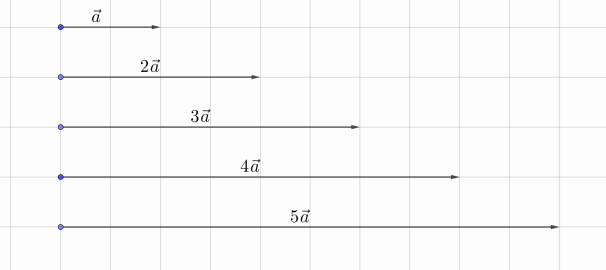
Рис. 2. Умножение вектора на положительное число
Аналогично можно построить векторы, которые больше исходного не в 2, а в 3, 4 и т.д. раз (рис. 2). А как умножать вектор на отрицательное число?
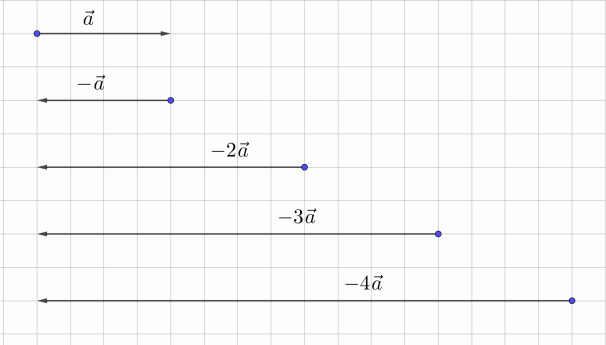
Рис. 3. Умножение вектора на отрицательное число
Здесь нужно использовать противоположный вектор. Логично считать, что он получается при умножении (– 1) на вектор
(рис. 3). Данные примеры показывают, что удобно ввести операцию умножения вектора на число, и подсказывают, как дать соответствующее определение.
Произведением
ненулевого вектора а→ на число k называется такой вектор b→, длина которого равна |k|∙|а→|, причем векторы а→ и b→
сонаправлены при k ≥ 0
и
противоположно направлены при
k < 0
.
Из определения следует, что
Произведением
нулевого вектора на любое число считается нулевой вектор.
Для любого числа k и любого вектора a→ векторы
a→
и
ka→
коллинеарны
.
Пример 1
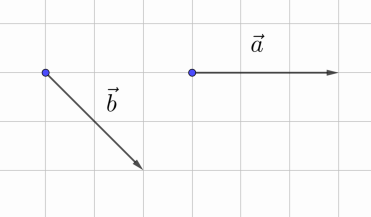
Рис. 4. Пример 1
На рисунке 4 изображены два вектора. Найдите векторы с→ = 4а→ + 2b→,
d→ = 4a→ – 2b→
Решение
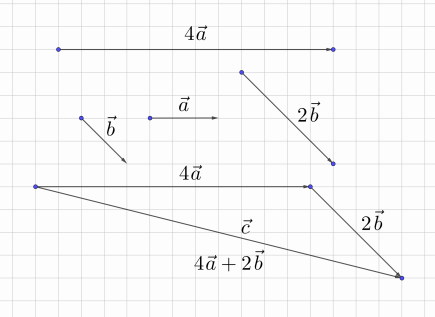
Рис. 5
1. Для построения
с→
нам надо сначала умножить исходные векторы на 4 и 2, а далее полученные результаты сложить по правилу треугольника (рис. 5).
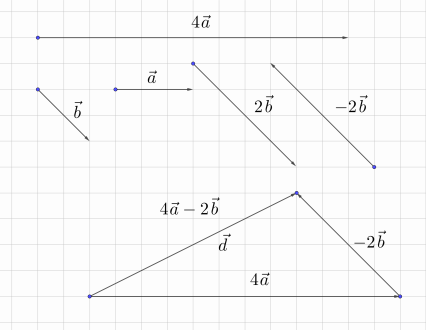
Рис. 6
Для нахождения вектора d→ надо построить вектор, противоположный вектору 2b→, и уже его складывать с 4a→ (рис. 6).
Умножение вектора на число обладает основными свойствами
Для любых чисел k, l и любых векторов a→, b→ справедливы равенства:
1.(kl)a→ = k(la→) (
сочетательный закон
);
2. (k + l)a→ = ka→ +la→ (
1-ый распределительный закон
);
3. k(a →+b→) = ka→ +kb→ (
2-ой распределительный закон
).
Рис. 7. Сочетательный закон
Проиллюстрируем свойства на примерах:
Сочетательный закон (рис. 7). Рассмотрим вектор 12a→ = (3·4)a ⃗= 3·(4a→).
Видно, что мы можем либо сразу умножить вектор а→ на число 12, либо сначала его умножить на 4, а потом на 3. Результат операции при этом не изменится
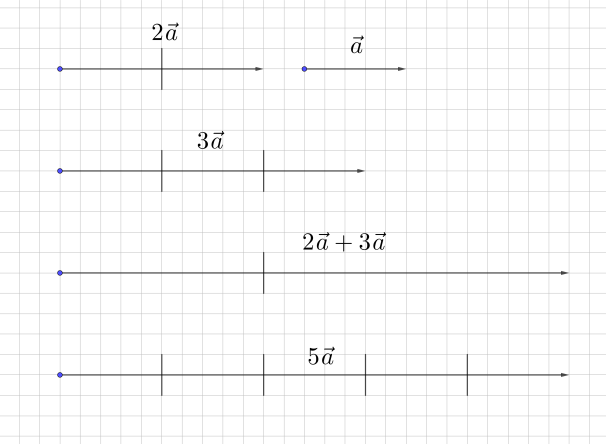
Рис. 8. 1-ый распределительный закон
2. 1-ый распределительный закон (рис.8)
Необходимо сложить векторы 2а→ и 3а→. Распределительный закон говорит, что мы можем поступить двумя способами. В первом случае мы просто строим векторы 2а→, 3а→ и складываем их. Во втором случае мы складываем только числа 2 и 3 (получаем 5), и далее уже умножаем вектор а→ на число 5.
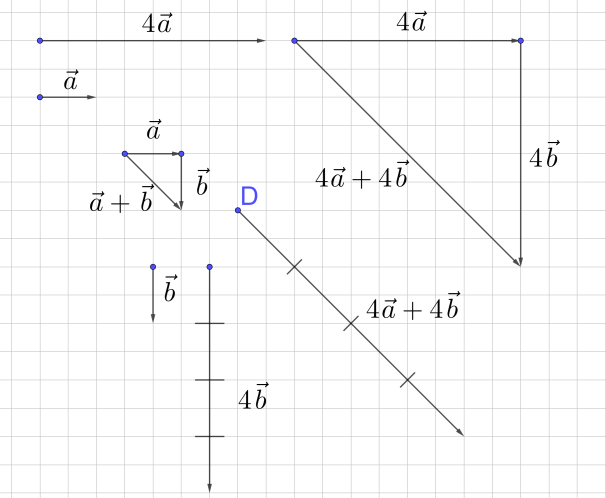
Рис. 9. 2-ой распределительный закон
3. 2-ой распределительный закон (рис. 9), в котором в скобках находится уже сумма векторов, а не чисел. Необходимо, например, сложить векторы 4а→ и 4b→. Конечно, можно просто построить их и сложить, однако закон говорит, что мы можем сначала сложить а→ и b→, и уже потом эту сумму умножить на 4.
Сформулированные нами законы сложения и умножения векторов позволяют выполнять действия с векторами так же, как с числами. В том числе можно упрощать выражения, содержащие векторные величины. Например, пусть известны векторы m→, n→ и k→, необходимо найти вектор
p→ = 2(m→ – n→) + (k→ + m→) – 3(n→ – k→ + m→).
Применим свойства: p→ = 2m→ – 2n→ + k→ + m→ – 3n→ + 3k→ – 3m→ = -5n→ + 4k→.
Видно, что выражение значительно упростилось.
Применение векторов к решению задач
Векторы активно используются в физике при решении многих задач, однако они также помогают доказывать геометрические теоремы. Рассмотрим несколько примеров, и начнем со вспомогательной задачи.
Пример 2
Известно, что M – это середина отрезка EF. Докажите, что для любой точки O выполняется равенство: ОМ→ = 12(ОЕ→ + OF→).
Доказательство:
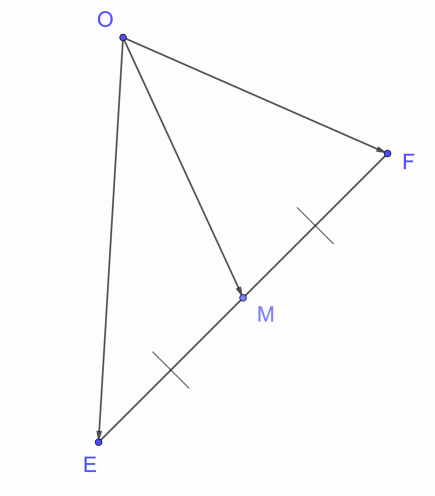
Рис. 10
1. Используя правило треугольника, вектор OM→ можно представить в виде двух различных сумм:
OM→ = OE→ + EM→, OM→ = OF→ + FM→
2. Сложим правые и левые части этих равенств:
2OM→ = OE→ + OF→ + EM→ + FM→.
3. Так как точка M – это середина отрезка EF, EM→ и FM→ – противоположные векторы, следовательно EM→ + FM→ = 0→ = 0.
4. Значит, 2OM→ = OE→ + OF→, OM→ =12 (OE→ + OF→).
Пример 3
Докажите, что если в трапеции провести прямую, проходящую через середины ее оснований, то она также пройдет через точку, в которой пересекаются продолжения боковых сторон трапеции.
Рис. 11. Пример 3
Доказательство
1. Построим трапецию DEFH, основаниями которой, будут отрезки EF и DH. M и N – их середины соответственно. Прямые DE и FH пересекаются в точке O. Необходимо доказать, что прямая MN также проходит через О.
2. Заметим, что ∆ОFE и ∆ОHD подобны по двум углам. Действительно, у них есть общий ∠DOH, а ∠ОFE = ∠OHD как соответственные углы при пересечении параллельных прямых секущей FH.
3. Обозначим коэффициент подобия буквой k, тогда можно записать, что OD = k ∙ OE,
OH = k ∙ OF.
4. Так как OD→↑↑OE→ и OH→↑↑OF→, то OD→ = k·OE→, OH→ = k·OF→.
5. M – это середина отрезка EF, поэтому OM→ = 12 (OE→ + OF)→ – см. доказательство Пример 2.
По аналогии ON→ = 12( OD→ + OH→)
6. Подставив в ON→ = 12( OD→ + OH→) вместо OD→ и OH→ соответствующие равенства, получим ON→ =k· 12( OE→ + OF→) = k·OM→, следовательно ON→∥OM→, N и M лежат на одной прямой (на параллельных прямых лежать не могут, т.к. имеют общую точку) и, значит, прямая MN проходит через О
Средняя линия трапеции
Отрезок, соединяющий середины боковых сторон трапеции, называется её
средней линией
.
Докажем теорему о средней линии трапеции, используя понятие вектор.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
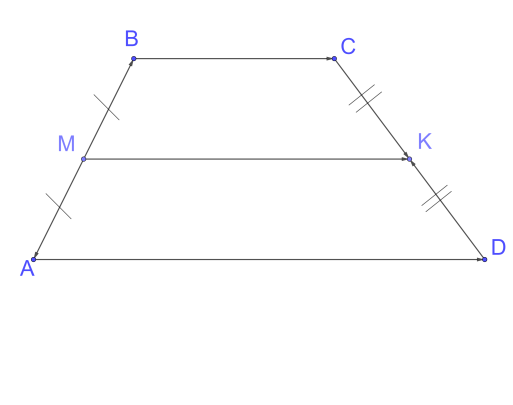
Рис. 12. Чертёж. Теорема
Доказательство
1. Построим трапецию ABCD так что, отрезки AD и BC являются основаниями трапеции, а отрезки АВ и CD – боковыми сторонами. Проведем среднюю линию МК. Необходимо доказать: МК∥AD, MK = 12 (AD+BC).
2. Выразим вектор MK→ через сумму векторов по правилу многоугольника сначала одним, а затем другим способом.
MK→ = MB→+ BC→+ CK→, MK→= MA→+ AD→+ DK→.
3. Сложим почленно два равенства и упростим получившееся выражение:
2MK→ = (MB→+ MA)→+ (BC→ +AD→) + (CK→+ DK→).
2MK→ = 0→ + (BC→ +AD→)+0→ = BC→ +AD→.
4. Выразим вектор МК через векторы BC→ и AD→: MK→ = 12 (BC→ + AD→), BC→↑↑ AD→, тогда MK→ ↑↑ AD→, т.е. MK∥AD.
5. Выразим длину вектора
MK→: 2|MK→| = |BC→ + AD→| = |BC→| + |AD→| = ВС + AD ,
значит MK = 12(ВС + AD).
Следовательно, длина средней линии трапеции равна полусумме её оснований.
Упражнение 1
1. На рисунке 4 изображены два вектора. Найдите вектор e→ = – 4a→ + 2b→.
2. Дан произвольный треугольник MNK. Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника MNK.
3. В равнобедренной трапеции MNKF перпендикуляр, опущенный из вершины N на большее основание MF, делит это основание на два отрезка, больший из которых равен 7 см. Найдите среднюю линию трапеции.
Контрольные вопросы
1. Какой вектор называется произведением данного вектора на число?
2. Чему равно произведение ka→, если: a→=0→, k = 0?
3. Могут ли векторы a→ и ka→ быть неколлинеарными?
4. Сформулируйте основные свойства умножения вектора на число.
5. Приведите пример применения векторов к решению задач.
6. Какой вектор называется разностью двух векторов? Постройте разность двух данных векторов.
7. Какой отрезок называется средней линией трапеции?
8. Сформулируйте и докажите теорему о средней линии трапеции.
Ответы
Упражнение 1
1. Рис. 13
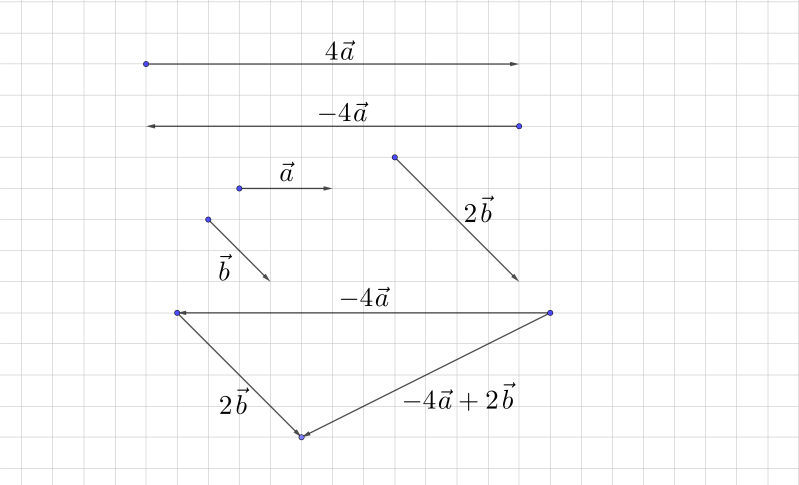
Рис. 13
2. Рис. 14
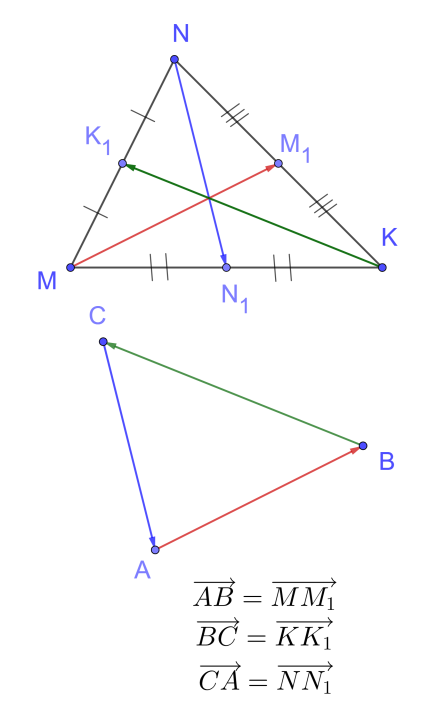
Рис. 14
3. 7 см
Предыдущий урок
Начальные сведения из стереометрии. Многогранники
Общие сведения из стереометрии
Следующий урок
Скалярное произведение векторов
Векторы на плоскости и в пространстве
В предыдущих уроках мы неоднократно решали следующую задачу: даны два неколлинеарных вектора, через которые в многоугольнике нужно выразить некоторые другие векторы. Выполним обобщение такого типа задач.
Теорема
Заданы векторы и . Векторы неколлинеарны. Доказать, что любой третий вектор однозначно выражается через векторы и , то есть найдутся такие числа х и у, что: .
Если данная теорема будет доказана, то в некотором смысле можно сказать, что, зная два неколлинеарных вектора, мы владеем всеми остальными векторами на плоскости.
Доказательство:
Из точки С, конца вектора , проведем прямые, параллельные векторам и . Получим точки А, В – пересечения построенных прямых с продолжениями векторов. Концы векторов обозначим за F и К соответственно (см. Рис. 1). Воспользуемся правилом треугольника и выразим вектор :
Вектор коллинеарен вектору , так как они
Рис. 1
принадлежат одной прямой согласно построению. Отсюда найдется такое число х, которое в произведении с вектором даст вектор : . С другой стороны, вектор равен вектору по построению, вектор коллинеарен вектору , значит, аналогично сказанному ранее, .
Таким образом, , то есть вектор является линейной комбинацией неколлинеарных векторов и . Кроме того, нашлась такая пара чисел х и у, с помощью которых любой вектор на плоскости можно выразить через два заданных неколлинеарных вектора.
Докажем, что такая пара единственная. Предположим противное: пусть существует такая пара чисел х1 и у1, что . Мы предположили, что есть еще одна линейная комбинация тех же двух неколлинеарных векторов для того же третьего вектора. Выполним вычитание полученных выражений:
Слева в выражении стоит нулевой вектор, справа – линейная комбинация двух неколлинеарных векторов, которые друг через друга не выражаются, таким образом, чтобы выполнялось равенство, коэффициенты при векторах в правой части должны быть нулевыми, то есть .
Вывод: разложение вектора по двум неколлинеарным векторам однозначно.
Пример 1 – задача 790: докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен их полуразности (см. Рис. 2).
Доказать: ; (при условии, что AD – большее основание, обозначим его за b, а ВС – меньшее основание, обозначим его за а).
Рис. 2
Доказательство:
Введем вектор . Выразим его через другие векторы, пользуясь правилом многоугольника. Напомним, что вектор , :
С другой стороны:
Выполним сложение полученных выражений:
Векторы очевидно противоположны, и их сумма составляет нулевой вектор, аналогично и векторы сокращаются. Получаем:
Поделим обе части выражения на два:
Из полученного равенства следует, что отрезок, соединяющий середины диагоналей трапеции, равен полуразности ее оснований. Кроме того, из равенства векторов в правой и левой частях следует, что они коллинеарны между собой, а также коллинеарны векторам и , таким образом, отрезок, соединяющий середины диагоналей трапеции, параллелен ее основаниям, что и требовалось доказать.
Обратим внимание, что несложно доказывается тот факт, что отрезок MN принадлежит средней линии трапеции, и данным фактом можно пользоваться при решении различных задач (см. Рис. 3). Напомним, что отрезок средней линии ММ1 – средняя линия треугольника , отсюда . Аналогично . Таким образом, можно найти длину отрезка, не пользуясь
Рис. 3
векторами, для этого следует вычесть из длины средней линии трапеции (она равна полусумме оснований) длины только что найденных отрезков:
Итак, мы рассмотрели применение векторов при решении различных задач, доказали некоторые свойства фигур и решили наиболее распространенные типы задач.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Terver.ru (Источник).
- Cleverstudents.ru (Источник).
Домашнее задание
1. Задание 1: точки M и N – середины диагоналей АС и BD четырехугольника ABCD. Докажите, что
2. Задание 2: дан произвольный треугольник . Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника
3. Задание 3: докажите, что отрезки, соединяющие середины противоположных сторон произвольного четырехугольника, точкой пересечения делятся пополам.
interneturok.ru
Трапеция. Свойства, признаки трапеции | Подготовка к ЕГЭ по математике
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
egemaximum.ru
Векторы в трапеции. П2
Данный модуль представляет собой задание повышенной сложности, состоящее из трех уровней. Для прохождения каждого уровня учащемуся необходимо два раза подряд правильно выполнить задание, при этом не использовать решение с ответом. Задание направлено на отработку умений и навыков учащихся решать задачи, используя свойства умножения вектора на число, коллинеарности векторов и правила параллелограмма. При прохождении уровней учащемуся предоставляется возможность использовать подсказки. Задание данного учебного модуля параметризировано. Это позволяет формировать индивидуальные задания для каждого учащегося.
Категория пользователей
Обучаемый, Преподаватель
Дисциплины
Математика
/ Умножение вектора на число
Уровень образования
Профессионально-техническая подготовка, повышение квалификации
Статус
Завершенный вариант (готовый, окончательный)
Тип ИР сферы образования
информационный модуль
Ключевые слова
вектор
Издатель
ООО «Кирилл и Мефодий»
ООО «Кирилл и Мефодий»
Россия, 127549, Москва, стр.1, ул. Пришвина, 8
Тел. — +7-495- 787-2610, +7-495- 787-2610
Сайт —
http://www.nmg.ru
Правообладатель
ООО «Кирилл и Мефодий»
ООО «Кирилл и Мефодий»
Россия, 127549, Москва, стр.1, ул. Пришвина, 8
Тел. — +7-495- 787-2610, +7-495- 787-2610
Сайт —
http://www.nmg.ru
Внимание! Для воспроизведения модуля необходимо установить на компьютере проигрыватель ресурсов.
Характеристики информационного ресурса
Тип используемых данных:
text/plain, text/html, image/jpeg
Объем цифрового ИР
1 212 451 байт
Проигрыватель
Категория модифицируемости компьютерного ИР
Признак платности
бесплатный
Наличие ограничений по использованию
нет ограничений
Рубрикация
Ступени образования
Основное общее образование
Целевое назначение
Учебное
Тип ресурса
Открытая образовательная модульная мультимедийная система (ОМС)
Классы общеобразовательной школы
9
Уровень образовательного стандарта
Федеральный
Характер обучения
Базовое

fcior.edu.ru
Трапеция
[{Large{text{Произвольная трапеция}}}]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна (180^circ).
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
Доказательство
1) Т.к. (ADparallel BC), то углы (angle BAD) и (angle ABC) – односторонние при этих прямых и секущей (AB), следовательно, (angle
BAD
+angle ABC=180^circ).
2) Т.к. (ADparallel BC) и (BD) – секущая, то (angle DBC=angle
BDA) как накрест лежащие.
Также (angle BOC=angle AOD) как вертикальные.
Следовательно, по двум углам (triangle BOC sim triangle AOD).
Докажем, что (S_{triangle AOB}=S_{triangle COD}). Пусть (h) – высота трапеции. Тогда (S_{triangle ABD}=frac12cdot hcdot
AD=S_{triangle ACD}). Тогда: [S_{triangle AOB}=S_{triangle ABD}-S_{triangle AOD}=S_{triangle ACD}-S_{triangle AOD}=S_{triangle
COD}]
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.

Проведем через точку (M) прямую (MN’parallel AD) ((N’in CD)). Тогда по теореме Фалеса (т.к. (MN’parallel ADparallel BC, AM=MB)) точка (N’) — середина отрезка (CD). Значит, точки (N) и (N’) совпадут.
2) Докажем формулу.
Проведем (BB’perp AD, CC’perp AD). Пусть (BB’cap MN=M’, CC’cap
MN=N’).
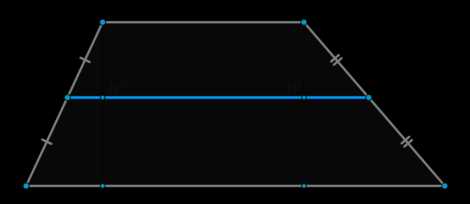
Тогда по теореме Фалеса (M’) и (N’) — середины отрезков (BB’) и (CC’) соответственно. Значит, (MM’) – средняя линия (triangle
ABB’), (NN’) — средняя линия (triangle DCC’). Поэтому: [MM’=dfrac12 AB’, quad NN’=dfrac12 DC’]
Т.к. (MNparallel ADparallel BC) и (BB’, CC’perp AD), то (B’M’N’C’) и (BM’N’C) – прямоугольники. По теореме Фалеса из (MNparallel AD) и (AM=MB) следует, что (B’M’=M’B). Значит, (B’M’N’C’) и (BM’N’C) – равные прямоугольники, следовательно, (M’N’=B’C’=BC).
Таким образом:
[MN=MM’+M’N’+N’N=dfrac12 AB’+B’C’+dfrac12 C’D=] [=dfrac12 left(AB’+B’C’+BC+C’Dright)=dfrac12left(AD+BCright)]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
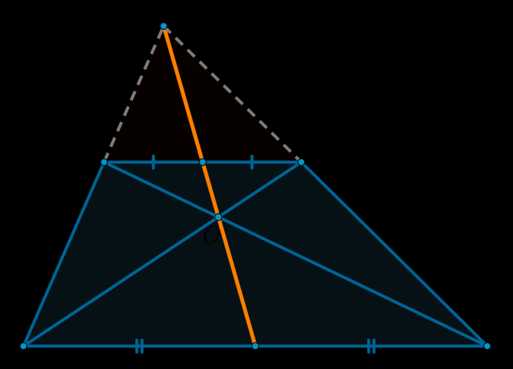
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки (P), (N) и (M) лежат на одной прямой.
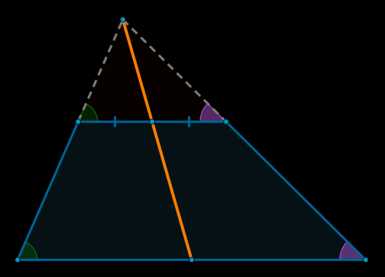
Проведем прямую (PN) ((P) – точка пересечения продолжений боковых сторон, (N) – середина (BC)). Пусть она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
Рассмотрим (triangle BPN) и (triangle APM). Они подобны по двум углам ((angle APM) – общий, (angle PAM=angle PBN) как соответственные при (ADparallel BC) и (AB) секущей). Значит: [dfrac{BN}{AM}=dfrac{PN}{PM}]
Рассмотрим (triangle CPN) и (triangle DPM). Они подобны по двум углам ((angle DPM) – общий, (angle PDM=angle PCN) как соответственные при (ADparallel BC) и (CD) секущей). Значит: [dfrac{CN}{DM}=dfrac{PN}{PM}]
Отсюда (dfrac{BN}{AM}=dfrac{CN}{DM}). Но (BN=NC), следовательно, (AM=DM).
2) Докажем, что точки (N, O, M) лежат на одной прямой.
Пусть (N) – середина (BC), (O) – точка пересечения диагоналей. Проведем прямую (NO), она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
(triangle BNOsim triangle DMO) по двум углам ((angle OBN=angle
ODM) как накрест лежащие при (BCparallel AD) и (BD) секущей; (angle BON=angle DOM) как вертикальные). Значит: [dfrac{BN}{MD}=dfrac{ON}{OM}]
Аналогично (triangle CONsim triangle AOM). Значит: [dfrac{CN}{MA}=dfrac{ON}{OM}]
Отсюда (dfrac{BN}{MD}=dfrac{CN}{MA}). Но (BN=CN), следовательно, (AM=MD).
[{Large{text{Равнобедренная трапеция}}}]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию (ABCD).
Из вершин (B) и (C) опустим на сторону (AD) перпендикуляры (BM) и (CN) соответственно. Так как (BMperp AD) и (CNperp AD), то (BMparallel CN); (ADparallel BC), тогда (MBCN) – параллелограмм, следовательно, (BM = CN).
Рассмотрим прямоугольные треугольники (ABM) и (CDN). Так как у них равны гипотенузы и катет (BM) равен катету (CN), то эти треугольники равны, следовательно, (angle DAB = angle CDA).
2) 
Т.к. (AB=CD, angle A=angle D, AD) – общая, то по первому признаку (triangle ABD=triangle ACD). Следовательно, (AC=BD).
3) Т.к. (triangle ABD=triangle ACD), то (angle BDA=angle CAD). Следовательно, треугольник (triangle AOD) – равнобедренный. Аналогично доказывается, что и (triangle BOC) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию (ABCD), такую что (angle A = angle D).

Достроим трапецию до треугольника (AED) как показано на рисунке. Так как (angle 1 = angle 2), то треугольник (AED) равнобедренный и (AE
= ED). Углы (1) и (3) равны как соответственные при параллельных прямых (AD) и (BC) и секущей (AB). Аналогично равны углы (2) и (4), но (angle 1 = angle 2), тогда (angle 3 = angle 1 = angle 2 =
angle 4), следовательно, треугольник (BEC) тоже равнобедренный и (BE = EC).
В итоге (AB = AE — BE = DE — CE = CD), то есть (AB = CD), что и требовалось доказать.
2) Пусть (AC=BD). Т.к. (triangle AODsim triangle BOC), то обозначим их коэффициент подобия за (k). Тогда если (BO=x), то (OD=kx). Аналогично (CO=y Rightarrow AO=ky).

Т.к. (AC=BD), то (x+kx=y+ky Rightarrow x=y). Значит (triangle AOD) – равнобедренный и (angle OAD=angle ODA).
Таким образом, по первому признаку (triangle ABD=triangle ACD) ((AC=BD, angle OAD=angle ODA, AD) – общая). Значит, (AB=CD), чтд.
shkolkovo.net
Трапеция
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.
Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие;
— прямоугольные
. 
Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У равнобокой трапеции боковые стороны равны, а основания параллельны.
У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии. Его длина
- Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые.
Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые, а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник, у которого линия сечения параллельна основанию треугольника.
Важно. Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h1h2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Площадь трапеции
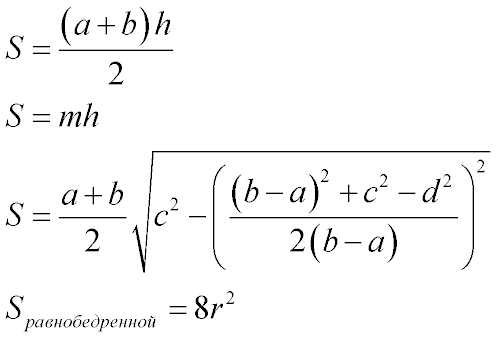
где
a и b — параллельные основания трапеции
c и d — боковые стороны трапеции
m — средняя линия трапеции
r — радиус вписанной в трапецию окружности
S — площадь трапеции
Содержание главы:
Ромб |
Описание курса
| Площадь трапеции
profmeter.com.ua
В трапеции ABCD вектор AC=вектору a,вектор DB=вектору b и AD=вектору c.
1. вектор AB + вектор BD= вектор AC + вектор CD
2. вектор AB + вектор BC= вектор AD + вектор DC
Это правило треугольника сложения векторов: Видим что конец первого вектора совпадает с началом второго. Значит результатом сложения будет вектор, обозначенный первой буквой первого вектора и второй буквой другого вектора:
АВ + ВD = AD, AC + CD = AD
Видим, что результаты сложения совпадают, что и требовалось доказать.
Аналогично и во втором примере:
AB + BC = AC, AD + DC = АС, что и треб. доказать.
АВСD — параллелограмм
1. CA = СВ + ВА = CD + DA
2. DA = DC + CA = DB + BA
1. вектор AB + вектор BC = AC
2. вектор MN + вектор NN = MN
3. вектор PQ+ вектор QR = PR
4.вектор EF + вектор DE = DE + EF = DF
выразите вектор BC через векторы AB и AC:
BC = AC — AB
взята точка D на стороне треугольника ABC. Выразите вектор BD через векторы AB и AD:
BD = AD — AB
Дан параллелограмм ABCD. Найдите разность:
1. вектор AB- вектор AC = CB
2. вектор BC — вектор CD = AB+BC = AC
Ты чё ебанутая ты блядь видишь что написано ТРАПЕЦИЯ
touch.otvet.mail.ru
Контрольная работа «Векторы. Средняя линия трапеции».
Контрольная работа № 11. 8 класс
Векторы. Средняя линия трапеции.
I вариант
Упростите выражение: а) AC + DE + CB + EA + BD; б) DK — EA — AB + KB — DB.Начертите два неколлинеарных вектора a и b. Постройте векторы: — 12a; 3a+12b.
M, N, K – середины сторон AB, BC и AC треугольника ABC, AM= a, AK = b. Выразите векторы AN, BC, BK через векторы a и b.
Одно из оснований трапеции больше другого на 8 см, а средняя линия равна 14 см. Найдите основания трапеции.
Контрольная работа № 11. 8 класс
Векторы. Средняя линия трапеции.
II вариант
Упростите выражение: а) AB + CA + BD + DC; б) XM- YN+ BX- TZ+ YZ+ MN.
Начертите два неколлинеарных вектора a и b. Постройте векторы: — 13b; 2a+12b.
M, N, K – середины сторон AB, BC и AC треугольника ABC, CK= a, CN = b. Выразите векторы CM, AB, AN через векторы a и b.
4. Основания трапеции относятся как 5:6, а средняя линия равна 22 см. Найдите основания трапеции.
Контрольная работа № 11. 8 класс
Векторы. Средняя линия трапеции.
I вариант
Упростите выражение: а) AC + DE + CB + EA + BD; б) DK — EA — AB + KB — DB.Начертите два неколлинеарных вектора a и b. Постройте векторы: — 12a; 3a+12b.
M, N, K – середины сторон AB, BC и AC треугольника ABC, AM= a, AK = b. Выразите векторы AN, BC, BK через векторы a и b.
Одно из оснований трапеции больше другого на 8 см, а средняя линия равна 14 см. Найдите основания трапеции.
Контрольная работа № 11. 8 класс
Векторы. Средняя линия трапеции.II вариант
Упростите выражение: а) AB + CA + BD + DC; б) XM- YN+ BX- TZ+ YZ+ MN.
Начертите два неколлинеарных вектора a и b. Постройте векторы: — 13b; 2a+12b.
M, N, K – середины сторон AB, BC и AC треугольника ABC, CK= a, CN = b. Выразите векторы CM, AB, AN через векторы a и b.
4. Основания трапеции относятся как 5:6, а средняя линия равна 22 см. Найдите основания трапеции.
Приложенные файлы
- 96322050615
Размер файла: 19 kB Загрузок: 8
weburok.com

| AB | .
2.1. Векторы на плоскости и в пространстве
Вектором (геометрическим вектором) называется направленный отрезок, т.е. отрезок, для которого указано, какой из его концов считается началом, а какой концом. При этом любые два направленных отрезка считаются равными, если они имеют одинаковые длину и направление. Таким образом, начало вектора можно помещать в любую точку пространства.
Если начало вектора находится в точке A, а конец – в точке B , то вектор обозначают AB . Векторы также принято обозначать строчными буквами латинского алфавита со стрелкой над ними: a , b , c .
Длиной вектора AB называется длина отрезка AB , обозначается Вектор, длина которого равна 0, называется нулевым и обозначается 0 . Нулевой вектор направления не имеет.
|
Два вектора a |
и b называются коллинеарными, если они параллельны |
||
|
одной и той же прямой. |
Если при этом векторы a и b имеют одинаковое |
||
|
направление, то они называются сонаправленными. |
|||
|
Три |
вектора |
a , b |
и c называются компланарными, если они |
параллельны однойи той же плоскости.
Углом между ненулевыми векторами a и b называется наименьший из двух углов, образуемых этими векторами при совмещении их начал (рис.2.1), обозначается α = (a ,b) . Векторы a и b называются ортогональными
(перпендикулярными), если (a ,b) = 90 .
Произведением вектора a на число λ называется вектор, обозначаемый λa , длина которого равна | λ || a |, а направление совпадает с направлением вектора a , если λ > 0 , и противоположно ему, если λ < 0 . Таким образом, векторы a и λa коллинеарны. Справедливо и обратное утверждение: если векторы a и b коллинеарны, то они связаны равенством a = λb , где λ – некоторое число.
30
ABCD (рис.2.3).
B
Суммой векторов AB и BC называется вектор AC (рис.2.2). Это определение называют правилом треугольника сложения векторов.
Сумма векторов a и b обозначается a +b .
Bb
C
a
Рис.2.2
Сложение нескольких векторов выполняется по правилу многоугольника:
A1A2 + A2 A3 +…+ An−1An = A1An .
Для сложения двух неколлинеарных векторов применяют также правило параллелограмма: суммой векторов AB и AD является вектор AC , где точка C
– вершина параллелограмма
C
aa +b
 D
D
A b
Рис.2.3
Пример 2.1. В треугольнике ABC даны стороны AB = 2 , AC = 3. Векторы a и b сонаправлены с векторами AB и AC соответственно и | a |=| b |=1. Точка E – середина стороны BC . Выразить векторы BC и AE через векторы a и b .
Р е ш е н и е. По правилу треугольника имеем
BC = CA + AB = −3b + 2a .
Для того чтобы выразить вектор AE , построим параллелограмм ABDC (рис.2.4). По правилу параллелограмма AD = AB + AC = 2a +3b . Так как диагонали параллелограмма в точке пересечения делятся пополам, имеем
|
1 |
1 |
||||||
|
AE = |
2 |
AD = |
2 |
(2a |
+3b )= a |
+1,5b . |
31

B D
E a 
A  C
C
bРис.2.4
Если вектор a может быть представлен в виде линейной комбинации векторов a1 ,a2 ,…,an , т.е.
a = λ1a1 +λ2a2 +… +λnan ,
где λi , i =1,…,n , – некоторые числа, то говорят, что вектор a линейно выражается через векторы a1 ,a2 ,…,an .
Базисом на плоскости называются любые два неколлинеарных вектора e1 ,e2 , взятые в определенном порядке. Любой компланарный с базисными векторами e1 ,e2 вектор a можно представить, и притом единственным образом, в виде их линейной комбинации:
Числа x и y в правой части равенства (2.1) называются координатами вектора a в базисе e1 ,e2 .
Базисом в пространстве называются любые три некомпланарных вектора e1 ,e2 ,e3 , взятые в определенном порядке. Любой вектор a можно представить, и притом единственным образом, в виде их линейной комбинации:
|
a = xe1 + ye2 |
+ ze3 , |
(2.2) |
||
|
где x, y , z – координаты вектора a в базисе e1 |
,e2 ,e3 . |
|||
|
Равенство (2.1) называется разложением вектора a |
по |
базису |
на |
|
|
плоскости, а равенство (2.2) – разложением вектора a |
по |
базису |
в |
|
|
пространстве. |
||||
|
Координаты вектора обычно записывают в круглых скобках после |
||||
|
буквенного обозначения вектора. Например, запись a (2;−1;3) |
означает, что |
|||
|
вектор a имеет координаты 2,−1 и 3 в выбранном базисе. |
||||
|
32 |
Два вектора, заданные координатами в фиксированном базисе, равны тогда и только тогда, когда равны их соответствующие координаты.
При умножении вектора на число все его координаты умножаются на это число. При сложении двух векторов складываются их соответствующие координаты.
Пример 2.2. При каком значении y векторы a(3;−2;5) и b(−6; y;−10) коллинеарны?
Р е ш е н и е. Векторы a и b λ , что выполняется равенство координаты векторов a и λb(−6λ;λ
коллинеарны, если существует такое число a = λb . Приравнивая соответствующие y;−10λ), получим:
3 = −6λ,−2 = λy ,5 = −10λ,
отсюда находим, что λ = − 12 и y = 4 .
Базис называется ортонормированным, если базисные векторы попарно ортогональны и имеют длину, равную единице. Векторы ортонормированного базиса на плоскости обозначают i , j , а в пространстве – i , j ,k . Если при указании координат вектора не дается ссылка на конкретный базис, то по умолчании считают базис ортонормированным.
Декартовой системой координат называется совокупность фиксированной точки O , называемой началом координат, и базиса e1 ,e2 ,e3 . Декартова система координат с ортонормированным базисом называется
прямоугольной (рис.2.5).
|
z |
||
|
k |
M |
|
|
O |
||
|
i |
j |
y |
Рис.2.5
33

Прямые, походящие через начало координат в направлении базисных векторов, называются координатными осями. Прямая Ox называется осью абсцисс, прямая Oy – осью ординат, прямая Oz – осью аппликат.
Вектор OM называется радиус-вектором точки M . Координатами точки M в рассматриваемой системе координат называются координаты ее радиус-вектора. Первая координата называется абсциссой, вторая –
ординатой, третья – аппликатой.
Длина вектора a (x; y; z) , заданного своими координатами в ортонормированном базисе, определяется равенством
a = 
 x2 + y2 + z2 .
x2 + y2 + z2 .
Если в декартовой системе координат даны две точки M1 (x1 ; y1 ; z1) и M2 (x2 ; y2; z2 ) , то вектор M1M2 в соответствующем базисе имеет координаты
|
x2 − x1, y2 − y1, z2 − z1, а расстояние между точками |
M1 |
и M2 (длина вектора |
||||||||||
|
M1M2 ) находится по формуле |
||||||||||||
|
= |
(x |
− x )2 |
+(y |
− y )2 +(z |
− z )2 |
. |
(2.3) |
|||||
|
M M |
2 |
2 |
2 |
|||||||||
|
1 |
2 |
1 |
1 |
1 |
||||||||
|
Разделить отрезок |
M1M2 |
в отношении |
λ |
означает |
найти точку |
M (x; y; z) , принадлежащую данному отрезку, удовлетворяющую условию M1M = λ MM2 . Координаты такой точки вычисляются по формулам:
|
x = |
x1 +λx2 |
; y = |
y1 +λy2 |
; |
z = |
z1 +λz2 |
. |
(2.4) |
||||||||
|
1+λ |
1+λ |
1+λ |
||||||||||||||
|
При λ =1 точка M |
делит |
отрезок |
M1M2 |
пополам и |
формулы (2.4) |
|||||||||||
|
определяют координаты середины отрезка: |
||||||||||||||||
|
x = |
x1 + x2 |
; |
y = |
y1 |
+ y2 |
; z |
ср |
= |
z1 + z2 |
. |
||||||
|
ср |
2 |
ср |
2 |
2 |
||||||||||||
|
Пример 2.3. Даны |
вершины A(1;−2), B(−2;4), C(5;−6) |
треугольника |
||||||||||||||
|
ABC . Точка K делит сторону AB в отношении |
2 :1, считая от вершины A. |
|||||||||||||||
|
Найти длину отрезка KC . |
||||||||||||||||
|
Р е ш е н и е. Так как |
AK : KB = 2 :1, |
то координаты точки K найдем по |
||||||||||||||
|
формулам (2.4) при λ = 2: |
34

|
xK = 1+ 2 (−2) = −1, |
yK = −2 + 2 4 |
= 2 , |
||||
|
1+ 2 |
1+ 2 |
|||||
|
т.е. K(−1;2) . Длину отрезка KC найдем по формуле (2.3) |
||||||
|
= |
(5 −(−1))2 + (−6 − 2)2 =10 . |
|||||
|
KC |
Задачи для самостоятельного решения
2.1. Изобразить два неколлинеарных вектора a и b и построить векторы:
а) a + 2b ; б) 3a −b ; в) − 12 a +3b .
|
2.2. Дан параллелограмм |
ABCD и два вектора p и q таких, что AB = 4 p , а |
||
|
AD = 3q . Точки |
M и |
N – середины сторон BC и CD соответственно. |
|
|
Выразить через векторы p и q : |
а) векторы CB,CD, AC , BD ; б) векторы |
||
|
AM , AN , MN . |
AE – медиана, a = AB, b = AC , c = AE . |
||
|
2.3. В треугольнике |
ABC |
отрезок |
Разложить геометрически и аналитически: а) вектор c по векторам a и b ; б) вектор a по векторам b и c .
2.4.В параллелограмме ABCD точки M и N – середины сторон BC и CD соответственно. Разложить геометрически и аналитически вектор AC = c по векторам a = AM и b = AN .
2.5.В трапеции ABCD имеем BC|| AD и BC : AD =1: 3. Выразить вектор c = CD через векторы a = AB и b = AD .
2.6.Медианы треугольника ABC пересекаются в точке O . Выразить векторы OA,OB,OC через векторы a = AB и b = AC . Проверить справедливость
|
равенства OA +OB +OC = 0. |
|||||||
|
2.7. Дан |
параллелепипед |
ABCDA1B1C1D1. Выразить |
векторы |
AC1 , A1C , |
|||
|
BD , B D через векторы a = AB, |
b = AD и c = AA |
1 |
. |
||||
|
1 |
1 |
||||||
|
2.8. Дан параллелепипед ABCDA1B1C1D1. Прямые AC и BD пересекаются в |
|||||||
|
точке O . Выразить |
векторы |
OA1 , OB1 , OC1 |
и |
OD1 через |
векторы |
||
|
a = AB, b = AD, c = AA . |
|||||||
|
1 |
35
2.9. При каком значении x векторы a (x;2;−4) и b(3;−6;12) коллинеарны?
2.10. Даны точки M (0;3), N(2;1), P(5;−1), Q (9;−3) . Доказать, что четырехугольник MNPQ является трапецией.
2.11.Даны координаты трех вершин параллелограмма ABCD : A(1;2) , B(3;7), D(8;−1) . Найти координаты вершины C .
2.12.Даныкоординатыдвухвершинтреугольника ABC : A(1;2) , B(3;4).Отрезок AE – медианатреугольникаи AE(4;−1) .Найтикоординатывершины C .
2.13. Найти положительное значение координаты x вектора a (x;−3;4) , если
|a |= 5
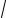 2 .
2 .
2.14.Найти диагонали параллелограмма, построенного на векторах m(3;4;−2)
и n (−1;2;5) .
2.15.Найти длину стороны BC треугольника ABC , если AB(1;−1;2) , AC(7;2;4) .
2.16.Даны точки A(2;3;−1) , B(8;12;−4) . Найти координаты: а) середины отрезка AB ; б) точек, делящих отрезок AB на три равные части.
2.17.Даны вершины A(4;−1) , B(5;5) , C(−3;1) треугольника ABC . Найти медиану, проведенную из вершины A.
2.18.На отрезке AB выбрана точка E так, что AE : EB =1: 4 . Найти координаты точки B , если A(1;−2;5) , E(3;−1;1) .
2.19.Разложить вектор a по векторам p и q , если:
а) a (2;−5) , p (1;3) , q (2;5); б) a(4;5) , p (3;2), q (2;1) .
2.20. Разложить вектор a по векторам p , q и r , если:
а) a (6;1;4) , p (4;5;1), q (3;2;1) , r (2;3;2) ;
б) a (10;−1;0) , p (3;1;−1) , q (2;−1;2) , r (3;2;1).
36
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
