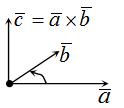Из всех операций, которые можно применять для решения физических задач, есть одна, знание которой позволяет практически “в уме” решать множество задач про электромагнитные силы и поля, вращение твердых тел и много-много других.
Более того, понимание сути данной математической операции ставит вас на целую голову выше остальных, в понимании физики.
На первый взгляд странная операция при ближайшем рассмотрении оказывается очень простой.
Итак, векторное произведение векторов
Но вначале кое-что важное.
Очень важное замечание!
Здесь и в дальнейшем (и в предыдущем изложении) мы всегда рассматриваем «Правую» систему координат.
Правая система координат! Берем правую руку. Раскрываем ладонь перед собой. Оттопыриваем большой палец – это положительное направление оси X. Четыре пальца перпендикулярных большому показывают положительное направление оси Y. Тогда из открытой ладони прямо на вас перпендикулярно осям X, Y будет выходить положительное направление оси Z.
Сильно хлопаем себя открытой ладонью правой руки по лбу! Навсегда запоминаем правильное расположение системы координат.
Если рисовать неправильную систему, то будут ошибки.
Итак, определим векторное произведение векторов:
Возьмем нашу правую систему координат и зададим три единичных вектора, по одному вдоль каждой из осей.
Тогда любой вектор
можно записать в виде суммы трех векторов
Легко заметить, что скалярные произведения наших единичных векторов
Эта удобная тройка векторов очень пригодится нам в дальнейшем.
Помним! Вектора при переходе от одной системы координат к другой не меняются.
И результаты векторных операций при переходе от одной системы координат к другой также не меняются!
И вот существует такая операция над векторами, называемая “векторное произведение векторов”
«Ну и ну! Как это? Для чего?»
Все очень просто!
Для начала убедимся, что векторные произведения наших единичных векторов между собой:
Надеюсь, все уже увидели, что от перемены местами сомножителей меняется знак векторного произведения?
Поиграв с единичными векторами, убедитесь что векторное произведение двух векторов дает в результате вектор, перпендикулярный плоскости, в которой лежат вектора сомножители, а по модулю равный площади параллелограмма, ограниченного векторами сомножителями!
Всегда во всех задачах выбирайте правую систему координат так, чтобы было просто и удобно! Как на картинке выше.
Зачем нужна операция векторного произведения векторов, определенная выше?
Рассмотрим задачу «о рычагах».
Пусть у нас есть твердое тело, представляющее из себя систему из трех стержней, жестко скрепленных в одной точке. И эта точка закреплена в пространстве так, что она является центром вращения («точка закрепления шарнира»). Как на рисунке ниже.
К концам стержней приложены силы
Силы создают вектора моментов сил – «крутящие моменты», приложенные к нашему твердому телу.
Момент силы – это модуль вектора момента силы. Синонимы вектора момента силы: крутящий момент, вращательный момент, вертящий момент, вращающий момент).
Наглядно представить себе вектор момента силы можно следующим образом:
Представьте себе юлу (детскую игрушку «волчок»). Чем сильнее мы его закрутим за ось, тем быстрее и дольше он вращается. Закрепим ось волчка на какой-то прямой так, чтобы она могла свободно вращаться. Представьте теперь, что вы будете тянуть за тело волчка, стараясь повернуть его вокруг закрепленной оси. А ваш товарищ будет пытаться удержать ось рукой. Представили?
Будет ли волчок поворачиваться вокруг оси?
И если вы будете тянуть его в одну сторону, а ваш товарищ в другую, то в какую сторону будет поворачиваться волчок?
В ту, чья сила больше?
Не совсем.
Представим ситуацию на картинке выше. Вы взялись ближе к оси, а ваш товарищ взялся за диск. Если ось достаточно тонкая, а диск достаточно большой, то как бы вы ни старались, волчок будет поворачиваться в сторону вашего товарища. Хотя силу вы приложите гораздо большую, чем он.
«Рычаг», скажете вы. И будете правы!
Задача о рычагах по сути аналогична. И решается она очень просто с использованием операции векторного произведения, которую мы с вами рассмотрели выше.
Из формул (74) – (76) мы знаем, что векторное произведение двух векторов есть вектор, который по направлению перпендикулярен плоскости, в которой лежат вектора сомножители. Величину этого вектора по модулю можно вычислить с учетом формул (71) – (73), а модуль вычисляется по простой формуле:
Так вот, вектор момента силы, приложенной к телу, равен векторному произведению радиус-вектора точки приложения силы умноженному на вектор силы.
Начало координат удобнее выбирать в точке закрепления тела на шарнире (например, в точке подвеса перекладины рычажных весов). Можно в любой другой.
Но мы с вами начало координат всегда берем в точке, относительно которой тело может поворачиваться. Потому, что так проще вычисления.
Складывая вектора моментов всех приложенных к телу сил мы автоматически находим результирующий вектор, который и определяет в какую сторону и насколько интенсивно будет вращаться наша тройная гантель, показанная на рисунке выше.
Вдумайтесь! Мы просто складываем три вектора момента, от каждой из сил.
Если сумма равна нулю, то наше твердое тело «стоит на месте». Если не равна нулю, то наше тело имеет ненулевой момент сил относительно «точки подвеса» в плоскости, перпендикулярной нашему вектору суммы моментов.
И угловое ускорение, которое пропорционально модулю этого вектора.
Можно обобщить задачу на произвольное твердое тело с закрепленной в пространстве точкой подвеса и неограниченным количеством приложенных сил, как показано на рисунке. ниже.
Оно будет вращаться относительно оси, в которой лежит наш результирующий вектор момента сил.
И вращение будет тем интенсивнее, чем больше этот результирующий вектор по модулю.
Направление вращения будет зависеть от направления этого вектора. Направлен в одну сторону, вращается тело в одну сторону, направлен в другую, тело вращается в обратную.
Причем, если тело закрепить на оси, как в случае рассмотренного нами волчка, то задача становится двумерной. Вращение может быть только относительно оси и, соответственно, можно рассматривать моменты сил, только в системе координат, перпендикулярной оси. Это вы можете рассмотреть сами.
Вопрос: каково условие невращения твердого тела в общем случае, показанном на рисунке 11? Другими словами, при каких условиях общий (суммарный) момент вращения тела равен нулю?
Ответ: Если сумма моментов всех сил равна нулю, то тело находится во «вращательном равновесии» – т.е. не имеет суммарного момента вращения.
Эта задача – более общая по отношению к школьной задаче о рычагах, изображенной на рисунке ниже.
Благодаря определенной нами операции векторного произведения векторов задача решается в одно действие.
Решите ее самостоятельно!
Или посмотрите решение в нашем учебнике.
Первому, кто ответит на вопрос, почему ось вращения вращающегося волчка (Юлы) обычно не “стоит” строго параллельно, а совершает некие колебания вокруг некой оси, получит в подарок цифровую ручку от нашего спонсора. Ответы можете писать на странице в facebook.
Так же, как всегда, получит подарок тот, кто первым найдет принципиальную ошибку в изложении материала.
Ну и как всегда ставьте лайки и подписывайтесь на канал!
Векторное произведение векторов
Определение
| Определение |
|
Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $. |
Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.
Формула
| Формула 1 |
|
Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле: $$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$ |
| Формула 2 |
|
В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$ где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $. |
Определитель во второй формуле можно раскрыть по первой строке:
$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 – a_3 b_2) – overline{j} (a_1 b_3 – a_3 b_1) + overline{k} (a_1 b_2 – a_2 b_1) $$
Итого вторая формула приобретает окончательный короткий вид:
$$ overline{a} times overline{b} = (a_2 b_3 – a_3 b_2; a_3 b_1 – a_1 b_3; a_1 b_2 – a_2 b_1) $$
Свойства
- При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
- Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
- $$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$
Примеры решений
| Пример 1 |
|
Найти векторное произведение векторов, заданных координатами $$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$ |
| Решение |
|
Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) – overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} – overline{j} + 3overline{k} $$ Полученный ответ можно записать в удобном виде: $$ overline{a} times overline{b} = (5, -1, 3) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ overline{a} times overline{b} = (5, -1, 3) $$ |
Геометрический смысл
- Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
- Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
- Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.
| Пример 2 |
| Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$ |
| Решение |
|
Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов. Находим определитель: $$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) – overline{j}(2+3) + overline{k}(4+1) = -5overline{i} – 5overline{j} + 5overline{k} $$ Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора: $$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$ По формуле нахождения площади треугольника имеем: $$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$ |
| Ответ |
| $$ S_Delta = 4.33 $$ |
Физика
Тестирование онлайн
Вектор
Вектор – это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало – точка. Модуль вектора (абсолютная величина) – длина этого направленного отрезка.
Если начало вектора совпадает с его концом, получим нулевой вектор.
Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.
На рисунке только вектор a равен вектору b. Вектор c им не равен, так как направлен в противоположную сторону
Вектор -c – это вектор c, но противоположного направления. Тогда
Проекция вектора
Проекция вектора на ось имеет положительное значение в том случае, когда направление вектора совпадает с направлением оси. Отрицательное значение – в противоположном случае.
Спроецируем вектор перемещения на ось Ox и на ось Oy. Для того, чтобы получить проекцию необходимо из координаты конца вектора отнять координату начала. На ось ОХ: sx=x-x0, на ось ОУ: sy=y-y0.
Частные случаи, когда проекция на ось Ox или Oy нулевая.
Сумма составляющих вектора по осям равна данному вектору, т.е.
Сложение векторов
Правило параллелограмма: диагональ параллелограмма – сумма двух векторов с общим началом.
Правило треугольника: от конца первого вектора отложить второй вектор, тогда их суммой будет вектор, начало которого совпадает с началом первого вектора, а конец с концом второго вектора.
Рассмотрим правила на примерах.
Вычитание векторов
Вычитание векторов – это сумма положительного и отрицательного вектора.
Упражнения
Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть численно равной одному из составляющих векторов?
Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть меньше меньшего из составляющих векторов?
Все действия с векторами в физике
Из предыдущего параграфа мы знаем, что есть скалярные физические величины и есть векторные физические величины. Например, скорость – вектор, перемещение – вектор. Длина пути – скаляр (просто одно число с размерностью расстояния). А перемещение имеет длину и направление. Поэтому, это вектор. В трехмерной прямоугольной системе координат вектор перемещения можно определить, как тройку чисел, компонентов вектора по осям X , Y , Z . Эта тройка чисел однозначно задает направление и величину вектора перемещения.
Для чего нам понадобились вектора? И какие операции можно производить с векторами? И все-таки, любая ли тройка чисел задает вектор?
Для начала, чтобы нагляднее представить себе, что можно делать с векторами, будем представлять себе все вектора, как операции перемещения в пространстве. Операции, которые задаются тройкой чисел (компонентов). Такие операции можно применить к любой точке пространства (обобщенно, к любому физическому телу).
Сразу становятся понятны операции сложения и вычитания векторов. Просто последовательно применяем к точке один вектор, потом другой. Понятно, почему можно изменить порядок слагаемых и сумма (общее перемещение) не изменится. Понятно, что вычитание – есть прибавление вектора с обратным знаком (меняем направление стрелки).
Для всех векторов это справедливо! Но что особенно важно – это справедливо для всех векторных функций.
Если у нас есть две векторные функции
Удобство применения векторов прежде всего заключается в краткости и понятности записи формул.
Например, материальная точка, движется по произвольной кривой в трехмерном пространстве с осями координат X , Y , Z .
где векто р ∆r = r(t1) – r(t 0 ) – есть вектор перемещения.
Приведенная выше векторная формула для скорости материальной точки в трехмерном пространстве означает, что
Вместо определенного момента t 0 мы можем выбрать произвольный момент времени t . И рассматривать функцию r ( t ) – векторную функцию зависимости координат от времени для случая трехмерного пространства. В общем случае неважно сколько размерностей в рассматриваемом нами пространстве – хоть две, хоть двадцать две. Одномерный случай – это тоже просто частный случай нашей векторной формулы. Вот чем удобны вектора!
Тогда v(t) – векторная функция зависимости мгновенной скорости нашего тела от времени
Где и запись с точками и запись дробью с буквой d – это всего лишь формы записи второй производной по времени. Просто векторную функцию r(t) продифференцировали два раза. После первого дифференцирования нашли первую производную – это функция скорости. После второго дифференцирования нашли вторую производную, которая есть функция зависимости ускорения от времени.
В обратном порядке a ( t ), v ( t ), r ( t ) – каждая следующая есть «первообразная» предыдущей. Напомним, операция, обратная дифференцированию, называется операцией интегрирования (или нахождения первообразной функции). Скажем упрощенно, нахождению функции, которая была до операции по ее дифференцированию.
Теперь, когда мы начали понимать физический смысл некоторых векторных функций, продолжим рассматривать другие операции, которые возможно выполнять с векторами.
Пусть у нас есть два вектора. F – вектор силы, действующей на материальную точку (Напомним: «материальная точка» – тело, имеющее массу, размерами которого можно пренебречь в данной задаче). И S – вектор перемещения нашей материальной точки под действием силы F .
Мы знаем, что работа (та, которая сила, умноженная на перемещение вдоль силы, или, по-другому, перемещение, умноженное на силу вдоль перемещения, или просто сила, умноженная на перемещение в одномерном случае) в нашем трехмерном «векторном» случае будет равняться скалярному произведению вектора силы на вектор перемещения материальной точки под действием этой силы.
Мы с вами помним из школьного курса физики, что механическая работа в общем случае равна модулю вектора силы, умноженному на модуль вектора перемещения и умноженному на косинус угла между векторами силы и перемещения.
В случае, если вектора силы и перемещения заданы в виде троек компонентов векторов по соответствующим осям прямоугольной системы координат, гораздо проще, чем вычислять модули и косинус угла между векторами, прямо посчитать работу по формуле скалярного произведения векторов. Это просто сумма произведений соответствующих компонент.
В физическом смысле, мы просто складываем между собой три работы (по каждой из осей отдельно как бы своя работа). Это возможно (складывать компоненты работы по разным осям) только в случае, когда эти компоненты скаляры. Мы не будем вдаваться в подробное доказательство. Отошлем читателя за подробностями в интернет.
Просто запомним формулу (67) и смысл скалярного произведения векторов.
Очень важное замечание!
Здесь и в дальнейшем (и в предыдущем изложении) мы всегда рассматриваем «Правую» систему координат.
Если вправо направить ось X , вверх ось Y , то ось Z будет как бы входить в нас (идти в положительном направлении на нас, а не от нас). Это очень важно никогда не забывать. В противном случае в формулах будут ошибки. И особенно большая путаница будет при изучении электромагнетизма с его правыми и левыми руками.
Правая система координат! Берем правую руку. Раскрываем ладонь перед собой. Оттопыриваем большой палец – это положительное направление оси X . Четыре пальца перпендикулярных большому показывают положительное направление оси Y . Тогда из открытой ладони прямо на вас перпендикулярно осям X , Y будет выходить положительное направление оси Z .
Необходимо запомнить и никогда не путать!
Теперь возьмем нашу правую систему координат и зададим три единичных вектора, по одному вдоль каждой из осей.
Тогда любой вектор A = (А x , Ay , Az ) можно записать в виде суммы трех векторов
Легко заметить, что скалярные произведения наших единичных векторов
Эта удобная тройка векторов очень пригодится нам в дальнейшем.
Теперь напомним, любую ли тройку чисел можно считать вектором? Или по-другому, любую ли тройку функций ( f x ( t ), fy ( t ), fz ( t )) можно назвать векторной функцией f ( t ) ?
Нет, не любую! А только если модуль значения и пространственное направление не меняется при повороте и перемещении системы координат. (И при переходе из одной системы координат к другой тоже)
Это очень важно!
Вектора при переходе от одной системы координат к другой не меняются.
И результаты векторных операций при переходе от одной системы координат к другой так же не меняются!
Какие еще есть операции над векторами?
Существует еще операция, называемая «векторное произведение» векторов
«Ну и ну! Как это? Для чего?»
Все очень просто!
Для начала убедимся, что векторные произведения наших единичных векторов между собой:
Поиграв с единичными векторами, вы наверняка уже догадались, что векторное произведение двух векторов дает в результате вектор, перпендикулярный плоскости, в которой лежат вектора сомножители, а по модулю равный площади параллелограмма, ограниченного векторами сомножителями. Как на рисунке ниже, где вектора сомножители i и s расположили в плоскости X , Y и один из них расположили вдоль оси X .
Хотя, правильнее сказать, что систему координат расположили таким образом. А мы помним, результат не зависит от выбора системы координат.
Поэтому, всегда во всех задачах мы выбираем систему координат так, как нам удобно!
Итак, зачем нужна операция векторного произведения векторов, определенная выше? Рассмотрим задачу «о рычагах». Пусть у нас есть твердое тело, представляющее из себя систему из трех стержней, жестко скрепленных в одной точке. И эта точка закреплена в пространстве так, что она является центром вращения («точка закрепления шарнира»). Как на рисунке ниже.
Имеем три вектора r1 , r2 , r3 , выходящих из точки в которой мы расположим начало нашей системы координат – точки (0,0,0).
К концам стержней приложили силы F1 , F2 , F3 . Силы создают вектора моментов сил – «крутящие моменты», приложенные к нашему твердому телу.
Момент силы – это модуль вектора момента силы. Синонимы вектора момента силы: крутящий момент, вращательный момент, вертящий момент, вращающий момент).
Наглядно представить себе вектор момента силы можно следующим образом: Представьте себе юлу (детскую игрушку «волчок»). Чем сильнее мы его закрутим за ось, тем быстрее и дольше он вращается. Закрепим ось волчка на какой-то прямой так, чтобы она могла свободно вращаться. Представьте теперь, что вы будете тянуть за тело волчка, стараясь повернуть его вокруг закрепленной оси. А ваш товарищ будет пытаться удержать ось рукой. Представили?
Будет ли волчок поворачиваться вокруг оси? И если вы будете тянуть его в одну сторону, а ваш товарищ в другую, то в какую сторону будет поворачиваться волчок? В ту, чья сила больше? Не совсем. Представим ситуацию на картинке. Вы взялись ближе к оси, а ваш товарищ взялся за диск. Если ось достаточно тонкая, а диск достаточно большой, то как бы вы ни старались, волчок будет поворачиваться в сторону вашего товарища. Хотя силу вы приложите гораздо большую, чем он.
«Рычаг», скажете вы. И будете правы! Задача о рычагах по сути аналогична. И решается она очень просто с использованием операции векторного произведения, которую мы с вами рассмотрели выше.
Из формул (74) – (76) мы знаем, что векторное произведение двух векторов есть вектор, который по направлению перпендикулярен плоскости, в которой лежат вектора сомножители. Величину этого вектора по модулю можно вычислить с учетом формул (71) – (73), а модуль вычисляется по простой формуле:
Так вот, вектор момента силы, приложенной к телу, равен векторному произведению радиус-вектора точки приложения силы умноженному на вектор силы. Начало координат выбирается в точке закрепления тела на шарнире (например, в точке подвеса перекладины рычажных весов). То есть начало координат всегда берем в точке, относительно которой тело может поворачиваться.
Складывая вектора моментов всех приложенных к телу сил мы автоматически находим результирующий вектор, который и определяет в какую сторону и насколько интенсивно будет вращаться тело, показанное на рисунке 9 выше.
Просто складываем три вектора момента, от каждой из сил. Если сумма равна нулю, то наше твердое тело «стоит на месте». Если не равна нулю, то наше тело имеет ненулевой момент сил относительно «точки подвеса» в плоскости, перпендикулярной нашему вектору суммы моментов M . И с угловым ускорением, которое пропорционально модулю этого вектора.
Можно обобщить задачу на произвольное твердое тело с закрепленной в пространстве точкой подвеса и неограниченным количеством приложенных сил, как показано на рисунке.
Оно будет вращаться относительно оси, в которой лежит наш результирующий вектор момента сил. И вращение будет тем интенсивнее, чем больше этот результирующий вектор по модулю. Направление вращения будет зависеть от направления этого вектора. Направлен в одну сторону, вращается тело в одну сторону, направлен в другую, тело вращается в обратную.
Причем, если тело закрепить на оси, как в случае рассмотренного нами волчка, то задача становится двумерной. Вращение может быть только относительно оси и, соответственно, можно рассматривать моменты сил, только в системе координат, перпендикулярной оси. Это мы рассмотрим в дальнейшем.
Вопрос: каково условие невращения твердого тела в общем случае, показанном на рисунке 11? Другими словами, при каких условиях общий (суммарный) момент вращения тела равен нулю?
Ответ: Если сумма моментов всех сил равна нулю, то тело находится во «вращательном равновесии» – т.е. не имеет суммарного момента вращения.
Эта задача – более общая по отношению к школьной задаче о рычагах, изображенной на рисунке 24.
Благодаря определенной нами операции векторного произведения векторов задача решается в одно действие.
Ответ: Условие отсутствия вращающего момента тела
Так как согласно условиям рисунка 13:
Тогда с учетом формул (70) – (72) получаем:
Получаем условия равновесия наших рычажных весов:
Получаем знакомое из школьного учебника соотношение:
Можно решать сразу в векторной форме:
Можно ли сократить вектор ускорения свободного падения в уравнении (101) из обеих частей уравнения?
Потому, что для этого нужно обе части уравнения «разделить» на вектор g .
А операции векторного деления не существует!
Внимание! При оперировании векторами всегда нужно помнить, что мы можем применять к векторным уравнениям только существующие векторные операции!
Распишем покомпонентно наше векторное уравнение (101) в соответствии с формулами для векторного произведения (74) – (76). Заметим, что мы «правильно» расположили нашу систему координат таки образом, чтобы уравнения были проще. В результате этого в векторном уравнении (101) только составляющие векторов по оси Z не равны нулю. Таким образом остается только найти условие при котором:
Получили скалярное уравнение, которое можно сократить:
Заметим, что модули r 1 и r 2 – это, по сути, координаты точек подвеса грузов m1 и m2 относительно начала оси X , которое (точку x = 0 ) мы выбрали в точке крепления шарнира рычага. Для того, чтобы выполнялось условие равновесия (107), r 1 и r 2 должны быть разных знаков
Что же означает эта, теперь уже скалярная, формула равновесия рычага?
1. Координаты расположения точек подвеса грузов должны быть расположены по разные стороны от точки шарнира рычага.
2. Массы подвешенных грузов должны быть обратно пропорциональны расстояниям от точки подвеса поперечины до точек подвеса грузов. Или по-другому – длина рычагов должна быть обратно пропорциональна массам подвешенных грузов.
Большая теория по векторам
И ты наверняка обратил внимание, что некоторые величины имеют только значение (число) – например, путь ((L)).
А некоторые имеют и число, и направление — например, перемещение ((vec)).
И сейчас ты узнаешь, почему это настолько важно.
Векторы — коротко о главном
Решать задачи с векторами — легко!
Векторы и… Колумб
В 1492 году Колумб приказал кораблям изменить курс на запад-юго-запад, полагая, что он и его команда уже прошли мимо Японии, не заметив ее островов.
Вскоре его экспедиция наткнулась на множество архипелагов, которые ошибочно принимали за земли Восточной Азии. И теперь, спустя века, американцы в октябре отмечают высадку Колумба в Новом Свете.
Кто знает, как повернулась бы история, если бы его корабли не поменяли свое направление?
О направлении
Направление – одна из важнейших характеристик движения.
Подумай, какие из этих величин являются просто числами, а какие тоже являются числами, но имеют еще и направление.
Наверное, ты без труда заметил, что направление имеют сила, скорость, перемещение, а время, длина, масса и температура – это просто числа.
Так вот, «просто числа» — это скалярные величины (их также называют скалярами).
А «числа с направлением» — это векторные величины (их иногда называют векторы).
В физике существует множество скалярных и векторных величин.
Что такое скалярная величина?
Скалярная величина, в отличие от вектора, не имеет направления и определяется лишь значением (числом)
Это, например, время, длина, масса, температура (продолжи сам!)
Что такое векторная величина?
Векторная величина – это величина, которая определяется и значением, и направлением.
В случае с векторами нам важно, куда мы, например, тянем груз или в какую сторону движемся.
Например, как на этом рисунке изображен вектор силы (нам важно не только с какой силой, но и куда мы тянем груз):
Как обозначаются векторы?
Векторы принято обозначать специальным символом – стрелочкой над названием. Вот, например, вектор перемещения: (vec)
Значение вектора – это модуль вектора, то есть его длина.
Обозначить это можно двумя способами: (left| <vec> right|) или (S)
Операции над векторами
Для решения задач необходимо уметь работать с векторами: складывать, вычитать, умножать их.
Давай научимся это делать. Мы пойдем от простого к сложному, но это вовсе не значит, что будет трудно!
Умножение вектора на число
Если вектор умножить на какое-либо число (скаляр), мы просто «растягиваем» вектор, сохраняя его направление. Получившийся вектор сонаправлен начальному, то есть они имеют одинаковое направление.
(Если направление противоположно, обозначаем так: (vecuparrow downarrow vec))
Рассмотрим на примере, используя клетку для точности построений:
Если вектор умножить на ноль, он станет нулевым.
Обязательно нужно ставить значок вектора над нулем! Нельзя говорить, что векторная величина просто равна скалярной:
Рассмотрим некоторые свойства нулевого вектора.
Если он нулевой, то его длина равна нулю! Логично, не правда ли?
А это значит, что его начало совпадает с концом, это просто какая-то точка.
Нулевой вектор – вектор, начало которого совпадает с концом.
Нулевой вектор принято считать сонаправленным любому вектору.
Его мы можем получить не только путем умножения вектора на ноль, но и путем сложения противонаправленных векторов:
А если к любому вектору прибавит нулевой, ничего не изменится:
Если вектор умножают на отрицательное число, он изменит свое направление на противоположное. Такой вектор называется обратным данному.
Но такие векторы должны быть коллинеарны. Звучит как скороговорка, но ничего страшного. Главное – понять суть.
Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых.
Две прямые параллельны: (qparallel p)
Векторы лежат на одной прямой: они коллинеарны. По направлению видно, что они противонаправлены, это обозначается так:
Векторы лежат на параллельных прямых, они коллинеарны. При этом они сонаправлены:
Эти двое тоже коллинеарны! Они ведь лежат на параллельных прямых. При этом они противонаправлены:
(vecuparrow downarrow vec)
Коллинеарные векторы, имеющие одинаковую длину и противоположные направления, называются обратными друг другу.
Параллельный перенос векторов
Одно из важных свойств вектора, которое очень часто помогает в операциях над ним, – параллельный перенос.
Если передвинуть вектор, не меняя его направления и длины, он будет идентичен начальному. Это свойство – параллельный перенос.
Сложение векторов по правилу треугольника
Сложение векторов – одна из самых легких и приятных вещей. Предположим, у нас есть два вектора:
Наша цель – найти такой вектор, который будет являться суммой двух данных:
Для начала нужно сделать так, чтобы конец одного вектора был началом другого. Для этого воспользуемся параллельным переносом:
Теперь достроим до треугольника.
Но как узнать направление нужного нам вектора?
Все просто: вектор суммы идет от начала первого слагаемого к концу второго, мы словно «идём» по векторам:
Это называется правилом треугольника.
Больше двух слагаемых векторов. Сложение по правилу многоугольника
Но что делать, нам нужно сложить не два, а три, пять векторов или даже больше?
Мы руководствуемся той же логикой: соединяем векторы и «идём» по ним:
Это называется правилом многоугольника.
Вычитание векторов через сложение
Вычитание векторов не сложнее. Это даже можно сделать через сумму! Для этого нам понадобится понятие обратного вектора. Запишем разность так:
Тогда нам лишь остается найти сумму с обратным вектором:
А сделать это очень легко по правилу треугольника:
Всегда помни, что вычитание можно представлять сложением, а деление — умножением на дробь.
Вычитание векторов через треугольник
Вычитать векторы можно через треугольник. Основная задача будет состоять в том, чтобы определить направление вектора разности.
Итак, векторы должны выходить из одной точки. Далее мы достраиваем рисунок до треугольника и определяем положение. Рассмотрим два случая:
Направление вектора разности зависит от того, из какого вектора мы вычитаем. У них совпадают концы.
Универсальное правило параллелограмма
Есть еще один способ сложения и вычитания векторов.
Способ параллелограмма наиболее востребован в физике и сейчас ты поймешь, почему. Основа в том, чтобы векторы выходили из одной точки, имели одинаковое начало.
Ничего не напоминает?
Именно! Когда мы делаем чертеж к задачам по физике, все силы, приложенные к телу, мы рисуем из одной точки.
В чем же заключается правило параллелограмма? С помощью параллельного переноса достроим до параллелограмма:
Тогда вектор суммы будет диагональю этой фигуры. Это легко проверяется правилом треугольника. Начало этого вектора совпадает с началом двух слагаемых векторов:
Другая диагональ будет являться разностью этих векторов. Направление определяем так же, как делали раньше.
Скалярное произведение векторов
Еще одной важной операцией является произведение векторов. Рассмотрим скалярное произведение. Его результатом является скаляр.
Уравнение очень простое: произведение длин этих векторов на косинус угла между ними.
Векторное произведение векторов
Векторное произведение векторов пригодится нам в электродинамике.
Его формула лишь немного отличается от предыдущей:
В отличие от скалярного произведения, результатом его является вектор и его даже можно изобразить!
После параллельного переноса векторов и нахождения угла между ними достроим их до параллелограмма и найдем его площадь. Площадь параллелограмма равна длине вектора произведения:
Этот вектор одновременно перпендикулярен двум другим. Его направление зависит от условного порядка векторов, который либо определен какими-то фактами (когда мы будем изучать силу Лоренца), либо является свободным.
Об этом мы поговорим подробнее, когда будем изучать электродинамику.
Итак, мы разобрали операции с векторами, рассмотрев даже самые сложные из них. Это было не так тяжело, верно? Так происходит не только с векторами, но и со многими другими темами. Идя от легкого к сложному, мы даже не заметили трудностей.
Ведь всегда стоит помнить о том, что даже самое длинное путешествие начинается с первого шага.
Проекции векторов
Что такое проекция вектора и с чем ее едят?
Мы уже выяснили, что над векторами можно проводить множество операций. Здорово, когда можешь начертить векторы, достроить их до треугольника и измерить результат линейкой.
Но зачастую физика не дает нам легких цифр. Наша задача – не отчаиваться и быть умнее, упрощая себе задачи.
Для того, чтобы работать с векторами как с числами и не переживать об их положении и о точности рисунков, были придуманы проекции.
Проекция вектора – словно тень, которую он отбрасывает на ось координат. И эта тень может о многом рассказать.
Ось координат — прямая с указанными на ней направлением, началом отсчёта и выбранной единицей масштаба.
Ось можно выбрать произвольно. В зависимости от ее выбора можно либо значительно упростить решение задачи, либо сделать его очень сложным.
Именно поэтому необходимо научиться работать с проекциями и осями.
Построение проекции. Определение знака
Возьмем вектор и начертим рядом с ним произвольную ось. Назвать ее тоже можно как угодно, но мы назовем ее осью Х.
Теперь опустим из начала и конца вектора перпендикуляры на эту ось. Отметим координаты начала (Х0) и конца (Х). Рассмотрим отрезок, заключенный между этими точками.
Казалось бы, мы нашли проекцию. Однако думать, что проекция является простым отрезком, – большое заблуждение.
Не все так просто: проекция может быть не только положительной. Чтобы найти проекцию, нужно из координаты конца вычесть координату начала:
Проекция вектора на ось — разность между координатами проекций точек конца и начала вектора на ось.
В случае выше определить знак довольно легко. Сразу видим, что координата конца численно больше координаты начала и делаем вывод о том, что проекция положительна:
Порой работать с буквами трудно. Поэтому предлагаю взять конкретный пример:
Рассмотрим другой случай. В этот раз координата начала больше координаты конца, следовательно, проекция отрицательна:
Рассмотрим еще один интересный случай.
Давай разместим ось так, чтобы вектор был ей перпендикулярен. Проекции точек начала и конца совпадут и проекция вектора будет равна нулю!
Анализ углов
Рассматривая эти ситуации, можно заметить, что знак, который принимает проекция вектора напрямую зависит от угла между вектором и осью, то есть от его направления!
Из начала вектора проведем луч, параллельный оси и направленный в ту же сторону, что и ось. Получим угол между вектором и осью.
Если угол острый, проекция положительна:
Если угол тупой, проекция отрицательна:
Обрати особое внимание на то, какой именно угол является углом между вектором и осью!
Частные случаи проекции
Настоящий подарок судьбы – тот момент, когда вектор параллелен оси. Это сохраняет драгоценное время при решении множества задач. Рассмотрим эти случаи.
Если вектор параллелен оси, угол между ними либо равен нулю, либо является развернутым (180 О ). Это зависит от направления.
При этом длина проекции совпадает с длиной вектора! Смотри!
Как и прежде, если вектор направлен туда же, куда и ось, проекция положительна:
Если вектор направлен в другую сторону, проекция отрицательна:
Если вектор направлен туда же, куда и ось, его проекция положительна. Если вектор направлен в другую сторону, его проекция отрицательна.
Эти утверждения применимы не только к векторам, которые параллельны оси. Это особенно удобно использовать в тех случаях, когда ось направлена под углом.
Что? Почему раньше не сказал? А… Ну…
Хватит вопросов! Вот тебе пример:
(vec) направлен противоположно оси. Его проекция отрицательна.
Еще один частный случай – работа с обратными векторами.
Давай выясним, как связаны проекции данного вектора и вектора, который является ему обратным. Начертим их и обозначим координаты начал и концов:
Проведем дополнительные линии и рассмотрим два получившихся треугольника. Они прямоугольны, так как проекция строится с помощью перпендикуляра к оси.
Наши векторы отличаются лишь направлением. При этом, если мы просто посмотрим на них как на прямые, мы можем сказать, что они параллельны. Их длины тоже одинаковы.
Прямоугольные треугольники равны по углу и гипотенузе. Это значит, что численно равны и их катеты, в том числе те, которые равны проекциям:
Мы помним, что обратные векторы всегда коллинеарны. Это значит, что прямые, на которых они расположены, находятся под одним углом к оси:
Остается лишь определиться со знаками. Данный вектор направлен по оси Х, а обратный ему – против. Значит, первый положителен, а второй отрицателен. Но модули их равны, так как равны их длины.
Проекции обратных векторов равны по модулю и противоположны по знаку.
Давайте еще раз уточним.
Вектор сам по себе не может быть отрицательным (обратный вектор есть вектор, умноженный на минус единицу).
Длина вектора так же не может быть отрицательной. Длина есть модуль вектора, а модуль всегда положителен.
Проекция вектора бывает отрицательной. Это зависит от направления вектора.
Способы нахождения проекций и векторов с помощью тригонометрии
Зная угол между вектором и осью, можно не прибегать к координатам. Углы, прямоугольные треугольники… Всегда стоит помнить, что, если ты видишь прямоугольный трегольник, тригонометрия протянет тебе руку помощи.
Именно тригонометрия чаще всего применяется в задачах, где требуется работать с проекциями. Особенно она помогает в задачах на второй закон Ньютона.
Рассмотрим вектор и его проекции на оси:
Можем заметить, что проекции вектора соответствуют катетам прямоугольного треугольника, который легко можно достроить:
Тогда обозначим прямой угол и угол между вектором и осью:
Зная, что проекции соответствуют катетам, мы можем записать, чему равны синус и косинус угла. Они равны отношению проекций к гипотенузе. За гипотенузу считаем длину данного вектора.
Из этих уравнений легко выражаются проекции.
А еще следует помнить, что из проекций мы можем найти длину данного вектора с помощью теоремы Пифагора:
Зная, как работать с проекциями векторов и часто практикуясь, можно довести свои навыки решения большинства задач механики до совершенства.
Действия над проекциями векторов. Решение задач
Умение применять свои знания на практике невероятно важны. Это касается не только физики.
Мы знаем, что проекции были придуманы для того, чтобы работать не с векторами, а с числами.
Сложение проекций. Доказательство главного свойства
Предположим, у нас есть два вектора и нам нужно найти их сумму. Посчитать по клеткам нам вряд ли удастся:
Спроецируем оба вектора на ось Х. Заметим, что конец одного вектора есть начало второго, то есть их координаты совпадают:
Давай посчитаем проекции векторов и проекцию вектора их суммы:
Мы можем заметить, что сумма проекций двух данных векторов оказалась равна проекции вектора их суммы!
Намного важнее уметь доказывать гипотезы в общем виде.
Тогда никто не сможет упрекнуть тебя в том, что твои утверждения – просто результат совпадения!
Согласно определению проекции, запишем уравнения проекций для двух данных векторов и вектора их суммы:
Затем запишем, чему равна сумма этих векторов.
Мы доказали нашу гипотезу.
Но что насчет разности?
Все очень просто! Помнишь, как мы считали разность через сумму? Здесь это делается аналогично!
Проекция суммы векторов равна сумме проекций векторов.
Проекция разности векторов равна разности проекций векторов.
Или можно записать так:
Простейшие задачи на нахождение проекций
Простейшие задачи на нахождение проекций чаще представлены в виде различных графиков или рисунков.
Давай научимся с ними работать.
Нам даны оси и векторы. Задача: найти проекции каждого из них на обе оси.
Будем делать все по порядку. Для каждого вектора предлагаю сначала определить знак проекций, а затем посчитать их.
В первом случае вектор направлен против оси Х.
Значит, его проекция на эту ось будет отрицательна. Мы убедимся в этом с помощью вычислений.
Сразу бросается в глаза то, что вектор расположен перпендикулярно оси Y. Его проекция на эту ось будет равна нулю, ведь расстояние между проекциями точек начала и конца равно нулю!
Рассмотрим второй вектор.
Он «сонаправлен» оси Y и «противонаправлен» оси Х. Значит, проекция на ось будет положительна, а на ось Х – отрицательна.
Убедимся в этом.
На осях для удобства отметим проекции точек начала и конца вектора, проведя перпендикуляры. Затем проведем вычисления:
Рассмотрим (vec). Заметим, что он является обратным для (vec): их длины равны, а направления противоположны.
Мы помним, что в таком случае их проекции отличаются лишь знаками. И это действительно так:
Поступаем с (vec) так же, как поступали с первым вектором.
Он перпендикулярен оси Х, а значит его проекция (что есть разность между проекциями точки конца и начала!) на эту ось равна нулю.
Проведя перпендикуляры, считаем проекцию на ось Y:
С (vec) работать приятно: он расположен по направлению обеих осей. Обе его проекции будут положительны, остается лишь посчитать их:
Задачи на нахождение вектора и его угла с осью
С помощью проекций можно найти длину вектора и его направление, а также угол, под которым он находится относительно оси.
Давай попробуем это сделать.
Даны проекции вектора на две оси. Для начала нарисуем оси:
Расположить вектор можно как угодно, поэтому произвольно отметим на осях его проекции. Мы помним, что проекции и вектор образуют прямоугольный треугольник. Давай попробуем его составить.
С проекцией на ось Х все понятно, просто поднимаем ее. Но куда поставить проекцию оси Y?
Для этого нам нужно определить направление вектора. Проекция на ось Х отрицательна, значит вектор направлен в другую сторону от оси.
Проекция на ось Y положительна. Вектор смотрит в ту же сторону, что и ось.
Исходя из этого, мы можем нарисовать вектор и получить прямоугольный треугольник:
Теперь нужно найти длину этого вектора. Используем старую добрую теорему Пифагора:
Обозначим угол (alpha ), который необходимо найти, мы учились это делать в начале изучения проекций. Он расположен вне треугольника. Мы ведь не ищем легких путей, верно?
Рассмотрим смежный ему угол (beta ). Его найти гораздо проще, а в сумме они дадут 180 градусов.
Чтобы сделать это, абстрагируемся от векторов, проекций и просто поработаем с треугольником, стороны которого равны 3, 4 и 5. Найдем синус угла (beta ) и по таблице Брадиса (либо с помощью инженерного калькулятора) определим его значение.
Вычитанием угла (beta ) из 180 градусов найдем угол (alpha ):
Главный метод работы с осями и проекциями в решении физических задач
В большинстве задач по физике, когда в условиях нам дают значения векторных величин, например, скорости, нам дают длину вектора.
Поэтому важно научиться искать проекции вектора и связывать их с ней.
Рассмотрим следующий рисунок (вектор F2 перпендикулярен вектору F3):
Чаще всего с подобным расположением векторов мы встречаемся в задачах, где необходимо обозначить все силы, действующие на тело.
Одним из важных этапов решение «векторной части» этих задач является правильный выбор расположения осей. Он заключается в том, чтобы расположить оси так, чтобы как можно большее число векторов оказались им параллельны.
Как правило, оси располагаются под прямым углом друг к другу, чтобы не получить лишней работы с углами.
Сделаем это для данного рисунка:
Мы видим, что остальные векторы расположены к осям под каким-то углом.
Пунктиром проведем горизонтальную линию и отметим этот угол, а затем отметим другие равные ему углы:
Пришло время искать проекции. У нас две оси, поэтому сделаем для удобства табличку:
Мы располагали оси так, чтобы некоторые векторы были расположены параллельно осям, значит их проекции будут равняться их длинам.
Оси перпендикулярны друг другу, поэтому некоторые проекции будут равняться нулю. Запишем это:
Переходим к векторам, которые расположены под углом.
Выглядит страшно, но это не так!
Дальше идет чистая геометрия. Чтобы не запутаться, рассмотрим лишь часть рисунка. А лучше и вовсе перерисовать его часть, могут открыться много новых вещей.
Из конца вектора F1 проведем перпендикуляр к оси Y. Мы получим прямоугольный треугольник, где нам известен угол (альфа) и гипотенуза (вектор).
Обозначим, что является проекцией. Это катет:
Здесь на помощь придет тригонометрия. Этот катет прилежащий к известному углу. Синус угла есть проекция катета, деленная на гипотенузу. Отсюда можно выразить катет (проекцию) и записать ее в таблицу.
Вспомни, когда мы первый раз встретились с тригонометрией, изучая векторы. Мы тоже рассматривали прямоугольный треугольник.
Найдем проекцию на ось Х. Это, кажется, сложнее, ведь мы не знаем угол…
Знаем! Ведь проекция вектора на ось Х – то же самое, что противолежащий катет уже рассмотренного треугольника, смотри:
Значит, проекцию на ось Х можно найти через косинус.
Не забываем смотреть на направления векторов!
Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.
Значит, проекцию на ось Х можно найти через косинус.
Не забываем смотреть на направления векторов!
Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.
Заключение
Итак, теперь мы знаем о векторах очень много! Мы выяснили, зачем они нужны и как с ними работать, а еще разобрали их роль в решении различных задач. Теперь векторы — наша прочная опора.
Именно из таких знаний складывается порой нечто более сложное и комплексное, что-то, что безусловно нам однажды поможет.
[spoiler title=”источники:”]
http://www.sites.google.com/site/fizikaetoprosto2016/13-operacii-nad-vektorami
[/spoiler]
План урока:
Угол между векторами
Понятие скалярного произведения векторов
Скалярное произведение в координатах
Определение перпендикулярности векторов и прямых
Вычисление угла между векторами
Свойства скалярного произведения
Угол между векторами
Любую пару векторов можно отложить от одной точки. Если при этом вектора не сонаправлены друг с другом, то они образуют некоторый угол. Его и именуют углом между векторами.
Если же пара векторов сонаправлена, то принято считать, что угол между такими векторами составляет 0°.
На рисунке показаны два вектора, a и b. Чтобы определить угол между a и b, надо отложить их от одной и той же точки:
В приведенном примере угол составил 135°. Для обозначения этого угла может быть использована такая запись:
Задание. В квадрате АВСD проведены диагонали, они пересекаются в точке О. Определите, какой угол образуют вектора:
Так как в квадрате диагонали пересекаются под углом 90°, а со сторонами образуют угол 45°, то мы легко определим, что
Здесь нам помог тот факт, что вектора из пунктов а) и б) изначально отложены из одной точки. С пунктом в) ситуация сложнее. Надо отложить от точки А вектор ОА и определить угол, образующийся при этом:
Пусть после откладывания вектора ОА от А получился вектора АА’. Нам надо найти ∠ВАА’. Нам уже известен ∠ОАВ, который является смежным с ∠ВАА’, поэтому можно записать равенство:
Ответ: а) 45°; б) 90°; в) 135°.
Понятие скалярного произведения векторов
Большое распространение в науке получила математическая операция, именуемая скалярным произведением векторов. В геометрии оно помогает находить угол между векторами, а в физике вычислять некоторые физические величины. В рамках школьной программы его используют для нахождения работы, совершенной той или иной силой. В рамках же более сложных дисциплин, с которыми мало кто сталкивается, оно применяется в квантовой механике и специальных разделах математики – тензорной алгебре, теории многообразий и т. п. Ввел его в науку Уильям Гамильтон в 1846 г, который разрабатывал теорию особых чисел – кватерионов. Они, кстати, используются компьютерами для расчетов трехмерной графики в играх и других приложениях.
Прежде, чем мы научимся применять на практике скалярное произведение, сначала сформулируем правило, позволяющее вычислить его.
Например, пусть есть вектора a и b, причем даны их длины:
Угол между a и b тоже известен и составляет 60°, это записывается таким образом:
Задание. Вычислите скалярное произведение векторов d и f, если их длины составляют 6 и 10 соответственно, а угол между векторами равен 45°.
Решение. Просто подставляем числа из условия в формулу:
Задание. АВС – равносторонний треугольник со стороной 4. Каково скалярное произведение векторов АВ и АС?
Решение. Все углы в равностороннем треугольнике равны 60°, поэтому и угол между АВ и АС также составляет 60°.
Ответ: 8.
Напомним, что косинус, взятый от острого угла – это положительная величина, а косинус тупого угла – это отрицательное число. У прямого же угла косинус равен нулю. Это означает, что по знаку скалярного произведения можно определить тип угла между векторами.
Часто скалярное произведение применяется в физике. Например, с его помощью рассчитывается работа, совершаемая силой при перемещении того или иного тела. И сила, и перемещение – это векторные величины. Чтобы найти работу силы, надо скалярно перемножить вектора силы и перемещения:
Эта формула отражает физический смысл скалярного произведения.
Задание. Под воздействием силы 10Н тело переместилось в горизонтальном направлении на 3 метра. При этом сила образует угол 60° с направлением перемещения тела. Какую работу совершила сила?
Решение.
Скалярное произведение в координатах
Оказывается, что для перемножения векторов достаточно знать только их координаты.
Докажем эту формулу. Сначала рассмотрим случай, когда один из перемножаемых векторов, например a, является нулевым. Тогда у него нулевая длина и нулевые координаты:
Теперь рассмотрим случай, когда оба перемножаемых вектора ненулевые. Тогда отложим их от некоторой точки О и, если вектора неколлинеарны, то мы получим ∆ОАВ:
Для частных случаев, когда a и b коллинеарны (то есть либо сонаправлены, либо противоположно направлены), эта формула также справедлива. Если aи b сонаправлены, то угол α принимается равным нулю (и cosα = 1):
Если же a и b направлены противоположно, то α = 180° (и cosα = – 1):
Итак, мы убедились, что в любой ситуации формула (1) справедлива. При этом вектор АВ можно представить как разность a и b:
Если вектор а имеет координаты {x1; у1}, а координаты b– это {x2; у2},то координаты их разности a – b будут записываться в виде {х1 – х2;у1 – у2}. С учетом этого (2) примет вид
В результате нам удалось доказать формулу скалярного произведения через координаты:
Задание. Перемножьте скалярно вектораa и b, если определены их координаты:
Ответ: а) 23; б) 0; в) 5.
Определение перпендикулярности векторов и прямых
Напомним, что скалярное произведение оказывается нулевым исключительно в случае перпендикулярности векторов. Это позволяет использовать его для проверки перпендикулярности векторов.
Задание. Проверьте, являются ли перпендикулярными вектора:
Решение. В каждом случае мы должны скалярно перемножить пару векторов. Если результат окажется нулевым, то можно сделать вывод о перпендикулярности векторов. В противном случае они не перпендикулярны. Первый вектор будет обозначать буквой а, а второй – буквой b:
Ответ: а) да; б) нет; в) да; г) нет.
Задание. При каком значении переменной х вектора а{4; 5} и b{x; – 6} окажутся перпендикулярными?
Решение. Перемножим скалярно вектора и получим некоторое выражение с переменной x:
Найдем, при каком х это выражение обращается в нуль, то есть вектора становятся перпендикулярными:
Задание. Определите, перпендикулярны ли прямые АВ и CD, если даны координаты точек: А(3; 8), В(4; 10), С(7;12) и D(5;13).
Решение. В этой задаче сначала надорассчитать координаты векторов АВ и CD по координатамих начальной и конечной точки:
Мы вычислили координаты векторов: АВ{1; 2} и CD{– 2; 1}. Теперь мы можем проверить их перпендикулярность, скалярно перемножив вектора:
Мы получили ноль. Это означает, что АВ и CD – перпендикулярные вектора. Значит, и прямые, на которых они лежат, также перпендикулярны.
Ответ: перпендикулярны.
Задание. Перпендикулярны ли друг другу прямые, задаваемые уравнениями
Названия точкам в данном примере присвоены произвольно. На следующем шаге по координатам точек мы находим координаты векторов, лежащих на исследуемых прямых:
Полученный ноль показывает, что исходные прямые перпендикулярны.
Ответ: перпендикулярны.
В случае, когда прямые заданы уравнениями, необязательно проделывать столь длительные вычисления для определения их перпендикулярности. Есть теорема, сокращающая объем вычислений.
Докажем это утверждение. Пусть две прямые заданы уравнениями
Найдем какие-нибудь точки этих прямых. Для этого подставим в уравнения значения х = 0 и х = 1:
Прямые окажутся перпендикулярными исключительно в том случае, если это выражение будет нулевым. Это условие перпендикулярности можно записать как уравнение:
В результате мы получили доказываемую нами формулу.
Задание. Проверьте, какие из этих пар прямых перпендикулярны:
Решение. В каждом случае надо просто перемножить угловые коэффициенты прямых, то есть числа, стоящие перед переменной х. Другие числа в этих уравнениях (свободные коэффициенты) никак не влияют на перпендикулярность. Если вычисленное произведение окажется равным (– 1), то из этого будет вытекать перпендикулярность прямых.
Вычисление угла между векторами
Мы научились по координатам векторов определять, перпендикулярны ли они. Однако в более общем случае можно рассчитать угол и между двумя неперпендикулярными векторами.
В самом деле, по известным координатам векторов легко как рассчитать длину каждого из них, так и скалярно перемножить вектора. Тогда из формулы скалярного произведения можно выразить значение косинуса угла между векторами:
Зная же косинус, можно рассчитать и сам угол, используя специальные таблицы либо функцию арккосинуса на калькуляторе.
Задание. Вычислите угол между векторами а{3; 4} и b{8; 15}.
Решение. Сначала рассчитываем длины векторов:
Задание. Точки А(2; 8), В(– 1; 5) и С(3; 1) соединили отрезками и получили ∆АВС. Вычислите угол ∠А в ∆АВС.
Решение.∠А данного треугольника представляет собой угол между двумя векторами АВ и АС. Вычислим координаты этих векторов:
Осталось лишь с помощью калькулятора найти сам ∠А:
Свойства скалярного произведения
Существует несколько важных свойств скалярного произведения. Эти свойства очень схожи с законами алгебры, которые используются при работе с обычными числами.
Переместительный закон легко доказать, опираясь только на определение операции скалярного произведения:
Задание. Известно, что угол между векторами a и с составлет 60°, так же как и угол между векторами b и с. Определены и длины векторов:
Задание. Найдите скалярное произведение векторов p и q, если
Решение. Сначала надо перемножить вектора и раскрыть при этом скобки также, как они раскрываются при перемножении обычных чисел:
Примечание. Иногда скалярное произведение вектора на самого себя именуют скалярным квадратом.
Тогда выражение (1) примет вид:
В сегодняшнем уроке мы узнали, что такое скалярное произведение. Оно имеет много приложений в физике и других науках, в частности, с его помощью вычисляется работа. В геометрии оно помогает вычислять углы между векторами, а значит, и между прямыми. В будущем, при более углубленном изучении геометрии, вы узнаете о существовании других типов произведений векторов – векторном и смешанном.
Содержание:
- Формула
- Примеры вычисления векторного произведения векторов
Формула
Для того чтобы найти векторное произведение
$[bar{a}, bar{b}]$ двух векторов, заданных своими координатами
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и
$bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$ соответственно, необходимо
вычислить следующий определитель
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$
Обычно такой определитель вычисляют разложением по первой строке. Отметим также, что результатом векторного произведения является вектор.
Примеры вычисления векторного произведения векторов
Пример
Задание. Найти векторное произведение векторов
$bar{a}=(1 ; 0 ; 0)$ и $bar{b}=(0 ; 1 ; 0)$
Решение. Для вычисления векторного произведения заданных векторов воспользуемся формулой
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$
Подставляя координаты заданных векторов, получим:
$$[bar{a}, bar{b}]=left|begin{array}{lll}bar{i} & bar{j} & bar{k} \ 1 & 0 & 0 \ 0 & 1 & 0end{array}right|$$
Раскладываем определитель по первой строке:
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ 1 & 0 & 0 \ 0 & 1 & 0end{array}right|=$$
$$=bar{i} cdotleft|begin{array}{cc}0 & 0 \ 1 & 0end{array}right|-bar{j} cdotleft|begin{array}{cc}1 & 0 \ 0 & 0end{array}right|+bar{k} cdotleft|begin{array}{cc}1 & 0 \ 0 & 1end{array}right|=$$
$$=0 cdot bar{i}-0 cdot bar{j}+1 cdot k$$
Первые два определителя равны нулю, так как они содержат нулевой столбец, а третий определитель вычисляем
как определитель второго порядка: от произведения элементов главной диагонали отнимаем произведение элементов побочной.
Итак, координаты искомого вектора равны коэффициентам при ортах, то есть
$$[bar{a}, bar{b}]=(0 ; 0 ; 1)$$
Ответ. $[bar{a}, bar{b}]=(0 ; 0 ; 1)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Даны векторы
$bar{a}=(5 ; 3 ;-4)$ и $bar{b}=(6 ; 7 ;-8)$ . Найти координаты векторного произведения
$[bar{a}, bar{b}]$
Решение. Координаты векторного произведения
$[bar{a}, bar{b}]$ вычисляются по формуле
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$
Подставляя координаты заданных векторов, получим:
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ 5 & 3 & -4 \ 6 & 7 & -8end{array}right|$$
Раскладываем полученный определитель по первой строке:
$$=bar{i} cdotleft|begin{array}{cc}3 & -4 \ 7 & -8end{array}right|-bar{j} cdotleft|begin{array}{cc}5 & -4 \ 6 & -8end{array}right|+bar{k} cdotleft|begin{array}{cc}5 & 3 \ 6 & 7end{array}right|=$$
$$=[3 cdot(-8)-7 cdot(-4)] cdot bar{i}-[5 cdot(-8)-6 cdot(-4)] cdot bar{j}+$$
$$+[5 cdot 7-6 cdot 3] cdot bar{k}=(-24+28) bar{i}-(-40+24) bar{j}+(35-18) bar{k}=$$
$$=4 cdot bar{i}+16 cdot bar{j}+17 cdot bar{k}$$
Тогда
$$[bar{a}, bar{b}]=(4 ; 16 ; 17)$$
Ответ. $[bar{a}, bar{b}]=(4 ; 16 ; 17)$
Читать дальше: как найти смешанное произведение векторов.