Как найти произведение всех простых чисел

Improve Article

Save Article

Like Article

Read

Discuss

Given a number n, we need to find the product of all prime numbers between 1 to n.
Examples: 
 

Input: 5
Output: 30
Explanation: product of prime numbers between 1 to 5 is 2 * 3 * 5 = 30 

Input : 7
Output : 210

Approach:  Basic brute-force method 

Steps:

• Initialize the product to be 1 and an empty list of primes.
• Iterate through all numbers i between 2 and n (inclusive).
• For each i, check if it is prime by iterating through all numbers j between 2 and i-1 (inclusive) and checking if i is divisible by j. If i is not divisible by any j, it is prime, so append i to the list of primes and multiply it with the running product.
• Return the product of all primes.

The time complexity of this approach is O(n^2).

The auxiliary space is O(n).

Efficient Approach:

Using Sieve of Eratosthenes to find all prime numbers from 1 to n then compute the product.
 

Following is the algorithm to find all the prime numbers less than or equal to a given integer n by Eratosthenes’ method: 
When the algorithm terminates, all the numbers in the list that are not marked are prime and using a loop we compute the product of prime numbers. 
 

Time Complexity: O(n log log n) // for sieve of erastosthenes

Auxiliary Space: O(N) //an extra array is used to store all the prime numbers hence algorithm takes up linear space

Last Updated :
25 Apr, 2023

Like Article

Save Article

Факториал — Википедия. Что такое Факториал

Факториа́л — функция, определённая на множестве неотрицательных целых чисел. Название происходит от лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л. Факториал натурального числа n определяется как произведение всех натуральных чисел от 1 до n включительно:

n!=1⋅2⋅…⋅n=∏k=1nk{displaystyle n!=1cdot 2cdot ldots cdot n=prod _{k=1}^{n}k}.

Например,

5!=1⋅2⋅3⋅4⋅5=120{displaystyle 5!=1cdot 2cdot 3cdot 4cdot 5=120}.

Из определения факториала следует соотношение (n−1)!=n!n{displaystyle (n-1)!={frac {n!}{n}}}, откуда при n=1{displaystyle n=1} формально находим

0!=1{displaystyle 0!=1}.

Последнее равенство обычно принимают в качестве соглашения, хотя, как показано выше, оно следует из определения факториала для натуральных чисел при условии, что все значения функции связаны единым рекуррентным соотношением.

Факториалы всех чисел составляют последовательность A000142 в OEIS; значения в научной нотации округляются

n	n!
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800
11	39916800
12	479001600
13	6227020800
14	87178291200
15	1307674368000
16	20922789888000
17	355687428096000
18	6402373705728000
19	121645100408832000
20	2432902008176640000
25	≈1,551121004 × 1025
50	≈3,041409320 × 1064
70	≈1,197857167 × 10100
100	≈9,332621544 × 10157
450	≈1,733368733 × 101000
1000	≈4,023872601 × 102567
3249	≈6,412337688 × 1010000
10000	≈2,846259681 × 1035659
25206	≈1,205703438 × 10100000
100000	≈2,824229408 × 10456573
205023	≈2,503898932 × 101000004
1000000	≈8,263931688 × 105565708
10100	≈109,956570552 × 10101
101000	≈10101003
1010 000	≈101010 004
10100 000	≈1010100 005
1010100	≈101010100

Факториал активно используется в различных разделах математики: комбинаторике, математическом анализе, теории чисел, функциональном анализе и др.

Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем любая показательная функция или любая степенная функция, а также быстрее, чем любая сумма произведений этих функций. Однако, степенно-показательная функция nn{displaystyle n^{n}} растёт быстрее факториала, так же как и большинство двойных степенных, например een{displaystyle e^{e^{n}}}.

Свойства

Рекуррентная формула

n!={1n=0,n⋅(n−1)!n>0.{displaystyle n!={begin{cases}1&n=0,\ncdot (n-1)!&n>0.end{cases}}}

Комбинаторная интерпретация

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала подтверждает целесообразность соглашения 0!=1{displaystyle 0!=1}. Так, формула для числа размещений из n{displaystyle n} элементов по m{displaystyle m}

Anm=n!(n−m)!{displaystyle A_{n}^{m}={frac {n!}{(n-m)!}}}

при n=m{displaystyle n=m} обращается в формулу для числа перестановок из n{displaystyle n} элементов (порядка n{displaystyle n}), которое равно n!{displaystyle n!}.

Связь с гамма-функцией

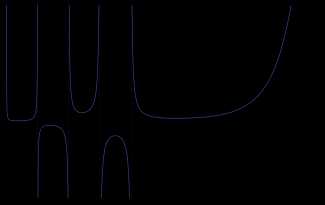Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением

n!=Γ(n+1){displaystyle n!=Gamma (n+1)}.

Это же выражение используют для обобщения понятия факториала на множество вещественных чисел. Используя аналитическое продолжение гамма-функции, область определения факториала также расширяют на всю комплексную плоскость, исключая особые точки при n=−1,−2,−3…{displaystyle n=-1,-2,-3ldots }.

Непосредственным обобщением факториала на множества вещественных и комплексных чисел служит пи-функция Π(z)=Γ(z+1){displaystyle Pi (z)=Gamma (z+1)}, которая при Re(z)>−1{displaystyle mathrm {Re} (z)>-1} может быть определена как

Π(z)=∫0∞tze−tdt{displaystyle Pi (z)=int _{0}^{infty }t^{z}e^{-t},mathrm {d} t} (интегральное определение).

Пи-функция натурального числа или нуля совпадает с его факториалом: Π(n)=n!{displaystyle Pi (n)=n!}. Как и факториал, пи-функция удовлетворяет рекуррентному соотношению Π(z)=zΠ(z−1){displaystyle Pi (z)=zPi (z-1)}.

Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

n!=2πn(ne)n(1+112n+1288n2−13951840n3−5712488320n4+163879209018880n5+524681975246796800n6+O(n−7)),{displaystyle n!={sqrt {2pi n}}left({frac {n}{e}}right)^{n}left(1+{frac {1}{12n}}+{frac {1}{288n^{2}}}-{frac {139}{51840n^{3}}}-{frac {571}{2488320n^{4}}}+{frac {163879}{209018880n^{5}}}+{frac {5246819}{75246796800n^{6}}}+Oleft(n^{-7}right)right),}

см. O-большое^[1].

Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:

n!≈2πn(ne)n.{displaystyle n!approx {sqrt {2pi n}}left({frac {n}{e}}right)^{n}.}

При этом можно утверждать, что

2πn(ne)ne1/(12n+1)<n!<2πn(ne)ne1/(12n).{displaystyle {sqrt {2pi n}}left({frac {n}{e}}right)^{n}e^{1/(12n+1)}<n!<{sqrt {2pi n}}left({frac {n}{e}}right)^{n}e^{1/(12n)}.}

Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Например, с помощью формулы Стирлинга легко подсчитать, что

• 100! ≈ 9,33×10¹⁵⁷;
• 1000! ≈ 4,02×10²⁵⁶⁷;
• 10 000! ≈ 2,85×10^35 659.

Разложение на простые числа

Каждое простое число p входит в разложение n! на простые множители в степени

⌊np⌋+⌊np2⌋+⌊np3⌋+….{displaystyle leftlfloor {frac {n}{p}}rightrfloor +leftlfloor {frac {n}{p^{2}}}rightrfloor +leftlfloor {frac {n}{p^{3}}}rightrfloor +ldots .}

Таким образом,

n!=∏pp⌊np⌋+⌊np2⌋+…,{displaystyle n!=prod _{p}p^{lfloor {frac {n}{p}}rfloor +lfloor {frac {n}{p^{2}}}rfloor +ldots },}

где произведение берётся по всем простым числам. Можно заметить, что для всякого простого p большего n соответствующий множитель в произведении равен 1, следовательно произведение можно брать лишь по простым p, не превосходящим n.

Связь с производной от степенной функции

Для целого неотрицательного числа n:

(xn)(n)=n!{displaystyle left(x^{n}right)^{(n)}=n!}

Например:

(x5)(5)=(5⋅x4)(4)=(5⋅4⋅x3)‴=(5⋅4⋅3⋅x2)″=(5⋅4⋅3⋅2⋅x)′=5⋅4⋅3⋅2⋅1=5!{displaystyle left(x^{5}right)^{(5)}=left(5cdot x^{4}right)^{(4)}=left(5cdot 4cdot x^{3}right)»’=left(5cdot 4cdot 3cdot x^{2}right)»=left(5cdot 4cdot 3cdot 2cdot xright)’={5cdot 4cdot 3cdot 2cdot 1}=5!}

Другие свойства

Для натурального числа n:

n!2⩾nn⩾n!⩾n{displaystyle n!^{2}geqslant n^{n}geqslant n!geqslant n}

Для любого n>1:

n!{displaystyle n!} не является квадратом целого числа.

Факториал дробного числа

Для дробного числа, факториал может определяться по формуле:

n!=[n]!⋅([n]+1){n}{displaystyle n!=[n]!cdot ([n]+1)^{left{nright}}}

где, [n]{displaystyle [n]}- целая часть от изначального числа ([4,5] = 4), a {n}{displaystyle {n}}- дробная часть ({4,5} = 0,5).

История

Факториальные выражения появились ещё в ранних исследованиях по комбинаторике, хотя компактное обозначение n!{displaystyle n!} предложил французский математик Кристиан Крамп только в 1808 году^[2]. Важным этапом стало открытие формулы Стирлинга, которую Джеймс Стирлинг опубликовал в своём трактате «Дифференциальный метод» (лат. Methodus differentialis, 1730 год). Немного ранее почти такую же формулу опубликовал друг Стирлинга Абрахам де Муавр, но в менее завершённом виде (вместо коэффициента 2π{displaystyle {sqrt {2pi }}} была неопределённая константа)^[3].

Стирлинг подробно исследовал свойства факториала, вплоть до выяснения вопроса о том, нельзя ли распространить это понятие на произвольные вещественные числа. Он описал несколько возможных путей к реализации этой идеи и высказал мнение, что:

(12)!=π2{displaystyle left({1 over 2}right)!={frac {sqrt {pi }}{2}}}

Стирлинг не знал, что годом ранее решение проблемы уже нашёл Леонард Эйлер. В письме к Кристиану Гольдбаху Эйлер описал требуемое обобщение^[4]:

x!=limm→∞mxm!(x+1)(x+2)…(x+m){displaystyle x!=lim _{mto infty }{frac {m^{x}m!}{(x+1)(x+2)dots (x+m)}}}

Развивая эту идею, Эйлер в следующем, 1730 году ввёл понятие гамма-функции в виде классического интеграла. Эти результаты он опубликовал в журнале Санкт-Петербургской Академии наук в 1729—1730 годах.

Обобщения

Двойной факториал

Двойной факториал числа n обозначается n‼ и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность, что и n.

n!!=2⋅4⋅6⋅…⋅n=∏i=1n22i=21n2⋅(n2)!{displaystyle n!!=2cdot 4cdot 6cdot ldots cdot n=prod _{i=1}^{frac {n}{2}}2i=2^{{color {white}1}^{!!!!{frac {n}{2}}}}cdot left({frac {n}{2}}right)!}

• Для нечётного n:

n!!=1⋅3⋅5⋅…⋅n=∏i=0n−12(2i+1)=n!21n−12⋅(n−12)!{displaystyle n!!={1cdot 3cdot 5cdot ldots cdot n}=prod _{i=0}^{frac {n-1}{2}}(2i+1)={frac {n!}{2^{{color {white}1}^{!!!!{frac {n-1}{2}}}}cdot left({frac {n-1}{2}}right)!}}}

Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.

n!!=(n+1)!(n+1)!!{displaystyle n!!={frac {(n+1)!}{(n+1)!!}}}

• Для нечётного n:

n!!=n!(n−1)!!{displaystyle n!!={frac {n!}{(n-1)!!}}}

Выведение формул

Осуществив замену n=2k{displaystyle n=2k} для чётного n и n=2k+1{displaystyle n=2k+1} для нечётного n соответственно, где k{displaystyle k} — целое неотрицательное число, получим:

• для чётного числа:

(2k)!!=2⋅4⋅6⋅…⋅2k=∏i=1k2i=2k⋅k!{displaystyle (2k)!!=2cdot 4cdot 6cdot ldots cdot 2k=prod _{i=1}^{k}2i=2^{k}cdot k!}

• для нечётного числа:

(2k+1)!!=1⋅3⋅5⋅…⋅(2k+1)=∏i=0k(2i+1)=(2k+1)!2k⋅k!{displaystyle (2k+1)!!=1cdot 3cdot 5cdot ldots cdot (2k+1)=prod _{i=0}^{k}(2i+1)={frac {(2k+1)!}{2^{k}cdot k!}}}

По договорённости: 0!!=1{displaystyle 0!!=1}. Также это равенство выполняется естественным образом:

0!!=20⋅0!=1⋅1=1{displaystyle 0!!=2^{0}cdot 0!=1cdot 1=1}

Двойной факториал, также как и обычный факториал, определён только для целых неотрицательных чисел.

Последовательность значений n!! начинается так^[5]:

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, …

Кратный факториал

m-кратный факториал числа n обозначается n!!…!⏟m{displaystyle textstyle nunderbrace {!!ldots !} _{m}} и определяется следующим образом. Пусть число n представимо в виде n=mk−r,{displaystyle n=mk-r,} где k∈Z,{displaystyle kin mathbb {Z} ,} r∈{0,1,…,m−1}.{displaystyle rin {0,1,ldots ,m-1}.} Тогда^[6]

n!!…!⏟m=∏i=1k(mi−r){displaystyle nunderbrace {!!ldots !} _{m}=prod _{i=1}^{k}(mi-r)}

Обычный и двойной факториалы являются частными случаями m-кратного факториала для m = 1 и m = 2 соответственно.

Кратный факториал связан с гамма-функцией следующим соотношением^[7]:

n!!…!⏟m=∏i=1k(mi−r)=mk⋅Γ(k−rm+1)Γ(1−rm).{displaystyle nunderbrace {!!ldots !} _{m}=prod _{i=1}^{k}(mi-r)=m^{k}cdot {frac {Gamma left(k-{frac {r}{m}}+1right)}{Gamma left(1-{frac {r}{m}}right)}}.}

Неполный факториал

Убывающий факториал

Убывающим факториалом называется выражение

(n)k=nk_=n[k]=n⋅(n−1)⋅…⋅(n−k+1)=n!(n−k)!=∏i=n−k+1ni{displaystyle (n)_{k}=n^{underline {k}}=n^{[k]}=ncdot (n-1)cdot ldots cdot (n-k+1)={frac {n!}{(n-k)!}}=prod _{i=n-k+1}^{n}i}.

Например:

n = 7; k = 4,

(n − k) + 1 = 4,

n^k = 7 • 6 • 5 • 4 = 840.

Убывающий факториал даёт число размещений из n по k.

Возрастающий факториал

Возрастающим факториалом называется выражение

n(k)=nk¯=n⋅(n+1)⋅…⋅(n+k−1)=(n+k−1)!(n−1)!=∏i=n(n+k)−1i.{displaystyle n^{(k)}=n^{overline {k}}=ncdot (n+1)cdot ldots cdot (n+k-1)={frac {(n+k-1)!}{(n-1)!}}=prod _{i=n}^{(n+k)-1}i.}

Праймориал или примориал

Праймориал или примориал (англ. primorial) числа n обозначается p_n# и определяется как произведение n первых простых чисел. Например,

p5#=2×3×5×7×11=2310{displaystyle p_{5}#=2times 3times 5times 7times 11=2310}.

Иногда праймориалом называют число n#{displaystyle n#}, определяемое как произведение всех простых чисел, не превышающих заданное n.

Последовательность праймориалов (включая 1#≡1{displaystyle {textstyle {1#equiv 1}}}) начинается так^[8]:

1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, …

Суперфакториалы

Нейл Слоан и Симон Плуффэ (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырёх равен

sf⁡(4)=1!×2!×3!×4!=288{displaystyle operatorname {sf} (4)=1!times 2!times 3!times 4!=288}

(поскольку устоявшегося обозначения нет, используется функциональное).

В общем

sf⁡(n)=∏k=1nk!=∏k=1nkn−k+1=1n⋅2n−1⋅3n−2⋯(n−1)2⋅n1.{displaystyle operatorname {sf} (n)=prod _{k=1}^{n}k!=prod _{k=1}^{n}k^{n-k+1}=1^{n}cdot 2^{n-1}cdot 3^{n-2}cdots (n-1)^{2}cdot n^{1}.}

Последовательность суперфакториалов чисел n⩾0{displaystyle ngeqslant 0} начинается так^[9]:

1, 1, 2, 12, 288, 34 560, 24 883 200, 125 411 328 000, 5 056 584 744 960 000, 1 834 933 472 251 084 800 000, 6 658 606 584 104 736 522 240 000 000, 265 790 267 296 391 946 810 949 632 000 000 000, 127 313 963 299 399 416 749 559 771 247 411 200 000 000 000, …

Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Hyperfactorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел n⩾0{displaystyle ngeqslant 0} начинается так^[10]:

1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 745 453 331 864 786 829 312 000 000, 3 769 447 945 987 085 350 501 386 572 267 520 000 000 000, 6 916 686 207 999 802 072 984 424 331 678 589 933 649 915 805 696 000 000 000 000 000, …

Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение (m − 1)-уровневых факториалов чисел от 1 до n, то есть

mf⁡(n,m)=mf⁡(n−1,m)mf⁡(n,m−1)=∏k=1nk(n−k+m−1n−k),{displaystyle operatorname {mf} (n,m)=operatorname {mf} (n-1,m)operatorname {mf} (n,m-1)=prod _{k=1}^{n}k^{n-k+m-1 choose n-k},}

где mf⁡(n,0)=n{displaystyle operatorname {mf} (n,0)=n} для n>0{displaystyle n>0} и mf⁡(0,m)=1.{displaystyle operatorname {mf} (0,m)=1.}

Субфакториал

Субфакториал !n определяется как количество беспорядков порядка n, то есть перестановок n-элементного множества без неподвижных точек.

См. также

Примечания

wiki.sc

Факториал — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Факториа́л числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно:

<math>n! = 1cdot 2cdotldotscdot n =prod_{i=1}^n i.</math>

Например:

<math>5 ! = 1 cdot 2 cdot 3 cdot 4 cdot 5 = 120</math>.

По договорённости: <math>0! = 1</math>. Также это равенство выполняется естественным образом:

<math>0! = Bigl.(n-1)!Bigr|_{n=1} = Bigl.frac{n!}{n}Bigr|_{n=1} = frac{1!}{1} = 1</math>

Факториал определён только для целых неотрицательных чисел.

Последовательность факториалов неотрицательных целых чисел начинается так^[1]:

1, 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880, 3 628 800, 39 916 800, 479 001 600, 6 227 020 800, 87 178 291 200, 1 307 674 368 000, 20 922 789 888 000, 355 687 428 096 000, 6 402 373 705 728 000, 121 645 100 408 832 000, 2 432 902 008 176 640 000, …

Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе. Обозначение факториала в формате <math>n!</math> предложил французский математик Кристиан Крамп в 1808 году^[2].

Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция <math>e^{e^n}</math>).

Свойства

Рекуррентная формула

<math>n!= begin{cases}

1 & n = 0,\
n cdot (n-1)! & n > 0.
end{cases}</math>

Комбинаторная интерпретация

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, так как пустое множество упорядочено единственным способом.

Связь с гамма-функцией

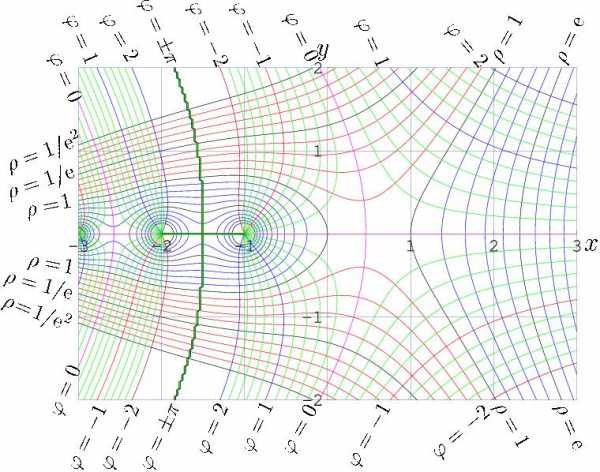
Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

<math>n! = Gamma(n+1).</math>

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.

Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при <math>n=-1, -2, -3ldots</math>.

Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как

<math>Pi(z)=int_0^infty t^{z} e^{-t}, mathrm{d}t</math>.

Поскольку <math>Pi(z) = Gamma(z+1) ,,</math> то пи-функция натурального числа совпадает с его факториалом: <math>Pi(n) = n!.</math> Как факториал, пи-функция удовлетворяет рекурсивному соотношению <math>Pi(z) = zPi(z-1),.</math>

Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

<math>n! = sqrt{2pi n}left(frac{n}{e}right)^n left(1 + frac{1}{12 n} + frac{1}{288 n^2} — frac{139}{51840 n^3} — frac{571}{2488320 n^4} + frac{163879}{209018880 n^5} + frac{5246819}{75246796800 n^6} + Oleft(n^{-7}right)right),</math>

см. O-большое^[3].

Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:

<math>n! approx sqrt{2pi n}left(frac{n}{e}right)^n.</math>

При этом можно утверждать, что

<math>sqrt{2pi n}left(frac{n}{e}right)^n e^{1/(12n+1)}< n! < sqrt{2pi n}left(frac{n}{e}right)^n e^{1/(12n)}.</math>

Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что

• 100! ≈ 9,33×10¹⁵⁷;
• 1000! ≈ 4,02×10²⁵⁶⁷;
• 10 000! ≈ 2,85×10^35 659.

Разложение на простые числа

Каждое простое число p входит в разложение n! на простые множители в степени

<math>leftlfloor frac{n}{p}rightrfloor + leftlfloor frac{n}{p^2}rightrfloor + leftlfloor frac{n}{p^3}rightrfloor + ldots.</math>

Таким образом,

<math>n! = prod_{p} p^{lfloor frac{n}{p}rfloor + lfloor frac{n}{p^2}rfloor +ldots},</math>

где произведение берётся по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.

Связь с производной от степенной функции

Для целого неотрицательного числа n:

<math>left( x^n right)^{(n)}=n!</math>

Например:

<math>left( x^5 right)^{(5)}

= left( 5 cdot x^4 right)^{(4)}
= left( 5 cdot 4 cdot x^3 right)
= left( 5 cdot 4 cdot 3 cdot x^2 right)
= left( 5 cdot 4 cdot 3 cdot 2 cdot x right)’
= {5 cdot 4 cdot 3 cdot 2 cdot 1} = 5!</math>

Другие свойства

• Для натурального числа n:

<math>n!^2 geqslant n^n geqslant n! geqslant n</math>

Обобщения

Двойной факториал

Двойной факториал числа n обозначается n‼ и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность, что и n.

<math>n!! = 2 cdot 4 cdot 6 cdot ldots cdot n = prod_{i=1}^{frac{n}{2}} 2i = 2^{{color{white}1}^{!!!! frac{n}{2}}} cdot left ( frac{n}{2} right )!</math>

• Для нечётного n:

<math>n!! = {1 cdot 3 cdot 5 cdot ldots cdot n} = prod_{i=0}^{frac{n-1}{2}} (2i+1) = frac{n!}{2^{{color{white}1}^{!!!! frac{n-1}{2}}} cdot left ( frac{n-1}{2} right )!}</math>

Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.

<math>n!! = frac{(n+1)!}{(n+1)!!}</math>

• Для нечётного n:

<math>n!! = frac{n!}{(n-1)!!}</math>

Выведение формул

• Формула для чётного n:

<math>n!! = 2^{{color{white}1}^{!!!! frac{n}{2}}} cdot left ( frac{n}{2} right )!</math>

Пример, иллюстрирующий использованное выше выведение формулы:

<math>begin{align} 14!! & = 2^{frac{14}{2}} cdot left ( frac{14}{2} right )! = 2^7 cdot 7! =

\ & = (2 cdot 2 cdot 2 cdot 2 cdot 2 cdot 2 cdot 2) cdot (1 cdot 2 cdot 3 cdot 4 cdot 5 cdot 6 cdot 7) =
\ & = (2 cdot 1) (2 cdot 2) (2 cdot 3) (2 cdot 4) (2 cdot 5) (2 cdot 6) (2 cdot 7) =
\ & = 2 cdot 4 cdot 6 cdot 8 cdot 10 cdot 12 cdot 14 = 645120 end{align}</math>

• Формула для нечётного n:

<math>n!! = frac{n!}{2^{{color{white}1}^{!!!! frac{n-1}{2}}} cdot left ( frac{n-1}{2} right )!}</math>

Пример, иллюстрирующий использованное выше выведение формулы:

<math>begin{align} 15!! & = frac{15!}{2^{{color{white}1}^{!!!! frac{15-1}{2}}} cdot left ( frac{15-1}{2} right )!}

\ & = {color{white}overbrace{color{Black}frac{1 cdot 2 cdot 3 cdot 4 cdot 5 cdot 6 cdot 7 cdot 8 cdot 9 cdot 10 cdot 11 cdot 12 cdot 13 cdot 14 cdot 15}{(2 cdot 2 cdot 2 cdot 2 cdot 2 cdot 2 cdot 2) cdot (1 cdot 2 cdot 3 cdot 4 cdot 5 cdot 6 cdot 7)}}} =
\ & = {color{white}overbrace{color{Black}frac{1 cdot 2 cdot 3 cdot 4 cdot 5 cdot 6 cdot 7 cdot 8 cdot 9 cdot 10 cdot 11 cdot 12 cdot 13 cdot 14 cdot 15}{(2 cdot 1) (2 cdot 2) (2 cdot 3) (2 cdot 4) (2 cdot 5) (2 cdot 6) (2 cdot 7)}}} =
\ & = {color{white}overbrace{color{Black}frac{1 cdot {color{OliveGreen}2} cdot 3 cdot {color{OliveGreen}4} cdot 5 cdot {color{OliveGreen}6} cdot 7 cdot {color{OliveGreen}8} cdot 9 cdot {color{OliveGreen}10} cdot 11 cdot {color{OliveGreen}12} cdot 13 cdot {color{OliveGreen}14} cdot 15}{color{OliveGreen}2 cdot 4 cdot 6 cdot 8 cdot 10 cdot 12 cdot 14}}} =
\ & = {color{white}overbrace{color{Black}1 cdot 3 cdot 5 cdot 7 cdot 9 cdot 11 cdot 13 cdot 15}} = 2027025 end{align}</math>

Осуществив замену <math>n=2k</math> для чётного n и <math>n=2k+1</math> для нечётного n соответственно, где <math>k</math> — целое неотрицательное число, получим:

• для чётного числа:

<math>(2k)!! = 2 cdot 4 cdot 6 cdot ldots cdot 2k =prod_{i=1}^{k} 2i = 2^kcdot k!</math>

• для нечётного числа:

<math>(2k+1)!! = 1 cdot 3 cdot 5 cdot ldots cdot (2k+1) = prod_{i=0}^{k} (2i+1) = frac{(2k+1)!}{2^kcdot k!}</math>

По договорённости: <math>0!! = 1</math>. Также это равенство выполняется естественным образом:

<math>0!! = 2^0 cdot 0! = 1 cdot 1 = 1</math>

</div></div>

Двойной факториал, также как и обычный факториал, определён только для целых неотрицательных чисел.

Последовательность значений n!! начинается так^[4]:

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, …

Кратный факториал

m-кратный факториал числа n обозначается <math>textstyle nunderbrace{!!ldots !}_m</math> и определяется следующим образом. Пусть число n представимо в виде <math>n=mk-r,</math> где <math>k in mathbb{Z},</math> <math>r in {0,1,ldots ,m-1}.</math> Тогда^[5]

<math>nunderbrace{!!ldots !}_m = prod_{i=1}^k (mi-r)</math>

Обычный и двойной факториалы являются частными случаями m-кратного факториала для m = 1 и m = 2 соответственно.

Кратный факториал связан с гамма-функцией следующим соотношением^[6]:

<math>nunderbrace{!!ldots !}_m = prod_{i=1}^{k} (mi-r)=m^k cdot frac {Gamma left (k-frac {r} {m} +1 right )} {Gamma left ( 1- frac {r} {m} right)}.</math>

Неполный факториал

Убывающий факториал

Убывающим факториалом называется выражение

<math>(n)_k = n^{underline{k}} = n^{[k]}= ncdot (n-1)cdot ldotscdot (n-k+1) = frac{n!}{(n-k)!} = prod_{i=n-k+1}^n i</math>.

Например:

n = 7; k = 4,

(n − k) + 1 = 4,

n^k = 7 • 6 • 5 • 4 = 840.

Убывающий факториал даёт число размещений из n по k.

Возрастающий факториал

Возрастающим факториалом называется выражение

<math>n^{(k)} = n^{overline{k}} = ncdot (n+1)cdot ldotscdot (n+k-1) = frac{(n+k-1)!}{(n-1)!}=prod_{i=n}^{(n+k)-1} i.</math>

Праймориал или примориал

Праймориал или примориал (англ. primorial) числа n обозначается p_n# и определяется как произведение n первых простых чисел. Например,

<math>p_5# = 2 times 3 times 5 times 7 times 11 = 2310</math>.

Иногда праймориалом называют число <math>n#</math>, определяемое как произведение всех простых чисел, не превышающих заданное n.

Последовательность праймориалов (включая <math>{textstyle{1# equiv 1}}</math>) начинается так^[7]:

1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, …

Суперфакториалы

Нейл Слоан и Симон Плуффэ (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырёх равен

<math> operatorname{sf}(4)=1! times 2! times 3! times 4!=288</math>

(поскольку устоявшегося обозначения нет, используется функциональное).

В общем

<math>

 operatorname{sf}(n)
 =prod_{k=1}^n k! =prod_{k=1}^n k^{n-k+1}
 =1^ncdot2^{n-1}cdot3^{n-2}cdots(n-1)^2cdot n^1.
</math>

Последовательность суперфакториалов чисел <math>n geqslant 0</math> начинается так^[8]:

1, 1, 2, 12, 288, 34 560, 24 883 200, 125 411 328 000, 5 056 584 744 960 000, 1 834 933 472 251 084 800 000, 6 658 606 584 104 736 522 240 000 000, 265 790 267 296 391 946 810 949 632 000 000 000, 127 313 963 299 399 416 749 559 771 247 411 200 000 000 000, …

Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Superduperfactorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел <math>n geqslant 0</math> начинается так^[9]:

1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 745 453 331 864 786 829 312 000 000, 3 769 447 945 987 085 350 501 386 572 267 520 000 000 000, 6 916 686 207 999 802 072 984 424 331 678 589 933 649 915 805 696 000 000 000 000 000, …

Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение (m − 1)-уровневых факториалов чисел от 1 до n, то есть

<math>operatorname{mf}(n,m) = operatorname{mf}(n-1,m)operatorname{mf}(n,m-1)=prod_{k=1}^n k^{n-k+m-1 choose n-k}, </math>

где <math>operatorname{mf}(n,0)=n</math> для <math>n>0</math> и <math>operatorname{mf}(0,m)=1.</math>

Субфакториал

Субфакториал !n определяется как количество беспорядков порядка n, то есть перестановок n-элементного множества без неподвижных точек.

См. также

Напишите отзыв о статье «Факториал»

Примечания

1. ↑ Последовательность A000142 в OEIS
2. ↑ [www-history.mcs.st-andrews.ac.uk/Biographies/Kramp.html Крамп, Кристиан]
3. ↑ Коэффициенты этого разложения дают A001163 (числители) и A001164 (знаменатели)
4. ↑ Последовательность A006882 в OEIS
5. ↑ «Энциклопедия для детей» Аванта+. Математика.
6. ↑ [www.wolframalpha.com/input/?i=product+%28m*i-r%29%2C+i%3D1..k wolframalpha.com].
7. ↑ Последовательность A002110 в OEIS
8. ↑ Последовательность A000178 в OEIS
9. ↑ Последовательность A055462 в OEIS

Отрывок, характеризующий Факториал

– Молодцы! – сказал, смеясь, Ростов. – Что, сено есть?
– И одинакие какие… – сказал Ильин.
– Развесе…oo…ооо…лая бесе… бесе… – распевали мужики с счастливыми улыбками.
Один мужик вышел из толпы и подошел к Ростову.
– Вы из каких будете? – спросил он.
– Французы, – отвечал, смеючись, Ильин. – Вот и Наполеон сам, – сказал он, указывая на Лаврушку.
– Стало быть, русские будете? – переспросил мужик.
– А много вашей силы тут? – спросил другой небольшой мужик, подходя к ним.
– Много, много, – отвечал Ростов. – Да вы что ж собрались тут? – прибавил он. – Праздник, что ль?
– Старички собрались, по мирскому делу, – отвечал мужик, отходя от него.
В это время по дороге от барского дома показались две женщины и человек в белой шляпе, шедшие к офицерам.
– В розовом моя, чур не отбивать! – сказал Ильин, заметив решительно подвигавшуюся к нему Дуняшу.
– Наша будет! – подмигнув, сказал Ильину Лаврушка.
– Что, моя красавица, нужно? – сказал Ильин, улыбаясь.
– Княжна приказали узнать, какого вы полка и ваши фамилии?
– Это граф Ростов, эскадронный командир, а я ваш покорный слуга.
– Бе…се…е…ду…шка! – распевал пьяный мужик, счастливо улыбаясь и глядя на Ильина, разговаривающего с девушкой. Вслед за Дуняшей подошел к Ростову Алпатыч, еще издали сняв свою шляпу.
– Осмелюсь обеспокоить, ваше благородие, – сказал он с почтительностью, но с относительным пренебрежением к юности этого офицера и заложив руку за пазуху. – Моя госпожа, дочь скончавшегося сего пятнадцатого числа генерал аншефа князя Николая Андреевича Болконского, находясь в затруднении по случаю невежества этих лиц, – он указал на мужиков, – просит вас пожаловать… не угодно ли будет, – с грустной улыбкой сказал Алпатыч, – отъехать несколько, а то не так удобно при… – Алпатыч указал на двух мужиков, которые сзади так и носились около него, как слепни около лошади.

– А!.. Алпатыч… А? Яков Алпатыч!.. Важно! прости ради Христа. Важно! А?.. – говорили мужики, радостно улыбаясь ему. Ростов посмотрел на пьяных стариков и улыбнулся.
– Или, может, это утешает ваше сиятельство? – сказал Яков Алпатыч с степенным видом, не заложенной за пазуху рукой указывая на стариков.
– Нет, тут утешенья мало, – сказал Ростов и отъехал. – В чем дело? – спросил он.
– Осмелюсь доложить вашему сиятельству, что грубый народ здешний не желает выпустить госпожу из имения и угрожает отпречь лошадей, так что с утра все уложено и ее сиятельство не могут выехать.
– Не может быть! – вскрикнул Ростов.
– Имею честь докладывать вам сущую правду, – повторил Алпатыч.
Ростов слез с лошади и, передав ее вестовому, пошел с Алпатычем к дому, расспрашивая его о подробностях дела. Действительно, вчерашнее предложение княжны мужикам хлеба, ее объяснение с Дроном и с сходкою так испортили дело, что Дрон окончательно сдал ключи, присоединился к мужикам и не являлся по требованию Алпатыча и что поутру, когда княжна велела закладывать, чтобы ехать, мужики вышли большой толпой к амбару и выслали сказать, что они не выпустят княжны из деревни, что есть приказ, чтобы не вывозиться, и они выпрягут лошадей. Алпатыч выходил к ним, усовещивая их, но ему отвечали (больше всех говорил Карп; Дрон не показывался из толпы), что княжну нельзя выпустить, что на то приказ есть; а что пускай княжна остается, и они по старому будут служить ей и во всем повиноваться.

В ту минуту, когда Ростов и Ильин проскакали по дороге, княжна Марья, несмотря на отговариванье Алпатыча, няни и девушек, велела закладывать и хотела ехать; но, увидав проскакавших кавалеристов, их приняли за французов, кучера разбежались, и в доме поднялся плач женщин.
– Батюшка! отец родной! бог тебя послал, – говорили умиленные голоса, в то время как Ростов проходил через переднюю.
Княжна Марья, потерянная и бессильная, сидела в зале, в то время как к ней ввели Ростова. Она не понимала, кто он, и зачем он, и что с нею будет. Увидав его русское лицо и по входу его и первым сказанным словам признав его за человека своего круга, она взглянула на него своим глубоким и лучистым взглядом и начала говорить обрывавшимся и дрожавшим от волнения голосом. Ростову тотчас же представилось что то романическое в этой встрече. «Беззащитная, убитая горем девушка, одна, оставленная на произвол грубых, бунтующих мужиков! И какая то странная судьба натолкнула меня сюда! – думал Ростов, слушяя ее и глядя на нее. – И какая кротость, благородство в ее чертах и в выражении! – думал он, слушая ее робкий рассказ.

Когда она заговорила о том, что все это случилось на другой день после похорон отца, ее голос задрожал. Она отвернулась и потом, как бы боясь, чтобы Ростов не принял ее слова за желание разжалобить его, вопросительно испуганно взглянула на него. У Ростова слезы стояли в глазах. Княжна Марья заметила это и благодарно посмотрела на Ростова тем своим лучистым взглядом, который заставлял забывать некрасивость ее лица.

– Не могу выразить, княжна, как я счастлив тем, что я случайно заехал сюда и буду в состоянии показать вам свою готовность, – сказал Ростов, вставая. – Извольте ехать, и я отвечаю вам своей честью, что ни один человек не посмеет сделать вам неприятность, ежели вы мне только позволите конвоировать вас, – и, почтительно поклонившись, как кланяются дамам царской крови, он направился к двери.
Почтительностью своего тона Ростов как будто показывал, что, несмотря на то, что он за счастье бы счел свое знакомство с нею, он не хотел пользоваться случаем ее несчастия для сближения с нею.
Княжна Марья поняла и оценила этот тон.
– Я очень, очень благодарна вам, – сказала ему княжна по французски, – но надеюсь, что все это было только недоразуменье и что никто не виноват в том. – Княжна вдруг заплакала. – Извините меня, – сказала она.
Ростов, нахмурившись, еще раз низко поклонился и вышел из комнаты.

– Ну что, мила? Нет, брат, розовая моя прелесть, и Дуняшей зовут… – Но, взглянув на лицо Ростова, Ильин замолк. Он видел, что его герой и командир находился совсем в другом строе мыслей.

Ростов злобно оглянулся на Ильина и, не отвечая ему, быстрыми шагами направился к деревне.
– Я им покажу, я им задам, разбойникам! – говорил он про себя.
Алпатыч плывущим шагом, чтобы только не бежать, рысью едва догнал Ростова.
– Какое решение изволили принять? – сказал он, догнав его.
Ростов остановился и, сжав кулаки, вдруг грозно подвинулся на Алпатыча.
– Решенье? Какое решенье? Старый хрыч! – крикнул он на него. – Ты чего смотрел? А? Мужики бунтуют, а ты не умеешь справиться? Ты сам изменник. Знаю я вас, шкуру спущу со всех… – И, как будто боясь растратить понапрасну запас своей горячности, он оставил Алпатыча и быстро пошел вперед. Алпатыч, подавив чувство оскорбления, плывущим шагом поспевал за Ростовым и продолжал сообщать ему свои соображения. Он говорил, что мужики находились в закоснелости, что в настоящую минуту было неблагоразумно противуборствовать им, не имея военной команды, что не лучше ли бы было послать прежде за командой.

– Я им дам воинскую команду… Я их попротивоборствую, – бессмысленно приговаривал Николай, задыхаясь от неразумной животной злобы и потребности излить эту злобу. Не соображая того, что будет делать, бессознательно, быстрым, решительным шагом он подвигался к толпе. И чем ближе он подвигался к ней, тем больше чувствовал Алпатыч, что неблагоразумный поступок его может произвести хорошие результаты. То же чувствовали и мужики толпы, глядя на его быструю и твердую походку и решительное, нахмуренное лицо.
После того как гусары въехали в деревню и Ростов прошел к княжне, в толпе произошло замешательство и раздор. Некоторые мужики стали говорить, что эти приехавшие были русские и как бы они не обиделись тем, что не выпускают барышню. Дрон был того же мнения; но как только он выразил его, так Карп и другие мужики напали на бывшего старосту.

– Ты мир то поедом ел сколько годов? – кричал на него Карп. – Тебе все одно! Ты кубышку выроешь, увезешь, тебе что, разори наши дома али нет?
– Сказано, порядок чтоб был, не езди никто из домов, чтобы ни синь пороха не вывозить, – вот она и вся! – кричал другой.
– Очередь на твоего сына была, а ты небось гладуха своего пожалел, – вдруг быстро заговорил маленький старичок, нападая на Дрона, – а моего Ваньку забрил. Эх, умирать будем!
– То то умирать будем!
– Я от миру не отказчик, – говорил Дрон.
– То то не отказчик, брюхо отрастил!..
Два длинные мужика говорили свое. Как только Ростов, сопутствуемый Ильиным, Лаврушкой и Алпатычем, подошел к толпе, Карп, заложив пальцы за кушак, слегка улыбаясь, вышел вперед. Дрон, напротив, зашел в задние ряды, и толпа сдвинулась плотнее.
– Эй! кто у вас староста тут? – крикнул Ростов, быстрым шагом подойдя к толпе.
– Староста то? На что вам?.. – спросил Карп. Но не успел он договорить, как шапка слетела с него и голова мотнулась набок от сильного удара.

– Шапки долой, изменники! – крикнул полнокровный голос Ростова. – Где староста? – неистовым голосом кричал он.
– Старосту, старосту кличет… Дрон Захарыч, вас, – послышались кое где торопливо покорные голоса, и шапки стали сниматься с голов.
– Нам бунтовать нельзя, мы порядки блюдем, – проговорил Карп, и несколько голосов сзади в то же мгновенье заговорили вдруг:
– Как старички пороптали, много вас начальства…
– Разговаривать?.. Бунт!.. Разбойники! Изменники! – бессмысленно, не своим голосом завопил Ростов, хватая за юрот Карпа. – Вяжи его, вяжи! – кричал он, хотя некому было вязать его, кроме Лаврушки и Алпатыча.
Лаврушка, однако, подбежал к Карпу и схватил его сзади за руки.
– Прикажете наших из под горы кликнуть? – крикнул он.
Алпатыч обратился к мужикам, вызывая двоих по именам, чтобы вязать Карпа. Мужики покорно вышли из толпы и стали распоясываться.

– Староста где? – кричал Ростов.
Дрон, с нахмуренным и бледным лицом, вышел из толпы.
– Ты староста? Вязать, Лаврушка! – кричал Ростов, как будто и это приказание не могло встретить препятствий. И действительно, еще два мужика стали вязать Дрона, который, как бы помогая им, снял с себя кушан и подал им.
– А вы все слушайте меня, – Ростов обратился к мужикам: – Сейчас марш по домам, и чтобы голоса вашего я не слыхал.
– Что ж, мы никакой обиды не делали. Мы только, значит, по глупости. Только вздор наделали… Я же сказывал, что непорядки, – послышались голоса, упрекавшие друг друга.
– Вот я же вам говорил, – сказал Алпатыч, вступая в свои права. – Нехорошо, ребята!
– Глупость наша, Яков Алпатыч, – отвечали голоса, и толпа тотчас же стала расходиться и рассыпаться по деревне.
Связанных двух мужиков повели на барский двор. Два пьяные мужика шли за ними.
– Эх, посмотрю я на тебя! – говорил один из них, обращаясь к Карпу.
– Разве можно так с господами говорить? Ты думал что?
– Дурак, – подтверждал другой, – право, дурак!
Через два часа подводы стояли на дворе богучаровского дома. Мужики оживленно выносили и укладывали на подводы господские вещи, и Дрон, по желанию княжны Марьи выпущенный из рундука, куда его заперли, стоя на дворе, распоряжался мужиками.
– Ты ее так дурно не клади, – говорил один из мужиков, высокий человек с круглым улыбающимся лицом, принимая из рук горничной шкатулку. – Она ведь тоже денег стоит. Что же ты ее так то вот бросишь или пол веревку – а она потрется. Я так не люблю. А чтоб все честно, по закону было. Вот так то под рогожку, да сенцом прикрой, вот и важно. Любо!
– Ишь книг то, книг, – сказал другой мужик, выносивший библиотечные шкафы князя Андрея. – Ты не цепляй! А грузно, ребята, книги здоровые!
– Да, писали, не гуляли! – значительно подмигнув, сказал высокий круглолицый мужик, указывая на толстые лексиконы, лежавшие сверху.

Ростов, не желая навязывать свое знакомство княжне, не пошел к ней, а остался в деревне, ожидая ее выезда. Дождавшись выезда экипажей княжны Марьи из дома, Ростов сел верхом и до пути, занятого нашими войсками, в двенадцати верстах от Богучарова, верхом провожал ее. В Янкове, на постоялом дворе, он простился с нею почтительно, в первый раз позволив себе поцеловать ее руку.
– Как вам не совестно, – краснея, отвечал он княжне Марье на выражение благодарности за ее спасенье (как она называла его поступок), – каждый становой сделал бы то же. Если бы нам только приходилось воевать с мужиками, мы бы не допустили так далеко неприятеля, – говорил он, стыдясь чего то и стараясь переменить разговор. – Я счастлив только, что имел случай познакомиться с вами. Прощайте, княжна, желаю вам счастия и утешения и желаю встретиться с вами при более счастливых условиях. Ежели вы не хотите заставить краснеть меня, пожалуйста, не благодарите.
Но княжна, если не благодарила более словами, благодарила его всем выражением своего сиявшего благодарностью и нежностью лица. Она не могла верить ему, что ей не за что благодарить его. Напротив, для нее несомненно было то, что ежели бы его не было, то она, наверное, должна была бы погибнуть и от бунтовщиков и от французов; что он, для того чтобы спасти ее, подвергал себя самым очевидным и страшным опасностям; и еще несомненнее было то, что он был человек с высокой и благородной душой, который умел понять ее положение и горе. Его добрые и честные глаза с выступившими на них слезами, в то время как она сама, заплакав, говорила с ним о своей потере, не выходили из ее воображения.

wiki-org.ru

Факториал простыми словами

Факториал: определение из Википедии

Факториа́л числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно:

n
!
=
1
⋅
2
⋅
…
⋅
n
=

∏

i
=
1

n

i
.

{displaystyle n!=1cdot 2cdot ldots cdot n=prod _{i=1}^{n}i.}

Например:

5
!
=
1
⋅
2
⋅
3
⋅
4
⋅
5
=
120

{displaystyle 5!=1cdot 2cdot 3cdot 4cdot 5=120}
.
По договорённости:

0
!
=
1

{displaystyle 0!=1}
. Также это равенство выполняется естественным образом:

0
!
=

(
n
−
1
)
!

|

n
=
1

=

n
!

n

|

n
=
1

=

1
!

1

=
1

{displaystyle 0!={Bigl .}(n-1)!{Bigr |}_{n=1}={Bigl .}{frac {n!}{n}}{Bigr |}_{n=1}={frac {1!}{1}}=1}

Факториал определён только для целых неотрицательных чисел.
Последовательность факториалов неотрицательных целых чисел начинается так:
1, 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880, 3 628 800, 39 916 800, 479 001 600, 6 227 020 800, 87 178 291 200, 1 307 674 368 000, 20 922 789 888 000, 355 687 428 096 000, 6 402 373 705 728 000, 121 645 100 408 832 000, 2 432 902 008 176 640 000, …
Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.
Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция

e

e

n

{displaystyle e^{e^{n}}}
).

Факториал: определение из словаря Ефремовой

м.
Произведение чисел натурального ряда от единицы до некоторого данного числа (в
математике).

На текущей странице дано определение слова факториал простым языком.
Надеемся, что после прочтения этого объяснения простыми словами, у вас больше не осталось вопросов,
что такое факториал.

wikisimple.ru

Факториал Википедия

Факториа́л — функция, определённая на множестве неотрицательных целых чисел. Название происходит от лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л. Факториал натурального числа n определяется как произведение всех натуральных чисел от 1 до n включительно:

n!=1⋅2⋅…⋅n=∏k=1nk{displaystyle n!=1cdot 2cdot ldots cdot n=prod _{k=1}^{n}k}.

Например,

5!=1⋅2⋅3⋅4⋅5=120{displaystyle 5!=1cdot 2cdot 3cdot 4cdot 5=120}.

Из определения факториала следует соотношение (n−1)!=n!n{displaystyle (n-1)!={frac {n!}{n}}}, откуда при n=1{displaystyle n=1} формально находим

0!=1{displaystyle 0!=1}.

Последнее равенство обычно принимают в качестве соглашения, хотя, как показано выше, оно следует из определения факториала для натуральных чисел при условии, что все значения функции связаны единым рекуррентным соотношением.

Факториалы всех чисел составляют последовательность A000142 в OEIS; значения в научной нотации округляются

n	n!
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800
11	39916800
12	479001600
13	6227020800
14	87178291200
15	1307674368000
16	20922789888000
17	355687428096000
18	6402373705728000
19	121645100408832000
20	2432902008176640000
25	≈1,551121004⋅1025
50	≈3,041409320⋅1064
70	≈1,197857167⋅10100
100	≈9,332621544⋅10157
450	≈1,733368733⋅101000
1000	≈4,023872601⋅102567
3249	≈6,412337688⋅1010000
10000	≈2,846259681⋅1035659
25206	≈1,205703438⋅10100000
100000	≈2,824229408⋅10456573
205023	≈2,503898932⋅101000004
1000000	≈8,263931688⋅105565708
10100	≈109,956570552⋅10101
101000	≈10101003
1010 000	≈101010 004
10100 000	≈1010100 005
1010100	≈101010100

Факториал активно используется в различных разделах математики: комбинаторике, математическом анализе,

ru-wiki.ru