Продолжаем изучать элементарные задачи по математике. Сегодня мы рассмотрим очень интересную физическую величину — производительность.
Что такое сила?
Сила — это физическое явление, способное изменять форму материальных тел, вызывать их движение, менять направление и скорость движения этих тел или приводить тело в состояние покоя.
Примеры сил:
- ребята слепили снеговика, а хулиганы его разрушили. Получается, что хулиганы приложили к снеговику свою силу, тем самым вызвали изменение формы снеговика;
- на дворе стояла тележка. Прохожий случайно задел её и тележка сдвинулась с места. Получается, что прохожий применил силу к тележке и вызвал её движение;
- далее тот же прохожий остановил тележку, чтобы она далеко не уехала. Получается, что прохожий применил силу, тем самым привел тележку в состояние покоя.
Сила является физической величиной — мерой воздействия на тело других тел. Сила обозначается заглавной латинской буквой F.
Что такое работа?
Работа — это количественная мера действия силы на тело. Работа зависит от количества силы, приложенной на тело и от направления этой силы, а также от перемещения данного тела.
Например, если мы попробуем сдвинуть шкаф с места и он сдвинется, то можно сказать, что мы совершили работу, поскольку сила, которую мы приложили, привела к тому, что шкаф совершил перемещение на некоторое расстояние.
Если же мы, к примеру, попробуем толкнуть стену, то стена с места не сдвинется, а значит и работа не будет совершена, поскольку сила была приложена, но эта сила не вызвала никакого перемещения стены.
Работа обозначается заглавной латинской буквой A.
Производительность
Производительностью называют работу, выполненную за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда. Производительность обозначается латинской буквой v
Рассмотрим следующий пример. Два пекаря пекли булочки. Первый пекарь испёк 40 булочек за 10 минут, а второй 15 булочек за 5 минут. Как узнать, кто из пекарей работал быстрее, первый или второй?
Работал быстрее тот, кто за одну минуту выпекает больше булочек. Говорят, что у него производительность больше. Для нахождения производительности предусмотрено следующее правило:
Чтобы найти производительность, надо выполненную работу разделить на время работы.
Также, можно воспользоваться формулой:
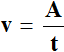
где v — производительность, A — выполненная работа, t — время работы.
Вернемся к нашей задаче. Зная правило или формулу нахождения производительности, можно определить сколько булочек приходится на одну минуту.
Найдём производительность первого пекаря. Разделим работу, которую он выполнил, на время которое он на нее затратил. Выполненная работа это количество испеченных им булочек, то есть 40, а время — 10 минут
40 : 10 = 4 булочки в минуту
Аналогично найдём производительность второго пекаря. Разделим 15 на 5
15 : 5 = 3 булочки в минуту
4 > 3
Первый пекарь в минуту выпекает больше булочек чем второй, значит его производительность выше. Отсюда делаем вывод, что работает он быстрее второго пекаря.
Также можно воспользоваться формулой нахождения производительности. В этом случае решение принимает следующий вид:
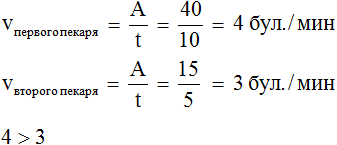
Под буквой v можно делать метки, указывающие для кого/чего мы находим производительность.
Задача 2. Тому нужно за 2 дня прочитать книгу, в которой 100 страниц. В первый день он читал 4 часа со скоростью 12 страниц в час. С какой скоростью ему надо читать оставшуюся часть книги, если у него есть на это 4 часа?
Узнаем сколько страниц Том прочитал в первый день. Он читал 12 страниц в час. Чтению в первый день он посвятил 4 часа, поэтому для нахождения количества прочитанных страниц в первый день, нужно 12 умножить на 4
12 × 4 = 48 страниц прочитано в первый день
Узнаем сколько страниц осталось прочесть. Вычтем из общего количества страниц (100) количество прочитанных страниц (48)
100 − 48 = 52 страницы осталось прочесть
Осталось прочесть 52 страницы. Теперь найдем такую производительность, при которой Том сможет прочесть 52 страницы за 4 часа. Раскидаем 52 страницы на 4 часа поровну
52 : 4 = 13 страниц в час
Ответ: чтобы прочитать оставшуюся часть книги за 4 часа, Том должен читать ее со скоростью 13 страниц в час.
Замечание. В некоторых источниках слово «производительность» может быть заменено на слова «скорость», «эффективность», «продуктивность», «плодотворность».
Задача 3. Один насос работал 4 часа, выкачивая 158 вёдер воды в час, а другой — 3 часа, выкачивая 169 вёдер воды в час. Определить какой из насосов выкачал больше вёдер.
Решение
Определим сколько всего вёдер выкачал каждый насос по отдельности. Для этого умножим их производительность на время их работы:
158 в/ч × 4 = 632 вёдер выкачал первый насос
169 в/ч × 3 = 507 вёдер выкачал второй насос
632 > 507
Ответ: первый насос выкачала больше вёдер, чем второй.
Задача 4. За 2 часа насос выкачал 80 литров воды. Определить сколько литров он выкачает за 5 часов.
Решение
Сначала нужно определить сколько литров воды насос выкачивает за час. Для этого 80 литров разделим на 2 часа — получим 40 литров
80 : 2 = 40 литров в час
За один час насос выкачивает 40 литров воды. За 5 часов выкачает в пять раз больше
40 × 5 = 200 литров
Ответ: за 5 часов насос выкачает 200 литров воды.
Если известны производительность и время работы, то можно найти выполненную работу. Выполненная работа равна производительности умноженной на время работы:
A = v × t
Например, если производительность пекаря составляет 50 булочек в час, и он проработал 4 часа, то можно найти всю выполненную работу за эти четыре часа. Для этого производительность (50 бул/ч) нужно умножить на время его работы (4ч)
50 × 4 = 200 булочек

Если известны работа и производительность, то можно найти время работы. Время работы равно отношению выполненной работы к производительности:
![]()
Например, если в неделю бригада отстраивает 2 этажа, то можно узнать сколько недель потребуется для отстройки 8 этажей. Чтобы определить время отстройки восьми этажей, нужно выполненную работу (8 этажей) разделить на производительность (2 эт./нед):
8 : 2 = 4 нед.
Либо с помощью формулы, приведенной выше:
![]()

Если в неделю строится 2 этажа, то 8 этажей будет отстроено за четыре недели. В данном случае вся работа была равна восьми. Производительность была равна двум, поскольку по определению производительность есть работа, выполненная за единицу времени – в нашем случае два этажа за неделю.
Задача 6. Принтер работает с производительностью 70 стр./ч. Сколько страниц он напечатает за 5 часов?
Решение
Если в час принтер печатает 70 страниц, то за 5 часов он напечатает в 5 раз больше:
70 × 5 = 350 страниц
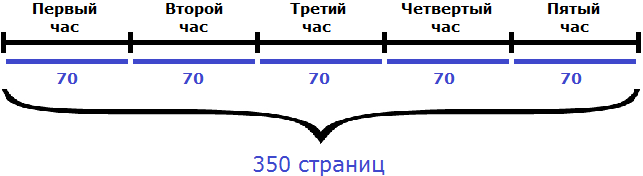
Также, решение можно записать с помощью формулы нахождения работы. В данном случае, количество напечатанных страниц являются выполненной работой:
A = v × t = 70 × 5 = 350 страниц
A = 350 страниц
Задача 7. Принтер напечатал 350 страниц за 5 часов. С какой производительностью он работал?
Решение
Если в течении пяти часов принтер напечатал 350 страниц, то в течении часа он печатал ![]() . То есть работал с производительностью 70 страниц в час:
. То есть работал с производительностью 70 страниц в час:
350 : 5 = 70 стр./ч.
Либо с помощью формулы нахождения производительности:
![]()
Задача 8. Принтер работал с производительностью 70 страниц в час и напечатал 350 страниц. Определить время работы принтера.
Решение
Выражение «работал с производительностью 70 страниц в час» означает, что в каждом часе принтер печатал по 70 страниц. И это продолжалось до тех пор, пока он не напечатал 350 страниц. Очевидно, что разделив 350 страниц по 70, мы определим время работы принтера, то есть узнаем сколько часов он работал
350 : 70 = 5 ч.
Либо с помощью формулы нахождения времени:
![]()
Задача 9. Машинистка в первый день напечатала 48 страниц рукописи, а во второй день — на 12 страниц больше, чем в первый. На всю работу в эти 2 дня она затратила 9 часов. Сколько часов работала она в каждый из этих дней, если производительность её не менялась ?
Решение
Определим сколько страниц напечатала машинистка во второй день. В условии сказано, что напечатала она на 12 страниц больше, чем в первый:
48 + 12 = 60 страниц во второй день.
Определим сколько страниц машинистка напечатала за два дня:
48 + 60 = 108 страниц за два дня.
На эту работу машинистка затратила 9 часов. Также сказано, что производительность её не менялась. Если мы разделим выполненную работу (108) на время выполнения (9), то определим производительность машинистки:
108 : 9 = 12 страниц в час.
Теперь мы можем определить сколько часов работала машинистка в каждый из двух дней. Для этого поочередно разделим выполненные работы в каждом из двух дней на производительность:
48 : 12 = 4 часа работала машинистка в первый день
60 : 12 = 5 часов работала машинистка во второй день.
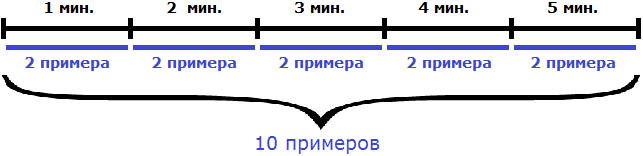
Задача 10. Джон решил 10 примеров за 5 минут. С какой производительностью он решал эти примеры?
10 примеров это выполненная Джоном работа. 5 минут — время работы. Разделим выполненную работу на время работы и определим производительность Джона:
10 : 5 = 2 примера в минуту.
Производительность Джона равна двум примерам в минуту.
Задача 11. Джон решил несколько примеров за 5 минут. С какой производительностью он решил эти примеры?
Это та же самая задача, что и предыдущая, но в ней работа не выражена каким-либо числом. Сказано лишь то, что Джон выполнил эту работу за 5 минут. Поэтому, конкретную производительность в такой задаче узнать нельзя. Но можно воспользоваться дробями. Обозначим выполненную работу через единицу. Тогда производительность работы Джона будет выражаться дробью – частью примеров, решенных за единицу времени. Если вы изучили задачи на дроби, то должны понимать о чем идёт речь.
Итак, обозначим выполненную работу через единицу:
A = 1
Мы знаем, что для нахождения производительности, выполненную работу нужно разделить на время. Время работы у нас равно пяти минутам. Поэтому, единицу делим на пять минут:
![]()
Дробь ![]() выражает часть работы, выполненную Джоном за единицу времени. Если мы вернемся к предыдущей задаче, где выполненная работа была равна десяти примерам и найдем одну пятую от этой работы, то получим 2
выражает часть работы, выполненную Джоном за единицу времени. Если мы вернемся к предыдущей задаче, где выполненная работа была равна десяти примерам и найдем одну пятую от этой работы, то получим 2
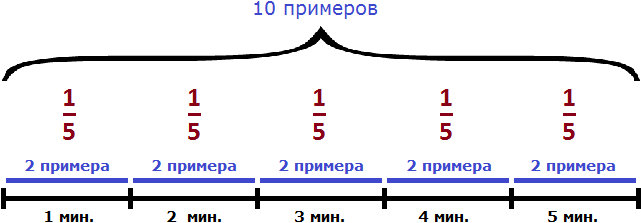
Выражать выполненную работу через единицу часто приходится при решении задач на совместную работу.
Задачи на совместную работу
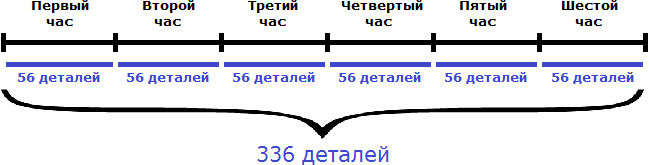
Задача 1. Первый мастер за 2 часа изготавливает 64 детали, а второй за 3 часа – 72 детали. За сколько часов они изготовят 336 деталей?
В данной задаче речь идет о совместной работе. Необходимо определить производительность обоих мастеров и найти время за которое они изготовят 336 деталей.
Для начала определим производительность первого мастера:
64 : 2 = 32 дет./час
Определим производительность второго мастера:
72 : 3 = 24 дет./час
Определим совместную производительность мастеров. Для этого сложим количество деталей, которые они изготавливают по отдельности за единицу времени. То есть сложим их производительности:
32 дет./час + 24 дет./час = 56 дет./час
Вместе за один час мастера изготавливают 56 деталей. Чтобы узнать за сколько часов они изготовят 336 деталей, нужно определить сколько раз 336 содержит по 56
336 : 56 = 6 часов
Задача 2. Первый мастер может покрасить забор за 20 минут, а второй мастер – за 30 минут. За сколько минут, работая вместе, они могут покрасить забор?
Решение
В данной задаче, в отличие от предыдущей, работа не выражена каким-либо числом. Сказано лишь то, что эту работу первый мастер может выполнить за 20 минут, а второй за 30 минут.
В такой ситуации можно воспользоваться дробями. Мы можем обозначить всю работу (покраску забора) через единицу.
Итак, обозначим работу (покраску забора) через единицу:
A = 1
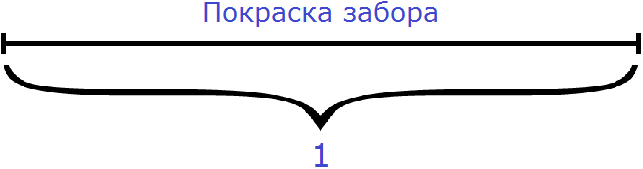
Производительность первого мастера будет выражáться дробью ![]() . То есть за одну минуту он покрасит одну двадцатую часть забора. Единица это вся работа, а двадцать минут это время работы. Запишем производительность первого мастера с помощью формулы нахождения производительности:
. То есть за одну минуту он покрасит одну двадцатую часть забора. Единица это вся работа, а двадцать минут это время работы. Запишем производительность первого мастера с помощью формулы нахождения производительности:
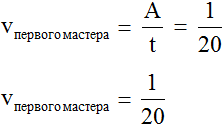
А производительность второго мастера будет выражáться дробью ![]() . То есть за одну минуту он покрасит одну тридцатую часть забора:
. То есть за одну минуту он покрасит одну тридцатую часть забора:
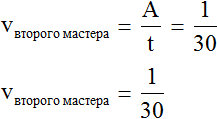
Определим общую производительность мастеров. Для этого сложим дроби, выражающие производительность первого и второго мастеров:
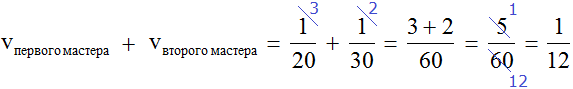
![]() это дробь, выражающая общую производительность обоих мастеров. То есть за одну минуту мастера вместе покрасят
это дробь, выражающая общую производительность обоих мастеров. То есть за одну минуту мастера вместе покрасят ![]() часть забора.
часть забора.
Определим время за которое мастера покрасят забор вместе. Для этого воспользуемся формулой нахождения времени: разделим выполненную работу на общую производительность мастеров. Выполненная работа у нас выражена единицей, а производительность — дробью ![]()
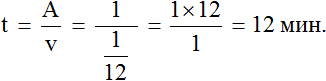
Ответ: работая вместе, мастера покрасят забор за 12 минут.
Задача 3. Первый рабочий может выполнить заказ за 8 часов, а второй за 6 часов. Два часа они работали вместе, а заканчивал работу один второй рабочий. Сколько времени потребовалось для выполнения этого заказа?
Решение
Обозначим всю работу через единицу
A = 1
Тогда первый рабочий за один час может выполнить ![]() часть работы, а второй рабочий
часть работы, а второй рабочий часть работы. А вместе за один час они могут выполнить
![]() часть работы
часть работы
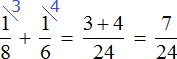
Рабочие работали вместе два часа, поэтому умножим часть работы, выполняемую ими за один час на 2:
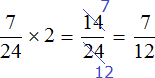
Остальную часть работы, а именно ![]() работы заканчивал один второй рабочий:
работы заканчивал один второй рабочий:
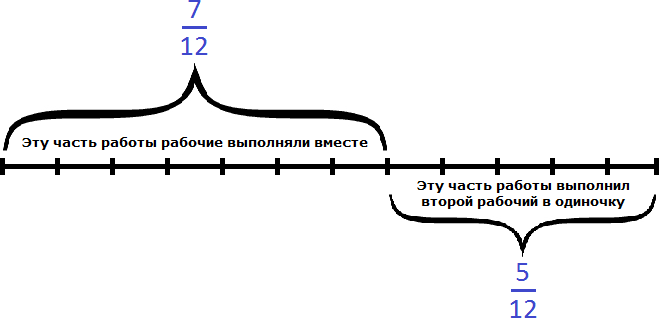
Второй рабочий за один час мог выполнить часть работы. Чтобы определить время за которое он завершил оставшуюся
![]() часть работы, воспользуемся формулой нахождения времени.
часть работы, воспользуемся формулой нахождения времени.
Переменная A теперь равна ![]() , переменная v —
, переменная v —
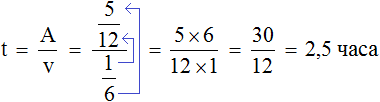
Теперь определим общее время заказа. Первые два часа рабочие работали вместе, остальную часть работы второй рабочий выполнил за два с половиной часа, отсюда имеем 4,5 ч.
2 + 2,5 = 4,5 ч.
Ответ: для выполнения заказа потребовалось 4,5 ч.
Задача 4. Одна труба наполняет бассейн за 6 ч, а другая – за 4 ч. За
сколько часов наполняют бассейн обе трубы, работая вместе?
Решение
Обозначим работу (наполнение бассейна) через единицу
A = 1
Тогда первая труба за один час выполнит часть работы, а вторая труба —
![]() часть работы. Работая вместе за один час они выполнят
часть работы. Работая вместе за один час они выполнят ![]() часть работы:
часть работы:
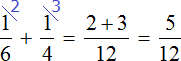
Определим время за которое обе трубы наполняют бассейн, работая вместе:
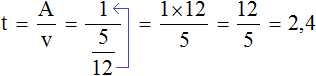
2,4 это два целых часа и четыре десятых часа
2,4 = 2 ч + 0,4 ч
А четыре десятых часа это 24 минуты
60 мин. × 0,4 = 24 мин.
Ответ: работая вместе обе трубы наполнят бассейн за 2 ч 24 мин.
Задачи для самостоятельного решения
Задача 1. Первая бригада может выполнить некоторое задание за 12 часов, вторая – за 4 часа. За сколько часов они выполнят задание, если будут работать вместе?
Решение
Обозначим работу через единицу:
A = 1
Тогда первая бригада за один час выполнит  часть работы, а вторая за один час
часть работы, а вторая за один час  часть работы. Их общая производительность равна сумме дробей
часть работы. Их общая производительность равна сумме дробей  и
и  :
:
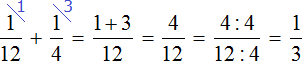
Определим время за которое обе бригады выполнят задание, работая вместе:
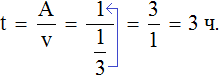
Ответ: обе бригады выполнят задание за 3 часа.
Задача 2. Лошадь съедает копну сена за 1 сутки, корова может съесть такую же копну за 3 суток, а овца за 6 суток. За какое время съедят эту копну лошадь, корова и овца вместе.
Решение
Работа в данном случае это съедание копны сена. Обозначим её через единицу:
A = 1
Тогда производительность лошади будет выражáться единицей, производительность коровы — дробью  , производительность овцы — дробью
, производительность овцы — дробью . Их совместная производительность равна следующей сумме:

Определим время, за которое лошадь, корова и овца съедят 1 копну сена:

Ответ: лошадь, корова и овца съедят 1 копну сена за суток или 16 часов.
Задача 3. Сосуд наполняется шлангом за 12 мин, а полный сосуд опорожняется при открытии крана за 20 мин. За какое время наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг?
Решение
Работа в данном случае это наполнение сосуда. Обозначим эту работу через единицу:
A = 1
В условии сказано, что сосуд наполняется шлангом за 12 минут. Значит в минуту будет наполняться  часть сосуда. При этом сказано, что одновременно открыт кран сосуда и из него вытекает вода, которой наполняется сосуд. Вода, которая вытекает равна
часть сосуда. При этом сказано, что одновременно открыт кран сосуда и из него вытекает вода, которой наполняется сосуд. Вода, которая вытекает равна  части сосуда, поскольку в условии сказано, что полный сосуд опорожняется за 20 минут.
части сосуда, поскольку в условии сказано, что полный сосуд опорожняется за 20 минут.
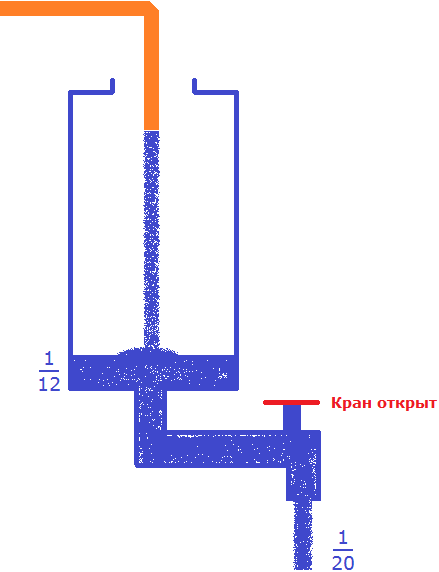
В сосуд поступает воды больше, чем вытекает. Дробь  больше, чем
больше, чем  .
.
Несмотря на то, что часть поступающей в сосуд воды будет вытекать, с каждой минутой сосуд будет пополняться на определенную часть. Узнаем, что эта за часть. Для этого из поступающей  части вычтем ту часть, которая вытекает:
части вычтем ту часть, которая вытекает:
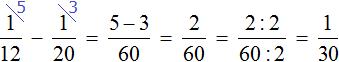
Каждую минуту сосуд будет наполняться на  .
.
Определим время за которое наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг:
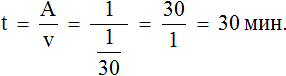
Ответ: если одновременно открыть кран и вливать в пустой сосуд воду через шланг, то он наполнится за 30 минут.
Задача 4. Через первую трубу бассейн можно заполнить за 20 ч, через вторую за 30 ч. Какая часть бассейна заполнится через обе трубы за 1 ч?
Решение
Работа в данном случае это заполнение бассейна. Обозначим эту работу через единицу:
A = 1
Производительность заполнения бассейна через первую трубу будет выражáться дробью  , через вторую трубу — дробью
, через вторую трубу — дробью  . Совместная производительность будет выражáться дробью
. Совместная производительность будет выражáться дробью 

Производительность по определению есть работа, выполненная за единицу времени. Значит дробь  является ответом к задаче, поскольку нас интересовало какая часть бассейна заполнится через обе трубы за 1 час. Это можно проверить, воспользовавшись формулой нахождения работы. Переменная v у нас имеет значение
является ответом к задаче, поскольку нас интересовало какая часть бассейна заполнится через обе трубы за 1 час. Это можно проверить, воспользовавшись формулой нахождения работы. Переменная v у нас имеет значение  , а переменная t равна единице (одному часу). Формула нахождения работы позволит нам определить какая часть работы будет выполнена за 1 час:
, а переменная t равна единице (одному часу). Формула нахождения работы позволит нам определить какая часть работы будет выполнена за 1 час:
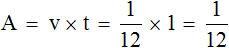
Ответ: за один час заполнится  часть бассейна.
часть бассейна.
Задача 5. На прокладку траншеи требуется затратить 10 ч. Экскаватор проработал 8 ч, после чего ему осталось пройти 50 м. Найти общую длину траншеи.
Решение
В задаче подразумевается, что экскаватор работал с одинаковой производительностью на протяжении всей работы. На работу требовалось затратить 10 ч. Проработано было 8 ч. Значит осталось еще 2 часа. На 2 часа приходятся оставшиеся 50 метров траншеи. Если разделить 50 метров на 2, то можно определить сколько метров экскаватор прокладывает за один час:
50 : 2 = 25 м./ч
В час экскаватор прокладывал 25 метров. Работал он 10 часов. Умножим 25 на 10, мы определим общую длину траншеи:
25 × 10 = 250 м
Ответ: общая длина траншеи составляет 250 м.
Задача 6. Ванна заполняется холодной водой за 6 мин 40 с, горячей – за 8 мин. Кроме того, если из полной ванны вынуть пробку, вода вытечет за 13 мин 20 с. Сколько времени понадобится, чтобы наполнить ванну полностью, при условии, что открыты оба крана, но ванна не заткнута пробкой?.
Решение
Для удобства переведем время данное в задаче в секунды
6 мин 40 с = 400 с
8 мин = 480 с
13 мин 20 с = 800 с
Обозначим заполнение ванны через единицу:
A = 1
Производительность первого крана будет выражáться дробью  , производительность второго крана — дробью
, производительность второго крана — дробью  . Совместная производительность обоих кранов равна сумме дробей
. Совместная производительность обоих кранов равна сумме дробей  и
и 
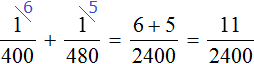
Одновременно с открытыми двумя кранами, вынута пробка из ванны. Поэтому часть поступающей в ванну воды сразу выходит через слив. Эта часть будет выражáться дробью 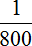 .
.
С каждой секундой ванна будет пополняться на определенную часть воды. Узнаем какая это часть. Для этого из поступающей части воды вычтем ту часть, которая вытекает через слив.

Определим сколько времени понадобится, чтобы наполнить ванну:
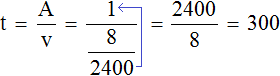
Ванна наполнится за 300 секунд. Поскольку задача завершена, секунды можно обратно перевести в минуты. Триста секунд это пять минут:
300 : 60 = 5 мин
Ответ: ванна заполнится за 5 мин.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Ничего сложного в задачах на формулу работы нет.
V – производительность труда – работа, которую выполнили за единицу времени.
t – время
А – работа.
Чтобы найти производительность, надо работу разделить на время:
V = A : t
Чтобы найти работу, надо производительность умножить на время.
A= V * t
Чтобы найти время, надо работу разделить на производительность.
t = A : V
Задачи для тренировки:
- Одна девочка рисует за неделю 25 рисунков, другая – 35 рисунков. Сколько всего рисунков нарисуют девочки за 2 дня?
- Производительность самого большого станка 5шт/час. За какое время на этом станке выточат 100 деталей?
- За 81 минут бабушка связала 9 шнурков. Сколько времени тратила бабушка на 1 шнурок.
- Дашин принтер за 10 секунд напечатал 500 листов. Какова производительность принтера?
- Я съедаю за 1 минуту 2 семечка. Сколько семечек я съем за 37 минут?
- Коля напечатал на компьютере 320 знаков за 8 минут. С какой скоростью печатает Коля?
- В первый день Наташа слепила из пластилина 12 шариков за 6 минут, а на следующий день за это же время 18 шариков. В какой день производительность Наташи была выше и насколько?
- Бригада Саши изготовляет 276 деталей за 6 часов, а бригада Поли – 336 деталей за 8 часов. У какой бригады производительность труда выше и на сколько?
- Производительность труда у бабушки 3 шарфика в месяц. Сколько шарфиков свяжет бабушка за год?
- Команда девочек за 3 часа собрала 33 кг яблок, а команда мальчиков за 5 часов собрала 55 кг яблок. У какой команды производительность труда выше и на сколько?
- Катя вышивает 3 цветочка за час. Сколько цветочков вышьет Катя за 3 часа?
- Люда прочитала книгу за 6 дней. Сколько страниц читывала Люда каждый день, если в книге 360 страниц? А Людина мама напечатала 240 страниц доклада за такое же количество дней. Сколько страниц в день печатала мама?
- Папа сделал 49 деревянных кубиков за 7 дней. Какова его производительность труда?
- За 100 дней сколько столяр сделает лавочек, если его производительность 2 лавочки в день?
- Тетя шьет 5 мягких игрушек за 25 дней. Какова ее производительность труда?
- Повар состряпал 45 пирожков за 3 часа. Какова его производительность?
Файл для распечатки.
2-й способ решения — без таблицы
Как обойтись без составления таблицы?
Сразу составить уравнение.
Для этого определим, какая величина нам не нужна в уравнении, чтобы затем приравнять.
Производительность? Ее и надо найти. Работа? Она нам дана по условию, поэтому глупо от нее избавляться. Остается время: оно нам и неизвестно, и не нужно.
Слева от знака равно будем писать формулу времени для первого рабочего, а справа – для второго.
Напомню, что первый работал на ( displaystyle 2) часа дольше, поэтому к времени второго надо будет прибавить ( displaystyle 2):
( displaystyle frac{112}{x}=frac{112}{x+1}+2)
То же самое уравнение, что и в первом способе, только без таблицы и системы уравнений.
А теперь вспомним, что я говорил в сааамом начале: задачи на работу и на движение – это то же самое. Спорное заявление, да? Ну, давай проверим, есть ли аналогия.
Во-первых, сравним формулы:
| Движение | Работа |
| ( displaystyle v=frac{S}{t}) | ( displaystyle P=frac{A}{t}) |
| Скорость движения | Скорость выполнения работы, т.е. производительность |
| Пройденный путь | Выполненная работа |
| Потраченное на движение время | Потраченное на работу время |
Теперь рассмотрим задачу:
Пример №1
Расстояние ( displaystyle 112) км первый велосипедист проезжает на ( displaystyle 2) часа дольше, чем второй.
Сколько км в час проезжает первый велосипедист, если известно, что второй за час проезжает на один километр больше, чем первый?
Ничего не напоминает? Да я же просто заменил слова: «Заказ» на «расстояние», «деталь» на «километр», «рабочий» на «велосипедист», «выполняет» на «проезжает». Суть осталась той же. Даже решение будет точно таким же (разберу здесь только II способ – без таблицы).
Пусть скорость первого ( displaystyle x), тогда второго ( displaystyle x+1). Сколько времени едет первый? ( displaystyle frac{112}{x}). Сколько времени едет второй? ( displaystyle frac{112}{x+1}). На сколько время первого больше, чем второго? На ( displaystyle 2) часа:
( displaystyle frac{112}{x}=frac{112}{x+1}+2).
То же самое уравнение! Вот и получается, что работа и движение – одно и то же.
Как решать задачи на совместную работу
Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).
Пример №2
Первая труба заполняет бассейн за ( displaystyle 6) часов, а вторая – за ( displaystyle 4).
За какое время они заполнят бассейн, работая вместе?
Решение
Во-первых, давай придумаем аналогию с движением.
Придумал?
Бассейн – это путь. Допустим, из ( displaystyle A) в ( displaystyle B). Итак, первый автомобиль проезжает путь ( displaystyle AB) за ( displaystyle 6) часов, второй – за ( displaystyle 4).
А теперь как сформулировать вопрос? За какое время они проедут весь путь, двигаясь вместе? Бред.
Если двигаться параллельно, то каждый проходит весь путь самостоятельно. А в какой ситуации нам важно, какой путь автомобили проходят в сумме? Все гениальное просто: если они движутся навстречу друг другу!
Тогда что нас просят найти? Время, через которое они встретятся.
Поразмысли немного над этой аналогией. Все понял? Тогда идем дальше.
Какова «скорость» (а по-настоящему, производительность) первого? Путь (работа) деленный на время: ( displaystyle {{P}_{1}}=frac{A}{{{t}_{1}}}=frac{A}{6}). А второго? ( displaystyle {{P}_{2}}=frac{A}{{{t}_{2}}}=frac{A}{4}).
С какой производительностью работают две трубы вместе (не забывай, это задачи на совместную работу)? Берем количество литров, которое налила в бассейн первая труба за один час, прибавляем количество литров, которое налила в бассейн вторая труба за один час, – именно столько наливают в бассейн обе трубы за один час. То есть производительности складываются:
( displaystyle P={{P}_{1}}+{{P}_{2}})
То же самое, что и относительная скорость: с какой скоростью второй автомобиль приближается к первому? Со скоростью, равной сумме скоростей: ( displaystyle v={{v}_{1}}+{{v}_{2}}).
Итак,
( displaystyle P={{P}_{1}}+{{P}_{2}}=frac{A}{6}+frac{A}{4}=frac{5A}{12}).
Тогда время, за которое с такой производительностью будет выполнена работа ( A):
( displaystyle t=frac{A}{P}=frac{A}{frac{5A}{12}}=frac{12}{5}=2,4) (ч)
Итак, правило:
При совместной работе производительности складываются
А теперь давай рассмотрим самый сложный пример, научившись решать который, ты сможешь с легкостью справится с любой задачей на ЕГЭ.
Пример 8
На изготовление ( displaystyle 600) деталей первый рабочий тратит на ( displaystyle 10) часов меньше, чем второй рабочий на изготовление ( displaystyle 500) таких же деталей. За какое время, работая совместно, они изготовят партию в ( displaystyle 1000) деталей, если известно, что за час первый рабочий делает на ( displaystyle 5) деталей больше?
Решение:
Давай определимся, что нам нужно найти? Нам нужно найти время, за которое рабочие изготовят ( displaystyle 1000) деталей, то есть: ( displaystyle frac{1000}{{{P}_{1}}+{{P}_{2}}}).
Значит, нужно найти ( displaystyle {{P}_{1}}) и ( displaystyle {{P}_{2}}).
Первый рабочий за час делает на ( displaystyle 5) деталей больше. Обозначим производительность первого рабочего за х, тогда производительность второго – ( displaystyle x-5).
( displaystyle 600) деталей первый рабочий делает за ( displaystyle {{t}_{1}}) часов, а ( displaystyle 500) таких же деталей второй рабочий делает за ( displaystyle {{t}_{2}}={{t}_{1}}+10) часов.
То есть: ( displaystyle {{t}_{1}}=frac{600}{x}, a {{t}_{2}}={{t}_{1}}+10=frac{500}{x-5}).
Приравняв ( displaystyle {{t}_{1}}), получаем уравнение:
Математика
5 класс
Урок № 69
Задачи на совместную работу
Перечень рассматриваемых вопросов:
– введение понятий производительность, общая производительность, время работы;
– алгоритм решения задач на совместную работу арифметическим способом;
– отработка применения алгоритма при решении задач.
Тезаурус
Производительность (Р) – объём работы, выполняемый за единицу времени.
Время работы (Т) – время выполнения всей работы.
Общая производительность – объём работы, выполняемый совместно всеми работниками за единицу времени.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 классы. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
На предыдущих уроках мы научились выполнять арифметические действия с обыкновенными дробями. Сегодня мы рассмотрим, как с помощью обыкновенных дробей решать задачи на совместное выполнение некоторой работы.
Под совместной работой можно понимать абсолютно любое действие: и одновременный поток воды из двух труб при наполнении бассейна, и изготовление деталей двумя рабочими, и вспашку поля несколькими тракторами, и набор текста на компьютере.
Всю работу мы будем принимать за единицу. А объём выполненной работы выражать как часть этой единицы.
Если какая-то работа выполняется за шесть часов, то за час выполняется одна шестая часть этой работы.


Объём работы, выполненный за единицу времени, называется производительностью. Она обозначается как Р.
Рассмотрим задачу.
Первый столяр может выполнить заказ за 36 часов, а второй – за 18 часов. За сколько часов этот заказ выполнят оба столяра, работая вместе?
Вся работа – 1
1-й столяр – 36 ч
2-й столяр – 18 ч
1-й и 2-й столяр – ? ч
(первый столяр за один час, или производительность Р1 первого столяра)


(второй столяр за один час, или производительность Р2 второго столяра)


(оба столяра за один час, или общая производительность Р)


(время выполнения всей работы совместно)


Ответ: за 12 ч.
Рассмотрим следующую задачу.
Одна труба заполняет бассейн за 60 минут, а вторая – за 20 минут. За сколько минут заполнится бассейн при включении обеих труб?
Вся работа – 1
1-я труба – 60 минут
2-я труба – 20 минут
Обе трубы – ?
часть бассейна (наполняет первая труба за одну минуту, или производительность Р1)


часть бассейна (наполняет вторая труба за одну минуту, или производительность Р2)


часть бассейна (заполняют обе трубы, работая вместе, или общая производительность Р)


минут (время заполнения бассейна двумя трубами)


Ответ: за 15 минут.
Рассмотрим задачу, в которой, зная время выполнения работы совместно, надо найти время работы одного из участников.
Работая вместе, два мастера Гжели выполняют заказ за шесть дней. Первый мастер, работая один, может выполнить этот заказ за 10 дней. За сколько дней этот заказ может выполнить второй мастер?
Вся работа – 1
1-й и 2-й мастер – 6 дней
1-й мастер – 10 дней
2-й мастер – ? дней
часть заказа (первый и второй мастера за один день, или общая производительность Р)


часть заказа (первый мастер за один день, или производительность Р1)


часть заказа (выполнит второй мастер за один день, или производительность Р2)


дней – время выполнения заказа вторым мастером


Ответ: за 15 дней.
Алгоритм решения задач на совместную работу
Т1 – время, за которое первый объект самостоятельно выполнит всю работу;
Т2 – время, за которое второй объект самостоятельно выполнит всю работу.
- Всю выполненную работа принимаем за единицу.
- Находим часть работы, выполненную первым объектом за единицу времени (производительность Р1 = 1 ꞉ Т1).
- Находим часть работы, выполненную вторым объектом за единицу времени (производительность Р2 = 1 ꞉ Т2).
- Находим часть работы, выполненную двумя (или более) объектами за единицу времени (общая производительность Р = Р1 + Р2).
- Находим время, затраченное на выполнение всей работы всеми объектами (Т = 1 ꞉ Р).
Тренировочные задания
№ 1. Путешественник планирует пройти маршрут за семь дней. Какую часть маршрута он пройдёт за один день? За три дня? За пять дней? Какая часть маршрута останется не пройденной за эти же промежутки времени? Используйте следующие значения ; ; ; ; .












За 1 день
Пройденная часть маршрута – ?
Осталось пройти – ?
За 3 дня
Пройденная часть маршрута – ?
Осталось пройти – ?
За 5 дней
Пройденная часть маршрута – ?
Осталось пройти – ?
Пройденная часть маршрута за день – это производительность путешественника. И находится она так же, как и другая производительность. Найдём часть маршрута, пройденную за один день:


Очевидно, что за три дня путешественник пройдет в три раза больше, чем за день. Рассчитаем эту часть пути:


Чтобы найти оставшуюся часть маршрута, надо из всего маршрута, то есть единицы, вычесть пройденную часть. Найдём, например, какую часть маршрута осталось пройти через три дня: .


Аналогично действуем и в остальных случаях.
Правильный ответ:
За 1 день
Пройденная часть маршрута –


Осталось пройти –


За 3 дня
Пройденная часть маршрута –


Осталось пройти –


За 5 дней
Пройденная часть маршрута –


Осталось пройти –


№ 2. Подберите к каждому действию правильное пояснение.
Два тракториста вспахали поле за 6 ч совместной работы. Первый тракторист мог бы один выполнить ту же работу за 10 ч. За сколько часов второй тракторист может вспахать поле?
Пояснения к действиям:
- Время выполнения всей работы вторым трактористом;
- Общая производительность обоих трактористов;
- Часть всей работы, выполняемая вторым трактористом за один час.
Действия:






Рассмотрим первое действие. Единица делится на шесть, где единица – это вся работа, а шесть – время совместной работы. Значит, этим действием мы находим общую производительность обоих тракторов.
Во втором действии из общей производительности вычитаем . Так как первый тракторист выполняет работу за 10 часов, то – это производительность первого тракториста. Значит, мы находим производительность второго тракториста, то есть объём работы, который он выполнил за один час.




В третьем действии единица (вся работа) делится на производительность второго тракториста: таким образом, мы находим время выполнения всей работы вторым трактористом.
Правильный ответ:
– это общая производительность обоих трактористов.


– это часть всей работы, выполняемая вторым трактористом за 1 ч.


ч – это время выполнения всей работы вторым трактористом.


Производительность труда в задаче 17
2 октября 2015
Задачи этого типа появились в ЕГЭ относительно недавно, но застали врасплох как учеников, так и многих учителей. А всё потому что решаются они с помощью производной — инструмента, совершенно непривычного для второй части экзамена.
Задача 17. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно ${{t}^{2}}$часов в неделю, то за эту неделю они производят $3t$единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно ${{t}^{2}}$часов в неделю, то за эту неделю они производят $4t$единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.
В приведённом условии есть важный момент, после осознания которого у вас вообще не будет проблем с решением подобных задач. Дело в том, что величина $t$, указанная для первого завода и для второго — это не одно и то же число! Другими словами, суммарное время рабочих на первом и другом заводе будет разным.
Для решения введём новые переменные: ${{a}^{2}}$ — суммарное время рабочих на первом заводе, ${{b}^{2}}$ — суммарное время на втором. С учётом производительности получим:
$begin{align}& {{a}^{2}}to 3a \& {{b}^{2}}to 4b \end{align}$
Таким образом, затратив суммарно ${{a}^{2}}+{{b}^{2}}$ часов времени, мы получим $3a+4b$ единиц продукции в неделю. Всё остальное — элементарная математика, подробно описанная в видеоуроке:
В прошлый раз мы рассматривали довольно «противные» задачи, связанные с вычислением времени в задачах про кредиты. Но это было очень просто по сравнению с тем, что мы будем рассматривать сегодня, а именно экономическую задачу 17 про производительность труда, в которой требуется применять производную. Эти задачи появились в ЕГЭ по математике относительно недавно, и те, кто уже с ними столкнулся, оценили, что, во-первых, условие таких задач довольно длинное, а, во-вторых, в каждой из таких задач есть неприятная зацепка, на которой «прогорели» очень многие ученики.
Думаю, вы уже догадались, что речь идет о той самой задачи 17, когда у Григория есть два завода, и еще указана производительность труда, и требуется оценить, какое наибольшее количество продукции можно произвести на этих двух заводах, если распределить нагрузку оптимально. Но на самом деле, в этих задачах 17 нет ничего сложного, даже чуть проще, чем многие задачи на кредиты. Поэтому сейчас мы рассмотрим одно из таких заданий, внимательно пробежимся по каждому пункту и посмотрим, как именно должно выглядеть идеальное ее решение.
Задача № 1
Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно ${{t}^{2}}$ часов в неделю, то за эту неделю они производят $3t$ единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно ${{t}^{2}}$ часов в неделю, то за эту неделю они производят $4t$. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.
Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Шаг первый: вводим переменные
Прежде всего, перед тем как переходить к непосредственному решению задачи 17 из ЕГЭ по математике, попытаться что-то посчитать, составить какие-то формулы, поймите одну простую вещь: величина ${{t}^{2}}$, данная и в первом, и во втором предложении, никак не связаны друг с другом. Коэффициент $t$ нам дан исключительно для того, чтобы сравнить производительность на разных заводах при одинаковом расходе времени. Думаю, это сравнение абсолютно очевидно: на первом производительность составляет $3t$, а на втором — $4t$, т.е. чуть побольше. На практике это означает следующее: давайте распишем, что происходит на каждом из них.
На первом заводе у нас расходуется ${{a}^{2}}$ времени (после замены) и производится $3a$ единиц продукции. На втором — ${{b}^{2}}$ времени и $4b$ продукции.
А теперь давайте сложим расходы времени и суммарный выпуск продукта.
Получим, что суммарный расход времени составляет ${{a}^{2}}+{{b}^{2}}$, а суммарный расход продукции — $3a+4b$. При этом еще раз обращаю ваше внимание: никто не говорил, что ${{a}^{2}}$ и ${{b}^{2}}$ должны быть равны. Ключевое слово здесь «если» и в первом, и во втором случае. Именно поэтому мы так смело меняем коэффициенты $t$ на $a$ в первом случае и на $b$ во втором случае.
Шаг второй: составляем и решаем уравнение
Давайте посмотрим, что у нас получилось. ${{a}^{2}}+{{b}^{2}}$ — это суммарный расход времени. Поскольку Григорий платит рабочему 500 рублей за каждый час работы, то всего он сможет заплатить такую сумму:
[500cdot left( {{a}^{2}}+{{b}^{2}} right)=5000000]
Вот и первое уравнение.
На самом деле, основная сложность этой задачи 17 про производительность труда — вовсе не составление уравнения. Она состоит в том, что нужно понять, что на первом и на втором заводе время разное. Именно поэтому для первого мы везде заменили $t$ на $a$, а для второго — $t$ на $b$. В итоге как вы сейчас увидите, мы получим одно уравнение с двумя неизвестными, которое легко упрощается — одна неизвестная легко выражается через другую. И поэтому вся функция, выражающая количество произведенного товара, на самом деле зависит от одной-единственной переменной, в нашем случае это будет переменная $a$.
Далее, я думаю, все понятно: у нас есть функция, отрезок, на котором эта функция рассматривается, а все, что нам требуется найти — это наибольшее значение этой функции на данном отрезке. Вообщем, классическая задача для применения производных, в нашем случае новая задача 17 из ЕГЭ по математике.
Суммарный выпуск продукции ($S$) равен:
[S=3a+4bto max ]
Вот теперь задача и проявилась: имея ограничение на $a$ и $b$, нам нужно добиться того, чтобы $S$ принимала свое максимальное значение. Для начала давайте немножко поработаем с уравнением: $$
[500cdot left( {{a}^{2}}+{{b}^{2}} right)=5000000left| :500 right.]
[{{a}^{2}}+{{b}^{2}}=10000]
Отсюда выразим $b$:
[{{b}^{2}}=10000-{{a}^{2}}]
[b=sqrt{10000-{{a}^{2}}}]
Конечно, тут следовало бы перед выражением поставить $pm $, однако у нас речь идет о времени, а оно не может быть отрицательным, поэтому мы берем положительное значение. Итого суммарный объем выпускаемого товара может быть выписан как функция от одной-единственной переменной $a$:
[S=3a+4sqrt{10000-{{a}^{2}}}]
Шаг третий: находим максимальное значение функции
Теперь нам нужно найти максимальное значение этой функции на всей области определения, а совершенно очевидно, что величину $a$, т.е. количество товара, выпущенного на первом заводе, увеличивать до бесконечности нельзя, просто потому что корень имеет конкретную область определения — величина, стоящая под корнем, не должна быть отрицательной. Давайте запишем это:
[10000-{{a}^{2}}ge 0]
[{{a}^{2}}le 10000]
[left| a right|le 100]
[ain left[ 0;100 right]]
Итого мы получили классическую задачу из первой части ЕГЭ по математике: у нас есть функция, есть интервал, соответственно, нужно найти максимальное значение этой функции на заданном интервале. Давайте считать производную:
[{S}’=3+4cdot frac{1cdot left( 10000-{{a}^{2}} right)}{2sqrt{10000-{{a}^{2}}}}=3+frac{4cdot left( -2a right)}{2sqrt{10000-{{a}^{2}}}}=]
[=3-frac{4a}{sqrt{10000-{{a}^{2}}}}]
[3-frac{4a}{sqrt{10000-{{a}^{2}}}}=0]
Решаем полученное уравнение:
[3=frac{4a}{sqrt{sqrt{10000-{{a}^{2}}}}}]
[3sqrt{10000-{{a}^{2}}}=4a]
[9left( 10000-{{a}^{2}} right)=16{{a}^{2}}]
[90000-9{{a}^{2}}=16{{a}^{2}}]
[25{{a}^{2}}=90000]
[5a=3cdot 100]
[a=frac{3cdot 100}{5}=60]
Теперь, зная, чему равно $a$, легко найти $b$:
[b=sqrt{10000-3600}=sqrt{6400}=80]
Однако для полного и обоснованного решения необходимо понять знак производной. Давайте начертим числовую прямую и отметим на ней $a=60$ и посмотрим, что происходит при $a gt 60$:
Например, если взять $a=99$ мы получим следующее:
[10000-{{99}^{2}}={{100}^{2}}-{{99}^{2}}=left( 100-99 right)left( 100+99 right)=199]
Если посмотрим на исходное выражение, то очевидно, что $sqrt{199} lt 99$, но посчитав его, получаем в ответе отрицательное число.
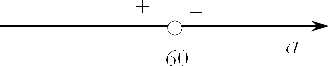
Отсюда следует, что$a=60$является точкой максимума, т.е. именно той, которую мы и хотели найти. Именно в ней наша исходная функция принимает исходное значение. Осталось подставить в $S$ полученное значение $a$ и $b$:
[S=3cdot 60+4cdot 80=180+320=500]
Окончательный ответ: 500 единиц товара.
Нюансы решения
Как видите, все оказалось не так уж и сложно. Единственно, что нам нужно запомнить — это то, что величина ${{t}^{2}}$, когда речь идет о первом заводе дает нам информацию о производительности труда именно на нем, т.е. связывает время, затраченное на производство и количество продукции в рамках только него.
Величина ${{t}^{2}}$, относящаяся ко второму заводу, говорит нам именно о нем и никак не связана с первым.
Более того, считать, что количество времени, затраченного рабочими на первом и на втором заводах, абсолютно одинаково — это вообще глупость, потому что в этом случае полученное уравнение оказалось бы намного проще и решалось бы как элементарное линейное: нам бы не потребовалось никаких производных, никаких доказательств, что мы получили точку максимума — мы просто бы разделили зарплату между рабочими первого и второго производств пополам.
Поэтому запомните: время, потраченное на первом и на втором заводах, разное, поэтому пусть на первом потрачено ${{a}^{2}}$ времени, а на втором — ${{b}^{2}}$. В этом случае задача действительно становится сложнее, при этом интересней и вполне достойной называться задачей 17 из ЕГЭ по математике.
Задача № 2
А в качестве десерта предлагаю решить еще одну такую же задачу 17 из ЕГЭ по математике, однако выкладки в этот раз будут минимальными, по возможности такими, какие и нужно делать на экзамене по математике.
Сергей владеет двумя промышленными заводами, выпускающими одинаковую продукцию. На втором заводе установлено современное оборудование, поэтому на нем может быть выпущено больше единиц продукции. Известно, что если рабочие первого завода суммарно трудятся ${{t}^{2}}$ часов в неделю, то выпускают $t$ единиц продукции. А если рабочие второго завода суммарно трудятся ${{t}^{2}}$ часов в неделю, то выпускают $2t$ единиц продукции. Ставка заработной платы рабочего составляет 500 рублей в час.
Сергей готов платить рабочим 30 250 000 рублей в неделю. На какое максимальное количество единиц продукции он может рассчитывать?
Шаг первый: вводим переменные
Если рабочие на первом заводе трудятся ${{x}^{2}}$, то это дает нам $x$ единиц товара. На втором ${{y}^{2}}$ времени дает нам $y$ товаров. Вновь складываем расходы времени — ${{x}^{2}}+{{y}^{2}}$ и отдельно складываем объем продукции — $x+2y$. Величина ${{x}^{2}}+{{y}^{2}}$ — это суммарный расход времени за неделю.
Шаг второй: составляем и решаем уравнение
Поскольку за каждый час работы платится 500 рублей, то суммарный расход денег за неделю составит:
[500cdot left( {{x}^{2}}+{{y}^{2}} right)=30250000]
[{{x}^{2}}+{{y}^{2}}=60500]
Таким способом, ограничения на ${{x}^{2}}$ и ${{y}^{2}}$ найдены.
Теперь необходимо записать сумму:
[S=x+2yto max ]
Опять же будем считать производную, но для этого сначала необходимо выразить $y$ через $x$:
[{{y}^{2}}=60500-{{x}^{2}}]
[y=sqrt{60500-{{x}^{2}}}]
Подставляем найденное значение $y$ в нашу формулу и получаем:
[S=x+2cdot sqrt{60500-{{x}^{2}}}]
Находим производную этой конструкции:
[{S}’=1+2frac{1left( -2x right)}{2sqrt{60500-{{x}^{2}}}}=1-frac{2x}{sqrt{60500-{{x}^{2}}}}]
Вновь приравниваем полученное выражение к нулю:
[1-frac{2x}{sqrt{60500-{{x}^{2}}}}=0]
[frac{1}{1}=frac{2x}{sqrt{60500-{{x}^{2}}}}]
[sqrt{60500-{{x}^{2}}}=2x]
[60500-{{x}^{2}}=4{{x}^{2}}]
[60500=5{{x}^{2}}]
[{{x}^{2}}=frac{60500}{5}=121cdot 100]
[x=11cdot 10=110]
Шаг третий: находим максимальное значение функции
Мы получили критическую точку функции $S$. Теперь необходимо доказать, что это точка максимума. Для этого начертим вновь прямую, отметим на ней полученную точку 110 и возьмем любое число, больше чем 110. Однако для упрощения дальнейших выкладок предлагаю взять не рандомное число как в прошлый раз, а посчитать его с помощью следующего метода. Для начала давайте найдем $y$. Запишем такое выражение:
[y=2x=220]
Очевидно, что 220 больше 110, и если мы поставим его в нашу функцию, то получим число на отмеченном интервале:
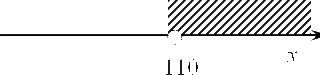
Давайте подставим:
${S}’left( 220 right)=1-frac{2cdot 220}{sqrt{60500-{{220}^{2}}}}=1-frac{440}{sqrt{60500-48400}}=$
$=1-frac{440}{sqrt{12100}}=1-frac{440}{110}=1-4=-3$
Следовательно, справа от числа 110 мы получаем отрицательную производную, а слева, естественно, будет положительная.
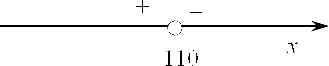
Итого 110 — точка максимума. Это является строгим обоснованием.
Теперь подставляем в выражение $x$ и $y$, которые мы нашли:
[S=110+2cdot 220=110+440=550]
Ответ: 550 единиц товара.
Ключевые моменты решения задач17 на производительность труда из ЕГЭ по математике
Все, что нам нужно знать — это:
- Правило вычисления производных сложных функций.
- Правила решения несложных уравнений.
Кроме того, хотел бы отметить, что не надо бояться работать с большими числами. Такие выражения, когда у нас появляются пятизначные и более числа, абсолютно типичны для последних задач 17 из ЕГЭ по математике, потому что они реально трудные. Но на самом деле, в этих задачах из ЕГЭ нет ничего трудного. Вам только нужно знать следующее:
- ${{a}^{2}}to a$ и ${{b}^{2}}to 2b$ — как связано затраченное время с объемом выпущенного товара;
- $S=a+2bto max $ — суммарный объем товара находится по несложной формуле.
Кроме того, необходимо понимать, как связано время, затраченное на первом производстве и на втором, т.е. каковы максимальны ограничения на это время.
А дальше дело техники: считаем производную, решаем уравнение, подставляем в исходное ограничение и получаем окончательный ответ.
Надеюсь, это видео поможет вам построить собственный завод, где вы будете платить рабочим по 30 млн. рублей в неделю, если такой суммы вам окажется недостаточно, заходите на наш сайт, подписывайтесь на паблик ВКонтакте и на канал в YouTube. До новых встреч!
Смотрите также:
- Задачи на кредит с плавающим платежом

- Задачи с экономическим содержанием — основные формулы

- Тест к уроку «Что такое логарифм» (средний)

- Решение задач B12: №440—447

- Как решать задачу 18: графический подход

- Нестандартные задачи B2: кредит в банке

