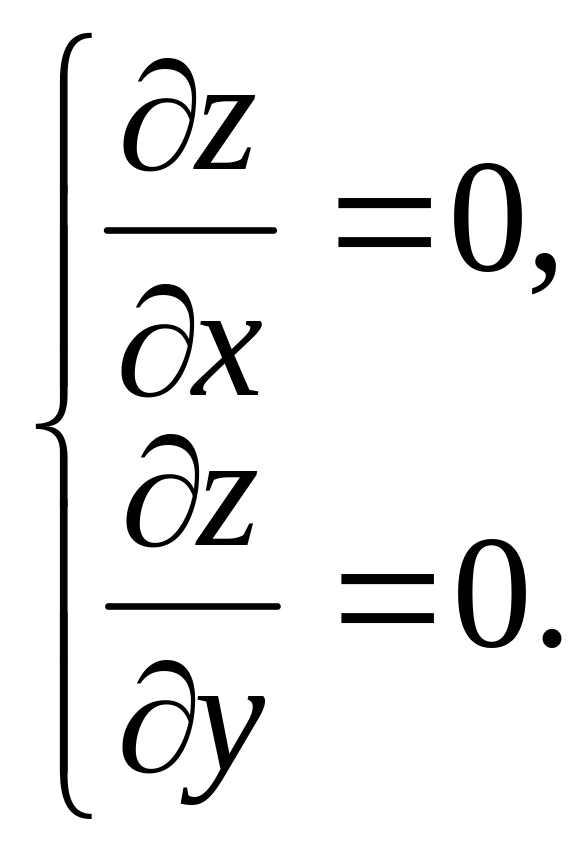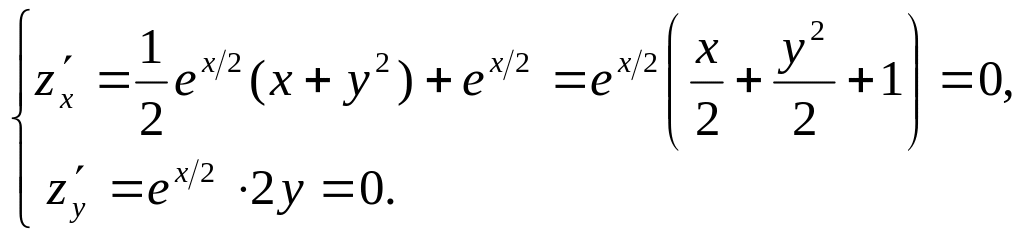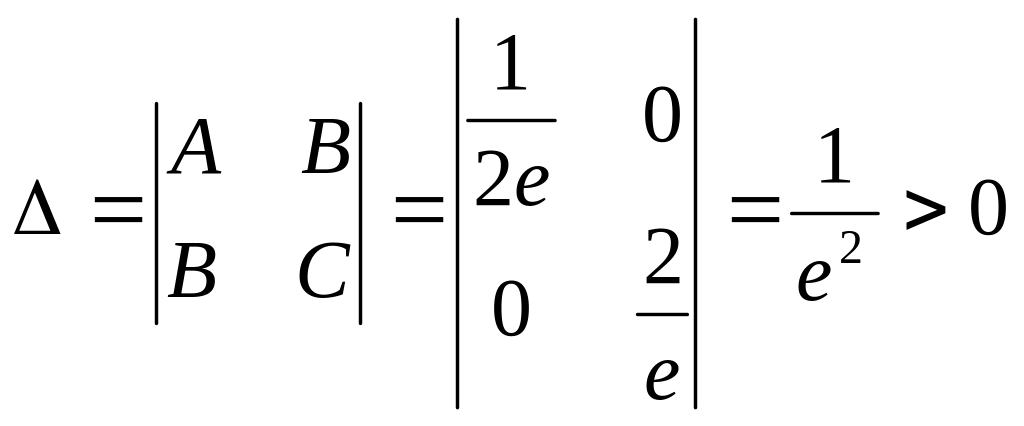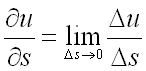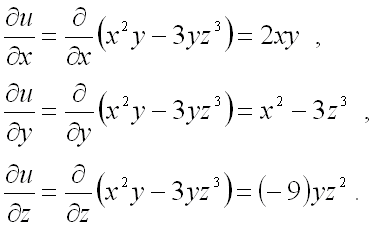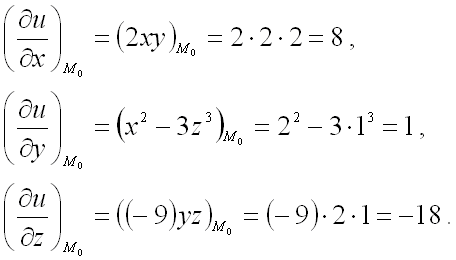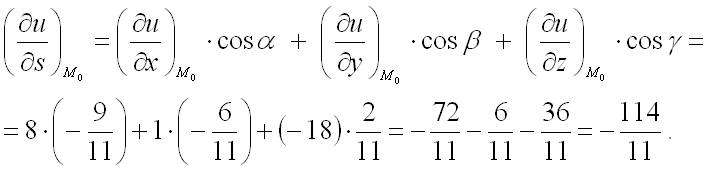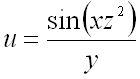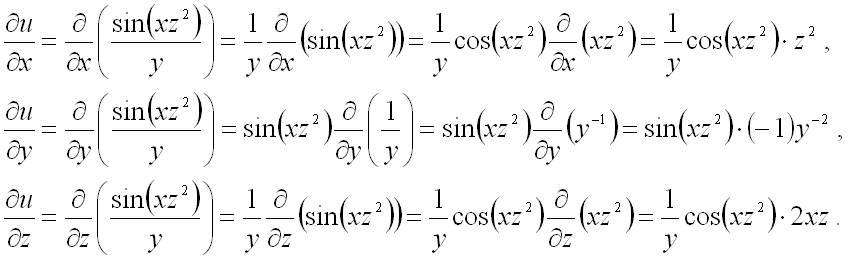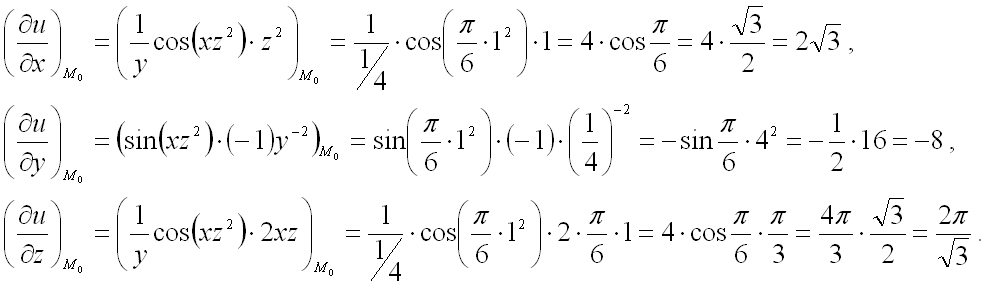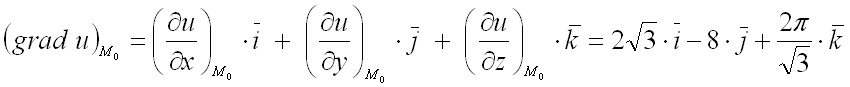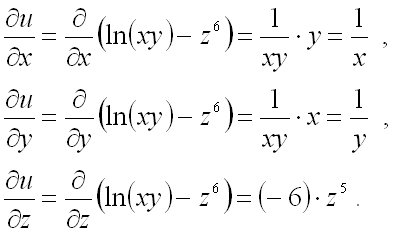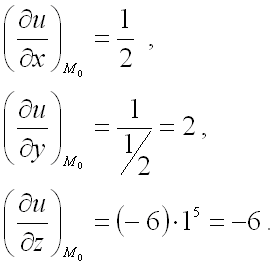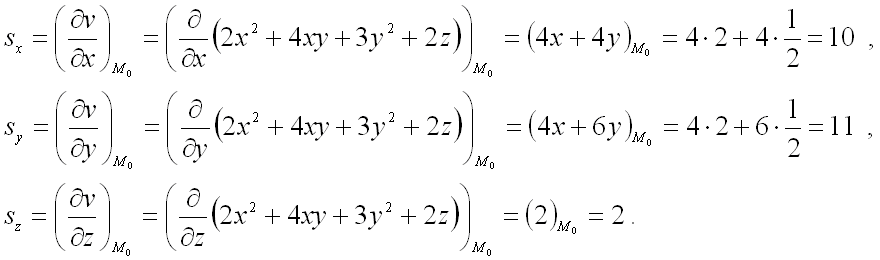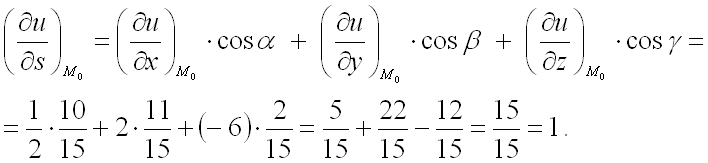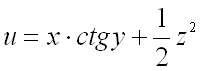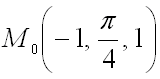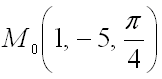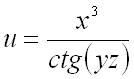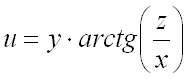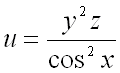Пусть F(x,y,z)F(x,y,z) – функция трех переменных, (x,y,z)(x,y,z) – декартовы координаты.
Градиентом функции F(x,y,z)F(x,y,z) называется векторное поле
∇F(x,y,z)=∂F∂xi+∂F∂yj+∂F∂zk,
nabla F(x,y,z)=frac{partial F}{partial x}mathbf{i}+frac{partial F}{partial y}mathbf{j}+frac{partial F}{partial z}mathbf{k},
где ∂F∂xfrac{partial F}{partial x}, ∂F∂yfrac{partial F}{partial y} и ∂F∂zfrac{partial F}{partial z} – частные производные функции F(x,y,z)F(x,y,z), а imathbf{i}, jmathbf{j} и kmathbf{k} – базис декартовой системы координат (x,y,z)(x,y,z).
Иногда градиент обозначается так: gradF(x,y,z)operatorname{grad} F(x,y,z).
Градиент функции в данной точке показывает направление наибольшего роста функции.
Пример 1
Найти градиент функции F(x,y,z)=ln(x2+y2+z2)F(x,y,z)=ln(x^2+y^2+z^2) в точке M(1,2,3)M(1,2,3).
Вычислим частные производные:
∂F∂x=∂∂xln(x2+y2+z2)=2xx2+y2+z2,
frac{partial F}{partial x}=frac{partial }{partial x}ln(x^2+y^2+z^2)=frac{2x}{x^2+y^2+z^2},
∂F∂y=∂∂yln(x2+y2+z2)=2yx2+y2+z2,
frac{partial F}{partial y}=frac{partial }{partial y}ln(x^2+y^2+z^2)=frac{2y}{x^2+y^2+z^2},
∂F∂z=∂∂zln(x2+y2+z2)=2zx2+y2+z2.
frac{partial F}{partial z}=frac{partial }{partial z}ln(x^2+y^2+z^2)=frac{2z}{x^2+y^2+z^2}.
Градиент в точке M(1,2,3)M(1,2,3) (подставляем в формулы для частных производных значения x=1x=1, y=2y=2, z=3z=3):
∇F(M)=17 i+27 j+37 k=17 OM→.
nabla F(M)=frac{1}{7},,mathbf{i}+frac{2}{7},,mathbf{j}+frac{3}{7},,mathbf{k}=frac{1}{7},,overrightarrow{OM}.
Производная по направлению
Пусть FF – функция на плоскости или в пространстве.
Производной функции FF по направлению вектора amathbf{a} в точке MM называется число
∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0,
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0},
если производная в правой части существует.
Пример 2
Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1).
Вычисляем значение функции в точке M+εaM+varepsilon mathbf{a} с координатами (−1+ε,−2ε,1+2ε)(-1+varepsilon,-2varepsilon,1+2varepsilon):
F(M+εa)=(−1+ε)2(−2ε)−(−2ε)2(1+2ε)+(1+2ε)2(−1+ε)=−6ε3−5ε−1.
Fleft(M+varepsilon mathbf{a}right)=(-1+varepsilon)^2(-2varepsilon)-(-2varepsilon)^2(1+2varepsilon)+(1+2varepsilon)^2(-1+varepsilon)=-6{varepsilon^{3}}-5varepsilon-1.
Длина вектора amathbf{a}:
∥a∥=a12+a22+a32=12+(−2)2+22=9=3.
|mathbf{a}|=sqrt{a_1^2+a_2^2+a_3^2}=sqrt{1^2+(-2)^2+2^2}=sqrt{9}=3.
Производная по направлению:
∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0=13ddε(−6ε3−5ε−1)∣ε=0=−53
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=frac{1}{3}left.frac{d}{dvarepsilon}left(-6{varepsilon^{3}}-5varepsilon-1right)right|_{varepsilon=0}=-frac{5}{3}
Выражение производной по направлению через градиент
Используя формулу Тейлора для функций нескольких переменных, легко получить выражение производной по направлению через градиент. Действительно, из равенства
F(M+εa)=F(M)+ε(∇F(M),a)+o(ε2)Fleft(M+varepsilon mathbf{a}right)=F(M)+varepsilonleft(nabla F(M),mathbf{a}right)+oleft(varepsilon^2right)
следует, что
ddεF(M+εa)∣ε=0=(∇F(M),a).
left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=left(nabla F(M),mathbf{a}right).
Таким образом,
∂F∂a(M)=(∇F(M),a)∥a∥.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}.
Пример 2′2′
Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1) используя градиент.
Частные производные:
∂F∂x(M)=2xy+z2∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial x}(M)=left.2xy+z^2right|_{(x,y,z)=(-1,0,1)}=1,
∂F∂y(M)=x2−2yz∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial y}(M)=left.x^2-2yzright|_{(x,y,z)=(-1,0,1)}=1,
∂F∂z(M)=−y2+2zx∣(x,y,z)=(−1,0,1)=−2.
frac{partial F}{partial z}(M)=left.-y^2+2zxright|_{(x,y,z)=(-1,0,1)}=-2.
Градиент:
∇F(M)=i+j−2k.
nabla F(M)=mathbf{i}+mathbf{j}-2mathbf{k}.
Скалярное произведение:
(∇F(M),a)=(i+j−2k,i−2j+2k)=1−2−4=−5.
left(nabla F(M),mathbf{a}right)=left(mathbf{i}+mathbf{j}-2mathbf{k},mathbf{i}-2mathbf{j}+2mathbf{k}right)=1-2-4=-5.
Производная по направлению:
∂F∂a(M)=(∇F(M),a)∥a∥=−53.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}=-frac{5}{3}.
Тест по теме “Градиент функции. Производная по направлению”
Частные производные функции нескольких
переменных, по своему смыслу, характеризуют
скорость изменения функции по направлениям
осей координат. Вполне естественно
выяснить с какой скоростью изменяется
функция в данной точке
в фиксированном направлении, задаваемом
вектором
.
Ответ на этот вопрос дает понятие
производной в точке
по
направлению вектора
.
Опуская точное определение такой
производной, которая естественно
является пределом отношения приращения
функции к приращению аргумента,
вычисленному в заданном направлении,
приведем формулы для её вычисления.
Для дифференцируемой функции трех
переменных
,
производная в направлении вектора
:
,
где
– направляющие косинусы вектора
,
которые вычисляются по формулам
,
,
и являются координатами единичного
вектора
того же направления:
.
Для дифференцируемой функции двух
переменных
формулы аналогичны, только будет
отсутствовать третья координата.
Определение. Градиентом функции
называется
вектор
,
координаты которого равны соответственно
частным производным
и
в точке
,
то есть
.
Для функции трех переменных
имеем
.
Используя определение градиента,
формулы для вычисления производной по
направлению можно записать в виде
скалярного произведения двух векторов:
или
Из этих формул, с учетом определения
скалярного произведения,
,
следуют основные свойства градиента:
-
градиент
это вектор, направленный в сторону
максимального роста функции
,
то есть производная по направлению в
данной точке принимает максимальное
значение в направлении её градиента
в этой точке; -
модуль
градиента равен максимальной производной
по направлению. -
градиент
перпендикулярен линии (поверхности)
уровня функции;
Пример 1. Найти градиент функции
и
его модуль в точке
,
и вычислить производную по направлению
вектора
.
Решение.1)Вычисляем
.
Подставляя координаты точки
,
получим
.
Модуль, полученного вектора
.
2) Вычисляем единичный вектор заданного
направления
.
Производная по направлению равна
=
.
Пример 2. Найти вектор нормальный
к линиям уровня функции
.
Решение. Поскольку градиент функции
перпендикулярен линиям уровня этой
функции в произвольной точке, получим
,
значит, вектор
– нормальный вектор к линиям уровня
,
которые образовывают множество
параллельных прямых, перпендикулярных
вектору
.
7.7. Экстремум функции двух переменных
Определение. Точка
является точкой максимума (минимума)
функции
,
если существует окрестность этой точки
такая, что для всех точек
из
этой окрестности
(
).
Максимум или минимум, как и ранее,
называют экстремумом. Далее, в силу
простоты и наглядности, исследование
на экстремум проведем для функций двух
переменных
,
тем более, что идеи и последовательность
действий такие же, как и для функции
одной переменной.
Прежде всего, находим стационарные
точки, то есть точки в которых
обращаются в нуль обе частные производные
– необходимое условие экстремума,
то есть решаем систему уравнений:
Пусть, например, точка
является решением этой системы, то
есть – стационарная точка. Для
того, чтобы выяснить будет ли в этой
точке экстремум, используем следующие
достаточные условия существования
экстремума в стационарной точке.
1) Находим частные производные второго
порядка исследуемой функции и вычисляем
их значения в точке
,
обозначая:
;
;
.
2) Составим определитель
.
3) Если
,
то в точке
будет экстремум:
-
максимум,
если
-
минимум,
если
4) Если
,
то в точке
нет экстремума.
5) Если
,
то требуется дальнейшее исследование.
Пример. Исследовать на экстремум
функцию
Решение. 1) Ищем стационарные точки:
Из второго уравнения системы получим
,
подставляя это значение в первое
уравнение, после очевидных вычислений
имеем
.
Таким образом далее предстоит исследовать
единственную стационарную точку
.
2) Находим производные второго порядка
данной функции:
;
;
.
3) Вычисляем значения вторых производных
в стационарной точке:
;
;
.
4) Составляем определитель
,
т.к.
,
то в точке
есть экстремум, а так как
,
это минимум.
5) Находим
.
Замечание. Исследование на наибольшее
и наименьшее значение функции нескольких
переменных непрерывной в замкнутой
ограниченной области подобно исследованию
функции одной переменной на замкнутом
промежутке
.
Сначала ищутся критические точки внутри
области и вычисляются значения функции
в этих критических точках. Затем находят
наибольшее и наименьшее значения
функции на границе области. И в заключение,
из всех полученных значений выбирают
наибольшее и наименьшее, которые и
являются решением задачи.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Производная
по направлению. Градиент
Пусть в некоторой области
задана функция
и точка .
Проведем из точки
вектор ,
направляющие косинусы которого .
На векторе ,
на расстоянии
от его начала рассмотрим точку ,
т.е. 
Будем предполагать, что функция
и ее частные производные первого порядка непрерывны в области .
Предел отношения
при называется
производной от функции
в точке по
направлению вектора
и обозначается ,
т.е.
.
Для нахождения производной от функции
в заданной точке по
направлению вектора
используют формулу: 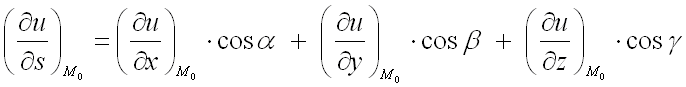
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
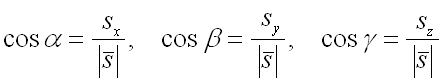
Пусть в каждой точке некоторой
области
задана функция .
Вектор, проекциями которого на оси координат являются значения частных производных
этой функции в соответствующей точке, называется градиентом функции
и обозначается
или
(читается «набла у»): 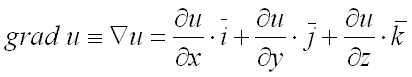
При этом говорят, что в области
определено векторное поле градиентов.
Для нахождения градиента функции
в заданной точке
используют формулу:
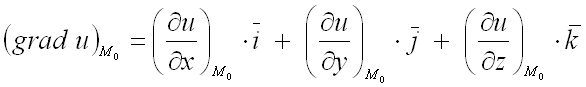
Свойства
градиента
1. Производная
в данной точке по направлению вектора
имеет наибольшее значение, если направление вектора
совпадает с направлением градиента. Это наибольшее значение производной равно
.
2. Производная
по направлению вектора, перпендикулярного к вектору ,
равна нулю.
Примеры
решения задач
Пример 1.
Найти производную от функции
в точке
по направлению вектора .
Решение.
Для решения задачи воспользуемся
формулой для нахождения производной от функции
в заданной точке
по направлению вектора :
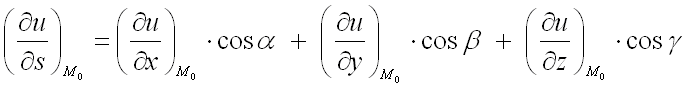
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
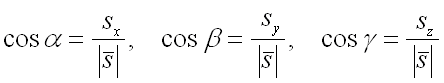
По условию задачи вектор
имеет координаты .
Тогда его длина равна:
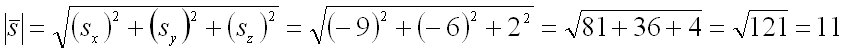
Следовательно, для направляющих косинусов вектора получим следующие значения:
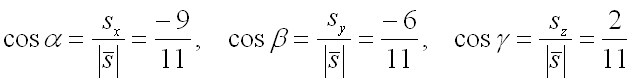
Далее для решения задачи необходимо найти все частные производные первого порядка
от функции :
Вычислим значения этих частных производных первого порядка в точке :
В заключении подставим полученные значения для направляющих косинусов вектора
и значения частных производных первого порядка от функции в
точке
в формулу для нахождения производной по направлению в заданной точке:
Ответ: производная от функции
в точке
по направлению вектора
равна 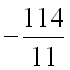
Пример 2.
Найти градиент функции
в точке 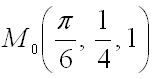
Решение.
Поскольку градиентом функции
называется вектор, проекциями которого на оси координат являются значения частных
производных этой функции в соответствующей точке, то для решения задачи сначала
найдем все частные производные первого порядка от заданной функции:
Далее вычислим значения этих частных производных первого порядка в точке 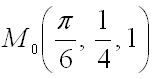
Подставим полученные значения в формулу градиента функции
в заданной точке :
.
Ответ: градиент функции
в точке
равен 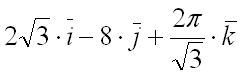
Пример 3.
Найти производную функции
в точке
по направлению градиента функции
в той же точке.
Решение.
Для нахождения производной
от функции
в заданной точке
по направлению вектора
используют формулу:
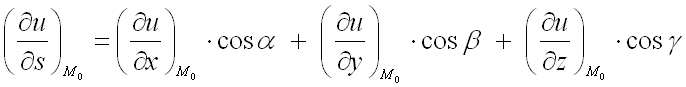
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
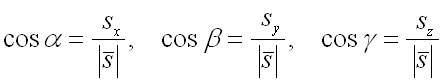
В данном случае вектор совпадает
с градиентом функции
в точке 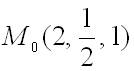
.
Следовательно, для решения задачи необходимо найти значения всех частных производных
первого порядка от функции
в точке ,
а также координаты и длину градиента функции
в той же точке.
Вычислим значения частных производных первого порядка от функции
в точке :
Для нахождения координат вектора ,
равного градиенту функции
в заданной точке ,
вычислим значения частных производных первого порядка от функции
в этой точке:
Длина вектора равна: 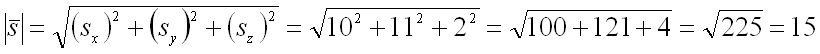
Найдем направляющие косинусы вектор по формулам:
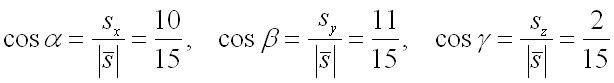
Подставим полученные значения в формулу для нахождения производной от функции
в заданной точке
по направлению вектора :
Ответ: производная функции
в точке 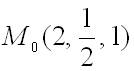
направлению градиента функции
в той же точке равна 1.
Задания
для самостоятельной работы
1.
Найти производную функции
в точке
по направлению вектора .
Ответ: .
2. Найти производную функции
в точке
по направлению вектора .
Ответ: .
3. Найти производную функции
в точке
по направлению вектора .
Ответ: .
4. Найти градиент функции
в точке 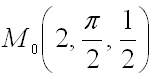
Ответ: .
5. Найти градиент функции
в точке .
Ответ: 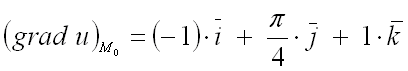
6. Найти градиент функции
в точке 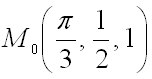
Ответ:
.
У этого термина существуют и другие значения, см. Производная.
В математическом анализе производная по направлению — одно из обобщений понятия производной на случай функции нескольких переменных.
Производная по направлению показывает, как быстро значение функции изменяется при движении в данном направлении.
Назначение[править | править код]
Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента.
Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной.
Именно это соображение и приводит к определению производной по направлению|[1].
Определение[править | править код]
Рассмотрим дифференцируемую функцию 






Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора 
Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.
В источниках встречаются разные обозначения для производной по направлению 
Производная по направлению имеет те же свойства, что и обычная производная функции одного аргумента:
Выражение производной по направлению через частные производные[править | править код]
Пусть направляющий вектор направления 

На языке векторного анализа эту формулу можно записать иначе. Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления|[2]:
Отсюда следует, что в заданной точке производная по направлению принимает максимальное значение тогда, когда её направление совпадает с направлением градиента функции в данной точке.
Нормальная производная[править | править код]
Нормальная производная — производная по направлению нормали некоторой поверхности. Понятие нормальной производной особенно важно при решении краевых задач[3] (см. пример в статье Задача Неймана). Если нормаль обозначить 

Для функции, заданной на плоскости, нормальная производная определяется как производная по направлению нормали некоторой кривой, лежащей в той же плоскости[3].
Вариации и обобщения[править | править код]
До сих пор рассматривались функции в евклидовом пространстве, однако производная по направлению может быть определена в произвольном гладком многообразии. Пусть 





Можно показать, что это определение зависит только от вектора 
Ещё одно обобщение — производная Гато.
См. также[править | править код]
- Полная производная функции
Примечания[править | править код]
- ↑ 1 2 Фихтенгольц, 1966, с. 391—393.
- ↑ Фихтенгольц, 1966, с. 393—394.
- ↑ 1 2 Нормальная производная // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 416. — 847 с.
Литература[править | править код]
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 6-е. — М.: Наука, 1966. — Т. I. — С. 391—394.
Ссылки[править | править код]
- Производная по направлению с примерами на YouTube
- “Свободный полет по производным” — перевод статьи Calculus: Building Intuition for the Derivative | BetterExplained (англ.)
Всех приветствую. Сегодня мы познакомимся с немало важной темой включающая в себя такие разделы как векторная алгебра и математический анализ. Данная практика является дополнением прошлой темы (ссылочка будет в конце урока) связанной с градиентом функции. Если связь будет неуловима мы всё распишем и разберёмся. Приступим к краткой теории.
Производная по направлению, хммм. Давайте подумаем логически, что мы можем найти с помощью производной. Всё правильно, можно найти интервалы возрастания и наибольшее значение функции. У нас идёт речь о “производной” следовательно она для функции берётся всего один раз и не более. У нас также сказано про направление, направление можно задавать на плоскости и в пространстве. Для плоскости определять направление возрастания можно, но не так интересно как для функций нескольких переменных и работать уже в пространстве. Этим мы сейчас и займёмся.
Запишем формулу для нахождения производной по направлению.
С теорией закончим, пора приступить к самим заданиям.
Долго не задумываясь “зарешаем” простенький примерчик в качестве разминки.
Мы с похожими заданиями уже сталкивались, алгоритм решения почти не отличается.
Попытаем счастье с двумя переменными.
Решение на много легче не стало из-за отсутствия одной переменной.
И наконец, то, чего все ждали, проведём связь между вычислением градиента и производной по направлению на примере задания.
Подошла к концу наша практика, ознакомились с понятием производной по направлению, закрепили как всегда всё на примерах. Думаю вы заметили что вычисление производной по направлению является “продолжением” или говоря иначе “дополнением” при нахождении градиента функции, вот и всё. Спасибо за внимание.
Другие темы: