
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки

Примеры
-
frac{d}{dx}(frac{3x+9}{2-x})
-
frac{d^2}{dx^2}(frac{3x+9}{2-x})
-
(sin^2(theta))”
-
производное:от:f(x)=3-4x^2,::x=5
-
неявная:производная:frac{dy}{dx},:(x-y)^2=x+y-1
-
frac{partial}{partial ypartial x}(sin (x^2y^2))
-
frac{partial }{partial x}(sin (x^2y^2))
- Показать больше
Описание
Поэтапное дифференцирование функций
derivative-calculator
frac{d}{dx}left(2lnxright)
ru
Блог-сообщения, имеющие отношение к Symbolab
High School Math Solutions – Derivative Calculator, the Chain Rule
In the previous posts we covered the basic derivative rules, trigonometric functions, logarithms and exponents…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Данный онлайн калькулятор вычисляет производную функции. Программа не только вычисляет ответ, она производит пошаговое решение. Выбирается порядок дифференцирования.
Как пользоваться калькулятором для нахождения производных онлайн:
1. Введите математическое выражение с переменной x, в выражении используйте стандартные операции: + сложение, –
вычитание, / деление, * умножение, ^ – возведение в степень, а также математические функции.
2. Выберите порядок дифференцирования (решения производных от первого до пятого порядка включительно).
3. Нажмите кнопку – Вычислить производную.
4. Через несколько секунд внизу отобразится пошаговое решение производной с подробными комментариями.
При помощи нашего калькулятора вы можете найти производную онлайн как от элементарной функции, так и от сложной, не имеющей решения в аналитическом виде.
Калькулятор поможет найти производную функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.

 : x^a
: x^a
модуль x: abs(x)
Для того, чтобы найти производную функции 
нужно написать в строке: f[x], x. Если Вам требуется
найти производную n-го порядка, то следует написать: f[x], {x, n}. В
том случае, если Вам требуется найти частную производную функции  напишите в окне гаджета: f[x, y, z,…,t], j, где
напишите в окне гаджета: f[x, y, z,…,t], j, где 
— интересующая Вас переменная. Если нужно найти частную производную по
некоторой переменной порядка n, то следует ввести: f[x, y, z,…,t], {j,
n}, где  означает тоже, что и Выше.
означает тоже, что и Выше.
Важно подчеркнуть, что калькулятор выдает пошаговое нахождение
производной при нажатии на «Show Steps» в правом верхнем углу
выдаваемого ей ответа.
- Примеры
- x*E^x, x;
- x^3*E^x, {x,17};
- x^3*y^2*Sin[x+y], x;
- x^3*y^2*Sin[x+y], y,
- x/(x+y^4), {x,6}.
Производная по-шагам

Примеры производных
- Производные от степенных функций
-
x^7/10
-
(x^2 - 1)/(x^a - 5)
- Производные от сложных функций
-
sin(ln(x))
-
ln(sin(x))
- Производные от показательных функций
-
e^(-x^2)
- Производные от логарифмов
-
1-log(x-5)
-
ln(a*x) / ln(x^3)
- Производные от обратных тригонометрических функций
-
arcsin(1-x)
-
arctan(a*x + b)
- Производная неявной функции
-
e^y/x = x*y + 1
- Частная производная функции
-
x^2*sin(-y) + y/x
-
x*y*cos(z)
Подробнее про Производная функции
.
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
-
квадратные корни sqrt(x),
кубические корни cbrt(x) -
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
-
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x) -
натуральные логарифмы ln(x),
десятичные логарифмы log(x) -
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x) -
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) -
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x) -
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) -
знак числа:
sign(x) -
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x) -
Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
-
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- – умножение
- 3/x
- – деление
- x^2
- – возведение в квадрат
- x^3
- – возведение в куб
- x^5
- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
- Действительные числа
- вводить в виде 7.5, не 7,5
Постоянные
- pi
- – число Пи
- e
- – основание натурального логарифма
- i
- – комплексное число
- oo
- – символ бесконечности
Найдем производную функции f(x)=lnxf(x)= ln x и приведем некоторые ее свойства и практические примеры использования.
Производная функции f(x)= ln x
Как известно, производной функции f(x)f(x), определенной в точке x0x_0 и в некотором интервале, содержащем x0x_0, называют предел следующего вида:
f′(x0)=dfdx∣x=x0=limΔx→0f(x0+Δx)−f(x0)Δxf^{‘}(x_0)=dfrac{df}{dx}Bigr|_{x=x_0}=limlimits_{Delta x to 0}dfrac{ f(x_0+ Delta x)-f(x_0 )}{ Delta x}
если только такой предел существует.
Таким образом, для вычисления производной функции f(x)f(x) необходимо последовательно:
- Записать выражение для приращения функции:
Δf(x0)=f(x0+Δx)−f(x0)Delta f(x_0 )=f(x_0+Delta x)-f(x_0 )
- Упростить, по возможности, дробь
Δf(x0)Δx=f(x0+Δx)−f(x0)Δxdfrac {Delta f(x_0)}{Delta x}=dfrac {f(x_0+Delta x)-f(x_0)}{Delta x}
- Вычислить предел дроби при Δx→0Delta x to 0 и записать полученное выражение для производной.
Применим этот алгоритм к вычислению производной натурального логарифма:
- Записываем приращение функции:
Δf(x0)=f(x0+Δx)−f(x0)=ln(x0+Δx)−lnx0=lnx0+Δxx0Delta f(x_0)= f(x_0+Delta x)-f(x_0)= ln (x_0+Delta x)-ln {x_0}=ln dfrac { x_0+Delta x }{ x_0}
- Получаем дробь:
Δf(x0)Δx=1Δx⋅lnx0+Δxx0=ln(1+Δxx0)1Δx=1x0ln(1+1×0/Δx)x0Δxdfrac {Delta f(x_0)}{Delta x}= dfrac {1}{Delta x} cdot ln {dfrac {x_0+Delta x }{ x_0}}=ln {Bigl( 1+dfrac {Delta x }{ x_0} Bigr)}^ {dfrac {1}{Delta x}}=dfrac {1}{x_0} ln {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}
- Вычисляем производную:
f′(x0)=limΔx→0(1x0ln(1+1×0/Δx)x0Δx)=1×0⋅limΔx→0ln(1+1×0/Δx)x0Δx=1×0⋅lnlimΔx→0(1+1×0/Δx)x0Δxf'(x_0 )=limlimits_{Delta x to 0} Bigl( dfrac {1}{ x_0} ln {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}Bigr) =dfrac {1}{ x_0} cdot limlimits_{Delta x to 0} ln {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}=dfrac {1}{ x_0} cdot ln limlimits_{Delta x to 0} {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}
Для вычисления предела
limΔx→0(1+1×0/Δx)x0Δxlimlimits_{Delta x to 0} {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}
обозначим:
x0Δx=ndfrac {x_0}{ Delta x }=n
Учитывая, что n→∞ntoinfty при условии, что Δx→0Delta x to 0, получаем:
limΔx→0(1+1×0/Δx)x0Δx=limn→∞(1+1n)nlimlimits_{Delta x to 0} {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}=limlimits_{ntoinfty } {Bigl( 1+dfrac {1 }{n} Bigr)}^{ n}
Полученный предел является одним из представлений экспоненты, числа e≈2,71828e≈2, 71828 (число Непера или число Эйлера):
e=limn→∞(1+1n)ne=limlimits_{ntoinfty } {Bigl( 1+dfrac {1 }{n} Bigr)}^{ n}
Тогда, искомая производная равна:
f′(x0)=1×0⋅lnlimΔx→0(1+1×0/Δx)x0Δx=1×0⋅lne=1x0f'(x_0) =dfrac {1}{ x_0} cdot ln limlimits_{Delta x to 0} {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}=dfrac {1}{ x_0}cdot ln e=dfrac {1}{ x_0}
Таким образом:
f′(x)=(lnx)′=1xf'(x)=(ln x) ‘=dfrac {1}{ x}
Некоторые свойства и практические примеры
- Приведем правило для нахождения производной обратной функции.
Пусть дана функция y=f(x)y=f(x), в которой переменная x является аргументом. Полагая теперь аргументом переменную y, получим функцию в виде x=g(y)x=g(y).
Очевидно, что f(g(y))=yf(g(y))=y или f(g(x))=xf(g(x))=x. Такую функцию g(x)g(x) называют обратной для f(x)f(x). Производную обратной функции можно найти по правилу:
yx′=dydx=1dxdy=1xy′y_x’=dfrac {dy}{dx}=dfrac {1}{dfrac {dx}{dy}}=dfrac {1}{x_y’}
Используя правило для обратной функции найти производную функции f(x)=lnx.f(x)= ln{x}.
Решение
Заметим, что обратной для логарифмической функции lnxln{x} является показательная функция exe^x. Действительно:
f(g(x))=lnex=xf(g(x)) = ln {e^x} = x
Воспользуемся далее формулой для производной экспоненты:
(ex)′=ex(e^{x})^{‘}=e^{x}
Получаем:
yx′=(lnx)′=1(ey)y′=1ey=1elnx=1xy_x’ = (ln {x})’ = dfrac {1}{(e^{y})^{‘}_y}= dfrac {1}{e^y}= dfrac {1}{e^{ln x}}= dfrac {1}{x}
Как и следовало ожидать, результат совпадает с полученным ранее.
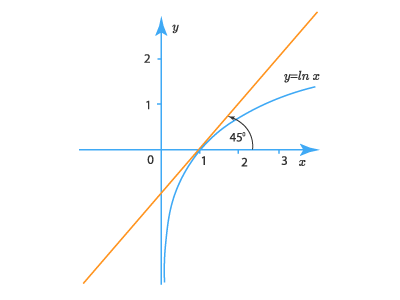
- Угол наклона αalpha касательной к графику функции y=lnxy= ln {x} в точке x=x0x=x_0 определяется соотношением:
tgα=y′(x0)=1x0tg alpha =y^{‘} (x_0 )= dfrac {1}{x_0}
Здесь угол αalpha это угол между касательной и осью OxOx отсчитываемый от положительного направления OxOx против часовой стрелки.
Производная функции f(x)=lnxf(x)= ln {x} в точке x0=1x_0=1 равна 11:
f′(x0)=(lnx)x0=1′=11=1f’ (x_0 ) = (ln {x})_{x_0=1}^{‘}=dfrac {1}{1}=1
Это означает, что касательная к графику в точке M(1;0),(x0=1,y0=ln1=0)M(1;0), (x_0=1, y_0=ln {1} = 0) составляют с осью OxOx угол 45°(tg45°=1)45° (tg {45°}=1)
- Производная сложной функции y=lng(x)y=ln {g(x)} согласно правил дифференцирования, равна:
y′=g′(x)1g(x)y’=g'(x) dfrac {1}{g(x)}
- Производная сложной функции y=u(v)y=u(v), где v=lnxv= ln {x} равна:
y′=uv′⋅v′=uv′⋅1xy’=u’_v cdot v’=u’_v cdot dfrac {1}{x}
Найти производную функции f(x)=ln(x2+2x)f(x)=ln {(x^2+2x)}
Решение
f′(x)=(ln(x2+2x))′=(x2+2x)′⋅1×2+2x=2x+2×2+2xf'(x)=(ln {(x^2+2x)})’=(x^2+2x)’ cdot dfrac {1}{x^2+2x}=dfrac {2x+2}{x^2+2x}
Найти производную функции
f(x)=sin(ln2x)f(x)= sin {(ln {2x})}
Решение
Полагаем ln2x=vln {2x}=v
Тогда:
f′(x)=(sinv)v′⋅v′=cosv⋅(ln2x)′=cos(ln2x)⋅(2x)′⋅12x=cos(ln2x)xf'(x)=(sin {v})’_v cdot v’ = cos {v} cdot (ln {2x})’ =cos{(ln {2x})} cdot (2x)’ cdot dfrac {1} {2x} = dfrac {cos(ln{2x})} {x}
Тест по теме «Производная натурального логарифма»
Онлайн калькулятор. Вычисление производных.
Онлайн-калькулятор позволяет решать математические выражения любой сложности с выводом подробного результата решения по шагам. 
Также универсальный калькулятор умеет вычислять производные любого порядка (дифференцирование).
Онлайн калькулятор производных
Перенос?
f”left(log left(frac{1-x^2}{1+x^2}right)right)
$$textbf{Вычисление производной 2-го порядка:} newline f”(x) = {{2xleft(-{{2x}over{x^2+1}}-{{2xleft(1-x^2right)}over{left(x^2+1right)^2}}right)}over{1-x^2}}+{{2xleft(x^2+1right)left(-{{2x}over{x^2+1}}-{{2xleft(1-x^2right)}over{left(x^2+1right)^2}}right)}over{left(1-x^2right)^2}}+{{left(x^2+1right)left(-{{2}over{x^2+1}}+{{8x^2}over{left(x^2+1right)^2}}-{{2left(1-x^2right)}over{left(x^2+1right)^2}}+{{8x^2left(1-x^2right)}over{left(x^2+1right)^3}}right)}over{1-x^2}} =newline -{{4left(3x^4+1right)}over{left(x-1right)^2left(x+1right)^2left(x^2+1right)^2}} =newline -{{12x^4+4}over{x^8-2x^4+1}}$$
Пояснения к калькулятору
- Для решения математического выражения необходимо набрать его в поле ввода с помощью предложенной виртуальной клавиатуры и нажать кнопку ↵.
- Управлять курсором можно кликами в нужное местоположение в поле ввода или с помощью клавиш со стрелками ← и →.
- ⌫ – удалить в поле ввода символ слева от курсора.
- C – очистить поле ввода.
- При использовании скобок ( ) в выражении в целях упрощения может производится автоматическое закрытие, ранее открытых скобок.
- Для того чтобы ввести смешанное число или дробь необходимо нажать кнопку ½, ввести сначала значение числителя, затем нажать кнопку со стрелкой вправо → и внести значение знаменателя дроби. Для ввода целой части смешанного числа необходимо установить курсор перед дробью с помощью клавиши ← и ввести число.
- Ввод числа в n-ой степени и квадратного корня прозводится кнопками ab и √ соответственно. Завершить ввод значения в степени или в корне можно клавишей →.
Вычисление производных
Математический калькулятор может дифференцировать функции (нахождение производной) произвольного порядка в точке “x”. Ввод производной в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:
f'(x) – производная первого порядка;
f”(x) – производная второго порядка;
f”'(x) – производная третьего порядка.
fn(x) – производная любого n-о порядка.

