Как найти производную аналитически

Г Л АВ А 3

Дифференцирование

Операция дифференцирования реализована в Mathcad как в численной, так и в аналитической форме и обозначается при помощи традиционного оператора, т. е. соответствующими математическими символами (подобно сложению или умножению). Если расчеты выполняются с помощью вычислительного процессора, необходимо хорошо представлять себе особенности численного алгоритма, действие которого остается для пользователя “за кадром”. С помощью Mathcad можно вычислять производные скалярных функций любого количества аргументов, причем как функции, так и аргументы могут быть и действительными, и комплексными.

Вне всякого сомнения, вы по достоинству оцените возможности символьного процессора, позволяющего с легкостью выполнять рутинные вычисления производных громоздких функций. В отличие от всех других операций, символьное дифференцирование выполняется успешно для подавляющего большинства аналитически заданных функций. Думаю, что многие читатели, которым иногда приходится аналитически дифференцировать функции, как и автор этих строк, единожды попробовав сделать это в среде Mathcad, уже никогда не возьмут в руки карандаша для расчета производных “вручную”.

3.1.1. Аналитическое дифференцирование функции

Для того чтобы аналитически найти производную функции f(x) в Mathcad:

1.Задайте функцию f(x).

2.Введите оператор дифференцирования нажатием кнопки Производная

(Derivative) на панели Математический анализ (Calculus) или введите с кла-

виатуры вопросительный знак <?>.

3.В появившихся местозаполнителях оператора дифференцирования (рис. 3.1) введите функцию, зависящую от аргумента x, т. е. f(x), и имя самого аргумента x.

Рис. 3.1. Оператор дифференцирования

4.Введите оператор < > символьного вычисления для получения ответа (лис-

тинг 3.1).

Листинг 3.1. Пример аналитического дифференцирования

f(x) sin(x) ln(x)

d		sin(x)
f(x)	cos(x) ln(x)
	x
dx

ПРИМЕЧАНИЕ 1

Помните о том, что в описанном применении оператора дифференцирования его результатом является функция той же переменной x. Пример визуализации операции дифференцирования с помощью графика приведен на рис. 3.2.

ПРИМЕЧАНИЕ 2

Исходная функция может зависеть не только от аргумента x, но и от других аргументов, например f(x,y,z,t) и т. п. В этом случае дифференцирование производится точно так же, причем становится более понятной необходимость определения переменной дифференцирования (в нижнем местозаполнителе оператора дифференцирования). Расчеты производных по разным аргументам (в этом случае говорят о частных производных), разумеется, будут давать совершенно разные результаты (см. разд. 3.4).

Рис. 3.2. График производной функции

3.1.2. Вычисление производной функции в точке

Для того чтобы рассчитать производную в точке, необходимо предварительно задать значение аргумента в этой точке (листинг 3.2, вторая строка). Результатом дифференцирования в этом случае будет число — значение производной в этой точке. Если результат удается отыскать аналитически, то он приводится в виде числового выражения, а для того чтобы получить его в форме числа, достаточно ввести после выданного выражения символ числового равенства <=> (последняя строка листинга 3.2).

Листинг 3.2. Аналитическое дифференцирование функции в точке

f(x)	sin(x) ln(x)
x 2
d		1
f(x)	cos(2) ln(2)	sin(2) 0.166
	2
dx

Для того чтобы продифференцировать функцию, вовсе не обязательно предварительно присваивать ей какое-либо имя, как это сделано в листингах 3.1 и 3.2. Можно определить функцию непосредственно в операторе дифференцирования (это демонстрирует первая строка листинга 3.3).

Листинг 3.3. Правильное и неправильное использование оператора дифференцирования

d sin(x) cos(x) dx

d sin(2) 0 dx

Как вы заметили, оператор дифференцирования, в основном, соответствует его общепринятому математическому обозначению, и поэтому его легко использовать интуитивно. Однако в некоторых случаях при вводе оператора дифференцирования следует проявить осторожность. Рассмотрим один показательный пример, приведенный во второй строке листинга 3.3, который демонстрирует неправильное применение оператора дифференцирования для вычисления производной в точке. Вместо вычисления производной sin(x) при x=2, как этого можно было ожидать, получено нулевое значение. Это случилось из-за того, что аргумент функции sin(x) введен не в виде переменной x, а в виде числа. Поэтому Mathcad воспринимает последнюю строку как вычисление сначала значения синуса в точке x=2, а затем дифференцирование этого значения (т. е. константы) также в точке x=2, в соответствии с требованием первой строки листинга. Поэтому ответ, на самом деле, неудивителен — в какой точке ни дифференцируй константу, результатом будет ноль.

ПРИМЕЧАНИЕ

То же самое касается и операции численного дифференцирования, т. е. применения опе-

ратора <=> вместо < > (см. листинг 3.3.2 на компакт-диске).

3.1.3. Определение функций пользователя через оператор дифференцирования

Разумеется, оператор дифференцирования, как и любой другой, можно применять для определения собственных функций пользователя. В листинге 3.4 через производную от f(x) определяется еще одна пользовательская функция g(x), затем при помощи оператора символьного вывода находится ее явный вид (предпоследняя строка листинга) и конкретное значение в точке x=1 (последняя строка).

Листинг 3.4. Определение функции посредством оператора дифференцирования

f(x) x4 2x3 7x2 3x 1

g(x) d f(x) dx

g(x) 4x3 6x2 14x 3 g(1) 1

3.1.4. Дифференцирование при помощи меню

Чтобы аналитически продифференцировать выражение по некоторой переменной, выделите в нем эту переменную и выберите команду Символьные операции / Пе-

ременная / Дифференцировать (Symbolics / Variable / Differentiate) (рис. 3.3).

Рис. 3.3. Аналитическое дифференцирование по переменной

Источник

Данный алгоритм реализован на языке Scala, характерной особенностью которого является использование case-классов, так удачно подходящих для написания алгоритма дифференцирования. В этой статье планируется описать лишь часть программы, содержащей алгоритм нахождения производной, поскольку разработка парсера для математических выражений это другая большая тема,
заслуживающая отдельной статьи

SingleToken будет реализовывать case-классы унарных операторов, таких как sin(a), -a, ln(a) и т.д.
DoubleToken описывает бинарные операторы: a+b, a^b и т.д.
LeafToken — «листья» дерева, т.е. константы, переменные и зарезервированные имена констант (число Пи и экспонента).

Опишем классы/объекты операторов и токенов:

case object Pi extends LeafToken
case object Exponenta extends LeafToken

case class Sin(override val a: MathAST) extends SingleToken
case class Cos(override val a: MathAST) extends SingleToken
…
case class Mul(override val a: MathAST, override val b: MathAST) extends DoubleToken
case class Add(override val a: MathAST, override val b: MathAST) extends DoubleToken
…
case class Differentiate(f: MathAST, dx: Variable) extends MathAST

case class Variable(name: String) extends LeafToken
case class Constant(value: BigDecimal) extends LeafToken

Обратите внимание на класс Differentiate, он имеет особую сигнатуру: f – исходная функция, dx – переменная, по которой происходит дифференцирование.

Теперь есть все, чтобы представить математическую функцию в виде дерева вычислений, для примера возьмем функцию: 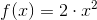$f(x)=2cdot x^{2}$ , которая примет вид:

Mul(Constant(BigDecimal(2)), Pow(x, Constant(BigDecimal(2)))

Конечно, чтобы получить дерево-выражение из обычной строки, введенной пользователем, нужно написать парсер, но, как было упомянуто выше, это уже другая тема. Скажу лишь что в программе используется самодельный парсер, наследующий трейт Parsers из пакета scala.util.parsing.combinator.

Алгоритм нахождения производной

def differentiate(f: MathAST)(implicit dx: String): MathAST

Аргумент dx, содержащий имя переменной (по которой происходит дифференцирование) помечен как неявный (implicit), это позволит не передавать ее в рекурсивные вызовы, пусть этим занимается компилятор.

На вход рекурсивной функции подается выражение — исходная функция f(x) (в формате MathAST), возвращаемое значение — функция-производная 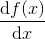$frac{mathrm{d} f(x)}{mathrm{d} x}$ в том же формате.

Примечание 1: Выражение может быть бинарным, унарным или токеном.
Примечание 2: Оператором может быть один из: «+», «-», «^», «*», «/», «abs», «sin», «cos», «tg», «ctg», «ln», «arcsin», «arccos», «arctg», «arcctg», «(», «)».
Примечание 3: Входные и выходные данные представлены в формате MathAST — дерево-выражение.

Общий алгоритм

В общем виде алгоритм слишком абстрактный, поэтому дальше разберем его подробнее.

Рекурсивная функция получает на вход данные и используя сопоставление с образцом (pattern-matching) выполняет необходимые действия, в зависимости от типа данных.
Функция высчитывает производную для входного выражения и возвращает выражение-результат. Может получиться, что аргументы a и/или b оказались не константой и не переменной, а сложной функцией u(x),
тогда понадобится рекурсивно посчитать еще и производную u’(x), т.е. вернуть [ differentiate(u(x)) ] — перейти к шагу 1 с новыми данными — u(x).
Если данные не корректны вернуть сообщение об ошибке.

Детали принципа работы и связь с математическими абстракциями

Функция приняла на вход данные — выражение-функцию, которую следует обработать в соответствии с правилами дифференцирования

Если бинарное выражение

Бинарные выражения помечены трейтом DoubleToken. Оператор проверяется на соответствие одному из доступных операторов («+», «-», «*», «/», «^»):

case Add(a, b) => Add(differentiate(a), differentiate(b))
case Sub(a, b) => Sub(differentiate(a), differentiate(b))
…

Если оператор «+»: вернуть [ differentiate(a) + differentiate(b) ].
Если оператор «-»: вернуть [ differentiate(a) — differentiate(b) ].
Если оператор «*»: Умножение представляет из себя более сложный случай, операнды a и b могут быть константами или переменными (всего 4 комбинации: u(x)*c, u(x)*v(x), c*c, c*u(x)).
Функция анализирует какой из 4 вариантов попался и возвращает выражение используя правило дифференцирования № 1, № 3, и №5,
если один из операндов – сложная функция. Например: если a = u(x), а b = v(x), то вернуть [ differentiate(a) * b + a * differentiate(b)) ].
Приватный метод isDependsOnVar проверяет, зависит ли подвыражение от переменной, по которой производится дифференцирование.
Если оператор «/»: Действия аналогичны, как и с оператором «*».
Если оператор возведения в степень «^»: Здесь имеется так же 4 варианта выражений: u(x)^c, u(x)^v(x), c^c, c^u(x).
Третий случай самый нетривиальный: u(x)^v(x), чтобы найти производную от такого выражения нужно использовать логарифм и его свойства (описание процедуры логарифмирования выходит за рамки этой статьи, поэтому сразу приведем готовую формулу – № 6).

В остальных трех случаях используются стандартные табличные формулы.

В качестве примера приведем обработку операции умножения:


case Mul(a, b) => {
	val u = isDependsOnVar(a)
	val v = isDependsOnVar(b)
	if (u && !v) {
		Mul(differentiate(a), b)
	} else if (!u && v){    // c^u(x), c=const
		Mul(a, differentiate(b))
	}else if (!u && !v){    // c^c, c=const
		Constant(BigDecimal(0))
	}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}

Если унарное выражение

Классы SingleToken обрабатываются следующим образом:


case e: SingleToken =>
val d = e match {
	case Sin(x) => Cos(x)
	case Cos(x) => Usub(Sin(x))
	case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2))))
	…
}
if (isLeaf(e.a)) d else Mul(d, differentiate(e.a))

Оператор проверяется на соответствие одному из доступных операторов («sin», «-», «cos», …)
Для примера, оператор «sin»: вернуть [ cos(a) ], если a = x, если же a — сложная функция u(x), то вернуть [ cos(a) * differentiate(a) ].

С остальными операторами происходят аналогичные действия, используя правило дифференцирования сложной функции и табличные правила взятия производной.

Отдельно следует рассмотреть оператор abs — модуль, поскольку его нет в таблице.

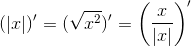
$(|x|)'=(sqrt{x^{2}})'=left( dfrac{x}{|x|} right)'$

Приватный метод isLeaf выясняет сложная функция или нет, в первом случае нужно вернуть текущий результат умноженный на производную вложенной функции, а во втором просто вернуть текущий результат.

Если один токен

Речь идет о переменной или константе

case Variable(a) => if (a == dx) Constant(BigDecimal(1)) else Constant(BigDecimal(0))
case Constant(a) => Constant(BigDecimal(0))
case Pi | Exponenta => Constant(BigDecimal(0))
case _ => throw new AbstractEvaluateException("Differentiate: Wrong input data")

Введены некорректные данные, вывести сообщение об ошибке и завершить работу.
Если переменная (по которой осуществляется дифференцирование, например x), вернуть [ 1 ].
Если константа, вернуть [ 0 ].

Напоследок добавим строку:

case Differentiate(_f, _dx) => differentiate(_f)(_dx.name)

Это на случай, если внутри функции есть вложенная производная, т.е. теперь можно считать производные высших порядков.

Приведу весь код дифференцирования, для лучшего понимания:

object Derivative {
  def apply(e: MathAST)(implicit dx: String): MathAST = differentiate(e)

  def differentiate(f: MathAST)(implicit dx: String): MathAST = f match {
    case Differentiate(_f, _dx) => differentiate(_f)(_dx.name)

    case Add(a, b) => Add(differentiate(a), differentiate(b))
    case Sub(a, b) => Sub(differentiate(a), differentiate(b))
    case Div(a, b) => Div(Sub(Mul(differentiate(a), b), Mul(a, differentiate(b))), Pow(b, Constant(BigDecimal(2))))

    case Pow(a, b) => {
      val u = isDependsOnVar(a)
      val v = isDependsOnVar(b)
      if (u && !v) Mul(Mul(Pow(a, Sub(b, Constant(BigDecimal(1)))), differentiate(a)), b) // u(x)^c, c=const
      else if (!u && v){  // c^u(x), c=const
        Mul(Mul(Pow(a, b), differentiate(b)), Ln(a))
      }else if(!u && !v){
        Constant(BigDecimal(0))
      }else Mul(Pow(a, Sub(b, Constant(BigDecimal(1)))), Add(Mul(b, differentiate(a)), Mul(Mul(a, Ln(a)), differentiate(b))))
    }
    case Mul(a, b) => {
      val u = isDependsOnVar(a)
      val v = isDependsOnVar(b)
      if (u && !v) {
        Mul(differentiate(a), b)
      } else if (!u && v){  // c^u(x), c=const
        Mul(a, differentiate(b))
      }else if (!u && !v){// c^c, c=const
        Constant(BigDecimal(0))
      }else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
    }

    case e: SingleToken =>
      val d = e match {
        case Sin(x) => Cos(x)
        case Cos(x) => Usub(Sin(x))
        case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2))))
        case Ctg(x) => Usub(Div(Constant(BigDecimal(1)), Pow(Sin(x), Constant(BigDecimal(2)))))
        case Abs(x) => Div(x, Abs(x))
        case Ln(x) => Div(Constant(BigDecimal(1)), x)
        case Sqrt(x) => Div(Constant(BigDecimal(1)), Mul(Constant(BigDecimal(2)), Sqrt(x)))
        case Usub(x) => Usub(differentiate(x))
        case Arcsin(x) => Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
        case Arccos(x) => Usub(Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))))
        case Arctg(x) => Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))
        case Arcctg(x) => Usub(Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
        case _ => throw new AbstractEvaluateException("Differentiate: Unknown unary operator")
      }
      if (isLeaf(e.a)) d else Mul(d, differentiate(e.a))

    case Variable(a) => if (a == dx) Constant(BigDecimal(1)) else Constant(BigDecimal(0))
    case Constant(a) => Constant(BigDecimal(0))
    case Pi | Exponenta => Constant(BigDecimal(0))
    case _ => throw new AbstractEvaluateException("Differentiate: Wrong input data")
  }

  private def isLeaf(e: MathAST): Boolean = e match {
    case Variable(_) | Constant(_) => true
    case  Pi | Exponenta => true
    case _ => false
  }

  private def isDependsOnVar(tree: MathAST)(implicit dx: String): Boolean = tree match{
    case e: DoubleToken => (e.a match {
      case Variable(name) => if(name == dx) true else false
      case _ => isDependsOnVar(e.a)
    })||(e.b match {
      case Variable(name) => if(name == dx) true else false
      case _ => isDependsOnVar(e.b)
    })
    case e: SingleToken => isDependsOnVar(e.a)
    case Variable(name) => if(name == dx) true else false
    case _ => false
  }
}

Заключение

Весь код исходников можно скачать на github’е, протестировать программу онлайн можно на сайте Калькулятор производных онлайн, приложение выполнено в виде REST сервиса и дополнено модулями упрощения выражений.

Список литературы

Математический портал «mathprofi.ru» mathprofi.ru/slozhnye_proizvodnye_logarifmicheskaja_proizvodnaja.html
Odersky M. «Programming in Scala (second edition)»
Хостманн К. «Scala для нетерпеливых»

Источник

Производная функции есть предел отношения приращения функции к приращению
независимой переменной при стремлении к нулю приращения независимой переменной

При численном нахождении производной заменим отношение
бесконечно малых приращений функций и аргумента отношением
конечных разностей. Очевидно, что чем меньше будет приращение аргумента, тем
точнее численное значение производной.

Первая производная. Двухточечные методы.

Для двухточечных методов при
вычислении производных используется значение функции в двух точках. Приращение
аргумента задается тремя способами, откладывая Δx = h
вправо, влево и в обе стороны от исследуемой точки. Соответственно получается
три двухточечных метода численного дифференцирования:

Суть указанных методов проиллюстрирована на рисунке.
Численное значение тангенса угла α образованного касательной к
графику y(x) и осью абсцисс, показывает точное значение
производной(геометрический смысл производной). Тангенсы углов α₁,
α₂, α₃ соответствуют приближенным значениям
производных, определенных методами 1,2,3 соответственно (подумайте почему?).

Пример. Вычислить точное и приближенное (тремя методами) значения производной
функции y=x*x в точке x=1 с шагом h=1 и h=0.001.

Этапы решения задачи приведены в таблице.

Таблица

Этап программирования	Выполнение
1. Постановка задачи	Вычислить точное и приближенное (тремя методами) значения производной функции y=x*x в точке x=1 с шагом h=1 и h=0.001.
2. Математическое описание	Аналитическое решение: y’=2x , y'(1)=2, Численное решение для шага: h=1 , для шага h=0.001
3. Разработка структограммы	Выполнить самостоятельно
4. Написание программы	Выполнить самостоятельно
5. Отладка и получени результатов	Выполнить самостоятельно

Вычисление первых производных по трёхточечным схемам.

Расчетные формулы для указанной трехточечной схемы имеют вид:

Вычисление производных второго порядка.

Вторая производная вычисляется как первая производная от первой производной. Для следующей пятиточечной схемы

расчетная формула имеет вид:

Пример. Написать
программу для нахождения второй производной функции y = 2 * x⁴

в точке x=1 с
шагом h=0.01, сравнить с точным значением.

Таблица

Технологическая операция

Выполнение

1. Постановка задачи

Написать программу для нахождения второй производной
функции y = 2 * x⁴ в точке x=1 с шагом h=0.01, сравнить с точным значением.

2. Математическое описание

Аналитическое значение

Приближенное значение

3. Разработка структограммы

Описание x,y,h

x=1; h=0.01

Вывод

4. Написание программы

Program P7;

Var x,ddy,h:real;

Function y(x:real):real;

begin

y:=2*sqr(sqr(x));

end;

begin

x:=1;h:=0.01;

ddy:=(y(x+h)-2*y(x)+y(x-h))/h/h;

writeln(ddy);

end.

5. Отладка и получение результатов

Выполнить сомостоятельно.

Вычисление производных третьего порядка.

Производные третьего порядка вычисляются как первая производная от производной второго порядка. Для рассмотренной пятиточечной схемы расчетная формула имеет вид

Контрольное задание. Лабораторная работа 2.

Численное дифференцирование

Вычислить значение производной в
произвольной точке x=x₀ аналитически и численно тремя методами для пяти
значений приращения аргумента Δx=1;
0.2; 0.1; 0.01; 0.001. Результаты расчета вывести на экран и распечатать в виде таблицы

Таблица вывода результатов расчета

Δx	y(x)	y'(x)
1
0.2
0.1
0.01
0.001

Построить графики
функций y'(x₀) = F(Δx). Варианты функций приведены в таблице.

Таблица

Варианты функций

Вар.	Вид функции	Вар.	Вид функции
1	x(t)=Ae^-at sin(ωt+b)	14	y=ctg^m (ax)
2	x(t)=Ae^at cos(ωt+b)	15	y(x)=(e^ax-e^-ax)ⁿ
3		16	x(t)=t^at
4	уυ(t)=cos²(at+b)	17	y(x)=(ax)^sin(bx)
5	yυ(t)=sin²(at+b)	18
6		19
7	q(t)=(a-btⁿ)ⁿ	20
8	y(x)=xⁿcos(ax)	21	R(φ)=arccos^m(a+bφⁿ)
9		22	r(φ)=c^sin(aφ+b)
10		23	y(x)=ln(tgⁿ(ax+b))
11		24	vυ(t)=log_a(tⁿ+b^m)^k
12	S(φ)=Вcоsⁿ(aφ+b)	25	S(φ)=Asinⁿ(aφ+b)
13	y=tg^ax( x/a )	26	X(t)=lg(atⁿ+b)

Примечание. Значение параметров a, b, c, d, m, n, A, B выбрать самостоятельно.

Содержание отчета:

Название, цель работы и задание.
Математическое описание, алгоритм (структограмма) и текст программы.
Таблица результатов расчета, четыре графика зависимости y'(x₀) = F(Δx) для трехчисленных методов и точного значения интеграла, выводы по работе.

Далее…

Источник

Тема 9. Численное дифференцирование и интегрирование.

Задача численного дифференцирования – приближенное вычисление значений производных заданной аналитически или таблично функции. Предположим, что нам дана таблично заданная функция y = f(x) набором пар точек (x_i, y_i) (i = 1, 2, … , n). Предположим, что точки являются равноотстоящими, т.е. x_i= x₀+ i·h, и значение величины h является достаточно малым. Тогда, исходя из математического определения производной функции, можно записать три приближенные формулы для вычисления производных первого порядка в точке x_i: