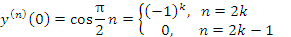Пусть
функция![]()
дифференцируема в некотором интервале.
Тогда её производная
![]() ,
,
вообще говоря, зависит отх
, то есть
является функцией от х.
Следовательно, по отношению к ней снова
можно ставить вопрос о существовании
производной.
Определение.
Производная
от первой производной называется
производной
второго порядка или второй производной
и обозначается символом
![]() или
или![]() ,
,
то есть
![]() .
.
Пример
1. Найти
вторую производную от функции
![]() .
.
Решение. Найдем
первую производную функции:
![]() .
.
Находим вторую
производную как производную первой
производной:
![]() .
.
Определение.
Производная
от второй производной называется
производной третьего порядка или третьей
производной и обозначается символом
![]() или
или![]() .
.
Определение.
Производной
n-ого
порядка функции
![]()
называется
первая производная от производной
(n-1)-го
порядка данной функции и обозначается
символом
![]() или
или![]() :
:
![]() .
.
Определение.
Производные
порядка выше первого называются
высшими
производными.
Пример
2. Найти
производную четвертого порядка функции
![]() .
.
Решение. Находим
последовательно первую, вторую, третью
и четвертую производные:
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Пример
3.Найти
производную n-ого
порядка для функции
![]() (k–const).
(k–const).
Решение. Имеем:
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Пример
4. Найти
производную n-ого
порядка для функции
![]() .
.
Решение. Имеем:
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
![]() Замечание.
Замечание.
Аналогично можно получить формулу n-ой
производной функции
![]() :
:
![]()
![]() .
.
![]() Пример
Пример
5. Найти
производную n-ого
порядка для степенной функции
![]() , где
, где![]() и
и![]() – любое вещественное число.
– любое вещественное число.
![]() Решение.
Решение.
Дифференцируя последовательно, получим:
![]()
![]() ,
,
![]() ,
,![]()
![]() ,
,
![]()
![]() .
.
![]() В
В
частном случае, когда
![]() ,
,
гдеm
– натуральное число, получим:
![]()
![]() ,
,
![]() при
при![]() .
.
![]() Замечание.
Замечание.
При строгом выводе формулы для производной
n-ого
порядка следует применять метод
математической индукции.
![]()
![]() Вторая
Вторая
производная параметрически заданной
функции
Если
функция задана параметрически уравнениями
![]() ,
,
то для нахождения производной второго
порядка нужно продифференцировать
выражение для её первой производной,
как сложной функции независимой
переменной.
Так
как
![]() ,
,
то
![]() ,
,
и с учетом того,
что
![]() ,
,
получим
![]() ,
,
то есть
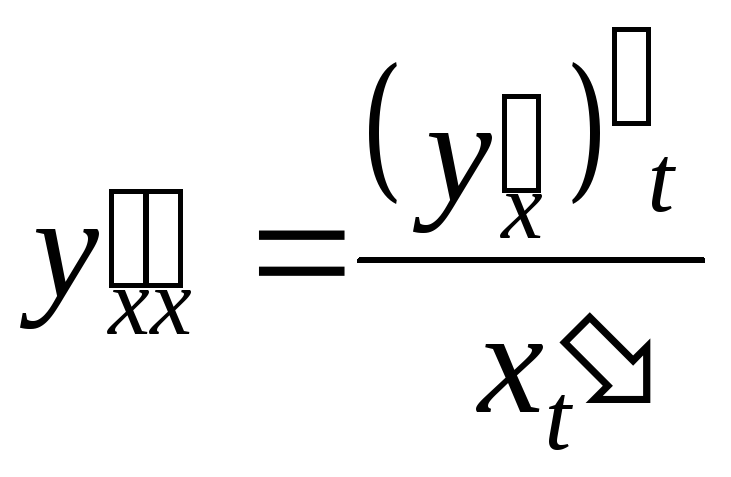 .
.
Аналогично можно найти третью
производную
![]()
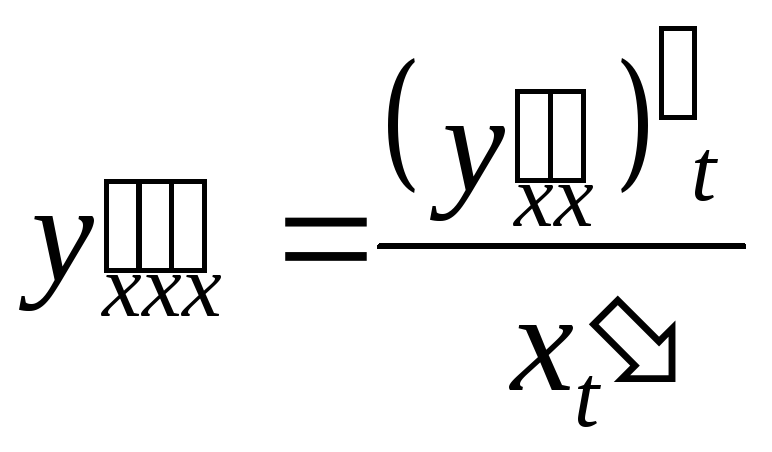 .
.
Пример
7. Найти
вторую производную параметрически
заданной функции
![]()
![]() ,
,![]() .
.
Решение.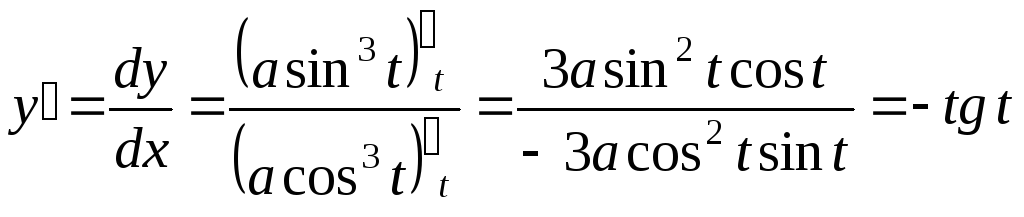 ,
,
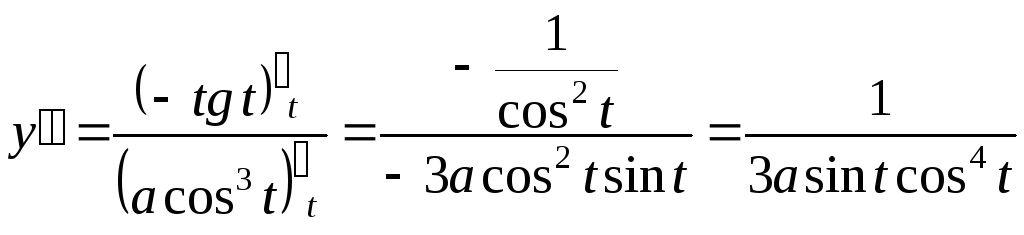 .
.
Формула Лейбница
Для
нахождения производной n-ого
порядка от произведения двух функций
большое практическое значение имеет
формула Лейбница.
Пусть
u
и
v
– некоторые
функции от переменной х,
имеющие производные любого порядка и
y=uv.
Выразим n-ую
производную
![]() через производные функцийu
через производные функцийu
и
v.
Имеем последовательно
![]() ,
,
![]() ,
,
![]() .
.
Легко подметить
аналогию между выражениями для второй
и третьей производных и разложением
бинома Ньютона соответственно во второй
и третьей степенях, но вместо показателей
степени стоят числа, определяющие
порядок производной, а сами функции
можно рассматривать как «производные
нулевого порядка». Учитывая это, получим
формулу Лейбница:
![]()
![]() . (2)
. (2)
Эту формулу
можно доказать методом математической
индукции.
Пример.
Найти пятую
производную функции
![]() .
.
Решение.
Положим
![]() и
и![]() .
.
Найдем![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() .
.
Подставляя эти выражения в формулу
Лейбница при![]() ,
,
получим
![]()
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Производные высших порядков
- Производные высших порядков с примерами
- Производные высших порядков сложных функций, обратных функций и функций, заданных параметрически
Производные высших порядков
Производная функции у = f (x) является также функцией: у’= f’ (x).
Эта функция также может иметь производную. Эта новая производная называется второй производной функции у = f (x) или производной функции f (x) второго порядка и обозначается  или
или  .
.
Производная второй производной, то есть функции называется третьей производной или производной третьего порядка и обозначается символом
называется третьей производной или производной третьего порядка и обозначается символом  или
или  . Так можно ввести производные четвертого, пятого и вообще n-го порядка, которые обозначают
. Так можно ввести производные четвертого, пятого и вообще n-го порядка, которые обозначают  .
.
Пример 1. Найти производную четвертого порядка функции  .
.
Решение. Имеем: 



Пример 2. Найти производные n-го порядка от функций
а) y = ex, б) y = sin x, в) y = cos x.
Решение.
а)
б)

и по индукции 
в) аналогично находим 
Производные высших порядков с примерами
Пусть функция 
 имеет производную
имеет производную  во всех точках некоторой окрестности точки
во всех точках некоторой окрестности точки  Если функция
Если функция  в свою очередь имеет в точке производную
в свою очередь имеет в точке производную  то она называется второй производной функции
то она называется второй производной функции  в точке
в точке  и обозначается
и обозначается  или
или  Таким образом, опуская обозначения аргумента, имеем
Таким образом, опуская обозначения аргумента, имеем

Аналогично определяются и производные  более высоких порядков
более высоких порядков 

где для удобства считается, что 
Примеры:
1. Если  то
то  вообще,
вообще,  В частности, если
В частности, если  то
то

2. Если 
 Заметив, что
Заметив, что  получим
получим

Вообще,

Аналогично,

По этой ссылке вы найдёте полный курс лекций по высшей математике:
Теорема 1. Если функции  имеют в точке
имеют в точке  производные порядка
производные порядка  то любая их линейная комбинация
то любая их линейная комбинация  и их произведение
и их произведение  имеют в точке
имеют в точке  производные порядка
производные порядка  причем
причем

Все производные в формулах (11.5) и (11.6) берутся в точке 
 биномиальные коэффициенты.
биномиальные коэффициенты.
Символическая запись  означает, что это выражение (см. среднюю часть формулы (11.6)) по своей структуре напоминает формулу бинома Ньютона
означает, что это выражение (см. среднюю часть формулы (11.6)) по своей структуре напоминает формулу бинома Ньютона

только вместо степеней  берутся производные соответствующих порядков функций
берутся производные соответствующих порядков функций  Формула (11.6) называется формулой Лейбница*).
Формула (11.6) называется формулой Лейбница*).
Докажем формулы (11.5) и (11.6) методом математической индукции. В п. 10.5 формула (11.5) была доказана для 

Пусть справедлива формула (11.5); покажем, что тогда будет справедлива и аналогичная формула для производной порядка 

Формула (11.5) доказана; докажем формулу (11.6).
Возможно вам будут полезны данные страницы:
Пусть справедлива формула (11.6) для производной порядка  от произведения функций. Докажем, что тогда будет справедлива и аналогичная формула для производной порядка
от произведения функций. Докажем, что тогда будет справедлива и аналогичная формула для производной порядка 


Вспомнив, что (см. п. 2.4)

получим

Производные высших порядков сложных функций, обратных функций и функций, заданных параметрически
С помощью формулы производной сложной функции (см. п. 10.7) можно вычислять и производные высших порядков сложной функции. Пусть функция  дважды дифференцируема в точке
дважды дифференцируема в точке  функция
функция  дважды дифференцируема в точке
дважды дифференцируема в точке  и имеет смысл сложная функция
и имеет смысл сложная функция  Вычислим вторую производную
Вычислим вторую производную  сложной функции
сложной функции  (для простоты записи аргумент писать не будем):
(для простоты записи аргумент писать не будем):

Аналогично вычисляются и производные более высоких порядков. С помощью формул производных обратной функции (см. п. 10.6) и сложной функции (см. п. 10.7) можно вычислять производные высших порядков обратных функций. Вычислим, например, вторую производную. Пусть функция  дважды дифференцируема в точке
дважды дифференцируема в точке  в ее окрестности непрерывна и строго монотонна, причем
в ее окрестности непрерывна и строго монотонна, причем  Тогда для второй производной
Тогда для второй производной  имеем в точке
имеем в точке 

Рассмотрим теперь параметрическое задание функций. Пусть на некотором множестве  задана пара функций
задана пара функций

причем одна из них, например,  строго монотонна на этом множестве и, следовательно, существует обратная функция
строго монотонна на этом множестве и, следовательно, существует обратная функция 
для которой  является множеством значений.
является множеством значений.
Тогда функция
называется параметрически заданной функцией (уравнениями (11.9)). Она определена на множестве значений функции
Если функции  и
и  дифференцируемы в точке
дифференцируемы в точке  функция
функция  непрерывна и строго монотонна в окрестности этой точки и
непрерывна и строго монотонна в окрестности этой точки и  то функция
то функция  дифференцируема в точке
дифференцируема в точке  причем
причем

ибо 
Аналогично вычисляются и производные высших порядков. Например, если функции (11.9) дважды дифференцируемы в точке  и
и  то
то

Выведенные здесь формулы не предназначены для запоминания. Достаточно усвоить метод их получения.


Лекции:
- Логарифмы: примеры и решения
- Производная и дифференциал
- Правило Лопиталя: пример решения
- Ряд тейлора примеры решения
- Каноническое уравнение эллипса
- Рациональные числа
- Предел числовой последовательности
- Пересекающиеся прямые
- Найти оптимум функции
- Метод неопределенных коэффициентов. Первая производная
Конев В.В. Дифференцирование функций
![]()
![]()
Производные высших порядков (примеры)
![]()
![]()
-
Пусть
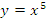 . Тогда
. Тогда
***
-
Получить общую формулу для производной n-го порядка от функции
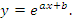
Решение.
Отметим, что полученная формула для производной n-го порядка оказывается справедливой и при n = 0:
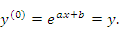
***
-
Вывести общую формулу для производной n-го порядка от функции

Решение.
При n = 0 эта формула дает правильное выражение для функции y.
***
-
Вывести общую формулу для производной n-го порядка от функции
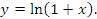
Решение.
Заметим, что полученная формула применима только при
 и, следовательно,
и, следовательно,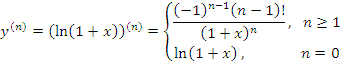
***
-
Вывести общую формулу для производной n-го порядка от функции

Решение. Представим предварительно эту функцию в виде алгебраической суммы простых дробей:
Используя формулу, полученную в примере 3, находим
***
-
Вывести общую формулу для производной n-го порядка от функции
 и вычислить эту производную в точке x = 0.
и вычислить эту производную в точке x = 0.
Решение.При каждом дифференцировании происходит сдвиг аргумента синуса на
 и, следовательно,
и, следовательно,
Очевидно, что
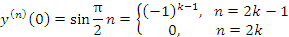
***
-
Аналогичным образом решается подобная задача для функции
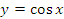 :
: