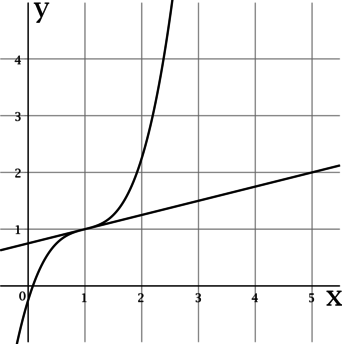
Геометрический смысл производной. Уравнение касательной к графику функции. Задание 7.
Вспомним определение производной:
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
Исходя из этого определения, рассмотрим, каким образом производная функции 
Посмотрите ВИДЕОУРОК, в котором я подробно объясняю, в чем заключается геометрический смысл производной, и как выводится уравнение касательной. А затем мы рассмотрим решение задач из Открытого банка заданий для подготовки к ЕГЭ по математике.
Итак.
Геометрический смысл производной.
Тангенс угла наклона касательной (угловой коэффициент наклона касательной), проведенной к графику функции 
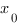

Заметим, что угол 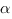
Уравнение касательной к графику функции 
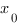
В этом уравнении:
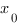
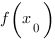



Приведем несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике, в которых используется знание геометрического смысла производной.
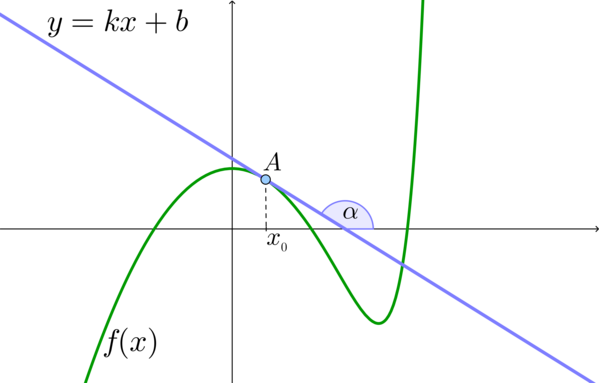
Пример 1. Задание В8 (№ 27504) На рисунке изображены график функции 
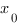

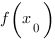
Значение производной функции 
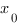
Проведем через точку А прямую параллельно оси ОХ, а через точку В – параллельно оси OY. Получим прямоугольный треугольник ABC:
Угол А треугольника АВС равен углу между касательной и положительным направлением оси ОХ.
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.
Длины катетов считаем по количеству клеточек.
Ответ: 0,25
Пример 2. Задание В8 (№ 27506) На рисунке изображены график функции 
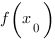

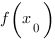
Эта задача очень похожа на предыдущую, за исключением того, что здесь касательная наклонена влево, и угол 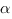
Построим, как предыдущей задаче, прямоугольный треугольник АВС:
Угол А треугольника ABC и угол 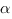
Запомните, если прямая наклонена влево, то коэффициент наклона прямой отрицателен.
Ответ: -0,25
Пример 3. Задание В8 (№ 40129) На рисунке изображен график функции 

Соединим отрезком точку начала координат с точкой касания:
Производная функции в точке касания равна тангенсу угла между касательной и положительным направлением оси ОХ:
Чтобы найти тангенс 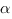
Ответ: 1,25
И.В. Фельдман, репетитор по математике.
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Значение производной в точке касания как тангенс угла наклона
Если к кривой (f(x)) проведена касательная в точке с абсциссой (x_0), то
[{large{color{royalblue}{f'(x_0)=mathrm{tg}, alpha, }}},]
где (alpha) – угол наклона касательной.
Значит, верна формула: (f'(x_0)=mathrm{tg}, alpha=k).
Заметим, что координаты точки (A) тогда можно записать как ( (x_0; f(x_0)) ) или ( (x_0; y_0) ),
где ( y_0=kx_0+b).
То есть ( y_0=f(x_0)).
Задание
1
#2090
Уровень задания: Равен ЕГЭ
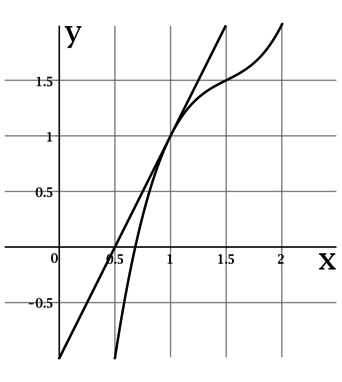
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))) (то есть угла между касательной к графику (f(x)) в точке ((x_0; f(x_0))) и положительным направлением оси (Ox)).
По рисунку видно, что касательная проходит через точки ((0,5; 0)) и ((1; 1)), тогда тангенс угла наклона касательной составляет (1 : 0,5
= 2), следовательно, (f'(x_0) = 2).
Ответ: 2
Задание
2
#2091
Уровень задания: Равен ЕГЭ
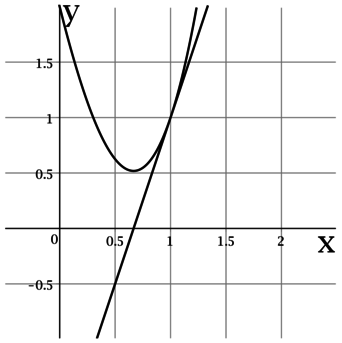
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((0,5; -0,5)) и ((1; 1)), тогда тангенс угла наклона касательной составляет (1,5 :
0,5 = 3), следовательно, (f'(x_0) = 3).
Ответ: 3
Задание
3
#2092
Уровень задания: Равен ЕГЭ
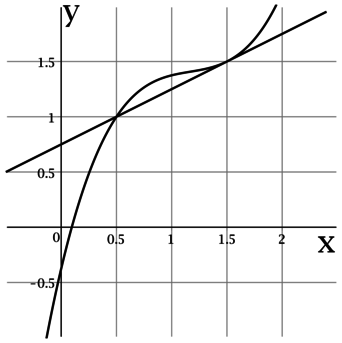
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((0,5; 1)) и ((1,5; 1,5)), тогда тангенс угла наклона касательной составляет (0,5
: 1 = 0,5), следовательно, (f'(x_0) = 0,5).
Ответ: 0,5
Задание
4
#2093
Уровень задания: Равен ЕГЭ
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f(x)) в точке (x_0).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((1; 1)) и ((5; 2)), тогда тангенс угла наклона касательной составляет ((2 – 1)
: (5 – 1) = 0,25), следовательно, (f'(x_0) = 0,25).
Ответ: 0,25
Задание
5
#3112
Уровень задания: Равен ЕГЭ
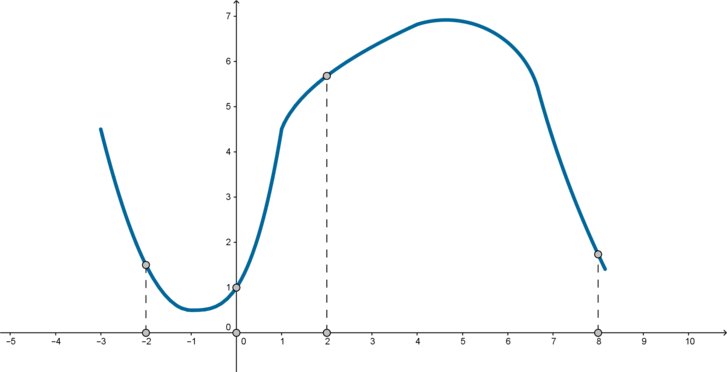
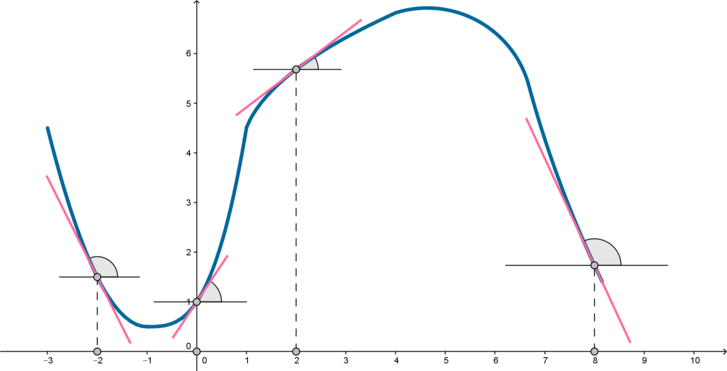
На рисунке изображен график функции (y=f(x)) и отмечены точки (-2;
0; 2; 8). В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Проведем касательные к графику функции в этих точках. Так как тангенс угла (alpha) наклона касательной равен значению производной (f'(x)) в точке касания (x_0) ((f'(x_0)=mathrm{tg},alpha)), то нужно сравнить тангенсы углов, отмеченных на рисунке.
Вспомним, что если угол тупой, то его тангенс отрицательный, если острый – положительный. Следовательно, так как мы ищем наибольший тангенс, имеет смысл рассматривать только острые углы. Это углы, образованные касательными в точках (0) и (2). Заметим, что угол в точке (0) больше, следовательно, его тангенс также больше, чем тангенс угла в точке (2). Таким образом, ответ: (0).
Ответ: 0
Задание
6
#718
Уровень задания: Сложнее ЕГЭ
Производная (f'(x)) функции (f(x)) в точке (x_0) равна (10). Найдите котангенс угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
При всех (alpha), при которых (mathrm{tg}, alpha) и (mathrm{ctg}, alpha) имеют смысл, выполнено (mathrm{tg}, alphacdotmathrm{ctg}, alpha = 1), откуда котангенс угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))) равен (0,1).
Ответ: 0,1
Задание
7
#719
Уровень задания: Сложнее ЕГЭ
Производная (f'(x)) функции (f(x)) в точке (x_0) равна (5). Найдите сумму тангенса и котангенса угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
При всех (alpha), при которых (mathrm{tg}, alpha) и (mathrm{ctg}, alpha) имеют смысл, выполнено (mathrm{tg}, alphacdotmathrm{ctg}, alpha = 1), откуда котангенс угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))) равен (0,2), тогда сумма тангенса и котангенса угла наклона касательной к графику функции (f(x)) в точке ((x_0; f(x_0))) равна (5,2).
Ответ: 5,2

УСТАЛ? Просто отдохни
Приветствую Вас, уважаемые Читатели! В одной из прошлых статей я рассказывал на очень простом языке о краеугольном понятии математического анализа – производной. В том материале я искал производную в виде мгновенной скорости движущегося объекта. Сегодня же я расскажу и о другом каноническом её определении – геометрическом – в максимально (иногда даже слишком) простой форме.
Что такое касательная к кривой?
Осведомленные Читатели, естественно вспоминают и знают, что с понятием производной тесно связано понятие касательной. Давайте формализуем его хотя бы чисто геометрически. Внимание на рисунок:
Пусть дана кривая линия, на которой отмечена точка А₀. Отметим на этой же прямой произвольную (в том смысле, что можем поставить её и справа) точку А₁ и проведем секущую через эти две точки.
Если теперь мы будем перемещать точку А₁ по кривой в сторону точки А₀, то секущая будет пытаться занять некоторое предельное положение, при котором у неё с кривой будет всего лишь одна общая точка. Именно тогда секущая и превращается в касательную.
- Конечно, касательная – это идеализированное понятие. Ведь чтобы понять, что значит “касается в одной точке”, нужно знать, что, собственно, из себя представляет эта точка. К счастью мы пользуемся в математике определением Евклида – “точка – это то, часть чего есть ничто“. Но вернемся к математике.
Определение производной
Итак, рассмотрим график функции y=f(x) и дадим пояснения рисунку:
Пусть на графике имеется точка М₀ (х₀,y₀), в которой функция принимает значение f(х₀). Зададим этой точке любое горизонтальное приращение ∆х (например, +0,1, что по сути без разницы). Тогда функция примет значение f(х₀+∆х), что соответствует точке М₁ на графике. Разница же между значениями функции в точках М₀ и М₁ равняется:
Давайте теперь ответим на вопрос, под каким углом секущая М₀М₁ встречается с горизонтальной осью?
Очевидно, исходя из простых геометрических соображений, что:
Тангенс – отношение противолежащего катета прямоугольного треугольника к прилежащему
Теперь начинаем как при определении касательной двигать точку М₁ в сторону точки М₀:
Сначала определимся, что “двигаем в сторону” – значит уменьшаем приращение ∆х.
На графике новому меньшему приращению ∆х (было + 0,1, а теперь пусть будет +0,05) соответствует точка М₂ и синяя секущая. Очевидно, что угол “встречи” секущей также изменился: в данном случае он увеличился.
- Если бы точка М₁ была слева от М₀, то угол бы наоборот увеличивался. Здесь всё зависит от конкретной точки конкретного графика, да и это не меняет сути вопроса.
Теперь же будем еще сильнее придвигать точку М₁, да так, что приращение ∆х будет всё меньше и меньше или, на языке матанализа, устремим его к нулю.
Как раз-таки в этой позиции предельной близости ∆х к нулю, секущая превратится в касательную к кривой в точке М₀. Как записать теперь угол встречи касательной с горизонтальной осью? Да почти так же, ведь изменений немного:
Т.е. значение производной функции в некоторой точке равняется тангенсу угла, образованного положительным направлением оси ОХ и касательной к графику функции в этой точке.
По рисунку видно, что в касательная точке М₀ встречается с осью ОХ по углом, меньшим 90 градусов, следовательно, тангенс угла больше 0. В таком случае говорят, что функция возрастает в точке М₀ (немного непонятно, что это такое, но с тем же самым мы встречались, когда говорили о мгновенной скорости).
Итак, с геометрическим понятием производной у меня всё. Если Вам понравился данный материал, он отвечает Вашим ожиданиям, да и просто Вы не прочь поддержать автора – ставьте “Нравится” и подписывайтесь на канал “Математика не для всех”. Спасибо за внимание!
- TELEGRAM и Facebook – там я публикую не только интересные статьи, но и математический юмор и многое другое.
Геометрический смысл производной
Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!
Рассмотрим график какой-то функции ( y=fleft( x right)):
Выберем на линии графика некую точку ( A). Пусть ее абсцисса ( {{x}_{0}}), тогда ордината равна ( fleft( {{x}_{0}} right)).
Затем выберем близкую к точке ( A) точку ( B) с абсциссой ( {{x}_{0}}+Delta x); ее ордината – это ( fleft( {{x}_{0}}+Delta x right)):
Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).
Обозначим угол наклона прямой к оси ( Ox) как ( alpha ).
Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.
Какие значения может принимать угол ( alpha )?
Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – ( 180{}^circ ), а минимально возможный – ( 0{}^circ ).
Значит, ( alpha in left[ 0{}^circ ;180{}^circ right)). Угол ( 180{}^circ ) не включается, поскольку положение прямой в этом случае в точности совпадает с ( 0{}^circ ), а логичнее выбирать меньший угол.
Возьмем на рисунке такую точку ( C), чтобы прямая ( AC) была параллельна оси абсцисс, а ( BC) – ординат:
По рисунку видно, что ( AC=Delta x), а ( BC=Delta f).
Тогда отношение приращений:
( frac{Delta f}{Delta x}=frac{BC}{AC}={tg}alpha )
(так как ( angle C=90{}^circ ), то ( triangle ABC) – прямоугольный).
Давай теперь уменьшать ( Delta x).
Тогда точка ( B) будет приближаться к точке ( A). Когда ( Delta x) станет бесконечно малым ( left( Delta xto 0 right)), отношение ( frac{Delta f}{Delta x}) станет равно производной функции в точке ( {{x}_{0}}).
Что же при этом станет с секущей?
Точка ( B) будет бесконечно близка к точке ( A), так что их можно будет считать одной и той же точкой.
Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки ( A), но этого достаточно).
Говорят, что при этом секущая занимает предельное положение.
Угол наклона секущей к оси ( displaystyle Ox) назовем ( varphi ). Тогда получится, что производная
( {f}’left( {{x}_{0}} right)underset{Delta xto 0}{mathop{=}},frac{Delta f}{Delta x}= {tg}varphi ),
то есть
Производная равна тангенсу угла наклона касательной к графику функции в данной точке
Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:
( y=kx+b).
За что отвечает коэффициент ( displaystyle k)? За наклон прямой. Он так и называется: угловой коэффициент.
Что это значит? А то, что равен он тангенсу угла между прямой и осью ( displaystyle Ox)!
То есть вот что получается:
( {f}’left( {{x}_{0}} right)= {tg}varphi =k).
Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?
Посмотрим: Теперь углы ( alpha ) и ( displaystyle varphi ) тупые. А приращение функции ( Delta f) – отрицательное.
Снова рассмотрим ( triangle ABC): ( angle B=180{}^circ -alpha text{ }Rightarrow text{ } {tg}angle B=- {tg}alpha ).
С другой стороны, ( {tg}angle B=frac{AC}{BC}=frac{-Delta f}{Delta x}).
Получаем: ( frac{-Delta f}{Delta x}=- {tg}alpha text{ }Rightarrow text{ }frac{Delta f}{Delta x}= {tg}alpha ), то есть все, как и в прошлый раз.
Снова устремим точку ( displaystyle B) к точке ( displaystyle A), и секущая ( displaystyle AB) примет предельное положение, то есть превратится в касательную к графику функции в точке ( displaystyle A).
Итак, сформулируем окончательно полученное правило:
Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:
( {f}’left( {{x}_{0}} right)= {tg}varphi =k)
Это и есть геометрический смысл производной.
Окей, все это интересно, но зачем оно нам? Вот пример:
На рисунке изображен график функции ( displaystyle y=mathsf{f}left( x right)) и касательная к нему в точке с абсциссой ( {{x}_{0}}).
Найдите значение производной функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}).
Решение.
Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:
( displaystyle f’left( x right)=k= {tg}varphi).
Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной.
На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!
Угол наклона касательной к оси ( displaystyle Ox) – это ( displaystyle angle BAC). Найдем тангенс этого угла:
( displaystyle {tg}angle BAC=frac{BC}{AC}=frac{6}{5}=1,2).
Таким образом, производная функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}) равна ( displaystyle 1,2).
Ответ: ( displaystyle 1,2).
Теперь попробуй сам.
Уравнение касательной к графику функций
А сейчас сосредоточимся на произвольных касательных.
Предположим, у нас есть какая-то функция, например, ( fleft( x right)=left( {{x}^{2}}+2 right)). Мы нарисовали ее график и хотим провести касательную к нему в какой-нибудь точке ( {{x}_{0}}). Например, в точке ( {{x}_{0}}=2).
Берем линейку, пристраиваем ее к графику и чертим:
Что мы знаем об этой прямой? Что самое важное нужно знать о прямой на координатной плоскости?
Поскольку прямая – это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты ( k) и ( b) в уравнении
( y=kx+b).
Но ведь ( k) мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке:
( k={f}’left( {{x}_{0}} right)).
В нашем примере будет так:
( {f}’left( x right)={{left( {{x}^{2}}+2 right)}^{prime }}=2x;)
( k={f}’left( {{x}_{0}} right)={f}’left( 2 right)=2cdot 2=4.)
Теперь остается найти ( b) . Это проще простого: ведь ( b) – значение ( y) при ( displaystyle x=0).
Графически ( b) – это координата пересечения прямой с осью ординат (ведь ( displaystyle x=0) во всех точках оси ( displaystyle Oy)):
Проведём ( BCparallel Ox) (так, что ( triangle ABC) – прямоугольный).
Тогда ( angle ABC=alpha )(тому самому углу между касательной и осью абсцисс). Чему равны ( displaystyle AC) и ( displaystyle BC)?
По рисунку явно видно, что ( BC={{x}_{0}}), а ( AC=fleft( {{x}_{0}} right)-b). Тогда получаем:
( {f}’left( {{x}_{0}} right)= {tg}alpha =frac{AC}{BC}=frac{fleft( {{x}_{0}} right)-b}{{{x}_{0}}}text{ }Rightarrow text{ }b=fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right)).
Соединяем все полученные формулы в уравнение прямой:
( y=kx+b={f}’left( {{x}_{0}} right)cdot x+fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right);)
( y={f}’left( {{x}_{0}} right)cdot left( x-{{x}_{0}} right)+fleft( {{x}_{0}} right))
Это и есть уравнение касательной к графику функции ( fleft( x right)) в точке ( {{x}_{0}}).
Пример:
Найди уравнение касательной к графику функции ( fleft( x right)={{x}^{2}}-2x+3) в точке ( {{x}_{0}}=3).
Решение:
На этом примере выработаем простой…
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
ЕГЭ №7. Производная функции — геометрический смысл, дифференцирование
На этом видео мы вспомним, что такое функция и её график, научимся искать производную некоторых функций, например, такой: y = 2×3 – 3×2 + x + 5.
Мы разберём от А до Я все 7 типов задач, которые могут попасться в задаче №7 из ЕГЭ. Узнаем, на какие 3 фразы в условии задачи нужно обратить особое внимание, чтобы с лёгкостью решить задачу и не потерять баллы на ровном месте.
Разберём все возможные ошибки, которые можно допустить в этих задачах. Мы поймём, что многие из этих задач решаются обычным подсчётом клеточек на графике! Главное – не перепутать, что нужно считать.
P.S. Не забудьте потом посмотреть родственную тему: «Интегралы на ЕГЭ. Первообразные элементарных функций».
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Решение:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Пример:
Решение:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.