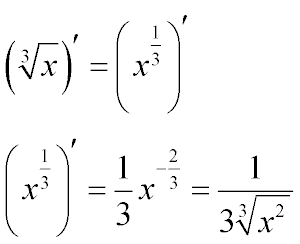Как найти производную числа с корнем

Как найти производную числа с корнем


Загрузить PDF


Загрузить PDF

На курсах дифференциального исчисления вы наверняка учили правила дифференцирования основных функций, в том числе правило дифференцирования степенной функции. Однако если функция содержит квадратный или другой корень, например {sqrt {x}}, может показаться, что данное правило не подходит. Тем не менее достаточно переписать ее в степенном виде, чтобы получить очевидный ответ. Если функция содержит несколько корней, такую подстановку можно делать сколько угодно раз и использовать правило дифференцирования сложной функции.

  1. Изображение с названием Differentiate the Square Root of X Step 1

    1

    Вспомните правило дифференцирования степенной функции. Обычно это правило учат в самом начале курса дифференциального исчисления. Оно гласит, что производная переменной x, возведенной в степень a, равна:[1]

  2. Изображение с названием Differentiate the Square Root of X Step 2

    2

  3. Изображение с названием Differentiate the Square Root of X Step 3

    3

    Примените правило дифференцирования степенной функции. Если под корнем стоит переменная x, f(x)={sqrt {x}}, производная берется следующим образом:[3]

  4. Изображение с названием Differentiate the Square Root of X Step 4

    4

    Упростите результат. На этом этапе необходимо вспомнить, что при отрицательной степени следует найти число, обратное данному числу в той же положительной степени. Степень -{frac {1}{2}} означает, что квадратный корень следует поставить в знаменателе дроби.[4]

    Реклама

  1. Изображение с названием Differentiate the Square Root of X Step 5

    1

    Вспомните правило дифференцирования сложных функций. Это правило применяется в тех случаях, когда необходимо продифференцировать функцию, аргументом которой выступает другая функция. Согласно данному правилу, комбинация двух функций, f(x) и g(x), дифференцируется следующим образом:[5]

  2. Изображение с названием Differentiate the Square Root of X Step 6

    2

    Определите функции. При использовании правила дифференцирования сложных функций первым делом следует выявить комбинацию функций. В случае квадратного корня в роли внешней функции f(g) выступает взятие корня, а внутренней функцией g(x) является то, что стоит под знаком корня.[6]

  3. Изображение с названием Differentiate the Square Root of X Step 7

    3

    Найдите производные обеих функций. Чтобы применить правило дифференцирования сложных функций к квадратному корню, сначала следует найти производную квадратного корня:[7]

  4. Изображение с названием Differentiate the Square Root of X Step 8

    4

    Реклама

  1. Изображение с названием Differentiate the Square Root of X Step 9

    1

    Запомните простое правило дифференцирования любых квадратных корней. Если необходимо найти производную квадратного корня, под которым стоит переменная или функция, используйте следующее правило. Результат всегда будет представлять собой производную подкоренного выражения, поделенную на удвоенный первоначальный квадратный корень. Это можно записать следующим образом:[9]

  2. Изображение с названием Differentiate the Square Root of X Step 10

    2

    Найдите производную подкоренного выражения. Как следует из названия, подкоренное выражение стоит под знаком квадратного корня. Чтобы применить данное правило, найдем производную этого выражения. Рассмотрим следующие примеры:[10]

  3. Изображение с названием Differentiate the Square Root of X Step 11

    3

    Запишите производную подкоренного выражения в числителе дроби. Производная корня представляет собой дробь, в числителе которой стоит производная подкоренного выражения. Для приведенных выше функций получаем следующие выражения:[11]

  4. Изображение с названием Differentiate the Square Root of X Step 12

    4

    Запишите знаменатель в виде удвоенного первоначального квадратного корня. Согласно данному правилу, в знаменателе следует написать удвоенный квадратный корень. Для приведенных выше функций получаем следующие знаменатели:[12]

  5. Изображение с названием Differentiate the Square Root of X Step 13

    5

    Скомбинируем числитель и знаменатель и получим искомую производную. Запишите полную дробь, и у вас получится производная первоначальной функции:[13]

    Реклама

Об этой статье

Эту страницу просматривали 52 041 раз.

Была ли эта статья полезной?

Источник

Производная корня

Опубликовано 10.07.2021

Производная корня из x – это формула определения производной функции, выраженной корнем из x или производной корня из выражения относительно x. Все производные смотрите в таблице производных.

Формула производной квадратного корня

Давайте выведем с вами формулу для производной корня для простой функции, опираясь на формулу производной степени (x^n)'=n cdot x^{n-1}:

displaystyle (sqrt{x})'=(x^{frac{1}{2}})'= frac{1}{2}x^{frac{1}{2}-1}=frac{1}{2}=x^{-frac{1}{2}}=frac{1}{2 sqrt{x}},  (x>0)

То есть, получается, что формула производной корня: displaystyle (sqrt{x})'=frac{1}{2 sqrt{x}}, где (x>0)

Производная корня любой степени

Аналогично определим производную корня любой степени. Например, пусть нам нужно определить производную кубического корня иначе находим производную корня третьей степени из x.

Формула производной корня

Формула производной корня

Производная кубического корня

Определим производную корня кубического: sqrt[3]{x^2}. Запишем этот корень как степень от x. Получим x^{frac{2}{3}}.

Находим производную:

displaystyle (sqrt[3]{x^2})'=(x^{frac{2}{3}})'=frac{2}{3} cdot x^{frac{2}{3}-1}=frac{2}{3} cdot x^{-frac{1}{3}} или

displaystyle (sqrt[3]{x^2})'=frac{2}{3 sqrt[3]{x}}

Примеры нахождения производной корня

Пример 1

Найдите производную функции: displaystyle y=sqrt{x} при x=4

Решение: находим производную функции: displaystyle y'=frac{1}{2sqrt{x}}, теперь подставим данное значение x. Получим displaystyle y'(4)=frac{1}{2sqrt{4}}=frac{1}{4}

Пример 2

Найдите производную функции f=sqrt[4]{x}. То есть нам нужно узнать, какова будет производная корня четвертой степени из x.

Решение: представим корень в виде степени. Получим displaystyle sqrt[4]{x}=x^{frac{1}{4}}. Теперь легко можно найти производную, зная формулу производной степени.

displaystyle f'(x)=(x^{frac{1}{4}})'=frac{1}{4} x^{frac{1}{4}-1}=frac{1}{4}x^{frac{-3}{4}}=frac{1}{4x^{frac{3}{4}}}=frac{1}{4 sqrt[4]{x^3}}

Таким образом, теперь легко определять производную корня любой степени, просто представляя сам корень в виде степени и зная формулу производной степени.

( 5 оценок, среднее 4.2 из 5 )

Источник

Содержание:

  • Формула
  • Примеры вычисления производной корня

Формула

$$(sqrt{x})^{prime}=frac{1}{2 sqrt{x}}$$

Производная от корня равна единице, деленной на два таких же корня.

Если под корнем находится сложная функция $u=u(x)$, то производная
от корня этой функции будет равна: единице, деленной на два таких же корня и умноженной на производную подкоренного выражения, то есть

$$(sqrt{u})^{prime}=frac{1}{2 sqrt{u}} cdot u^{prime}$$

Примеры вычисления производной корня

Пример

Задание. Найти производную функции $y(x)=2 sqrt{x}$

Решение. Искомая производная равна:

$$y^{prime}(x)=(2 sqrt{x})^{prime}$$

Согласно правилам дифференцирования, вынесем константу 2 за знак производной, в итоге будем иметь:

$$y^{prime}(x)=2 cdot(sqrt{x})^{prime}=2 cdot frac{1}{2 sqrt{x}}=frac{1}{sqrt{x}}$$

Ответ. $y^{prime}(x)=frac{1}{sqrt{x}}$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Вычислить производную функции $y(x)=sqrt{2 x}$

Решение. Искомая производная

$$y^{prime}(x)=(sqrt{2 x})$$

Находим как производную сложной функции, то есть вначале находим как производную от корня, а затем умножаем на производную
подкоренного выражения. В результате будем иметь:

$$y^{prime}(x)=(sqrt{2 x})^{prime}=frac{1}{2 sqrt{2 x}} cdot(2 x)^{prime}$$

Константу выносим за знак производной, а
производная независимой переменной равна единице, тогда получаем:

$$y^{prime}(x)=frac{1}{2 sqrt{2 x}} cdot 2 cdot(x)^{prime}=frac{1}{sqrt{2 x}} cdot 1=frac{1}{sqrt{2 x}}$$

Ответ. $y^{prime}(x)==frac{1}{sqrt{2 x}}$

Читать дальше: производная синуса (sinx)’.

Источник

См. также: 

таблица производных простых функций

таблица производных логарифмических функций

таблица производных тригонометрических функций

Производная корня. Формулы для нахождения производной корня

Формула нахождения производной квадратного корня, кубического корня и корня произвольной степени

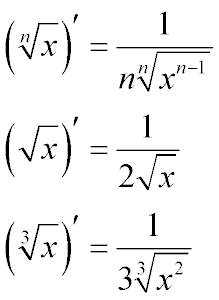
  1. Общий случай формулы производной корня произвольной степени – дробь, в числителе которой единица, а в знаменателе число, равное степени корня, для которого вычислялась производная, умноженная на корень такой же степени, подкоренное выражение которого – переменная в степени корня, для которого вычислялась производная, уменьшенной на единицу
  2. Производная квадратного корня – является частным случаем предыдущей формулы. Производная квадратного корня из x – это дробь, числитель которого равен единице, а знаменатель – двойка, умноженная на квадратный корень х
  3. Производная кубического корня, также частный случай общей формулы. Производная кубического корня – это единица, деленная на три кубических корня из икс квадрат.

Ниже приведены преобразования, поясняющие, почему формулы нахождения производной квадратного и кубического корня именно такие, как приведены на рисунке. 

Разумеется, данные формулы можно вообще не запоминать, если принять во внимание, что извлечение корня производной степени – это то же самое, что возведение в степень дроби, знаменатель которой равен той же степени. Тогда нахождение производной корня сводится к применению формулы нахождения производной степени соответствующей дроби.

Производная переменной под квадратным корнем

( √x )’ = 1 / ( 2√x )   или 1/2 х-1/2  

 

Пояснение:

( √x )’ = ( х1/2 )’   

Квадратный корень – это точно то же самое действие, что и возведение в степень 1/2, значит для нахождения производной корня можно применить формулу из правила нахождения производной от переменной в произвольной степени:

( х1/2 )’ = 1/2 х-1/2 = 1 / (2√х)  

Производная кубического корня  (производная корня третьей степени)

Производная кубического корня находится точно по такому же принципу, что и квадратного.

Представим себе кубический корень как степень 1/3 и найдем производную по общим правилам дифференцирования. Краткую формулу можно посмотреть на картинке выше, а ниже расписано пояснение, почему именно так.

Нахождение производной кубического корня представлением через степенную функцию

Степень -2/3 получается в следствие вычитания единицы из 1/3

Производная переменной под корнем произвольной степени 

Данная формула пригодна для нахождения производной корня любой степени:

( n√x )’ = 1 / ( n n√xn-1 ) 

В более удобном для глаза виде она представлена на картинке выше.

Здесь:

n – степень корня, для которой находится производная

x – переменная, для которой находится производная


2080.1947
 

 Производная дроби |

Описание курса

| Нахождение экстремума функции 

Источник

Производная корня икс

ОПРЕДЕЛЕНИЕ

Производная корня икс равна единице, деленной на два таких же корня.

Данную формулу можно получить из формулы производной степенной функции , представив корень в виде дробного показателя:

Примеры решения задач по теме «Производная корня»

ПРИМЕР 1

  • Задание

    • Найти производную функции

  • Решение

    • Искомая производная

    По правилам дифференцирования производная суммы равна сумме производных. То есть тогда

    Производная первого слагаемого, как константы, равна 0:

    Найдем производную второго слагаемого

    Вначале по правилу дифференцирования вынесем константу за знак производной:

    Далее находим производную от корня по формуле . И так как подкоренное выражение есть сложная функция (оно отлично от просто x), то еще дробь нужно будет умножить на производную от подкоренного выражения:

    Производная от суммы равна сумме производных:

    Первая производная от независимой переменной равна единице, а производная от константы 2 равна нулю, то есть имеем:


    Итак,

    Ответ

    ПРИМЕР 2

  • Задание

    • Найти производную функции

  • Решение

    • Искомая производная

    Производная от корня равна единице деленной на два таких же корня. Но так как подкоренное выражение является сложной функцией (под корнем стоит не просто x, а sin x ), то еще надо домножить на производную от подкоренного выражения, то есть синуса. Производная от синуса равна косинусу . Тогда имеем:

    Ответ

    Источник

    Добавить комментарий