Как найти производную для неявно заданной функции

Производная неявной функции

Формула

Рассмотрим функцию y(x), которая записывается неявным способом в общем виде $ F(x,y(x)) = 0 $. Производная неявной функции находится двумя способами:

1. Дифференцированием обеих частей уравнения
2. С помощью использования готовой формулы $ y’ = – frac{F’_x}{F’_y} $

Как найти?

Способ 1

Не требуется приводить функцию к явному виду. Нужно сразу приступать к дифференцированию левой и правой части уравнения по $ x $. Стоит обратить внимание, что производная $ y’ $ вычисляется по правилу дифференцирования сложной функции. Например, $ (y^2)’_x = 2yy’ $. После нахождения производной необходимо выразить $ y’ $ из полученного уравнения и разместить $ y’ $ в левой части.

Способ 2

Можно воспользоваться формулой, в которой используются в числителе и знаменателе частные производные неявной функции $ F(x,y(x)) = 0 $. Для нахождения числителя берем производную по $ x $, а для знаменателя производную по $ y $. 

Вторую производную неявной функции можно найти с помощью повторного дифференцирования первой производной неявной функции.

Примеры решений

Рассмотрим практические примеры решений на вычисление производной неявно заданной функции.

Пример 1

Найти производную неявной функции $ 3x^2y^2 -5x = 3y – 1 $

Решение

Воспользуемся способом №1. А именно продифференцируем левую и правую часть уравнения: $$ (3x^2y^2 -5x)’_x = (3y – 1)’_x $$ Не забываем при дифференцировании использовать формулу производной произведения функций: $$ (3x^2)’_x y^2 + 3x^2 (y^2)’_x – (5x)’_x = (3y)’_x – (1)’_x $$ $$ 6x y^2 + 3x^2 2yy’ – 5 = 3y’ $$ Далее выражаем y’ из уравнения: $$ 6x y^2 – 5 = 3y’ – 6x^2 yy’ $$ $$ 6x y^2 – 5 = y'(3-6x^2 y) $$ $$ y’ = frac{6x y^2 – 5}{3 – 6x^2y } $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ y’ = frac{6x y^2 – 5}{3 – 6x^2y } $$

Пример 2

Функция задана неявно, найти производную $ 3x^4 y^5 + e^{7x-4y} -4x^5 -2y^4 = 0 $

Решение

Воспользуемся способом №2. Находим частные производные функции $ F(x,y) = 0 $ Положим $ y $ постоянной и продифференцируем по $ x $: $$ F’_x = 12x^3 y^5 + e^{7x-4y} cdot 7 – 20x^4 $$ $$ F’_x = 12x^3 y^5 + 7e^{7x-4y} – 20x^4 $$ Считаем теперь $ x $ константой и дифференцируем по $ y $: $$ F’_y = 15x^4 y^4 + e^{7x-4y} cdot (-4) – 8y^3 $$ $$ F’_y = 15x^4 y^4 – 4e^{7x-4y} – 8y^3 $$ Подставляем теперь в формулу $ y’ = -frac{F’_x}{F’_y} $ и получаем: $$ y’ = -frac{12x^3 y^5 + 7e^{7x-4y} – 20x^4}{15x^4 y^4 – 4e^{7x-4y} – 8y^3} $$

Ответ

$$ y’ = -frac{12x^3 y^5 + 7e^{7x-4y} – 20x^4}{15x^4 y^4 – 4e^{7x-4y} – 8y^3} $$

Дифференцирование функции, заданной неявно

Определение
1. Равенство
F(x,
y)
= 0 определяет
у как функцию у
= у(х), задает
эту функцию неявно.

Для нахождения
производной функции у,
заданной неявно, нужно продифференцировать
равенство F(x,
y)
= 0 по аргументу
х
и решить уравнение относительно у’.

Примеры 1 – 4.
Продифференцировать функцию у
= у(х), заданную
неявно.

1. х³
   + у²
   – 5х = 0.

Решение.
Продифференцируем это равенство:

(х³
+ у²
– 5х)’ = 0;

3х²
+ 2уу’ = 0;

Решим полученное
равенство относительно у’:

1. ху²
   + sin y – 2x = 3.

Решение.
Продифференцируем равенство по х,
считая у функцией по х:

(ху²)’
+ (sin y)’
– 2(x)’
= (3)’;

(х)’
у²
+ х
(у²)’
+ cos
у 
y’
– 2 = 0;

у²
+ х

2у

у‘
+ cos
y

y’
= 2;

Решим уравнение
относительно у’:

2х

у

у‘
+ cos
y

y’
= 2 – у²
;

у‘(2х

у
+ cos
y)
= 2 – у²;

Пользуясь формулами
и правилами дифференцирования, найдем
производные следующих функций.

Пример 1. Найти
производные следующих функций

Решение. Имеем:

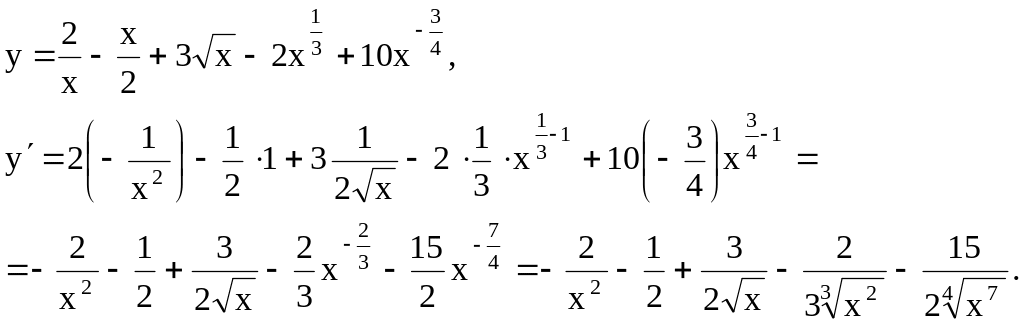
Пример 2. у
= х² (cos
x
– 4 sin
x).

Решение. Воспользуемся
формулой 9 и таблицей производных.

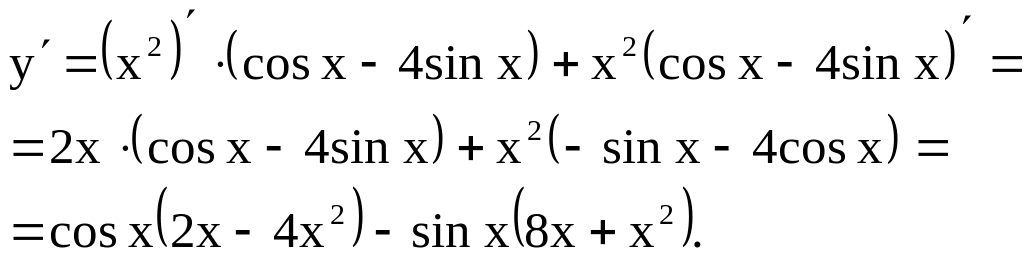
Пример 3. у
= (3х²
+ 5х
– 1)³.

Решение. Имеем
сложную функцию, последнее действие
производится над выражением u
= 3х²
+ 5х
– 1.

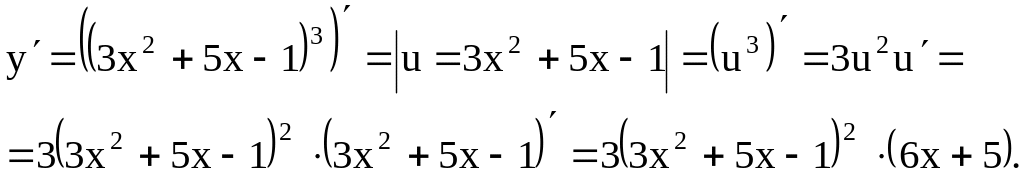
Пример 4. y
= arctg⁸
x

Решение. Имеем
сложную функцию, последнее действие –
возведение в 8ую степень производится
над u
= arctg
x.

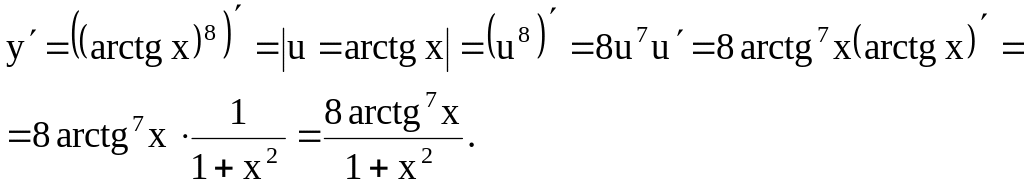
Пример 5. у =

Решение. Имеем
дважды сложную функцию

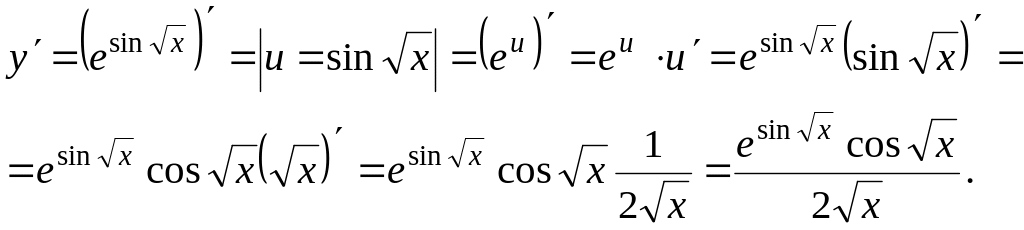
Пример 6.

Решение. Воспользуемся
формулой 11

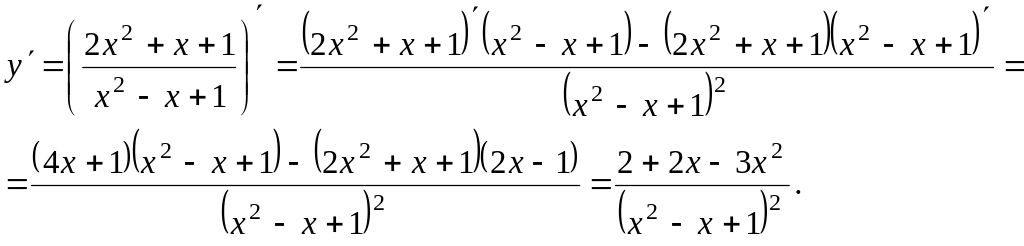
Пример
7. y
= arctg (ln x) + ln (arctg x).

Решение. Имеем
сумму двух сложных функций, воспользуемся
правилами дифференцирования суммы
функций, при вычислении значения функции
в первом слагаемом последнее действие
– (вычисление арктангенса) производится
над логарифмом, значит, промежуточный
аргумент – ln
x,
а во втором слагаемом (вычисление
логарифма) – над arctg
x,
значит промежуточный аргумент – arctg
x.

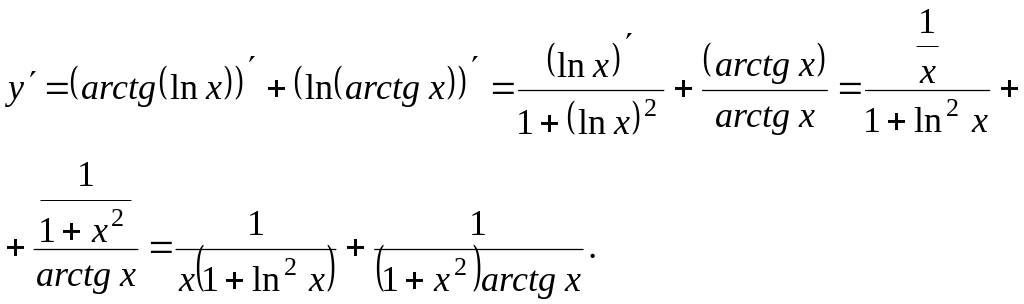
Пример 8.

Решение.
Имеем функцию у
= у(х), заданную
неявно. Продифференцируем это равенство,
считая, что sin
y,
e
^{– y}
– сложные функции:

В
левой части группируем слагаемые с у’,
в правую часть переносим слагаемые, не
содержащие у’.

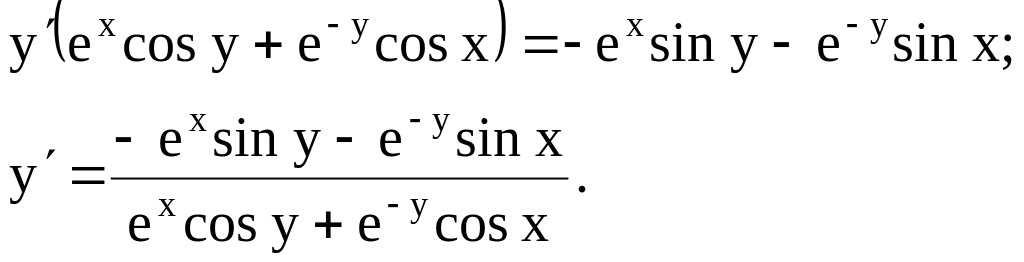
Пример 9.

.

Решение. Имеем
показательно-степенную функцию

.

Прологарифмируем
данное равенство:

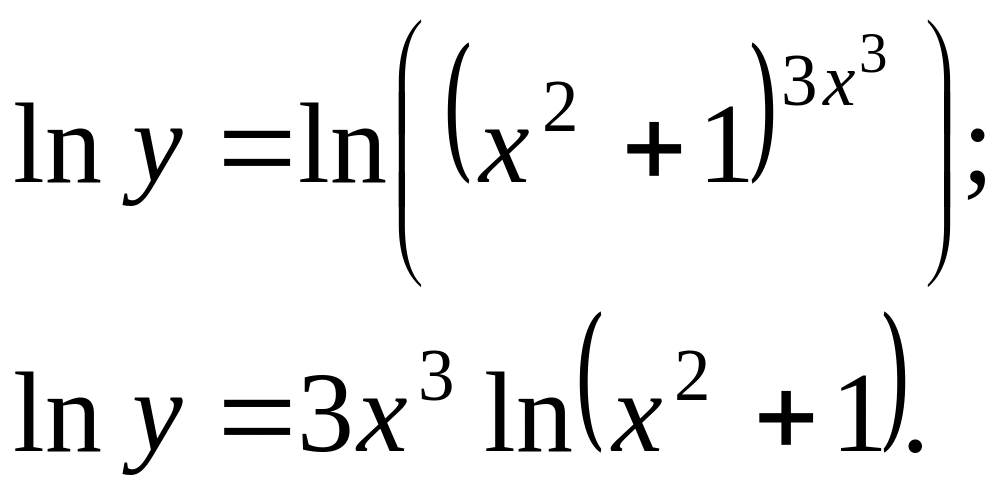
Продифференцируем
данное равенство:

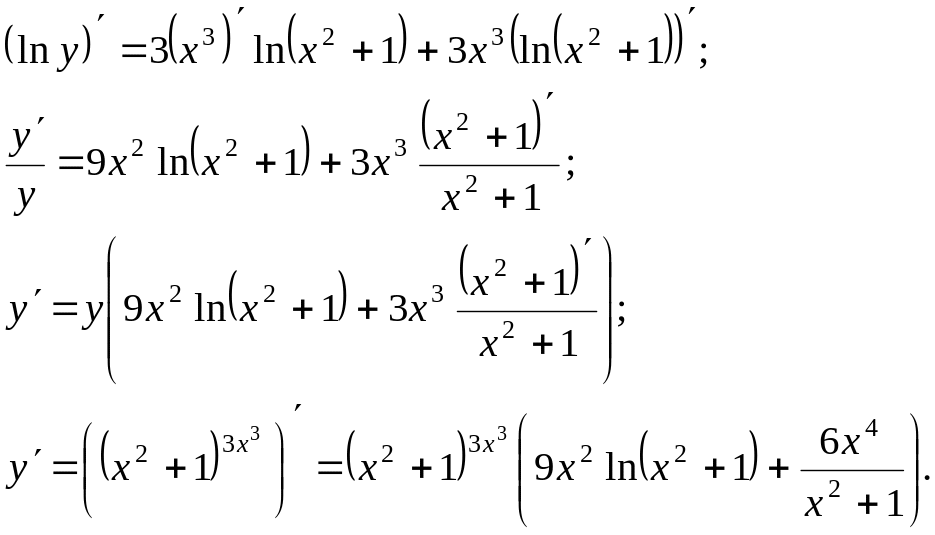
Дифференциал функции и его приложение

Пусть функция y
= f(x)
дифференцируема в точке х,
тогда f
’(x)
=

,
а по теореме о связи функции, имеющей
предел и бесконечно-малой

,
т.е. приращение функции можно представить
в виде двух слагаемых, одно зависит от
х
линейно, а второе содержит степени х
не ниже второй.

Опр. 1. Дифференциалом
функции называется главная часть ее
приращения, линейная относительно
приращения аргумента.

Обозначается:

(34)

Для f
(x)
= x;
dx
= х,
тогда dy
= f
’(x)dx

Поэтому производную
функции y
= f(x)
можно обозначить:

(35.)

Из определения
(4.29) следует, что свойства дифференциалов
аналогичны свойствам производной:

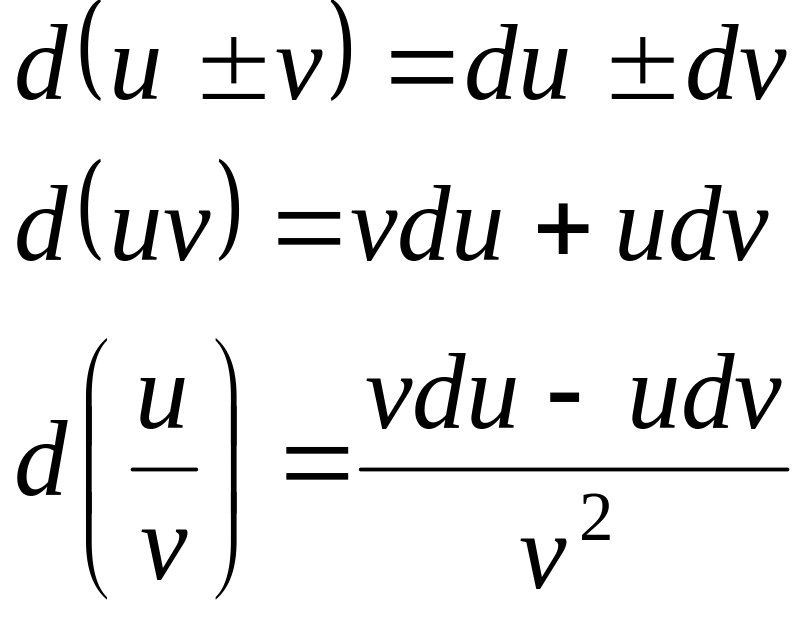
Приложения
дифференциала основываются на приближенной
формуле:

(36)

1. Приближенные
   вычисления.

Пусть известно
значение функции y
= f
(x)
в точке х₀,
т.е. f
(х₀).
Тогда

.
Обозначим х
= х₀
+ х,
получим

(37)

Пример. Вычислить
приближенно значение

1)

.

Решение. Имеем

х
= 4,01; х
= х – х₀=0,01.

Поэтому

1. 

Имеем
f
(x)
= sin
x;
x=33⁰=
,
берем

sin
33⁰
= sin

1. Оценка погрешности.

Пусть имеем
зависимость y
= f
(x),
а х
измеряется с ошибкой х,
тогда у
получит ошибку у:

.

Например, найдем
ошибку при вычислении ln
2,1. Т.к. х
= 2,1, то ошибка х
= 0,05, f
(x)
= ln
x;

поэтому

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Явные и неявные

В этой статье мы познакомимся с неявными функциями и техникой их дифференцирования. Вспомним для начала, как выглядят функции, заданные явно. Это “обычные” функции вида y=f(x)y=f(x), с которыми вы уже имели дело и умеете вычислять их производные. Запись y=f(x)y=f(x) обозначает, что мы функцию yy смогли выразить (явно представить) через её аргумент xx. З неявными функциями дело обстоит иначе. Здесь мы не можем “перетащить” yy в левую сторону выражения, а все что содержит xx — в правую. Такие функциональные зависимости в общем виде можно записать так:

F(x,y)=0F(x, y)=0

Эта запись означает, что величины xx и yy как-то связанны между собой, но ничего не говорится о том, как yy выражается через xx (и можно ли это вообще сделать). Одну и ту же функцию (но не каждую) можно записать как в явном так и в неявном виде. Например, неявно заданную функцию F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x} можно записать явно: y(x)=−53x2y(x)=-frac{5}{3x^2}. В этом случае нам удалось выразить yy через xx. Или, если:

F(x,y)=x2+y2−1=0F(x, y)=x^2+y^2-1=0

то

y=±1−x2y=pm sqrt{1-x^2}

Здесь функция получилась многозадачной (именно двузначной, отвечающей двум знакам), но это не страшно. Мы все-равно представили yy как выражение зависящее от xx. В правой стороне у нас присутствует только xx.
Но существуют случаи, когда этого сделать нельзя. Можно навести множество примеров таких функций. Например:

F(x,y)=yln⁡x+eyy2F(x, y)=yln x+e^yy^2

Ну попробуйте выразить отсюда yy через xx. То есть запишите эту функцию в виде y=f(x)y=f(x). Вот вам и пример неявной заданной функции. Ещё пример:

F(x,y)=xsin⁡x+ysin⁡y−12F(x, y)=xsin x+ysin y-12

Здесь, мы хотя и не можем выразить yy через xx, но мы все-равно можем считать yy функцией от аргумента xx. Так как каждому значению xx будут соответствовать какие-то значения yy.
Естественно, возникает вопрос о дифференцировании подобных функций. Вы уже понимаете, что эта операция очень важна, и было бы тяжело поверить, что математики ничего не придумали на этот счет.

Дифференцирование неявно заданных функций

Оказывается, что для того чтобы посчитать производную от yy по xx нам не обязательно решать уравнение:

F(x,y)=0F(x, y)=0

Теоретически можно доказать (пользуюсь определением производной, производя предельный переход и т. д.), что:

Формула дифференцирования неявной функции

dydx=−∂F(x,y)∂x∂F(x,y)∂yfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}

Обозначение ∂partial обозначает частную производную. Мы здесь имеем дело с двумя переменными xx и yy и берем производные от функции F(x,y)F(x, y) по этим величинам. Так, выражение:

∂F(x,y)∂xfrac{partial F(x, y)}{partial x}

говорит, что берется производная от F(x,y)F(x, y) по xx, при этом величина yy считается постоянной. Следует обратить внимание на знак “минус” перед дробью, а также на то, что мы не можем сократить числитель и знаменатель на ∂F(x,y)partial F(x, y), так как производные берутся по разным величинам. Вооружившись этой главной формулой вычисления производных от неявных функций, перейдем к разбору нескольких примеров.

Примеры

Пример 1

F(x,y)=x2+y2−1F(x, y)=x^2+y^2-1

∂F(x,y)∂x=2x,     ∂F(x,y)∂y=2yfrac{partial F(x, y)}{partial x}=2x, frac{partial F(x, y)}{partial y}=2y

dydx=−∂F(x,y)∂x∂F(x,y)∂y=−2x2y=−xyfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{2x}{2y}=-frac{x}{y}

Пример 2

F(x,y)=xsin⁡x+ysin⁡y−12F(x, y)=xsin x+ysin y-12

∂F(x,y)∂x=sin⁡x+xcos⁡x,     ∂F(x,y)∂y=sin⁡y+ycos⁡yfrac{partial F(x, y)}{partial x}=sin x+x cos x, frac{partial F(x, y)}{partial y}=sin y+y cos y

dydx=−∂F(x,y)∂x∂F(x,y)∂y=−sin⁡x+xcos⁡xsin⁡y+ycos⁡yfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{sin x+xcos x}{sin y+ycos y}

Пример 3

1. F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x}

∂F(x,y)∂x=3y−5×2,     ∂F(x,y)∂y=3xfrac{partial F(x, y)}{partial x}=3y-frac{5}{x^2}, frac{partial F(x, y)}{partial y}=3x

dydx=−∂F(x,y)∂x∂F(x,y)∂y=−3y−5x23x=−3yx2−53x3frac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{3y-frac{5}{x^2}}{3x}=-frac{3yx^2-5}{3x^3}

Но здесь мы можем выразить yy через xx явно:

y=−53x2y=-frac{5}{3x^2}

Подставим это выражение в формулу для производной выше:

dydx=103x3frac{dy}{dx}=frac{10}{3x^3}

А теперь поступим так, как будто нам с самого начала была известна явная зависимость y=f(x)y=f(x). То есть продифференцируем функцию y(x)=−53x2y(x)=-frac{5}{3x^2} по xx:

dydx=ddx(−53×2)=−53(−2)1×3=103x3frac{dy}{dx}=frac{d}{dx}Big(-frac{5}{3x^2}Big)=-frac{5}{3}(-2)frac{1}{x^3}=frac{10}{3x^3}

Получили то же самое. Значит мы все сделали правильно.

Производные различных порядков от неявных функций

Щебетун Виктор

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Как найти первую и вторую производные параметрической функции

Параметрическое представление функциональной зависимости y от x для функции y = f(x) имеет вид:

Пусть функции x = x(t) и y = y(t) определены и непрерывны на интервале изменения параметра t. Продифференцируем данные функции.

Для нахождения первой производной необходимо разделить второе уравнение на первое:

Для нахождения второй производной:

Пример 1

Найти вторую производную параметрической функции

[left{begin{array}{l} {x=ln t} \ {y=3t^{2} } end{array}right. ]

Решение.

1. Найдем первую производную по формуле:

[y’_{x} =frac{y’_{t} }{x’_{t} } ]

[y’_{t} =left(t^{3} right)^{{‘} } =6t x’_{t} =left(ln tright)^{{‘} } =frac{1}{t} ]

[y’_{x} =frac{6t}{frac{1}{t} } =6t^{2} ]

2. Найдем вторую производную

[y”_{xx} =left(6t^{2} right)^{{‘} } =12t]

Что такое неявно заданная функция, и как ее найти

Определение

Если функция вида y=y(x) задана уравнением F(x;y(x)) = 0, то функция является неявно заданной.

Для нахождения дифференциала неявной функции необходимо выполнить следующие действия:

1. Продифференцировать обе части уравнения по х.
2. Поскольку у — дифференцируемая функция, для ее нахождения используется правило вычисления производной сложной функции.
3. В правой части уравнения должно получится значение 0.

Примечание

Это значит перенести все слева направо и привести к уравнению вида F(x;y(x)) = 0

1. Решить полученное уравнение относительно y`(x)

Пусть неявная функция у от x определяется равенством:

[frac{x^{2} }{a^{2} } +frac{y^{2} }{b^{2} } -1=0]

Дифференцируем по x все члены этого равенства:

[frac{2x}{a^{2} } +frac{2ydy}{b^{2} dx} =0]

[frac{dy}{dx} =-frac{b^{2} x}{a^{2} y} ]

Последнее равенство снова дифференцируем по х:

[frac{d^{2} y}{dx^{2} } =-frac{b^{2} (y-x)frac{dy}{dx} }{a^{2} y} ]

Заменим производную dy/dx ее выражением:

[frac{d^{2} y}{dx^{2} } =-frac{b^{2} (y+x)frac{b^{2} }{a^{2} } frac{x}{y} }{a^{2} y} ]

[frac{d^{2} y}{dx^{2} } =-frac{b^{2} left(a^{2} y^{2} +b^{2} x^{2} right)}{a^{4} y^{3} } ]

Поскольку $a^2y^2 + b^2x^2 = a^2b^2$, вторую производную можно представить в виде

[frac{d^{2} y}{dx^{2} } =frac{b^{4} }{a^{2} y^{3} } ]

Дифференцируя по х последнее равенство, найдем $frac{d^{3} y}{dx^{3} } $ и т. д.

«Производные различных порядков от неявных функций» 👇

Пример 2

Найти вторую производную неявно заданной функции

[2x^{3} -xy^{2} =4]

Решение.

1. Перенесем все части выражения в левую часть, приравняем к нулю и продифференцируем:

[left(2x^{3} -xy^{2} -4right)^{{‘} } =0]

[left(2x^{3} right)^{{‘} } -left(xy^{2} right)^{{‘} } -left(4right)^{{‘} } =0]

[6x^{2} -left(x’y^{2} +xleft(y^{2} right)^{{‘} } right)=0]

[6x^{2} -y^{2} -2xyy’=0]

2. Выразим y`

[y’=frac{6x^{2} -y^{2} }{2xy} ]

3. Повторно дифференцируем равенство

[left(6x^{2} -y^{2} -2xyy’right)^{{‘} } =12x-2y-2left(xyright)^{{‘} } y’-2xyy’]

[12x-2y-2left(xyright)^{{‘} } y-2xyy’=12x-2y-2x’y’-2xy’-2xyy”]

[12x-2y-2x’y’-2xy’-2xyy”=12x-2y-2y’-2xy’-2xyy”]

4. Выполним замену y`

[12x-2y-2frac{6x^{2} -y^{2} }{2xy} -2xfrac{6x^{2} -y^{2} }{2xy} -2xyy”=0]

5. Упростим

[frac{12x^{2} y-2xy^{2} }{xy} -frac{6x^{2} -y^{2} }{xy} -frac{6x^{3} -y^{2} }{xy} -2xyy”=0]

[frac{12x^{2} y-2xy^{2} -6x^{2} +2y^{2} -6x^{3} }{xy} -2xyy”=0]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 15.12.2022

Дифференцирование функции, заданной неявно

Пусть дано уравнение F(x,y)=0, не разрешенное относительно y. Если существует y=f(x) такая, что F[x,f(x)]=0, то говорят, что уравнение F(x,y)=0 задает y как функцию от x неявно. Обычное задание функции y=f(x) называют явным.

При таком способе задания функции производную находим, дифференцируя уравнение F(x,y)=0, считая y функцией от x (по правилу дифференцирования сложной функции).

• Решение онлайн
• Видеоинструкция

Правила ввода функции, заданной в неявном виде

Примеры

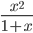≡ x^2/(1+y)

cos2(2x+y) ≡ (cos(2*x+y))^2

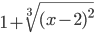≡ 1+(x-y)^(2/3)

см. также Производная от параметрической функции

Пример 1. Найти производную y’, не решая уравнения: x³ – x²y – x²y⁴ + 5 = 0 относительно y.

Решение. Так как в правой части уравнения стоит нуль, а производная постоянной равна нулю, то .

Применяя почленное дифференцирование, найдем 3x² – 2xy – x²y’ – 2xy⁴ – 4x²y³y’ = 0, откуда .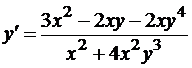

Пример 2. Найти y’ функции, заданной неявно уравнением y*lnx – x2ey + 1 = 0 (x>0).

Решение. 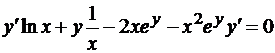(производную от e^y берем как производную сложной функции). Разрешая уравнение относительно y’ (что не всегда возможно), найдем .

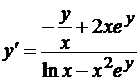Пример 3. Найти производную y’_x функции y(x), заданной неявно: x⁴ + x²y + y³ + 5 = 0.

Решение.

Продифференцируем уравнение по х, рассматривая у как функцию от х, и решим полученное уравнение относительно y’_x.

.

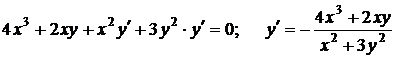Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).