Как найти производную дробного числа

Как найти производную дробного числа

Формула производной от дроби, примеры

Автор статьи

Александр Мельник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Формула производной от дроби

Раздел о производных является отдельным самостоятельным разделом в математическом анализе. Условимся, что читателю известно понятия предела, производной, дифференциала, а также ряд свойств производной.

В данной статье рассмотрим одно из свойств производной, а именно формулу производной от дроби. Приведём эту формулу. Пусть функция $v(x)$ имеет производную в точке $x$ и $v(x)neq0$, тогда:

$(frac{u}{v})’=frac{u’v-uv’}{v^2}.$

Напомним формулы производных элементарных функций:

Формулы производных элементарных функций. Автор24 — интернет-биржа студенческих работ

Рисунок 1. Формулы производных элементарных функций. Автор24 — интернет-биржа студенческих работ

Примеры

Решим примеры. Преобразования, позволяющие применить другие свойства производной, мы применять не будем. В решениях будем использовать только формулу производной от дроби.

По условию даются функции. Нужно найти производные.

Пример 1

Пример. Автор24 — интернет-биржа студенческих работ

Рисунок 2. Пример. Автор24 — интернет-биржа студенческих работ

Пример. Автор24 — интернет-биржа студенческих работ

Рисунок 3. Пример. Автор24 — интернет-биржа студенческих работ

Пример. Автор24 — интернет-биржа студенческих работ

Рисунок 4. Пример. Автор24 — интернет-биржа студенческих работ

Пример 2

Пример. Автор24 — интернет-биржа студенческих работ

Рисунок 5. Пример. Автор24 — интернет-биржа студенческих работ

Пример. Автор24 — интернет-биржа студенческих работ

Рисунок 6. Пример. Автор24 — интернет-биржа студенческих работ

Пример 3

Пример. Автор24 — интернет-биржа студенческих работ

Рисунок 7. Пример. Автор24 — интернет-биржа студенческих работ

Пример. Автор24 — интернет-биржа студенческих работ

Рисунок 8. Пример. Автор24 — интернет-биржа студенческих работ

Пример 4

Пример. Автор24 — интернет-биржа студенческих работ

Рисунок 9. Пример. Автор24 — интернет-биржа студенческих работ

Пример. Автор24 — интернет-биржа студенческих работ

Рисунок 10. Пример. Автор24 — интернет-биржа студенческих работ

Пример 5

Рисунок 11.

Пример. Автор24 — интернет-биржа студенческих работ

Рисунок 12. Пример. Автор24 — интернет-биржа студенческих работ

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 15.05.2023

Источник

Производная дроби

Производная дроби равна произведению производной числителя на знаменатель минус произведение числителя на производную знаменателя и всё делить на квадрат знаменателя:

$$ bigg (frac{u}{v} bigg )’ = frac{u’v-uv’}{v^2} $$

Следует понимать, что производная дроби НЕ РАВНА отношению производных числителя и знаменателя!

Примеры с решением

Пример 1
Найти производную дроби $ y = frac{x}{ln x} $
Решение

Из формулы следует, что числитель $$ u = x $$ а знаменатель $$ v = ln x $$ Находим их производные: $$ u’ = (x)’ = 1 $$ $$ v’ = (ln x)’ = frac{1}{x} $$

Подставляем найденные $ u’ $ и $ v’ $ в формулу производной дроби:

$$ y’=bigg (frac{x}{ln x} bigg )’ = frac{(x)’ln x – x(ln x)’}{(ln x)^2} = $$

$$ = frac{ln x – x frac{1}{x}}{ln^2 x} = frac{ln x – 1}{ln^2 x} $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$ y’ = frac{ln x – 1}{ln^2 x} $$
Пример 2
Найти производную от дроби $ y = frac{cos x}{x} $
Решение

По формуле производной частного:

$$ y’=bigg (frac{cos x}{x} bigg ) = frac{(cos x)’x-cos x (x)’}{(x)^2} = $$

Производная косинуса равна отрицательному синусу: $$ (cos x)’ = -sin x $$

Тогда:

$$ y’ = frac{-xsin x – cos x}{x^2} = -frac{xsin x + cos x}{x^2} $$
Ответ
$$ y’ = -frac{xsin x + cos x}{x^2} $$
Источник

Производная дроби – что это такое

Определение

Производная дроби – это значение, которое получается, если производную числителя умножить на знаменатель и прибавить числитель, умноженный на производную знаменателя, а затем все это разделить на квадрат знаменателя.

Формула производной от дроби

Формула ПД имеет следующий вид:

(left(fracupsilonnuright)’=frac{upsilon’nu-upsilonnu’}{v^2})

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

При этом важно отметить, что нахождение ПД нельзя осуществлять с помощью деления производной числителя на производную знаменателя. Два эти действия будут иметь разные значения после подсчетов.

Приведем доказательство данной формулы. Рассмотрим выражение y=fracupsilonnu. Все представленные переменные – это функции от х. Умножим их на (nu). Получим (ytimesnu=upsilon).

Дифференцируем по х, применяя формулу производной произведения двух функций, то есть:

(left(upsilontimesnuright)’=upsilon’timesnu+upsilontimesnu’)

Тогда выводим:

(y’timesnu+ytimesnu’=upsilon’)

Из этого вычисляем нужную нам производную:

(y’timesnu=upsilon’-ytimesnu’=upsilon’-fracupsilonnutimesnu’=frac{upsilon’v-upsilonnu’}nu;;y’=frac{upsilon’v-upsilonnu’}{nu^2})

Что и требовалось доказать.

Следует также привести таблицу с производными часто встречающихся функций:

Производные

 

Как решать производные функции с дробями, примеры

Чтобы понять, как решать ПФ с дробями, приведем несколько примеров.

Пример 1

Найти производную дроби (y=frac x{In;x}.)

Решение

Из формулы следует, что числитель (upsilon=х), а знаменатель (nu=In;х). Найдем их производные:

(upsilon’=left(хright)’=1,;nu’=left(In;xright)’=frac1x)

Подставляем решенные (upsilon’;и;nu’) в формулу и получаем:

( y’=left(frac x{In;x}right)’=frac{left(xright)’In;x-xleft(In;xright)’}{left(In;xright)^2}=frac{In;x;-x{displaystylefrac1x}}{In^2x}=frac{In;x-1}{In^2x})

Ответ: (y’=frac{In;x-1}{In^2x}.)

Пример 2

Найти производную дроби, равную (y=frac{cos;x}x).

Решение

По формуле производной частного:

(y’=left(frac{cos;x}xright)=frac{left(cos;xright)’x-cos;xleft(xright)’}{left(xright)^2})

Производная косинуса дает нам синус с минусом:

(left(cos;xright)’=-sin;x)

В таком случае:

(y’=frac{-x;sin;x-cos;x}{x^2}=-frac{x;sin;x+cos;x}{x^2})

Ответ: (y’=-frac{x;sin;x+cos;x}{x^2}.)

Пример 3

Найти производную дроби (yleft(xright)=frac{e^x-1}{e^x+1}.)

Решение

Из таблицы производных находим:

(left(e^xright)’=e^x)

Применяем правила дифференцирования постоянной и суммы:

(left(e^x-1right)’=left(e^xright)’-left(1right)’=e^x-0=e^x;;left(e^x+1right)’=left(e^xright)’+left(1right)’=e^x-0=e^x)

Используем формулу производной дроби:

(left(fracupsilonnuright)’=frac{upsilon’nu-upsilonnu’}{nu^2};left(frac{e^x-1}{e^x+1}right)’=frac1{left(e^x+1right)^2}timeslbrackleft(e^x-1right)’left(e^x+1right)-left(e^x-1right)left(e^x+1right)’rbrack=frac1{left(e^x+1right)^2}timeslbrack e^xleft(e^x+1right)-left(e^x-1right)e^xrbrack=frac{2e^x}{left(e^x+1right)^2})

Ответ: (y’=frac{2e^x}{left(e^x+1right)^2}.)

Источник

Один из важнейших разделов математики – производные. Для их нахождения существуют специальные формулы производных. Для работы с ними необходимо знать основные формулы элементарных функций.

Таблица формул производных

Ниже приведена таблица формул производных элементарных функций.

[C^{prime}=0] [(ln ln x)^{prime}=frac{1}{x}]
[x^{prime}=1] [(sin sin x)^{prime}=cos cos x]
[left(x^{2}right)^{prime}=2 x] [(cos cos x)^{prime}=-sin sin x]
[left(x^{n}right)^{prime}=n * x^{n-1}] [(operatorname{tg} x)^{prime}=frac{1}{cos ^{2}(x)}]
[left(a^{x}right)^{prime}=a^{x} * ln (a)] [(operatorname{ctg} x)^{prime}=-frac{1}{sin ^{2}(x)}]
[left(e^{x}right)^{prime}=e^{x}] [(arcsin arcsin x)^{prime}=frac{1}{sqrt{1-x^{2}}}]
[(x)^{prime}=frac{1}{x * ln (a)}] [begin{aligned}
(arccos &arccos x)^{prime}
&=-frac{1}{sqrt{1-x^{2}}}
end{aligned}]
[(operatorname{arctg} x)^{prime}=frac{1}{1+x^{2}}] [(operatorname{arcctg} x)^{prime}=-frac{1}{1+x^{2}}]
Таблица 1 – Производные элементарных функций

Смысл производной

В математике производная имеет геометрический и физический смыслы.

Допустим, что некоторая функция f(x) задана в интервале (a, b). При этом есть две точки x и x0, которые находятся в указанном интервале. Если значение x будет изменяться, то и f(x) тоже изменится. Изменение аргумента находится из выражения (x – x0). Эта разность обозначается как Δx – приращение аргумента. В таком случае приращением функции будет являться разность между ее значениями в двух точках. Исходя из этого, можно дать определение производной. Ей называется предел отношения приращения функции к приращению аргумента в указанной точке. При этом сам аргумент стремится к нулю.

В математике формулы производных функций записываются так:

[begin{gathered} f^{prime}left(x_{0}right)=left(frac{fleft(x_{0}+Delta xright)-fleft(x_{0}right)}{Delta x}right). \ y^{prime}left(x_{0}right)=lim _{Delta x rightarrow 0}left(frac{Delta y}{Delta x}right) . end{gathered}]

Смысл этих формул, а точнее нахождения их значений, может быть описан с точки зрения геометрии и физики.

Геометрический смысл состоит в том, что производная функции в конкретной точке равняется тангенсу угла, который образован осью абсцисс и касательной линией к графику. Пример показан на рисунке ниже.

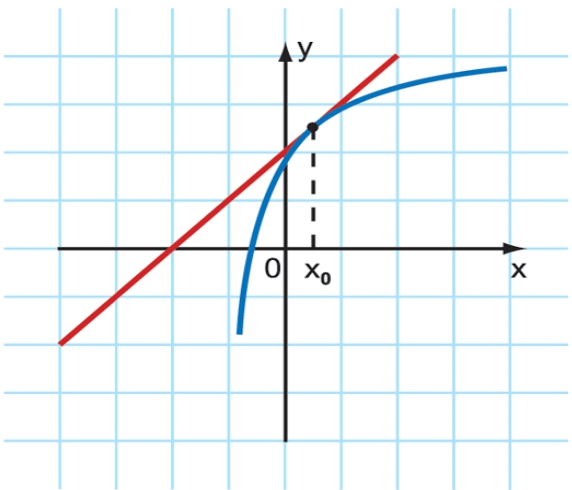
Геометрический смысл производной
Рисунок 1 – Геометрический смысл производной

В физике смысл состоит в том, что производная от пройденного расстояния по времени есть скорость движения точки.

Нет времени решать самому?

Наши эксперты помогут!

Формула вычисления производной дроби

Рассмотрим формулу вычисления производной дроби. Функция v(x) имеет производную в определенной точке x. При этом v(x) не равна нулю (v(x) ≠ 0). В таком случае справедлива следующая формула:

[left(frac{u}{v}right)^{prime}=frac{u^{prime} v-u v^{prime}}{v^{2}}]

Рассмотрим примеры использования формулы производной дроби при решении задач.

Примеры 1 — 2

Первый пример с выражениями из тригонометрии: [y=frac{cos cos x}{x^{2}}]

Пользуясь таблицей 1 найдем:

[begin{gathered}
y^{prime}=frac{left.(cos cos x)^{prime} * (x^{2}-xright) *left(x^{2}right)^{prime}}{left(x^{2}right)^{2}} =\
frac{(-sin sin x) * x^{2}-(cos cos x) * 2 x}{x^{4}} .
end{gathered}]

Вынесем x за скобки и преобразуем полученное выражение: [y^{prime}=frac{(-sin sin x) * x-2 cos cos x}{x^{3}}]

Другой пример:

[begin{gathered}
y=frac{x^{3}}{x^{3}+2} \
y^{prime}=frac{left(x^{3}right)^{prime} *left(x^{3}+2right)-x^{3} *left(x^{3}+2right)^{prime}}{left(x^{3}+2right)^{2}} \
y^{prime}=frac{3 x^{2} *left(x^{3}+2right)-x^{3} * 3 x^{2}}{left(x^{3}+2right)^{2}} \
y^{prime}=frac{3 x^{5}+6 x^{2}-3 x^{5}}{left(x^{3}+2right)^{2}}=frac{6 x^{2}}{left(x^{3}+2right)^{2}}
end{gathered}]

Решение примеров на нахождение производных в математике называется дифференцированием. Они бывают двух типов:

  • частными;
  • полными.

Между этими типами есть одно основное отличие. При нахождении частной производной функция аппроксимируется только по одному аргументу. Так во всех предыдущих примерах аппроксимация производилась только по x.

Источник

Дробная производная (или производная дробного порядка) является обобщением математического понятия производной. Существует несколько разных способов обобщить это понятие, но все они совпадают с понятием обычной производной в случае натурального порядка. Когда рассматриваются не только дробные, но и отрицательные порядки производной, к такой производной обычно применяется термин дифферинтеграл.

Дробные производные на отрезке вещественной оси[править | править код]

Для функции f(x), заданной на отрезке {displaystyle [a,,b]}, каждое из выражений

{displaystyle D_{a+}^{alpha },f(x)={frac {1}{Gamma (1-alpha )}}{frac {d}{dx}}int limits _{a}^{x}{frac {f(t),dt}{(x-t)^{alpha }}},quad ,D_{b-}^{alpha },f(x)=-{frac {1}{Gamma (1-alpha )}}{frac {d}{dx}}int limits _{x}^{b}{frac {f(t),dt}{(t-x)^{alpha }}},}

где Gamma — гамма-функция, называется дробной производной порядка alpha , 0 < alpha < 1, соответственно левосторонней и правосторонней. Дробные производные в приведенном виде называют обычно производными Римана — Лиувилля.

Определение через интеграл Коши[править | править код]

Дробная производная порядка p (p — вещественное положительное число) определяется через интеграл Коши: {displaystyle D_{C}^{p}f(t)={frac {1}{Gamma (p)}}!int limits _{C}{frac {f(u)}{(t-u)^{p+1}}},du}, где интегрирование ведется по выбранному заранее контуру C на комплексной плоскости. Непосредственное применение этой формулы затруднено из-за ветвления функции при дробном показателе степени в знаменателе.

Определение через преобразование Фурье[править | править код]

Основано на следующем свойстве интегрального преобразования Фурье

{displaystyle F[D^{k}psi (x)](omega )=(-iomega )^{k}(Fpsi )(omega )quad (kin mathbb {N} ).}[1]

Определение через общую формулу n-й производной[править | править код]

В случае, если есть общее аналитическое выражение для производной n-го порядка, понятие дробной производной может быть введено естественным образом путём обобщения данного выражения (когда это возможно) на случай произвольного числа n.

Пример 1: дифференцирование многочленов[править | править код]

Пусть f(x) есть моном вида

{displaystyle f(x)=x^{k},.}

Первая производная, как и обычно

{displaystyle f'(x)={d over dx}f(x)=kx^{k-1},.}

Повторение данной процедуры даёт более общий результат

{displaystyle {d^{n} over dx^{n}}x^{k}={k! over (k-n)!}x^{k-n},,}

который после замены факториалов гамма-функциями приводит к

{displaystyle {d^{n} over dx^{n}}x^{k}={Gamma (k+1) over Gamma (k-n+1)}x^{k-n},.}

Поэтому, например, половинная производная функции x есть

{displaystyle {d^{1 over 2} over dx^{1 over 2}}x={Gamma (1+1) over Gamma (1-{1 over 2}+1)}x^{1-{1 over 2}}={Gamma (2) over Gamma ({3 over 2})}x^{1 over 2}={2pi ^{-{1 over 2}}}x^{1 over 2};={frac {2,x^{1 over 2}}{sqrt {pi }}},.}

Повторяя процедуру, будем иметь

{displaystyle {d^{1 over 2} over dx^{1 over 2}}{2pi ^{-{1 over 2}}}x^{1 over 2}={2pi ^{-{1 over 2}}}{Gamma (1+{1 over 2}) over Gamma ({1 over 2}-{1 over 2}+1)}x^{{1 over 2}-{1 over 2}}={2pi ^{-{1 over 2}}}{Gamma ({3 over 2}) over Gamma (1)}x^{0}={1 over Gamma (1)}=1,,}

что представляет собой ожидаемый результат

{displaystyle left({frac {d^{1/2}}{dx^{1/2}}}{frac {d^{1/2}}{dx^{1/2}}}right)x={d over dx}x=1,.}

Таким образом можно ввести дробные производные произвольного положительного порядка от многочлена. Определение также естественно обобщается на аналитические функции. Рассматривая Gamma как мероморфную функцию комплексного переменного, можно обобщить определение на случай произвольного порядка дифференцирования. При этом

{displaystyle {left({d over dx}right)}^{a}{left({d over dx}right)}^{b}={left({d over dx}right)}^{a+b}}

на всех x^{k}, таких что {displaystyle k-a}, {displaystyle k-b} и {displaystyle k-a-b} не являются целыми отрицательными числами.

Следует заметить, что производная в рассмотренном смысле имеет место при целых отрицательных n, однако такая производная отличается от понятия первообразной n-го порядка, поскольку первообразная определена неоднозначно, в то время как производная совпадает лишь с одной из первообразных. В этом случае можно говорить о главном значении первообразной.

Пример 2: дифференцирование тригонометрических функций[править | править код]

Пусть

{displaystyle f(x)=sin(ax+b),.}

Поскольку для любых a и b

{displaystyle {d^{n} over dx^{n}}sin(ax+b)=a^{n}sin left(ax+b+{pi n over 2}right),,}

то, полагая {displaystyle n=1/2},

{displaystyle {{d^{1/2}} over {dx^{1/2}}}sin(ax+b)={sqrt {a}},sin left(ax+b+{pi over 4}right),.}

Действительно,

{displaystyle {{d^{1/2}} over {dx^{1/2}}}left({{d^{1/2}} over {dx^{1/2}}}sin(ax+b)right)={sqrt {a}};{sqrt {a}},sin left(ax+b+{pi over 4}+{pi over 4}right)=a,cos(ax+b)=f'(x),.}

В рассмотренном примере понятие производной обобщается на случай любого действительного и даже комплексного порядка. Так, при n=-1 формула n-й производной даёт одну из первообразных функции f(x).

Свойства[править | править код]

Основные свойства производной нецелого порядка:

  • Линейность
{displaystyle D_{t}^{q}(f(t)+g(t))=D_{t}^{q}(f(t))+D_{t}^{q}(g(t))}
{displaystyle D^{q}(ax)=aD^{q}(x)}
  • Правило нуля
{displaystyle D^{0}x=x}
  • Дробная производная произведения
{displaystyle D_{t}^{q}(f(t)g(t))=sum _{j=0}^{infty }{q choose j}D_{t}^{j}(f(t))D_{t}^{q-j}(g(t))}
  • Полугрупповое свойство
{displaystyle D^{a}D^{b}f(t)=D^{a+b}f(t)}

в общем случае не выполняется [1].

Примечания[править | править код]

  1. ↑ 1 2 см. Формулу (1.3.11) (стр. 11) в книге A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Applications of Fractional Differential Equations. (Elsevier, 2006)

См. также[править | править код]

  • Дифферинтеграл
  • Дробная динамика
  • Наследственная механика

Литература[править | править код]

  • Риман Б. Опыт обобщения действий интегрирования и дифференцирования. — Москва, Ленинград: ГИТТЛ, 1948. — 544 с.
  • Самко С. Г., Килбас А. А., Маричев О. И. Интегралы и производные дробного порядка и некоторые их приложения. — Минск: Наука и техника, 1987. — 688 с.
  • Псху А. В. Уравнения в частных производных дробного порядка. — Москва: Наука, 2005. — 199 с.
  • Нахушев А. М. Дробное исчисление и его применение. — Москва: ФИЗМАТЛИТ, 2003. — 272 с. — 5−9221−0440−3 экз. Архивная копия от 20 июля 2013 на Wayback Machine
  • Учайкин В. В. Метод дробных производных. — Ульяновск: Артишок, 2008. — 512 с. — 400 экз. — ISBN 978-5-904198-01-5. (недоступная ссылка)
  • Тарасов В. Е. Модели теоретической физики с интегро-дифференцированием дробного порядка. — Москва, Ижевск: РХД, 2010. — 568 с.
  • В. В. Васильев, Л. А. Симак. Дробное исчисление и аппроксимационные методы в моделировании динамических систем. — Киев: НАН Украины, 2008. — P. 256. — ISBN 978-966-02-4384-2.
  • F. Mainardi,. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models. — Imperial College Press, 2010. — 368 с. Архивная копия от 19 мая 2012 на Wayback Machine
  • V. E. Tarasov. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Mediaю. — 2010. — 450 с.
  • V. V. Uchaikin. Fractional Derivatives for Physicists and Engineers. — Higher Education Press, 2012. — 385 с.
  • R. Herrmann. Fractional Calculus. An Introduction for Physicists. — Singapore: World Scientific, 2014. — ISBN 978-981-4551-09-0.
  • A.A. Kilbas, H.M. Srivastava, J.J. Trujillo. Theory and Applications of Fractional Differential Equations. — Elsevier. — Амстердам, 2006.
  • S. G. Samko, A. A. Kilbas, O.I. Marichev. Fractional Integrals and Derivatives Theory and Аpplications. — Нью-Йорк: Gordon and Breach, 1993.
  • K. Miller, B. Ross. An Introduction to the Fractional Calculus and Fractional Differential Equations. — Нью-Йорк: Wiley, 1993.
  • I. Podlubny. Fractional Differential Equations. — Сан Диего: Academic Press, 1999.
  • B. Ross. A brief history and exposition of the fundamental theory of fractional calculus. — Notes Math, 1975.

Ссылки[править | править код]

  • журнал: «Fractional Calculus & Applied Analysis», (с 1998 по 2014) и Fractional Calculus and Applied Analysis (с 2015)
  • журнал: Fractional Differential Equations (FDE)
  • журнал Journal of Fractional Calculus and Applications (JFCA)
  • журнал: Progress in Fractional Differentiation and Applications
  • журнал: Communications in Fractional Calculus (ISSN 2218-3892)
  • Applications of Fractional Calculus (англ.)
  • Fractional Calculus, the Riemann-Liouville definition of the fractional integral, a definition of fractional derivatives, and a list of applications of the calculus. (англ.)
  • Fractional Calculus (англ.)
  • Fractional Calculus — Contains introductory notes on fractional calculus (англ.)
  • Weisstein, Eric W. Fractional Calculus (англ.) на сайте Wolfram MathWorld..
  • Интегралы и производные дробного порядка и их приложения. С. Г. Самко, А. А. Килбас, О. И. Маричев, Минск, 1987 (недоступная ссылка)
Источник

Добавить комментарий