Производная функции, заданной параметрически
4 января 2022
Сегодня мы научимся считать производную параметрической функции. Для этого разберём основную формулу, несколько примеров, но главное — одну из самых частых и глупых ошибок, которые допускают начинающие студенты.
План такой:
- Параметрическое задание функции — основные понятия
- Производная функции, заданной параметрически
- Типичные ошибки на примере второй производной
- Третья производная — разминка для мозгов
Начнём с ключевых определений и соображений.
1. Функция, заданная параметрически
Считая производные, мы привыкли работать с функциями, заданными аналитически, т.е. формулой $y=fleft( x right)$. Подставляя в эту формулу разные значения $x$, мы легко находим значение $y$.
Несколько примеров таких функций:
- Квадратичная функция: $y={{x}^{2}}$. График — парабола.
- Показательная функция: $y={{text{e}}^{x}}$. Она же «экспонента».
- Тригонометрическая функция: $y=sin x$. График — синусоида.
Но что если величины $y$ и $x$ зависят не друг от друга, а от некой третьей переменной? Скажем, от параметра $t$?
Пример 1. Функция, заданная параметрически:
[left{ begin{align} & x=cos t \ & y=sin t \ end{align} right.]
Перебирая разные $tin mathbb{R}$, мы будем получать точки с координатами $left( x;y right)$, которые в итоге превратятся в график:
Да это же тригонометрическая окружность! Она задаётся уравнением ${{x}^{2}}+{{y}^{2}}=1$.
График такого уравнения не является функцией (если забыли почему, гляньте урок про графики уравнений с двумя переменными). Но его можно «составить» из графиков двух функций:
[begin{align} & {{y}_{1}}=sqrt{1-{{x}^{2}}} \ & {{y}_{2}}=-sqrt{1-{{x}^{2}}} \ end{align}]
А вот это уже привычные нам аналитические функции, и для них можно посчитать производную!
К сожалению, далеко не всегда параметрическое уравнение вида
[left{ begin{align} & x=varphi left( t right) \ & y=psi left( t right) \ end{align} right.]
можно свести к привычными выражениям вида $y=fleft( x right)$. Но это ни в коем случае не означает, что для таких параметрических функций нельзя посчитать производную. Можно и даже нужно. И поможет нам в этом следующая формула.
2. Производная функции, заданной параметрически
Итак, основная теорема.
Теорема 1. Пусть функция $y=fleft( x right)$ задана параметрически:
[left{ begin{align} & x=varphi left( t right) \ & y=psi left( t right) \ end{align} right.]
Тогда производная этой функции считается по формуле
[{{{y}’}_{x}}left( x right)=frac{{{{{y}’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]
Эту теорему очень легко доказать. В самом деле, если функция $x=varphi left( t right)$ рассматривается на интервале $tin left( a;b right)$ таком, что существует обратная функция $t={{varphi }^{-1}}left( x right)$, то можно определить сложную функцию
[yleft( x right)=psi left( {{varphi }^{-1}}left( x right) right)]
По теореме о производной сложной функции:
[{{{y}’}_{x}}left( x right)={{{psi }’}_{x}}left( {{varphi }^{-1}}left( x right) right)={{{psi }’}_{x}}left( t right)={{{psi }’}_{t}}left( t right)cdot {{{t}’}_{x}}left( x right)]
[begin{align} {{{{y}’}}_{x}}left( x right) & ={{{{psi }’}}_{x}}left( {{varphi }^{-1}}left( x right) right)= \ & ={{{{psi }’}}_{x}}left( t right)= \ & ={{{{psi }’}}_{t}}left( t right)cdot {{{{t}’}}_{x}}left( x right) end{align}]
Но по теореме об обратной функции ${{{t}’}_{x}}={1}/{{{{{x}’}}_{t}}};$, поэтому
[{{{y}’}_{x}}left( x right)=frac{{{{{psi }’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]
Что и требовалось доказать.
Замечание. Когда выражение дифференцируется по разным переменным, целесообразно указывать в нижним индексе ту переменную, по которой выполняется дифференцирование: ${{{y}’}_{x}}$, ${{{y}’}_{t}}$, ${{{x}’}_{t}}$ и т.д.
Это поможет избежать недоразумений и глупых вычислительных ошибок. Кроме того, подобные обозначения активно используются в дифференциальном исчислении функций нескольких переменных.
Детальное руководство по работе с нижними индексами и переменными дифференцирования — см. урок «Производная сложной функции». Сейчас просто отметим, что мы привыкли считать производную по переменной $x$. Но с тем же успехом можно считать производную и по $t$, и по какому-нибудь $varphi $, и вообще по любой переменной, которую мы увидим в функции.
2.1. Примеры
Приведённые выше формулы могут показаться сложными и страшными. Но на деле это одна из самых лёгких тем в производных. Взгляните:
Пример 1. Найдите ${{{y}’}_{x}}$, если
[left{ begin{align} & x=2t \ & y=3{{t}^{2}}-5t \ end{align} right.]
Считаем производные ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{left( 2t right)}^{prime }}_{t}=2 \ & {{{{y}’}}_{t}}={{left( 3{{t}^{2}}-5t right)}^{prime }}_{t}=6t-5 end{align}]
Теперь считаем ${{{y}’}_{x}}$ по формуле производной параметрической функции:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{6t-5}{2}]
Вот и всё! Готовое выражение можно разбить на две дроби, а можно оставить и так.
Пример 2. Найдите ${{{y}’}_{x}}$, если
[left{ begin{align} & x={{2}^{-t}} \ & y={{2}^{2t}} \ end{align} right.]
Вместо многочленов видим показательные функции. Это ничего не меняет, снова считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{left( {{2}^{-t}} right)}^{prime }}_{t}={{2}^{-t}}cdot left( -ln 2 right) \ & {{{{y}’}}_{t}}={{left( {{2}^{2t}} right)}^{prime }}_{t}={{2}^{2t}}cdot 2ln 2 end{align}]
Теперь находим ${{{y}’}_{x}}$ по формуле:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{{{2}^{2t}}cdot 2ln 2}{{{2}^{-t}}cdot left( -ln 2 right)}=-{{2}^{3t+1}}]
Для решения этого задания пришлось вспомнить производную показательной функции и некоторые свойства степеней.:)
Пример 3. Найдите ${{{y}’}_{x}}$, если
[left{ begin{align} & x=acos varphi \ & y=bsin varphi \ end{align} right.]
Здесь переменной-параметром является $varphi $, а буквы $a$ и $b$ — просто числа, которые будут частью ответа. Считаем ${{{x}’}_{varphi }}$ и ${{{y}’}_{varphi }}$ — производные тригонометрических функций:
[begin{align} & {{{{x}’}}_{varphi }}={{left( acos varphi right)}^{prime }}_{varphi }=-asin varphi\ & {{{{y}’}}_{varphi }}={{left( bsin varphi right)}^{prime }}_{varphi }=bcos varphiend{align}]
Находим ${{{y}’}_{x}}$:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{varphi }}}{{{{{x}’}}_{varphi }}}=frac{bcos varphi }{-asin varphi }=-frac{b}{a}operatorname{ctg}varphi ]
2.2. Производная в точке
Понятно, что это были совсем простые задачи. Буквально через минуту мы рассмотрим примеры посерьёзнее, но сначала важное дополнение.
Часто нам требуется посчитать не производную функции вообще, а лишь в конкретной точке. Например, чтобы провести касательную или нормаль к кривой, заданной параметрически, в некой точке ${{M}_{0}}left( {{x}_{0}};{{y}_{0}} right)$, лежащей на этой кривой.
В этом случае задача ещё более упрощается.
Пример 4. Найдите ${{{y}’}_{x}}$ при $t={pi }/{4};$, если
[begin{align} & xleft( t right)=tcdot left( tcos t-2sin t right) \ & yleft( t right)=tcdot left( tsin t+2cos t right) \ end{align}]
Задача явно серьёзнее, чем все предыдущие. Считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{left( tcdot left( tcos t-2sin t right) right)}^{prime }}_{t}=-left( {{t}^{2}}+2 right)cdot sin t \ & {{{{y}’}}_{t}}={{left( tcdot left( tsin t+2cos t right) right)}^{prime }}_{t}=left( {{t}^{2}}+2 right)cdot cos t end{align}]
[begin{align} {{{{x}’}}_{t}} & ={{left( tcdot left( tcos t-2sin t right) right)}^{prime }}_{t}= \ & =-left( {{t}^{2}}+2 right)cdot sin t \ {{{{y}’}}_{t}} & ={{left( tcdot left( tsin t+2cos t right) right)}^{prime }}_{t}= \ & =left( {{t}^{2}}+2 right)cdot cos tend{align}]
И сразу подставляем $t={pi }/{4};$:
[begin{align} & {{{{x}’}}_{t}}left( frac{pi }{4} right)=-left( frac{{{pi }^{2}}}{16}+2 right)cdot frac{sqrt{2}}{2} \ & {{{{y}’}}_{t}}left( frac{pi }{4} right)=left( frac{{{pi }^{2}}}{16}+2 right)cdot frac{sqrt{2}}{2} end{align}]
Осталось найти ${{{y}’}_{x}}$:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=-frac{32+{{pi }^{2}}}{32+{{pi }^{2}}}=-1]
Разумеется, можно было сначала найти общую формулу для ${{{y}’}_{x}}$, а уже затем подставить в неё $t={pi }/{4};$ — результат получится точно такой же.
3. Типичные ошибки при вычислении производных
А теперь, пожалуй, ключевой момент, связанный с дифференцированием параметрических функций. Ошибка, которую я сам допустил много лет назад.
Давайте ещё раз взглянем на функцию, заданную параметрически:
[left{ begin{align} & x=varphi left( t right) \ & y=psi left( t right) \ end{align} right.]
И на производную этой функции:
[{{{y}’}_{x}}left( x right)=frac{{{{{y}’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]
А теперь представьте, что надо посчитать вторую производную: ${{{y}”}_{xx}}$. И тут у многих проскакивает мысль: а что если взять формулу для первой производной и просто увеличить в ней количество «штрихов»?
Получится что-то типа вот этого:
[{{{y}”}_{xx}}left( x right)=frac{{{{{y}”}}_{tt}}left( t right)}{{{{{x}”}}_{tt}}left( t right)}]
Так вот: эта формула не верна!
Чтобы правильно найти вторую производную функции, заданной параметрически, достаточно вспомнить, что вторая производная — это просто производная от производной:
[{{{y}”}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}]
Проще говоря, сначала мы находим ${{{y}’}_{x}}$ — это будет какая-то функция от $t$. Затем уже от этой функции вновь считаем производную — всё по той же формуле, которую мы сегодня уже много раз использовали. Получится так:
[{{{y}”}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}]
Тут нас ждёт две новости:
- Хорошая: мы уже знаем ${{{x}’}_{t}}$. Это значит, что каждая последующая производная будет считаться чуть проще и быстрее;
- Плохая: можно легко запутаться во всех этих штрихах и переменных.
Чтобы разобраться с плохой новостью, достаточно просто небольшой практики. Поэтому сейчас мы разберём три примера. А точнее, три задачи из контрольных работ МГТУ им. Баумана. А там знают толк в производных.:)
Пример 5. Найдите ${{{y}”}_{xx}}$, если
[left{ begin{align} & x=cos 2t \ & y=sin t \ end{align} right.]
1. Сначала находим первую производную. Для этого считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}=-2sin 2t=-4sin tcos t \ & {{{{y}’}}_{t}}=cos t end{align}]
Откуда находим саму производную ${{{y}’}_{x}}$:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{cos t}{-4sin tcos t}=-frac{1}{4sin t}]
2. Теперь находим вторую производную. Для этого считаем ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:
[{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}={{left( -frac{1}{4sin t} right)}^{prime }}_{t}=frac{cos t}{4{{sin }^{2}}t}]
Кроме того, мы уже знаем ${{{x}’}_{t}}$. Поэтому находим вторую производную ${{{y}”}_{xx}}$:
[{{{y}”}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{cos t}{4{{sin }^{2}}t}cdot frac{1}{-4sin tcos t}=-frac{1}{16}cdot frac{1}{{{sin }^{3}}t}]
[begin{align} {{{{y}”}}_{xx}} & ={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}= \ & =frac{cos t}{4{{sin }^{2}}t}cdot frac{1}{-4sin tcos t}= \ & =-frac{1}{16}cdot frac{1}{{{sin }^{3}}t} end{align}]
Вторая производная найдена.
Для сравнения посчитаем «производную» по неправильной формуле:
[frac{{{{{y}”}}_{tt}}}{{{{{x}”}}_{tt}}}=frac{{{left( {{{{y}’}}_{t}} right)}^{prime }}_{t}}{{{left( {{{{x}’}}_{t}} right)}^{prime }}_{t}}=frac{{{left( cos t right)}^{prime }}_{t}}{{{left( -2sin 2t right)}^{prime }}_{t}}=frac{-sin t}{-4cos 2t}=frac{1}{4}cdot frac{sin t}{cos 2t}]
[begin{align} frac{{{{{y}”}}_{tt}}}{{{{{x}”}}_{tt}}} & =frac{{{left( {{{{y}’}}_{t}} right)}^{prime }}_{t}}{{{left( {{{{x}’}}_{t}} right)}^{prime }}_{t}}=frac{{{left( cos t right)}^{prime }}_{t}}{{{left( -2sin 2t right)}^{prime }}_{t}}= \ & =frac{-sin t}{-4cos 2t}=frac{1}{4}cdot frac{sin t}{cos 2t} end{align}]
Получили совершенно другое выражение, которое не является второй производной.
Итак, вторая производная считается из первой ровно по той же формуле, по какой первая производная считается из исходной функции.
Пример 6. Найдите ${{{y}”}_{xx}}$, если
[left{ begin{align} & x={{text{e}}^{t}}+1 \ & y=left( {{t}^{2}}-2t+2 right)cdot {{text{e}}^{t}} \ end{align} right.]
Первая производная ${{{y}’}_{x}}$ через ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{text{e}}^{t}} \ & {{{{y}’}}_{t}}={{t}^{2}}cdot {{text{e}}^{t}} \ & {{{{y}’}}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{{{t}^{2}}cdot {{text{e}}^{t}}}{{{text{e}}^{t}}}={{t}^{2}} \ end{align}]
Вторая производная ${{{y}”}_{xx}}$ через ${{{x}’}_{t}}$ и ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:
[begin{align} & {{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}=2t \ & {{{{y}”}}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{2t}{{{text{e}}^{t}}} \ end{align}]
Замечание. Когда освоитесь с основной формулой, выкладки можно сократить буквально до двух строк:
[begin{align} & {{{{y}’}}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{{{t}^{2}}cdot {{text{e}}^{t}}}{{{text{e}}^{t}}}={{t}^{2}} \ & {{{{y}”}}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{2t}{{{text{e}}^{t}}} \ end{align}]
Впрочем, не стоит увлекаться сокращением выкладок, если у вас есть хоть малейшее сомнение или недопонимание на любом этапе вычислений.
Пара дополнительных минут — сомнительная экономия по сравнению с парой баллов на контрольной. И уж тем более по сравнению с недопониманием материала.
Пример 7. Найдите ${{{y}”}_{xx}}$, если
[left{ begin{align} & x={1}/{left( 1+{{t}^{2}} right)}; \ & y=2operatorname{arctg}t \ end{align} right.]
Дифференцирование арктангенса дробно-рациональной функции — довольно громоздкие действия. Тут в пару строк не уложиться.
1. Считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{left( frac{1}{1+{{t}^{2}}} right)}^{prime }}_{t}=frac{-2t}{{{left( 1+{{t}^{2}} right)}^{2}}} \ & {{{{y}’}}_{t}}={{left( 2operatorname{arctg}t right)}^{prime }}_{t}=frac{2}{1+{{t}^{2}}} \ end{align}]
Первая производная ${{{y}’}_{x}}$:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{2}{1+{{t}^{2}}}cdot frac{{{left( 1+{{t}^{2}} right)}^{2}}}{-2t}=-frac{1+{{t}^{2}}}{t}]
2. Считаем ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:
[{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}=-frac{2tcdot t-left( 1+{{t}^{2}} right)}{{{t}^{2}}}=frac{1-{{t}^{2}}}{{{t}^{2}}}]
Вторая производная ${{{y}”}_{xx}}$:
[{{{y}”}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{1-{{t}^{2}}}{{{t}^{2}}}cdot frac{{{left( 1+{{t}^{2}} right)}^{2}}}{-2t}=frac{{{left( 1+{{t}^{2}} right)}^{2}}left( {{t}^{2}}-1 right)}{2{{t}^{3}}}]
[begin{align} {{{{y}”}}_{xx}} & ={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}= \ & =frac{1-{{t}^{2}}}{{{t}^{2}}}cdot frac{{{left( 1+{{t}^{2}} right)}^{2}}}{-2t}= \ & =frac{{{left( 1+{{t}^{2}} right)}^{2}}left( {{t}^{2}}-1 right)}{2{{t}^{3}}} end{align}]
Замечание. При делении дробных выражений полезно заменять их умножением на обратное:
[frac{Aleft( x right)}{Bleft( x right)}:frac{Pleft( x right)}{Qleft( x right)}=frac{Aleft( x right)}{Bleft( x right)}cdot frac{Qleft( x right)}{Pleft( x right)}]
Именно так мы и поступили при вычислении ${{{y}’}_{x}}$ и ${{{y}”}_{xx}}$ в последнем примере. И не только в последнем.:)
4. Третья производная
Пример 8. Найдите производную третьего порядка ${{{y}”’}_{xxx}}$ для функции, заданной параметрически:
[left{ begin{align} & xleft( t right)={{text{e}}^{t}}left( cos t+sin t right) \ & yleft( t right)={{text{e}}^{t}}left( cos t-sin t right) \ end{align} right.]
Решение будет состоять из трёх шагов.
1. Найдём первую производную ${{{y}’}_{x}}$. Для этого считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} {{{{x}’}}_{t}} & =2cos tcdot {{text{e}}^{t}} \ {{{{y}’}}_{t}} & =-2sin tcdot {{text{e}}^{t}} \ end{align}]
Первая производная ${{{y}’}_{t}}$ равна
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{-2sin tcdot {{text{e}}^{t}}}{2cos tcdot {{text{e}}^{t}}}=-operatorname{tg}t]
2. Считаем вторую производную. При этом ${{{x}’}_{t}}$ уже посчитано, осталось найти ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:
[{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}={{left( -operatorname{tg}t right)}^{prime }}_{t}=-frac{1}{{{cos }^{2}}t}]
Находим вторую производную по всё той же формуле:
[{{{y}”}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=-frac{1}{{{cos }^{2}}t}cdot frac{1}{2cos tcdot {{text{e}}^{t}}}=-frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t}]
[begin{align} {{{{y}”}}_{xx}} & ={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}= \ & =-frac{1}{{{cos }^{2}}t}cdot frac{1}{2cos tcdot {{text{e}}^{t}}}= \ & =-frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t} end{align}]
3. Считаем третью производную. Вновь нужно лишь найти ${{left( {{{{y}”}}_{xx}} right)}^{prime }}_{t}$:
[{{left( {{{{y}”}}_{xx}} right)}^{prime }}_{t}={{left( -frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t} right)}^{prime }}_{t}=frac{cos t-3sin t}{2{{text{e}}^{t}}{{cos }^{4}}t}]
[begin{align} {{left( {{{{y}”}}_{xx}} right)}^{prime }}_{t} & ={{left( -frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t} right)}^{prime }}_{t}= \ & =frac{cos t-3sin t}{2{{text{e}}^{t}}{{cos }^{4}}t} end{align}]
Для сокращения вычислений я сразу записал готовую формулу ${{left( {{{{y}”}}_{xx}} right)}^{prime }}_{t}$ — проверьте её самостоятельно. А дальше вновь используем формулу производной для параметрической функции:
[{{{y}”’}_{xxx}}=frac{{{left( {{{{y}”}}_{xx}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{cos t-3sin t}{4{{text{e}}^{2t}}cdot {{cos }^{5}}t}]
Задача решена. Хотя вычислений получилось довольно много.
В любом случае помните главную формулу:
[{{{y}’}_{x}}left( x right)=frac{{{{{psi }’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]
И помните, что вторая производная не равна частному вторых производных:
[{{{y}”}_{xx}}left( x right)ne frac{{{{{psi }”}}_{tt}}left( t right)}{{{{{x}”}}_{tt}}left( t right)}]
Попытка использовать эту формулу для нахождения производных высших порядков будет считаться грубой ошибкой.
Вот и вся теория. Теперь — за практику!:)
Смотрите также:
- Частные производные для функции нескольких переменных

- Формула полной вероятности

- Тест по теории вероятностей (1 вариант)

- Видеоурок по задачам C2: уравнение плоскости через определитель

- Процент: неизвестно начальное значение (метод пропорции)

- Производительность совместного труда

Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
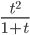 ≡ t^2/(1+t)
≡ t^2/(1+t)
cos2(t) ≡ cos(t)^2
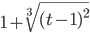 ≡ 1+(t-1)^(2/3)
≡ 1+(t-1)^(2/3)
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
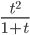 ≡ t^2/(1+t)
≡ t^2/(1+t)
cos2(t) ≡ cos(t)^2
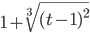 ≡ 1+(t-1)^(2/3)
≡ 1+(t-1)^(2/3)
Пример 1. Найти производную функции y по x, заданной параметрически: 
Решение.
 .
.
 .
.
Пример 2. Найти y’’xx функции 
Решение. Найдем y’x по формуле (*):  .
.
Производную y’x запишем в параметрической форме 
К этой функции снова применим формулу (*):
 .
.
Пример 3. Для функции  найти y’’’xxx.
найти y’’’xxx.
Решение.  тогда
тогда  и
и 
 .
.
 .
.
 .
.
Производная параметрически заданной функции
Производная параметрически заданной функции находится по обычным правилам дифференцирования, но с использованием дополнительных формул, которые будут рассмотрены далее, а пока напомним как выглядит параметрическая функция.
Параметрическая функция задаётся в виде:
$$ begin{cases} y = phi(t) \ x = psi(t) end{cases}, t in [a;b] $$
Здесь $ t $ это параметр функции. Для нахождения производной такой функции нужно знать таблицу производных элементарных функций.
Формула первой производной
$$ y’_x = frac{y’_t}{x’_t} $$
| Пример 1 |
| Найти производную функции, заданной параметрически $$ begin{cases} y = t^2 – 16 \ x = t – 4 end{cases} $$ |
| Решение |
|
Рассмотрев формулу понимаем, что для решения примера нужно найти неизвестные $ y’_t $ и $ x’_t $. Займемся этим: $$ y’_t = (t^2 – 16)’_t = 2t $$ $$ x’_t = (t-4)’_t = 1 $$ Обратите внимание! При записи производной нужно обязательно внизу писать $ t $. Теперь подставляем найденное в формулу: $$ y’_x = frac{y’_t}{x’_t} = frac{2t}{1} = 2t $$ Ответ необходимо записывать в следующем виде: $$ begin{cases} y’_x = 2t \ x = t – 4 end{cases} $$ Обратите внимание, что обязательно составляется система, в которой кроме $ y’_x $ пишем ещё $ x = t – 4 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ begin{cases} y’_x = 2t \ x = t – 4 end{cases} $$ |
| Пример 2 |
| Вычислить первую производную функции заданной параметрически: $$ begin{cases} y = e^t cos t \ x = e^t sin t end{cases} $$ |
| Решение |
|
Начинаем с нахождения производных функций $ y(t) $ и $ x(t) $. Не забываем правило дифференцирования сложной функции: $$ y’_t = (e^t cos t)’_t = (e^t)’_t cos t + e^t (cos t)’_t = $$ $$ = e^t cos t – e^t sin t = e^t (cos t – sin t) $$ Аналогично находим производную $ x’_t $: $$ x’_t = (e^t sin t)’_t = (e^t)’_t sin t + e^t (sin t)’_t = $$ $$ = e^t sin t + e^t cos t = e^t (sin t + cos t) $$ Подставляем в формулу найденные $ y’_t $ и $ x’_t $. Получаем: $$ y’_x = frac{y’_t}{x’_t} = frac{e^t (cos t – sin t)}{e^t (sin t + cos t)} = frac{cos t – sin t}{sin t + cos t} $$ |
| Ответ |
| $$ begin{cases} y’_t = frac{cos t – sin t}{sin t + cos t} \ x = e^t sin t end{cases} $$ |
Формула второй производной
$$ y”_{xx} = frac{(y’_x)’_t}{x’_t} $$
| Пример 3 |
| Найти вторую производную параметрически заданной функции $$ begin{cases} y = sin 2t \ x = cos^2 t end{cases} $$ |
| Решение |
|
Как видно из формулы для начала нужно найти первую производную $ y’_x $, а затем уже можно получить вторую. Приступаем: $$ y’_t = (sin 2t)’_t = cos 2t cdot (2t)’_t = 2cos 2t $$ $$ x’_t = (cos^2 t)’_t = 2cos t cdot (cos t)’_t = -2cos t sin t = -sin 2t $$ Тогда первая производная параметрической функции равна: $$ y’_x = frac{2cos 2t}{-sin 2t} = -2 ctg 2t $$ Зная первую производную находим вторую. Используем формулу: $$ y”_{xx} = frac{ (y’_x)’_t }{x’_t} = frac{(-2 ctg 2t)’_t}{-sin 2t} = $$ $$ = frac{2 frac{2}{sin^2 2t} }{-sin 2t} = – frac{4}{sin^3 2t} $$ |
| Ответ |
| $$ begin{cases} y”_{xx} = – frac{4}{sin^3 2t} \ x = cos^2 t end{cases} $$ |
Предположим, что функциональная
зависимость ![]() от
от![]() не
не
задана непосредственно![]() ,
,
а через промежуточную величину —![]() .
.
Тогда формулы

задают параметрическое
представление функцииодной
переменной.
Пример:
Задание.Найти вторую
производную![]() для
для
функции заданной
заданной
параметрически.
Решение.Вначале находим
первую производную![]() по
по
формуле:
![]()
Производная функции ![]() по
по
переменной![]() равна:
равна:
![]()
производная ![]() по
по![]() :
:
![]()
Тогда
![]()
Вторая производная равна
![]()
Ответ.![]()
Вывод формулы производной
параметрически заданной функции.
Пусть ![]() определены
определены
и дифференцируемы при ![]() ,
,
причем ![]() и
и ![]() имеет
имеет
обратную функцию ![]() .
.
Сначала переходим от
параметрического задания к явному. При
этом получаем сложную функцию ![]() ,
,
аргументом которой является x.
По правилу
нахождения производной сложной
функции имеем: ![]() .
.
Так как ![]() и
и ![]() обратные
обратные
функции, то по формуле
производной обратной функции ![]() ,
,
поэтому  .
.
Для
нахождения производной второго порядка
параметрически заданной функции,
можно к найденной производной первого
порядка вновь применить формулу:

21. Функции, заданные неявно. Пример. Производная неявной функции. Производные старших порядков.

22. Возрастание и убывание в точке. Условия возрастания и убывания функции.
Возрастание и убывание в точке:
– Функция f(х) называется
возрастающей в точке хо,
в окрестности которой она определена,
если для как угодно малого положительногоhимеет место условие:
f(хо-h)<f(хо)<f(хо+h)
-Функция f(x)
называется убывающей в точке хо,
в окрестности которой она определена,
если для как угодно малого положительногоhимеет место условие:
f(хо-h)>f(хо)>f(хо+h)
Условия возрастания и убывания ф-ии:
Достаточное условие:
-Для того чтобы ф-ия f(x), дифференцируемая
в точке хо (а,b), возрастала (убывала) в
точке хо,
достаточно, чтобыf’(хо)>0
(f’(хо)<0).
Необходимые условия:
-Для того чтобы ф-ия f(x), дифференцируемая
в точке хо (а,b), возрастала (убывала) в
точке хо,
необходимо, чтобы ее производная в точке
хобыла
неотрицательнойf’(хо)>=0
(неположительнойf’(хо)
<=0).
-Если ф-ия f(x) определена на отрезке [a,b], дифференцируема в
точкахx(a,b)
иf’(x)>0,
(f’(x)<0),
то ф-ияf(x)
возрастает (убывает) на отрезке [a,b].
23. Экстремум функции. Теорема Ферма. Геометрический смысл.
Определение 1.Точка
![]() называетсяточкой максимума[точкой минимума]
называетсяточкой максимума[точкой минимума]
функции
![]() ,
,
если существует такая
![]() –окрестность
–окрестность
![]() точки
точки
![]() ,
,
что для всех значений
![]() из
из
этой окрестности выполняется неравенство
![]()
![]() .
.
Определение 2. Значение функции
в точке максимума (точке минимума)
называетсямаксимумом(минимумом)
функции
![]() .
.
Определение 3. Точки минимума и
точки максимума называютсяточками
экстремумафункции
![]() ,
,
а значения функции в этих точках —экстремумамифункции
![]() .
.
Теорема 1. Если функция
![]() непрерывна
непрерывна
в точке
![]() ,
,
а
![]() на
на
промежутке
![]() и
и
![]() на
на
промежутке
![]() ,
,
то
![]() является
является
точкой максимума функции
![]() .
.
Теорема 2. Если функция
![]() непрерывна
непрерывна
в точке
![]() ,
,
а
![]() на
на
промежутке
![]() и
и
![]() на
на
промежутке
![]() ,
,
то
![]() —
—
точка минимума функции
![]() .
.
Теорема 3.Пусть функция
![]() дифференцируема
дифференцируема
в некоторой окрестности точки
![]() ,
,
кроме, быть может, самой точки
![]() ,
,
и непрерывна в точке
![]() .
.
Тогда, если
![]() меняет
меняет
знак с «![]() »
»
на «![]() »
»
(с «![]() »
»
на «![]() »)
»)
при переходе через точку
![]() ,
,
то
![]() —
—
точка минимума (точка максимума) функции
![]() .
.
Теорема Ферма. (Ферма, 1601-1665 –
французский математик).
Пусть функция f(x),
определенная в интервале (a,
b), принимает в
некоторой точкеx=cэтого интервала наибольшее или наименьшее
значение. В таком случае, если в точкеx=cсуществует производная этой функции,
то она равна нулю.
Доказательство. Пустьf(с)=M,
гдеМ– наибольшее значение функции
в интервале (a, b).
Покажем, чтоf/(c)=0.По определению производной:f/(c)=![]() .
.
Так как в точке x=c
функция принимает наибольшее значение,
то при любом знакеxимеем:f(c)f(c+x)
иf(c+x)-f(c)0
Отсюда, если x>0,
то
![]() и
и
по теореме 2 имеем:f/(c)=![]() .
.
Если же x<0,
то
![]() иf/(c)=
иf/(c)=![]() .
.
Сравнивая полученные для f/(c)неравенства видим, что оба они
удовлетворяются только тогда, когдаf/(c)=0,
что и требовалось доказать. Геометрический
смысл теоремы Ферма: касательная к
графику функцииy=f(x)в точке экстремума, в которой функция
дифференцируема, параллельна осиOx
(так какy/=tg=0),=0.

Определение
Предположим, что функциональная зависимость $y$ от
$x$ не задана непосредственно
$y=f(x)$, а через промежуточную величину —
$-t$. Тогда формулы
$left{begin{array}{l}x=x(t) \ y=y(t)end{array}right.$
задают параметрическое представление функции одной переменной.
Пусть функция $y=y(x)$ задана в параметрической форме,
то есть в виде:
$$left{begin{array}{l}x=x(t) \ y=y(t)end{array}right$$
где функции $x=x(t)$ и
$y=y(t)$ определены и непрерывны на некотором интервале
изменения параметра $t$. Найдем дифференциалы от
правых и левых частей каждого из равенств:
$$left{begin{array}{l}
d x=x_{t}^{prime} d t \
d y=y_{t}^{prime} d t
end{array}right.$$
Далее, разделив второе уравнение на первое, и с учетом того, что
$frac{d y}{d x}=y_{x}^{prime}$, получим выражение для первой производной функции,
заданной параметрически:
$$frac{d y}{d x}=y_{x}^{prime}=frac{y_{t}^{prime}}{x_{t}^{prime}}$$
Для нахождения второй производной $frac{d^{2} y}{d x^{2}}=y_{x x}^{prime prime}$ выполним следующие преобразования:
$$frac{d^{2} y}{d x^{2}}=y_{x x}^{prime prime}=left(y_{x}^{prime}right)^{prime}=frac{d y_{x}^{prime}}{d x}=frac{frac{d y_{x}^{prime}}{d t}}{frac{d x}{d t}}=frac{left(y_{x}^{prime}right)_{t}^{prime}}{x_{t}^{prime}}$$
Пример
Задание. Найти вторую производную $y_{c x}^{prime prime}$
для функции $left{begin{array}{l}x=ln t \ y=t^{3}end{array}right.$ заданной параметрически.
Решение. Вначале находим первую производную $y_{x}^{prime}$ по формуле:
$$y_{x}^{prime}=frac{y_{t}^{prime}}{x_{t}^{prime}}$$
Производная функции $y$ по переменной
$t$ равна:
$$y_{t}^{prime}=left(t^{3}right)^{prime}=3 t^{2}$$
производная $x$ по $t$:
$$x_{t}^{prime}=(ln t)^{prime}=frac{1}{t}$$
Тогда
$$y_{x}^{prime}=frac{3 t^{2}}{frac{1}{t}}=3 t^{3}$$
Вторая производная равна
$$y_{x x}^{prime prime}=left(3 t^{3}right)^{prime} cdot frac{1}{frac{1}{t}}=3 cdotleft(t^{3}right)^{prime} cdot t=3 t cdot 3 t^{2}=9 t^{3}$$
Ответ. $y_{x x}^{prime prime}=9 t^{3}$
Читать дальше: логарифмическое дифференцирование.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

