Как найти производную если в степени логарифм

ВНИМАНИЕ, когда я готовил ответ, то предполагал, что там написано (ln(x+5))^4, если же в степень возводится не логарифм, а выражение в нём, то надо пересчитать, и там всё будет значительно проще даже 🙂

Разберёмся как считается производная сложной функции

найдём производную функции a(b(x)) по dx
заменим b(x) = u
тогда
a`(u) = (a(u + du) – a(u))/du
как мы знаем u` = du/dx; du = u`*dx
a`(u) = (a(u + du) – a(u))/(u`*dx)
заменим обратно, с учётом того, что du = b(x+dx) – b(x)
a`(u) = (a(b(x) + b(x+dx) – b(x)) – a(b(x)))/(u`*dx)
a`(u)*u` = (a(b(x+dx)) – a(b(x)))/dx

Итак, доказали, что
a`(b(x)) = a`(b)*b`(x)

(этого делать по сути в школе не требуется, но я посчитал, что знание откуда берётся производная сложной функции, не помешает).

Теперь решим предложенный пример
y = 4x – ln(x + 5)^4;
x + 5 = u;
y` = (4x)` – u`*(ln(u)^4)` = (4x)` – (x + 5)`*(ln(u)^4)`;
y` = 4 – 1*(ln(u)^4)` = 4 – (ln(u)^4)`;
ln(u) = v;
y` = 4 – v`*(v^4)` = 4 – (ln(u))`*(v^4)` = 4 – (1/u)*(4v³)`;
y` = 4 – 4v³/u = 4 – 4*ln(x + 5)³/(x + 5);

Если нигде не ошибся, то
y` = 4 – 4*ln(x + 5)³/(x + 5)

Когда нам нужно выполнить дифференцирование показательно степенной функции вида y=(f(x))g(x) или преобразовать громоздкое выражение с дробями, можно использовать логарифмическую производную. В рамках этого материала мы приведем несколько примеров применения этой формулы.

Чтобы понять эту тему, необходимо знать, как пользоваться таблицей производных, быть знакомым с основными правилами дифференцирования и представлять себе, что такое производная сложной функции.

Как вывести формулу логарифмической производной

Для получения этой формулы нужно сначала произвести логарифмирование по основанию e, а затем упростить получившуюся функцию, применив основные свойства логарифма. После этого надо вычислить производную неявно заданной функции:

y=f(x)ln y=ln(f(x))(ln y)’=(ln(f(x)))’1y·y’=(ln(f(x)))’⇒y’=y·(ln(f(x)))’

Примеры использования формулы

Покажем на примере, как это делается.

Такую задачу можно решить и другим способом, без логарифмической производной. Сначала нам надо преобразовать исходное выражение так, чтобы перейти от дифференцирования показательно степенной функции к вычислению производной сложной функции, например:

y=xx=eln xx=ex·ln x⇒y’=(ex·ln x)’=ex·ln x·x·ln x’=xx·x’·ln x+x·(ln x)’==xx·1·ln x+x·1x=xx·ln x+1

Рассмотрим еще одну задачу.

Чтобы закрепить материал, изучите еще пару следующих примеров. Здесь будут приведены только вычисления с минимумом комментариев.

Содержание:

Производные показательной и логарифмической функций:

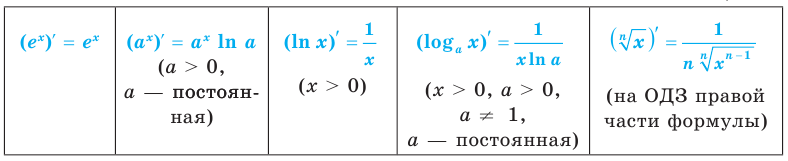
Объяснение и обоснование

Чтобы обосновать формулы производных показательных и логарифмических функций, используем без доказательства свойство функции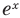

При а > 0 по основному логарифмическому тождеству имеем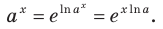

Тогда по правилу нахождения производной сложной функции: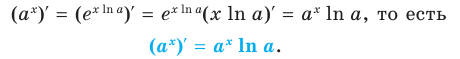

По полученной формуле мы можем найти значение производной показательной функции для любого значения 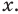Следовательно, показательная функция дифференцируема в каждой точке области определения, а значит, и непрерывна в каждой точке своей области определения (при всех действительных значениях ).

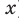Для логарифмической функции сначала найдем производную функции 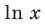(принимая без доказательства существование ее производной). Область определения этой функции — 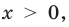то есть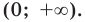

При 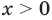по основному логарифмическому тождеству имеем 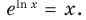Это равенство означает, что при 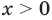функции 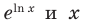совпадают (это одна и та же функция, заданная на множестве 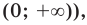а значит, совпадают и их производные. Используя для левой части равенства правило нахождения производной сложной функции, получаем: 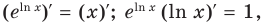то есть 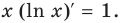Отсюда

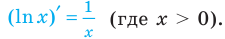
Поскольку 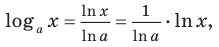то

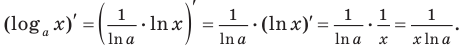Следовательно,

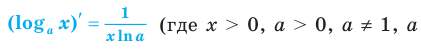– постоянная).

Замечание. Формула 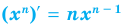была обоснована только для целых значений Докажем, что она выполняется при любых действительных значениях

*Напомним , что 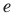— иррациональное число, первые знаки которого следующие: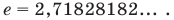

Если 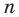— любое нецелое число, то функция 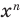определена только при 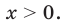Тогда поосновному логарифмическому тождеству 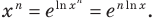По правилу вычисления производной сложной функции получаем:

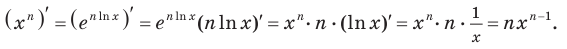
Следовательно, далее формулой 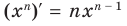можно пользоваться при любых действительных значениях 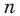(в этом случае только при тех значениях 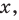при которых определена ее правая часть).

Опираясь на полученный результат, обоснуем также формулу

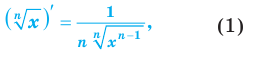
которую можно использовать при тех значениях 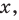при которых определена ее правая часть.

Если 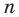— четное число, то ОДЗ правой части формулы (1): 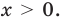Но при этом условии

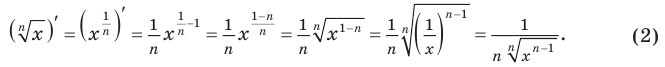
Если 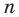— нечетное число, то ОДЗ правой части формулы (1) задается условием: 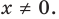При остается справедливым равенство (2). При 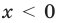учтем, что 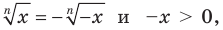а также то, что при нечетном 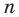число 1 – 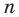будет четным (поэтому 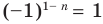). Тогда

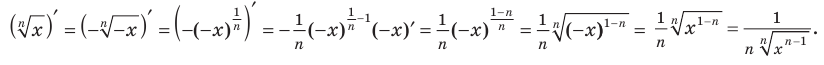
Следовательно, и для нечетного 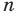при всех 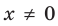формула (1) также выполняется.

В последнем случае такие громоздкие преобразования пришлось вы- 1 полнить вследствие того, что при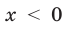 выражение 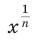не определено, а выражение 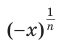существует, поскольку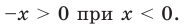

Примеры решения задач

Пример №1

Найдите производную функции:

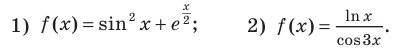
Решение:

Комментарий:

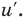Последовательно определяем, от какого выражения берется производная (ориентируясь на результат последнего действия). В задании 1 сначала берется производная суммы: Затем для каждого из слагаемых используется правило вычисления производной сложной функции: берется производная от и умножается на Полученный результат желательно упростить по формуле: 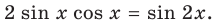В задании 2 сначала берется производная частного: 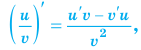а для производной знаменателя используется правило вычисления производной сложной функции (производная умножается на ).

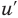Пример №2

Найдите уравнение касательной к графику функции 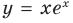точке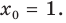

Решение:

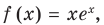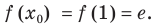
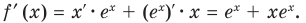Если то Тогда 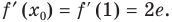Подставляя эти значения в уравнение касательной 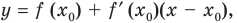получаем: 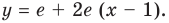То есть 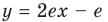— искомое уравнение касательной.

Комментарий:

Уравнение касательной к графику функции 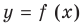в точке с абсциссой 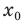в общем виде записывается так: 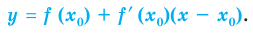Чтобы записать это уравнение для данной функции, необходимо найти 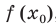производную 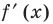и значение 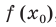. Д ля выполнения соответствующих вычислений удобно обозначить данную функцию через 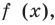а для нахождения ее производной воспользоваться формулой производной произведения:

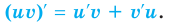
Пример №3

1) Постройте график функции 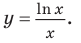2) Найдите наибольшее значение параметра 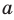, при котором уравнение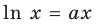имеет единственный корень.

Комментарий:

Для выполнения задания 1 исследуем функцию 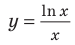по общей схеме и по результатам исследования строим ее график. При исследовании функции на четность и нечетность можно воспользоваться тем, что учетной или нечетной функции в область определения входят точки Следовательно, для таких функций область определения должна быть симметричной относительно точки 0. Если же это условие не выполняется, то функция не может быть ни четной, ни нечетной. Для лучшего представления о виде графика целесообразно уточнить поведение функции на концах области определения 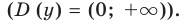При 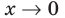справа (при 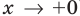) значение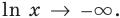

Тогда 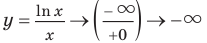(рис. 18.2). Но при 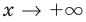мы не можем выполнить такую оценку (получаем неопределенность вида 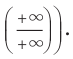В таком случае поведение функции при 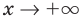можно уточнить с помощью дополнительных точек.

При выполнении задания 2 целесообразно использовать графическую иллюстрацию решения. Это можно сделать двумя способами:

Решение:

1) Исследуем функцию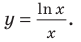

1. Область определения: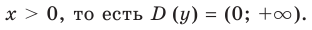

2. Функция ни четная, ни нечетная, поскольку ее область определения не симметрична относительно точки 0. 3. Точки пересечения графика с осями координат. График не пересекает ось На оси 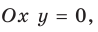то есть 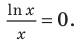Тогда при получаем: 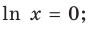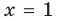— абсцисса точки пересечения графика с осью 4. Производная и критические точки.

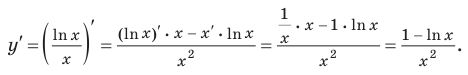
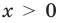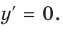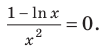Производная существует на всей области определения функции (то есть при ), следовательно, функция непрерывна на всей области определения. Тогда Отсюда при 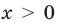получаем 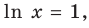следовательно, 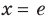— критическая точка.

5. Отмечаем критические точки на области определения функции и находим знак 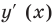в каждом из полученных промежутков (рис. 18.1).

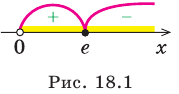
Составляем таблицу, в которой отмечаем промежутки возрастания, убывания и экстремумы функции.

6. Найдем координаты еще нескольких точек графика функции:

Заметим, что при 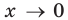справа ()) значение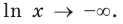 Действительно,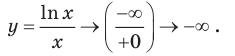

7. Используя результаты исследования, строим график функции 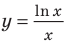(см. рис. 18.2).

I способ решения задания 2

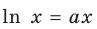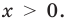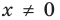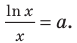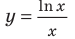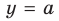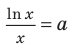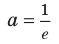Область допустимых значений данного уравнения задается неравенством Но тогда и данное уравнение на его ОДЗ равносильно уравнению Решим последнее уравнение графически. Для этого построим график функции (см. задание 1) и график функции (18.3). Как видим, уравнение имеет единственный корень только при и при (при 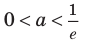уравнение имеет два корня, а при 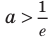– уравнение не имеет корней). Следовательно, наибольшее значение параметра 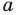, при котором уравнение 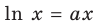имеет единственный корень, — это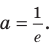

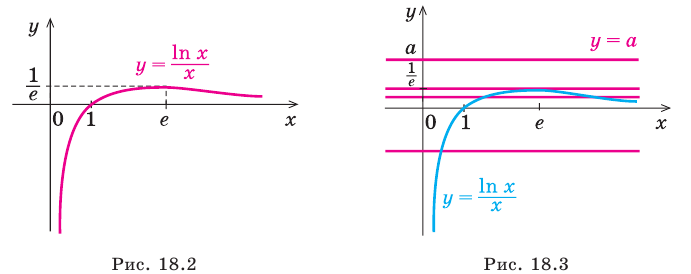
II способ решения задания 2

Рассмотрим графическую иллюстрацию (рис. 18.4) решения данного уравнения

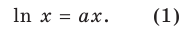
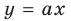Функция возрастающая и принимает все значения от График функции — прямая, проходящая через начало координат. При 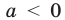прямая 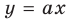пересекает график функции 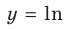только в одной точке (прямая 1 на рис. 18.4). Следовательно, уравнение (1) имеет единственный корень (действительно, функция 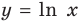возрастающая, а функция 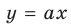убывающая, поэтому уравнение (1) может иметь только один корень).

При 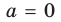уравнение (1) имеет вид 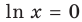и также имеет единственный корень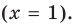

При 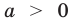прямая 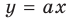может касаться графика функции 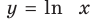(прямая 2 на рис. 18.4). Тогда уравнение (1) будет иметь единственный корень. Также прямая 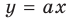может проходить в первой четверти ниже касательной (прямая 3 на рис. 18.4).

Тогда уравнение (1) будет иметь два корня. Если же прямая будет проходить в первой четверти выше касательной (прямая 4 на рис. 18.4), то уравнение(1) не будет иметь корней.

Выясним, когда прямая 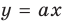будет касательной к графику функции 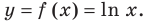Пусть точка касания 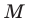имеет абсциссу 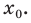Учитывая геометрический смысл производной, получаем, что 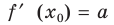(значение производной в точке 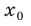равно угловому коэффициенту касательной, проведенной через точку 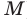). Поскольку 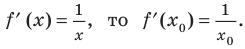Тогда из равенства 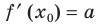имеем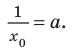 Отсюда 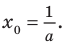Тогда уп = In -. С другой стороны, поскольку точка касания 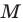лежит на касательной 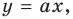то ее координаты удовлетворяют и уравнению касательной. Получаем 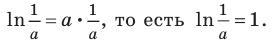Тогда 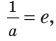следовательно, 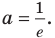Таким образом, данное уравнение будет иметь единственный корень только 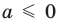при и при 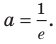. Тогда наибольшее значение параметра 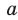, при котором уравнение 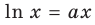имеет единственный корень, — это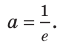

Пример №4

Докажите, что при всех действительных значениях 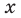выполняется неравенство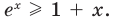

Решение:

Рассмотрим функцию

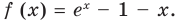
Область определения: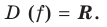

Производная 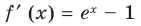существует на всей области определения. Следовательно, функция 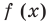непрерывна на всей числовой прямой:

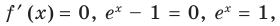
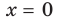— критическая точка. Отмечаем критическую точку на области определения функции 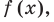определяем знаки производной и поведение функции в каждом из полученных промежутков (рис. 18.5).

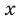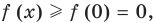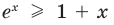Как видим, непрерывная функция имеет на интервале только одну критическую точку, — точку минимума, в которой функция принимает наименьшее значение на этом интервале. Тогда при всех действительных значениях значения то есть Следовательно, при всех действительных значениях .

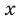Комментарий:

Используем производную для доказательства данного неравенства. Для этого исследуем функцию 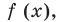которая является разностью левой и правой частей неравенства. При всех действительных значениях 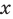эта функция не является ни возрастающей, ни убывающей, поэтому рассуждения, приведенные при решении предыдущих задач, нельзя использовать. Тогда в результате исследования попробуем найти наибольшее или наименьшее значение функции 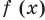на всей числовой прямой. Для этого можно использовать свойство: если непрерывная функция 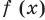имеет на заданном интервале только одну точку экстремума 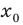и это точка минимума, то на этом интервале функция принимает свое наименьшее значение в точке 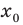. Далее воспользуемся тем, что когда в точке 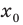функция принимает наименьшее значение на заданном интервале, то для всех значений 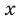из этого интервала (если необходимо, то можно также уточнить, что знак равенства достигается только в точке ).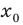

При доказательстве числовых неравенств или для сравнения двух чисел часто бывает удобно перейти к более общему функциональному неравенству

Пример №5

Сравните числа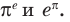

Комментарий:

Чтобы составить план решения, можно рассуждать следующим образом. Мы не знаем, какое из данных чисел больше: 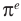или 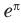, поэтому в ходе анализа поставим между ними знак «». Этот знак неравенства, направленный вниз острым концом, свидетельствует о том, что мы не знаем, в какую сторону его следует направить. Будем выполнять преобразование неравенства до тех пор, пока не выясним, какое число больше.

Затем заменим знак «» соответствующим знаком неравенства: «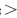» или «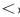», которое и запишем в решении. (В ходе анализа, если необходимо поменять знак неравенства, знак «» меняем на знак «», а в записи решения в соответствующем месте меняем знак неравенства.) При анализе запись вида также будем называть неравенством (но, конечно, не в решении). Рассмотрим неравенство Это неравенство с положительными членами (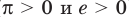), следовательно, обе его части можно прологарифмировать. Поскольку функция 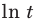является возрастающей, то после логарифмирования обеих частей по основанию 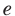знак неравенства не изменится, и мы получим неравенство 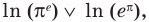то есть неравенство Так как 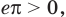то после деления обеих частей последнего неравенства на 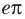знак неравенства не изменится, и мы получим неравенство 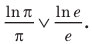Замечаем, что в левой и правой частях этого неравенства стоят значения одной и той же функции 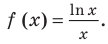Исследуем эту функцию с помощью производной на возрастание и убывание.

Далее, учитывая, что сравним полученные выражения, а затем и данные выражения (выполняя все те преобразования, что и в ходе анализа, только в обратном порядке).

Решение:

Рассмотрим функцию 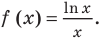Ее область определения: 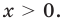Производная 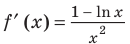существует на всей области определения. Выясним, когда 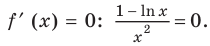Тогда на области определения получаем равносильное уравнение 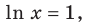то есть 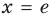— критическая точка. Отмечаем критическую точку на области определения функции 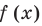и определяем знаки производной и поведение функции в каждом из полученных промежутков (рис. 18.6).

Функция убывает на интервале 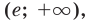а так как она непрерывна на всей области определения, то убывает и на промежутке 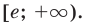Поскольку то 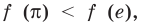то есть 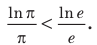Умножив обе части этого неравенства на положительное число 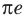(знак неравенства не меняется), получаем неравенство 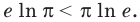Тогда 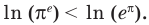Так как функция 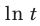возрастающая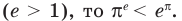

Ответ: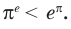

Пример №6

Решите уравнение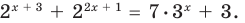

Комментарий:

Если попытаться применить к данному уравнению схему решения показательных уравнений (см. с. 178), то удается реализовать только первый ее пункт — избавиться от числовых слагаемых в показателях степеней. А привести все степени к одному основанию (с удобными показателями) или к двум основаниям так, чтобы получить однородное уравнение, или перенести все члены в одну сторону и разложить полученное выражение на множители — не удается. Попробуем применить свойства соответствующих функций. Но и на этом пути нам не удается использовать конечность ОДЗ (она бесконечна), оценку значений левой и правой частей уравнения (они обе в пределах от 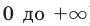). Также не получается использовать теоремы о корнях уравнений (в обеих частях данного уравнения стоят возрастающие функции). Тогда попробуем подобрать корни этого уравнения и доказать, что других корней оно не имеет (удобно предварительно привести уравнение к виду 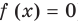). Последовательно подставляя 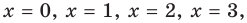выясняем, что 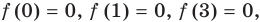то есть уравнение 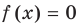имеет три корня. Чтобы убедиться, что других корней нет, достаточно доказать, что у функции 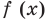не больше трех промежутков возрастания или убывания; а учитывая непрерывность 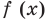на всей числовой прямой, для этого достаточно доказать, что у нее не больше двух критических точек, то есть уравнение 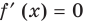имеет не больше двух корней. Рассматривая теперь уравнение 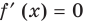мы после его преобразования можем провести аналогичные рассуждения, но уже для двух корней (как это было сделано в примере на с. 139). Выполняя преобразования уравнения 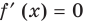, учтем, что все его члены имеют одинаковую степень — 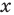(то есть оно является однородным относительно трех функций от переменной 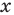, а именно: 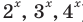). Делением обеих частей уравнения 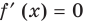на степень с основанием 2, 3 или 4 удается уменьшить количество выражений с переменной на одно.

Решение:

Данное уравнение равносильно уравнению 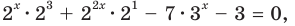то есть,

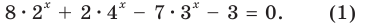
Обозначим 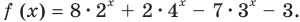Так как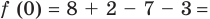

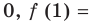
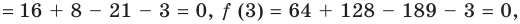то уравнение 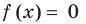имеет три корня: 0, 1, 3. Докажем, что других корней уравнение (1) не имеет. Для этого достаточно доказать, что у функции 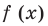есть не больше трех промежутков возрастания или убывания, а учитывая непрерывность функции 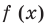на всей числовой прямой, достаточно доказать, что функция имеет не больше двух критических точек. Область определения: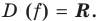

Производная 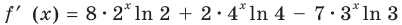существует при всех значениях 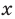. Следовательно, критическим и точкам и могут быть только те значения 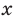, при которых 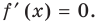Получаем уравнение

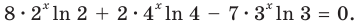
Поскольку 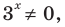то после деления обеих частей последнего уравнения на 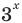получаем равносильное уравнение

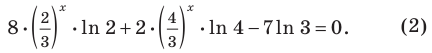
Чтобы доказать, что уравнение (2) имеет не больше двух корней, достаточно доказать, что функция 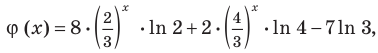стоящая в левой части уравнения, имеет не больше двух промежутков возрастания или убывания. Учитывая непрерывность этой функции на всей числовой прямой, достаточно доказать, что она имеет только одну критическую точку. Действительно, 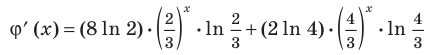существует при всех значениях 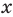. Следовательно, критическими точками могут быть только те значения 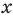, при которых 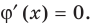Получаем однородное уравнение

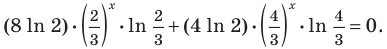
Поскольку 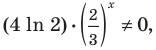то после деления обеих частей уравнения на это выражение получаем равносильное уравнение 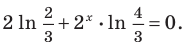Отсюда 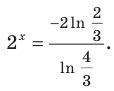. Учитывая, что 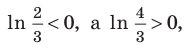получаем: 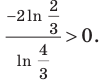Следовательно, последнее уравнение имеет единственный корень. Тогда функция 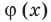имеет единственную критическую точку, поэтому уравнение (2) имеет не больше двух корней. Это означает, что функция 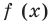имеет не больше двух критических точек. Тогда уравнение (1) (а значит, и данное уравнение) имеет не больше трех корней. Но три корня данного уравнения мы уже знаем: 0, 1, 3, следовательно, других корней данное уравнение не имеет. Ответ: 0, 1, 3.

• Заказать решение задач по высшей математике

Производные показательной и логарифмической функций – формулы и доказательство

Докажем следующие формулы производных:

1. Пусть дана функция 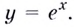 Зафиксируем произвольное значение  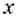её аргумента и дадим ему приращение  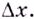Тогда приращение функции

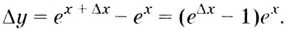
Следовательно,

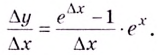
Если 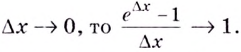 Это следует из того, что угловой коэффициент касательной к графику функции  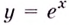в точке  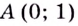равен 1 рис. 22. В математическом анализе доказывают следующее утверждение: если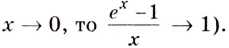  

Если значение 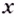 зафиксировано, то когда  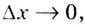значение  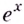не меняется. Следовательно, если  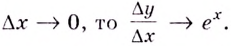Это и означает, что функция  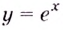дифференцируема в каждой точке  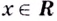и

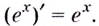
2.Как известно, при каждом 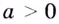 выполняется равенство  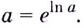Поэтому

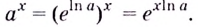
По теореме о производной сложной функции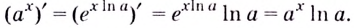

Итак, формула 2 доказана.

3.    Если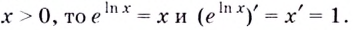 

А по теореме о производной сложной функции 

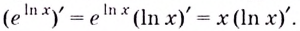
Следовательно, 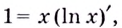 отсюда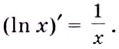 

4. При каждом 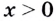 по формуле перехода

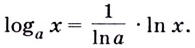
Следовательно,

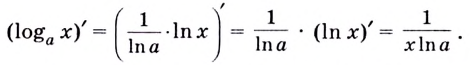
По доказанным формулам можно находить производные любых показательных или логарифмических функций, а значит, и исследовать эти функции.

Обратите внимание! Если функция содержит логарифм сложного выражения, то прежде чем находить её производную, целесообразно это выражение прологарифмировать.

Пример №7

Найдите производную функции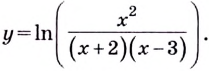 

Решение:

 

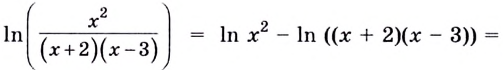
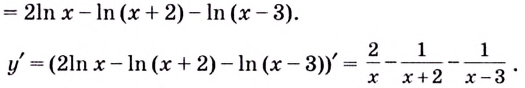
Теперь можно вывести формулу производной степенной функции 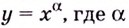 — произвольное действительное число. Если  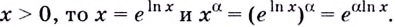Поэтому

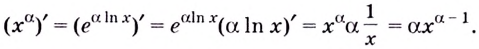
Итак, формула 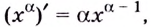 доказанная ранее только для натурального показателя степени  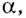верна и для любого действительного  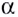и положительного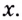 

 Формулу для нахождения производной логарифмической функции можно вывести иначе, используя тот факт, что функция 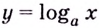 обратная к функции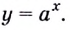 

Выясним, как связаны между собой производные взаимно обратных функций.

Теорема. Если функция 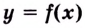 обратима (строго монотонная) на интервале  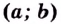и имеет отличную от нуля производную  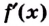в произвольной точке этого интервала, тогда существует обратная функция  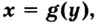которая также имеет производную  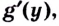причём:

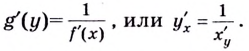
Обоснуем эти формулы, используя геометрический смысл производной. 

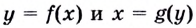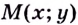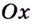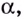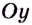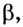Пусть   — взаимно обратные функции. Тогда они задают одну и ту же кривую (рис. 69). Если касательная к этой кривой в точке  образует с осью  угол  а с осью  угол  то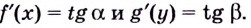 
Поскольку 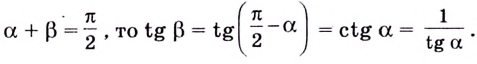 Из этого соотношения следует, что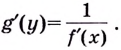 
Строгое доказательство этой теоремы рассматривается в университетском курсе математического анализа.

Применим формулу 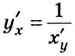 для дифференцирования функции  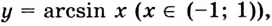обратной к функции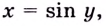  

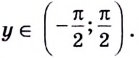
Получим: 

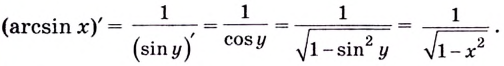
Пример №8

Найдите производную функции:

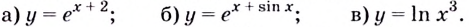
Решение:

 

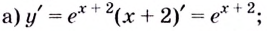
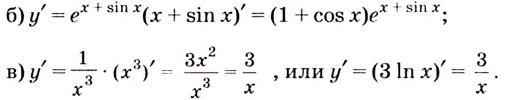
Пример №9

Запишите уравнение касательной к графику функции 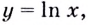 если точка касания имеет ординату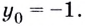 

Решение:

Найдём абсциссу точки касания: 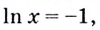 отсюда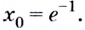 

Найдём производную функции 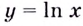 и её значение в точке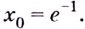 

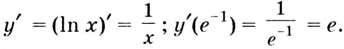
Уравнение касательной запишем в виде 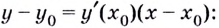 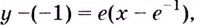или 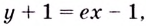 отсюда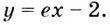 

Пример №10

Найдите производную функции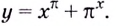 

Решение:

Заданная функция является суммой степенной и показательной функций. Для нахождения её производной воспользуемся соответствующими формулами: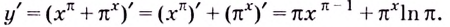 

Определение производной показательной и логарифмической функций

Существует ли функция, производная которой равна самой функции? Ответить на этот вопрос легко. Например, функция, которая является нулевой константой, обладает этим свойством.

А можно ли указать такую функцию 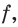определенную на 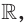отличную от нулевой константы, чтобы 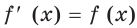для любого 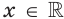? Ответ на этот вопрос неочевиден.

Оказывается, что среди показательных функций 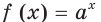существует единственная функция такая, что 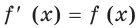для всех 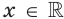. Для этой функции число, которое является

основанием степени, обозначают буквой 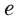, а сама функция имеет вид 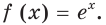Следовательно,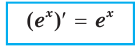

Установлено, что число 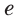— иррациональное. Его можно записать в виде бесконечной непериодической десятичной дроби: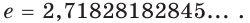

Функцию 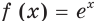называют экспонентой.

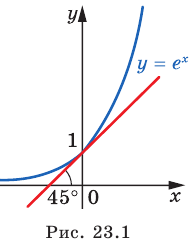
Отметим одну особенность графика экспоненты.

Имеем: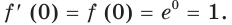

Следовательно, касательная к графику экспоненты в точке с абсциссой, равной нулю, имеет угловой коэффициент, равный 1. То есть эта касательная образует угол 45° с положительным направлением оси абсцисс (рис. 23.1).

Выведем формулу для нахождения производной показательной функции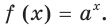

Имеем: 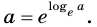Тогда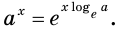

Пользуясь правилом вычисления производной сложной функции, запишем: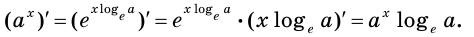

Логарифм по основанию 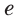называют натуральным логарифмом и обозначают 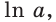то есть 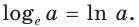Тогда при 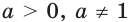можно записать:

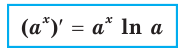
Эта формула показывает, что между значением производной показательной функции и соответствующим значением самой функции существует прямая пропорциональная зависимость. Коэффициент пропорциональности равен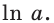

В пункте 20 мы определили, что логарифмическая функция 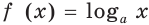является дифференцируемой. Найдем формулу для вычисления производной логарифмической функции.

Для любого 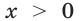выполняется равенство 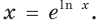Тогда функци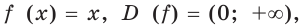и и 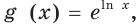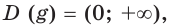представляют собой одну и ту же функцию. Поэтому для любого 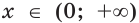выполняется равенство 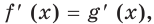то есть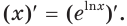

Левая часть этого равенства равна 1. В правой части получаем: 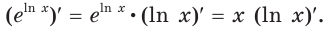Тогда 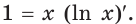Отсюда

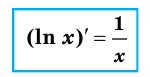
Имеем: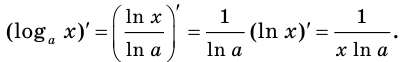

Следовательно,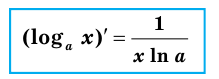

Пример №11

Найдите производную функции:

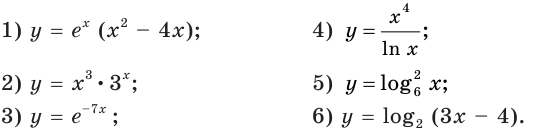
Решение:

1) Применяя теорему о производной произведения двух функций, получаем:

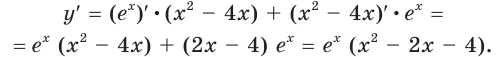
2) Имеем: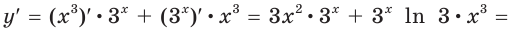

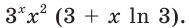
3) Используя теорему о производной сложной функции, запишем: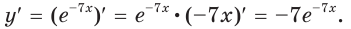

4) Имеем: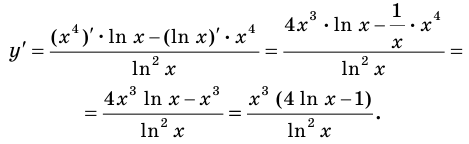

5) Применив теорему о производной сложной функции, получаем:

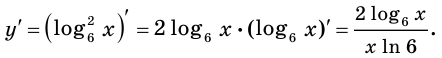
6) Имеем:

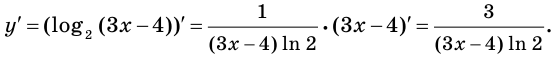
Пример №12

Составьте уравнение касательной к графику функции 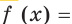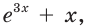если эта касательная параллельна прямой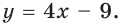

Решение:

Поскольку угловой коэффициент прямой 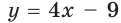равен 4, то угловой коэффициент искомой касательной 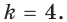Найдем абсциссу 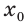точки касания. Имеем: 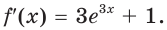Поскольку 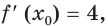то 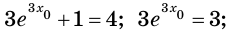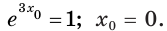Отсюда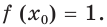

Тогда искомое уравнение имеет вид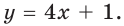

Ответ: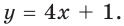

Ответ: у = 4х + 1.

Пример №13

Найдите промежутки возрастания и убывания и точки экстремума функции:

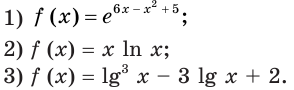
Решение:

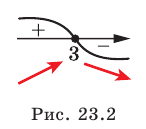
1) Имеем: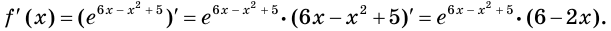

Исследовав знак производной функции 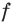(рис. 23.2), получаем, что функция 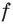возрастает на промежутке 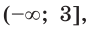убывает на промежутке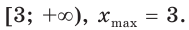

2) Имеем: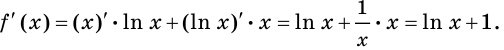

Исследуем знак 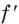на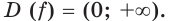

Имеем: 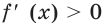при 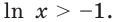Отсюда 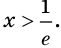Аналогично находим, что 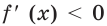при

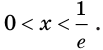
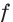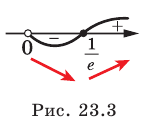
Получаем, что функция возрастает на промежутке 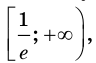убывает на промежутке 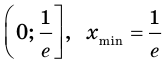(рис. 23.3).

3) Имеем:

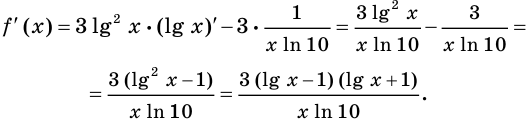
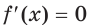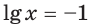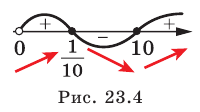
Тогда при или 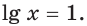Следовательно, данная функция имеет две критические точки: 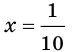и И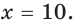сследовав знак производной функции 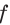на 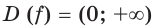(рис. 23.4), приходим к выводу, что функция 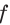возрастает на промежутках 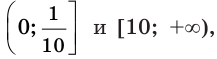убывает на промежутке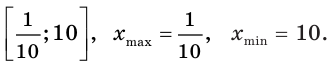

Пример №14

Докажите, что: 1) показательная функция 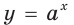является выпуклой вниз; 2) при 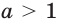логарифмическая функция 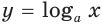является выпуклой вверх, а при 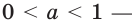выпуклой вниз.

Решение:

1) Имеем:

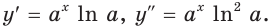
Поскольку для всех 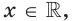то показательная функция 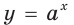является выпуклой вниз.

2) Запишем: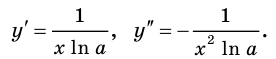

Если 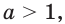то 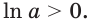Поэтому 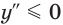для всех 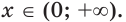Следовательно, при 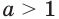логарифмическая функция 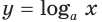является выпуклой вверх.

При 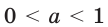аналогично доказываем, что 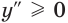и логарифмическая функция 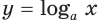является выпуклой вниз.

Содержание:

• Суть метода логарифмического дифференцирования
• Производная показательно-степенной функции

Для функций вида $y(x)=frac{u_{1}(x) cdot u_{2}(x) cdot ldots cdot u_{k}(x)}{v_{1}(x) cdot v_{2}(x) cdot ldots cdot v_{m}(x)}$ для упрощения нахождения
производной рациональнее использовать логарифмическое дифференцирование.

Суть метода логарифмического дифференцирования

Суть такого дифференцирования заключается в следующем: вначале находится
логарифм заданной функции, а уже затем
вычисляется от него производная. Пусть задана некоторая функция
$y=f(x)$. Прологарифмируем левую и правую части данного выражения:

$$ln y=ln f(x)$$

Далее продифференцируем полученное равенство при условии, что
$y$ является функцией от $x$, то есть найдем
производную сложной функции:

$$(ln y)^{prime}=(ln f(x))^{prime} Rightarrow frac{1}{y} cdot y^{prime}=(ln f(x))^{prime}$$

А тогда, выражая искомую производную $y^{prime}$, в
результате имеем:

$$y^{prime}=y cdot(ln f(x))^{prime}$$

Производная показательно-степенной функции

Рационально использовать логарифмическое дифференцирование и при нахождении
производной показательно-степенной
(или степенно-показательной) функции или “функции в степени функция”, то есть в случае, когда заданная функция имеет
вид $y(x)=u(x)^{v(x)}$. Логарифмируем левую и правую часть:

$$ln y(x)=ln u(x)^{v(x)}$$
$$ln y(x)=v(x) cdot ln u(x)$$

Тогда

$$(ln y(x))^{prime}=(v(x) cdot ln u(x))^{prime}$$

Производную в левой части равенства находим как производную сложной функции, а в правой – как производную произведения:

$$begin{array}{c}
frac{y^{prime}(x)}{y(x)}=v^{prime}(x) cdot ln u(x)+v(x) cdot frac{u^{prime}(x)}{u(x)} Rightarrow \
Rightarrow y^{prime}(x)=y(x) cdotleft(v^{prime}(x) cdot ln u(x)+v(x) cdot frac{u^{prime}(x)}{u(x)}right)
end{array}$$

Читать дальше: производная степенно-показательной функции.