Формула производной от дроби, примеры
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Формула производной от дроби
Раздел о производных является отдельным самостоятельным разделом в математическом анализе. Условимся, что читателю известно понятия предела, производной, дифференциала, а также ряд свойств производной.
В данной статье рассмотрим одно из свойств производной, а именно формулу производной от дроби. Приведём эту формулу. Пусть функция $v(x)$ имеет производную в точке $x$ и $v(x)neq0$, тогда:
$(frac{u}{v})’=frac{u’v-uv’}{v^2}.$
Напомним формулы производных элементарных функций:
Рисунок 1. Формулы производных элементарных функций. Автор24 — интернет-биржа студенческих работ
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Примеры
Решим примеры. Преобразования, позволяющие применить другие свойства производной, мы применять не будем. В решениях будем использовать только формулу производной от дроби.
По условию даются функции. Нужно найти производные.
Пример 1
Рисунок 2. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 3. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 4. Пример. Автор24 — интернет-биржа студенческих работ
Пример 2
Рисунок 5. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 6. Пример. Автор24 — интернет-биржа студенческих работ
Пример 3
Рисунок 7. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 8. Пример. Автор24 — интернет-биржа студенческих работ
Пример 4
Рисунок 9. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 10. Пример. Автор24 — интернет-биржа студенческих работ
Пример 5
Рисунок 11.
Рисунок 12. Пример. Автор24 — интернет-биржа студенческих работ
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 15.05.2023
Один из важнейших разделов математики – производные. Для их нахождения существуют специальные формулы производных. Для работы с ними необходимо знать основные формулы элементарных функций.
Таблица формул производных
Ниже приведена таблица формул производных элементарных функций.
| [C^{prime}=0] | [(ln ln x)^{prime}=frac{1}{x}] |
| [x^{prime}=1] | [(sin sin x)^{prime}=cos cos x] |
| [left(x^{2}right)^{prime}=2 x] | [(cos cos x)^{prime}=-sin sin x] |
| [left(x^{n}right)^{prime}=n * x^{n-1}] | [(operatorname{tg} x)^{prime}=frac{1}{cos ^{2}(x)}] |
| [left(a^{x}right)^{prime}=a^{x} * ln (a)] | [(operatorname{ctg} x)^{prime}=-frac{1}{sin ^{2}(x)}] |
| [left(e^{x}right)^{prime}=e^{x}] | [(arcsin arcsin x)^{prime}=frac{1}{sqrt{1-x^{2}}}] |
| [(x)^{prime}=frac{1}{x * ln (a)}] | [begin{aligned} (arccos &arccos x)^{prime} &=-frac{1}{sqrt{1-x^{2}}} end{aligned}] |
| [(operatorname{arctg} x)^{prime}=frac{1}{1+x^{2}}] | [(operatorname{arcctg} x)^{prime}=-frac{1}{1+x^{2}}] |
Смысл производной
В математике производная имеет геометрический и физический смыслы.
Допустим, что некоторая функция f(x) задана в интервале (a, b). При этом есть две точки x и x0, которые находятся в указанном интервале. Если значение x будет изменяться, то и f(x) тоже изменится. Изменение аргумента находится из выражения (x – x0). Эта разность обозначается как Δx – приращение аргумента. В таком случае приращением функции будет являться разность между ее значениями в двух точках. Исходя из этого, можно дать определение производной. Ей называется предел отношения приращения функции к приращению аргумента в указанной точке. При этом сам аргумент стремится к нулю.
В математике формулы производных функций записываются так:
[begin{gathered}
f^{prime}left(x_{0}right)=left(frac{fleft(x_{0}+Delta xright)-fleft(x_{0}right)}{Delta x}right). \
y^{prime}left(x_{0}right)=lim _{Delta x rightarrow 0}left(frac{Delta y}{Delta x}right) .
end{gathered}]
Смысл этих формул, а точнее нахождения их значений, может быть описан с точки зрения геометрии и физики.
Геометрический смысл состоит в том, что производная функции в конкретной точке равняется тангенсу угла, который образован осью абсцисс и касательной линией к графику. Пример показан на рисунке ниже.
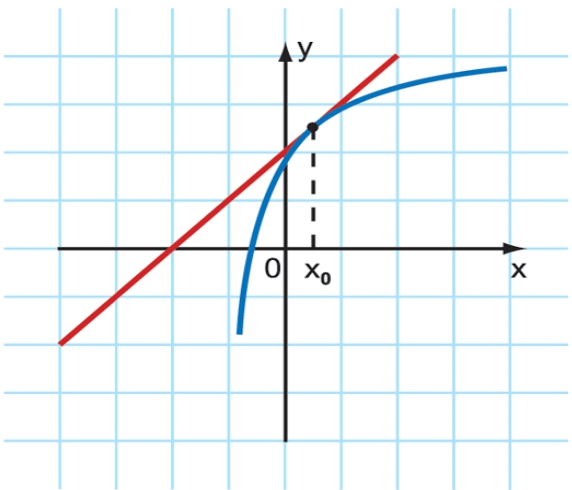
В физике смысл состоит в том, что производная от пройденного расстояния по времени есть скорость движения точки.
Нет времени решать самому?
Наши эксперты помогут!
Формула вычисления производной дроби
Рассмотрим формулу вычисления производной дроби. Функция v(x) имеет производную в определенной точке x. При этом v(x) не равна нулю (v(x) ≠ 0). В таком случае справедлива следующая формула:
[left(frac{u}{v}right)^{prime}=frac{u^{prime} v-u v^{prime}}{v^{2}}]
Рассмотрим примеры использования формулы производной дроби при решении задач.
Примеры 1 — 2
Первый пример с выражениями из тригонометрии: [y=frac{cos cos x}{x^{2}}]
Пользуясь таблицей 1 найдем:
[begin{gathered}
y^{prime}=frac{left.(cos cos x)^{prime} * (x^{2}-xright) *left(x^{2}right)^{prime}}{left(x^{2}right)^{2}} =\
frac{(-sin sin x) * x^{2}-(cos cos x) * 2 x}{x^{4}} .
end{gathered}]
Вынесем x за скобки и преобразуем полученное выражение: [y^{prime}=frac{(-sin sin x) * x-2 cos cos x}{x^{3}}]
Другой пример:
[begin{gathered}
y=frac{x^{3}}{x^{3}+2} \
y^{prime}=frac{left(x^{3}right)^{prime} *left(x^{3}+2right)-x^{3} *left(x^{3}+2right)^{prime}}{left(x^{3}+2right)^{2}} \
y^{prime}=frac{3 x^{2} *left(x^{3}+2right)-x^{3} * 3 x^{2}}{left(x^{3}+2right)^{2}} \
y^{prime}=frac{3 x^{5}+6 x^{2}-3 x^{5}}{left(x^{3}+2right)^{2}}=frac{6 x^{2}}{left(x^{3}+2right)^{2}}
end{gathered}]
Решение примеров на нахождение производных в математике называется дифференцированием. Они бывают двух типов:
- частными;
- полными.
Между этими типами есть одно основное отличие. При нахождении частной производной функция аппроксимируется только по одному аргументу. Так во всех предыдущих примерах аппроксимация производилась только по x.
Производная дроби
Производная дроби равна произведению производной числителя на знаменатель минус произведение числителя на производную знаменателя и всё делить на квадрат знаменателя:
$$ bigg (frac{u}{v} bigg )’ = frac{u’v-uv’}{v^2} $$
Следует понимать, что производная дроби НЕ РАВНА отношению производных числителя и знаменателя!
Примеры с решением
| Пример 1 |
| Найти производную дроби $ y = frac{x}{ln x} $ |
| Решение |
|
Из формулы следует, что числитель $$ u = x $$ а знаменатель $$ v = ln x $$ Находим их производные: $$ u’ = (x)’ = 1 $$ $$ v’ = (ln x)’ = frac{1}{x} $$ Подставляем найденные $ u’ $ и $ v’ $ в формулу производной дроби: $$ y’=bigg (frac{x}{ln x} bigg )’ = frac{(x)’ln x – x(ln x)’}{(ln x)^2} = $$ $$ = frac{ln x – x frac{1}{x}}{ln^2 x} = frac{ln x – 1}{ln^2 x} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ y’ = frac{ln x – 1}{ln^2 x} $$ |
| Пример 2 |
| Найти производную от дроби $ y = frac{cos x}{x} $ |
| Решение |
|
По формуле производной частного: $$ y’=bigg (frac{cos x}{x} bigg ) = frac{(cos x)’x-cos x (x)’}{(x)^2} = $$ Производная косинуса равна отрицательному синусу: $$ (cos x)’ = -sin x $$ Тогда: $$ y’ = frac{-xsin x – cos x}{x^2} = -frac{xsin x + cos x}{x^2} $$ |
| Ответ |
| $$ y’ = -frac{xsin x + cos x}{x^2} $$ |
Производная дроби – что это такое
Определение
Производная дроби – это значение, которое получается, если производную числителя умножить на знаменатель и прибавить числитель, умноженный на производную знаменателя, а затем все это разделить на квадрат знаменателя.
Формула производной от дроби
Формула ПД имеет следующий вид:
(left(fracupsilonnuright)’=frac{upsilon’nu-upsilonnu’}{v^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
При этом важно отметить, что нахождение ПД нельзя осуществлять с помощью деления производной числителя на производную знаменателя. Два эти действия будут иметь разные значения после подсчетов.
Приведем доказательство данной формулы. Рассмотрим выражение y=fracupsilonnu. Все представленные переменные – это функции от х. Умножим их на (nu). Получим (ytimesnu=upsilon).
Дифференцируем по х, применяя формулу производной произведения двух функций, то есть:
(left(upsilontimesnuright)’=upsilon’timesnu+upsilontimesnu’)
Тогда выводим:
(y’timesnu+ytimesnu’=upsilon’)
Из этого вычисляем нужную нам производную:
(y’timesnu=upsilon’-ytimesnu’=upsilon’-fracupsilonnutimesnu’=frac{upsilon’v-upsilonnu’}nu;;y’=frac{upsilon’v-upsilonnu’}{nu^2})
Что и требовалось доказать.
Следует также привести таблицу с производными часто встречающихся функций:
Как решать производные функции с дробями, примеры
Чтобы понять, как решать ПФ с дробями, приведем несколько примеров.
Пример 1
Найти производную дроби (y=frac x{In;x}.)
Решение
Из формулы следует, что числитель (upsilon=х), а знаменатель (nu=In;х). Найдем их производные:
(upsilon’=left(хright)’=1,;nu’=left(In;xright)’=frac1x)
Подставляем решенные (upsilon’;и;nu’) в формулу и получаем:
( y’=left(frac x{In;x}right)’=frac{left(xright)’In;x-xleft(In;xright)’}{left(In;xright)^2}=frac{In;x;-x{displaystylefrac1x}}{In^2x}=frac{In;x-1}{In^2x})
Ответ: (y’=frac{In;x-1}{In^2x}.)
Пример 2
Найти производную дроби, равную (y=frac{cos;x}x).
Решение
По формуле производной частного:
(y’=left(frac{cos;x}xright)=frac{left(cos;xright)’x-cos;xleft(xright)’}{left(xright)^2})
Производная косинуса дает нам синус с минусом:
(left(cos;xright)’=-sin;x)
В таком случае:
(y’=frac{-x;sin;x-cos;x}{x^2}=-frac{x;sin;x+cos;x}{x^2})
Ответ: (y’=-frac{x;sin;x+cos;x}{x^2}.)
Пример 3
Найти производную дроби (yleft(xright)=frac{e^x-1}{e^x+1}.)
Решение
Из таблицы производных находим:
(left(e^xright)’=e^x)
Применяем правила дифференцирования постоянной и суммы:
(left(e^x-1right)’=left(e^xright)’-left(1right)’=e^x-0=e^x;;left(e^x+1right)’=left(e^xright)’+left(1right)’=e^x-0=e^x)
Используем формулу производной дроби:
(left(fracupsilonnuright)’=frac{upsilon’nu-upsilonnu’}{nu^2};left(frac{e^x-1}{e^x+1}right)’=frac1{left(e^x+1right)^2}timeslbrackleft(e^x-1right)’left(e^x+1right)-left(e^x-1right)left(e^x+1right)’rbrack=frac1{left(e^x+1right)^2}timeslbrack e^xleft(e^x+1right)-left(e^x-1right)e^xrbrack=frac{2e^x}{left(e^x+1right)^2})
Ответ: (y’=frac{2e^x}{left(e^x+1right)^2}.)
2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
При этом важно отметить, что нахождение ПД нельзя осуществлять с помощью деления производной числителя на производную знаменателя. Два эти действия будут иметь разные значения после подсчетов.
Приведем доказательство данной формулы. Рассмотрим выражение y=fracupsilonnu. Все представленные переменные – это функции от х. Умножим их на (nu). Получим (ytimesnu=upsilon).
Дифференцируем по х, применяя формулу производной произведения двух функций, то есть:
(left(upsilontimesnuright)’=upsilon’timesnu+upsilontimesnu’)
Тогда выводим:
(y’timesnu+ytimesnu’=upsilon’)
Из этого вычисляем нужную нам производную:
(y’timesnu=upsilon’-ytimesnu’=upsilon’-fracupsilonnutimesnu’=frac{upsilon’v-upsilonnu’}nu;;y’=frac{upsilon’v-upsilonnu’}{nu^2})
Что и требовалось доказать. 2}.)
Чему равна производная дроби. Как найти производную от дроби
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x)
, заданная в некотором интервале (a, b)
. Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0
. Эта разность записывается как дельта икс
и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной:
производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t)
и времени t
. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0
нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте
.
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций.
То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.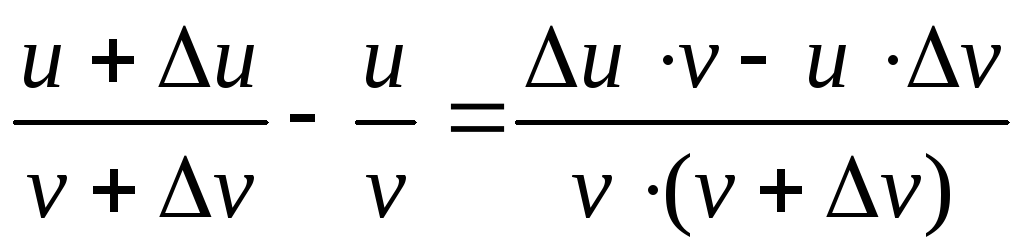
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Определение.
Пусть функция (y = f(x) ) определена в некотором интервале, содержащем внутри себя точку (x_0 ).
Дадим аргументу приращение (Delta x ) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции
(Delta y ) (при переходе от точки (x_0 ) к точке (x_0 + Delta x )) и составим отношение
(frac{Delta y}{Delta x} ). Если существует предел этого отношения при (Delta x rightarrow 0 ), то
указанный предел называют производной функции
(y=f(x) ) в точке (x_0 ) и обозначают (f»(x_0) ).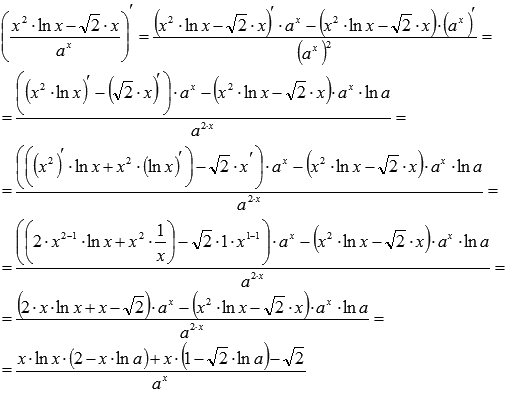
$$ lim_{Delta x to 0} frac{Delta y}{Delta x} = f»(x_0) $$
Для обозначения производной часто используют символ y».
Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых
существует указанный выше предел. Эту функцию называют так: производная функции у = f(x)
.
Геометрический смысл производной
состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно
провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
(k = f»(a) )
Поскольку (k = tg(a) ), то верно равенство (f»(a) = tg(a) ) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция (y = f(x) ) имеет
производную в конкретной точке (x ):
$$ lim_{Delta x to 0} frac{Delta y}{Delta x} = f»(x) $$
Это означает, что около точки х выполняется приближенное равенство (frac{Delta y}{Delta x} approx f»(x) ), т.
2 ) справедливо приближенное равенство (Delta y approx 2x cdot Delta x ).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение (x ), найти (f(x) )
2. Дать аргументу (x ) приращение (Delta x ), перейти в новую точку (x+ Delta x ), найти (f(x+ Delta x) )
3. Найти приращение функции: (Delta y = f(x + Delta x) — f(x) )
4. Составить отношение (frac{Delta y}{Delta x} )
5. Вычислить $$ lim_{Delta x to 0} frac{Delta y}{Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной
функции у = f(x) называют дифференцированием
функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную,
причем, напомним, угловой коэффициент касательной равен f»(x). Такой график не может «разрываться» в точке М, т. е. функция
обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то
выполняется приближенное равенство (Delta y approx f»(x) cdot Delta x ). Если в этом равенстве (Delta x ) устремить к
нулю, то и (Delta y ) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке
.
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция (y=sqrt{x} ) непрерывна на всей числовой прямой, в том числе в точке х = 0.
И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у,
т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и
(f»(0) )
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее
дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси
абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она
перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием
.
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями.
2} $$
Вычисление производной
— одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:
- Таблица производных экспоненциальных и логарифмических функций
Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена «шпаргалка» основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.
Производные простых функций
1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0
Пояснение
:
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.
2. Производная переменной
равна единице
x´ = 1
Пояснение
:
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение
:
В данном случае, при каждом изменении аргумента функции (х
) ее значение (y) растет в с
раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с
.
Откуда следует, что
(cx + b)» = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю
равна частному этой переменной к ее модулю
|x|»
= x / |x| при условии, что х ≠ 0
Пояснение
:
Поскольку производная переменной (см.
формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени
равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)»= cx c-1
, при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)» = 2x
(x 3)» = 3x 2
Для запоминания формулы
:
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х.
То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.
6. Производная дроби
1/х
(1/х)» = — 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)» = (x -1)» , тогда можно применить формулу из правила 5 таблицы производных
(x -1)» = -1x -2 = — 1 / х 2
7. Производная дроби
с переменной произвольной степени
в знаменателе
(1 / x c)» =
— c / x c+1
Пример:
(1 / x 2)» = — 2 / x 3
8. Производная корня
(производная переменной под квадратным корнем)
(√x)» = 1 / (2√x)
или 1/2 х -1/2
Пример:
(√x)» = (х 1/2)» значит можно применить формулу из правила 5
(х 1/2)» = 1/2 х -1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
(n √x)» = 1 / (n n √x n-1)
Исчисление
— Как найти производную дроби?
спросил
8 лет, 4 месяца назад
Изменено
8 лет, 4 месяца назад
Просмотрено
111 тысяч раз
$begingroup$
Итак, у меня есть интересная задача, над которой я работал два дня: 97$ найти $f'(t)$, чем найти $f'(2)$.
Как преобразовать эту задачу в более читаемый формат? (без дробей и деления), иначе, как мне составить его с дробями?
Спасибо
- исчисление
- пределы
- производные
$endgroup$
$begingroup$
Я вижу, что были представлены некоторые методы перезаписи, и в данном случае это самый простой и быстрый метод. Но его также можно решить как дробь, используя правило частных, поэтому для справки здесь приведен действительный метод решения его как дроби. 9{-7-1})$$
Сможете ли вы выполнить это?
$endgroup$
5
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
