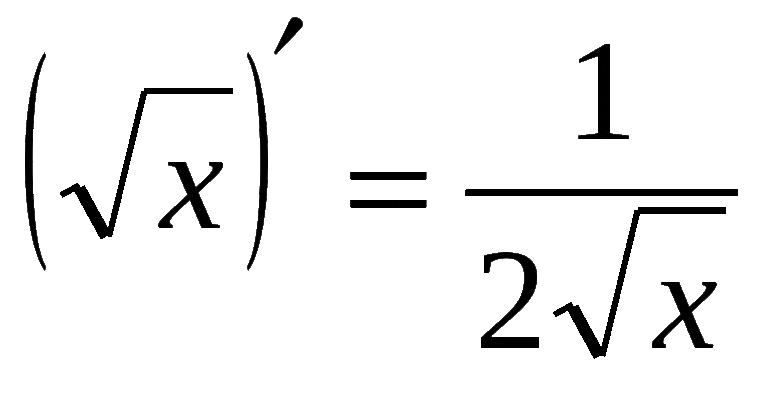Загрузить PDF
Загрузить PDF
На курсах дифференциального исчисления вы наверняка учили правила дифференцирования основных функций, в том числе правило дифференцирования степенной функции. Однако если функция содержит квадратный или другой корень, например 
, может показаться, что данное правило не подходит. Тем не менее достаточно переписать ее в степенном виде, чтобы получить очевидный ответ. Если функция содержит несколько корней, такую подстановку можно делать сколько угодно раз и использовать правило дифференцирования сложной функции.
-
1
Вспомните правило дифференцирования степенной функции. Обычно это правило учат в самом начале курса дифференциального исчисления. Оно гласит, что производная переменной
, возведенной в степень , равна:[1]
-
2
-
3
Примените правило дифференцирования степенной функции. Если под корнем стоит переменная x,
, производная берется следующим образом:[3]
-
4
Упростите результат. На этом этапе необходимо вспомнить, что при отрицательной степени следует найти число, обратное данному числу в той же положительной степени. Степень
означает, что квадратный корень следует поставить в знаменателе дроби.[4]
Реклама
-
1
Вспомните правило дифференцирования сложных функций. Это правило применяется в тех случаях, когда необходимо продифференцировать функцию, аргументом которой выступает другая функция. Согласно данному правилу, комбинация двух функций,
и , дифференцируется следующим образом:[5]
-
2
Определите функции. При использовании правила дифференцирования сложных функций первым делом следует выявить комбинацию функций. В случае квадратного корня в роли внешней функции
выступает взятие корня, а внутренней функцией является то, что стоит под знаком корня.[6]
-
3
Найдите производные обеих функций. Чтобы применить правило дифференцирования сложных функций к квадратному корню, сначала следует найти производную квадратного корня:[7]
-
4
Реклама
-
1
Запомните простое правило дифференцирования любых квадратных корней. Если необходимо найти производную квадратного корня, под которым стоит переменная или функция, используйте следующее правило. Результат всегда будет представлять собой производную подкоренного выражения, поделенную на удвоенный первоначальный квадратный корень. Это можно записать следующим образом:[9]
-
2
Найдите производную подкоренного выражения. Как следует из названия, подкоренное выражение стоит под знаком квадратного корня. Чтобы применить данное правило, найдем производную этого выражения. Рассмотрим следующие примеры:[10]
-
3
Запишите производную подкоренного выражения в числителе дроби. Производная корня представляет собой дробь, в числителе которой стоит производная подкоренного выражения. Для приведенных выше функций получаем следующие выражения:[11]
-
4
Запишите знаменатель в виде удвоенного первоначального квадратного корня. Согласно данному правилу, в знаменателе следует написать удвоенный квадратный корень. Для приведенных выше функций получаем следующие знаменатели:[12]
-
5
Скомбинируем числитель и знаменатель и получим искомую производную. Запишите полную дробь, и у вас получится производная первоначальной функции:[13]
Реклама
Об этой статье
Эту страницу просматривали 52 258 раз.
Была ли эта статья полезной?
Производная корня
Опубликовано 10.07.2021
Производная корня из x – это формула определения производной функции, выраженной корнем из x или производной корня из выражения относительно x. Все производные смотрите в таблице производных.
Формула производной квадратного корня
Давайте выведем с вами формулу для производной корня для простой функции, опираясь на формулу производной степени :
,
То есть, получается, что формула производной корня: 
, где
Производная корня любой степени
Аналогично определим производную корня любой степени. Например, пусть нам нужно определить производную кубического корня иначе находим производную корня третьей степени из x.
Производная кубического корня
Определим производную корня кубического: . Запишем этот корень как степень от
. Получим
.
Находим производную:
![displaystyle (sqrt[3]{x^2})'=(x^{frac{2}{3}})'=frac{2}{3} cdot x^{frac{2}{3}-1}=frac{2}{3} cdot x^{-frac{1}{3}}](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-d6c3e357fc6da02b27538f28f112d685_l3.png "Rendered by QuickLaTeX.com")
или
![displaystyle (sqrt[3]{x^2})'=frac{2}{3 sqrt[3]{x}}](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-bf7745aa3d3a8553e2ae667731748f79_l3.png "Rendered by QuickLaTeX.com")
Примеры нахождения производной корня
Пример 1
Найдите производную функции: при
Решение: находим производную функции: , теперь подставим данное значение
. Получим
Пример 2
Найдите производную функции . То есть нам нужно узнать, какова будет производная корня четвертой степени из x.
Решение: представим корень в виде степени. Получим . Теперь легко можно найти производную, зная формулу производной степени.
![displaystyle f'(x)=(x^{frac{1}{4}})'=frac{1}{4} x^{frac{1}{4}-1}=frac{1}{4}x^{frac{-3}{4}}=frac{1}{4x^{frac{3}{4}}}=frac{1}{4 sqrt[4]{x^3}}](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-9010e8e042cffe58bc345b55f2d60efd_l3.png "Rendered by QuickLaTeX.com")
Таким образом, теперь легко определять производную корня любой степени, просто представляя сам корень в виде степени и зная формулу производной степени.
( 5 оценок, среднее 4.2 из 5 )
Содержание:
- Формула
- Примеры вычисления производной корня
Формула
$$(sqrt{x})^{prime}=frac{1}{2 sqrt{x}}$$
Производная от корня равна единице, деленной на два таких же корня.
Если под корнем находится сложная функция $u=u(x)$, то производная
от корня этой функции будет равна: единице, деленной на два таких же корня и умноженной на производную подкоренного выражения, то есть
$$(sqrt{u})^{prime}=frac{1}{2 sqrt{u}} cdot u^{prime}$$
Примеры вычисления производной корня
Пример
Задание. Найти производную функции $y(x)=2 sqrt{x}$
Решение. Искомая производная равна:
$$y^{prime}(x)=(2 sqrt{x})^{prime}$$
Согласно правилам дифференцирования, вынесем константу 2 за знак производной, в итоге будем иметь:
$$y^{prime}(x)=2 cdot(sqrt{x})^{prime}=2 cdot frac{1}{2 sqrt{x}}=frac{1}{sqrt{x}}$$
Ответ. $y^{prime}(x)=frac{1}{sqrt{x}}$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить производную функции $y(x)=sqrt{2 x}$
Решение. Искомая производная
$$y^{prime}(x)=(sqrt{2 x})$$
Находим как производную сложной функции, то есть вначале находим как производную от корня, а затем умножаем на производную
подкоренного выражения. В результате будем иметь:
$$y^{prime}(x)=(sqrt{2 x})^{prime}=frac{1}{2 sqrt{2 x}} cdot(2 x)^{prime}$$
Константу выносим за знак производной, а
производная независимой переменной равна единице, тогда получаем:
$$y^{prime}(x)=frac{1}{2 sqrt{2 x}} cdot 2 cdot(x)^{prime}=frac{1}{sqrt{2 x}} cdot 1=frac{1}{sqrt{2 x}}$$
Ответ. $y^{prime}(x)==frac{1}{sqrt{2 x}}$
Читать дальше: производная синуса (sinx)’.
Производная: корень из х
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
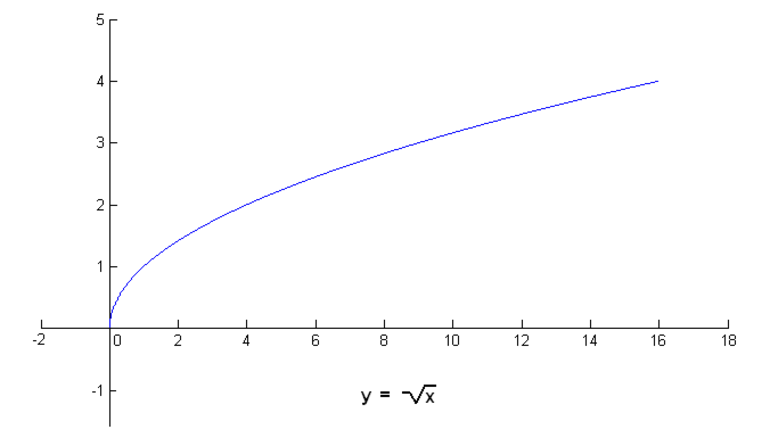
Найдём производную от функции игрек, равной квадратному корню из икс $y=sqrt{x}$.
Для этого проведём стандартную процедуру вывода формулы производной.
Сначала дадим функции y, равной $f(x)$ в точке x, приращение $Δx$:
$f(x+ Δx)=sqrt{x+ Δx}$.
Теперь рассмотрим, чему равно приращение $y$:
$Δy=f(x+Δx)-f(x)=sqrt{x+ Δx}- sqrt{x}$;
Из этого следует, что:
$frac{Δy}{ Δx}=frac{sqrt{x+ Δx}- sqrt{x}}{Δx}$.
Домножим всё полученное выражение на $(sqrt{x+ Δx}+ sqrt{x})$, в результате чего в числителе получается разность квадратов, равная $(x+ Δx)-x= Δx$, а дробь преображается до следующей формы:
$frac{Δy}{Δx}=frac{1}{sqrt{x+ Δx}+ sqrt{x}}$.
Теперь возьмём предел полученного отношения при $Δx to 0$:
$lim_{ Δx to 0}= frac{Δy}{Δx}=lim_{ Δx to 0}frac{1}{sqrt{x+ Δx}+ sqrt{x}}=frac{1}{sqrt{x}+sqrt{x}}=frac{1}{2sqrt{x}}$.
Таким образом, мы осуществили доказательство того, что производная корня из $x$ равна $frac{1}{2sqrt{x}}$:
$(sqrt{x})’=frac{1}{2 cdot sqrt{x}}$.
Формула для производной от икса под знаком кубического корня выглядит подобным образом:
$(sqrt[3]{x})’=frac{1}{3 cdot sqrt[3]{x^2}}$.
Пример 1
Продифференцируйте следующие функции:
-
$y=sqrt{x} – 9x^2$
-
$y=sqrt{x}-5x^2$.
Решение:
-
$(sqrt{x} – 9x^2)’=frac{1}{2sqrt{x}-18x}$;
-
$(sqrt{x}-5x^2)’=frac{1}{2sqrt{x}-10x}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 16.04.2023
Производная корень из Х – формулы и примеры вычислений
Понятие производной
Смысл производной основан на понятии предела функции. Состоит запись выражения из трёх частей, в одной из которых указывается, к чему стремится неизвестное. Оно может достигать как нуля, так и бесконечности. Таким образом, предел представляет собой динамическую величину. Например, пусть имеется некая функция f (x) = (1 + x) 1/x .
При иксе, который равен нулю, функция будет не определена, но можно исследовать, как она будет себя вести при приближении переменной к нулю. Для этого можно взять какое-либо значение икса и, подставив его в уравнение, вычислить функцию. Затем в формулу подставить иное произвольное число, но такое, чтобы оно было меньше предыдущего, то есть приближалось к нулю.
Выполнив несколько таких вычислений, можно увидеть, что значение функции начнёт приближаться к некой величине. Это значение и считается пределом рассматриваемого выражения при иксе, стремящемся к нулю.
Следует рассмотреть другую функцию: f (x) = 1 / x. Подставляя вместо икса различные числа, можно будет отметить, что при уменьшении исходной величины переменной числовое значение в ответе увеличивается, то есть результат функции ничем не ограничивается. Это означает, что при иксе, который стремится к нулю, предел будет равняться бесконечности.
Понятие предела помогает дать определение непрерывности. Функция f (x) непрерывна в точке x = c только тогда, когда знак предела и выражения можно поменять друг с другом местами: lim f (x) = f (lim x) = f с. Используя это свойство, можно определить точки разрыва и непрерывность. Зная определения можно понять, что представляет собой производная.
Пусть имеется линейная функция y = k * x + b, графиком которой будет прямая. При изменении икса на дельту по игреку будет происходить прирост на Δy = k * Δx. Получается, что величина k является скоростью роста функции: k = (f (x + Δx) — f (x)) / Δx. В этом случае график прямой имеет постоянный наклон, поэтому коэффициент k — константа.
Если же функция имеет произвольный вид, например, она состоит из сложного многочлена с дробями и квадратами, то, как вычислить постоянную k, непонятно. Вот тут на помощь и приходит понятие производной. Можно взять отношение дельта-икс на дельта-игрек и посмотреть, какой предел будет у функции: f'(x) = lim (f (x + Δx) — f (x)) / Δx. По сути, это действие и является нахождением производной.
Свойства корня
Находить производные подкоренных выражений невозможно без знания свойств степеней и корней. По определению, корнем квадратным из произвольного числа, которое больше нуля, называется такое неотрицательное число, которое при возведении в квадрат равняется этому числу.
То есть выражение √a = b тождественно равенству: b 2 = a. Например, √16 = 4, так как 4 2 = 16. Таким образом, можно утверждать, что корнем энной степени числа а будет такое выражение, которое при возведении в эту степень будет равняться а. Степень корня указывается в верхнем регистре значка, а основание записывается под знаком корня и называется подкоренным выражением.
Выделяют следующие свойства корней:
- Если подкоренное выражение представляет умножение неотрицательных чисел, то корень квадратный будет равняться произведению корней членов выражения: √ a * b * … * n = √ a * √ b * … * √ n.
- Когда под корнем находится отношение двух положительных чисел, то для решения выражения нужно извлечь корень из числителя и знаменателя, а после выполнить деление: √ a / b = √ a / b = √ a / √ b.
- В случае когда а больше или равняется нулю и при этом n является натуральным, то корень из подкоренного выражения будет равняться а в степени n: √ a 2 n = a n .
- При действительном числе и чётном значении показателей подкоренного выражения будет справедливым равенство: 2*m √ a 2*m = | a |. Если же показатель нечётный, то в ответе действительное число будет всегда положительное.
- При извлечении корня из корня n √ m √ действие можно заменить произведением показателей при неизменном подкоренном выражении.
- Сложение и вычитание корней возможно только в том случае, когда количественные или буквенные значения подкоренных выражений совпадают: n √ m + k √ m = (n + k) √ m.
- Умножить корни с одинаковыми показателями возможно лишь тогда, когда показатель у всех перемножаемых членов одинаков: √ n * √ m = √ n * m.
Для любой степени существует основная формула, по которой может быть найдена производная.
Выглядит она как (x n )’ = n * x n -1 . Эта формула используется и для дифференцирования корней. Кроме этого, для успешного решения задач на нахождение производной квадратного корня из х необходимо знать и свойства степеней.
Нахождение выражения из Х
В общем случае формула производной корня из х равна дроби, в числителе которой стоит единица, а в знаменателе произведение степени корня на корень той же степени в подкоренном выражении, где находится неизвестное, уменьшенное на единицу, в степени. Математически это теорема записывается следующей формулой: ( n √x)’ = 1 / (n * n √ x n -1 ).
Эта формула имеет название первообразной. Она подходит для использования в выражениях любой кратности. В качестве примера можно рассмотреть взятие производной квадратного и кубического корня.
Так, для квадратного степенного уравнения справедливо выражение: (n√x)’ = 1 / 2 * √x. То есть производная квадратного корня х является дробью, делимое которой равняется единице, а делитель состоит из двойки, умножаемой на квадратный корень из неизвестного.
Аналогично можно сформулировать теорему и для нахождения производной кубического корня из x. Для этого случая решением задания на вычисление производной будет дробь, в числителе которой находится единица, а в знаменателе произведение тройки на корень кубический из икса в степени два. Формула для вычисления выглядит следующим образом: ( 3 √x)’ = 1 / (3 3 √x 2 ).
Можно обратить внимание, что, по сути, операция сводится к таким же действиям, как и при возведении дробей в степень, когда делитель равняется тому же показателю.
Иными словами, вычисление производной коренного выражения сводится к использованию формул для нахождения функции дроби.
Для доказательства формул используют следующие рассуждения. Производная переменной под квадратным корнем это то же, что и нахождение функции при возведении многочлена в степень одна вторая: (√x)’ = (х ½ )’. Поэтому можно воспользоваться формулой для расчёта производной неизвестного числа в степени эн. А значит, запись вида (х ½ )’ = ½ х -½ = 1 / (2√х) будет верной.
Формула производной третьей степени доказывается по такому же принципу. Используя правило дифференцирования и переписав кубический корень как тройную степень, можно записать: ( 3 √x)’ = (х 1/3 )’ = 1 / 3 * (x- 2/3 ) = 1 / 3 * ( 3 √х 2 ). Тут следует отметить, что степень -2/3 образовывается путём вычитания единицы из дроби, в числителе которой стоит два, а в знаменателе три.
Примеры заданий
При взятии производной функции f (x) = n √х m необходимо привести корень к степенному виду: f (x)’ = ( n √х m )’ = x m/n .
Так как из производных степени известно, что (x m )’ = m * x m-1 , то и алгоритм решения для нахождения ответа коренного выражения сводится к преобразованию исходного уравнения путём перехода к степени: f (x)’ = ( n √х m )’ = (x m/n )’ = m/n * x ( m/n) -1 = (m/n * n √х m-n ).
Этот подход позволяет не запоминать сложную формулу, что часто и используется на практике.
Для закрепления теории следует решить несколько типовых примеров:
- Определить, чему будет равна производная от корня квадратного, кратного разности три минус икс в квадрате. Запись условия задачи выглядит так: (√ 3 — x 2 )’. Мысленно можно обозначить выражение в скобках буквой S. Получается, что задача будет состоять в поиске производной (√ S)’. Используя знание формулы, можно утверждать, что (√ S)’ = S’ / (2 * √ S). Ту же самую формулу можно будет получить, воспользовавшись преобразованием задания в степенную функцию: (√ S)’ = (S ½ ) ‘ = (½) * S (½ — 1 ) * S’ = S -½ * S’ / 2 = S’ / (2 * √ S). Таким образом, (√ 3 — x 2 )’ = (3 — x 2 )’ / (2 * √ 3 — x 2 ) = – 2* x / 2 * √ 3 — x 2 = – x / √ 3 — x 2 .
- Рассчитать, чему будет равна производная функции 1 / (2 * 3√ x7). Исходное выражение нужно преобразовать так, чтобы неизвестная оказалась в числителе, а затем уже воспользоваться стандартным алгоритмом: (1 / 2 * 3√ x7)’ = 1 / 2 * (x-7/3)’. Теперь нужно взять производную от степенной функции. В итоге получится выражение: 1 / 2 * (-7 / 3) * x (-7/3) — 1 = -(7 / 6) * x-10/3 = (-7 / 6) * (1 / 3√ x10).
- Необходимо найти производную суммы многочленов: p (x) = 3 + 4 √ x+3. По теореме дифференцирования ответ будет равняться сумме производных каждого члена равенства: p (x)’ = (3)’ + (4 √ x+3)’. Первое слагаемое равняется нулю, поэтому останется только найти производную корня. Используя снова правило производной, выражение можно переписать как 4 * (√ x+3)’. На следующем этапе многочлен в скобках нужно представить в виде степенной функции: (√x + 3)’ = 1 / ((2√x + 2)) * (x + 2)’ = 2 * (x +2)’ / √x+2. Так как производная суммы, это то же самое, что сумма производных, то будет верным записать: (4 √ x+2)’ = (2 / √x+2) *(<(x)’ + (2)’>). Производная для двойки равна нулю, поэтому плюсовать её смысла нет. В итоге получится: p (x)’ = (3 + 4 √ x+3)’ = 2/ √x +2 = 2 / √x +2.
Расчёт на онлайн-калькуляторе
Попрактиковавшись в решении различных примеров, найти производную корня простых выражений будет довольно просто. Но если в заданиях будут стоять двойные корни или сама функция будет содержать большой многочлен, могут возникнуть проблемы. Связаны они обычно не с алгоритмом решения, а с трудностью вычисления и преобразования.
Такого рода задачи требуют повышенного внимания и скрупулёзности в расчётах. При этом поиску ответа понадобится уделить довольно много времени. Поэтому для помощи в нахождении производных коренных функций и существуют в интернете математические онлайн-калькуляторы.
Это сервисы, предлагающие бесплатно услуги по автоматическому расчёту производной любой сложности. Воспользоваться ими может каждый желающий, имеющий доступ к интернету. Для нахождения ответа не нужно обладать какими-то особыми знаниями. Всё что требуется от пользователя — ввести в предложенную форму условие и нажать кнопку «Вычислить». Весь процесс расчёта займёт одну-две секунды.
При этом большинство сервисов, кроме предоставления ответа на своих страницах, дает возможность ознакомиться с теоретическим материалом и предлагает рассмотреть решения заданий различной сложности. Поэтому вопроса, каким образом получился тот или иной ответ, возникнуть не должно.
Из различных онлайн-калькуляторов, считающих производные, можно выделить следующие:
- Webmath.
- Kontrolnaya-rabota
- Onlinemschool.
- Сalc.
- Nauchniestati.
Сайты, используемые для вычислений, характеризуются интуитивно понятным интерфейсом, не содержащим нагромождения ненужной информации. На их страницах нет рекламного и вирусного кода.
Примечательно и то, что, выполнив пару вычислений, пользователь научится самостоятельно вычислять производную. А всё дело в том, что особенностью таких ресурсов является возможность обучения. Кроме непосредственно ответа, программа-расчётчик выдаст пошаговое вычисление с комментариями.
Кроме учащихся, онлайн-калькуляторы будут полезны и инженерам. Даже незначительная ошибка, допущенная в расчёте, приведёт к неверному ответу. В то же время при автоматических вычислениях появление ошибки исключено.
Производная корня икс
Формула
Производная от корня равна единице, деленной на два таких же корня.
Если под корнем находится сложная функция $u=u(x)$, то производная от корня этой функции будет равна: единице, деленной на два таких же корня и умноженной на производную подкоренного выражения, то есть
Примеры вычисления производной корня
Задание. Найти производную функции $y(x)=2 sqrt$
Решение. Искомая производная равна:
Согласно правилам дифференцирования, вынесем константу 2 за знак производной, в итоге будем иметь:
Найти производную: алгоритм и примеры решений
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную, надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного – в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
.
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
.
Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
.
Пример 2. Найти производную функции
.
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200. ), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего “икса”. Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной:
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций”.
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u‘v , в котором u – число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями”.
Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.
Пошаговые примеры – как найти производную
Пример 3. Найти производную функции
.
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
А проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями”.
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций”.
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на :
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Найти производные самостоятельно, а затем посмотреть решения
Пример 7. Найти производную функции
.
Пример 8. Найти производную функции
.
Пример 9. Найти производную функции
, где a и b – константы.
Пример 10. Найти производную функции
.
Пример 11. Найти производную функции
.
Ещё больше домашних заданий на нахождение производных
Продолжаем искать производные вместе
Пример 12. Найти производную функции
.
Решение. Применяя правила вычисления производной алгебраической суммы функций, вынесения постоянного множителя за знак производной и формулу производной степени (в таблице производных – под номером 3), получим
.
Пример 13. Найти производную функции
Решение. Применим правило дифференцирования произведения, а затем найдём производные сомножителей, так же, как в предыдущей задаче, пользуясь формулой 3 из таблицы производных. Тогда получим
Пример 14. Найти производную функции
Решение. Как и в примерах 4 и 6, применим правило дифференцирования частного:
Теперь вычислим производные в числителе и перед нами уже требуемый результат:
Пример 15.Найти производную функции
Шаг1. Применяем правило дифференцирования суммы:
Шаг2. Найдём производную первого слагаемого. Это табличная производная квадратного корня (в таблице производных – номер 5):
Шаг3. В частном знаменатель – также корень, только не квадратный. Поэтому преобразуем этот корень в степень:
и далее дифференцируем частное, не забывая, что число 2 в первом слагаемом числителя – это константа, производная которой равна нулю, и, следовательно всё первое слагаемое равно нулю:
Корень из константы, как не трудно догадаться, является также константой, а производная константы, как мы знаем из таблицы производных, равна нулю:
,
а производная, требуемая в условии задачи:
Ещё больше домашних заданий на нахождение производных
Напоминаем, что чуть более сложные примеры на производную произведения и частного – в статьях “Производная произведения и частного функций” и “Производная суммы дробей со степенями и корнями”.
Также настоятельно рекомендуем изучить производную сложной функции.
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/formules_10_6.php
http://function-x.ru/derivative.html
[/spoiler]
