Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью

Тема: Максимумы, минимумы функций
1. Изучить весь предложенный теоритический материал по данной теме и записать в тетрадь.
2. Рассмотреть пример 1,2 и записать в тетрадь.
3. Решить самостоятельно в тетради (отправить мне на эл. почту) – за третий пункт будет выставлена оценка!
1. Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
2. Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике ниже, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. y. Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке ниже, −5 точка минимума, а 1 – минимум (или экстремум – смотрим по ОУ).
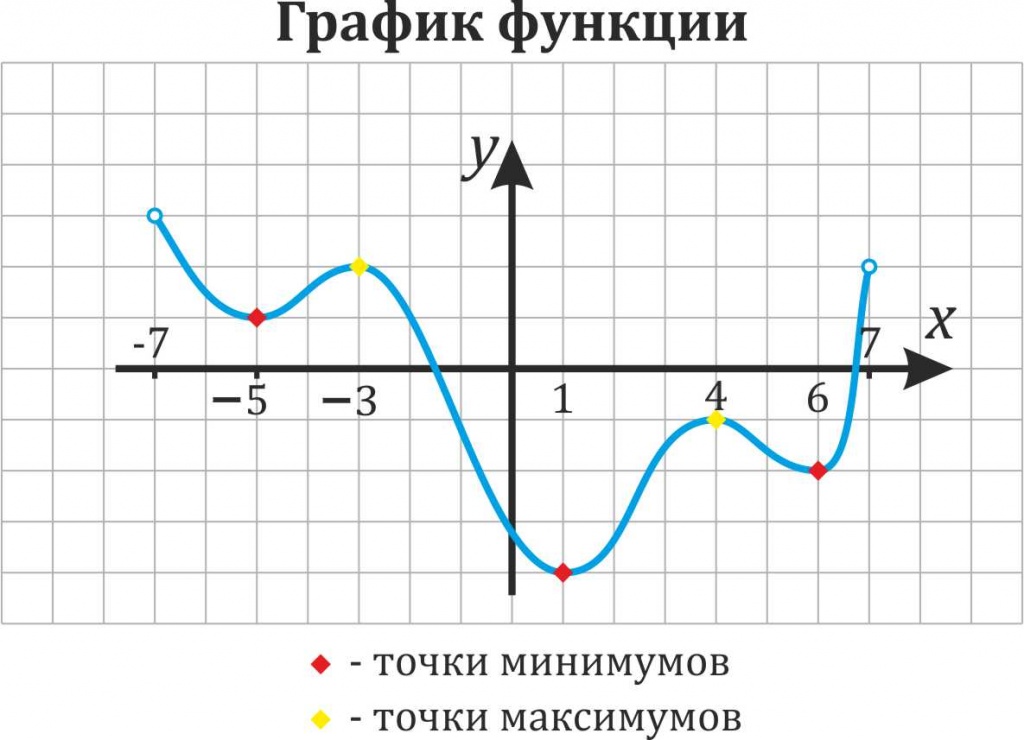
3. Как найти точки экстремумов функции по графику производной?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производной — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки −13, −11, −9,−7 и 3. Количество точек экстремума функции 5.
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось x).
4. Как найти точки максимумов или минимумов функции по графику производной)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает. – Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди −13, −11, −9,−7 и 3.
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с−13: до −13 производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что −13 – точка максимума.
−11: производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что −11 – это минимум.
−9: функция возрастает, а потом убывает – максимум.
−7: минимум.
3: максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус. – Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции f′(x).
- Найдите корни уравнения f′(x)=0.
- Нарисуйте ось x и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью f′(x), а под осью f(x).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2: – если f′(x) изменила знак с «+» на «−», то x1 – точка максимума; – если f′(x) изменила знак с «−» на «+», то x3 – точка минимума; – если f′(x) не изменила знак, то x2 – может быть точкой перегиба.
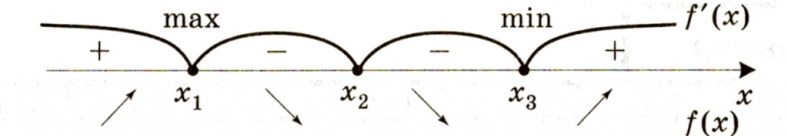
Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.
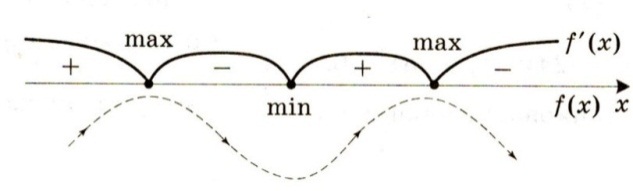
2.Рассмотрим примеры:
Пример 1.
Найдите точку максимума функции y=3x5−20x3−54. Решение:
1.Найдем производную функции: y′=15x4−60x2. 2. Приравняем её к нулю и решим уравнение:
15x4−60x2=0 |:15 x4−4x2=0 x2(x2−4)=0 x=0 x2−4=0 x=±2
3. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
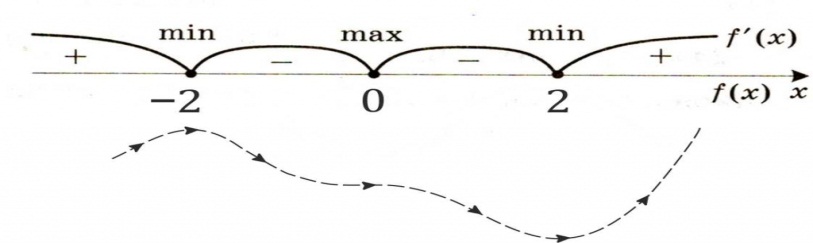
Теперь очевидно, что точкой максимума является −2.
Ответ. −2.
Пример 2.
Найдите точку максимума функции 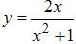
Решение 1. Найдём производную (по правилу производная дроби) и приравниваем её к нулю:
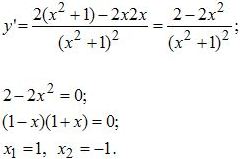 Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -2, тогда производная будет равна -0,24, для второго возьмём 0, тогда производная будет 2, а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.
Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -2, тогда производная будет равна -0,24, для второго возьмём 0, тогда производная будет 2, а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.
 Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума. Ответ: 1.
Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума. Ответ: 1.
3. Исследовать на экстремумы функцию (самостоятельно):
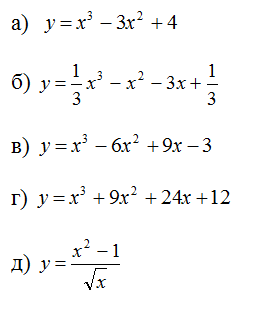
КРИТЕРИИ «5» – все 5 функций
«4» – 3,4 функции
«3» – 2 функции
Решение 3 пункта записываете в тетрадь и предоставляете для проверки, оценка выставляется в ГИС
Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
Тема 7.
Взаимосвязь функции и ее производной
7
.
06
Производная и точки экстремума функции
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
взаимосвязь функции и ее производной
Решаем задачи
На рисунке изображен график производной функции определенной на отрезке
Найдите количество точек
максимума функции на отрезке
Показать ответ и решение
Точка максимума — значение в котором производная меняет свой знак с «+» на «-» при движении слева направо.
Следовательно, в этой точке график производной пересекает ось абсцисс «сверху вниз». На отрезке таких точек две.
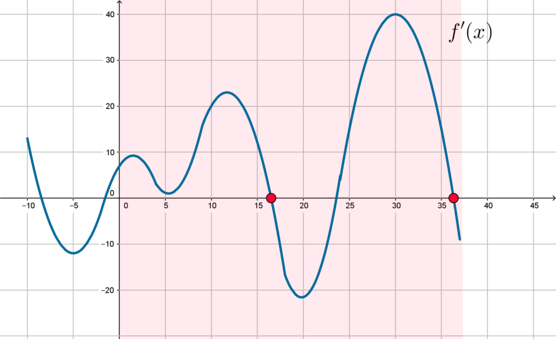
На рисунке изображен график функции , определенной на интервале
. Найдите
произведение точек экстремума этой функции.
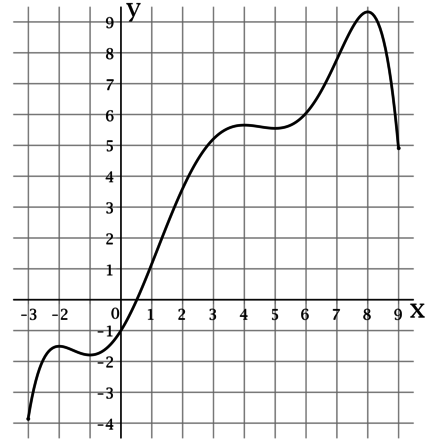
На рисунке изображен график функции , определенной на интервале
. Найдите
сумму точек экстремума этой функции на отрезке .
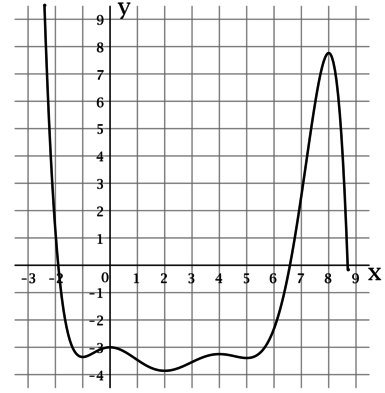
На рисунке изображен график функции , определенной на интервале
. Найдите
произведение точек экстремума этой функции.
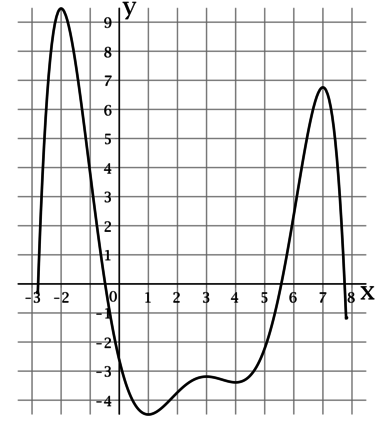
На рисунке изображен график функции , определенной на интервале
. Найдите сумму точек экстремума этой
функции.
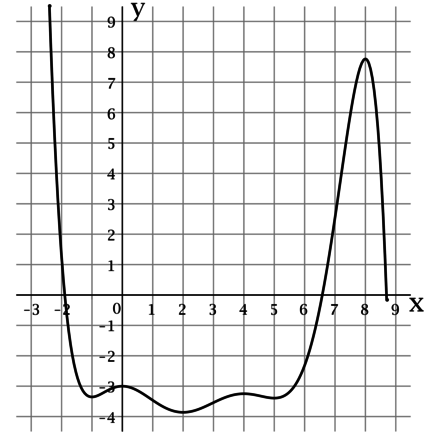
На рисунке изображен график функции , определенной на интервале
. Найдите
сумму точек экстремума этой функции.
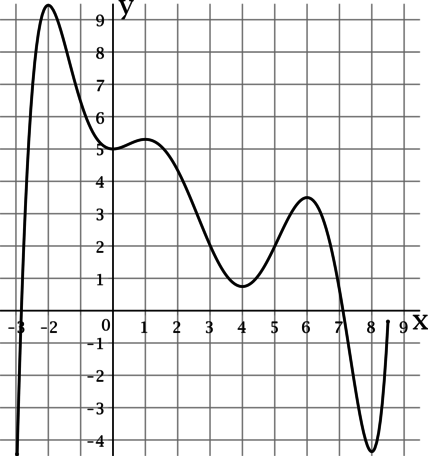
На рисунке изображён график производной функции
определённой на интервале Найдите количество точек максимума
функции принадлежащих отрезку
Показать ответ и решение
Точки максимума — это точки, в которых функция меняет свой характер
монотонности с возрастания на убывание, если смотреть слева направо.
Следовательно, в них производная меняет свой знак с плюса на минус.
Значит, на рисунке нужно найти те точки отрезка в которых
график функции пересекает ось причем сверху вниз. Таких точек
две.
На рисунке изображён график функции определённой на интервале
Найдите наименьшее значение функции
на отрезке
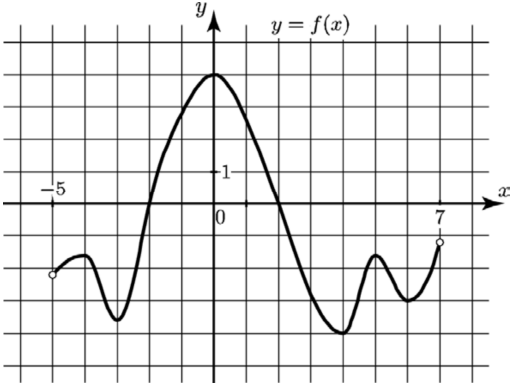
Показать ответ и решение
Наименьшее значение функции достигается при и равно
На рисунке изображен график функции определенной на интервале
Найдите количество точек, в которых
производная функции равна 0.
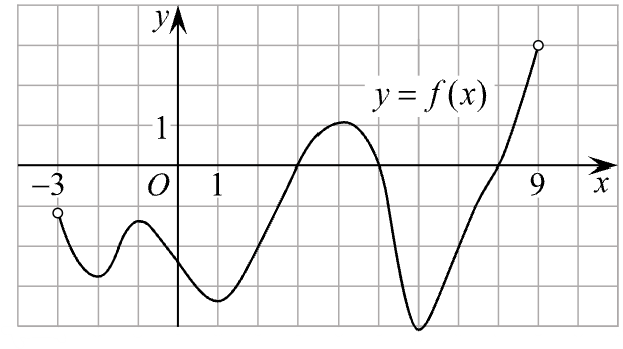
Показать ответ и решение
Производная равна нулю в точках экстремума функции. Таких точек пять:
На рисунке изображен график — производной функции
определённой на интервале
Найдите
количество точек минимума функции принадлежащих отрезку
![]()
На рисунке изображен график — производной функции
, определенной на интервале
. В
какой точке отрезка функция
принимает наименьшее значение?
На рисунке изображен график функции , определенной на интервале
. Найдите количество точек, в которых
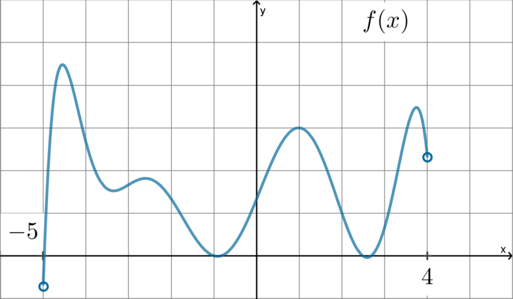
касательная к графику функции параллельна прямой или совпадает с ней.
Показать ответ и решение
Так как на рисунке изображен график самой функции, то условие задачи нужно свести к функции.
Если касательная параллельна прямой , то угловой коэффициент касательной равен угловому коэффициенту прямой
, то есть
. Следовательно,
, где
— некоторое число.
Если — касательная к графику
, то ее угловой коэффициент равен
, где
— абсцисса точки касания.
Количество таких точек нам и нужно найти.
Следовательно, . Но производная функции равна 0 в точках экстремума, следовательно, раз у нас
нарисован график самой функции, то нам нужно найти количество точек максимума и минимума. Таких точек у нас 7.
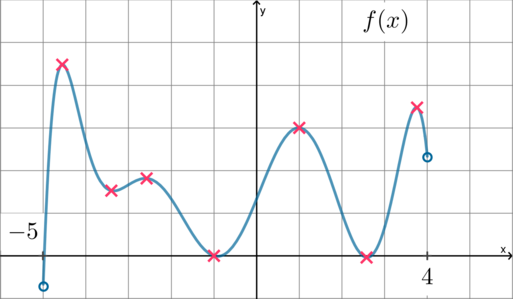
На рисунке изображен график — производной функции
, определенной на интервале
. Найдите
количество точек максимума функции , принадлежащих отрезку
.
На рисунке изображен график — производной функции
определенной на интервале
Найдите
количество точек минимума функции принадлежащих полуинтервалу
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Связь производной с точками экстремума функции
В данных задачах речь идет о непрерывных функциях (простым языком, функция будет непрерывна на интервале, если ее график можно нарисовать на этом интервале, не отрывая ручку от листа).
(blacktriangleright) (color{royalblue}{text{Точки}}) (локального) (color{royalblue}{text{экстремума}}) функции – это точки (локального) максимума и минимума.
Окрестность – это интервал вокруг точки некоторого радиуса. Например, окрестностью точки (x=0) можно назвать интервал ((-1;1)), или ((-0,1;0,1)), или ((-0,0000001;0,0000001)) и т.д.
(blacktriangleright) (color{royalblue}{text{Точка}}) (color{royalblue}{text{максимума}}) (x_{max}) – такая внутренняя точка области определения функции, для которой выполнено: (f(x)leqslant
f(x_{max})) для любого (x) из некоторой окрестности точки (x_{max}).
То есть можно найти такую окрестность, что для любой точки из этой окрестности будет выполнено данное неравенство.
Заметим, что, например, если функция определена на отрезке ([0;2]), то все точки интервала ((0;2)) будут внутренними, а вот точки (0) и (2) – граничными (то есть не внутренними).
(blacktriangleright) (color{royalblue}{text{Точка}}) (color{royalblue}{text{минимума}}) (x_{min}) – такая внутренняя точка области определения функции, для которой выполнено: (f(x)geqslant
f(x_{min})) для любого (x) из некоторой окрестности точки (x_{min}).
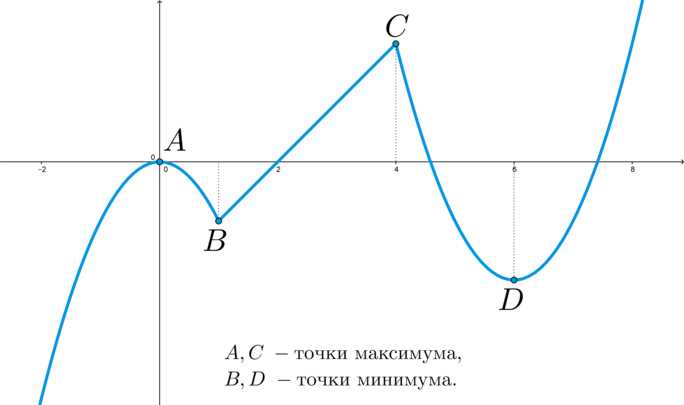
Например, для точки (C) за окрестность можно взять интервал ((3;5)) или даже ((2;6)), а можно совсем маленький — ((4-0,01;4+0,01)).

Следующие факты помогают искать точки экстремума функции.
(blacktriangleright) Если производная (f’) в точке (x) равна нулю и меняет свой знак слева направо с “(+)” на “(-)” , то эта точка является точкой максимума.
Заметим также, что если производная (f’) в точке (x) не существует и меняет свой знак слева направо с “(+)” на “(-)” (но (x) – внутренняя точка области определения функции (f,)!), то эта точка является точкой максимума.
Пример: в точке (A) производная равна нулю и эта точка является точкой максимума; в точке (C) производная не “равна нулю”, а не существует, при этом точка (C) также является точкой максимума.
(blacktriangleright) Если производная в точке (x) равна нулю и меняет свой знак слева направо с “(-)” на “(+)” , то эта точка является точкой минимума.
Также, если производная (f’) в точке (x) не существует и меняет свой знак слева направо с “(-)” на “(+)” (но (x) – внутренняя точка области определения функции (f,)!), то эта точка является точкой минимума.
(blacktriangleright) Заметим, что точки экстремума – это значение абсциссы (x).
(blacktriangleright) Заметим, что существует такое понятие, как критические точки — это все точки, в которых производная функции либо равна нулю, либо не существует.
Таким образом, только часть критических точек является точками экстремума.
Задание
1
#3107
Уровень задания: Равен ЕГЭ
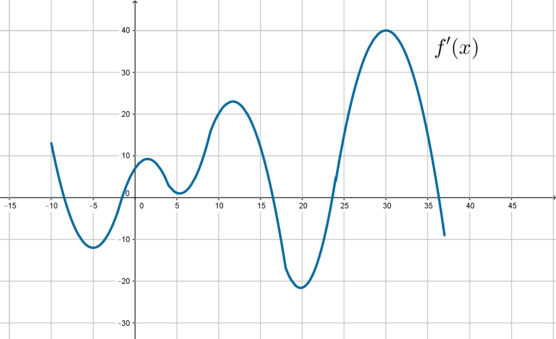
На рисунке изображен график производной функции (f(x)), определенной на отрезке ([-10;37]). Найдите количество точек максимума функции (f(x)) на отрезке ([0;37]).
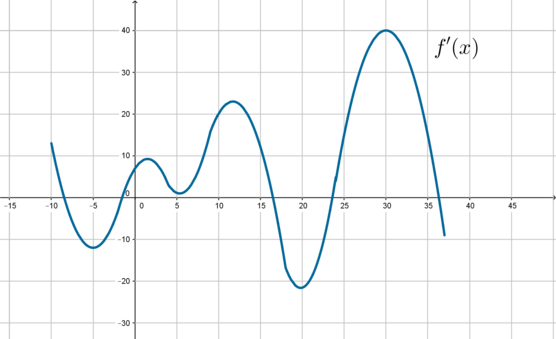
Точка максимума – значение (x), в котором производная меняет свой знак с “(+)” на “(-)”. Следовательно, в этой точке ее график пересекает ось абсцисс “сверху вниз” (если двигаться по рисунку слева направо). Отметим отрезок ([0;37]) и увидим, что таких точек 2:
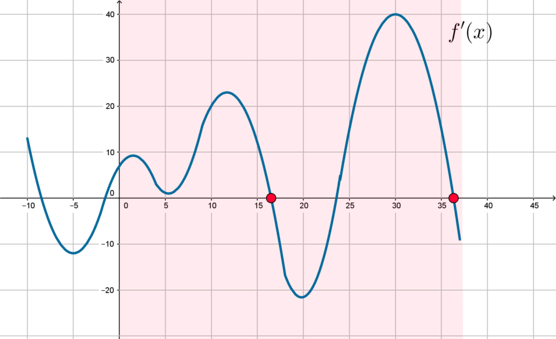
Ответ: 2
Задание
2
#2962
Уровень задания: Равен ЕГЭ
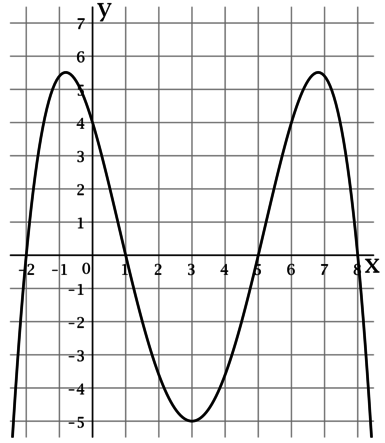
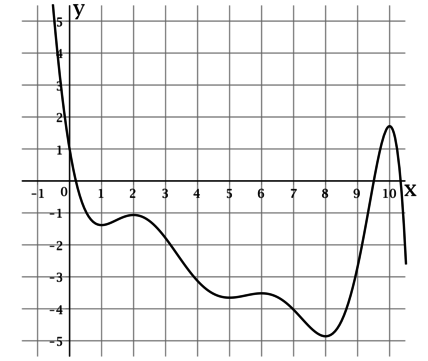
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-2,4; 8,7)). Найдите сумму точек экстремума этой функции на отрезке ([1;6]).
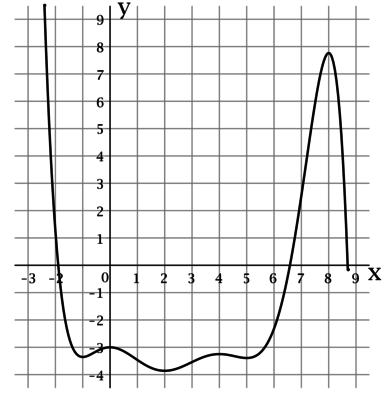
Так как на рисунке изображен график функции, то точки экстремума – это точки на графике, в которых функция меняется с возрастания на убывание или наоборот. Эти точки: (x=-1; 0; 2; 4; 5; 8.) Из них на отрезке ([1;6]) лежат только точки (2; 4; 5), следовательно, их сумма равна (2+4+5=11.)
Ответ: 11
Задание
3
#730
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-3; 8,5)). Найдите сумму точек экстремума этой функции.
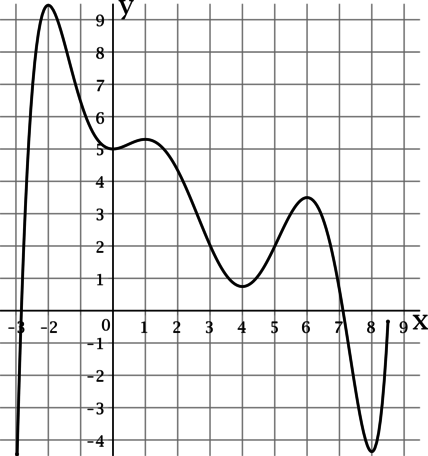
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (0), (4) и (8), а локально максимальные значения в точках (-2), (1) и (6). Таким образом, сумма точек экстремума этой функции равна (0 + 4 + 8 + (-2) + 1 + 6 = 17).
Ответ: 17
Задание
4
#731
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-2,4; 8,7)). Найдите сумму точек экстремума этой функции.
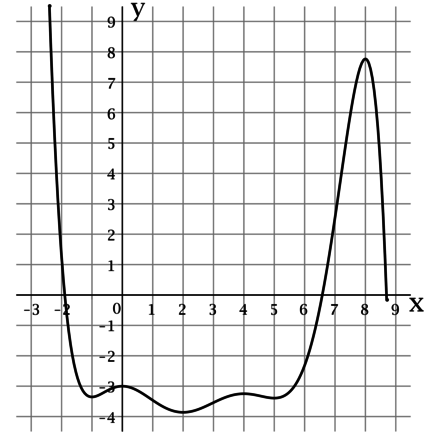
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (-1), (2) и (5), а локально максимальные значения в точках (0), (4) и (8). Таким образом, сумма точек экстремума этой функции равна (-1 + 2 + 5 + 0 + 4 + 8 = 18).
Ответ: 18
Задание
5
#732
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-3; 9)). Найдите произведение точек экстремума этой функции.
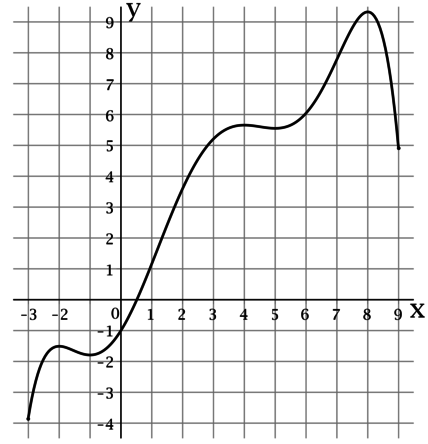
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (-1) и (5), а локально максимальные значения в точках (-2), (4) и (8). Таким образом, произведение точек экстремума этой функции равно ((-1)cdot 5cdot (-2)cdot 4cdot 8 = 320).
Ответ: 320
Задание
6
#733
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-2.8; 7.8)). Найдите произведение точек экстремума этой функции.
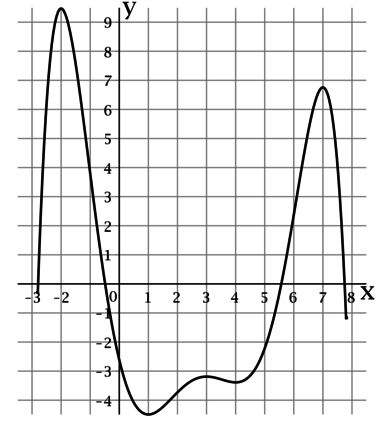
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (1) и (4), а локально максимальные значения в точках (-2), (3) и (7). Таким образом, произведение точек экстремума этой функции равно (1cdot 4cdot (-2)cdot 3cdot 7 = -168).
Ответ: -168
Задание
7
#734
Уровень задания: Равен ЕГЭ
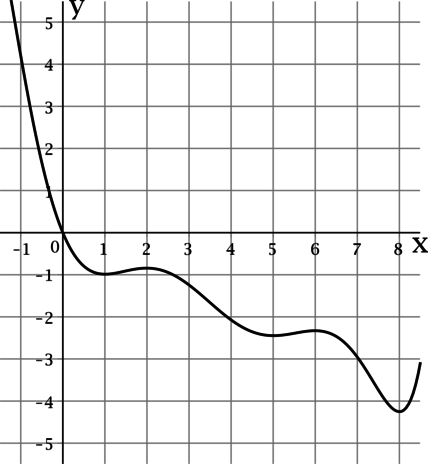
На рисунке изображен график (y = f'(x)) – производной функции (y = f(x)), определенной на интервале ((-1; 8)). В какой точке отрезка ([2; 5]) функция (y = f(x)) принимает наибольшее значение?
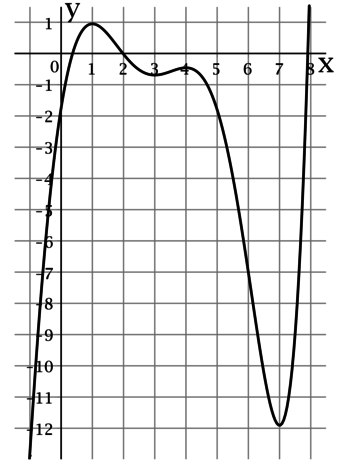
По рисунку можно определить, что функция (y = f'(x)) на отрезке ([2; 5]) принимает неположительные значения, при этом (f'(2) = 0). Так как на полуинтервале ((2; 5]) производная функции (f(x)) отрицательна, то сама функция (f(x)) на ((2; 5]) убывает, тогда (y = f(x)) на отрезке ([2; 5]) принимает наибольшее значение при (x = 2).
Ответ: 2
Итоговый экзамен по математике для выпускников 11-х классов обязательно включает задания на поиск точек максимума и минимума функциональных зависимостей. Их решение проводится аналитически – методом дифференцирования. Применение производной для исследования функции на экстремум сокращает время анализа и позволяет представить общий вид графика зависимости еще до выполнения построений.
Обучающий ресурс «Школково» позволит учащимся освежить в памяти главные моменты темы – уточнить теоретические знания и отработать их в решении ряда задач. Наш подход к обучению в отношении поиска точек экстремума функции через производную в типовых заданиях ЕГЭ основан на принципе глубокой взаимосвязи теории и практики. Сначала ученик читает правила «Теоретической справки», потом смотрит видео с объяснениями учителя, а затем работает с реальным педагогом. В процессе просмотра предлагаемых на сайте вебинаров можно задать интересующие вопросы и получить помощь в решении конкретных задач.
В разделе «Каталог» имеются подборки тематических заданий на нахождение точек экстремума функции с помощью производной, а также нахождения производной угла наклона касательной. Каждый пример содержит готовое решение и правильный ответ, с которыми можно ознакомиться после окончания самостоятельной работы. «Конструктор» примерных вариантов ЕГЭ позволит провести исследование экстремумов функций с помощью производных в ходе пробного выполнения экзаменационной работы.

УСТАЛ? Просто отдохни
