 Популярные ответы
Популярные ответы
- Когда буквы е, ё, ю, я обозначают два звука?
- Каким членом предложения может быть местоимение?
- Как правильно произносятся слова термин, шинель, темп?
- Как найти точки экстремума функции по графику производной?
- Как правильно: по средам (ударение на «а» или на «е»)?
- Какой официальный сайт Московского энергетического института (МЭИ)?
- На какие вопросы отвечает наречие?
- Где найти примеры сравнительных оборотов и других конструкций со словом «как»?
- Как в физике обозначается скорость движения?
- Где скачать задания по английскому языку олимпиады для школьников «Покори Воробьевы горы!»?
Степенной называют функцию вида f(x) = k·xa, где коэффициент k и показатель a — вещественные (действительные) постоянные.
Производную степенной функции f(x) = k·xa можно найти по формуле:
f'(x) = d(k·xa)/dx = k·xa−1.
В частных случаях показателя a:
| a | f(x) | f'(x) | Название исходной функции |
| −2 | x−2 = 1/x2 | −2x−3 = −2/x3 | обратный квадрат |
| −1 | x−1 = 1/x | −x−2 = −1/x2 | обратная пропорциональность |
| 0 | x0 = 1 | 0 | константа |
| 1/3 | x1/3 = 3√x | (1/3)x−2/3 = 1/(3·3√(x2)) | кубический корень |
| 1/2 | x1/2 = √x | (1/2)x−1/2 = 1/(2√x) | квадратный корень |
| 1 | x1 = x | 1 | прямая пропорциональность |
| 2 | x2 | 2x | квадрат |
| 3 | x3 | 3x2 | куб |
| 4 | x4 | 4x2 | четвертая степень |
Источник:
- fxyz.ru — производные алгебраических функций.
Дополнительно на Геноне:
- Что такое степенная функция?
Последнее редактирование ответа: 16.11.2012
-
Оставить отзывОставить отзыв
Вы можете написать свои замечания к ответу, предложения об улучшении или просто поблагодарить автора. Комментарий, после проверки, увидят автор и редактор ответа. Будьте, пожалуйста, вежливыми. Спасибо!
Если Вы хотите получить уведомление об
исправлении ответа укажите свой e-mail:Неправильный формат адреса электронной почты
 Похожие вопросы
Похожие вопросы
В соответствии с пользовательским соглашением администрация не несет ответственности за содержание материалов, которые размещают пользователи. Для урегулирования спорных вопросов и претензий Вы можете связаться с администрацией сайта genon.ru.
Размещенные на сайте материалы могут содержать информацию, предназначенную для пользователей старше 18 лет, согласно Федерального закона №436-ФЗ от 29.12.2010 года “О защите детей от информации, причиняющей вред их здоровью и развитию”. Обращение к пользователям 18+.
Заказать задачи по любым предметам можно здесь от 10 минут
Производная функции
Процесс нахождения производной функции называется дифференцированием. Производную приходится находить в ряде задач курса математического анализа. Например, при отыскании точек экстремума и перегиба графика функции.
Как найти?
Чтобы найти производную функции нужно знать таблицу производных элементарных функций и применять основные правила дифференцирования:
- Вынос константы за знак производной: $$ (Cu)’ = C(u)’ $$
- Производная суммы/разности функций: $$ (u pm v)’ = (u)’ pm (v)’ $$
- Производная произведения двух функций: $$ (u cdot v)’ = u’v + uv’ $$
- Производная дроби: $$ bigg (frac{u}{v} bigg )’ = frac{u’v – uv’}{v^2} $$
- Производная сложной функции: $$ ( f(g(x)) )’ = f'(g(x)) cdot g'(x) $$
Примеры решения
| Пример 1 |
| Найти производную функции $ y = x^3 – 2x^2 + 7x – 1 $ |
| Решение |
|
Производная суммы/разности функций равна сумме/разности производных: $$ y’ = (x^3 – 2x^2 + 7x – 1)’ = (x^3)’ – (2x^2)’ + (7x)’ – (1)’ = $$ Используя правило производной степенной функции $ (x^p)’ = px^{p-1} $ имеем: $$ y’ = 3x^{3-1} – 2 cdot 2 x^{2-1} + 7 – 0 = 3x^2 – 4x + 7 $$ Так же было учтено, что производная от константы равна нулю. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ y’ = 3x^2 – 4x + 7 $$ |
| Пример 2 |
| Найти производную функции $ y = sin x – ln 3x $ |
| Решение |
|
По правилу производной разности: $$ y’ = (sin x – ln 3x)’ = (sin x)’ – (ln 3x)’ = $$ По таблице интегрирования находим: $$ (sin x)’ = cos x $$ $$ (ln x)’ = frac{1}{x} $$ С учетом того, что аргумент натурального логарифма отличен от $ x $, то нужно домножить ещё на производную самого аргумента: $$ y’ = (sin x)’ – (ln 3x)’ = cos x – frac{1}{3x} cdot (3x)’ = $$ После упрощения получаем: $$ = cos x – frac{1}{3x} cdot 3 = cos x – frac{1}{x} $$ |
| Ответ |
| $$ y’ = cos x – frac{1}{x} $$ |
| Пример 3 |
| Найти производную функции $ y = (3x-1) cdot 5^x $ |
| Решение |
|
В данном примере стоит произведение двух функций, а производная произведения находится по формуле номер 3: $$ (u cdot v)’ = u’v + uv’ $$ $$ y’ = ( (3x-1) cdot 5^x )’ = (3x-1)’ 5^x + (3x-1) (5^x)’ = $$ Производная первой функции вычисляется как разность фунций: $$ (3x-1)’ = (3x)’ – (1)’ = 3(x)’ – (1)’ = 3 $$ Вторая функция является показательной, производная которой находится по формуле: $ (a^x)’ = a^x ln a $: $$ (5^x)’ = 5^x ln 5 $$ Продолжаем решение с учетом найденных производных: $$ y’ = (3x-1)’ 5^x + (3x-1) (5^x)’ = 3 cdot 5^x + (3x-1) 5^x ln 5 $$ |
| Ответ |
| $$ y’ = 3cdot 5^x + (3x-1) 5^x ln 5 $$ |
| Пример 4 |
| Найти производную функции $ y = frac{ln x}{sqrt{x}} $ |
| Решение |
|
Производную дроби найдем по четвертой формуле. Положим $ u = ln x $ и $ v = sqrt{x} $. Тогда их производные по таблице основных элементарных функций равны: $$ u’ = (ln x)’ = frac{1}{x} $$ $$ v’ = (sqrt{x})’ = frac{1}{2sqrt{x}} $$ Используя формулу №4 получаем: $$ y’ = bigg ( frac{ln x}{sqrt{x}} bigg )’ = frac{ frac{1}{x} cdot sqrt{x} – ln x cdot frac{1}{2sqrt{x}} }{x} = $$ Выносим множитель $ frac{1}{2sqrt{x}} $ в числителе за скобку: $$ y’ = frac{2-ln x}{2xsqrt{x}} $$ |
| Ответ |
| $$ y’ = frac{2-ln x}{2xsqrt{x}} $$ |
| Пример 5 |
| Найти производную функции $ y = ln sin 3x $ |
| Решение |
|
Данная функция является сложной, потому производную будем брать по цепочке. Сначала от внешней функции, затем от внутренней. При этом выполняя их перемножение. $$ y’ = (ln sin 3x )’ = frac{1}{sin 3x} cdot (sin 3x)’ = $$ Заметим, что аргумент синуса отличен от $ x $, поэтому тоже является сложной функцией: $$ = frac{1}{sin 3x} cdot cos 3x cdot (3x)’ = frac{1}{sin 3x} cdot cos 3x cdot 3 $$ Учитывая определение котангенса $ ctg x = frac{cos 3x}{sin 3x} $ перепишем полученную производную в удобном компактном виде: $$ y’ = 3ctg 3x $$ |
| Ответ |
| $$ y’ = 3ctg 3x $$ |
График кубической функции (кубическая парабола)
Куби́ческая фу́нкция в математике — это числовая функция 
где
Другими словами, кубическая функция задаётся многочленом третьей степени.
Аналитические свойства[править | править код]
Производная кубической функции 






График[править | править код]
График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции 




Кроме того, кубическая парабола
- центрально-симметрична относительно точки перегиба,
- всегда пересекает линию абсцисс хотя бы в одной точке,
- не имеет общих точек со своей касательной в точке перегиба, кроме как в самой точке касания.
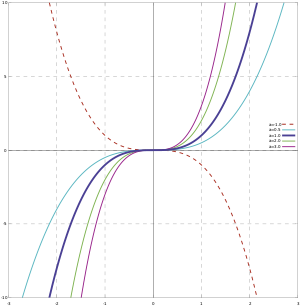
|
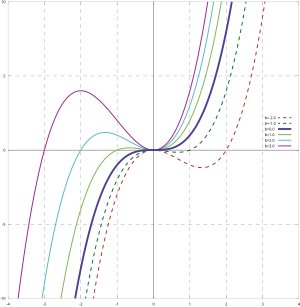
|

|
| Коэффициент при кубе | Коэффициент при квадрате | Коэффициент при первой степени |
Коллинеарность[править | править код]
Касающиеся прямые в трёх коллинеарных точках графика кубической функции пересекают график снова в коллинеарных точках.[1]
Применение[править | править код]
Кубическую параболу иногда применяют для расчёта переходной кривой на транспорте, так как её вычисление намного проще, чем построение клотоиды.
См. также[править | править код]
- Парабола
- Кубика
- Кубическое уравнение
- Сплайн
Примечания[править | править код]
- ↑ Whitworth, William Allen. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions, Forgotten Books, 2012 (orig. Deighton, Bell, and Co., 1866). http://www.forgottenbooks.com/search?q=Trilinear+coordinates&t=books Архивная копия от 24 марта 2016 на Wayback Machine
Литература[править | править код]
- Л. С. Понтрягин, Кубическая парабола // «Квант», 1984, № 3.
- И. Н. Бронштейн, К. А. Семендяев, «Справочник по математике», издательство «Наука», М. 1967, с. 84
Раз ты зашел сюда, то уже, наверное, успел увидеть в учебнике эту формулу
((f(g(x)))’=f'(g(x))cdot g'(x))
и сделать вот такое лицо:

Друг, не переживай! На самом деле все просто до безобразия. Ты обязательно все поймешь. Только одна просьба – прочитай статью не торопясь, старайся понять каждый шаг. Я писал максимально просто и наглядно, но вникнуть в идею всё равно надо. И обязательно реши задания из статьи.
Содержание:
- Что такое сложная функция?
“Распаковка” сложной функции
Внутренняя и внешняя функция
Производная сложной функции. Примеры
Что такое сложная функция?
Представь, что ты переезжаешь в другую квартиру и поэтому собираешь вещи в большие коробки. Пусть надо собрать какие-нибудь мелкие предметы, например, школьные письменные принадлежности. Если просто скидать их в огромную коробку, то они затеряются среди других вещей. Чтобы этого избежать, ты сначала кладешь их, например, в пакет, который затем укладываешь в большую коробку, после чего ее запечатываешь. Этот “сложнейший” процесс представлен на схеме ниже:

Казалось бы, причем здесь математика? Да притом, что сложная функция формируется ТОЧНО ТАКИМ ЖЕ способом! Только «упаковываем» мы не тетради и ручки, а (x), при этом «пакетами» и «коробками» служат разные функции.
Например, возьмем x и «запакуем» его в функцию косинуса:

В результате получим, ясное дело, (cosx). Это наш «пакет с вещами». А теперь кладем его в «коробку» – запаковываем, например, в кубическую функцию.

Что получится в итоге? Да, верно, будет «пакет с вещами в коробке», то есть «косинус икса в кубе».

Получившаяся конструкция и есть сложная функция. Она отличается от простой тем, что к одному иксу применяется НЕСКОЛЬКО «воздействий» (упаковок) подряд и получается как бы «функция от функции» – «упаковка в упаковке».
В школьном курсе видов этих самых «упаковок» совсем мало, всего четыре :

Давай теперь «упакуем» икс сначала в показательную функцию с основанием 7, а потом в тригонометрическую функцию тангенс. Получим:
(x → 7^x → tg(7^x))
А теперь «упакуем» икс два раза в тригонометрические функции, сначала в синус, а потом в котангенс:
(x → sinx → ctg (sinx ))
Просто, правда?
Напиши теперь сам функции, где икс:
– сначала «упаковывается» в косинус, а потом в показательную функцию с основанием (3);
– сначала в пятую степень, а затем в тангенс;
– сначала в логарифм по основанию (4), затем в степень (-2).
Ответы на это задание посмотри в конце статьи.
А можем ли мы «упаковать» икс не два, а три раза? Да, без проблем! И четыре, и пять, и двадцать пять раз. Вот, например, функция, в которой икс «упакован» (4) раза:
(y=5^{log_2{sin(x^4 )}})
Но такие формулы в школьной практике не встретятся (студентам повезло больше – у них может быть и посложнее☺).
«Распаковка» сложной функции
Посмотри на предыдущую функцию еще раз. Сможешь ли ты разобраться в последовательности «упаковки»? Во что икс запихнули сначала, во что потом и так далее до самого конца. То есть – какая функция вложена в какую? Возьми листок и запиши, как ты считаешь. Можно сделать это цепочкой со стрелками как мы писали выше или любым другим способом.
Сделал?
Теперь правильный ответ: сначала икс «упаковали» в (4)-ую степень, потом результат упаковали в синус, его в свою очередь поместили в логарифм по основанию (2), и в конце концов всю эту конструкцию засунули в степень пятерки.
То есть разматывать последовательность надо В ОБРАТНОМ ПОРЯДКЕ. И тут подсказка как это делать проще: сразу смотри на икс – от него и надо плясать. Давай разберем несколько примеров.
Например, вот такая функция: (y=tg(log_2x )). Смотрим на икс – что с ним происходит сначала? Берется логарифм от него. А потом? Берется тангенс от результата. Вот и последовательность будет такая же:
(x → log_2x → tg(log_2x ))
Еще пример: (y=cos{(x^3 )}). Анализируем – сначала икс возвели в куб, а потом от результата взяли косинус. Значит, последовательность будет: (x → x^3 → cos{(x^3 )}). Обрати внимание, функция вроде бы похожа на самую первую (там, где с картинками). Но это совсем другая функция: здесь в кубе икс (то есть (cos{(x·x·x)})), а там в кубе косинус (x) (то есть, (cosx·cosx·cosx)). Эта разница возникает из-за разных последовательностей «упаковки».
Последний пример (с важной информацией в нем): (y=sin{(2x+5)}). Понятно, что здесь сначала сделали арифметические действия с иксом, потом от результата взяли синус: (x → 2x+5 → sin{(2x+5)}). И это важный момент: несмотря на то, что арифметические действия функциями сами по себе не являются, здесь они тоже выступают как способ «упаковки». Давай немного углубимся в эту тонкость.
Как я уже говорил выше, в простых функциях икс «упаковывается» один раз, а в сложных – два и более. При этом любая комбинация простых функций (то есть их сумма, разность, умножение или деление) – тоже простая функция. Например, (x^7) – простая функция и (ctg x) – тоже. Значит и все их комбинации являются простыми функциями:
(x^7+ ctg x) – простая,
(x^7· ctg x) – простая,
(frac{x^7}{ctg x}) – простая и т.д.
Однако если к такой комбинации применить еще одну функцию – будет уже сложная функция, так как «упаковок» станет две. Смотри схему:

Хорошо, давай теперь сам. Напиши последовательность «заворачивания» функций:
(y=cos{(sinx)})
(y=5^{x^7})
(y=arctg{11^x})
(y=log_2(1+x))
Ответы опять в конце статьи.
Внутренняя и внешняя функции
Зачем же нам нужно разбираться во вложенности функций? Что нам это дает? Дело в том, что без такого анализа мы не сможем надежно находить производные разобранных выше функций.
И для того, чтобы двигаться дальше, нам будут нужны еще два понятия: внутренняя и внешняя функции. Это очень простая вещь, более того, на самом деле мы их уже разобрали выше: если вспомнить нашу аналогию в самом начале, то внутренняя функция – это «пакет», а внешняя – это «коробка». Т.е. то, во что икс «заворачивают» сначала – это внутренняя функция, а то, во что «заворачивают» внутреннюю – уже внешняя. Ну, понятно почему – она ж снаружи, значит внешняя.
Вот в этом примере: (y=tg(log_2x )), функция (log_2x) – внутренняя, а – внешняя.
А в этом: (y=cos{(x^3+2x+1)}), (x^3+2x+1) – внутренняя, а – внешняя.
Выполни последнюю практику анализа сложных функций, и перейдем, наконец, к тому, ради чего всё затевалось – будем находить производные сложных функций:
Заполни пропуски в таблице:
Производная сложной функции
Браво нам, мы всё ж таки добрались до «босса» этой темы – собственно, производной сложной функции, а конкретно, до той самой ужасной формулы из начала статьи.☺
((f(g(x)))’=f'(g(x))cdot g'(x))
Формула эта читается так:
Производная сложной функции равна произведению производной внешней функции по неизменной внутренней на производную внутренней функции.
И сразу смотри схему разбора “по словам” чтобы понимать, что к чему относится:

Надеюсь, термины «производная» и «произведение» затруднений не вызывают. «Сложную функцию» – мы уже разобрали. Загвоздка в «производной внешней функции по неизменной внутренней». Что это такое?
Ответ: это обычная производная внешней функции, при которой изменяется только внешняя функция, а внутренняя остается такой же. Все равно непонятно? Хорошо, давай на примере.
Пусть у нас есть функция (y=sin(x^3 )). Понятно, что внутренняя функция здесь (x^3), а внешняя . Найдем теперь производную внешней по неизменной внутренней.
Из таблицы производных мы знаем, что производная синуса икс есть косинус икс (табличные значения надо знать наизусть!): (({sin{x}})’=cos{x}).
Тогда производная внешней функции по неизменной внутренней для нашего случая будет (cos(x^3)). То есть, мы взяли ее как обычную производную синуса, а содержимое синуса (внутреннюю функцию) просто скопировали в полученную производную (косинус), ничего в ней не меняя.
Таким образом, на данный момент имеем:

Осталась «производная внутренней функции». Ну, это совсем легко – обычная производная от внутренней функции, при этом внешняя не влияет вообще никак. В нашем примере, производная от (x^3).
((x^3 )’=3x^2)
Все, теперь можем писать ответ:

Вот так. Давай еще один пример разберем.
Пусть надо найти производную функции (y=(sinx )^3).
Анализируем. Последовательность «заворачивания» у нас такая: (x → sinx → (sinx )^3). Значит, в данном примере внутренняя функция это (sinx), а внешняя .
Производная внешней по внутренней – это производная куба (содержимое куба при этом не меняется). Так как , а в нашем случае в куб «завернут» (sinx), то производная внешней будет (3(sinx)^2). То есть, имеем:

Ну, а производная внутренней – это просто производная синуса икс, то есть косинус икс.
В итоге, имеем:
(y’=((sinx )^3 )’=3(sinx )^2·(sinx )’=3(sinx )^2·cosx)
Понятно?
Ладно, ладно, вот еще один пример с разбором. ☺
Пример. Найти производную сложной функции (y=ln(x^2-x)).
Разбираем вложенность функций: (x → x^2-x → ln(x^2-x)).
Внутренняя: (x^2-x). Внешняя: .
Из таблицы производных знаем:.
То есть производная внешней по внутренней будет: (ln(x^2-x)’=) (frac{1}{x^2-x}).
Производная внутренней: ((x^2-x)’= (x^2)’-(x)’=2x-1).
В итоге, согласно большой и страшной формуле имеем:
(y ‘=(ln(x^2-x) )’=)(frac{1}{x^2-x})(·(2x-1))
Ну и напоследок можно немного «причесать» ответ, чтоб никто не докопался:
(y ‘=(ln(x^2-x))’=)(frac{1}{x^2-x})(·(2x-1)=)(frac{2x-1}{x^2-x})
Готово.
Что, еще примеров желаешь? Легко.
Пример. Найти производную сложной функции (y=sin{(cosx)}).
Вложенность функций: (x → cosx → sin{(cosx)})
Внутренняя: (cosx) Внешняя:
Производная внешней по внутренней: (sin{(cosx )}’=cos{cosx})
Производная внутренней: ((cosx )’= -sinx)
Имеем: (y’=(sin{(cosx)})’=cos{cosx}·(-sinx )=-cos{cosx} ·sinx)
Замечание: Обрати внимание, что заменить запись (cos{cosx}) на (cos^2x) НЕЛЬЗЯ, так как (cos^2x) – это комбинация простых функций (cos^ 2x=cosx·cosx), а (cos{cosx}) – сложная функция: косинус от косинуса икс. Это абсолютно разные функции.
Еще пример с важным замечанием в нем.
Пример. Найти производную сложной функции (y=sqrt{x^6} )
Вложенность функций: (x → x^6 → sqrt{x^6})
Внутренняя: (x^6) Внешняя:
Производная внешней по внутренней: (sqrt{x^6}’=)(frac{1}{2sqrt{x^6}})
Производная внутренней: ((x^6)’= 6x^5)
Имеем: ((sqrt{x^6})’=)(frac{1}{2sqrt{x^6}})(·6x^5)
И теперь упростим ответ. Вспомним свойство корня: (sqrt[b]{x^a} =x^{frac{a}{b}}). Тогда (sqrt{x^6}=x^{frac{6}{2}}=x^3). С учетом этого получаем:
(y’=( sqrt{x^6})’=)(frac{1}{2sqrt{x^6}})(·6x^5=)(frac{1}{2x^3})(·6x^5=)(frac{6x^5}{2x^3})(=3x^2)
Всё. А теперь, собственно, важное замечание:
Тот же самый ответ, но значительно меньшими усилиями мы могли бы получить, упростив исходную функцию сразу. Воспользуемся тем же свойством корня: (sqrt[b]{x^a} =x^{frac{a}{b}}). Тогда исходная функция приобретает вид: (y=sqrt{x^6}=x^{frac{6}{2}}=x^3). А производная куба это практически табличное значение! Готов ответ: (y’=(sqrt{x^6})’=(x^3 )’=3x^2). Немножко проще предыдущего решения, правда ☺? Поэтому прежде чем искать производную, посмотрите, можно ли исходную функцию упростить, чтоб решать было проще.
Давай рассмотрим пример, где эта идея нам сильно поможет.
Пример. Найти производную сложной функции (y=ln(x^3)).
Можно, конечно, рассмотреть вложенность функций: (x → x^3 → ln(x^3 )), разобрать на внутреннюю и внешнюю и так далее. Но можно вспомнить свойство логарифма: (log_a{b^c}=c·log_a{b}). И тогда функция получается (y=ln(x^3 )=3lnx). Отлично! Берем производную:
(y’=(ln(x^3 ) )’=(3lnx )’=3(lnx )’=3·)(frac{1}{x}=frac{3}{x})
Вуаля!
Теперь задачка посложнее, для продвинутых. Решим пример с тройной вложенностью!
Пример. Найти производную сложной функции (y=3^{sin(x^4+1)}).
Вложенность функций: (x → x^4+1 → sin(x^4+1) → 3^{sin(x^4+1)})
Внутренняя: (x^4+1) Средняя: Внешняя:
Сначала производная внешней по средней. Вспоминаем таблицу производных: . Значит, в нашем случае будет (3^{sin(x^4+1)}·ln3).
Хорошо, теперь производная средней по внутренней. По таблице: . Значит, мы получим, (sin(x^4+1)’=cos(x^4+1)).
И наконец, производная внутренней: ((x^4+1)’=(x^4 )’+(1)’=4x^3).
Отлично. Теперь собираем все вместе, перемножая отдельные производные:
((3^{sin(x^4+1)})’=3^{sin(x^4+1)} ·ln3·cos{(x^4+1)}·4x^3)
Готово. Да, это ответ. ☺
Ну, а что ты хотел, я сразу сказал – пример для продвинутых! А представь, что будет с четырехкратной или пятикратной вложенностью? ☺
Пример: Найти производную сложной функции (y=tg(7^x)).
Разбираем вложенность функций: (x : → :7^x : → :tg(7^x)).
Внутренняя: (7^x) Внешняя: (tg(7^x)).
Ищем производную самой внешней функции, внутреннюю при этом не трогаем.
Из таблицы производных знаем: .
То есть, в нашем случае производная внешней по внутренней будет: (frac{1}{cos^2(7^x)}).
Теперь ищем производную внутренней. Этой формулой мы уже пользовались, так что сразу пишем ответ: ((7^x)’=7^x·ln7).
И перемножаем результаты:
(y’=tg(7^x)’=)(frac{1}{cos^2(7^x)}·7^x·ln7)
И “причесываем”: (y’=(tg(7)^x))’=)(frac{1}{cos^2(7^x )})( ·7^x·ln7=)(frac{ln7·7^x}{cos^2(7^x)}).
Ну, теперь думаю всё понятно? И снова повторю – не пугайся сложных конструкций в ответах и промежуточных вычислениях. Они «на лицо ужасные», но зато добрые (в смысле простые) внутри. ☺ Пойми принцип и делай все последовательно.
Последний пример. Такие задания в разных вариациях весьма часто дают на контрольных и тестах. Он вроде как считается сложным. ☺ Хех, наивные учителя. ☺
Пример: Найти производную сложной функции (y=sqrt[3]{(x^5+2x-5)^2}).
Казалось бы, опять у нас тройная вложенность функций:
(x → x^5+2x-5 → (x^5+2x-5)^2 → sqrt[3]{(x^5+2x-5)^2}).
Но давай снова воспользуемся свойством корня (sqrt[b]{x^a} =x^{frac{a}{b}}) и преобразуем нашу функцию к виду:
(y=sqrt[3]{(x^5+2x-5)^2}=(x^5+2x-5)^{frac{2}{3}})
Вот так. И теперь у нас вложенность двойная: (x → x^5+2x-5 → (x^5+2x-5)^{frac{2}{3}})
При этом функция осталась той же! Удобное свойство, однако. Стоит его запомнить, да? ☺ Ладно, поехали дальше.
Внутренняя функция: (x^5+2x-5). Внешняя: .
Производная внешней по внутренней. По таблице производных общая формула производной степенной функции: . Получаем:
. Тогда в нашем случае будет: (frac{2}{3}(x^5+2x-5)^{-frac{1}{3}}).
Производная внутренней: ((x^5+2x-5)’=5x^4+2).
Общий результат: (y ‘=(sqrt[3]{(x^5+2x-5)^2})’=((x^5+2x-5)^{frac{2}{3}} )’=frac{2}{3}(x^5+2x-5)^{-frac{1}{3}}·(5x^4+2)).
В принципе, ответ найден. Но здесь можно сильно «причесать» результаты. Это может показаться сложным, но это не так, просто опять нагромождения символов большое и возникает такое ложное ощущение. На всякий случай помни: «не причесанный» ответ – тоже ответ. Поэтому если не поймешь дальнейших преобразований – не критично. Ладно, расческу в руки и вперед.
Вспоминаем свойство отрицательной степени (a^{-n}=)(frac{1}{a^n}). Получаем:
(y ‘=frac{2}{3}(x^5+2x-5)^{-frac{1}{3}}·(5x^4+2)=)(frac{2}{3})(·)(frac{1}{(x^5+2x-5)^{frac{1}{3}}})(·(5x^4+2))
А теперь применяем свойство корня (sqrt[b]{x^a} =x^{frac{a}{b}}) в обратную сторону. То есть, вот так (x^{frac{a}{b}}=sqrt[b]{x^a}). В результате имеем:
(y’=)(frac{2}{3})(frac{1}{(x^5+2x-5)^{frac{1}{3}}})(·(5x^4+2)=)(frac{2}{3})(frac{1}{sqrt[3]{x^5+2x-5}})(·(5x^4+2))
Ну, и перемножаем дроби.
(y’=)(frac{2}{3})(frac{1}{sqrt[3]{x^5+2x-5}})(·(5x^4+2)=)(frac{2(5x^4+2)}{3sqrt[3]{x^5+2x-5}})(=)(frac{10x^4+4}{3sqrt[3]{x^5+2x-5}})
ВСЁ!!! А теперь сам.
Найти производные функций:
a. (y=ctg(x^7))
b. (y=e^{x^4+5x^3})
c. (y=sqrt{cosx})
d. (y=log_5{5^x})
e. (y=(tgx)^3)
f. (y=sin(ln(x^2)))
Ответы ко всем заданиям (вперемежку).
(y=tg(x^5))
(y=log^{-2}_{4}{x})
(y=3^{cosx})
(x → 1+x → log_2{(1+x)} )
(x → 11^x → arctg(11^x) )
(x → x^7 → 5^{x^7})
(x → sinx → cos(sinx))


Сошлось? Красавчик!

Таблица производных и правила дифференцирования
О том, что такое производная, мы рассказали в статье «Геометрический смысл производной». Если функция задана графиком, её производная в каждой точке равна тангенсу угла наклона касательной к графику функции. А если функция задана формулой — вам помогут таблица производных и правила дифференцирования, то есть правила нахождения производной.
Для решения задач на исследование функции в вариантах ЕГЭ необходима таблица производных и правила дифференцирования, а также знания о том, как связана производная с поведением функции.
Смотри также, как решаются задачи ЕГЭ на применение производной: задача 7 и задача 11.
Прокомментируем несколько строк из таблицы производных.
1. Производная постоянной величины, то есть константы, равна ей самой. Так и должно быть. Ведь константа не меняется. Это постоянная величина, она всегда принимает одинаковые значения.
А производная функции, как мы знаем, – это скорость изменения функции. Подробнее об этом здесь:
Производная функции.
И поэтому производная константы равна нулю.
2. Производная функции у=х равна 1. Вспомним, что производная функции в точке – это тангенс угла наклона касательной, проведенной к графику функции в этой точке. График функции у=х образует угол 45 градусов с положительным направлением оси Х. А тангенс 45 градусов равен 1.
3. Производная функции равна самой этой функции. И действительно, чем больше значение х, тем больше значение функции
… и тем круче вверх идет график по отношению к оси Х. Вот такая это функция, экспонента. Чем дальше, тем быстрее она растет.
4. Производная синуса и косинуса – тоже тригонометрические функции. Например, производная синуса – это косинус. Как это отражается в физике? Если координата тела меняется по закону синуса, то производная координаты, скорость, будет меняться по закону косинуса. Это описание гармонических колебаний: и координата, и скорость, и ускорение тела меняются по законам синуса и косинуса.
5. Производная логарифма в точке обратно пропорциональна
. Чем дальше, тем медленнее растет логарифмическая функция.
Вспомним, как связаны производная и поведение функции.
Если производная положительна, то функция
возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | – | 0 | + |
Разберем задачи ЕГЭ по теме «Таблица производных, нахождение наибольших и наименьших значений функции, нахождение точек максимума и минимума». Во всех этих примерах мы пользуемся формулами из таблицы производных.
Задача 1. Найдите точки максимумам функции
Решение:
Область определения функции:
Найдем производную функции, пользуясь формулой производной частного из таблицы.
если
Точки х = 5 и х = -5, а также точка ноль, разбивают числовую прямую на интервалы, на каждом из которых производная сохраняет свой знак. Это метод интервалов.
Найдем знаки производной на каждом интервале.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». Это точка 5 на рисунке.
Ответ: 5.
Задача 2. Найдите точки минимума функции
Решение:
Применим формулу производной произведения.
Приравняем производную к нулю:
, если
Если то
функция убывает.
Если то
функция возрастает, значит,
– точка минимума функции
В этой точке производная равна нулю и меняет знак с «минуса» на «плюс».
Ответ: -0,625.
Задача 3. Найдите значение функции в точке максимума.
Решение:
Найдем производную функции:
Мы применили формулы производной степени.
Решим уравнение:
Получили критические точки, в которых производная равна нулю. Отметим их на оси Х и найдём знаки производной.
– точка максимума.
Найдём значение функции в этой точке:
Ответ: 16.
Рассмотрим задачи ЕГЭ на нахождение наибольших и наименьших значений функций.
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке:
Это значит, что у нас есть алгоритм для нахождения наибольших и наименьших значений функции на интервале.
Пусть функция f(x) определена на некотором интервале. Чтобы найти ее наибольшее или наименьшее значение, действуем следующим образом:
- Находим производную функции.
- Приравниваем производную к нулю, находим точки, в которых она равна нулю.
- Если производная меняет знак с «плюса» на «минус» в точке
, то
– точка максимума функции.
- Если производная меняет знак с «минуса» на «плюс» в точке
, то
– точка минимума функции.
- Чтобы найти наибольшее значение функции на отрезке, сравниваем значения в точке максимума и концах отрезка.
Чтобы найти наименьшее значение функции на отрезке, сравниваем значения в точке минимума и концах отрезка.
Задача 4. Найдите наибольшее значение функции на отрезке
Решение:
Найдем производную:
Приравняем производную к нулю:
Если то
Так как
Точка – точка максимума функции
В этой точке функция принимает наибольшее значение на указанном отрезке.
Ответ: 4.
Задача 5. Найдите наименьшее значение функции на отрезке
Решение:
Найдем производную функции:
при
Найдем знаки производной слева и справа от точки
Если то
Если то
Значит, – точка минимума. Наименьшее значение функции на отрезке достигается при
Это значение равно
Ответ: -1.
Задача 6. Найдите наибольшее значение функции на отрезке
Решение:
Область определения функции:
Найдем производную функции и приравняем ее к нулю:
если
или
Второй корень не принадлежит отрезку
Найдем знаки производной на отрезке:
В точке производная равна нулю и меняет знак с «плюса» на «минус». Значит, это точка максимума, и наибольшее значение функции на отрезке
достигается при
Найдем значение функции при
Ответ: -5.
В следующих задачах наименьшее значение функции достигается на конце отрезка.
Задача 7. Найдите наименьшее значение функции на отрезке
Решение:
Найдем производную функции и приравняем ее к нулю.
У этого уравнения нет решений, так как
Это значит, что при любых
то есть
а это означает, что
– убывает, наименьшее значение функции достигается в правом конце отрезка
Ответ: -3.
Задача 8. Найдите наибольшее значение функции на отрезке
Решение:
Найдем производную функции:
Производная функции не равна нулю ни при каком
.
Мы знаем, что Тогда
Прибавим 7 ко всем частям неравенства:
для всех
Значит, производная положительна при любом значении переменной, функция монотонно возрастает. Наибольшее значение функции будет достигаться в правом конце отрезка, то есть при
Ответ: 8.
Задача 9. Найдите наименьшее значение функции на отрезке
Решение:
Найдем производную функции и приравняем ее к нулю:
тогда
На указанном отрезке это уравнение имеет единственное решение
Слева от этой точки Если производная отрицательна.
Справа от этой точки производная положительна.
Значит, – точка минимума функции, и наименьшее значение функции на отрезке достигается в этой точке.
Найдем значения функции в этой точке:
Ответ: 7.
В задачах ЕГЭ встречаются сложные функции. И найти нужно их точки максимума или минимума, наибольшие или наименьшие значения. Но производную сложной функции в школьной программе по-настоящему не проходят. Как же быть? Покажем полезные приемы, помогающие решить такие задания ЕГЭ.
Задача 10. Найдите наименьшее значение функции
Решение:
Рассмотрим функцию
Так как функция монотонно возрастает, точка минимума функции
будет при том же значении
, что и точка минимума функции
А ее найти легко:
при
В точке производная
меняет знак с «минуса» на «плюс». Значит,
– единственная точка минимума функции
и функции
Ответ: -2.
Задача 11. Найдите наибольшее значение функции на отрезке
Решение:
Так как функция монотонно возрастает при
точка минимума функции
соответствует точке минимума подкоренного выражения
Заметим, что подкоренное выражение всегда положительно.
Функция задает квадратичную параболу с ветвями вверх и точкой минимума в вершине параболы, то есть при
Если – монотонно убывает.
Если – монотонно возрастает.
Значит, наибольшее значение функции на отрезке
достигается в одном из концов этого отрезка.
Сравним и
Ответ: 6.
Задача 12. Найдите точку максимума функции
Решение:
Рассмотрим функцию
Ее график – парабола с ветвями вниз, и точка максимума будет в вершине параболы, при Функция
монотонно возрастает, и значит, большему значению
будет соответствовать большее значение
Точка максимума функции будет такой же, как у функции
то есть
Ответ: 1.
Читайте также: Задание 11 на ЕГЭ по математике.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Таблица производных и правила дифференцирования» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023












