Как найти производную функции одной переменной

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

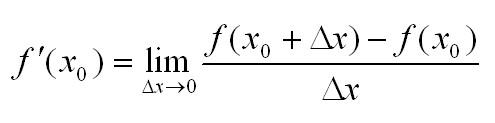
Иначе это можно записать так:

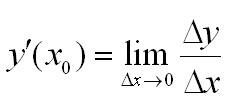
Какой смысл в нахождении такого предела? А вот какой:

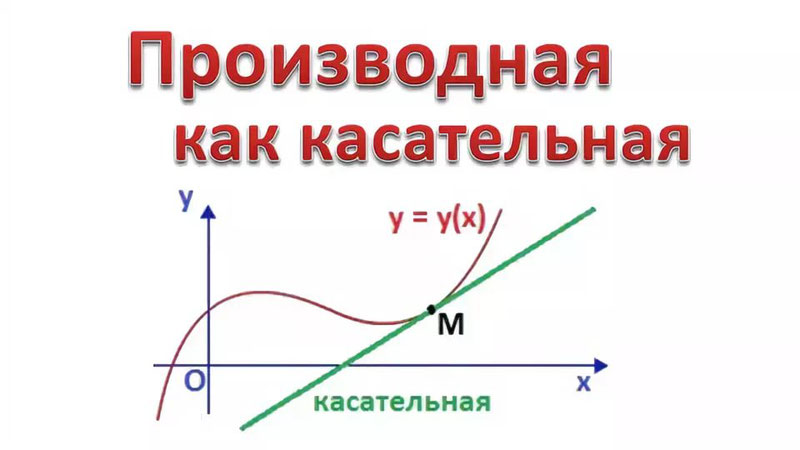
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

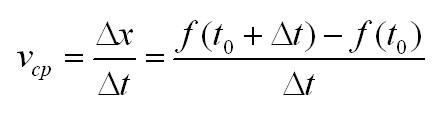
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

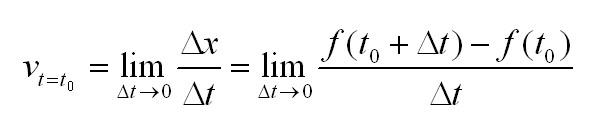
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.

Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

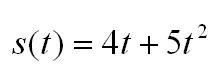
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

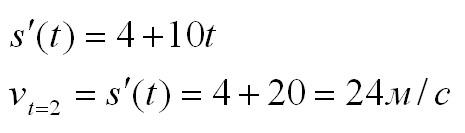
Правила нахождения производных

Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.

Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

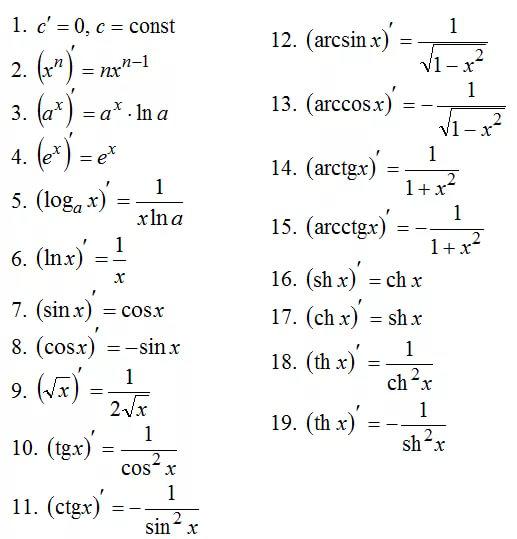
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.

Пример. Вычислим производную:

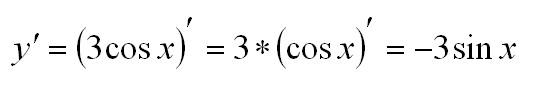
Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

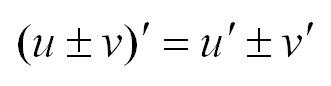
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

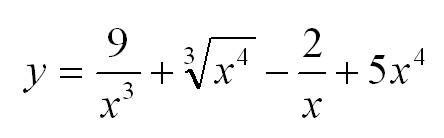
Решение:

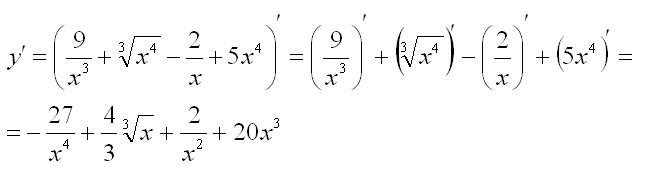
Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

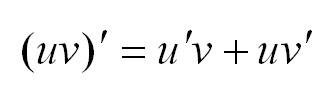
Пример: найти производную функции:

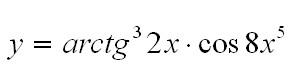
Решение: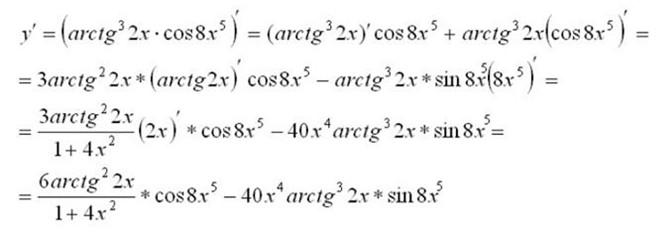

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

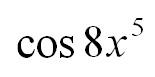
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

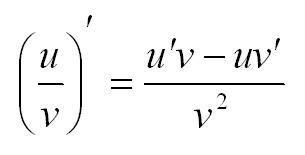
Пример:

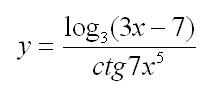
Решение:

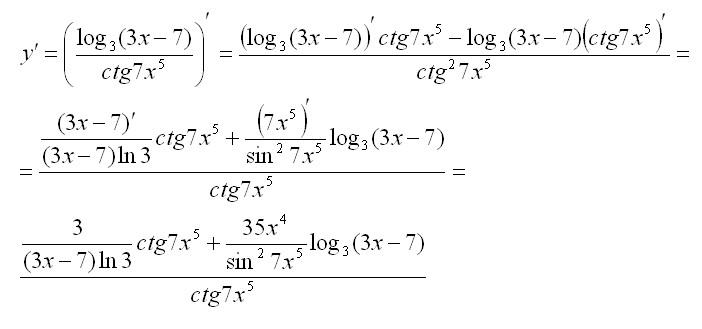
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Содержание:

Определение производной, её геометрический смысл:

Рассмотрим функцию

называется разностным отношением (в данной точке). Разностное отношение – это функция, которая определена для всех значений аргумента, кроме 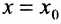. Это дает нам право рассматривать вопрос о существовании предела функции (11.1.1) при .

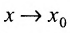Определение 11.1.1. Пусть функция y=f(x) определена в некоторой окрестности точки 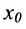и пусть х – некоторая точка этой окрестности, 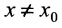. Если отношение

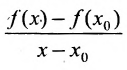имеет предел при 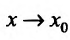, то этот предел называется производной функции f e точке 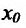и обозначается 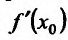, т.е.

Если ввести обозначения 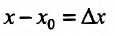и 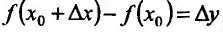, то формула (11.1.2) запишется в виде:

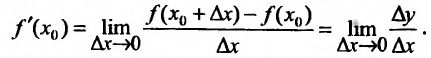
Если для некоторого значения 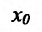выполняется условие

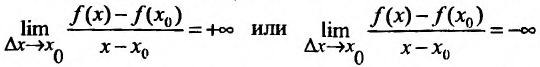, то говорят, что для этого значения 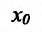существует бесконечная производная, равная л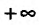ибо,либо.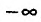

В дальнейшем под выражением «функция имеет производную» мы будем понимать, что функция имеет конечную производную, которую будем обозначать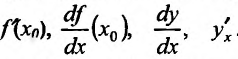

Определение 11.1.2, Если функция f определена в правосторонней (левосторонней) окрестности точки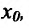 или существует конечный или бесконечный предел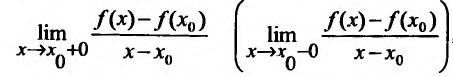

то он называется конечной или бесконечной производной справа (слева) функции f в точке х и обозначается f+(xq) (или f’.(x0)).

Из теоремы 10.2.1 об односторонних пределах следует, что функция f, определенная в некоторой окрестности точки 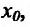, имеет производную 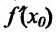тогда и только тогда, когда 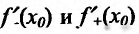суше-ствуют и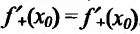. В этом случае

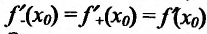
Заметим, что если у функции 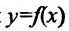существуют правая и левая производные в точке 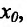, но эти производные не равны друг другу, то у этой функции не существует производной в точке 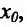Например, функция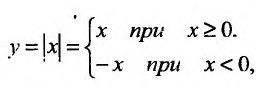

не имеет производной в точке 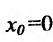, так как,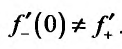. Поскольку правая производная равна: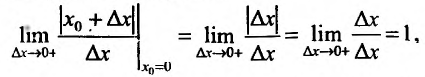

а левая производная равна: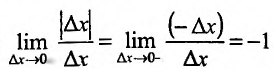

Понятие производной в данной точке связано с понятием касательной к графику функции в этой точке. Чтобы выяснить эту связь, определим, прежде всего, касательную.

Пусть функция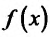 определена на интервале (а; b), непрерывна в точке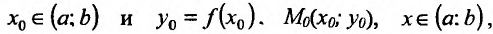 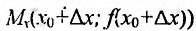. Уравнение секущей, как уравнение прямой, проходящей через две точки 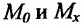имеет вид

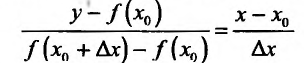
или

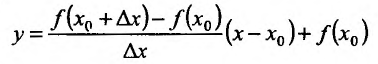
или

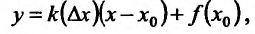
где

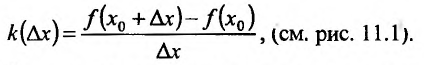
Если существует предельное положение секущей 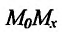при стремлении точки 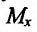графика функции к точке 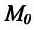(или, что то же самое, при стремлении 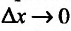), то это предельное положение называется касательной к графику функции 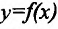в данной фиксированной точке 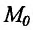этого графика. Отсюда следует, что для того, чтобы существовала касательная к графику функции 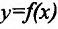в точке 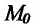достаточно, чтобы существовал предел

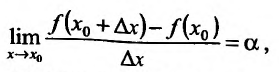
причем указанный предел 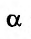равен углу наклона касательной к оси Ох.

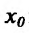Предположим, что функция имеет в данной точке изводную. Докажем, что существует касательная к графику фу ции 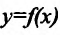в точке 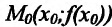, причем угловой коэффициент касательной (т.е. тангенс угла наклона ее к оси Ох) равен производной .

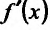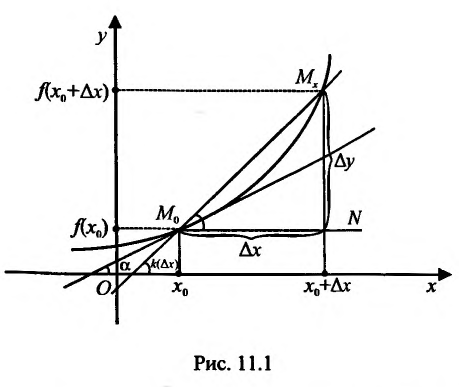
Рассмотрим рис. 11.1. Из треугольника 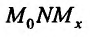найдём

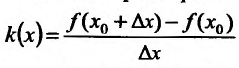и вычислим предел k(х) при.

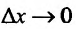Поскольку в точке 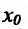существует производная, то существует пред

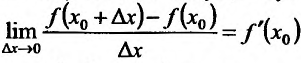но тогда и существ”

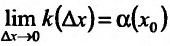. Отсюда и из непрерывности функции f(x) следует, что 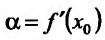. А это означает, что существует касателые графику функции y=f(x) в точке 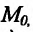, угловой коэффициент ко равен производной функции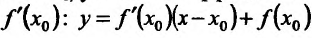

Правила вычисления производных, связанные с арифметическими действиями над функциями

Предположим, что все функции, рассматриваемые ниже, определены в некоторой окрестности точки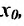

Теорема 11.2.1. Если функция f имеет производную в некоторой точке 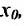, то она непрерывна в этой точке.

Доказательство. Рассмотрим разность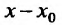 и соответствующее приращение функции 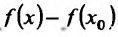. Найдём предел приращения функции при :

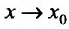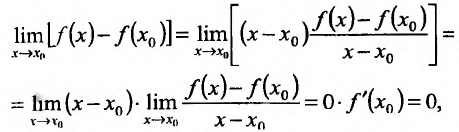
т.е. бесконечно малому приращению независимой переменной соответствует бесконечно малое приращение функции, значит, / непрерывна в точке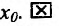

Заметим, что обратная теорема не верна, т.е. функция может быть непрерывной в точке 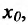но не иметь производной в этой точке. Примером служит функция 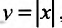которая непрерывна в точке х=0, но, как мы уже показывали в п. 11.1. не имеет в этой точке производной

Теорема 11.2.2. Если функции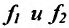 имеют производные в данной точке 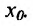то и сумма функций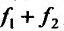, разность функций 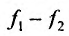имеют производные в точке 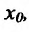которые вычисляются по формулам:

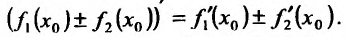
Доказательство. Пусть функции 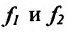имеют производные в точке 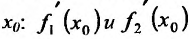. Докажем, что их сумма 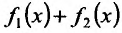так-же имеет в точке 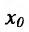производную и 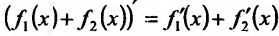Обозначим

и вычислим приращение функции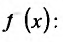

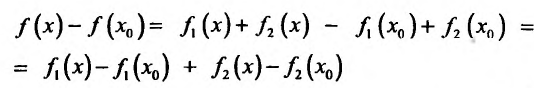
Составим разностное отношение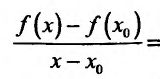

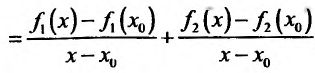
, если 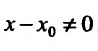, и вычислим предел этого разностного отношения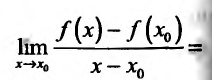 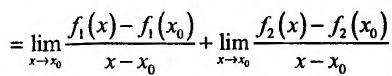Предел суммы равен сумме пределов, так как пределы слагаемых существуют. Пределы слагаемых равны, соответственно, 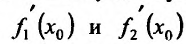. Следовательно, в точке 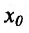предел правой части равенства существует и он равен 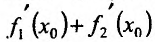• Значит, существует предел левой части, который силу определения производной равен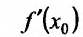. Поскольку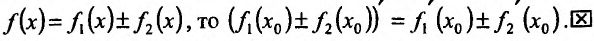

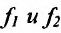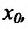Теорема 11.2.3. Пусть функции имеют производные точке , тогда и произведение 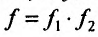имеет в точке 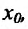производную, причём

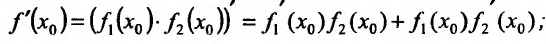
а если 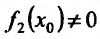, то и частное 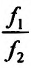также имеет в точке 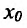проводную, вычисляемую по формуле:

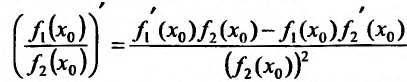
Доказательство. Пусть 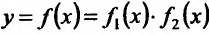. Тогда приращение функции равно 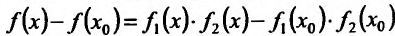. Обозначая 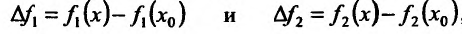, выразим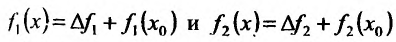

Подставим эти выражения в формулу приращения функции f, получим:

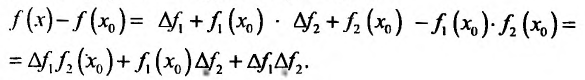
Составим разностное отношение

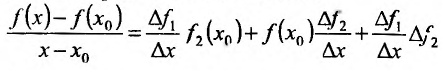
Рассматривая предел разностного отношения при 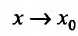, т.е. при 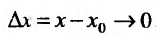, будем иметь

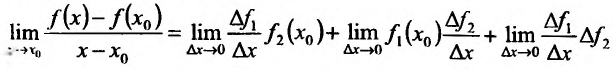
или

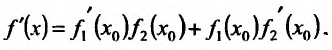
так как 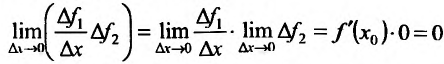(функция 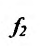имеет производную в точке 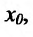следовательно, она непрерывна, и значит).

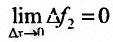Пуста 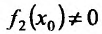. Тогда существует такое h>0, что 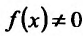для всех 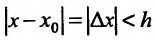. Выбрав 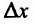такое, что 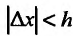, рассмотрим приращение функции

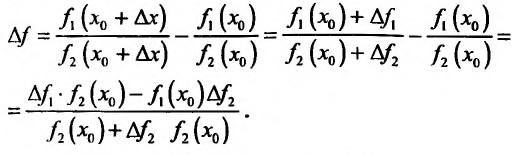
Поэтому 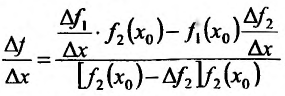Вычислив предел разкостного отношения при 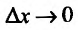и воспользовавшись определением производной, как и при доказательстве предыдущей формулы,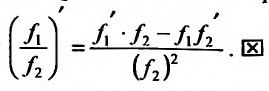

Следствие 11.2.1. Пусть функция f имеет производную в точке 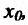, тогда функция cf(x) (с- постоянная) также имеет в этой точке производную, причём ‘.

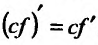Следствие 11.2.2. Пусть функции 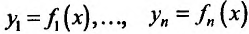имеют производные в точке 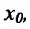, тогда функция 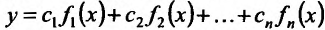также имеет в точке 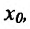производную, причём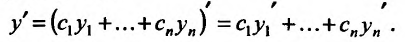

Производные сложной и обратной функций

Определим правила, позволяющие вычислять производные обратных и сложных функций.

Теорема 11.3.1. Пусть функция f определена, непрерывна и строго монотонна в некоторой окрестности точки 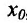и пусть в точке хо существует производная 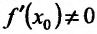, тогда и обратная функция 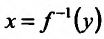, определенная в некоторой окрестности точки 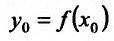имеет производную в точке 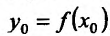, причём 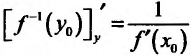т.е. производная обратной функции равна обратной величине производной данной функции.

Доказательство. Зафиксируем некоторую окрестность точки 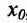, на которой функция f определена, непрерывна и строго монотонна и рассмотрим функцию только в этой окрестности. Тогда существует однозначная обратная функция непрерывная, строго монотонная на некотором интервале, содержащем точку 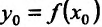(на образе указанной выше окрестности точки 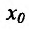и поэтому условия 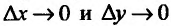эквивалентны).

Зададим аргументу у функции 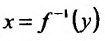произвольное достаточно малое и отличное от нуля приращение 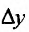. Этому приращению соответствует приращение обратной функции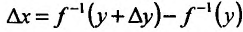, отличное от нуля. Тогда отношение 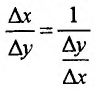имеет предел и 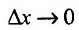при и при 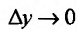, т.е.

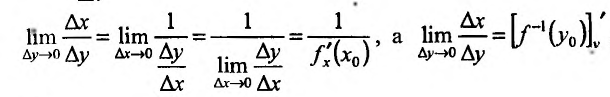, поэтому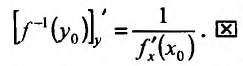

Эта теорема допускает наглядную геометрическую интерпретацию (рис. 11.2).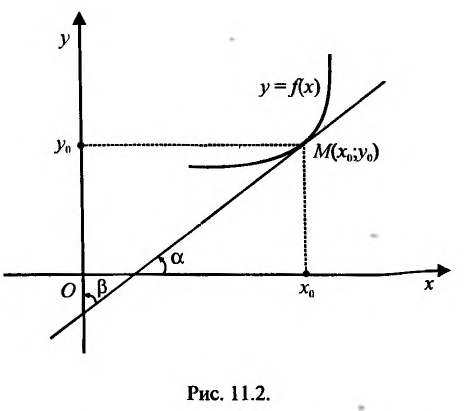

Известно, что производная функции в точке 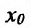равна тангенсу угла наклона касательной к графику функции в точке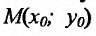

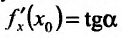
Поскольку у функции 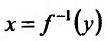аргументом является переменная у, то в силу геометрической интерпретации производной можно утверждать, что производная обратной функции с геометрической точки зрения – это тангенс угла, который образует касательная к графику функции 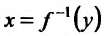в точке М, с положительным направлением оси Оу, т.е. .

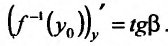Поскольку 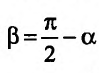, то,

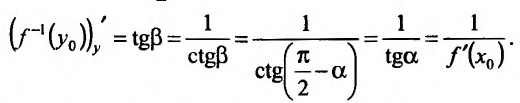
Пример №1

Найти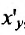, если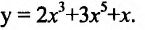

Решение:

Имеем 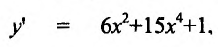тогда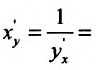

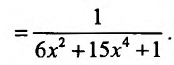
Теорема 11.3.2. Пусть 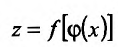– сложная функция, и пусть функция 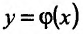имеет производную в точке 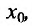, а функция 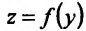имеет производную в точке 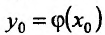. Тогда сложная функция 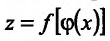так же имеет производную в точке 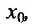причём:

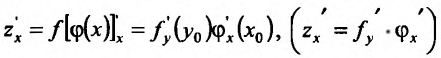
Доказательство. Придадим приращение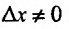 независимой переменной х функции 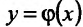. Этому приращению соответствует некоторое приращение 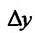функции у, равное 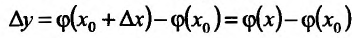. Пусть 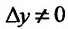. Тогда приращению соответствует приращение функции 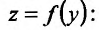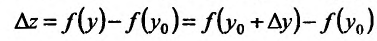и пус^ оно не Равно НУЛЮ

Составим разностное отношение 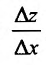, которое представим в виде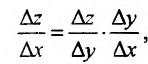

поскольку 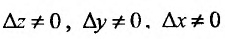. Из непрерывности Дх Ау Ах

функции 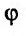следует, что, при 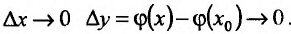. Следовательно,

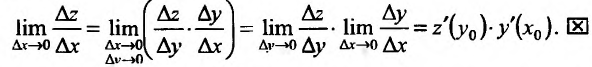
Заметим, что, используя правило вычисления производной сложной функции, можно находить производные функций, заданных неявно

Действительно, пусть функция 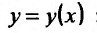задана неявно уравнением F(x,y)= 0. Вычисляя производную правой и левой части тождества 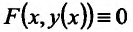как производную сложной функции, находим 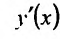разрешая полученное равенство после вычисления производной относительно .

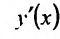Пример №2

Найти 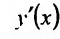, если :

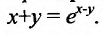
Решение:

Дифференцируем данное уравнение по х, считая у функцией от х:

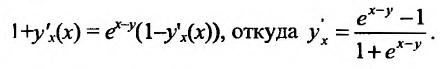
Таблица производных

Для непосредственного вычисления производной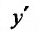 функции 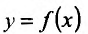на основании определения производной выполняют операции по следующему правилу:

1. выбирают приращение аргумента 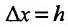, находят соответствующее приращение функции 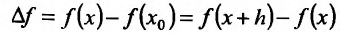и составляют разностное отношение ;
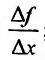2. преобразуют разностное отношение;
3. вычисляют предел преобразованного разностного отношения, при

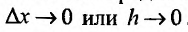
Если предел существует, то и производная существует и она равна пределу разностного отношения.

Применим это правило для определения производных простейших функций.

Свойство 11.4.1. у = с (const).

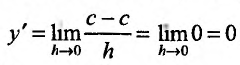,т.е. производная постоянной, равна нулю.

Свойство 11.4.2. у = sin x .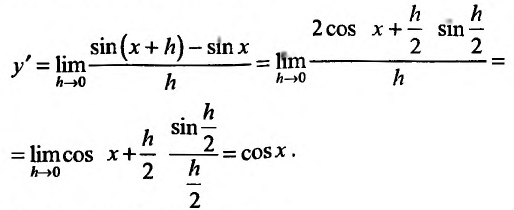

Свойство 11.4.3. у = cos x.

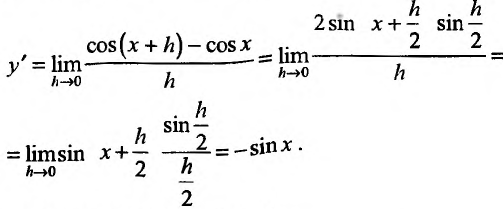
Свойство 11.4.4.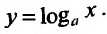

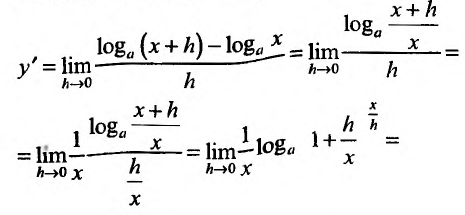
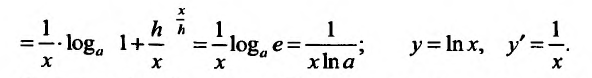
Свойство 11.4.5. у = tg x. Применим правило для производной частного двух функций:

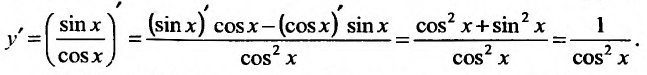
Свойство 11.4.6. у = ctgx Применяя правило дифференцирования частного, будем иметь: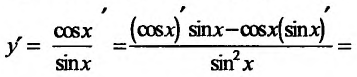

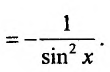
Свойство 11.4.7.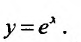

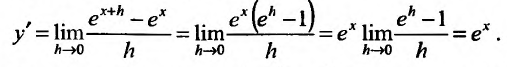
Свойство 14.4.8. 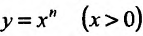. Пользуясь определением логарифма, мы можем представить нашу функцию в виде сложной функции 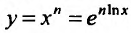. По правилу вычисления производной сложной функции, получим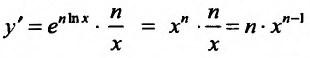

Свойство 11.4.9. у = arcsinх. Если 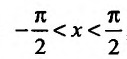то функция 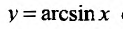обратная по отношению к функции x = siny, и применив правило вычисления производной обратной функции, имеем: 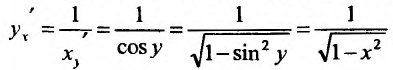, причем у радикала надо брать знак «+», т.к. cos y имеет в интервале 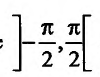знак«+». Аналогично,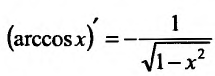

Свойство 11.4.10. у = arctgx. Если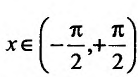 то Функция у = arctg x обратная по отношению к функции x = tg у ; следовательно, 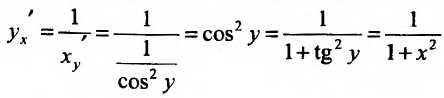. Аналогично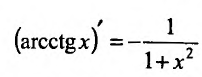

Свойство 11.4.11. 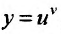, где u и v функции от х ( называется степенно-показательной функцией). Воспользовавшись определением логарифма, заданную функцию 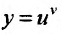можно представить в виде 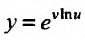. Применяя правило вычисления производной сложной функции, получим:

Свойство 11.4.12. 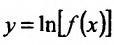, где f(x) – постоянно положительная функция. Применяя правило вычисления производной сложной функции, получим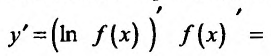 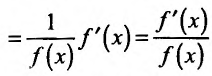. Выражение 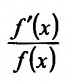называется логарифмической производной.

Приведём таблицу производных простейших элементарных функций:

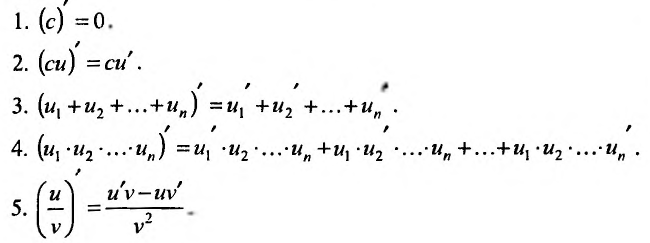
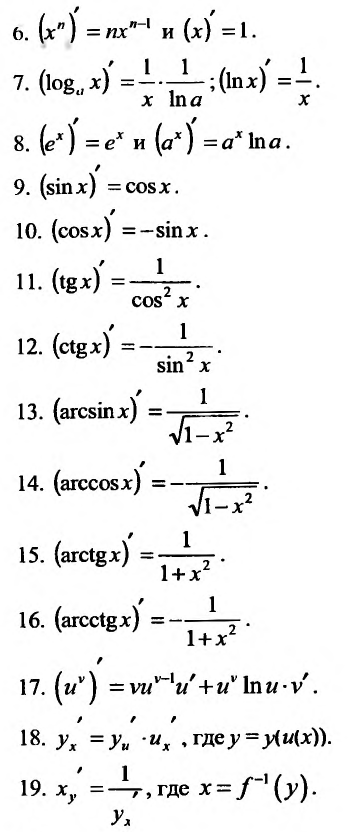
Пример №3

Вычислить производную функции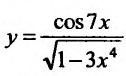

Решение:

Воспользовавшись формулой вычисления производной частного, получим:

• Заказать решение задач по высшей математике

Пример №4

Вычислить производную функции ;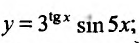

Решение:

Воспользовавшись формулой вычисления производной произведения, получим:

Пример:

Вычислить производную функции у = In arcsin/6х;

Решение:

Воспользовавшись формулой вычисления производной сложной функции, получим:

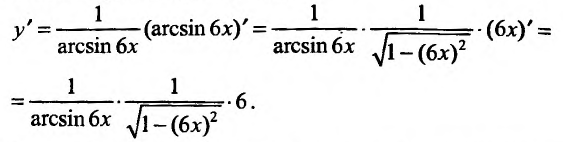
Выведем ещё формулу для вычисления производной параметрически заданных функций, т.е. функций, заданных формулами вида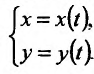

Если функции x = x(t) И y = y(t) имеют в точке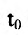 производные и если 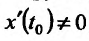, то параметрически заданная функция 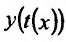также имеет в точке 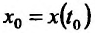производную, причём

В самом деле, по правилу вычисления производной сложной функции имеем 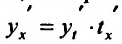. Поскольку t=t(x) – функция, обратная к функции x=x(t), то 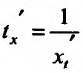. Тогда, подставив значение производной 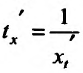в формулу 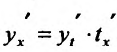.получим (11.4.1).

Производные высших порядков

Производная 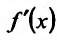функции 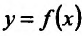, определенной на интервале (а, b) и имеющей производную в каждой точке этого интервала (a,b), представляет собой функцию, также определенную на интервале (a,b). И если эта функция 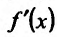имеет производную в некоторой точке, то можно ввести следующее определение:

Определение 11.5.1. Пусть функция f определённая на интервале (а.b), в каждой точке 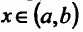имеет производную 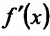и пусть 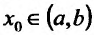. Производная функции 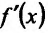в точке 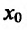называется второй производной функции f и обозначается ,

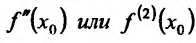т.е.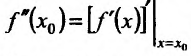

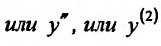
После того, как введено определение второй производной, можно последовательно ввести определение третьей производной, затем четвертой производной, и т.д. Если предположить, что уже введено определение (n-1)-ой производной и что (n-1)-ая производная имеет производную в некоторой точке 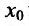интервала (a,b),то эту производную называют n-ой производной (или производной n-ого порядка) функции 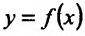в точке 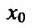и обозначают 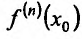или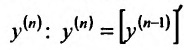

Кроме того считают, что 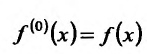. Ясно, что 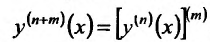– Заметим, что если функция f имеет в точке 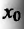. производную порядка n, т.е. если существует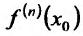. то отскг следует, в силу определения производной, что в некоторой о ности существуют все производные низших порядков.

Определение 11.5.2. Функция f называется n раз непрерывной дифференцируемой на некотором промежутке, если на этом промежутке существует непрерывная производная n-ого порядка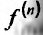 функции f.

По индукции можно доказать, что: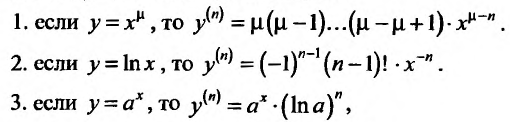

в частности , если

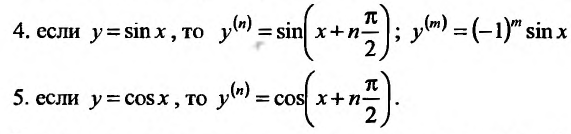
Кроме того, по индукции можно доказать, что сумма функций,, слагаемые которой имеют производные n-го порядка, также имеет производную n-го порядка, вычисляемую по формуле:’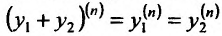 и произведение функций имеет производную n-го порядка, вычисляемую по формуле Лейбница:

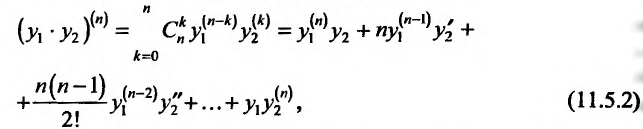
где 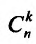– число сочетаний из n элементов по к: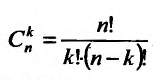

Рассмотрим некоторые производные 2-го порядка:

– для сложной функции 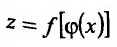вторая производная вычисляется по формуле:

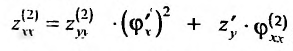
– для обратной функции 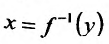вторая производная вычисляется по формуле;

так как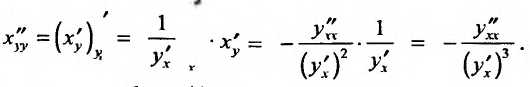

для функции 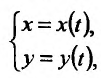заданной параметрически, производная второго порядка вычисляется по формуле:

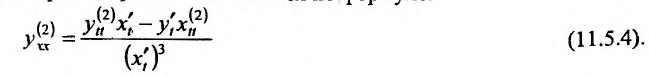
Действительно, так как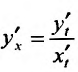, то

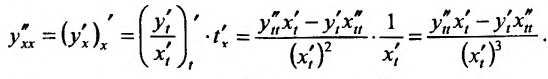
Пример №5

Найти 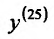если .

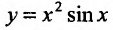Решение:

Полагая в формуле Лейбница (11.5.2) ,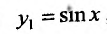

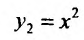и учитывая, что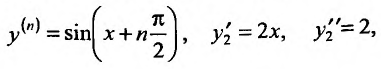

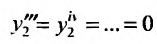, получим:

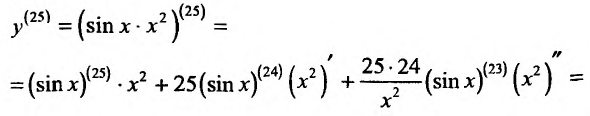
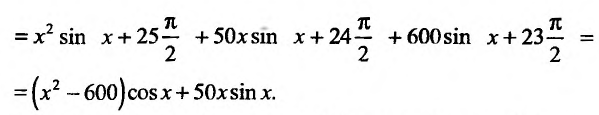
Подчеркнем, что формула Лейбница особенно эффективна в том случае, когда одна из перемножаемых функций имеет лишь конечное число отличных от нуля производных и не представляет затруднения вычисление всех производных другой из перемножаемых функций.

Если вы ничего не смыслите в том, что такое производная и какими методами можно её вычислить, то совершенно невозможно решать примеры по математике или задачи по физике. Ведь такое понятие, как производная, является одним из самых важных в математическом анализе.

В этой статье мы расскажем вам, что является производной, какой она имеет геометрический и физический смысл. В общем, мы с вами попытаемся понять производную.

Геометрический и физический смысл производной

Задаём функцию f(x) в интервале (a, b). А точки x и x0 этому интервалу принадлежат. Если изменится x, то и функция тоже изменится. Изменением аргумента является разность его значений x-x0. Записывается эта разность, как дельта икс и имеет название: приращение аргумента. Разность значений функций в двух точках называется приращением или изменением функции. Так каково определение производной?

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Можно записать ещё следующим образом:

Встаёт вопрос, для чего нужно находить такой предел? Вот и ответ:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Ещё в школе нас учили тому, что скорость – это частное пути x=f(t) и времени (t). Вычисляем среднюю скорость за какой-то временной промежуток:

Для того чтобы нам узнать какова скорость движения в момент t0, необходимо вычислить предел:

Сейчас мы разберем один пример, который продемонстрирует вам применение производной на практике. Допустим, тело движется по закону:

Нам необходимо рассчитать скорость в момент времени t=2c. Вычисляем производную:

Правила нахождения производных

Дифференцирование – это процесс нахождения производной. А дифференцируемая функция – это функция, которая имеет производную в данной точке.

Каким образом нам найти саму производную? Нам необходимо составить отношения приращения функции и аргумента, а после вычислить предел при условии стремящегося к нулю приращения аргумента. Но практика показывает, что такой путь вычисления является очень долгим. Всё, что нам необходимо, уже посчитано. И специально для вас, мы подготовили таблицу с производными элементарных функций.

После таблицы мы рассмотрим правила по вычисления производных. Коснёмся мы и вычисления производных сложных функций. Подробно разберём всё на примерах.

Правило первое: выносим константу

Вынести константы можно за знак производной. Причём делать это необходимо! Когда вы решаете примеры по математике, то всегда помните правило – если есть возможность упростить выражение, то делайте это.

Для примера вычислил с вами производную:

Правило второе: производная суммы функций

Производная суммы двух функций равняется сумме производных этих функций. Это касается и производной разности функций.

Сейчас мы с вами на практике рассмотрим пример доказательства этой теоремы.

Найти производную функции:

Решение:

Правило третье: производная произведения функций

По следующей формуле мы сможем вычислить производную произведения двух дифференцируемых функций:

К примеру: необходимо найти производную функции:

Решение:

Необходимо сказать о том, каким образом вычисляются производные сложных функций.

Производная сложной функции равняется произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В примере, который указан выше, мы можем встретить выражение:

В этом примере промежуточным аргументом является 8x в пятой степени. Чтобы нам вычислить производную данного выражения, то для начала необходимо высчитать производную внешней функции по промежуточному аргументу, а после необходимо умножить на производную непосредственно сам промежуточный аргумент по независимой переменной.

Правило четвертое: производная частного двух функций

Ниже приведена формула для того, чтобы определить производную от частного двух функций:

Пример:

Решение:

В данной статье мы попытались рассказать о производных для тех, кто совершенно не знаком с этой темой. Когда вы будете решать примеры, то будьте очень внимательны, ведь в них часто можно встретить ловушки. Эта тема не так уж и проста, какой кажется на первый взгляд.

Вы можете обратиться в наш студенческий сервис по любым вопросам. Мы с удовольствием поможем решить для вас задачи любой сложности. А занимались вы раньше вычислением производных или нет, не имеет никакого значения. Мы помогаем всем!

Содержание:

1. Дифференциальное вычисление функции одной переменной 
2. Определение производной
3. Основные правила и формулы дифференцирования 
4. Логарифмическое дифференцирование
5. Производная неявной функции
6. Параметрическое задание функции 
7. Производные высших порядков 
8. Механическое и геометрическое содержание производной
9. Геометрическое содержание производной 
10. Касательная и нормаль к кривой
11. Дифференциал функции
12. Вычисление основных дифференциалов 
13. Инвариантность формы первого дифференциала 
14. Использование дифференциала для приближенных значений
15. Экономическое использование дифференциала. Мультипликатор
16. Правило Лопиталя и использование его к нахождению границ функции 
17. Некоторые основные теоремы дифференциального вычисления
18. Теорема Лагранжа (про оконченные прироста функции)
19. Экономическое содержание теоремы Лагранжа 
20. Формула Тейлора 
21. Использование формулы Тейлора в экономических задачах 
22. Разложение основных элементарных функций по формуле Тейлора 
23. Экономическое содержание производной
24. Задача на продуктивность работы 
25. Эластичность 
26. Эластичность элементарных функций
27. Использование эластичности в экономическом анализе
28. Исследование функций и построение их графиков
29. Возрастание и спад функции
30. Определение максимума и минимума функции
31. Необходимое условие экстремума
32. Первое достаточное условие существования экстремума функции
33.  Правило для исследования функции на экстремум с помощью первой производной (первый способ)
34. Правило для исследования функции на экстремума по второму признаку (второй способ)
35. Наибольшее и наименьшее значение функции на отрезке
36. Задачи про наибольшие и наименьшие значение величин
37. Использование производной для исследования динамики функций
38. Выпуклость и вогнутость функции
39. Общий план доказательства функции и построение ее графиков 
40. Дифференциальное исчисление функции одной переменной
41. Определение производной, общий порядок ее нахождения, связь производной с непрерывностью функции
42. Интерпретация производной в различных областях знаний
43. Задача об определении уравнения касательной и нормали
44. Задача о нахождении скорости прямолинейного движения
45. Задача о нахождении предельных издержек производства
46. Таблица производных и правила дифференцирования
47. Дифференцирование составленных функций и функций различной формы задания
48. Производная обратной функции
49. Производная неявной функции
50. Логарифмическое дифференцирование
51. Производная функции, заданной параметрически
52. Дифференциал функции и его свойства
53. Применение дифференциала в приближенных вычислениях
54. Производные функции и ее дифференциалы высших порядков
55. Задача о нахождении ускорения прямолинейного движения материальной точки.
56. Задача о нахождении скорости изменения экономических показателей
57. Применение производных высших порядков в приближенных вычислениях. Формула Тейлора для многочлена и произвольной функции
58. Формула Тейлора для многочлена
59. Формула Тейлора для произвольной функции

Дифференциальное вычисление функции одной переменной 

Во время изучения экономических понятий, таких. как спрос, затраты производства, национальный прирост, часто приходится обозначать скорость смены значений соответственных величин. Решая такие задачи, используют методы дифференциального вычисления. 

Определение производной

Производной функции  к аргумента  называется граница отношение ее прироста  к соответственному прироста  независимой переменной, когда 

Производная обозначается  или   или  Операция нахождения производной  заданной функции  называется дифференцированием этой функции. 

Функция называется дифференцированной в некоторой точке  если в этой точке она имеет определенную производную  то есть если  существует и имеет одно и то же значение, если  любым способом. При этом функция будет и непрерывной в этой точке 

Непрерывность функции является необходимым условием дифференциации функции. 

Для непосредственного нахождения производной  от функции  служит следующее правило: 

 Дадим аргументу   произвольный прирост  и подставляя в заданное выражение функции вместо  наращенное значение   получим наращенное значение функции 

 Отнимая из наращенного значения функции ее начальное значение, находим прирост функции 

 делим прирост функции на прирост аргумента, то есть складывается отношение 

 Находим границу этого отношения, если  Эта граница и дает искомую производную  от функции 

Пример 4.1 

Путем нахождения границы  найти производные следующих функций: 

Решение. Воспользовавшись указанными общими правилами для непосредственного нахождения производной, последовательно находим: 

1) Для функции 

2) Для функции 

Основные правила и формулы дифференцирования 

Практически же производные функции находят по основным правилам и основными формулами дифференцирования. 

Основные правила дифференцирования: 

7. Пусть  сложная функция, то есть  Если для соответствия один к одному значению   и  существует производные   и  то существует производная от  к  причем 

Воспользовавшись этим соотношением, таблицу формул дифференцирования можно подать так; ( – постоянная величина). 

Пример 4.2 

Найти производные, воспользовавшись формулами дифференцирования: 

 вычислить 

Решение 

2) Введем дробные и отрицательные показатели, преобразуем заданную функцию: 

воспользовавшись формулами (9а, 4, 2), получим: 

3) По формуле (5) получим при 

после упрощения:

5) используем формулу (6). получим:

8) используя формулу (8) получим 

9) Введем дробные и отрицательные показатели, а потом найдем производную от суммы и по формуле (18а), получим: 

Вычислим  Подставим в значение производной 

10) сначала находим производную синуса, а так как синус берется от  то находим производную от  производная заданной функции равна произведению этих производных.

11) Во первых необходимо продифференцировать тангенс. но так как он берется от дроби, то следует найти производную дроби и полученные производные умножить: 

Постоянный множитель 3 выносим за знак производной. Потом продифференцируем степень, а так как в степень заноситься  то дифференцируем и  найденные результаты перемножаем. 

14) Рассмотрим формулу (14): 

Производная от функции  находится так: единица делится на квадратный корень из единицы минус квадрат той функции, которая стоит под знаком арксинуса, и эта дробь умножается на производную этой функции. Через это можно выразить: 

запомним, что производная функции  равна дроби. в котором числитель равен 1, а знаменатель равен 1 плюс квадрат функции, что стоит под знаком арктангенса и дробь умножается на производную этой функции 

продифференцируем сначала степень. Так как степень преподноситься  то есть взять производную от  а потом производную от  

по формуле (18а) получим: 

по формуле (18б) получим: 

по формуле (19б) если  то  получим, 

тут сначала дифференцируется степень логарифма. а потом берется производная от  логарифмической функции. 

Сначала преобразуем заданную функцию согласно свойствам логарифмов, а потом дифференцируем по формуле:  

заданная функция является показательно – степенной –  где  производная которой находится по формуле: 

Логарифмическое дифференцирование

если необходимо продифференцировать произведение нескольких функций или дробей, числитель и знаменатель которого содержать произведение, часто целесообразно обе части выражения сначала прологарифмировать с основой   а потом приступить к дифференцировании. этот способ получил название логарифмического дифференцирования. Производная от логарифма функции называется логарифмической производной. 

К этому способу удобно прибегать и при дифференцировании выражений, что содержат корни дробей. Этим способом воспользуются тогда, когда необходимо продифференцировать функцию вида:  то есть, когда основа степени и показатель степени является функцией от 

Пример 4.3

Найти производную функции: 

Решение 

Сначала прологарифмируем с основой обе части равенства, а потом будем дифференцировать 

Производная неявной функции

Если независимая переменная   и функция связаны уравнением вида  которое не решено относительно , то  называется неявной функцией . 

 Метод нахождения производной в этом случае состоит в том, что обе части уравнения  дифференцируем к  с учетом, что  является функциейи из полученного уравнения определим 

Пример 4.5

Найти производную  функции . 

Решение 

Прологарифмируем обе части данного уравнения, потом продифференцируем к рассматривая   как функцию .

Параметрическое задание функции 

В геометрии часто вводится так называемый параметрический способ задания уравнения кривой. Кривую линию можно рассмотреть как геометрическое место последовательных положений движущейся точки, а координаты  и  этой точки выразить в виде непрерывной функции вспомогательной переменной  которая называется  параметром. Плоская кривая в таком случае обозначается двумя уравнениями: 

Например. Кривая задана параметрическими уравнениями 

 – это эллипс 

Производная функции 

что задана параметрическим уравнением. находятся по формуле: 

Производная второго порядка обозначается по формуле: 

Пример 4.6 

Найти при  производные   и   функции 

Решение 

Найдем: 

Производные высших порядков 

Производная  от функции  в общем случае является функцией  Если от этой функции  найти производную, то получим производную второго порядка, или вторую производную функции  и она обозначается  или  или 

Аналогично определяются производные любого порядка: 

Производная третьего порядка: 

Производная четвертого порядка: 

Производная порядка: 

Для нахождения производной любого высшего порядка от заданной функции нудно последовательно находить все ее производные нижних порядков. 

Для произведения двух функций можно получить производную любого   порядка, воспользовавшись формулой Лейбница: 

Пример 4.7

  Найти  

Решение 

Пример 4.8

  Найти  

Решение 

Пример 4.9

  Найти  

Решение 

Механическое и геометрическое содержание производной

Источником дифференциального вычисления стали, как известно, два вопроса: 

• 1) про поиск скорости в случае произвольного закона движения;
• 2) про поиск касательной к произвольной кривой. 

Они обе привели к одной и той же задачи, которая была положена в начало дифференциального вычисления. 

В механике соответственная задача формируется так: найти скорость тела, что движется по закону  в некоторый момент времени  Учтем, что расстояние   и время  – физические величины, которые можно измерить.

Пусть на время от  к  тело прошло путь 

Тогда 

Средняя скорость тела, что движется вдоль некоторой линии, обозначается по формуле: 

Чтобы найти мгновенную скорость  такого тела, нужно перейти к границе отношения  при 

Мгновенной скоростью тела, что движется вдоль линии называется производная функции  за время : 

Пример 4.13 

Точка движется по кубической параболе  которая из ее координат изменится быстрее? 

Решение. Учитывая в уравнении параболы  сложной функцией от часа  и дифференцирования его по , получим: 

отсюда находим соотношение скорости ординаты и абсциссы: 

При  это отношение будет меньше 1, при  равно 1, и при  оно будет больше 1.

Следует: 

Геометрическое содержание производной 

Пусть дана функция   график которой приведен на рис. 4.1. Отношение   равно тангенсу угла   образованного секущей. что проходит через точки   и   которые имеют соответственно абсциссы   и  с положительным направлением оси  Если прирост  то точка  направляется к точке . а угол  – к углу  образованного касательной к рассматриваемой кривой в данной точке с положительным направлением оси 

Следует, получим 

Значение производной в некоторой точке равно тангенсу угла, образованного касательной к кривой в этой точке с положительным направлением оси  – в этом заключается геометрическое содержание производной.
 

Касательная и нормаль к кривой

Рассмотрим уравнение кривой  (рис. 4.2) Возьмем на кривой точку  и сложим уравнение касательной к этой кривой в точке  допуская, что касательная не параллельна ни одной координатной оси. Получим: 

Для касательной  потому уравнение касательной будет:  

из определения нормали получается, что ее угловой коэффициент  связанный с угловым коэффициентом  равенством: 

то есть 

Следует, получим уравнение нормали к кривой  в точке 

 

Пример 4.14 

Сложить уравнение касательной и нормали: 

1) к параболе  в точке, где 

2) к кривой  в точке 

3) к кривой   в точке 

Решение.

1) подставим в уравнение параболы заданную абсциссу точки касания    и найдем ее ординату: 

для определения углового коэффициента касательной найдем производную  из уравнения параболы и вычислим значение производной в точке 

Подставляя  в уравнение касательной  получим уравнение касательной:  или  и уравнение нормали  или 

2) Проверим, заданная  точка  является ли тоской касания: 

найдем угловой коэффициент: 

Уравнение касательной: 

Уравнение нормали: 

3) находим производную по правилу дифференцирования  неполной функции 

Уравнение касательной: 

Уравнение нормали: 

Пример 4.15 

Найти  уравнение касательной и нормали к кривой: 

в точке, где 

Для того, чтобы воспользоваться формулами уравнений касательной и нормали, необходимо обозначить  при   Сначала обозначим  и 

после этого находим  производной в точке 

Уравнение касательной: 

Уравнение нормали: 

Дифференциал функции

Из определение производной   и границе переменной следует, что   или  где  если   то есть прирост функции может быть предоставлен в виде суммы двух множителей. Первый множитель   содержит прирост  независимой переменной в первой степени, то есть он линейный относительно . Это первый множитель является главной частью прироста функции. 

Главная часть прироста функции  линейная относительно прироста независимой переменной, называется дифференциалом функции и обозначается знаком

Дифференциал независимой переменной  равен ее приросту 

Через это 

то есть дифференциал функции равен ее производной, умноженной на дифференциал независимой переменной. Следует, чтобы найти дифференциал какой – нибудь функции, необходимо найти производную этой функции и умножить ее на дифференциал независимой переменной. 

Вычисление основных дифференциалов 

Таблица для вычисления дифференциалов основных элементарных функции получится из таблицы производных этих функций путем умножения соответственной производной на дифференциал независимой переменной 

Правила вычисления дифференциалов: 

 где 

Инвариантность формы первого дифференциала 

Пусть  где  является независимой переменной, тогда дифференциал этой функции запишется в виде 

Если   где  тогда функция  будет сложной функцией от переменной  Вычислим дифференциал этой функции: 

Следует, мы вернулись к виду дифференциала, который был записан с допущением, что переменная  является переменной. получим свойство дифференциала, которая называется инвариантностью. 

Использование дифференциала для приближенных значений

Известно, что 

Если  то 

Полученная формула позволяет с известными значениями функции и ее производной в точке   найти приближенное значение функции в точке  что близка к  и тем самым дает возможность   использовать дифференциал функции для нахождения приближенных значений. 

Экономическое использование дифференциала. Мультипликатор

Рассмотрим простейшую модель, которая описывает динамику возрастания прибыли зависимо от инвестиций  где  – прибыль,  – потребление,  – инвестиции. Пусть   Как получается изменение инвестиций  на прибыль?

Пусть  Из уравнения  найдем зависимость между инвестициями и скоростью возрастания прибыли:

 

то есть 

или в дифференциалах 

Выражение    называется мультипликатором 

Мультипликатором – числовой коэффициент, который показывает, сколько раз сумма прироста или сокращение прибыли превышает начальную сумму инвестиций. 

Термин впервые был введен в 1931 р. Ф. Каюмом и был приобрел дальнейшее развитие в кейнсианский модели определения равна равновесию прибыли. 

В рассмотренной модели получим: если  то 

Следует, дополнительные инвестиции усиливают прибыль.

Решение примеров:

Пример 4.18

Найти дифференциал функции 

Решение. Находим производную данной функции и умножим на дифференциал независимой переменной, получим дифференциал данной функции 

Пример 4.19 

Вычислить приблизительно 

Решение. Если необходимо вычислить   и если проще вычислить    и   то при достаточно малой к абсолютному значению разницы  можно заменить прирост функции ее дифференциалом 

Пусть  является значение функции  при 

Пусть   тогда 

Воспользовавшись формулой  получим: 

Правило Лопиталя и использование его к нахождению границ функции 

Раньше были пояснены элементарные способы нахождения границ функции в тех случаях, когда аргумент неограниченно возрастает или направляется к значению, которые не входят в область определения функции. Кроме этих элементарных способов, эффективным способом для нахождения этих элементарных способов, эффективным способом для нахождения границы функции в указанных особенных случаях является следующее правило Лопиталя: граница отношения двух бесконечно малых или бесконечно больших величин равна границы отношения их производных. 

4.5.1 Случаи   и 

Случаи нахождения границ:

1)   – когда функция представляет отношение двух бесконечно малых величин; 

2)   – когда функция представляет отношение двух бесконечно больших величин; 

Согласно правилу Лопиталя в этих случаях можно заменить отношение функций отношений их производных, то есть если   и   одновременно направляются к нулю или к бесконечности при   или   то 

если остальная граница существует или равна бесконечности, то она будет равна искомой границе. Если же отношение производных так же представлять случай   или  то можно использовать правило Лопиталя, если это полезно для получения результате. 

Пример 4.22 

Найти границу: 

Решение. Если в заданной дроби подставить  вместо  то получим “неопределенность” вида . Используем правило Лопиталя получим: 

Пример 4.23 

Вычислить 

Решение. Если заменить в данной дроби  нулем, то получим “неопределенность” вида . Используем правило Лопиталя: заменим числитель и знаменатель дроби их производными, потом еще раз и еще раз их производными и придем к нахождению границы нового отношения. 

Пример 4.24 

Вычислить 

Решение. При  функции   и  – величины бесконечно большие, то мы получим “неопределенность” вида . Используем правило Лопиталя, то есть заменим отношение функции отношением их производным и будем находить границу этого нового отношения. 

Случаи  и :

Случаи нахождения границ 

3)  – когда функция представляет произведение бесконечно  малой величины на бесконечно большую величину;

4)  когда функция представляет разницу двух положительных бесконечно больших величин.

в этих случаях нахождения границы функции приводится к случаю   или  путем преобразования функции к виду дроби. 

Пример 4.25 

Найти границы: 

Решение. Установив, что имеет место случай   или  преобразуем функцию к виду дроби, числитель и знаменатель которого одновременно направляются к нулю или бесконечности, а потом используют правило Лопиталя: 

Случаи  и :

Случаи нахождения границы: 

5)  – когда функция представляет степень, основа которого направляется к единице, а показатель – к бесконечности; 

6)  – когда функция представляет степень, основа которого направляется к бесконечности, а показатель – к нулю;

7)  – когда функция представляет степень, основа и показатель которой направляется к нулю. 

Эти случаи нахождения границы функции приводятся к случаям   а потом к случаю   или  следующим образом: функция логарифмуется и сначала находят границу ее логарифма, а потом по найденной границей логарифма находят и границу самой функции.  

 Пример 4.26 

Найти границы: 

Решение.

  Установим, что имеет место случай  , обозначим, что   Потом прологарифмируем полученную функцию: 

Найдем границу его логарифма 

  Находим границу функции 

Следует, 

2)  Установим, что имеет место случай  выполняем преобразование: 

Следует, 

Некоторые основные теоремы дифференциального вычисления

Теорема Лагранжа (про оконченные прироста функции)

Если функция  непрерывна на отрезке  и дифференцированна на интервала  посередине этого интервала существует хотя бы одна точка  такая, что выполняется равенство: 

Экономическое содержание теоремы Лагранжа 

Пусть   выражает зависимость выпуска  от затрат  некоторого специфического ресурса. Если объем затрат увеличивается от  к    единиц, то разница  выражает соответственное изменение выпуска. 

Отношение  показывает, на сколько единиц в среднем изменяется выпуск продукции, если затраты выросли на одну единицу. Другими словами,  – среднее производство ресурса на промежутке 

Граничное производство ресурса равно значению производной функции выпуска при данном уровне затрат. Если затраты ресурса складывают  единиц, то   – соответственное им граничное отношение ресурса. 

На основе теоремы Лагранжа можно утверждать, что для процесса производства, который описан функцией выпуска  которая непрерывна на отрезке  и дифференцирована на   существует хотя бы один граничный уровень затрат , при котором граничное производство соответственного ресурса совпадает с его средним производством. 

Формула Тейлора 

Функция  что дифференцирована  раз в некотором интервале. которому принадлежит точка  может быть представлена в виде суммы многочлена  – ой степени и остаточного члена  

где  – некоторое значение границ   и 

Формула Тейлора  (Т)  позволяет приблизительно представить произвольную функцию   в виде многочлена: 

и вместе с тем позволяет оценить погрешность, которая при этом возникает. 

Частичный, простой вид формулы Тейлора при   принято называть формулой Маклорена: 

Формула Маклорена (М) дает расклад функции к степеням той же независимой переменной. 

Использование формулы Тейлора в экономических задачах 

Приближено равенство 

используется в задач экономической статистики. Например, рассмотрим такую задачу: предположим, что для чисел введено среднее арифметическое 

и среднее квадратичная погрешность 

Как обозначить среднее арифметическое вида 

если числа  неизвестные, или известный отрезок, которому они принадлежат. 

Значение  можно, очевидно, найти приближенно. Подставим вместо   многочлен Тейлора второго порядка в точке 

Поскольку 

получим 

Разложение основных элементарных функций по формуле Тейлора 

1. Разложим по формуле Тейлора функцию   в точке  Для этого вычислим: 

Далее по формуле Тейлора получим: 

2. Разложим по формуле Тейлора функцию   в точке  Для этого вычислим: 

Далее по формуле Тейлора получим: 

2. Разложим по формуле Тейлора функцию   в точке  Для этого вычислим: 

Далее по формуле Тейлора получим: 

1. Разложим функции    где  – произвольное число. Например: 

Далее по формуле Тейлора получим: 

Этот ряд называется формулой бинома Ньютона в честь ее открытия. Если  – натуральное число, то ряд содержит оконченное число множителей. 

5. Разложение функции  Например:

или 

Экономическое содержание производной

Задача на продуктивность работы 

Пусть функция   выражается количество изготовленной продукции  за время   и необходимо найти продуктивность работы в момент 

Очевидно за время от   к  количество выполненной продукции изменится от значения  к значению  Тогда, средняя продуктивность работы по этому термину 

Продуктивность работы в момент  можно обозначить как граничное значение средней продуктивности в период времени от  к   при   то есть 

Следует, производная объема сделанной продукции за время  является продуктивность работы в момент . В этом экономическое содержание производной. 

На практике экономических исследований широко используется производственные функции, которые используют для установления . например, выпуска продукции от затрат ресурсов, затрат производства от объема продукции, прибыли от проданного товара.

Рассмотрим производные для определения типов производственной функции. 

1) Пусть производственная функция  – функция затрат производства, что зависит от количества продукции  Предположим, что количество продукции увеличится на  Количеству продукции   соответствуют затраты производства 

Средний прирост затрат производства  Этот прирост затрат производства на единицу количеству продукции. 

Граничными затратами производства называется граница 

граничные затраты производства сходится со скоростью изменения затрат производства. Величина  характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции. 

2. Обозначим    выручка от продажи   единиц товара. 

Граничной выручкой называется граница 

3. Пусть производственная функция  устанавливает зависимость выпуска продукции  от затрат ресурса  

Граничным продуктом называется граница 

Эластичность 

Пусть аргумент   функции   получил прирост  Тогда значение функции изменяется на величину 

 Приросты   и  называются абсолютным приростом аргумента и функции соответственно. Сложим относительные приросты переменных   и 

Граница отношения относительного прироста функции  к  отношения относительного прироста аргумента   при условии, что абсолютный прирост аргумента  направляется к нулю, называется эластичностью функции  к переменной  и обозначается символом 

Эластичность   показывает при приблизительно на сколько процентов изменяется значение функции  при изменении независимой переменной  на 1% 

Формулу (21) можно переписать в виде: 

это означает, что для функции выпуска  эластичность равна отношению граничного производства ресурса к его среднему значению производства. 

Пример 4.28

Найти  если 

Решение. Эластичность заданной функции вычислим по формуле: 

Найдем 

это означает, что при увеличении  с 2 к 2,02 значения функции возрастает на 0,6%.

1. Если  то функция называется не эластичной 

2. Если  то функция называется эластичной 

Свойства: 

Эластичность элементарных функций

1. Эластичность степенной функции  постоянная и равна показательной степени: 

На самом деле: 

2. Эластичность показательной функции  пропорциональна к 

На самом деле: 

3. Эластичность линейной функции 

На самом деле: 

Использование эластичности в экономическом анализе

В экономике рассматривают несколько видов эластичности.

 Эластичность спроса относительно цены. 

Изучается зависимость спроса   на товар от цены  на него. Зависимость спроса от цены опишем с помощью формулы 

Во многих экономических исследованиях необходимо установить не величину спроса при каждом конкретном уровне цены, а характер изменения спроса при указанном изменении цены. В таком случае находят эластичность спроса относительно цены. В наших определениях: 

Эластичность спроса относительно цены обозначает, на сколько процентов измениться спрос на товар, если цена на него увеличится на 1%. 

так как в большинстве случаев, спрос является спадающей функцией цены   и  то чтобы избежать отрицательных чисел, в таких случаях при изучении эластичности спроса принимают 

Знак  показывает, что спрос уменьшается при увеличении цены. 

Пример 4.28 

Пусть функция спроса линейна  то 

Если   то   Это означает, что при увеличении цены на 1% спрос  спадает на  Если   показатель эластичности равен 1. Увеличение цены с 5 у 5, 05 приводит к уменьшению спроса на 1%. Если  спрос уменьшается на 9%. 

Другими словами, спрос на товар эластичный, если небольшое изменение цены товара ведет к значимому изменению величины спроса.  Когда изменение цены ведет к  небольшому изменению величины спроса, спрос является не эластичным. 

Исследуем динамику выручки при разных видах спроса.

Выручка от продажи данного товара при цене  складывается 

Граничная выручка равна 

а) Если спрос эластичный, то есть  то   и с повышением цены выручка от продажи товара понижается. 

б) При нейтральном спросе  и выручка практически не зависит от цены 

в) При не эластичном спросе  выручка увеличивается с ростом цены, так как в этом случае 

Из рассмотренного выше понятно, что знание эластичности спроса на данный товар позволяет прогнозировать направление изменения выручки под влиянием роста или снижения цены. Очевидно, что каждой фирме выгодно, чтоб спрос на ее продукцию был как можно больше не эластичным, так как в такой ситуации существует возможность придания товару высокой цены. 

Эластичность предложения обозначается аналогично эластичности спроса. Для дифференцированной функции  Форма эластичности принимает вид 

В отличие от формулы эластичности спроса  формулы эластичности предложения отрицательный знак  Это связано с тем, что с ростом рыночной цены на товар,  предложения на этот товар возрастают. Каждому предприятию выгодно реализовать свою продукцию, через это  – возрастающая функция и

Предложение называется эластичной, если   не эластичной, если   и нейтральной, если  

Цена, при которой величина спроса равна величины предложения, называется ценой равновесия. 

В точке   величина спроса равна величины предложения,  – цена равновесия. 

Решение задач:

Задача 4.30

Пусть функция  устанавливает зависимость затрат производства от количества  продукции, что выпускается. Найти граничные затраты и коэффициент эластичности, если объем продукции складывается 100 единиц, 20 единиц. 

Решение. 

1. Граничные затраты производства является производная от функции затрат 

При соответственных объемах продукции: 

Следует, чем больше изготовляется продукции, тем медленнее растут затраты на ее выпуск. 

2. Эластичность функции

В нашем случае 

Следует, если при объеме выпуска 100 единиц количества продукции, что выпускается, увеличивается на 1%, то есть на 1, то относительно затрат производства увеличивается приблизительно на 0,67%: при объеме 20 единиц увеличения выпуска продукции на 1% произведет к увеличению относительно затрат приблизительно на 0,95%. 

Задача 4.31 

Зависимость между затратами производства  и объемом продукции   что выпускается, выражается функцией  (ден. ед). Обозначить средние и граничные затраты, если объем продукции 10 ед. 

Решение.  Функция средних затрат выражается отношением 

  (ден. ед).

Граничные затраты:  (ден. ед).

Следует. если средние затраты на производство единицы продукции складывают 45 ден. ед., то граничные затраты, то есть дополнительные затраты на производство дополнительной единицы продукции при данном уровне производства, складывают 35 ден. ед. 

Задача 4.32 

Зависимость между себестоимостью единицы продукции  (тыс. ден. ед.) выражается функцией  Найти эластичность себестоимости. если выпуск продукции равна 60 млрд. ден. ед. 

Решение. Эластичность себестоимости 

Это означает, что в случае выпуска продукции на 60 млрд ден. ед. увеличения его на 1% приведет к снижению себестоимости на 0,6%. 

Задача 4.33 

Опытным путем установлена функция спроса  и предложения  где   – количество товара, что покупается и предлагается на продажи соответственно, в единицу времени,  – цена товара. Найти:

а) цена равновесия, то есть цена, при которой спрос и предложение уравниваются; 

б) эластичность спроса и предложения для этой цены;

в) изменение прибыли в случае цены на 5%  от цены равновесия. 

Решение. 

а) Цена равновесия обозначает из условия 

откуда  то есть цена равновесия равна 2 ден. ед. 

б) Найдем эластичность спроса и предложения по формуле 

Тогда 

для цены равновесия  получим: 

поскольку полученные значения эластичности по абсолютной величиной меньше единицы, и спрос, и предложение данного товара при цене равновесия не эластичны относительно цены. Это означает, что изменение цены не произведет резкого изменения спроса и предложения. 

Так, при увеличении цены   на 1% спрос уменьшиться на 0,3%, а предложение увеличится на 0,8%.

в) При увеличении цены  на 5% от равновесный спрос увеличивается на  следует, прибыль возрастает на 

Задача 4.34 

Фирма планирует выпускать солнечные батареи. На основе исследований была установлена в=зависимость спроса  от цены  за батарею:  где  – количество батарей на продажу в год. Затраты фирмы на выпуск  солнечных батарей складывают 

Вычислить прибыль, обозначить его максимальное значение. 

Решение. Валовая прибыль  

Из условия запишем функцию  как функцию переменной :  потому 

тогда прибыль 

Следует, 

Обозначим максимальную прибыль 

Следует, при  единиц выпуска достигает  максимума.  ден. ед – максимальное значение прибыли. 

Задача 4.35 

Предприятие изготовляет  единиц продукции по цене  а затраты производства задаются функцией 

найти оптимальный для предприятия объем продукции и соответственная ему максимальная прибыль. 

Решение. Пусть  – валовая прибыль,  – прибыль от реализации  единиц продукции по цене  Тогда, 

где  – заданные функции. 

Для решения задачи следует исследовать функцию  на экстремум. При этом прибыль будет максимальной для такого объема  выпуска продукции, для которого 

Проведем эти исследования. 

1. Формируем , находим  и решив уравнение  находим критическую точку. 

Учтем, что 

 – критичная точка. 

2. Находим  и обозначим ее знак при 

Следует,  – точка максимума функции  то есть оптимальный объем производства складывается 150 единиц продукции.

3. Находим максимальную прибыль производства, то есть 

При  цена  валовая прибыль 

Затраты производства 

Максимальная от продажи прибыль 

Задача 4.36 

Капитал в 1 млрд ден. ед. может быть размещен в банк под 50% годовых. или инвестированных в производство, причем эффективность вложения ожидается в размере 100%, а затраты задаются квадратичной зависимостью. Прибыль облагается в  При каких значениях  вложения в производство является эффективным, чем просто вложение капитала в банк?

Решение. Пусть  инвестируется в производство, а  – размещается под проценты. Тогда размещенный капитал через год станет равным

а капитал, вложенный в производство. обозначается по формуле 

Затраты складывают  поскольку по условию они задаются квадратичной зависимостью, то есть прибыль от вложения в производство 

Налоги сложат  то есть чистая прибыль получится: 

Общая сумма через год сложит: 

Нужно найти максимальное значение этой функции на отрезке  Получим 

 то есть  – точка максимума.

Чтобы  Необходимо выполнить условие 

 или 

Таким образом, если  то выгоднее ничего не вкладывать производство и разместить весь капитал в банк. Если  то можно показать, что при 

То есть вложение в производство выгоднее, чем чистое размещение под проценты. 

Исследование функций и построение их графиков

Возрастание и спад функции

Функция  называется строго возрастающей на промежутке  если для некоторых двух чисел  и   на этом промежутке из неравенства  следует неравенство 

Если из неравенства следует нестрогое неравенство  то функция называется возрастающей на данном промежутке .

Функция  называется строго спадающей на промежутке  если для некоторых двух чисел  и   на этом промежутке из неравенства  следует неравенство 

Если из неравенства следует нестрогое неравенство  то функция называется возрастающей на данном промежутке .

Функции возрастающие и спадающие, а также функции строго возрастающие и строго  спадающие называются монотонными. 

Если во всех точках интервала первая производная  то функция  на этом интервале возрастает. Если во всех точках некоторого интервала первая производная  то функция на этом интервале спадает. 

Это достаточный признак возрастания и спада функции на интервале. Точка  называется критичной точкой первого рода, или просто критичной, если имеет место одно из условий; 

  функция  определена на точке , но   не существует. 

Чтобы найти интервалы монотонности функции , необходимо на числовую ось нанести граничные точки области определения функции на все ее критичные точки. 

Область определения при этом разобьется на некоторое число интервалов, на каждом из них производная не изменяет знак. Это и будут интервалы монотонности функции. Для того чтобы узнать, спадает или возрастает функция на данном интервале монотонности, достаточно выяснить, какой знак имеет производна в какой – нибудь точкой этого интервала. Если в этой точке  то функция возрастает, если  – спадает. 

Пример 4.48.

Обозначить интервалы возрастание и спада функций: 

Решение 

а) Областью существования функции   является вся ось . Найти производную функции 

Точки  разбивают область определения на интервале 

Находим знак функции в каждом интервале   Следует,  и  – интервалы возрастания функции, а   – интервал спадания функции. 

б) Областью существования функции  является интервал  Производная  Находим критичные точки  В интервале  а это означает, что  является интервалом возрастания функции. В интервале  а это означает, что  ч- интервал спадания функции. 

Пример 4.49

Затраты производства  зависят от объема продукции   по формуле  При каких значениях  затраты производства начнут спадать? 

Решение. Найдем производную  Затраты спадают, если  то есть Откуда  или  Неравенство выполняется, если  или   По условию задачи  не может быть решением. Следует, затраты производства начинают спадать при объемах 

Определение максимума и минимума функции

Функция  имеет точки  максимум, если значение функции в этой точке больше, чем ее значение во всех точках, достаточно близких к 

То есть функция  имеет максимум при  если  для любого  – как положительного, так и отрицательного, но достаточно малых по абсолютной величине. 

Функция  имеет точки  минимум, если значение функции в этой точке меньше, чем ее значение во всех точках, достаточно близких к 

То есть функция  имеет минимум при  если  для любого  – как положительного, так и отрицательного, но достаточно малых по абсолютной величине. 

Если в некоторой точке функция имеет максимум или минимум, то говорят, что в этой точке имеет место экстремум. 

В экономических дисциплинах экстремумом функции называют ее локальным оптимумом, а процесс нахождения экстремального значения функции называют оптимизацией. 

Следует запомнить:  

1) Максимум (минимум) не является обязательно наибольшим (наименьшим) значением, что принимает функция. После рассмотренного около точки  функция может принимать большие (меньшие) значения, чем в этой точке. 

2)Функция может иметь несколько максимумов и минимумов. 

3)Функция, что обозначена на отрезке, может достигнуть экстремума только во внутренних точках этого отрезка. 

Необходимое условие экстремума

Если функция  имеет экстремум при  то ее производная в этой точке равна нулю, или бесконечности. или вообще не существует.

Из этого следует, что точки экстремума функции необходимо находить только среди тех,  в которых ее первая производная    или не существует. Следует выяснить, что указанный признак экстремума и только необходимо, или не достаточно. 

укажем два достаточных условия существования экстремума функции. 

Первое достаточное условие существования экстремума функции

Пусть точка  является критической точкой функции  а сама функция  непрерывна и дифференцирована во всех точках некоторого интервала, который содержит эту точку. 

Тогда: 

1) Если при  производная функции  а при    то при  имеет место максимум, то есть если при переходе слева направо критичную точку первая производная изменяет знак из плюса и минус, то в этой точке функция достигает максимума. 

2) Если при  а при  то при  имеет место минимум, то есть, если при переходе через критичную точку первая производная функции изменяет знак с минуса на плюс, то в этой точке функция достигает минимума. 

3) Если же при переходе через критичную точку первая производная не изменяет знак, то экстремума нет.

 Правило для исследования функции на экстремум с помощью первой производной (первый способ)

Для исследования функции на экстремум по первой производной необходимо: 

1. Найти  – первую производную функции.

1. Решить уравнение  а также обозначить эти значения    при которых   или не существует (то есть: найти критичные точки функции ).

Пусть этими точками будут точки с абсциссами  которые находится в интервале 

3. Все критичные точки расположено в порядке возрастания их абсцисс в интервале 

4. Посередине каждого из интервалов  взять некоторую точку и установить в этой точке знак первой производной функции . 

5. Рассмотреть знак  в двух соседних точках, переходя последовательно слева направо от первого интервала до последнему. Если при таком переходе знаки в двух соседних интервалах разные, имеет место сохранения знака первой производной, то экстремума в рассмотренной критичной точки нет. 

6. Найти значение функции в точках, где она достигает, где она достигает экстремума (экстремальное значение функции).

Правило для исследования функции на экстремума по второму признаку (второй способ)

Для того, чтобы исследовать экстремум по второй производной, необходимо:

1. найти  – первую производную функцию. 

2. решить уравнение 

3. найти  – вторую производную функцию. 

4. исследовать знак  – вторую производную функцию – в каждой точке, что найден в пункте 2. 

Если в рассмотренной точке  то в этой точке будет минимум, а если  то в этой будет максимум. Если в рассмотренной точке  то исследование необходимо провести по правилу первой производной. 

Наибольшее и наименьшее значение функции на отрезке

Если функция  непрерывна на отрезке  то не этом отрезке всегда находятся точки, в которых она принимает наибольшее и наименьшее значение. Этих значений функция достигает или в критическихточках, или на концах отрезка  через это, чтобы обозначить наибольшее и наименьшее значение функции на отрезке, необходимо: 

1) обозначить критичные точки функции

2)вычислить значение функции в критическихточках и на концах 

3) наибольшее из значений в п. 2, будет наибольшим, а наименьшее – наименьшим значением функции на отрезке 

Пример 4.49.

Найти экстремум функции 

а так же обозначить ее наибольшее и наименьшее значение на отрезке 

Решение. Проведем решение сначала по первому правилу. Область определения функции является весь бесконечный интервал 

1. найдем первую производную: 

2. решим уравнение  то уравнение: 

3. Разместим критичные точки в порядке возрастания абсцисс: 

4. Рассмотрим интервалы: 

5. Исследование характера полученных точек проведем с помощью первого достаточного условия. Для этого сложим таблицу изменение знаков первой производной. 

Находим экстремальные значения функции 

строим по найденным точках график (рис. 4.4). 

Объяснение таблицы. В первом порядке указывается интервал монотонности и их граничные точки. Чтобы заполнить второй порядок, необходимо взять любое значение  из интервала монотонности и вычислить  и знак полученного числа записать в таблицу. 

В третьем ряду под знаком  второго ряда ставим знак  который обозначает спад функции, а под знаком  ставим  – знак возрастания функции. В третьем ряду вносятся также значения минимума и максимума функции. 

Теперь проведем решение по правилу. 

У нас критичные точки уже обозначены точки:  найдем вторую производную, получим:   и согласно второму правилу обозначаем знак второй производной в каждой критической точке: 

 функция имеет минимум при 

  функция имеет максимум 

 функция имеет минимум 

Дадим ответ на второй вопрос: обозначим наибольшее и наименьшее значение функции на отрезке 

Этот отрезок содержит в себе все критические  точки. Значение в критических точках уже вычислены. Вычислим значение функции на концах отрезка, то есть   и 

  и 

Сравнивая эти значения функции с значениями в критических точках, мы видим, что наибольшим из этих значений будет  а наименьшим  то есть наибольшее значения функция достигает на левом конце отрезка при  а наименьшее – в кривой точке 

Пример 4.50

Исследовать на максимум и минимум функции: 

Решение. 

1. Областью определения функции 

критическими точками должны быть точки: 

При значениях  производная не существует. Но критическими точками является только точки  они находятся посередине области существования функции  которая является отрезком  и в них заданная функция непрерывна. 

Точки  не являются критическими, так как они находятся не в середине области определения функции, а на ее границах. 

Исследуем критические точки по знаку производной  соседних с ними точках. Сложим таблицу 

согласно таблицы функция  имеет две точки экстремума: точка минимума  где   и точки максимума  где 

См. рис. 4.5

2. Функция  обозначена и непрерывна на всей оси. находим производную: 

Критическими точками будут точки  . Так как функция  обозначена на интервале   то точки   и  являются критическими. Исследуем критические точки. Сложим таблицу

Из таблицы следует, что функция  имеет две точки экстремума: точки максимума  где  и точка минимума  где   Построим график, рис. 4.6

Пример 4.51 

Вычислить наименьшее и наибольшее значение функции   на отрезке 

Решение. Обозначим точки максимума и минимума. Найдем первую производную: 

точки  являются критическими точками. 

Найдем вторую производную: 

Найдем:  – это означает. что в точке  функция имеет максимум. Находим:  – точка   является точкой минимума. Находим  Вычислить значение функции на концах интервала  Сравнивая полученные значения получим, что на интервале   и 

Следует, наибольшее значения при  функция принимает в правом конце отрезка при  Наименьшее значение достигается в двух точках минимума функции и в левом конце отрезка, при 

Задачи про наибольшие и наименьшие значение величин

Во многих геометрических  и технических задачах необходимо найти наибольшее и наименьшее значение величины, которая связана функциональной зависимостью с другой величиной. Для решения таких задач необходимо из ее условия выбрать независимую переменную и выразить ее величину, а потом найти искомое наибольшее или наименьшее значение полученной функции. При этом интервал изменения независимой переменной также обозначается из условия задач. 

Пример 4.56 

Необходимо изготовить закрытий цилиндрический бак объемом  Какие должны быть размеры, чтобы на его изготовление ушло наименьшее количество материала? 

Решение. В задаче необходимо обозначить, в каком отношении находится радиус и высота цилиндра, чтобы при заданном объеме  его полная поверхность была наименьшей. 

Полная поверхность цилиндра: 

Наименьшее значение этой функции и необходимо найти. Видим, что   является функцией двух  независимых переменных, одну из которых необходимо исключить. Известно, что объем цилиндра  В  – величина известна. Выразим  через  С этим значением  полная поверхность цилиндра равна: 

 или 

Теперь уже  – функция одной независимой переменной 

Находим 

и при любом  получим, что  Из уравнения  получим, что  Так как  то значение  является минимумом функции, а вместе с этим и наименьшим значением. Запишем значение 

  либо 

Таким образом, на изготовление цилиндра заданному объема пойдет наименьшее количество материала, если взять высоту цилиндра, равную диаметру. 

Задача 4.57

Окно имеет форму прямоугольника, обрамленного полукругом. Обозначить размеры окна является заданное число   необходимо найти   и  чтобы площадь окна была наибольшей.

Площадь окна   где  – площадь полукруга,  – площадь прямоугольника. Получим функцию двух независимых переменных. Выразим  через 

Следует, площадь окна 

Находим 

А это означает, что при   функция  имеет максимум найдем . 

таким образом, чтобы окно пропускало наибольшее количество света, необходимо, чтобы ширина окна была в два раза больше высоты. 

Задача 4.58 

Затраты на топливо для парохода делятся на две части. Первая из них не зависит от скорости и равна 480 рублей в час. А вторая часть затрат пропорциональна кубу скорости, причем при скорости 10 км/ час эта часть затрат равна 30 рублей в час. Необходимо найти, при какой скорости сумма затрат на 1 км пути будет наименьшей. 

Решение. Обозначим через  ( км/час) – скорость парохода. Тогда вторая его часть затрат равна  где  – коэффициент пропорциональности. Для обозначения  подставим  тогда:  откуда 

Пароход пройдет 1 км пути за  часов. Затраты за топливо будут равны 

необходимо найти наименьшее значение функции 

на промежутке 

найдем первую производную: 

Если 

Проверим, что при  функция  достигает минимального значения. 

Следует, при скорости 20 км/час общая сумма затрат на 1 км пути будет наименьшей. 

Использование производной для исследования динамики функций

Темп изменения функции:

Рассмотрим функцию  Скорость ее изменения обозначается, как известно, производной   Относительной скоростью или темпом изменения функции называют отношение   С тем: 

Следует, темп изменения функции равен ее логарифмической производной. 

Задача 4.66

Объем продукции    изготовленной предприятием на протяжении рабочего дня, представлено функцией: 

 (ед.)

где    – рабочее время.

необходимо найти: 

1) продуктивность работы, скорость и темп ее изменения:

2) при каком времени  после начала работы продуктивность работы максимальна;

3) значение продуктивности работы, скорости и темпа ее изменения через  через начала работы. 

Результаты вычисления привести в таблицу и проанализировать.

Решение 

1. продуктивность работы выражается производной  а скорость и темп изменения продуктивности работы – соответственно производной  и логарифмической производной 

 (ед/час)

(ед/час)

 

2. Найдем максимум функции  

 – критическая точка 

  при    при  Отсюда получается, что  – точка максимума функции 

Найдем    (ед/час)

Сложим таблицу значений   при 

Результат вычислений показывают, что до конца рабочего дня продуктивность работы существенно уменьшается: при этом смена знака   и   с плюса на минус указывает на то, что повышение продуктивности работы в первый рабочий день изменяется ее снижением в последние часы. 

Выпуклость и вогнутость функции

Темп изменения функции показывает, насколько единиц увеличивается или уменьшается скорость в течении процесса, который описан заданной функцией, при каждом конкретном значении ее аргумента. Чем выше темп, тем скорее изменяется скоростью. Как это отображается на форме графика функции? Как имея график функции, отличить один от другого с разными знаками и абсолютной величины темпом? Получается, графики функции, что изменяются в положительном темпе имеют одно и то же свойство. Все они размещены выше своей касательной. В связи с этим, введем понятие выпуклость и вогнутость функции и установим из признаки. 

Кривая  называется выпуклой на интервале  если все точки графика функции лежат ниже ее касательных на этом интервале. 

Кривая  называется вогнутой на интервале  если все точки графика функции лежат выше ее касательных на этом интервале. 

Функция изображена на рис. 4.9, на интервале  выпуклая, а на интервале  вогнута. 

Если на интервале  функция  обозначена, имеет первую и вторую производные и  для  то функция выпуклая на  этом интервале. 

Если для всех  функция   обозначена, имеет первую и вторую производные и то функция вогнутая на  этом интервале. 

Интервалы, в которых дуги кривой выпуклые, обозначаются из неравенства   а интервалы в которых дуги кривой вогнуты – из неравенства 

Темп изменения функции   выражается ее второй производной, то функция на нем выпукла. 

Если на интервале  темп изменения функции отрицательный,  то функция на нем вогнута. Функция с положительным темпом изменения выпукла на соответственном интервале. В этом и заключается геометрическое содержание темпа изменения функции. 

Точка кривой, что отделяет ее выпуклую часть от вогнутой называется точкой пересечения. Точки кривой, в которых   или  а также те из них, в которых  не существует, называются критическими точками второго рода. Точки пересечения необходимо находить среди критических точек второго рода. В критической точке второго рода   пересечение будет только в том случае, когда при переходе через эту точку   изменяет знак. 

Для обозначения точек пересечения кривой необходимо найти все критические точки второго рода и рассмотреть знак  в каждых двух соседних интервалах, на эти точки делят область существования функции. В случае, если знаки   в двух соседних интервалах разные, критическая точка второго рода является точкой пересечения. Если же в двух соседних интервалах  имеет один и тот же знак, то в рассмотренной точке второго рода пересечения нет. В точке пересечения кривая пересекает касательную. 

Пример 4.67 Обозначить точки пересечения на интервале выпуклости и вогнутости кривой 

Решение. Функция обозначена и два раза дифференцирована для всех   Для определения критических точек второго рода находим 

Полученные точки являются критическими точками второго рода. Сложим таблицу значений 

точка   не является точкой пересечения. Точки  являются точками пересечения, потому, что при переходе слева направо через эти точки вторая производная изменяет знак на противоположный. 

найдем 

Задача 4.68 Обозначить точку пересечения, интервал выпуклости и вогнутости кривой  (кривая Гаусса). 

Решение. Функция обозначена на интервале  Находим первую и вторую производные: 

 

Находим критические точки второго рода: 

Сложим таблицу изменения знаков 

Находим 

 

Следует, кривая имеет две точки пересечения:   и  Смотреть рис. 4.10.

4.8.10 Асимптоты.

Асимптотой кривой называется такая прямая, к которой бесконечно приближается точка кривой при бесконечном отдалении ее он начала координат. Кривая может приближаться к своей асимптоты теми же способами, как и переменная к своей границе : оставаясь с одной стороны от асимптоты или с разных сторон, несколько раз пересекая асимптоты и переходя с одной стороны на вторую.

Различают асимптоты: вертикальные, горизонтальные и производные. 

а) если при   кривая   имеет разрыв  -ого рода, то есть если при   или при  функция направляется к бесконечности, то прямая  является вертикальной асимптотой. 

б) Кривая  имеет горизонтальную асимптоту  только в том случае, если существует ограниченная граница функции  при   или  и эта граница равна  то есть, если   или 

в) Для нахождения производной асимптоты  кривой  необходимо найти числа     и   по формулам: 

При нахождении границ удобно использовать правило Лопиталя. 

Пример 4.70.

Найти асимптоты кривой: 

Решение

а) при  заданная кривая имеет бесконечный разрыв, через это прямая  является ее вертикальной асимптотой. 

б) находим погрешности асимптоты: 

Подставляя найденные значения   и  уравнение производной асимптоты, получим:  Других погрешностей асимптот нет, так как при   значения   и   будут такими же. Кривая изображена на рис. 4.11. Асимптоты кривой   являются прямые  и 

2)  (равносторонняя гипербола) 

а) Обозначить вертикальную асимптоту: для этого находим те значения  вблизи которых   бесконечно возрастает по абсолютной величиной. Таким значением будет  то есть ось   (рис. 4.12). 

б) находим горизонтальные асимптоты 

и кривая имеет одну горизонтальную асимптоту  то есть горизонтальной асимптотой является ось 

3) 

а) Кривая имеет вертикальных асимптот, так как она непрерывная. 

в) Зайдем наклонность асимптоты: 

то есть при  угловой коэффициент асимптоты не существует, вследствие чего, при  кривая не имеет асимптоты

Следует, при  имеет горизонтальные асимптоту   (ось )

а) Кривая имеет две вертикальные асимптоты   и  так как при  она имеет бесконечные разрывы. 

в) Наклонных асимптот  кривая не имеет, так как ее областью определения является интервал   и через это  не может направляется к бесконечности. (См. рис. 4.13), 

Общий план доказательства функции и построение ее графиков 

Общее исследование функции и построение ее графиков удобно использовать следующую схему: 

1.  Найти область определения функции
2.  Найти точки разрыва функции и ее односторонние границы
3.  Выяснить, является ли функция четной, нечетной или периодической
4.   Найти точку пересечения с осями координат
5.  Найти асимптоты графика функции: а) вертикальные б) наклонные 
6.  Найти точки экстремума и интервалы возрастания и спада функции 
7.   Найти точки пересечения графика функции и интервалы выпуклости и вогнутости кривой
8.  Построить график функции, используя оси, полученные результаты исследования. Если их будет недостаточно, то необходимо найти еще несколько точек графика функции, выходя из ее уравнения. 

Пример 4.72 

Исследовать функции и построить их графики 

Решение 

 Область определения функции   – вся числовая прямая   то есть 

  Точек разрыва нет. 

 Выясним, является ли функция четной, нечетной или не четной и не нечетной

Следует, функция является  не четной и не нечетной. Функция периодичная. 

 Найти точку пересечения с осями координат

а) с осью 

б) с осью 

 Найти асимптоты графика функции:

а) вертикальных асимптот нет

б) наклонные 

наклонных асимптот нет. 

  Найти точки экстремума и интервалы монотонности: 

 – критические точки первого рода. 

Дальше решение можно оформить в виде таблицы. 

  Найти точки пересечения графика функции и интервалы выпуклости и вогнутости функций: 

Сложим таблицу 

 Строим график (рис. 4.14). 

 Найдем область определения заданной функции. Функция обозначена при всех значениях    кроме   при котором знаменатель дроби преобразуется в ноль. Следует функция определена на интервалах  и 

 Найти точки разрыва функции и ее односторонние границы в точках разрыва. 

Точка разрыва одна 

 Выясним, является ли функция четной, нечетной или периодической

функция является ни четной, ни нечетной. Функция не периодичная. 

 Найти точку пересечения с осями координат

а) с осью 

б) с осью 

 Найти асимптоты графика функции:

а) вертикальных асимптоты находим так: 

это означает, вертикальных асимптот нет

б) наклонные асимптоты находим так: 

наклонная асимптота одна: 

 Найти точки экстремума и интервалы возрастания и спада функции. 

находим производную:

Найдем критичные точки: 

но при  функция неопределенная. 

Разбиваем область определения критическими точками на интервалы и установим интервалы монотонности и экстремума: 

Сложим таблицу: 

  Найти точки пересечения графика функции и интервалы выпуклости и вогнутости кривой: 

Найдем критичные точки второго рода: 

Разбиваем область определения функции критическими точками   и  на интервале и устанавливаем интервалы выпуклости и вогнутости кривой и точки пересечения кривой

Сложим таблицу: 

Это точка 

 Строим график

 Найдем область определения заданной функции. Функция обозначена при всех значениях   то есть

 Функция непрерывна на всей оси. 

 Выясним, является ли функция четной, нечетной или периодической: 

Следует функция не четная  и не нечетная. Функция не периодичная. 

 Найти точку пересечения с осями координат

а) с осью 

б) с осью 

Потому  и    – точки пересечения графика с осью    точки пересечения графика с осью  

 Найти асимптоты кривой:

Вертикальных асимптот нет.

Наклонные: 

Следует,  – наклонная асимптоты. 

  Находим   и обозначаем критические точки:  

Из уравнения 

 – критические точки. 

Разбиваем область определения критическими точками на интервале и по знаку наклонной в этих интервалах установим интервалы монотонности и экстремумы: 

Следует, 

 Найдем точки пересечения и интервалы вогнутости и выпуклости кривой:

  – критические точки второго рода. 

Сложим таблицу и исследуем знак   вблизи каждой точки второго рода. 

 Строим график 

 Найдем область определения заданной функции. Функция определена при всех значениях   кроме   то есть в интервалах  и 

  Найдем точки разрыва и ее односторонние границы в точках разрыва: 

Функция непрерывна на интервалах  и  Функция не периодическая.  

 Выясним, функция четная или нечетная: 

Ни одна из неравенств  не имеет место. Следует, функция не четная и не нечетная. 

 График функции не пересекает осей координат, так как  и 

 Обозначим асимптоты графика функции: 

а) значение   (то есть вся ось ) является вертикальной асимптотой кривой. 

б) горизонтальные асимптоты: 

Горизонтальной асимптотой является ось 

в) найдем наклонные асимптоты, уравнение которых 

Это означает. что при   наклонных асимптот нет.

 

 (наклонная асимптота совпадает с горизонтальной). 

 Обозначим точки экстремума и спадания функции. 

Находим критичные точки: 

1) Из уравнения  то есть  следует, что 

2)   при  но при   функция не определена. Таким образом, функция имеет критическую точку  Область определения функции поделим на интервалы 

Сложим таблицу: 

Следует, 

  Найдем точки пересечения и интервалы выпуклости и вогнутости кривой: 

Найдем критические точки второго рода.

Из уравнения   учитывая что,  то но дискриминант квадратного уравнения меньше, чем ноль.. Следует, нет действительных значений  при которых вторая наклонная равна 0. Найдем значение  при которых   Таким единственным значением является  но точка перегиба при  не может быть, так как при    заданная функция не существует. Следует, точки точки перегиба функции не существует. 

Для определения интервалов выпуклости и вогнутости графика функции рассмотрим знак   на интервалах   и 

   на  кривая выпуклая 

 на  кривая вогнута

 Построим график. Рис. 4.17. 

функция которая играет важную роль в теории вероятностей, а также в математической и экономической статистиках.

 Функция определена для любого действительного значения   Она принимает только положительные значения: 

  Точек разрыва нет. Функция непрерывна на интервале 

 Функция четная: 

так как 

График функции симметричный относительно оси ординат 

 При   значение 

Точек пересечения с осью   нет,  так как 

 Найдем асимптоты: 

Следует, ось   является асимптотой кривой.

 Найдем точки экстремума и интервалы монотонности. находим первую наклонную функции: 

Очевидно,   для    и    для  

При   функция достигает максимума 

 Находим точки перегиба и интервалы выпуклости и вогнутости кривой. 

Вторая касательная функции имеет вид: 

Так как  то знак  зависит от знака  Критические точки будут две. Это  и 

Схема знаков второй касательной имеет вид: 

 Построим график. Рис. 4.18

 Функция определена в интервалах 

 Точками разрыва функции являются точки   и 

Находим односторонние границы в точках разрыва: 

 Функция является не четной,  не нечетной. 

 Находим точки пересечения графика функции с осями координат. С осью   график не пересекается, потому  с осью  он также не пересекается. 

 Находим асимптоты графика. Поскольку    то  – вертикальная асимптоты. Находим наклонные асимптоты: 

Получим: 

следует, наклонные асимптот нет. 

 Находим точки экстремума и интервалы монотонности функции: 

Учитывая область определения функции: 

Далее решение можно оформить в виде таблицы: 

 Находим вогнутость и выпуклость и точки пересечения графика функции: 

Точек пересечения нет, ибо   не обращается в ноль ни по одному значению 

 при  график функции вогнутый;   при  график функции выпуклый. 

 Построим график функции с учетом того, что   при   Рис. 4.19

Задача 4.73. Пусть зависимость спроса от цены описывается функцией   Спрос спадает с возрастанием цены, так как  меньше нуля. Темп возрастания функции  отрицательный, если   и положительный, если цена больше   Это означает: для  спрос спадает больше произвольно, а когда цена превышает   спрос спадает более быстро. 

На промежутке  график спроса выпуклый, а на  – вогнутый. Точкам   – точка перегиба (рис. 4.20) для более точного графика вычислим: 

Выручка от реализации товара по цене   станет:

  денежных единиц. 

Наклонная этой функции: 

 положительная, если   и отрицательная для   Это означает, что с ростом цены выручка сначала увеличивается (несмотря на  спадание спроса) а при   достигает максимального значения, что равно   Далее увеличение цены не правильно, так как оно ведет к укорочению спроса. 

Темп изменения выручки   положительный. если    и отрицательный, пока 

Проанализируем схему знаков первой и второй наклонных: 

На промежутке  функция возрастает больше произвольно. Соответственная часть графика выпуклая. Как уже мы обозначили, далее повышение цены невыгодно. Сначала выручка спадает с отрицательным темпом для  а потом темп спадания  станет положительным. Для  выручка спадает все быстрее и приближается к нулю к бесконечному возрастанию цены. На промежутке   функция   вогнута. В точке   график перегибается (см. рис. 4.21). 

Дифференциальное исчисление функции одной переменной

Продолжая тему функциональной зависимости характеристик экономических процессов, мы переходим к изучению дифференциального исчисления как одного из основных методов исследования скорости изменений этих процессов во времени или под влиянием факторов внешней среды и направления их протекания.

После изучения данной темы вы сможете:

• ● понимать смысл производной в экономике и ее применение при проведении предельного анализа;
• ● знать методы дифференцирования функций;
• ● применять инструменты дифференциального исчисления для решения реальных экономических задач;
• ● использовать дифференциал функции для приближенных вычислений величин в экономике;
• ● уметь находить эластичность функций в экономике и давать интерпретацию полученных результатов;
• ● приобрести навыков применения производных при исследовании функций и построении их графиков;
• ● выполнять простейшие расчеты для оптимизации производства и максимизации прибыли предприятия.

Определение производной, общий порядок ее нахождения, связь производной с непрерывностью функции

Основные понятия этого раздела – производная и дифференциал – сложились как результат дальнейшего развития теории границ в связи с существованием широкого класса задач из разных областей знаний, решение которых требовало вычисления границ специального вида. Это, например, задачи о вычислении скорости движения материального объекта или протекания химической реакции, рост численности населения, себестоимости продукции и др.

Дифференциальное исчисление – это раздел математического анализа, в котором определяются свойства производной и дифференциала функции, а также их применение к исследованию функций.

Датой становления дифференциального исчисления считается май 1684, когда немецкий философ, математик, юрист и дипломат фон Лейбниц опубликовал свое исследование «Новый метод максимумов и минимумов», в котором изложил основы нового метода.

Пусть функция определена в промежутке . Исходя из некоторого значения аргумента , предоставим ему прирост (положительный или отрицательный), такой, что . Тогда функция получает соответствующий прирост . Рассмотрим отношение .

Производной функции по аргументу при данном его значении (или в данной точке) называется предел отношения прироста функции к приращению аргумента , когда прирост аргумента произвольным образом стремится к нулю, и пишут:

Процесс нахождения производной от данной функции называется дифференцированием. Если функция имеет производную в каждой точке из интервала , то говорят, что она дифференцирована на интервале . Конечно, когда функция имеет производную в точке , то – определенное число; если же функция дифференцирована на интервале, то ее производная, в свою очередь, является некоторой функцией от , то есть . Наряду с обозначением для производной употребляют и другие: , а конкретное значение производной при обозначают так:

где – символ подстановки, который означает, что .

Анализируя определение производной, получаем общий порядок нахождения производной от функции в некоторой точке :

1) предоставляем аргументу x прирост и находим соответствующий ему приращение функции

2) делим прирост функции на приращение аргумента, то есть находим отношение приростов

3) находим предел этого отношения, когда приращение аргумента стремится к нулю, то есть находим производную

Выполнение последнего шага требует учета структуры конкретного отношения, а поэтому нет общих указаний о нахождении его границы.

Найдем, например, производную функции для произвольной точки . Следуя только что наведенной схеме, имеем:

Таким образом, мы получили 

При нахождении производной, как видим, отношение при порождает неопределенность , то есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, и это не случайность.

Теорема 15.1 (о непрерывности дифференцированной функции). Если функция дифференцированная в точке , то она непрерывна в этой точке.

Доказательство. Пусть функция имеет производную (напомним, что является определенным числом, то есть 

По критерию существования границы «языком бесконечно малых» имеем:

где  – бесконечно малая при 

Следовательно, . Учитывая арифметические свойства границ и бесконечно малых, получаем:

Это и означает, что функция является непрерывной в точке .

Обратное теореме 15.1 утверждение, вообще говоря, не является справедливым, то есть с непрерывности функции не следует ее дифференцированность. В этом можно убедиться на примере функции

Интерпретация производной в различных областях знаний

Задача об определении уравнения касательной и нормали

Задача об определении уравнения касательной и нормали к графику функции в точке (рис. 15.1).

Рис. 15.1

Касательной к кривой в точке называется предельное положение секущей, проведенной через точки и при

Обозначим угол наклона секущей к оси через , а касательной – через .

Запишем уравнение касательной к кривой, определяется функцией в точке :

Находим угловой коэффициент касательной:

то есть

Приведенная задача считается классической задачей Лейбница о нахождении углового коэффициента касательной в точке.

Из этой задачи следует геометрическая интерпретация производной: производная функции в некоторой точке равна угловому коэффициенту касательной к графику функции в точке . Таким образом, уравнение касательной приобретает вид:

С учетом свойства угловых коэффициентов взаимно перпендикулярных прямых  получим уравнение нормали (перпендикуляра к касательной):

Задача о нахождении скорости прямолинейного движения

Задача о нахождении скорости прямолинейного движения, если известна функция , которая определяет зависимость пути от времени. Эта задача была исторически одной из первых и считается задачей Ньютона об определении производной. Из нее следует механический смысл производной.

Пусть некоторая точка движется вдоль прямой по закону , где  – время, а – путь, который она проходит за это время. Если на интервале считать движение точки равномерным, то скорость движения определяется как . Если скорость движения меняется со временем, то мгновенная скорость в определенной точке определяется как предел этого отношения: . Отсюда следует, что скорость движения в произвольный момент времени является производной от функции, которая выражает зависимость пути от времени:

Если термин «скорость» понимать в общем смысле, то производную можно трактовать как скорость изменения величины, которую описывает функция , в зависимости от изменения .

Задача о нахождении предельных издержек производства

Остановимся подробнее на экономической интерпретации производной. Прежде всего, введем в рассмотрение некоторые экономические понятия. Пусть предприятие производит однородную продукцию. Под производственными затратами понимают совокупность человеческих, материальных, энергетических ресурсов и т.п., которые тратятся на изготовление и реализацию продукции. Если эти расходы выражены в денежной форме, то их называют себестоимостью продукции. Сюда входят: стоимость сырья, материалов, топлива, технических средств, обще хозяйственных расходов, заработная плата и др. Функцию , которая устанавливает зависимость производственных затрат от объема произведенной продукции , называют производственной функцией.

Важным показателем эффективности работы предприятия является предельная себестоимость , что при определенном объеме производства определяет себестоимость каждой последующей единицы продукции. Пусть объем произведенной продукции возрастает на величину , тогда издержки производства изменяются соответственно на величину , следовательно, предельная себестоимость единицы продукции определяет соотношение:

Слово «предельный» в данном случае означает скорость изменения, характеризующееся производной соответствующей функции. Следует подчеркнуть, что предельные величины характеризуют не состояние, а скорость изменения показателей экономического процесса в зависимости от каких-либо факторов. Понятно, что предельные экономические показатели можно определить, если функция, их характеризует, является дифференцируемой.

Таблица производных и правила дифференцирования

Производную любой элементарной функции можно найти, применив общую схему нахождения производных. Основные трудности при этом заключаются в раскрытии неопределенности Чтобы упростить задачу дифференцирования, по общей схеме устанавливают производные только основных элементарных функций, которые приведены в таблице 15.1.

Таблица основных производных                                                                               Таблица 15.1

Рассмотрим арифметические свойства производных.

Пусть функции имеют производные в определенной точке .
Тогда в той же точке:

в частности, 

Доказательство проведем для частного функций , используя опять же общую схему нахождения производных.

Предоставим аргументу прирост , тогда функции  и получат соответственно приращения и
Их новые значения и связаны таким же соотношением, а именно:

Отсюда

Направим к нулю, тогда согласно теореме о непрерывности дифференцируемой функции и , а границы отношений при дают соответственно . Таким образом, выражение при стремится к конечной границе:

Итак, производная  существует и определяется формулой (15.9). 

Аналогично доводятся соотношения (15.6) – (15.8). Правило (15.6) распространяется на произвольное конечное число слагаемых.
Производную от функции можно найти по обычной схеме. Однако найдем ее как производную от доли функций :

Следовательно, , то есть мы получили ту же формулу, что содержится в таблице производных основных элементарных функций (см. Табл. 15.1).

Дифференцирование составленных функций и функций различной формы задания

Нахождение производных составленных функций , где и , занимает центральное место в технике дифференцировки, то есть умении находить производную, и поэтому очень важна следующая теорема.

Теорема 15.2 (о производной сложной функции). Если функция при некотором значении имеет производную , а функция дифференцированная в точке , которой соответствует значение , то производную сложной функции  можно найти по формуле:

Доказательство. Предположение о существовании производной по определению равносильно равенству

Отсюда, согласно критерию существования границы, имеем:

где  – бесконечно малая при 

Тогда 

При согласно непрерывностью дифференцируемой функции  получим , а значит и ; предел отношения  при равен Таким образом, последнее равенство при и дает (15.10).

Согласно (15.10) получаем правило нахождения производной от сложной функции. Чтобы продифференцировать составленную функцию по независимой переменной , необходимо найти производную от функции по промежуточным аргументом и умножить ее на производную промежуточного аргумента по независимой переменной . Итак, мы получаем следующий алгоритм:
1) найти производную внешней функции по аргументу ;
2) найти производную внутренней функции по переменной ;
3) записать их произведение.

Основное, кроме знания таблицы производных и правил дифференцирования, при нахождении производной сложной функции – это умение определять внешнюю функцию и промежуточный аргумент, то есть внутреннюю функцию.

Так, функция является составной, где внешней является степенная функция , а внутренней – тригонометрическая , следовательно, 

А вот для функции , где , имеем:

Случай сложной функции как суперпозиции функций, количество которых больше двух, исчерпывается последовательным применением приведенного правила. Так, для функции , что является суперпозицией трех функций: и , имеем 

Например, если , то и
Тогда имеем производную

Следовательно, 

В результате с только что доказанной теоремы вытекают утверждения о связи производных прямой и обратной функций (1), о дифференцировки функций, заданных в неявной (2) и параметрической (3) формах.

Производная обратной функции

Напомним определение: если из равенства по каждому допустимым значением величины можно восстановить одно и только одно значение величины , говорится, что это равенство определяет функцию , которая является обратной к исходной функции . В свою очередь,  можно рассматривать как функцию, обратную к функции , то есть эти функции являются взаимообратные.

Найдем производную от функции по переменной , если функция в некоторой точке имеет отличную от нуля производную. По определению обратной функции ее можно рассматривать как составную функцию: .

Возьмем производную этой функции по переменной
Таким образом, 

Найдем производную функции , считая, что производная функции уже известна. Тогда: . По формуле (15.11) находим:

Поскольку , перейдем в последнем выражении от функции к функции . Теперь получаем:

Окончательно имеем:

Производная неявной функции

Напомним, что функция y от x называют заданной в неявной форме, если она определяется уравнением , не решен относительно , где под символом понимают выражение, содержащее переменные и

Для нахождения производной от функции y нет необходимости решать уравнения относительно функции (это, кстати, не всегда можно сделать). Необходимо найти производную левой части равенства  как производную сложной функции, и получить уравнение которое затем решить относительно

Рассмотрим уравнение окружности радиусом r с центром в точке : . Переписав это уравнение в виде , продифференцируем его по переменной , получим:

Решив последнее уравнение относительно , имеем: .

Подытоживая рассмотрен, получаем правило дифференцирования неявной функции. Чтобы найти производную неявной функции от , надо:
1) продифференцировать по переменной обе части равенства , которой определяется в зависимости , применяя правило нахождения производной от сложной функции;
2) решить полученное уравнение относительно искомой производной .

Логарифмическое дифференцирование

Иногда, чтобы упростить задачу дифференцирования функции логарифмическое дифференцирование, переходят от явного задания функции к неявного. Для этого логарифмируют левую и правую части равенства , получая . Для упрощения записи модуль можно опускать, поскольку после взятия производной от логарифма модуля переменной этот модуль исчезает: .

Такой подход к нахождению производной называют логарифмическим дифференцированием.

Логарифмическое дифференцирование применяют чаще всего в степенно-показательных функций или к другим функциям, удобных для логарифмирования.

Например, найдем производную функции .

После логарифмирования получим:

Окончательно получаем 

Производная функции, заданной параметрически

Функцию от называют заданной параметрически, если она определяется с помощью двух функций от вспомогательной переменной (параметра) :

В прикладных задачах при параметрической форме задания функции часто роль параметра играет время.

Функцию, которая заданная параметрически, можно продифференцировать как неявную, без представления ее в явной форме.

Найдем производную функции от , представленной в параметрической форме (15.12), при условии, что функции и имеют производные по аргументу , а функция имеет обратную . Исходя из условия задачи, делаем вывод, что функция от можно рассматривать как составную функцию: . Тогда по правилу дифференцирования сложной функции имеем:

 поскольку 

Таким образом,

Найдем тангенс угла наклона касательной к графику функции, заданная параметрически системой уравнений:

где – угол между радиусом-вектором точки, принадлежащей линии, и положительным направлением оси .

Эта система уравнений является параметрическим заданием эллипса. Действительно, если исключить параметр , получим каноническое уравнение эллипса:

Напомним, что тангенсом угла наклона касательной к графику функции есть производная от этой функции. Итак, имеем:

Дифференциал функции и его свойства

При введении понятия производной первого порядка от функции в некоторой точке оперируют приростами аргумента и соответствующим ему приростом функции . Если производная существует, то функция  является непрерывной в точке и ее прирост можно представить в виде:

где – бесконечно малая при .

Если в точке производная конечна и отлична от нуля, то оба слагаемые в (15.14) является бесконечно малыми при сравним бесконечно малый прирост функции с первым слагаемым формулы (15.14). Для этого по выражению (15.14) составим отношение (учитывая, что производная функции в точке является постоянной величиной и ) и перейдем к его границы при :

Итак, бесконечно мала, которая созданная как произведение производной с приростом аргумента , эквивалентная прироста функции , то есть

Это означает, что первое слагаемое в формуле (15.14) представляет собой главную часть приращения функции , которая линейно зависит от прироста аргумента , а второе слагаемое – бесконечно малая более высокого порядка, чем .

Дифференциалом функции в точке называется главная часть прироста функции , которая является линейной относительно прироста аргумента , и обозначается символом , или :

 или 

Замечания. Формула дифференциала остается правильной и в том случае, когда . Тогда дифференциал функции в точке равен нулю.

Из определения дифференциала следует, что:
1) дифференциал независимой переменной равен ее приросту. Действительно, если положить , отсюда

2) дифференциал функции равен произведению ее производной с дифференциалом аргумента:

 или 

3) производная функции является отношением дифференциала функции к дифференциалу аргумента: ; следовательно, символ , которым ранее обозначалась производная, теперь можно толковать как отношение дифференциалов функции и аргумента.

Связь между производной функции и ее дифференциалом с учетом геометрического содержания производной позволяет предоставить геометрическую интерпретацию дифференциала функции (рис. 15.2). Так, из прямоугольного треугольника имеем:

Рис. 15.2

Отсюда имеем геометрическую интерпретацию дифференциала. Дифференциалом функции в точке есть прирост ординаты касательной к графику функции в этой точке при переходе от нее к точке (то есть когда x приобретает прироста ).

Основные свойства дифференциала. Дифференциал функции отличается от ее производной только множителем , поэтому получаем аналогичные арифметические свойства дифференциала, а именно:

Правильность каждого из соотношений (15.19) легко проверить, умножив обе части равенств, описывающих правила дифференцирования, на дифференциал аргумента , и воспользовавшись определением дифференциала.

Вычислим, например, дифференциал произведения функций и :

Инвариантность (неизменность) формы первого дифференциала: форма (вид) первого дифференциала функции не зависит от того, является ли аргумент функции независимой переменной, или он является функцией какой-то другой переменной.

Действительно, если является промежуточным аргументом, то есть функцией от независимой переменной , а именно , то по правилу нахождения производной сложной функции получим:

Отсюда Но по определению дифференциала произведение равна , то есть: Таким образом, мы получили соотношение: Следовательно, формула определения дифференциала сложной функции сохраняет тот же вид, что и в соотношении (15.18). Свойство инвариантности дифференциала играет важную роль в разделе «интегральное исчисление».

Применение дифференциала в приближенных вычислениях

Задача приближенного вычисления значения функции базируется на эквивалентности прироста функции  и ее дифференциала  при движении приращению аргумента к нулю, то есть на соотношении (15.16), которое можно представить следующим образом:

 если 

Эквивалентность бесконечно малых   и означает, что при относительно малом иметь место приближенное равенство:

по которой получаем:

Следовательно, имеем формулу для расчетов:

Правило, по которому можно приближенно вычислить значение функции, сформулируем следующим образом. Для того чтобы по заданному значению функции в точке найти ее приближенное значение в точке , надо вычислить ее дифференциал в этой точке и воспользоваться формулой ( 15.23).

Для оценки точности приближенного вычисления применяют такие характеристики, как абсолютная и относительная погрешности.

Абсолютная погрешность вычисляется по формуле:

Она измеряется в тех же единицах, что и функция, для которой она вычисляется.

Относительная погрешность вычисляется по формуле:

и выражается, как правило, в процентах.

Точность приближенных вычислений зависит не только от величины прироста аргумента (чем меньше , тем выше точность вычислений), но и от поведения функции в окрестности точки (чем меньше есть колебания значений функции вблизи точки , тем точнее есть вычисления).

Вычислим дифференциал и приращение функции при переходе от до и сравниваем их. Находим производную , и вычисляем ее значение в точке . Далее в точке по формуле (15.18) определяем дифференциал:

Теперь подсчитываем прирост функции:

Следовательно, абсолютная погрешность вычисления составляет

Производные функции и ее дифференциалы высших порядков

Если функция имеет производную на некотором множестве , то эту производную можно рассматривать как некоторую функцию от . Производная от производной называется производной второго порядка, или второй производной от функции . То есть

Считая, что производная является производной первого порядка, или первой производной, называть по определению вторую производную производной первого порядка от первой производной. Вторая производная обозначается как
или

Производная первого порядка от второй производной называется производной третьего порядка и обозначается через или

Производной -го порядка (или –й производной) называют производную первого порядка от производной -го порядка, если производная -го порядка является дифференцированной функцией:

Производную -го порядка обозначают или 

Производными высшего порядка называют производные, имеющие порядок выше первого. Для того чтобы найти -ю производную, необходимо последовательно вычислить первую производную от функции, затем производную от ее первой производной, затем производную от второй производной, то есть последовательно осуществлять дифференцировки предыдущего выражения. Соответственно, находим  

Рассмотрим производные высших порядков от функции, заданной параметрически с помощью двух функций: . Считая, что функции и дважды дифференцируемы, остановимся на нахождении второй производной функции , а именно . Для первой производной функции имеем уже известную формулу: , то есть является составной функцией аргумента

Найдем производную от по правилу дифференцирования сложной функции. Итак, получаем:

Найдем , если 

Сначала ищем , а именно

Далее определяем производную второго порядка:

Заметим, что в некоторых случаях можно записать общее выражение -й производной, которое напрямую зависит от произвольного .

Например, определим производные -го порядка от функции:

Соответственно … . Тогда получим общую формулу , в частности ;

Тогда:
Таким образом, получаем общую формулу для производной -го порядка

Приведем некоторые примеры применения второй производной.

Задача о нахождении ускорения прямолинейного движения материальной точки.

Если на интервале времени считать движение точки равномерно ускоренным, то ускорение определяется как . Если ускорение меняется во времени, то мгновенное ускорение в определенной точке определяется как предел этого отношения: Отсюда ускорение движения в произвольный момент времени является производной первого порядка от функции скорости. Поскольку в свою очередь то ускорение является производной второго порядка от функции, описывающей зависимость пути от времени:

Утверждение (15.28) считается механической интерпретацией производной второго порядка.

Задача о нахождении скорости изменения экономических показателей

Как и производная первого порядка, которая характеризует  предельные значения показателей производственных процессов, вторая производная часто используется для анализа изменения этих значений. Понятно, что вторая производная имеет определенный экономический смысл в зависимости от функции, для которой она рассматривается. Так, вторая производная от производственной функции , описывает затраты на производство продукции в зависимости от ее объема является скоростью изменения себестоимости продукции:

Вторая производная по времени от объема является скоростью изменения производительности труда

Вернемся к определению производной второго порядка и введем понятие дифференциала второго порядка. Поскольку прирост аргумента не зависит от значения независимой переменной (для любой точки с области определения функции его можно выбирать произвольно), то от дифференциала функции , который тоже можно рассматривать как функцию от , можно создать дифференциал .

Дифференциалом второго порядка, или вторым дифференциалом, называют дифференциал от дифференциала функции и обозначают символом или

Считают, что дифференциал является дифференциалом первого порядка. Несмотря на общепринятую договоренность писать , …, , получаем окончательно:

Аналогично ищут третий дифференциал и дифференциалы высших порядков.

Дифференциалом n-го порядка называют дифференциал первого порядка от дифференциала -го порядка:

По формуле (15.32) получаем выражение для производной любого конечного порядка через отношение дифференциалов -го порядка:

Применение производных высших порядков в приближенных вычислениях. Формула Тейлора для многочлена и произвольной функции

Задача вычисления значения функции по значениям аргумента в техническом отношении не всегда является тривиальной. Проще она решается, конечно, для целой рациональной функции-многочлена: выполняют определенное количество действий сложения (вычитания) и умножения. Когда же аналитическое задание функции другое, например,   то нельзя указать, какие именно арифметические операции и в каком количестве необходимо выполнить над значением аргумента, чтобы получить значения функции.

Формула Тейлора позволяет подавать приближенно функции в виде многочлена и, пользуясь этим, составлять таблицы логарифмов, тригонометрических функций, корней и т.д., и разрабатывать соответствующие компьютерные программы.

Формула Тейлора для многочлена

Многочлен  степени , который представлен в виде:

где – постоянная (коэффициенты многочлена), называют многочленом по степеням переменной .

Продифференцируем его последовательно раз:

и положим в этих формулах и в (15.33) , тогда получим выражения для коэффициентов многочлена через значения самого многочлена и его производных при :

С учетом (15.34) получим формулу:

которую называют формулой Тейлора для многочлена по степеням переменной ; она отличается от формулы (15.33) только способом записи коэффициентов.

Многочлен, который представлен в виде:

где – коэффициенты многочлена, – некоторая фиксированная стоимость аргумента, называют многочленом по степеням разности

Аналогично рассмотренному выше получим формулу Тейлора для многочлена (15.36):

Понятно, что формула (15.35) – частный случай (15.37), когда .

Формулой Тейлора удобно пользоваться при исчислении стоимости многочлена для значений аргумента, близких к , потому, начиная с некоторого степени разницы , слагаемым можно пренебречь, упрощая таким образом вычисления.

Найдем значение многочлена  при с точностью до

Запишем многочлен по степеням . Имеем:

Следовательно,

Формула Тейлора для произвольной функции

Пусть функция имеет производные до -го порядка включительно в некотором промежутке, который содержит точку . Запишем вроде (15.37) многочлен

Как видно, этот многочлен и его производные (до -й включительно) в точке имеют те же значения, что и функция и ее производные. Если – не целый многочлен -й степени, то нельзя утверждать равенства . Многочлен дает лишь некоторое приближение к функции ; потому особый интерес представляет изучение разницы . Если обозначить эту разницу через , то получим:

Функцию называют остаточным членом формулы Тейлора для функции . Существуют различные формы остаточного члена; одна из них имеет вид:

где – промежуточная точка между и .

Формулу (15.40) называют остаточным членом в форме Лагранжа, а соответствующую формулу (15.39) – формулой Тейлора для  с остаточным членом в форме Лагранжа.

Как видим, (15.39) отличается от (15.38) только последним членом: он имеет такую же форму, как и другие члены, но производная исчисляется не в точке x0, а в промежуточной точке между и .

Если , то получим отдельный, очень важный, случай формулы Тейлора:

где – число, находящееся между нулем и .

В этом случае вместо часто пишут , где – параметр 

Запишем формулу Тейлора при для функции:

Устанавливаем выражение производной -го порядка и используем (15.41):

а) для функции имеем: , поэтому при получаем: , и (15.41) принимает вид:

б) функция имеет такое выражение для -й производной: Откуда при получаем: , если нечетное; , если , если .
Следовательно,

Замечания.

1. Формула теоремы Лагранжа является частным случаем, при , формулы Тейлора:

2. Формула Тейлора для применяется не только в практике приближения функций многочленами, но и играет очень важную роль в теоретических исследованиях, в частности, в теории рядов, которая будет рассматриваться позже.