Определение производной
Определение. Пусть функция ( y = f(x) ) определена в некотором интервале, содержащем внутри себя точку ( x_0 ).
Дадим аргументу приращение ( Delta x ) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции
( Delta y ) (при переходе от точки ( x_0 ) к точке ( x_0 + Delta x ) ) и составим отношение
( frac{Delta y}{Delta x} ). Если существует предел этого отношения при ( Delta x rightarrow 0 ), то
указанный предел называют производной функции ( y=f(x) ) в точке ( x_0 ) и обозначают ( f'(x_0) ).
$$ lim_{Delta x to 0} frac{Delta y}{Delta x} = f'(x_0) $$
Для обозначения производной часто используют символ ( y’ ).
Отметим, что ( y’ = f(x) ) – это новая функция, но, естественно, связанная с функцией ( y = f(x) ), определенная во всех точках (x), в которых
существует указанный выше предел. Эту функцию называют так: производная функции ( y = f(x) ).
Геометрический смысл производной состоит в следующем. Если к графику функции ( y = f(x) ) в точке с абсциссой ( x=a ) можно
провести касательную, непараллельную оси (y), то ( f(a) ) выражает угловой коэффициент касательной:
( k = f'(a) )
Поскольку ( k = tg(a) ), то верно равенство ( f'(a) = tg(a) ) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция ( y = f(x) ) имеет
производную в конкретной точке ( x ):
$$ lim_{Delta x to 0} frac{Delta y}{Delta x} = f'(x) $$
Это означает, что около точки (x) выполняется приближенное равенство ( frac{Delta y}{Delta x} approx f'(x) ), т.е.
( Delta y approx f'(x) cdot Delta x ).
Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально»
приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке (x).
Например, для функции ( y = x^2 ) справедливо приближенное равенство ( Delta y approx 2x cdot Delta x ).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение ( x ), найти ( f(x) )
2. Дать аргументу ( x ) приращение ( Delta x ), перейти в новую точку ( x+ Delta x ), найти ( f(x+ Delta x) )
3. Найти приращение функции: ( Delta y = f(x + Delta x) – f(x) )
4. Составить отношение ( frac{Delta y}{Delta x} )
5. Вычислить $$ lim_{Delta x to 0} frac{Delta y}{Delta x} $$
Этот предел и есть производная функции в точке (x).
Если функция (y=f(x)) имеет производную в точке (x), то ее называют дифференцируемой в точке (x). Процедуру нахождения производной
функции (y=f(x)) называют дифференцированием функции (y=f(x)).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция (y=f(x)) дифференцируема в точке (x). Тогда к графику функции в точке ( M(x; ; f(x)) ) можно провести касательную,
причем, напомним, угловой коэффициент касательной равен ( f'(x) ). Такой график не может «разрываться» в точке (M), т. е. функция
обязана быть непрерывной в точке (x).
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция (y=f(x)) дифференцируема в точке (x), то
выполняется приближенное равенство ( Delta y approx f'(x) cdot Delta x ). Если в этом равенстве ( Delta x ) устремить к
нулю, то и ( Delta y ) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Обратное утверждение неверно. Например: функция ( y=|x|) непрерывна везде, в частности в точке (x=0), но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция ( y=sqrt[3]{x} ) непрерывна на всей числовой прямой, в том числе в точке (x=0).
И касательная к графику функции существует в любой точке, в том числе в точке (x=0). Но в этой точке касательная совпадает с осью (y),
т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид (x=0). Углового коэффициента у такой прямой нет, значит, не существует и
( f'(0) )
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее
дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси
абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она
перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием.
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если (C) — постоянное число и ( f=f(x), ; g=g(x) ) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
$$ C’=0 $$
$$ x’=1 $$
$$ ( f+g)’=f’+g’ $$
$$ (fg)’=f’g + fg’ $$
$$ (Cf)’=Cf’ $$
$$ left(frac{f}{g} right) ‘ = frac{f’g-fg’}{g^2} $$
$$ left(frac{C}{g} right) ‘ = -frac{Cg’}{g^2} $$
Производная сложной функции:
$$ f’_x(g(x)) = f’_g cdot g’_x $$
Таблица производных некоторых функций
$$ left( frac{1}{x} right) ‘ = -frac{1}{x^2} $$
$$ ( sqrt{x} ) ‘ = frac{1}{2sqrt{x}} $$
$$ left( x^a right) ‘ = a x^{a-1} $$
$$ left( a^x right) ‘ = a^x cdot ln a $$
$$ left( e^x right) ‘ = e^x $$
$$ ( ln x )’ = frac{1}{x} $$
$$ ( log_a x )’ = frac{1}{xln a} $$
$$ ( sin x )’ = cos x $$
$$ ( cos x )’ = -sin x $$
$$ ( text{tg} x )’ = frac{1}{cos^2 x} $$
$$ ( text{ctg} x )’ = -frac{1}{sin^2 x} $$
$$ ( arcsin x )’ = frac{1}{sqrt{1-x^2}} $$
$$ ( arccos x )’ = frac{-1}{sqrt{1-x^2}} $$
$$ ( text{arctg} x )’ = frac{1}{1+x^2} $$
$$ ( text{arcctg} x )’ = frac{-1}{1+x^2} $$
Производная функции
Производной функции y=f(x) в точке x0 называется конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (см. пример).
Если необходимо найти производные функции нескольких переменных z=f(x,y), то можно воспользоваться данным онлайн-калькулятором. Решение оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
Примеры
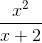 ≡ x^2/(x+2)
≡ x^2/(x+2)
cos2(2x+π) ≡ (cos(2*x+pi))^2
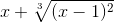 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)
Правила ввода функции, заданной в неявном виде
Примеры
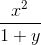 ≡ x^2/(1+y)
≡ x^2/(1+y)
cos2(2x+y) ≡ (cos(2*x+y))^2
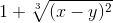 ≡ 1+(x-y)^(2/3)
≡ 1+(x-y)^(2/3)
Если функция задана в виде y2-x=cos(y), то ее необходимо записать так: y^2-x-cos(y).
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
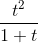 ≡ t^2/(1+t)
≡ t^2/(1+t)
cos2(t) ≡ cos(t)^2
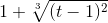 ≡ 1+(t-1)^(2/3)
≡ 1+(t-1)^(2/3)
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
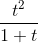 ≡ t^2/(1+t)
≡ t^2/(1+t)
cos2(t) ≡ cos(t)^2
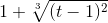 ≡ 1+(t-1)^(2/3)
≡ 1+(t-1)^(2/3)
Как найти производную, исходяя из ее определения?
Правила нахождения производных
Пример 1. Найти производную функции y=cos4x.
Решение.
Внешней функцией здесь служит степенная функция: cos(x) возводится в четвертую степень. Дифференцируя эту степенную функцию по промежуточному аргументу cos(x), получим
(cos4x)′cos x = 4cos4-1x = 4cos3x
но промежуточный аргумент cos(x) – функция независимой переменной х; поэтому надо полученный результат умножить на производную от cos(x) по независимой переменной х . Таким образом, получим
y′x = (cos4x)′cos x·(cosx)′x = 4·cos3x·(-sin x) = -4·cos3x·sin x
При дифференцировании функций нет необходимости в таких подробных записях. Результат следует писать сразу, представляя последовательно в уме промежуточные аргументы.
Пример 2. Найти производную функции
![]() .
.

 .
.
В некоторых случаях, если, например, нужно найти производную функции y = (u(x))v(x), или функции, заданной в виде произведения большого числа сомножителей, используется так называемый способ логарифмического дифференцирования.
Пример 3. Найти производную функции
 .
.
Решение.
Применим метод логарифмического дифференцирования. Рассмотрим функцию

Учитывая, что  , будем иметь
, будем иметь

Но  , откуда
, откуда
 .
.
Пример 4. Найти производную функции y=xex
Решение.
![]()
 ;
;
 .
.
Прикладное использование производной
Вычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.
- Нахождение экстремумов функции одной переменной осуществляют приравниванием к нулю производной:
f'(x)=0. Этот этап является основным для построения графика функции методом дифференциального исчисления. - Значение производной в точке x0 позволяет находить уравнение касательной к графику функции.
- Отношение производных позволяет вычислять пределы по правилу Лопиталя.
- В математической статистике плотность распределения f(x) определяют как производную от функции распределения F(x).
- При отыскании частного решения линейного дифференциального уравнения требуется вычислять производную в точке.
- В методе Ньютона с помощью производной отделяют корни нелинейных уравнений.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Производная по-шагам

Примеры производных
- Производные от степенных функций
-
x^7/10
-
(x^2 - 1)/(x^a - 5)
- Производные от сложных функций
-
sin(ln(x))
-
ln(sin(x))
- Производные от показательных функций
-
e^(-x^2)
- Производные от логарифмов
-
1-log(x-5)
-
ln(a*x) / ln(x^3)
- Производные от обратных тригонометрических функций
-
arcsin(1-x)
-
arctan(a*x + b)
- Производная неявной функции
-
e^y/x = x*y + 1
- Частная производная функции
-
x^2*sin(-y) + y/x
-
x*y*cos(z)
Подробнее про Производная функции
.
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
-
квадратные корни sqrt(x),
кубические корни cbrt(x) -
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
-
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x) -
натуральные логарифмы ln(x),
десятичные логарифмы log(x) -
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x) -
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) -
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x) -
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) -
знак числа:
sign(x) -
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x) -
Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
-
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- – умножение
- 3/x
- – деление
- x^2
- – возведение в квадрат
- x^3
- – возведение в куб
- x^5
- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
- Действительные числа
- вводить в виде 7.5, не 7,5
Постоянные
- pi
- – число Пи
- e
- – основание натурального логарифма
- i
- – комплексное число
- oo
- – символ бесконечности
Данный онлайн калькулятор вычисляет производную функции. Программа не только вычисляет ответ, она производит пошаговое решение. Выбирается порядок дифференцирования.
Как пользоваться калькулятором для нахождения производных онлайн:
1. Введите математическое выражение с переменной x, в выражении используйте стандартные операции: + сложение, –
вычитание, / деление, * умножение, ^ – возведение в степень, а также математические функции.
2. Выберите порядок дифференцирования (решения производных от первого до пятого порядка включительно).
3. Нажмите кнопку – Вычислить производную.
4. Через несколько секунд внизу отобразится пошаговое решение производной с подробными комментариями.
При помощи нашего калькулятора вы можете найти производную онлайн как от элементарной функции, так и от сложной, не имеющей решения в аналитическом виде.
Калькулятор поможет найти производную функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.

 : x^a
: x^a
модуль x: abs(x)
Для того, чтобы найти производную функции 
нужно написать в строке: f[x], x. Если Вам требуется
найти производную n-го порядка, то следует написать: f[x], {x, n}. В
том случае, если Вам требуется найти частную производную функции  напишите в окне гаджета: f[x, y, z,…,t], j, где
напишите в окне гаджета: f[x, y, z,…,t], j, где 
— интересующая Вас переменная. Если нужно найти частную производную по
некоторой переменной порядка n, то следует ввести: f[x, y, z,…,t], {j,
n}, где  означает тоже, что и Выше.
означает тоже, что и Выше.
Важно подчеркнуть, что калькулятор выдает пошаговое нахождение
производной при нажатии на «Show Steps» в правом верхнем углу
выдаваемого ей ответа.
- Примеры
- x*E^x, x;
- x^3*E^x, {x,17};
- x^3*y^2*Sin[x+y], x;
- x^3*y^2*Sin[x+y], y,
- x/(x+y^4), {x,6}.
Решение производных
Что такое производная и как её решить
В науке под производной имеют в виду скорость изменения чего-либо, например скорость движения материальной точки. Производная функции — это предел отношения приращения функции к приращению аргумента при стремлении последнего к 0. Чтобы найти производную функции, необходимо ее продифференцировать.
Данный калькулятор решает задачи по вычислению производной как от элементарной, так и от сложной функции. Для решения задачи: введите функцию с переменной х, для которой нужно найти производную и за пару секунд получите результат.
Пример вычисления производной
Предположим перед нами стоит задача вычисления производной, как приведено на нижеследующей картинке:
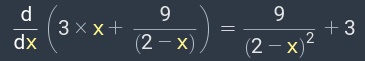
Комбинация клавиш, которые нам необходимо использовать для вычислений на онлайн-калькуляторе выглядит следующим образом:
