Формула производной от дроби, примеры
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Формула производной от дроби
Раздел о производных является отдельным самостоятельным разделом в математическом анализе. Условимся, что читателю известно понятия предела, производной, дифференциала, а также ряд свойств производной.
В данной статье рассмотрим одно из свойств производной, а именно формулу производной от дроби. Приведём эту формулу. Пусть функция $v(x)$ имеет производную в точке $x$ и $v(x)neq0$, тогда:
$(frac{u}{v})’=frac{u’v-uv’}{v^2}.$
Напомним формулы производных элементарных функций:
Рисунок 1. Формулы производных элементарных функций. Автор24 — интернет-биржа студенческих работ
Примеры
Решим примеры. Преобразования, позволяющие применить другие свойства производной, мы применять не будем. В решениях будем использовать только формулу производной от дроби.
По условию даются функции. Нужно найти производные.
Пример 1
Рисунок 2. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 3. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 4. Пример. Автор24 — интернет-биржа студенческих работ
Пример 2
Рисунок 5. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 6. Пример. Автор24 — интернет-биржа студенческих работ
Пример 3
Рисунок 7. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 8. Пример. Автор24 — интернет-биржа студенческих работ
Пример 4
Рисунок 9. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 10. Пример. Автор24 — интернет-биржа студенческих работ
Пример 5
Рисунок 11.
Рисунок 12. Пример. Автор24 — интернет-биржа студенческих работ
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 15.05.2023
Производная дроби – что это такое
Определение
Производная дроби – это значение, которое получается, если производную числителя умножить на знаменатель и прибавить числитель, умноженный на производную знаменателя, а затем все это разделить на квадрат знаменателя.
Формула производной от дроби
Формула ПД имеет следующий вид:
(left(fracupsilonnuright)’=frac{upsilon’nu-upsilonnu’}{v^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
При этом важно отметить, что нахождение ПД нельзя осуществлять с помощью деления производной числителя на производную знаменателя. Два эти действия будут иметь разные значения после подсчетов.
Приведем доказательство данной формулы. Рассмотрим выражение y=fracupsilonnu. Все представленные переменные – это функции от х. Умножим их на (nu). Получим (ytimesnu=upsilon).
Дифференцируем по х, применяя формулу производной произведения двух функций, то есть:
(left(upsilontimesnuright)’=upsilon’timesnu+upsilontimesnu’)
Тогда выводим:
(y’timesnu+ytimesnu’=upsilon’)
Из этого вычисляем нужную нам производную:
(y’timesnu=upsilon’-ytimesnu’=upsilon’-fracupsilonnutimesnu’=frac{upsilon’v-upsilonnu’}nu;;y’=frac{upsilon’v-upsilonnu’}{nu^2})
Что и требовалось доказать.
Следует также привести таблицу с производными часто встречающихся функций:
Как решать производные функции с дробями, примеры
Чтобы понять, как решать ПФ с дробями, приведем несколько примеров.
Пример 1
Найти производную дроби (y=frac x{In;x}.)
Решение
Из формулы следует, что числитель (upsilon=х), а знаменатель (nu=In;х). Найдем их производные:
(upsilon’=left(хright)’=1,;nu’=left(In;xright)’=frac1x)
Подставляем решенные (upsilon’;и;nu’) в формулу и получаем:
( y’=left(frac x{In;x}right)’=frac{left(xright)’In;x-xleft(In;xright)’}{left(In;xright)^2}=frac{In;x;-x{displaystylefrac1x}}{In^2x}=frac{In;x-1}{In^2x})
Ответ: (y’=frac{In;x-1}{In^2x}.)
Пример 2
Найти производную дроби, равную (y=frac{cos;x}x).
Решение
По формуле производной частного:
(y’=left(frac{cos;x}xright)=frac{left(cos;xright)’x-cos;xleft(xright)’}{left(xright)^2})
Производная косинуса дает нам синус с минусом:
(left(cos;xright)’=-sin;x)
В таком случае:
(y’=frac{-x;sin;x-cos;x}{x^2}=-frac{x;sin;x+cos;x}{x^2})
Ответ: (y’=-frac{x;sin;x+cos;x}{x^2}.)
Пример 3
Найти производную дроби (yleft(xright)=frac{e^x-1}{e^x+1}.)
Решение
Из таблицы производных находим:
(left(e^xright)’=e^x)
Применяем правила дифференцирования постоянной и суммы:
(left(e^x-1right)’=left(e^xright)’-left(1right)’=e^x-0=e^x;;left(e^x+1right)’=left(e^xright)’+left(1right)’=e^x-0=e^x)
Используем формулу производной дроби:
(left(fracupsilonnuright)’=frac{upsilon’nu-upsilonnu’}{nu^2};left(frac{e^x-1}{e^x+1}right)’=frac1{left(e^x+1right)^2}timeslbrackleft(e^x-1right)’left(e^x+1right)-left(e^x-1right)left(e^x+1right)’rbrack=frac1{left(e^x+1right)^2}timeslbrack e^xleft(e^x+1right)-left(e^x-1right)e^xrbrack=frac{2e^x}{left(e^x+1right)^2})
Ответ: (y’=frac{2e^x}{left(e^x+1right)^2}.)
Один из важнейших разделов математики – производные. Для их нахождения существуют специальные формулы производных. Для работы с ними необходимо знать основные формулы элементарных функций.
Таблица формул производных
Ниже приведена таблица формул производных элементарных функций.
| [C^{prime}=0] | [(ln ln x)^{prime}=frac{1}{x}] |
| [x^{prime}=1] | [(sin sin x)^{prime}=cos cos x] |
| [left(x^{2}right)^{prime}=2 x] | [(cos cos x)^{prime}=-sin sin x] |
| [left(x^{n}right)^{prime}=n * x^{n-1}] | [(operatorname{tg} x)^{prime}=frac{1}{cos ^{2}(x)}] |
| [left(a^{x}right)^{prime}=a^{x} * ln (a)] | [(operatorname{ctg} x)^{prime}=-frac{1}{sin ^{2}(x)}] |
| [left(e^{x}right)^{prime}=e^{x}] | [(arcsin arcsin x)^{prime}=frac{1}{sqrt{1-x^{2}}}] |
| [(x)^{prime}=frac{1}{x * ln (a)}] | [begin{aligned} (arccos &arccos x)^{prime} &=-frac{1}{sqrt{1-x^{2}}} end{aligned}] |
| [(operatorname{arctg} x)^{prime}=frac{1}{1+x^{2}}] | [(operatorname{arcctg} x)^{prime}=-frac{1}{1+x^{2}}] |
Смысл производной
В математике производная имеет геометрический и физический смыслы.
Допустим, что некоторая функция f(x) задана в интервале (a, b). При этом есть две точки x и x0, которые находятся в указанном интервале. Если значение x будет изменяться, то и f(x) тоже изменится. Изменение аргумента находится из выражения (x – x0). Эта разность обозначается как Δx – приращение аргумента. В таком случае приращением функции будет являться разность между ее значениями в двух точках. Исходя из этого, можно дать определение производной. Ей называется предел отношения приращения функции к приращению аргумента в указанной точке. При этом сам аргумент стремится к нулю.
В математике формулы производных функций записываются так:
[begin{gathered} f^{prime}left(x_{0}right)=left(frac{fleft(x_{0}+Delta xright)-fleft(x_{0}right)}{Delta x}right). \ y^{prime}left(x_{0}right)=lim _{Delta x rightarrow 0}left(frac{Delta y}{Delta x}right) . end{gathered}]
Смысл этих формул, а точнее нахождения их значений, может быть описан с точки зрения геометрии и физики.
Геометрический смысл состоит в том, что производная функции в конкретной точке равняется тангенсу угла, который образован осью абсцисс и касательной линией к графику. Пример показан на рисунке ниже.
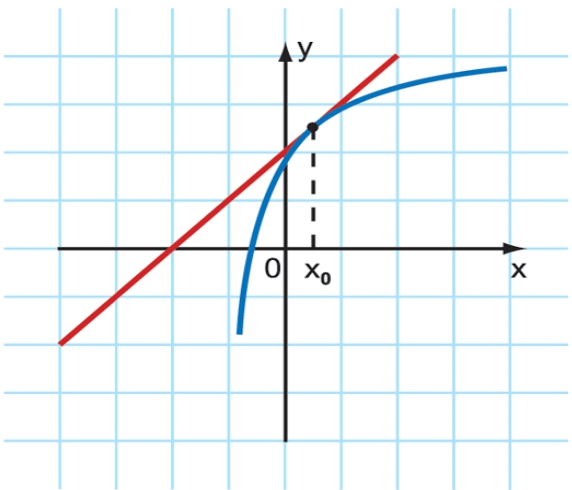
В физике смысл состоит в том, что производная от пройденного расстояния по времени есть скорость движения точки.
Нет времени решать самому?
Наши эксперты помогут!
Формула вычисления производной дроби
Рассмотрим формулу вычисления производной дроби. Функция v(x) имеет производную в определенной точке x. При этом v(x) не равна нулю (v(x) ≠ 0). В таком случае справедлива следующая формула:
[left(frac{u}{v}right)^{prime}=frac{u^{prime} v-u v^{prime}}{v^{2}}]
Рассмотрим примеры использования формулы производной дроби при решении задач.
Примеры 1 — 2
Первый пример с выражениями из тригонометрии: [y=frac{cos cos x}{x^{2}}]
Пользуясь таблицей 1 найдем:
[begin{gathered}
y^{prime}=frac{left.(cos cos x)^{prime} * (x^{2}-xright) *left(x^{2}right)^{prime}}{left(x^{2}right)^{2}} =\
frac{(-sin sin x) * x^{2}-(cos cos x) * 2 x}{x^{4}} .
end{gathered}]
Вынесем x за скобки и преобразуем полученное выражение: [y^{prime}=frac{(-sin sin x) * x-2 cos cos x}{x^{3}}]
Другой пример:
[begin{gathered}
y=frac{x^{3}}{x^{3}+2} \
y^{prime}=frac{left(x^{3}right)^{prime} *left(x^{3}+2right)-x^{3} *left(x^{3}+2right)^{prime}}{left(x^{3}+2right)^{2}} \
y^{prime}=frac{3 x^{2} *left(x^{3}+2right)-x^{3} * 3 x^{2}}{left(x^{3}+2right)^{2}} \
y^{prime}=frac{3 x^{5}+6 x^{2}-3 x^{5}}{left(x^{3}+2right)^{2}}=frac{6 x^{2}}{left(x^{3}+2right)^{2}}
end{gathered}]
Решение примеров на нахождение производных в математике называется дифференцированием. Они бывают двух типов:
- частными;
- полными.
Между этими типами есть одно основное отличие. При нахождении частной производной функция аппроксимируется только по одному аргументу. Так во всех предыдущих примерах аппроксимация производилась только по x.
Производная дроби
Производная дроби равна произведению производной числителя на знаменатель минус произведение числителя на производную знаменателя и всё делить на квадрат знаменателя:
$$ bigg (frac{u}{v} bigg )’ = frac{u’v-uv’}{v^2} $$
Следует понимать, что производная дроби НЕ РАВНА отношению производных числителя и знаменателя!
Примеры с решением
| Пример 1 |
| Найти производную дроби $ y = frac{x}{ln x} $ |
| Решение |
|
Из формулы следует, что числитель $$ u = x $$ а знаменатель $$ v = ln x $$ Находим их производные: $$ u’ = (x)’ = 1 $$ $$ v’ = (ln x)’ = frac{1}{x} $$ Подставляем найденные $ u’ $ и $ v’ $ в формулу производной дроби: $$ y’=bigg (frac{x}{ln x} bigg )’ = frac{(x)’ln x – x(ln x)’}{(ln x)^2} = $$ $$ = frac{ln x – x frac{1}{x}}{ln^2 x} = frac{ln x – 1}{ln^2 x} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ y’ = frac{ln x – 1}{ln^2 x} $$ |
| Пример 2 |
| Найти производную от дроби $ y = frac{cos x}{x} $ |
| Решение |
|
По формуле производной частного: $$ y’=bigg (frac{cos x}{x} bigg ) = frac{(cos x)’x-cos x (x)’}{(x)^2} = $$ Производная косинуса равна отрицательному синусу: $$ (cos x)’ = -sin x $$ Тогда: $$ y’ = frac{-xsin x – cos x}{x^2} = -frac{xsin x + cos x}{x^2} $$ |
| Ответ |
| $$ y’ = -frac{xsin x + cos x}{x^2} $$ |
Квадратное уравнения имеет 4 корня, число Пи может быть равно 2, факториал можно вычислить для нецелого аргумента – обо всё этом я писал на своём канале…Сегодня я хочу выдать Вам еще один замечательный математический этюд.
Давайте подумаем, как возвести число в 4-ю степень? Ну
, например, сначала возвести в квадрат, а затем еще раз; или же возвести в 8-ю степень, а потом в степень 1/2. Ничего же противоестественного нет!
То же самое и с производной: вторую производную от функции можно получить последовательно применяя операцию дифференцирования.
Напрашивается такой вопрос: а есть ли такой оператор (назовём его А), что если его применить к функции ДВА раза, то получится обычная производная?
Оказывается, и это доказывается в курсе продвинутого математического анализа, такие операторы существуют и в самом обобщенном случае. Давайте лучше на простом примере:
Что мы сделали выше? Мы нашли обобщенную формулу производной n-ного порядка для указанной функции.
А теперь моё любимое: подставим вместо n число 1/2. Посмотрим, что получилось:
“Ну и что, скажете Вы, – это какое-то искусственное сооружение” В ответ на это я применю операцию вычисления дробной производной еще разок:
Мы получили как раз тот самый оператор A (некое правило вычисления), который при двойном применении к функции возвращает её производную. Будем называть его полупроизводной.
Естественно, никакой сложности не составит обобщить этот случай для производной порядка 1/n.
Первопроходцами применения дробной производной как обобщенного случая знакомой нам со школы операции являются математики Лопиталь, Лейбниц и Абель.
Операция – далеко не бесполезная, хотя и не имеет такого явного физического смысла как её полноценная сестра.
Дробная производная возникает в огромном количестве практических задач в метеорологии, химии, применяется при моделировании перемещения потоков жидкости, распространения сложных акустических колебаний и, конечно, на самом переднем крае науки – квантовой физике.
Конечно, рассказанное мной не претендует ни на какую математическую строгость, ведь, чтобы рассказать о дробной производной нужно знать немного больше школьного курса математики. Несмотря на это, в следующих выпусках я на очень простом языке это сделаю.
Там еще много интересного! Например, дробная производная константы отнюдь не равна нулю!
Подписывайтесь на канал! Ставьте “Нравится” этой публикации, мотивируя меня писать дальше. Спасибо за внимание!













