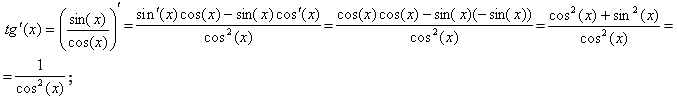Как найти производную функции sinx cosx - Сайт, где вы сможете решить свои вопросы

Голосование за лучший ответ

Евгений Фомин

Мудрец

(13846)

7 лет назад

Согласен с Романом
Действительно: y = (sinx)^cosx
Прологорифмируем обе части равенства.
lny = ln((sinx)^cosx) = cosx*ln(sinx)
Находим дифференциалы обеих частей
dy/y = (-sinx*ln(sinx) + ctg(x) * cos(x))dx
Поделим на dx
dy/dx = y’
y’/y = -sinx*ln(sinx) + ctg(x) * cos(x)
Отсюда
y’ = (-sinx*ln(sinx) + ctg(x) * cos(x)) * y = (-sinx*ln(sinx) + ctg(x) * cos(x))*(sinx)^cosx

Владимир Втюрин

Профи

(950)

7 лет назад

Запишем:
y = (sin x) ^ cos x

ЛОГАРИФМИРУЕМ:
ln y = ln [ (sin x) ^ cos x ]
ln y = (cos x) * ln (sin x)

НАХОДИМ ПРОИЗВОДНУЮ:
1/y * y’ = (-sin x)*ln(sin x) + (cos x)* (1/sin x) * cos x)

y’ = y*[(-sin x)*ln (sin x) + (cos x)^2 / sin x)]

Источник

Заказать задачи по любым предметам можно здесь от 10 минут

Производная синуса

Определение

Производная синуса равна положительному косинусу одно и того же аргумента: $$ (sin x)’ = cos x $$

Если же аргумент синуса представляе собой функцию $ f(x) $, то производная синуса сложной функции находится по формуле: $$ (sin f(x))’ = cos f(x) cdot ( f(x) )’ = f'(x) cos f(x) $$

Пример 1

Найти производную синуса двойного угла: $ y = sin 2x $

Решение

Так как аргумент синуса представляет собой сложную функцию $ f(x)=2x $, то используем вторую формулу.

Находим производную $ f(x) $:

$$ f'(x) = (2x)’ = 2 $$

Теперь подставляем всё в формулу и записываем:

$$ y’ = (sin 2x)’ = cos 2x cdot (2x)’ = 2cos 2x $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ y’ = 2cos 2x $$

Пример 2

Чему равна производная синуса в квадрате? $ y = sin^2 x $

Решение

В этом примере синус представляет собой степенную функцию. Поэтому сначала берем производную по правилу: $ (x^p)’=px^{p-1} $, а затем производную от $ sin x $.

Записываем:

$$ y’=(sin^2 x)’ = 2sin^2 x cdot (sin x)’ = 2sin^2 x cdot cos x $$

Ответ

$$ y’ = 2sin^2 x cos x $$

Пример 3

Найти производную синуса в кубе: $ y = sin^3 x $

Решение

Это задание полностью аналогичное предыдущему, только вместо квадрата стоит куб:

$$ y’ = (sin^3 x)’ = 3sin^2 x cdot (sin x)’ = 3sin^2 x cdot cos x $$

Ответ

$$ y’ = 3sin^2 x cos x $$

Пример 4

Чему равна производная сложной функции синус корень икс? $ y = sin sqrt{x} $

Решение

Формула производной квадратного корня: $$ (sqrt{x})’ = frac{1}{2sqrt{x}} $$

Возвращаемся к заданию и находим производную:

$$ y’ = (sin sqrt{x})’ = cos sqrt{x} cdot (sqrt{x})’ = cos sqrt{x} cdot frac{1}{2sqrt{x}} = frac{cos sqrt{x}}{2sqrt{x}} $$

Ответ

$$ y’ = frac{cos sqrt{x}}{2sqrt{x}} $$

Источник

Решение

$$sin^{cos{left(x right)}}{left(x right)}$$

d /   cos(x)   
--sin      (x)/
dx

$$frac{d}{d x} sin^{cos{left(x right)}}{left(x right)}$$

Подробное решение

Не могу найти шаги в поиске этой производной.

Но производная

Ответ:

Первая производная
[src]

             /   2                        
   cos(x)    |cos (x)                     |
sin      (x)*|------- - log(sin(x))*sin(x)|
              sin(x)                     /

$$left(- log{left(sin{left(x right)} right)} sin{left(x right)} + frac{cos^{2}{left(x right)}}{sin{left(x right)}}right) sin^{cos{left(x right)}}{left(x right)}$$

Вторая производная
[src]

             /                              2                                     
             |/                        2       /       2                        |
   cos(x)    ||                     cos (x)|    |    cos (x)              |       |
sin      (x)*||log(sin(x))*sin(x) - -------|  - |3 + ------- + log(sin(x))|*cos(x)|
             |                      sin(x)/    |       2                 |       |
                                                   sin (x)              /       /

$$left(left(log{left(sin{left(x right)} right)} sin{left(x right)} – frac{cos^{2}{left(x right)}}{sin{left(x right)}}right)^{2} – left(log{left(sin{left(x right)} right)} + 3 + frac{cos^{2}{left(x right)}}{sin^{2}{left(x right)}}right) cos{left(x right)}right) sin^{cos{left(x right)}}{left(x right)}$$

Третья производная
[src]

             /                                3                                                                                                                              
             |  /                        2                                            2           4        /                        2    /       2                        |
   cos(x)    |  |                     cos (x)|                                    2*cos (x)   2*cos (x)     |                     cos (x)| |    cos (x)              |       |
sin      (x)*|- |log(sin(x))*sin(x) - -------|  + 3*sin(x) + log(sin(x))*sin(x) + --------- + --------- + 3*|log(sin(x))*sin(x) - -------|*|3 + ------- + log(sin(x))|*cos(x)|
             |                        sin(x)/                                      sin(x)        3                               sin(x)/ |       2                 |       |
                                                                                              sin (x)                                         sin (x)              /       /

$$left(- left(log{left(sin{left(x right)} right)} sin{left(x right)} – frac{cos^{2}{left(x right)}}{sin{left(x right)}}right)^{3} + 3 left(log{left(sin{left(x right)} right)} sin{left(x right)} – frac{cos^{2}{left(x right)}}{sin{left(x right)}}right) left(log{left(sin{left(x right)} right)} + 3 + frac{cos^{2}{left(x right)}}{sin^{2}{left(x right)}}right) cos{left(x right)} + log{left(sin{left(x right)} right)} sin{left(x right)} + 3 sin{left(x right)} + frac{2 cos^{2}{left(x right)}}{sin{left(x right)}} + frac{2 cos^{4}{left(x right)}}{sin^{3}{left(x right)}}right) sin^{cos{left(x right)}}{left(x right)}$$

График

Источник

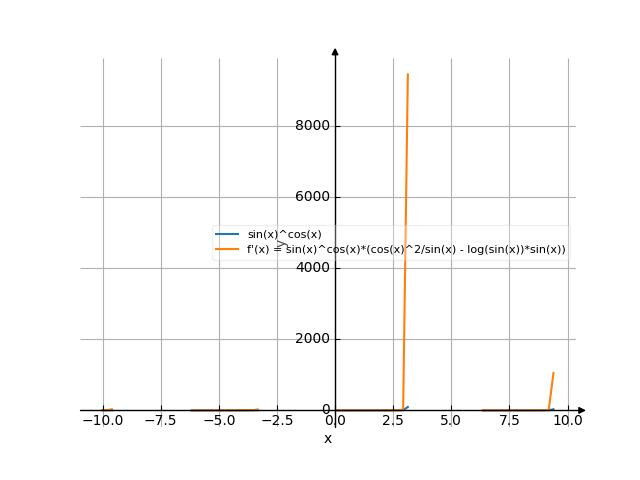
Выведем формулы производных некоторых функций.

1. sin'(x) = cos(x).

Доказательство:

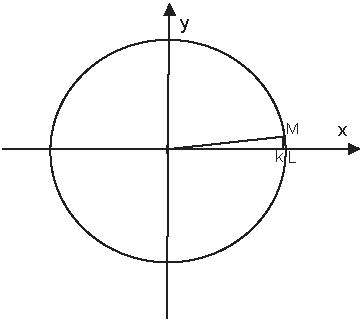
при h стремящемся к нулю, cos(h) стремится к 1, a sin(h) стремится к h. Строгое утверждение последнего утверждения выходит за рамки школьной программы, однако, чисто интуитивно можно в этом убедиться, посмотрев на следующий рисунок.