Марина Тарасюк
Ученик
(103),
на голосовании
10 лет назад
Голосование за лучший ответ
Alexander Bashirov
Мудрец
(12557)
10 лет назад
Это 5cos5x
Похожие вопросы
Предмет: Математика,
автор: FreaCKk
Приложения:
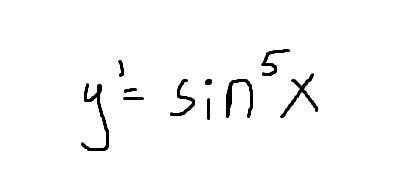
Ответы
Автор ответа: bena20192
5
Ответ:
Пошаговое объяснение:
y=sin⁵x
это производная сложной функции
формула f'(g(x))=f'(g)*g'(x)
сначала берем производную степенной функции считая sinx аргументом по формуле (tⁿ)’=ntⁿ⁻¹ и умножаем на производную аргумента то есть (sinx)’=cosx
y’=5(sin⁴x)cosx
FreaCKk:
Могу я вас попросить объяснить решение, и по какой формуле вы раскрывали
JulijaYulija:
y=sin⁵x
y’=5(sin⁴x)cosx ,в принципи так же …
bena20192:
написал
bena20192:
забыли 4 написать
bena20192:
вместо 5
JulijaYulija:
Вы правы)
bena20192:
бывает
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Математика,
автор: valeriazolotyh355
Під час сушіння яблука втрачають 91% своєї маси. Скільки сухих яблук одержимо з 250 кг свіжих?
Будь ласка, терміново!!!!
4 года назад
Предмет: Литература,
автор: zhanarka83
Художественное пространство и время в рассказе И.С. Тургенева «Бежин луг»
ІЯ В
ва
Вставь пропущенные слова в схеме.
Схема художественного пространства и времени
(рассказы Ильюши)
вр…
BILIM
Land
рольня
• Авдей
1
Назаров
2
• Ермила
• приказчик
• барашек
4 года назад
Предмет: Қазақ тiлi,
автор: Аноним
1. Қазақ хандарының мемлекетті нығайтудағы рөлін анықтаңыз.
4 года назад
Предмет: Алгебра,
автор: BetB
Построить график функции, подробно
1) (2/x)+(1/2)
2) 3/(2x-2)
3) 2/(2x-3)
7 лет назад
Предмет: Информатика,
автор: botko2016
як написати дріб на клавіатурі
7 лет назад
Решение
$$sin{left(frac{5}{x} right)}$$
d / /5\ --|sin|-|| dx x//
$$frac{d}{d x} sin{left(frac{5}{x} right)}$$
Подробное решение
-
Заменим .
-
Производная синуса есть косинус:
-
Затем примените цепочку правил. Умножим на :
-
Производная произведения константы на функцию есть произведение этой константы на производную данной функции.
-
В силу правила, применим: получим
Таким образом, в результате:
-
В результате последовательности правил:
-
Ответ:
Первая производная
[src]
/5
-5*cos|-|
x/
---------
2
x
$$- frac{5 cos{left(frac{5}{x} right)}}{x^{2}}$$
Вторая производная
[src]
/ /5\
| 5*sin|-||
| /5 x/|
5*|2*cos|-| - --------|
x/ x /
-----------------------
3
x
$$frac{5 cdot left(2 cos{left(frac{5}{x} right)} – frac{5 sin{left(frac{5}{x} right)}}{x}right)}{x^{3}}$$
Третья производная
[src]
/ /5 /5\
| 25*cos|-| 30*sin|-||
| /5 x/ x/|
5*|- 6*cos|-| + --------- + ---------|
| x/ 2 x |
x /
--------------------------------------
4
x
$$frac{5 left(- 6 cos{left(frac{5}{x} right)} + frac{30 sin{left(frac{5}{x} right)}}{x} + frac{25 cos{left(frac{5}{x} right)}}{x^{2}}right)}{x^{4}}$$
График


35 БАЛЛОВ
Нахождение производных функций
Sin 5x=y
y’=

Светило науки – 2 ответа – 0 раз оказано помощи
Чтобы найти производную функции у = sin5x, необходимо найти производную тригонометрической функции sin5x и выражения 5х. Для этого воспользуемся формулами:
1) (sinx)’ = cosx,
2) (ax)’ = a, где а – некоторое число.
Отсюда получим, что у’ = (sin5x)’ = (5x)'(sin5x)’ = 5cos5x.
Ответ: у’ = 5сos5x.

Светило науки – 3667 ответов – 10853 помощи
Ответ:
5cos5x
Пошаговое объяснение:
это производная сложной функции, здесь тригонометрическая функция синус зависит от линейной функции 5х, поэтому находим производные этих функций и перемножаем. получаем
у’=(cos5x)*(5x)’=5cos5x
Калькулятор Производных
Производная sin(5*x) по x
=
5*cos(5*x)
Калькулятор Производных вычисляет производную от функции по заданной перемеренной с использованием аналитического дифференцирования.
Показать правила синтаксиса
Производные Примеры калькулятор
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
中文
日本語
한국어
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.
© 2023
numberempire.com
Все права защищены
