При работе с функциями часто приходится учитывать их специфику, производя сложение, умножение или деление производных. Последнее из действий чаще всего вызывает вопросы у обучающегося, поэтому этот аспект стоит рассмотреть подробнее.
Производная частного
Когда выполняется деление производных, формула для преобразования выглядит как разность производной числителя, помноженного на знаменатель, и производной знаменателя, умноженного на числитель, и поделённое на квадрат знаменателя. При этом необходимо учитывать, что значение в нижней части дроби должно быть не равным нулю. При решении первых примеров преобразование производной частного нередко возникает проблема, поэтому лучше всего иметь перед глазами эту формулу:
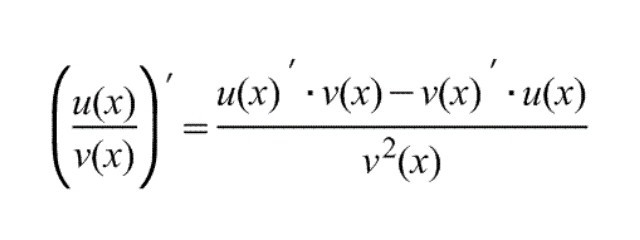
Благодаря этой формуле удаётся привести пример в более простую форму, которую можно разделить на табличные функции производных, после чего решить данную задачу не составит большого труда.
Пример решения
В качестве примера, демонстрирующего ход решения, где выполняется деление производных, стоит рассмотреть следующий:
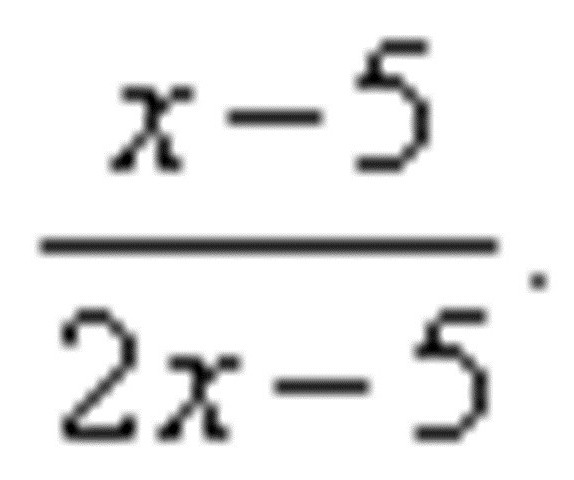
Согласно заданию, необходимо найти производную данного выражения. Воспользовавшись формулой, упрощающей деление производных, преобразуем исходный пример к следующему виду:
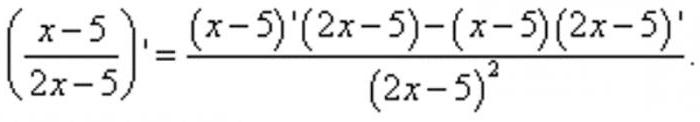
В результате в числителе оказалось две производные табличного вида, значения которых можно вычислить без дополнительных преобразований. В первом случае результатом будет единица, во втором – двойка. Подставив вычисленные данные в пример, получим дробь, в которой останется лишь произвести несложные вычисления в числителе, получив итоговый результат:
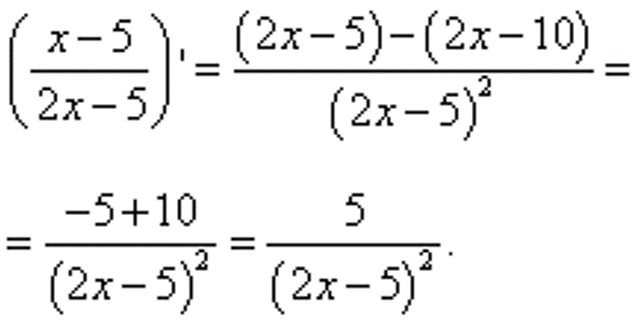
Маленькие хитрости
Перед применением формулы стоит внимательно посмотреть на деление производных. В некоторых случаях дробь можно упростить, благодаря чему приведенная в начале формула может оказаться ненужной или станет более простой. Упрощение дроби можно выполнить несколькими способами, включая деление числителя на знаменатель с целью определения целой части, а также домножением обеих частей дроби на одно и то же ненулевое число – этот приём часто применяется при наличии иррациональности под знаком производной.
Стоит отметить, что перед вначале необходимо проверить пример на наличие решения. Для этого нужно найти область допустимых значений (ОДЗ), и если она будет существовать, не создавая неопределённостей различного вида, можно приступать к вычислениям.
Правила вычисления производных
7 апреля 2011
- Скачать все правила
Если следовать определению, то производная функции в точке — это предел отношения приращения функции Δy к приращению аргумента Δx:
![]()
Вроде бы все понятно. Но попробуйте посчитать по этой формуле, скажем, производную функции f(x) = x
2 + (2x + 3) · e
x
· sin x. Если все делать по определению, то через пару страниц вычислений вы просто уснете. Поэтому существуют более простые и эффективные способы.
Для начала заметим, что из всего многообразия функций можно выделить так называемые элементарные функции. Это относительно простые выражения, производные которых давно вычислены и занесены в таблицу. Такие функции достаточно просто запомнить — вместе с их производными.
Производные элементарных функций
Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.
Итак, производные элементарных функций:
| Название | Функция | Производная |
| Константа | f(x) = C, C ∈ R | 0 (да-да, ноль!) |
| Степень с рациональным показателем |
f(x) = x n |
n · x n − 1 |
| Синус | f(x) = sin x | cos x |
| Косинус | f(x) = cos x | − sin x (минус синус) |
| Тангенс | f(x) = tg x | 1/cos2 x |
| Котангенс | f(x) = ctg x | − 1/sin2 x |
| Натуральный логарифм | f(x) = ln x | 1/x |
| Произвольный логарифм |
f(x) = log a x |
1/(x · ln a) |
| Показательная функция |
f(x) = e x |
e x (ничего не изменилось) |
Если элементарную функцию умножить на произвольную постоянную, то производная новой функции тоже легко считается:
(C · f)’ = C · f ’.
В общем, константы можно выносить за знак производной. Например:
(2x
3)’ = 2 · (x
3)’ = 2 · 3x
2 = 6x
2.
Очевидно, элементарные функции можно складывать друг с другом, умножать, делить — и многое другое. Так появятся новые функции, уже не особо элементарные, но тоже дифференцируемые по определенным правилам. Эти правила рассмотрены ниже.
Производная суммы и разности
Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:
- (f + g)’ = f ’ + g ’
- (f − g)’ = f ’ − g ’
Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.
Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.
Задача. Найти производные функций: f(x) = x
2 + sin x; g(x) = x
4 + 2x
2 − 3.
Функция f(x) — это сумма двух элементарных функций, поэтому:
f ’(x) = (x
2 + sin x)’ = (x
2)’ + (sin x)’ = 2x + cos x;
Аналогично рассуждаем для функции g(x). Только там уже три слагаемых (с точки зрения алгебры):
g ’(x) = (x
4 + 2x
2 − 3)’ = (x
4 + 2x
2 + (−3))’ = (x
4)’ + (2x
2)’ + (−3)’ = 4x
3 + 4x + 0 = 4x · (x
2 + 1).
Ответ:
f ’(x) = 2x + cos x;
g ’(x) = 4x · (x
2 + 1).
Производная произведения
Математика — наука логичная, поэтому многие считают, что если производная суммы равна сумме производных, то производная произведения strike“>равна произведению производных. А вот фиг вам! Производная произведения считается совсем по другой формуле. А именно:
(f · g) ’ = f ’ · g + f · g ’
Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.
Задача. Найти производные функций: f(x) = x
3 · cos x; g(x) = (x
2 + 7x − 7) · e
x
.
Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:
f ’(x) = (x
3 · cos x)’ = (x
3)’ · cos x + x
3 · (cos x)’ = 3x
2 · cos x + x
3 · (− sin x) = x
2 · (3cos x − x · sin x)
У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:
g ’(x) = ((x
2 + 7x − 7) · e
x
)’ = (x
2 + 7x − 7)’ · e
x
+ (x
2 + 7x − 7) · (e
x
)’ = (2x + 7) · e
x
+ (x
2 + 7x − 7) · e
x
= e
x
· (2x + 7 + x
2 + 7x −7) = (x
2 + 9x) · e
x
= x(x + 9) · e
x
.
Ответ:
f ’(x) = x
2 · (3cos x − x · sin x);
g ’(x) = x(x + 9) · e
x
.
Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.
Производная частного
Если есть две функции f(x) и g(x), причем g(x) ≠ 0 на интересующем нас множестве, можно определить новую функцию h(x) = f(x)/g(x). Для такой функции тоже можно найти производную:
![]()
Неслабо, да? Откуда взялся минус? Почему g
2? А вот так! Это одна из самых сложных формул — без бутылки не разберешься. Поэтому лучше изучать ее на конкретных примерах.
Задача. Найти производные функций:
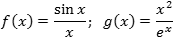
В числителе и знаменателе каждой дроби стоят элементарные функции, поэтому все, что нам нужно — это формула производной частного:
![]()
![]()
По традиции, разложим числитель на множители — это значительно упростит ответ:
![]()
Ответ:
![]()
Производная сложной функции
Сложная функция — это не обязательно формула длиной в полкилометра. Например, достаточно взять функцию f(x) = sin x и заменить переменную x, скажем, на x
2 + ln x. Получится f(x) = sin (x
2 + ln x) — это и есть сложная функция. У нее тоже есть производная, однако найти ее по правилам, рассмотренным выше, не получится.
Как быть? В таких случаях помогает замена переменной и формула производной сложной функции:
f ’(x) = f ’(t) · t ’, если x заменяется на t(x).
Как правило, с пониманием этой формулы дело обстоит еще более печально, чем с производной частного. Поэтому ее тоже лучше объяснить на конкретных примерах, с подробным описанием каждого шага.
Задача. Найти производные функций: f(x) = e
2x + 3; g(x) = sin (x
2 + ln x)
Заметим, что если в функции f(x) вместо выражения 2x + 3 будет просто x, то получится элементарная функция f(x) = e
x
. Поэтому делаем замену: пусть 2x + 3 = t, f(x) = f(t) = e
t
. Ищем производную сложной функции по формуле:
f ’(x) = f ’(t) · t ’ = (e
t
)’ · t ’ = e
t
· t ’
А теперь — внимание! Выполняем обратную замену: t = 2x + 3. Получим:
f ’(x) = e
t
· t ’ = e
2x + 3 · (2x + 3)’ = e
2x + 3 · 2 = 2 · e
2x + 3
Теперь разберемся с функцией g(x). Очевидно, надо заменить x
2 + ln x = t. Имеем:
g ’(x) = g ’(t) · t ’ = (sin t)’ · t ’ = cos t · t ’
Обратная замена: t = x
2 + ln x. Тогда:
g ’(x) = cos (x
2 + ln x) · (x
2 + ln x)’ = cos (x
2 + ln x) · (2x + 1/x).
Вот и все! Как видно из последнего выражения, вся задача свелась к вычислению производной суммы.
Ответ:
f ’(x) = 2 · e
2x + 3;
g ’(x) = (2x + 1/x) · cos (x
2 + ln x).
Очень часто на своих уроках вместо термина «производная» я использую слово «штрих». Например, штрих от суммы равен сумме штрихов. Так понятнее? Ну, вот и хорошо.
Таким образом, вычисление производной сводится к избавлению от этих самых штрихов по правилам, рассмотренным выше. В качестве последнего примера вернемся к производной степени с рациональным показателем:
(x
n
)’ = n · x
n − 1
Немногие знают, что в роли n вполне может выступать дробное число. Например, корень — это x
0,5. А что, если под корнем будет стоять что-нибудь навороченное? Снова получится сложная функция — такие конструкции любят давать на контрольных работах и экзаменах.
Задача. Найти производную функции:
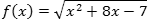
Для начала перепишем корень в виде степени с рациональным показателем:
f(x) = (x
2 + 8x − 7)0,5.
Теперь делаем замену: пусть x
2 + 8x − 7 = t. Находим производную по формуле:
f ’(x) = f ’(t) · t ’ = (t
0,5)’ · t ’ = 0,5 · t
−0,5 · t ’.
Делаем обратную замену: t = x
2 + 8x − 7. Имеем:
f ’(x) = 0,5 · (x
2 + 8x − 7)−0,5 · (x
2 + 8x − 7)’ = 0,5 · (2x + 8) · (x
2 + 8x − 7)−0,5.
Наконец, возвращаемся к корням:
![]()
Ответ:
![]()
Смотрите также:
- Вводный урок по вычислению производных степенной функции

- Уравнение касательной к графику функции

- Тест к параграфу «Что такое логарифм» (легкий)

- Комбинаторика в задаче B6: легкий тест

- Задача B2: лекарство и таблетки

- Задача B4 про шерсть и свитер

Чтобы успешно решать задачи на дифференцирование, нужно уметь находить разные виды производных. Данная статья посвящена основным правилам дифференцирования, которые постоянно используются на практике. С помощью самого определения производной функции мы сформулируем доказательства всех этих правил и подробно рассмотрим несколько примеров, чтобы понять, как они применяются при решении задач.
Условимся заранее, что все функции f(x) и g(x), упомянутые здесь, будем считать дифференцируемыми на промежутке x, иными словами, для любого x0=x∈X будет справедливо равенство f'(x)=lim∆x→0∆f(x)∆x, g'(x)=lim∆x→0∆g(x)∆x. Здесь ∆f(x)=f(x+∆x)-f(x), ∆g(x)=g(x+∆x)-g(x) считаются приращениями указанных функций. Также это можно записать как f(x+∆x)=f(x)+∆f(x), g(x+∆x)=g(x)+∆g(x).
Сформулируем основные проблемы дифференцирования:
- Как вынести постоянный множитель за знак производной.
- Как вычислить производную суммы и производную разности.
- Как вычислить производную произведения функций.
- Как вычислить производную частного двух функций (дробного выражения с функциями).
Разберем все эти случаи по порядку.
C·f(x)’=C·f'(x), C∈R(f(x)±g(x))’=f'(x)±g'(x)(f(x)·g(x))’=f'(x)·g(x)+f(x)·g'(x)f(x)g(x)’=f'(x)·g(x)-f(x)·g'(x)g2(x)
Как вынести постоянный множитель за знак производной
Для начала нам нужно доказать следующую формулу:
C·f(x)’=C·f'(x), C∈R
Используя определение производной, запишем следующее:
C·f(x)’=lim∆x→0∆(C·f(x))∆x=lim∆x→0C·f(x+∆x)-C·f(x)∆x==lim∆x→0C·f(x+∆x)-f(x)∆x=lim∆x→0C·∆f(x)∆x
Если в таком выражении у нас есть произвольный множитель, он может быть вынесен за знак предельного перехода (мы доказывали это утверждение, когда изучали свойства предела). Значит, C·f(x)’=lim∆x→0C·∆f(x)∆x=C·lim∆x→0∆f(x)∆x=C·f'(x).
Этим мы доказали первое правило дифференцирования. Разберем задачу на его применение.
Дана функция y=2·cos x. Необходимо вычислить ее производную.
Решение
Обратимся к таблице производных для тригонометрических функций и выясним, что cos x’=-sin x.
Вынесем множитель за знак производной и получим:
y’=2·cos x’=2·cos x’=-2·sin x
Ответ: y’=2·cos x’=2·cos x’=-2·sin x.
Это самый простой пример. На практике чаще всего приходится предварительно преобразовывать дифференцируемую функцию, чтобы увидеть нужное значение в таблице производных и применить соответствующее правило.
Продифференцировать функцию f(x)=log3x2-1.
Решение
Зная свойства логарифмической функции, мы можем сразу записать, что f(x)=log3x2-1=2-1·log3x. Теперь вспоминаем, как вычислить для нее производную, и выносим постоянный множитель:
f(x)=log3x2-1’=2-1·log3x’==2-1·log3x’=2-1x·ln 3
Ответ: f(x)=2-1x·ln 3
Дана функция y=12-x+3. Вычислите ее производную.
Решение
Сначала нам нужно выполнить преобразование исходной функции.
y=12-x+3=12-x·23=2×23
Далее применяем изученное выше правило и берем из таблицы производных соответствующее значение:
y’=2×23’=123·2x’=123·2x·ln 2=2x-3·ln 2
Ответ: y’=2x-3·ln 2
Как вычислить производную суммы и производную разности
Чтобы доказать второе правило дифференцирования f(x)±g(x)’=f'(x)±g'(x), нам нужно вспомнить определение производной, а также одно из свойств, которым обладает предел непрерывной функции.
f(x)±g(x)’=lim∆x→0∆(f(x)±g(x))∆x==lim∆x→0fx+∆x±gx+∆x-(f(x)±g(x))∆x==lim∆x→0f(x+∆x)-f(x)±(g(x+∆x)-g(x))∆x==lim∆x→0f(x+∆x)-f(x)∆x±lim∆x→0g(x+∆x)-g(x)∆x==lim∆x→0∆f(x)∆x±lim∆x→0∆g(x)∆x=f'(x)±g'(x)
Так мы можем доказать равенство производной суммы или разности n-ного количества функций сумме или разности их производных:
f1(x)±f2(x)±…±fn(x)’=f1′(x)±f2’±…±fn'(x)
Вычислить производную y=x3+3x+1-ln xln5+3.
Решение
Первым делом упрощаем данную функцию.
y=x3+3x+1-ln xln5+3=x3+3·3x-ln(5+3)·ln x
После этого применяем второе правило – производной суммы/разности:
y’=(x3)’+3·3x’-ln5+3·ln x’
Первое правило говорит нам о том, что можно вынести постоянный множитель за знак производной, значит:
y’=(x3)’+3·3x’-ln5+3·ln x’==(x3)’+3·3x’-ln(5+3)·ln x’
Нам остается только заглянуть в таблицу производных и взять оттуда соответствующее значение:
y’=(x3)’+3·3x’-ln(5+3)·ln x’==3·x3-1+3·3x·ln 3-ln5+3x=3·x2+3x+1·ln 3-ln(5+3)x
Ответ: y’=3·x2+3x+1·ln 3-ln(5+3)x
Как вычислить производную произведения функций
Правило дифференцирования произведения двух функций выглядит следующим образом: fx·g(x)’=f'(x)·g(x)’+f(x)·g'(x)
Попробуем доказать его.
Для начала вычислим предел отношения приращения произведения функций к приращению аргумента. Здесь нужно вспомнить, что f(x+∆x)=f(x)+∆f(x), g(x+∆x)=g(x)+∆g(x), а lim∆x→0∆g(x)=0, lim∆x→0∆f(x)=0, то есть если приращение аргумента стремится к 0, то и приращение функции также будет к нему стремиться.
(f(x)·g(x))’=lim∆x→0∆(f(x)·g(x))∆x=lim∆x→0f(x+∆x)·g(x+∆x)-f(x)·g(x)∆x==lim∆x→0(f(x)+∆f(x))+(g(x)·∆g(x))-f(x)·g(x)∆x==lim∆x→0f(x)·g(x)+g(x)·∆f(x)+f(x)·∆g(x)+∆f(x)·∆g(x)-f(x)·g(x)∆x==lim∆x→0g(x)·∆f(x)+f(x)·∆g(x)+∆f(x)·∆g(x)∆x==lim∆x→0g(x)·∆f(x)∆x+lim∆x→0f(x)·∆g∆x+lim∆x→0∆f(x)∆x·lim∆x→0∆g(x)==g(x)·lim∆x→0∆f(x)∆x+f(x)·lim∆x→0∆g(x)∆x+f'(x)·0==f'(x)·g(x)+f(x)·g'(x)
Это и есть результат, который нам нужно было доказать.
Продифференцируйте функцию y=tg x·arcsin x.
Решение
Здесь f(x)=tg x, g(x)=arcsin x. Можем воспользоваться правилом производной произведения:
y’=(tg x·arcsin x)’=(tg x)’·arcsin x+tg x·(arcsin x)’
Берем нужное значение из таблицы производных основных элементарных функций и записываем ответ:
y’=(tg x·arcsin x)’=(tg x)’·arcsin x+tg x·(arcsin x)’==arcsin xcos2x+tg x1-x2
Ответ: y’=arcsin xcos2x+tg x1-x2
Дана функция y=exx3. Вычислите производную.
Решение
Здесь мы имеем f(x)=ex, g(x)=1×3=x-13. Значит,
y’=exx3=ex·x-13’=ex’·x-13+ex·x-13==ex·x-13+ex·-13·x-13-1=exx3-exx43=exx3·1-1x
Ответ: y’=exx3·1-1x
Теперь разберем, что нужно делать в случае, когда производную нужно найти для произведения трех функций. По той же схеме решаются задачи с произведениями четырех, пяти и большего количества функций.
Продифференцируйте функцию y=(1+x)·sin x·ln x.
Решение
Возьмем за основу правило для двух функций. Будем считать функцией f(x) произведение (1+x)·sin x, а g(x) – ln x.
У нас получится следующее:
y’=((1+x)·sin x·ln x)’=1+x·sin x’·ln x+1+x·sin x·ln x’
Чтобы найти 1+x·sin x’, нам снова потребуется правило вычисления производной произведения:
1+x·sin x’=(1+x)’·sin x+1+x·(sin x)’
С помощью этого правила и таблицы производных получим:
1+x·sin x’=(1+x)’·sin x+1+x·(sin x)’==1’+x’·sin x+(1+x)·cos x=0+1·x1-1·sin x+(1+x)·cos x==(0+1)·sin x+1+x·cos x=sin x+cos x+x·cos x
Теперь подставим в формулу то, что у нас получилось:
y’=1+x·sin x·ln x’=1+x·sin x’·ln x+(1+x)·sin x·(ln x)’==sin x+cos x+x·cos x·ln x+(1+x)·sin xx
Ответ: y’=sin x+cos x+x·cos x·ln x+(1+x)·sin xx
Из этого примера видно, что иногда приходится применять несколько правил дифференцирования подряд для вычисления нужного результата. Это не так сложно, как кажется, главное – соблюдать нужную последовательность действий.
Дана функция y=2·sh x-2x·arctg x, вычислите ее производную.
Решение
Исходная функция является разностью выражений 2·sh x и 2x·arctg x, значит, y’=2·sh x-2x·arctg x’=2·sh x’-2x·arctg x’. Здесь можно вынести за знак производной число 2, а в другом произведении применить подходящее для произведений правило:
y’=2·sh x’-2x·arctg x’=2·sh x’-2x’·arctg x+2x·(arctg x)’==2·ch x-2x·ln 2·arctg x+2×1+x2=2·ch x-2x·ln 2·arctg x-2×1+x2
Ответ: y’=2·ch x-2x·ln 2·arctg x-2×1+x2
Как вычислить производную частного двух функций (дробного выражения с функциями)
Данное правило выглядит следующим образом: f(x)g(x)’=f'(x)·g(x)-f(x)·g'(x)g2(x).
Докажем его.
Сразу отметим, что g(x) не будет обращаться в 0 ни при каких значениях x из указанного промежутка. Согласно определению производной, получим:
f(x)g(x)’==lim∆x→0∆f(x)g(x)∆x=lim∆x→0f(x+∆x)g(x+∆x)-f(x)g(x)∆x=lim∆x→0f(x+∆x)·g(x)-g(x+∆x)·f(x)∆x·g(x+∆x)·g(x)==1g2(x)·lim∆x→0(f(x)+∆f(x))·g(x)-(g(x)+∆g(x))·f(x)∆x==1g2(x)·lim∆x→0f(x)·g(x)+g(x)·∆f(x)-f(x)·g(x)-f(x)·∆g(x)∆x==1g2(x)·lim∆x→0gx·∆f(x)-f(x)·∆g(x)∆x==1g2(x)·g(x)·lim∆x→0∆f(x)∆x-f(x)·lim∆x→0∆g(x)∆x==f'(x)·g(x)-f(x)·g'(x)g2(x)
Продифференцируйте функцию y=sin x2·x+1.
Решение
Эта функция является отношением двух выражений 2x+1 и sin x. Воспользуемся приведенным выше правилом дифференцирования дробного выражения и получим:
y’=sin x2·x+1’=sin x’·2·x+1-sin x·2·x+1’2·x+12
После этого нам потребуется правило для суммы, а также правило вынесения постоянного множителя за знак производной:
y’=sin x’·2·x+1-sin x·2·x+1’2·x+12==cos x·(2·x+1)-sin x·2x’+1′(2·x+1)2=cos x·(2·x+1)-sin x·(2·x’+0)(2·x+1)2==cos x·2·x+1-sin x·(2·1·x1-1+0)(2·x+1)2=2·x·cos x+cos x-2·sin x(2·x+1)2
Ответ: y’=2·x·cos x+cos x-2·sin x(2·x+1)2
Возьмем задачу на применение всех изученных правил.
Дана функция y=3ex-x2·ln x-2·xax+2sin x·arccos x, где значение undefined является положительным действительным числом. Вычислите производную.
Решение
y’=3·ex’-x2·ln x-2·xax’+2sin x·arccos x’
Поясним, как это получилось.
Первым слагаемым будет 3·ex’=3·ex’=3·ex.
Вычисляем второе:
x2·ln x-2·xax’=x2·ln x-2·x·ax-x2·ln x-2·x·ax’ax2==x2·ln x’-2·x’·ax-x2·ln x-2·x·ax·ln aa2·x==2·x2-1·ln x+x2·1x-2·1·x1-1·ax-x2·ln x-2·x·ax·ln aa2·x==2·x2-1·ln x+x2·1x-2·1·x1-1·ax-x2·ln x-2·x·ax·ln aa2·x==2·x·ln x+x-2·ax-x2·ln x-2·x·ax·ln aa2·x==x·ln x·(2-x·ln a)+x·1-2·ln a-2ax
Вычисляем третье слагаемое:
2sin x·arccos x’=2·sin x·arccos x’==2·sin x’·arccos x+sin x·arccos x’==2·cos x·arccos x-sin x1-x2
Теперь собираем все, что у нас получилось:
y’=3·ex’-x2·ln x-2·xax+2sin x·arccos x’==3·ex-x·ln x·(2-x·ln a)+x·1-2·ln a-2ax++2·cos x·arccos x-sin x1-x2
В задачах, которые мы разобрали в этой статье, использовались только основные элементарные функции, которые были связаны между собой знаками простых арифметических действий. Они нагляднее всего иллюстрируют правила дифференцирования. Однако возможно их применение и к более сложным функциям.
После того, как мы разберем, что такое производная сложной функции, мы сможете проводить дифференцирование выражений любой сложности.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Используем свойства
предела для доказательства правил
дифференцирования.
1.
![]()
![]() . (1)
. (1)
2.
![]()
![]() . (2)
. (2)
3.
![]()
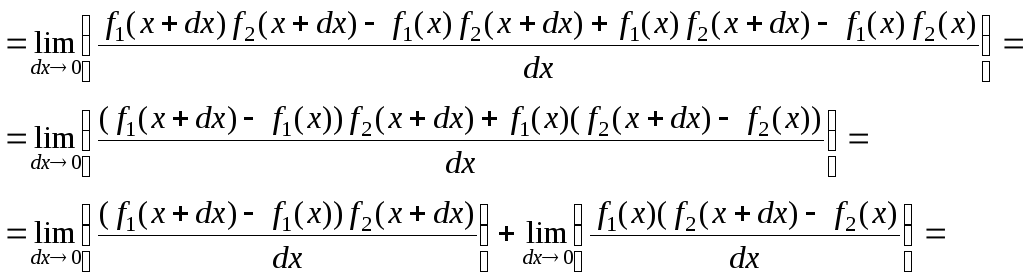
![]() (3)
(3)
4.
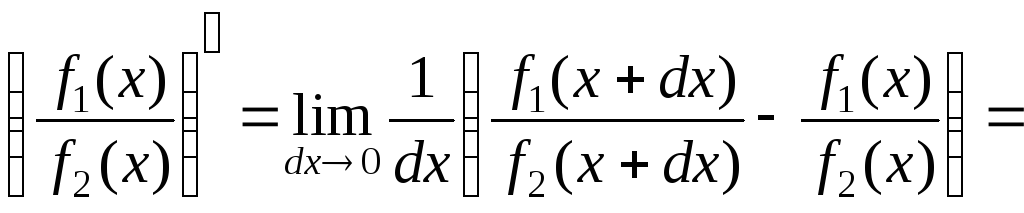
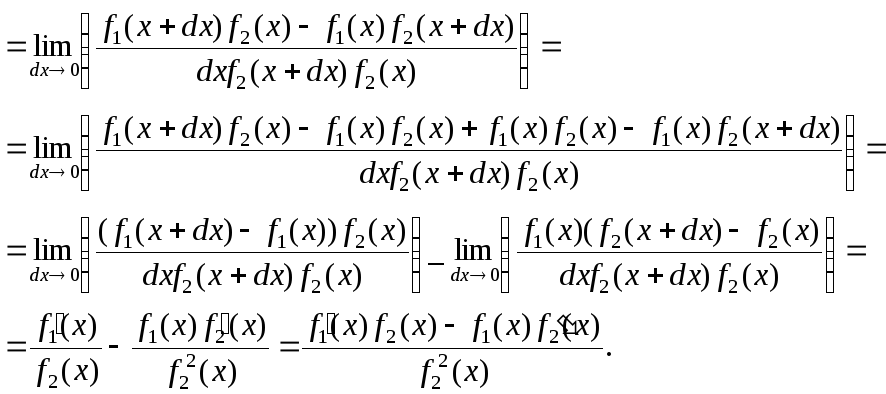 (4)
(4)
4. Производная сложной и обратной функций.
Пусть функция
![]() в некоторой окрестности точки
в некоторой окрестности точки![]() является непрерывной, монотонной, а в
является непрерывной, монотонной, а в
самой точке![]() – дифференцируемой. Тогда по теореме о
– дифференцируемой. Тогда по теореме о
непрерывных функциях она имеет обратную![]() .
.
Найдем связь между производными прямой
и обратной функций
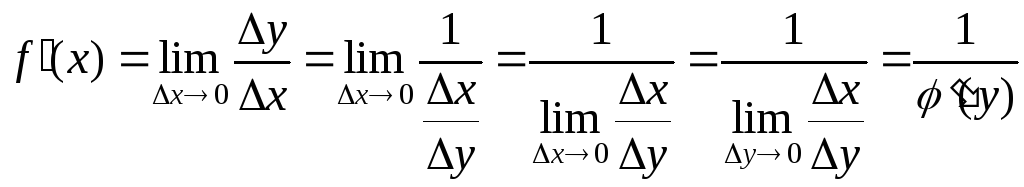 . (1)
. (1)
Формулу (1) следует
понимать так, что производные в ее левой
и правой части вычисляются при значениях
аргументов, связанных между собой
соотношениями
![]() или
или![]() .
.
Определение.Сложнойназывается функция, которая
зависит от своего аргумента, таким
образом, что эту зависимость можно
представить посредством как минимум
одного промежуточного аргумента.
Например, пусть
![]() и
и![]() .
.
Тогда![]() – сложная функция с промежуточным
– сложная функция с промежуточным
аргументом![]() и независимым аргументом
и независимым аргументом![]() .
.
Теорема.
Если функция![]() имеет производную
имеет производную![]() в точке
в точке![]() ,
,
а функция![]() имеет производную
имеет производную![]() в точке
в точке![]() ,
,
соответствующей точке![]() ,
,
то сложная функция![]() имеет производную
имеет производную![]() в точке
в точке![]() ,
,
которая находится по формуле
![]() . (2)
. (2)
Доказательство
В окрестности
точки
![]() дадим приращение
дадим приращение![]() аргументу
аргументу![]() .
.
Тогда промежуточный аргумент![]() получит приращение
получит приращение![]() ,
,
а функция![]() – приращение
– приращение![]() .
.
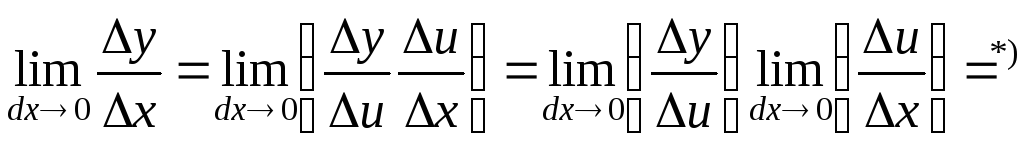 .
.
Поскольку в силу
существования производной
![]() функция
функция![]() является непрерывной в рассматриваемой
является непрерывной в рассматриваемой
точке, то при![]() следует, что
следует, что![]() .
.
Тогда продолжая выкладки, получаем
![]() .
.
5. Таблица производных
Получим сейчас
формулы для дифференцирования основных
элементарных функций. Знание этих формул
совместно с ранее полученными правилами
дифференцирования позволит нам выполнять
дифференцирование элементарных функций.
-
Пусть
 .
.
Применяя формулу (1) получим
![]() . (1)
. (1)
-
Пусть
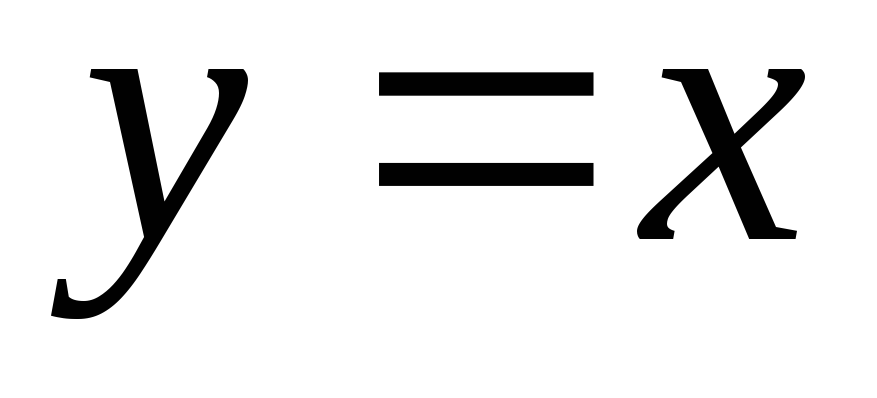 .
.
Тогда
![]() . (2)
. (2)
3. Получим производную
степенной функции
![]() с вещественным показателем степени
с вещественным показателем степени![]() .
.
При этом воспользуемся таблицей
эквивалентных бесконечно малых величин.
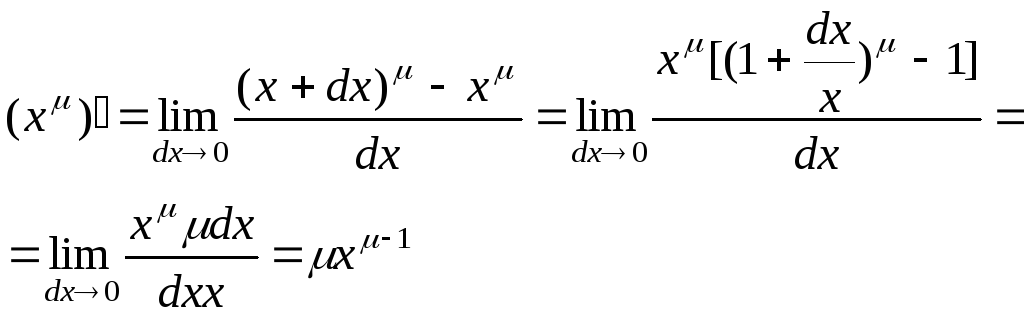 . (3)
. (3)
В частном случае,
когда
![]() = целое число
= целое число
![]() . (4)
. (4)
4. Для получения
формулы дифференцирования показательной
функции
![]() (
(![]() также воспользуемся таблицей эквивалентных
также воспользуемся таблицей эквивалентных
бесконечно малых величин
![]() . (5)
. (5)
В частном случае,
когда
![]()
![]() . (6)
. (6)
5. Для получения
формулы дифференцирования логарифмической
функции
![]() (
(![]() также воспользуемся таблицей эквивалентных
также воспользуемся таблицей эквивалентных
бесконечно малых величин. В результате
получим
 . (1)
. (1)
В частном случае,
когда
![]()
![]() . (2)
. (2)
Перейдем теперь
к вычислению производных тригонометрических
функций.
6. Найдем производную
функции
![]() .
.
Пользуясь таблицей эквивалентных
бесконечно малых величин, получим
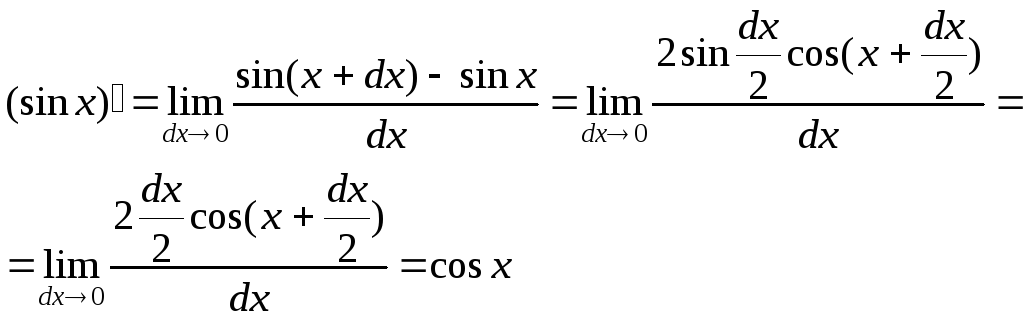 . (9)
. (9)
7. Найдем производную
функции
![]() .
.
Пользуясь таблицей эквивалентных
бесконечно малых величин, получим
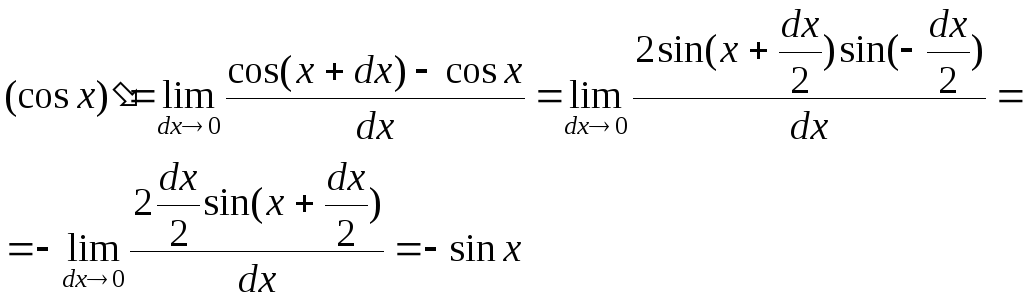 . (10)
. (10)
8. Найдем производную
функции
![]() .
.
Пользуясь правилами дифференцирования,
получим
![]() . (11)
. (11)
9. Найдем производную
функции
![]() .
.
Пользуясь правилом дифференцирования
частного от деления двух функций, получим
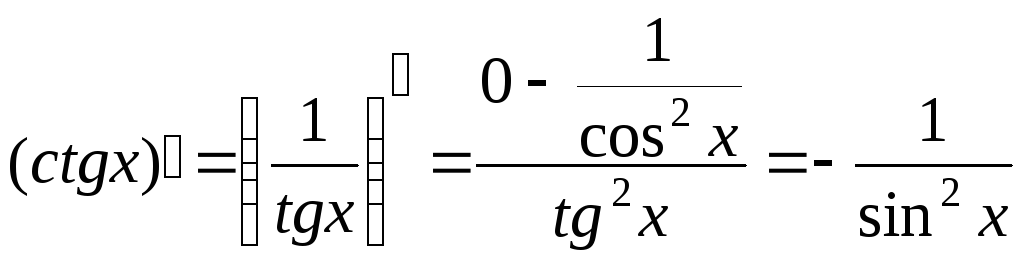 . (12)
. (12)
10. Найдем производную
функции
![]() ,
,
где![]() ,
,
а![]() .
.
Очевидно![]() ,
,
тогда пользуясь формулами (3.1) и (9),
получим
![]() . (13)
. (13)
Здесь было
использовано свойство функции
![]() на промежутке
на промежутке![]() .
.
11. Найдем производную
функции
![]() ,
,
где![]() ,
,
а![]() .
.
Очевидно![]() ,
,
тогда пользуясь формулами (3.1) и (10),
получим
![]() . (14)
. (14)
Здесь было
использовано свойство функции
![]() на промежутке
на промежутке![]() .
.
12. Найдем производную
функции
![]() ,
,
где![]() ,
,
а![]() .
.
Очевидно![]() ,
,
тогда пользуясь формулами (3.1) и (11),
получим
![]() . (15)
. (15)
13. Найдем производную
функции
![]() ,
,
где![]() ,
,
а![]() .
.
Очевидно![]() ,
,
тогда пользуясь формулами (3.1) и (12),
получим
![]() . (16)
. (16)
14. Так как
гиперболический синус определяется
соотношением
![]() ,
,
то
![]() . (17)
. (17)
15. Так как
гиперболический косинус определяется
соотношением
![]() ,
,
то
![]() . (18)
. (18)
Графики
гиперболического синуса и косинуса
представлены на рис. 1.
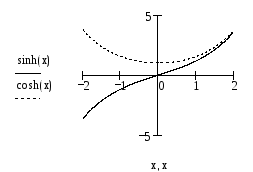
Рис. 1. Синус и
косинус гиперболические1
16. Так как
гиперболический тангенс определяется
соотношением
![]() ,
,
то
![]() . (19)
. (19)
17. Так как
гиперболический котангенс определяется
соотношением
![]() ,
,
то
![]() . (20)
. (20)
Графики гиперболического тангенса и
котангенса представлены на рис. 2.
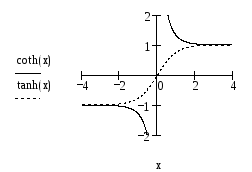
Рис. 2. Тангенс и
котангенс гиперболические2
Результаты
вычисления производных представлены
в таблице.
Таблица
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Производная от деления между двумя функциями равна знаменателю, умноженному на производную числителя, минус производная знаменателя, умноженная на числитель, и это между знаменателем в квадрате.
С математической точки зрения, мы могли бы резюмировать это следующим образом:

Мы должны помнить, что производная – это математическая функция, которая позволяет нам вычислить скорость или скорость изменения (зависимой) переменной. Это когда изменение зарегистрировано в другой переменной (которая будет независимой), которая влияет на нее.
Пример производной от деления
Чтобы лучше понять, как вычисляется производная от деления, давайте рассмотрим несколько примеров.





Теперь давайте посмотрим на пример, который немного сложнее, с тригонометрической функцией и логарифмом функции:






