Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Решение:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Пример:
Решение:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
Монотонность.
Функция называется
возрастающей если большему значению
аргумента соответствует большее значение
функции, а меньшему соответствует
меньше.
Функция называется
убывающей если большему значению
аргумента соответствует меньшее значение
функции, а меньшему соответствует
большее.
Теорема.
У возрастающей функции производная
больше 0 ().
Доказательство:
|
x |
|
-1 |
|
|
|
min |
||
|
|
– |
0 |
+ |
Экстремумы
функции.
Т
очка
-называется
точкой max,
если существует некоторая окрестность
точки, что для любой точки x
из этой
окрестности
.
Точка
-называется
точкой min,
если существует некоторая окрестность
точки, что для любой точки x
из этой
окрестности
.
Необходимый признак
экстремума, если
-точка экстремума.

Если
и
,
то это точка экстремума.
Если
– точка экстремума и существует
,
то производная
=0.
Точка, в которой
производная, равна нулю, называется
критической точкой.
,
теорема Логранжа.
Первый достаточный
признак экстремума.
Если при переходе
через критическую точку производная
меняет знак с ”+”
на “-“,то
в этой точке максимум.
Если при переходе
через критическую точку производная
меняет знак с ”-”
на “+“,то
в этой точке минимум.
Второй достаточный
признак экстремума.
Если в критической точке 2-ая производная больше нуля, то это точка минимума, а если в критической точке 2-ая производная меньше нуля, то это точка максимума.
Пример:
|
x |
|
1 |
|
3 |
|
|
|
|
Max |
Min |
||||
|
|
+ |
0 |
– |
0 |
+ |
Выпуклость и
вогнутость.
Если
в окрестности точки, график функции
ниже касательной, то в окрестности этой
точки график функции выпуклый.
Если
в окрестности точки, график функции
выше касательной, то в окрестности этой
точки график функции вогнутый.
Теорема.
В точке
выпуклости 2-ая производная меньше 0. В
точке вогнутости вторая производная
больше 0.
Доказательство:
Если
прямая проходит через точку
Применим
теорему Логранжа:
Поставим
“-“
в
,
учитывая, что
>0
тогда
должна
быть <0.
Второй
раз применим теорему Логранжа:
Для вогнутости
поставим “+”
должно
быть >0.
Точка, в которой
вторая производная равна нулю, называется
точкой перегиба.
|
|
|
|
|
|
|
|
|
п |
п |
|||
|
|
+ |
0 |
– |
0 |
+ |
Асимптоты.
Асимптотой к кривой
называется прямая, к которой график
функции неограниченно приближается.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Взаимосвязи графика функции и графика ее производной
Приближенное и точное определение производной функции
Приближенным значением производной функции в точке $x_{0}$ со сдвигом 0,01 называется значение
$f’left(x_0right)approx frac{fleft(x_0+0,01right)-fleft(x_0right)}{left(x_0+0,01right)-left(x_0right)}$ $f’left(aright)approx frac{fleft(a+hright)-fleft(aright)}{left(a+hright)-left(aright)}$ Точное: $f’left(aright)=lim frac{fleft(a+hright)-fleft(aright)}{left(a+hright)-left(aright)}$ при $lim h=0$
- Производная в точке – это отношение: (приращение самой функции) / (малое приращение аргумента в этой точке).
- Физический смысл – производная функции показывает скорость изменения функции: роста или убывания функции.
- Геометрический смысл – производная в каждой точке равна тангенсу угла наклона касательной, проведенной к ее графику.
Пример 1: Дана функция $fleft(xright)=x^3-3x+2$ . Вычислить приближенное производную $f’left(x_0right)$
- в точке $x_0=1,2$ со сдвигом $h=0,2$ ? $Rightarrow$ $f’left(1,2right)approx frac{bigtriangleup fleft(xright)}{bigtriangleup x}approx frac{fleft(1,2+0,2right)-fleft(1,2right)}{1,4-1,2}=frac{1,4^3-3cdot 1,4+2-left(1,2^3-3cdot 1,2+2right)}{0,2}=1,555$
- В реальности мы получили тангенс угла наклона секущей, проходящей в точках графика $left(1,2;fleft(1,2right)right)$ и $left(1,4;fleft(1,4right)right)$
- в точке $x_0=0,5$ со сдвигом $h=0,0001$ ? $Rightarrow$ $f’left(0,4right)approx frac{fleft(0,4+hright)-fleft(0,4right)}{left(0,4+hright)-0,4}=frac{left(0,4+hright)^3-3cdot left(0,4+hright)+2-left(0,4^3-3cdot 0,4+2right)}{h}=frac{left(0,4+hright)^3-0,4^3}{h}-frac{3cdot left(0,4+hright)-3cdot 0,4}{h}=frac{0,4^3+3cdot 0,4^2cdot h+3cdot 0,4h^2+h^3-0,4^3}{h}-3=left(3cdot 0,4^2-3right)+hcdot left(3cdot 0,4+hright)approx 2,5201$
- точное производное $f’left(0,4right)=3cdot 0,4^2-3=2,52$ при $hsim 0$ !
- в точке $x_0=0,5$ со сдвигом $h=0,0001$ ? $Rightarrow$ $f’left(0,4right)approx frac{fleft(0,4+hright)-fleft(0,4right)}{left(0,4+hright)-0,4}=frac{left(0,4+hright)^3-3cdot left(0,4+hright)+2-left(0,4^3-3cdot 0,4+2right)}{h}=frac{left(0,4+hright)^3-0,4^3}{h}-frac{3cdot left(0,4+hright)-3cdot 0,4}{h}=frac{0,4^3+3cdot 0,4^2cdot h+3cdot 0,4h^2+h^3-0,4^3}{h}-3=left(3cdot 0,4^2-3right)+hcdot left(3cdot 0,4+hright)approx 2,5201$
- точное производное $f’left(0,4right)=3cdot 0,4^2-3=2,52$ при $hsim 0$ !
- $f’left(-0,6right)$ “На глаз по графику” ? $Rightarrow$ значения $fleft(-0,6right)approx 3,6$ и в сдвинутой $fleft(-0,4right)approx 3,1$. скорость изменения, наклон $f’left(-0,6right)approx frac{fleft(-0,4right)-fleft(-0,6right)}{-0,4-left(-0,6right)}approx frac{3,1-3,6}{0,2}=-2,5$
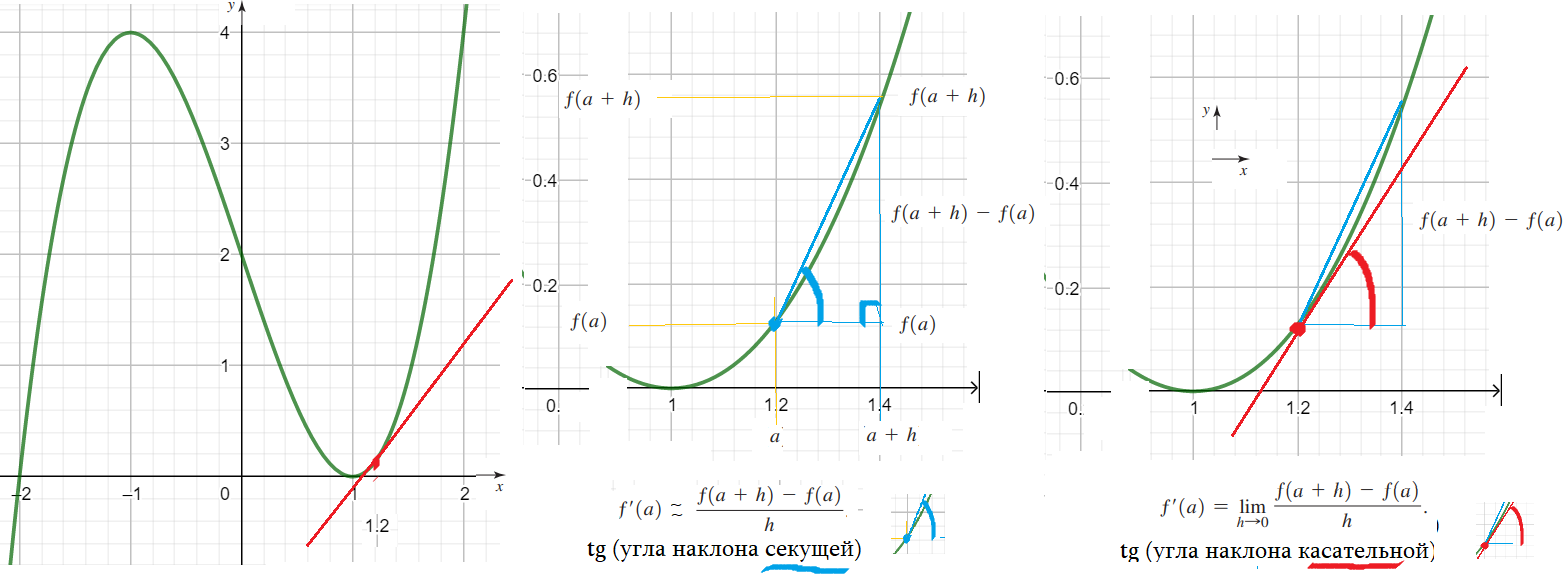
- Секущая графика функции – прямая, проходящая в точках графика $left(x_1;fleft(x_1right)right) и left(x_2;fleft(x_2right)right)$.
- Наклон секущей – тангенс угла наклона секущей к х – оси, равен $tg s=frac{fleft(x_2right)-fleft(x_1right)}{x_2-x_1}$.
- Касательной к графику в точке х = а – предел секущих в точках $left(a;fleft(aright)right) и left(a+h;fleft(a+hright)right)$ при h стремящемся к нулю.
- Наклон касательной – тангенс угла $k=frac{fleft(x+0,000001right)-fleft(xright)}{x+0,000001-x}$ . Точнее, “примерно равен”. Точнее: при малом h !.
- ….еще точнее “в пределе равен”. lim $frac{fleft(a+hright)-fleft(aright)}{h}$. Точка (a+h; f(a+h)) сближается с точкой (a; f(a)) при малом h !.
- Производная f'(a) равен тангенсу угла наклона касательной к графику функции f в точке (a, f(a)).
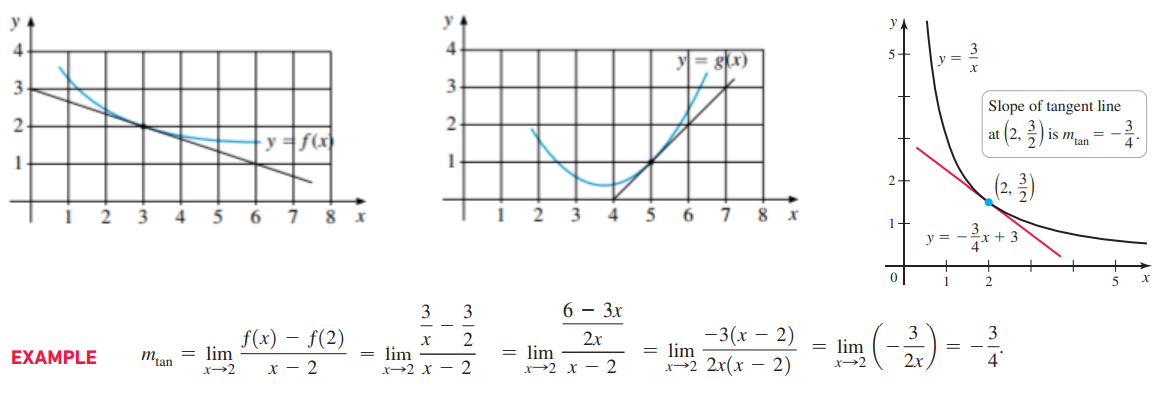
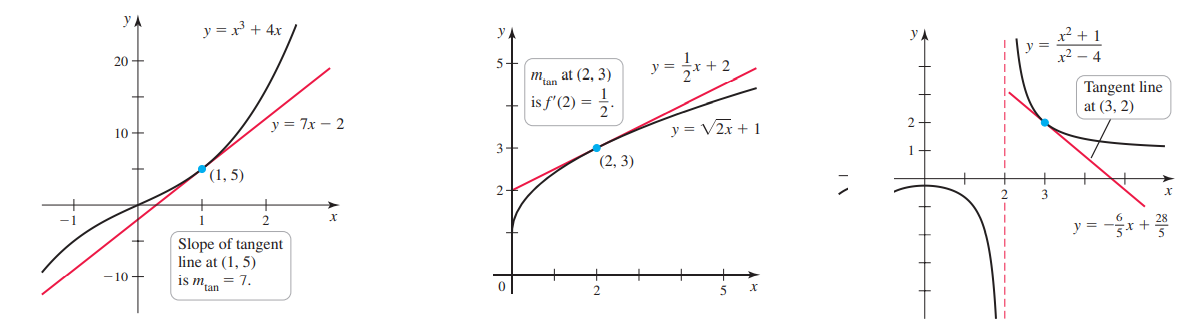
Пример 2: По графику функции найти производную – наклон касательной в указанной точке.
- Смотрим на касательную в точке х = 3. Для нахождения тангенса наклона надо “увидеть” прямоугольный треугольник с катетами вдоль х- и у- осей и с гипотенузой вдоль касательной.
- Считаем по клеткам: f'(3) = – 1 : 3 1 клетка по у – оси вниз (-), 3 клетки по х – оси вправо (+) .
- На 2-м рисунке: g'(5) = 2 : 2 2 клетки по у – оси вверх (+), 2 клетки по х – оси вправо (+) .
Уравнение касательной к графику функции $y=fleft(xright)$ в точке $x=x_0$ : $y=fleft(x_0right)+f’left(x_0right)cdotleft(x-x_0right)$ – касательная, прямая
- Функция $y=fleft(xright)$ и её касательная $y=ax+b$ в точке касания $x=x_0$ имеют одинаковые значения, наклон, производные.
- Наклон касательной = производное функции $a=f’left(x_0right)$ определяет как “течет” график: растет, убывает?
- Наклон положительный – касательная справа-налево – производная положительна – функция растет – график функции “течет” вверх.
- Наклон отрицательный – касательная слево-направо – производная отрицательна – функция убывает – график функции “течет” вниз, по склону.
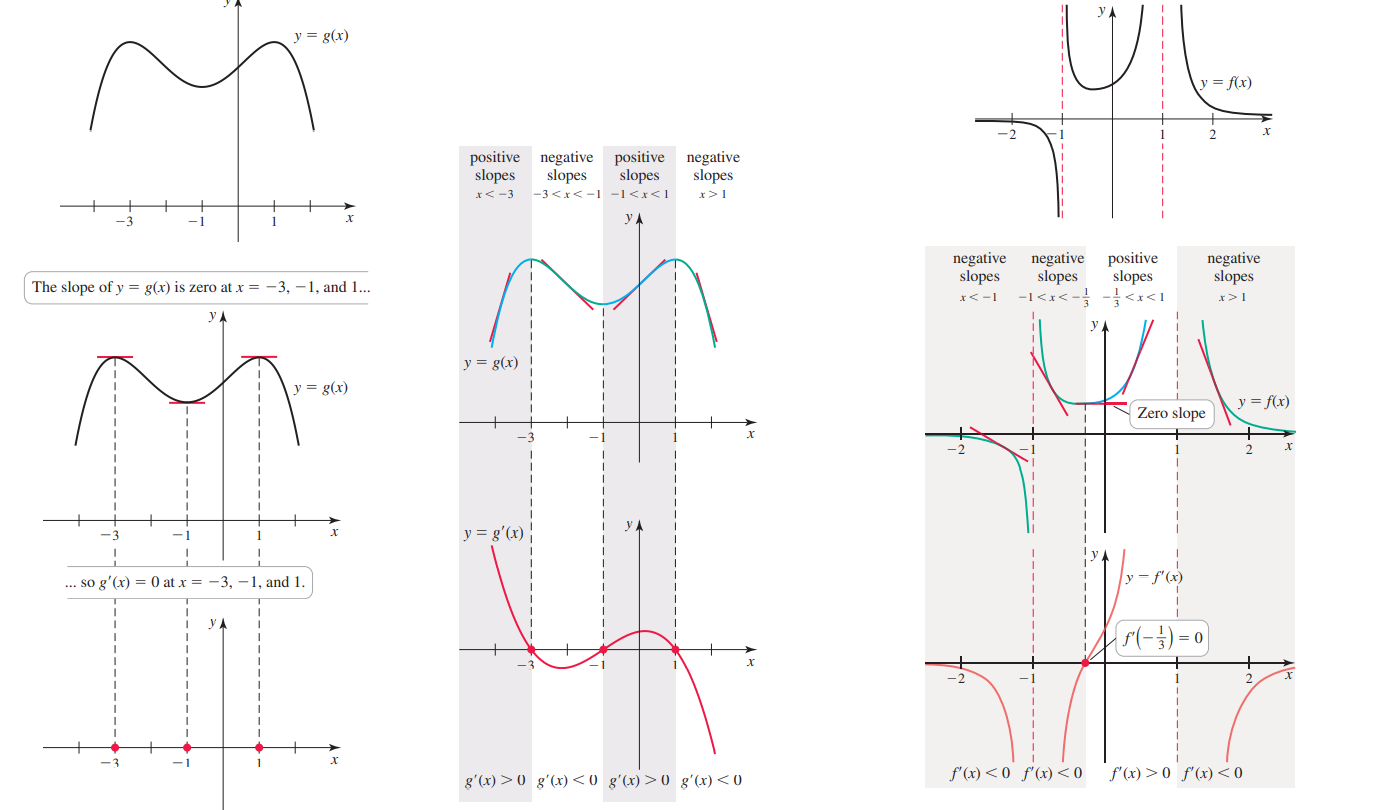
Производная – как детектор поведения функции
Вопрос: Как влияет на поведение функции $fleft(x_0right)$ около точки $x=x_0$ значение производной $f’left(x_0right)$ ?
- Из определения производной в точке $x=x_0$ $Rightarrow$ $f’left(x_0right)approxfrac{fleft(x_0+0,01right)-fleft(x_0right)}{x_0+0,01-x_0}$
- выразим значение функции чуть правее точки $x_0$ : $fleft(x_0+0,01right)approx fleft(x_0right)+0,01f’left(x_0right)$. Значит, функция будет иметь большее значение правее от $x_0$ , если только $f’left(x_0right) > 0$.
- Аналогичные рассуждения для значения функции чуть левее. Из $f’left(x_0right)approxfrac{fleft(x_0-0,01right)-fleft(x_0right)}{x_0-0,01-x_0}$ $Rightarrow$ $fleft(x_0-0,01right)approx fleft(x_0right)-0,01cdot f’left(x_0right)$ $Leftrightarrow$ понятно почему поведение функции левее $x_0$ зависит от знака производной в точке $x_0$.
- Сформулирует ответы на вопрос о влиянии знака производной в данной точке:
- если $f’left(x_0right) > 0$ то $fleft(x_0-0,01right) < fleft(x_0right) < fleft(x_0+0,01right)$ $Rightarrow $ функция растет (см. слева направо).
- если $f’left(x_0right) < 0$ то $fleft(x_0-0,01right) > fleft(x_0right) > fleft(x_0+0,01right)$ $Rightarrow $ функция убывает, график идет вниз.
- если $f’left(x_0right)=0$ то ситуации более запутанные: при $fleft(x_0-0,01right) < fleft(x_0right) > fleft(x_0+0,01right)$ точка $x=x_0$ называется точкой максимума. В нем функция “выше”, чем по-соседству хоть слева, хоть справа.
В случае $fleft(x_0-0,01right) > fleft(x_0right) < fleft(x_0+0,01right)$, $x=x_0$ – точка минимума. Если ни то, ни другое, то точка перегиба.
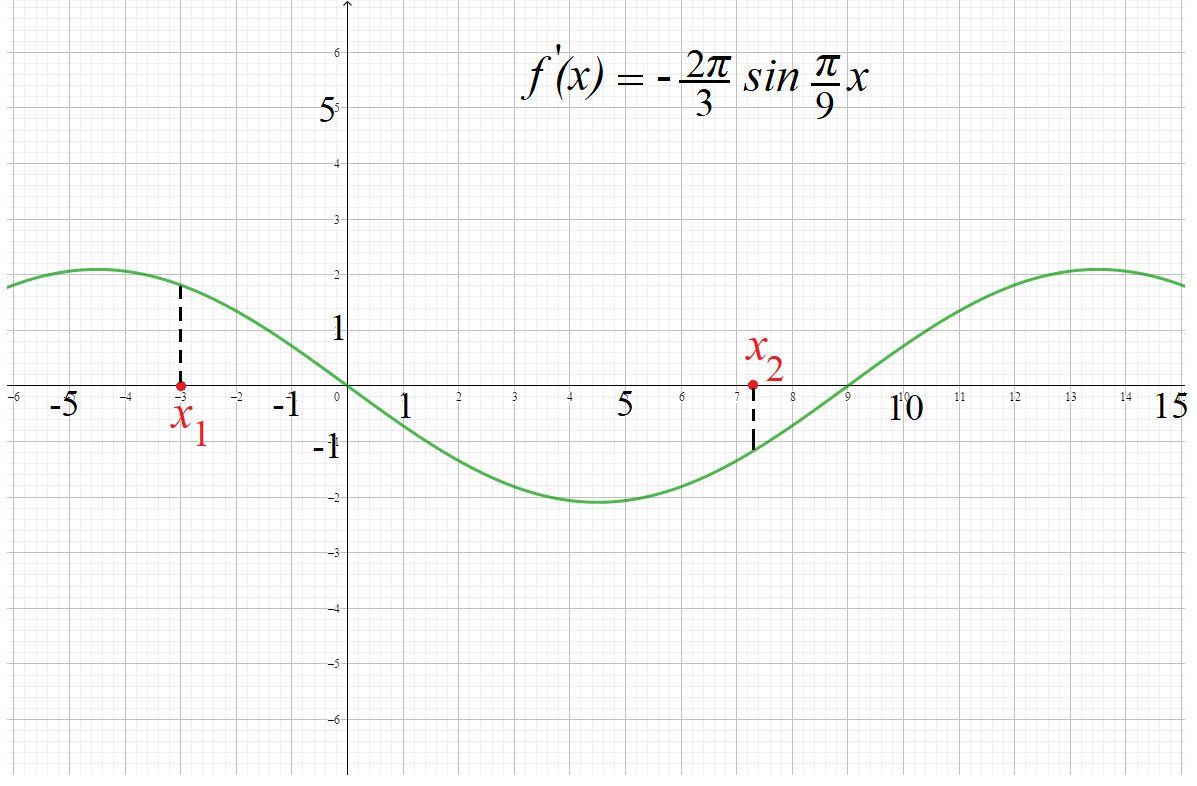
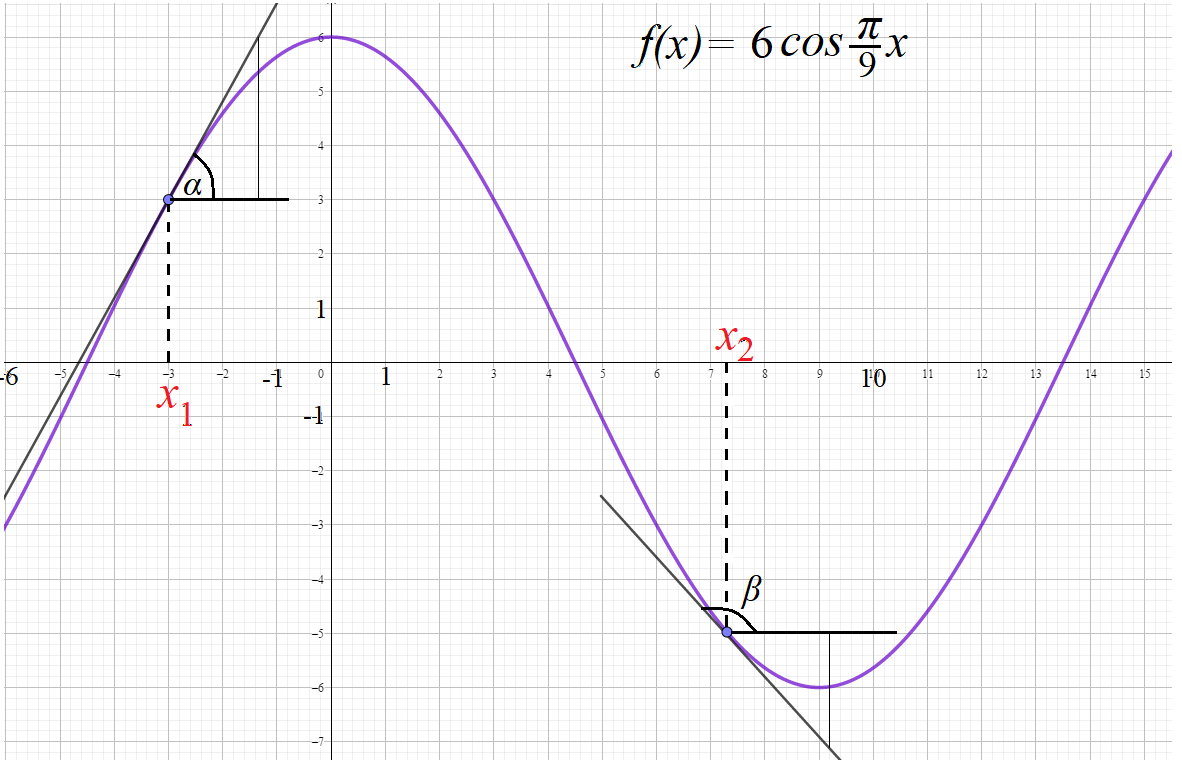
Пример 2: Каково взаимовлияние графика $fleft(xright)=6cosfrac{pi}{9}x$ и графике ее производной $f’left(xright)=-frac{2pi}{3}sinfrac{pi}{9}x$
- Производная от какой-то функции – это некая, связанная с ней функция, характеризующая поведение самой функции
- Рассмотрим точку $x_1=-3$ . В нем сама функция равна $fleft(-3right)=6cosfrac{pi}{9}(-3)=3$ , а ее производная – $f’left(-3right)=-frac{2pi}{3}sinfrac{pi}{9}(-3)approx1,77$,
- График график проходит в точке $(-3;3)$. Каково поведение графика около этой точки? Растет или убывает?
- Насколько быстро растет или убывает? На все эти вопросы ответы дает производная. Производная здесь $(-3;3)$ положительна, поэтому растет!
- Около точки $x_1=-3$ функция приближенно $fleft(xright)approx 3+1,77cdot(x+7)$
- Т.к. производная равна $1$, то тангенс угла наклона касательной, проведенной к графику нашей функции в данной точке ($-3; 3$) равен $1$.
- Значит, касательная направлена под углом $45$ градусов, ведь $tg45=1$.
- Значит, функция около этой точки растет “умеренно”, примерно под углом 45 градусов.
Значение производной $f’left(x_0right)$ в какой-либо точке указывает на рост или убывание исходной функции $fleft(xright)$ около этой точки $x_0$. Зная числовое значение производной, можно определить как ведет себя функция: стоит ли на месте, растет или убывает и как быстро изменяется. Производная от функции помогает узнать в каждой точке характер скорости изменений, поведения графика самой функции.
-
В тех точках, где функция растет – график поднимается вверх (если смотреть слева направо) – касательная к графику в этой точке наклонена вправо – – тангенс наклона положительный – производная в этой точке имеет положительное значение.
-
В тех точках, где функция убывает – график опускается вниз (если смотреть слева направо) – касательная к графику в этой точке наклонена влево – – тангенс наклона отрицательный, тупой угол – производная в этой точке имеет отрицательное значение.
-
Производная = 0 функция “остановилась”, “касательная горизонтальна” точка экстремума: минимум, максимум или перегиб.
-
Вторая производная в точке x показывает скорость изменения скорости, т.е. ускорение в этой точке. Вторая производная = 0 означает “ускорение обнулилось”. больше нуля – выпоукло вниз (min), меньше нуля – вверх (max).
Пример 3: Указать интервалы монотонности функции $fleft(xright)=x^3-3x+2$ . ;
- $f’left(xright)=left(x^3-3x+2right)’=3x^2-3$ находим производную от нашей функции
- $f’left(xright)>0$ $3x^2-3>0$ $left(-infty ;-1right) left(1;infty right)$ интервалы возрастания, неравенство больше
- $f’left(xright)<0$ $3x^2-3<0$ $left(-1;1right)$ интервалы убывания, производное минус
- $M_f$ области монотонности $ left(-infty ;-1right)+left(-1;1right)+left(1;infty right)$
Точки экстремумов функции. min-max
Из $f’left(x_0right)approxfrac{fleft(x_0+0,01right)-fleft(x_0right)}{x_0+0,01-x_0}$ выразим значение функции чуть правее точки $x_0$ : $fleft(x_0+0,01right)approx fleft(x_0right)+0,01f’left(x_0right)$.
Значит, функция будет иметь большее значение правее от $x_0$ , если только $f’left(x_0right) > 0$.
Аналогичные рассуждения для значения функции чуть левее. Из $f’left(x_0right)approxfrac{fleft(x_0-0,01right)-fleft(x_0right)}{x_0-0,01-x_0}$ $Rightarrow$ $fleft(x_0-0,01right)approx fleft(x_0right)-0,01cdot f’left(x_0right)$ $Leftrightarrow$ понятно почему поведение функции левее $x_0$ зависит от знака производной в точке $x_0$.
Итак:
-
если $f’left(x_0right) > 0$ то $fleft(x_0-0,01right) < fleft(x_0right) < fleft(x_0+0,01right)$ $Rightarrow $ функция растет (см. слева направо).
-
если $f’left(x_0right) < 0$ то $fleft(x_0-0,01right) > fleft(x_0right) > fleft(x_0+0,01right)$ $Rightarrow $ функция убывает, график идет вниз.
-
если $f’left(x_0right)=0$ то ситуации более запутанные: при $fleft(x_0-0,01right) < fleft(x_0right) > fleft(x_0+0,01right)$ точка $x=x_0$ называется точкой максимума. В нем функция “выше”, чем по-соседству хоть слева, хоть справа.
В случае $fleft(x_0-0,01right) > fleft(x_0right) < fleft(x_0+0,01right)$, $x=x_0$ – точка минимума. Если ни то, ни другое, то точка перегиба.
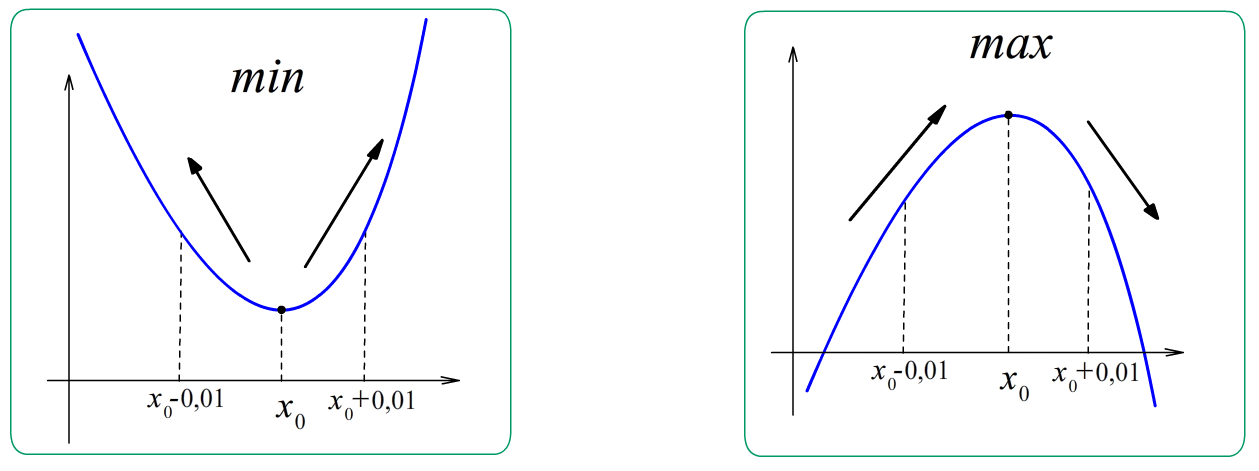
Определение: Точка, в которой производная обнуляется, называется экстремумом (минимум, максимум, перегиб).
В этой точке наклон графика равен нулю, т.е. касательная к графику горизонтальна.
Точка максимума – если функция растет, “застывает” в $x_0$” , затем убывает.
Производная функции больше нуля, в $x_0$ обнуляется, затем отрицательна.
Точка минимума наоборот – если функция убывает, “застывает” в $x_0$” , затем растет.
Производная меньше нуля, равна нулю в $x_0$”, затем положительна.
Нахождение точки минимума (максимума) функции $y=fleft(xright)$:
Точка минимума – это $x$ – число, в котором производная равна нулю, а сама исходная функция от убывания переходит к возрастанию. Надо “взять” производную исходной функции и составить уравнение экстремума “производная равна нулю”. Среди точек экстремума найти точку минимума.
Есть три способа:
- по поведению “рост / убывание” исходной функции ;
- либо поведение “отрицательности / положительности” производной;
- либо знак второй производной в этой точке; если 2-ая производная (“производная от производной”) в точке $x_0$ положительна, то это минимум.
min: $f’left(x_0right)=0$ , $fleft(x_0-0,01right) > fleft(x_0right) < fleft(x_0+0,01right)$ , $f’left(x_0-0.01right) < 0$ , $f’left(x_0+0.01right) > 0$ ; $f”left(x_0right) > 0$.
max: $f’left(x_0right)=0$ , $fleft(x_0-0,01right) < fleft(x_0right) > fleft(x_0+0,01right)$ , $f’left(x_0-0.01right) > 0$ , $f’left(x_0+0.01right) < 0$ ; $f”left(x_0right) < 0$.
Обозначения множеств, областей
$D_f$ область определения функции
$Z_f$ область знакопостоянства, интервалы положительности, отрицательности
$M_f$ области монотонности функции, интервалы возрастания, убывания
$X_f$ экстремумы функции, перечисление х – точек
$T_f$ уравнение касательной к функции в указанной х – точке
$E_f$ области значений функции, все у – значений
Упражнения:
Если вы ничего не смыслите в том, что такое производная и какими методами можно её вычислить, то совершенно невозможно решать примеры по математике или задачи по физике. Ведь такое понятие, как производная, является одним из самых важных в математическом анализе.
В этой статье мы расскажем вам, что является производной, какой она имеет геометрический и физический смысл. В общем, мы с вами попытаемся понять производную.
Геометрический и физический смысл производной
Задаём функцию f(x) в интервале (a, b). А точки x и x0 этому интервалу принадлежат. Если изменится x, то и функция тоже изменится. Изменением аргумента является разность его значений x-x0. Записывается эта разность, как дельта икс и имеет название: приращение аргумента. Разность значений функций в двух точках называется приращением или изменением функции. Так каково определение производной?
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Можно записать ещё следующим образом:
Встаёт вопрос, для чего нужно находить такой предел? Вот и ответ:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Ещё в школе нас учили тому, что скорость – это частное пути x=f(t) и времени (t). Вычисляем среднюю скорость за какой-то временной промежуток:
Для того чтобы нам узнать какова скорость движения в момент t0, необходимо вычислить предел:
Сейчас мы разберем один пример, который продемонстрирует вам применение производной на практике. Допустим, тело движется по закону:
Нам необходимо рассчитать скорость в момент времени t=2c. Вычисляем производную:
Правила нахождения производных
Дифференцирование – это процесс нахождения производной. А дифференцируемая функция – это функция, которая имеет производную в данной точке.
Каким образом нам найти саму производную? Нам необходимо составить отношения приращения функции и аргумента, а после вычислить предел при условии стремящегося к нулю приращения аргумента. Но практика показывает, что такой путь вычисления является очень долгим. Всё, что нам необходимо, уже посчитано. И специально для вас, мы подготовили таблицу с производными элементарных функций.
После таблицы мы рассмотрим правила по вычисления производных. Коснёмся мы и вычисления производных сложных функций. Подробно разберём всё на примерах.
Правило первое: выносим константу
Вынести константы можно за знак производной. Причём делать это необходимо! Когда вы решаете примеры по математике, то всегда помните правило – если есть возможность упростить выражение, то делайте это.
Для примера вычислил с вами производную:
Правило второе: производная суммы функций
Производная суммы двух функций равняется сумме производных этих функций. Это касается и производной разности функций.
Сейчас мы с вами на практике рассмотрим пример доказательства этой теоремы.
Найти производную функции:
Решение:
Правило третье: производная произведения функций
По следующей формуле мы сможем вычислить производную произведения двух дифференцируемых функций:
К примеру: необходимо найти производную функции:
Решение:
Необходимо сказать о том, каким образом вычисляются производные сложных функций.
Производная сложной функции равняется произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В примере, который указан выше, мы можем встретить выражение:
В этом примере промежуточным аргументом является 8x в пятой степени. Чтобы нам вычислить производную данного выражения, то для начала необходимо высчитать производную внешней функции по промежуточному аргументу, а после необходимо умножить на производную непосредственно сам промежуточный аргумент по независимой переменной.
Правило четвертое: производная частного двух функций
Ниже приведена формула для того, чтобы определить производную от частного двух функций:
Пример:
Решение:
В данной статье мы попытались рассказать о производных для тех, кто совершенно не знаком с этой темой. Когда вы будете решать примеры, то будьте очень внимательны, ведь в них часто можно встретить ловушки. Эта тема не так уж и проста, какой кажется на первый взгляд.
Вы можете обратиться в наш студенческий сервис по любым вопросам. Мы с удовольствием поможем решить для вас задачи любой сложности. А занимались вы раньше вычислением производных или нет, не имеет никакого значения. Мы помогаем всем!






















 y
y













 y
y