Как найти производную n ого порядка - Сайт, где вы сможете решить свои вопросы

Пусть
функция
дифференцируема в некотором интервале.
Тогда её производная
,
вообще говоря, зависит отх
, то есть
является функцией от х.
Следовательно, по отношению к ней снова
можно ставить вопрос о существовании
производной.

Определение.
Производная
от первой производной называется
производной
второго порядка или второй производной
и обозначается символом
или,
то есть

Пример
1. Найти
вторую производную от функции
.

Решение. Найдем
первую производную функции:

Находим вторую
производную как производную первой
производной:

Определение.
Производная
от второй производной называется
производной третьего порядка или третьей
производной и обозначается символом
или.

Определение.
Производной
n-ого
порядка функции

называется
первая производная от производной
(n-1)-го
порядка данной функции и обозначается
символом
или:

Определение.
Производные
порядка выше первого называются
высшими
производными.

Пример
2. Найти
производную четвертого порядка функции
.

Решение. Находим
последовательно первую, вторую, третью
и четвертую производные:

,,.

Пример
3.Найти
производную n-ого
порядка для функции
(k–const).

Решение. Имеем:

,,.

Пример
4. Найти
производную n-ого
порядка для функции
.

Решение. Имеем:

Замечание.
Аналогично можно получить формулу n-ой
производной функции
:

Пример
5. Найти
производную n-ого
порядка для степенной функции
, гдеи– любое вещественное число.

Решение.
Дифференцируя последовательно, получим:

В
частном случае, когда
,
гдеm
– натуральное число, получим:

при.

Замечание.
При строгом выводе формулы для производной
n-ого
порядка следует применять метод
математической индукции.

Вторая
производная параметрически заданной
функции

Если
функция задана параметрически уравнениями
,
то для нахождения производной второго
порядка нужно продифференцировать
выражение для её первой производной,
как сложной функции независимой
переменной.

Так
как
,
то

и с учетом того,
что

получим

,
то есть

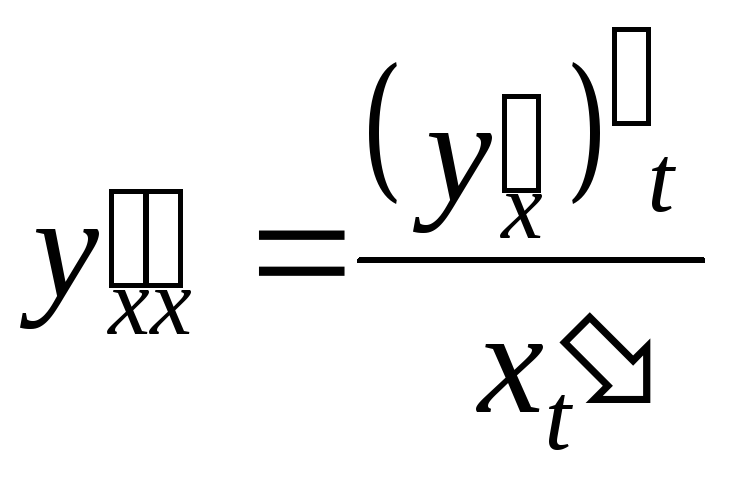Аналогично можно найти третью
производную

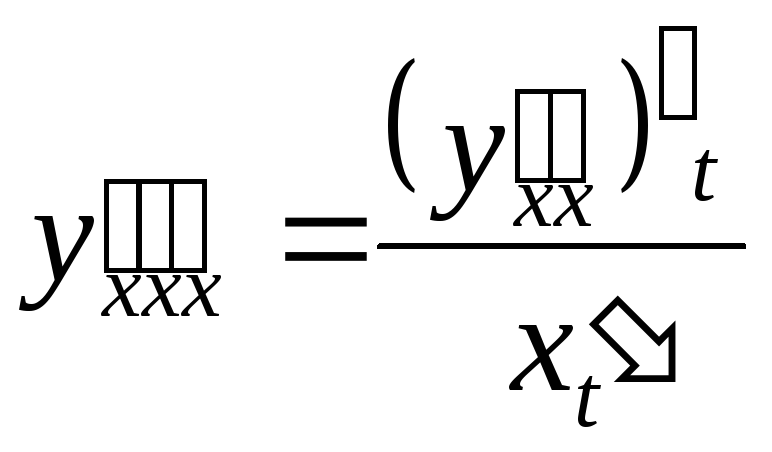Пример
7. Найти
вторую производную параметрически
заданной функции
,.

Решение.,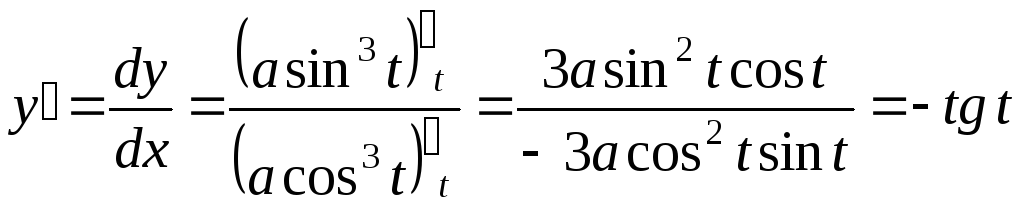

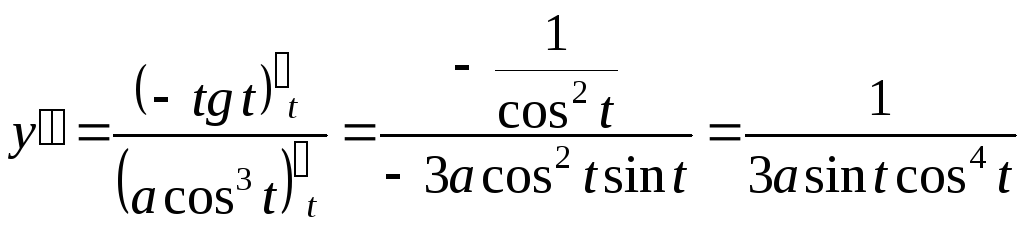Формула Лейбница

Для
нахождения производной n-ого
порядка от произведения двух функций
большое практическое значение имеет
формула Лейбница.

Пусть
u
и
v
– некоторые
функции от переменной х,
имеющие производные любого порядка и
y=uv.
Выразим n-ую
производную
через производные функцийu
и
v.

Имеем последовательно

Легко подметить
аналогию между выражениями для второй
и третьей производных и разложением
бинома Ньютона соответственно во второй
и третьей степенях, но вместо показателей
степени стоят числа, определяющие
порядок производной, а сами функции
можно рассматривать как «производные
нулевого порядка». Учитывая это, получим
формулу Лейбница:

. (2)

Эту формулу
можно доказать методом математической
индукции.

Пример.
Найти пятую
производную функции
.

Решение.
Положим
и.
Найдем,,,,;.
Подставляя эти выражения в формулу
Лейбница при,
получим

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Производная n-го порядка.

Начать изучение
Вторая производная.

Начать изучение
Производная n-го порядка.

Начать изучение
Формула Лейбница.

Начать изучение
Дифференциал n-го порядка.

Начать изучение

Производная n-го порядка.

Вторая производная.

Определение.

Пусть функция (f(x)) имеет производную во всех точках интервала ((a,b)). Если функция (f'(x)) дифференцируема в точке (x_0in (a,b)), то ее производную называют второй производной или производной второго порядка функции (f(x)) в точке (x_0) и обозначают (f″(x_0)), (f^{(2)}(x_{0})), (displaystyle frac{d^{2}f(x_{0})}{dx^{2}}), (f_{xx}″(x_0)). Таким образом, по определению
$$
f″(x_{0})=lim_{Delta xrightarrow 0}frac{f'(x_{0}+Delta x)-f'(x_{0})}{Delta x}.nonumber
$$

Заметим, что функцию (f'(x)) часто называют первой производной или производной первого порядка функции (f(x)), а под производной нулевого порядка (f^{(0)}(x)) подразумевается функция (f(x)), то есть (f^{(0)}(x)equiv f(x)).

Пример 1.

Найти (f″(x)), если:

(f(x)=sin^{2}x);
(f(x)=e^{-x^{2}});
(f(x)=operatorname{ln}(x+sqrt{x^2+1}));
(f(x)=|x|^{3}).

Решение.

(triangle) Так как (f'(x)=2sin {x}cos {x}=sin 2x), то (f″(x)=2cos{2x}).
(f'(x)=-2xe^{-x^2},;f″(x)=-2e^{-2x^2}+(-2x)^2e^{-2x^2}=2e^{-x^2}(2x^2-1)).
Так как (f'(x)=displaystyle frac{1}{sqrt{x^2+1}}), то (f″(x)=-x(x^2+1)^{-3/2}).
Если (xneq 0), то
$$
f'(x)=left{begin{array}{l}3x^2quad приquad x;>;0\-3x^2quad приquad x;<;0end{array}right.label{ref1}
$$
а если (x=0), то по определению производной
$$
f'(0)=lim_{xrightarrow 0}frac{f(x)-f(0)}{x}=displaystyle lim_{xrightarrow 0}frac{|x|^{3}}{x}=0.label{ref2}
$$
Следовательно,
$$
f'(x)=3x^{2}operatorname{sign}x.label{ref3}
$$
Из равенства eqref{ref1} следует, что
$$
f″(x)=left{begin{array}{l}6xquad приquad x;>;0\-6xquad приquad x;<;0end{array}right.nonumber
$$Покажем, пользуясь определением производной, что (f″(0)) существует и (f″(0)=0). Из eqref{ref2} и eqref{ref3} находим
$$
f″(0)=lim_{xrightarrow 0}frac{f'(x)-f'(0)}{x}=lim_{xrightarrow 0}frac{3x^{2}operatorname{sign}x}{x}=0.nonumber
$$Таким образом, (f″(x)=6|x|), то есть
$$
(|x|)^{3})″=6|x|.quadblacktrianglenonumber
$$

Дадим физическое истолкование второй производном. Пусть материальная точка движется прямолинейно, и пусть (S=S(t)) — путь, пройденный ею за время (t) от начала движения. Тогда (v=S'(t)) — скорость точки в момент времени (t).

Отношение (displaystyle frac{Delta v}{Delta t}=frac{S'(t+Delta t)-S'(t)}{Delta t}) представляет собой среднее ускорение точки на промежутке времени от (t) до (t+Delta t), а предел этого отношения (если он существует), равный (S″(t)) , называют ускорением точки в момент (t).

Таким образом, вторая производная пути по времени есть ускорение точки в момент времени (t).

Выведем, далее, формулу для второй производной функции в случае, когда эта функция задана параметрически. Пусть функции (x=x(t)) и (y=y(t)) удовлетворяют условиям, указанным нами ранее, и пусть, кроме того, существуют производные (x″(t_0)) и (y″(t_{0})), которые будем обозначать соответственно (x_{tt}″, y_{tt}″). Тогда функция (y=у(x)) имеет в точке (x_0), где (x_0=x(t_{0})), вторую производную (y_{xx}″=y_{xx}″(x_{0})), причем
$$
y_{xx}″=left(frac{y_{t}’}{x_{t}’}right)_{t}’frac{1}{x_{t}’},label{ref4}
$$
или
$$
y_{xx}″=frac{y_{tt}″x_{t}’-y_{t}’x_{tt}″}{(x_{t}’)^{3}}.label{ref5}
$$
(circ) Действительно, по правилу дифференцирования сложной функции
$$
y_{xx}″=(y_{x}’)_{t}’t_{x}’,nonumber
$$
где (y_{x}’=displaystyle frac{y_{t}’}{x_{t}}), (t_{x}’=displaystyle frac{1}{x_{t}’}), откуда следует формула eqref{ref4}, которую можно представить в виде eqref{ref5}. (bullet)

Пример 2.

Найти (y_{xx}″), если (displaystyle x=frac{1}{cos t}, y=operatorname{tg}t-t, 0 < t <displaystyle frac{pi}{2}).

Решение.

(triangle) Так как (x_{t}’=displaystyle frac{sin t}{cos^{2}t}), (y_{t}’=displaystyle frac{1}{cos^{2}t}-1=frac{sin^{2}t}{cos^{2}t}), то (y_{x}’=displaystyle frac{y_{t}’}{x_{t}}=sin t), и по формуле eqref{ref4} получаем
$$
y_{xx}″=cos tfrac{1}{x_{t}’}=frac{cos^{3}t}{sin t}.quadblacktrianglenonumber
$$

Обратимся к вопросу о вычислении второй производной сложной и неявной функции.

Если функция (y=y(x)) имеет вторую производную в точке (x_0), а функция (z=z(y)) — вторую производную в точке (y_0), где (y_0=y(x_0)), то существует вторая производная в точке (x_0) сложной функции (w=z(y(x))), причем
$$
w″(x_{0})=z_{yy}″(y_{x}’)^{2}+z_{y}’y_{xx}″,label{ref6}
$$
где в правой части формулы eqref{ref6} опущены обозначения аргументов.

(circ) Заметим сначала, что в некоторой окрестности точки (x_0) определена сложная функция (w=z(y(x))), так как функции (y(x)) и (z(y)) непрерывны соответственно в точках (x_0) и (y_0), причем (y_0=у(x_0)). По правилу дифференцирования сложной функции (w_{x}’=z_{y}’y_{x}’), откуда (w_{xx}″=(z_{y}’)_{x}’y_{x}’+z_{y}’y_{xx}″), где ((z_{y}’)_{x}’=z_{yy}″y_{x}’). Формула eqref{ref6} доказана. (bullet)

Вторую производную неявной функции в простейших случаях часто удается найти с помощью дифференцирования тождества, которое получается при вычислении первой производной.

Пример 3.

Найти (y_{xx}″), где (y=y(x)) — неявная функция, определяемая уравнением
$$
frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1.nonumber
$$

Решение.

Ранее мы уже доказали, что
$$
y_{x}’=-frac{b^2x}{a^2y}.label{ref7}
$$
Дифференцируя тождество eqref{ref7} по (x) получаем (y_{xx}″=-displaystyle frac{b^{2}}{a^{2}y}+frac{b^{2}x}{a^{2}y^{2}}y_{x}’), откуда, используя формулу eqref{ref7} и равенство (a^2y^2+b^2x^2=a^2b^2), находим
$$
y_{xx}″=-frac{b^{4}}{a^{2}y^{3}}.quadblacktrianglenonumber
$$

Производная n-го порядка.

Производную от второй производной функции (f(x)) называют третьей производной или производной третьего порядка этой функции и обозначают (f′′′(x)) или (f^{(3)}(x)). Аналогично определяются производные любого порядка.

Пусть функция (f(x)) имеет на интервале ((a,b)) производные (f'(x),ldots, f^{(n-1)}(x)). Если в точке (xin(a,b)) существует производная функции (f^{(n-1)}(x)), то эту производную называют производной n-го порядка или n-й производной функции (f(x)) и обозначают (f^{(n)}(x)).

Таким образом, если функция (f(x)) имеет в точке (x) производные до n-го порядка включительно, то
$$
f^{(n)}(x)=(f^{(n-1)}(x))’,nonumber
$$
то есть
$$
f^{(n)}(x)=lim_{Delta xrightarrow 0}frac{f^{(n-1)}(x+Delta x)-f^{(n-1)}(x)}{Delta x}.nonumber
$$
Функцию, имеющую в каждой точке множества (E) производные до n-го порядка включительно, называют n раз дифференцируемой на множестве (E).

Пусть функции (f(x)) и (g(x)) имеют в точке (x) производные (n)-го порядка. Тогда функция (Af(x)+Bg(x)), где (A) и (B) — постоянные, также имеет производную n-го порядка в точке (x) причем
$$
(Af(x)+Bg(x))^{(n)}=Af^{(n)}(x)+Bg^{(n)}(x).label{ref8}
$$

При вычислении производных любого порядка часто используют следующие основные формулы.
$$
(x^alpha)^{(n)}=alpha(alpha-1)ldots(alpha-(n-1))x^{alpha-n}.label{ref9}
$$
В частности, если (alpha=m), где (minmathbb{N}), то
$$
{(x^m)}^{(n)}=left{begin{array}{l}m!quad приquad n=m\0quad приquad n;>;mend{array}right.label{ref10}
$$
$$
(a^x)^{(n)}=a^xoperatorname{ln}^na,quad a;>;0,quad aneq 1label{ref11}
$$
В частности,
$$
(e^{x})^{(n)}=e^{x}.label{ref12}
$$
Далее,
$$
left(frac{1}{x+alpha}right)^{(n)}=frac{(-1)^{n}n!}{(x+alpha)^{n+1}}.label{ref13}
$$
$$
(operatorname{ln}|x+alpha|)^{(n)}=frac{(-1)^{n-1}(n-1)!}{(x+alpha)^{n}}.label{ref14}
$$
$$
(sin x)^{(n)}=sin {left(x+nfrac{pi}{2}right)},label{ref15}
$$
$$
(cos x)^{(n)}=cos {left(x+nfrac{pi}{2}right)}.label{ref16}
$$
Формулы eqref{ref9}-eqref{ref14} легко проверяются с помощью индукции. Докажем формулу eqref{ref15}. Так как ((sin x)’=cos x), то из равенства (cos x=sin {left(x+displaystyle frac{pi}{2}right)}) следует справедливость формулы eqref{ref15} при (n=1). Применив метод индукции, докажем, что формула eqref{ref15} верна при любом (ninmathbb{N}). Аналогично проверяется формула eqref{ref16}. Из равенств eqref{ref15} и eqref{ref16} следует, что если (alpha=operatorname{const}), то
begin{align}
(sin {alpha x})^{(n)}=alpha^nsin {left(alpha x+nfrac{pi}{2}right)},nonumber\
(cos {alpha x})^{(n)}=alpha^n cos {left(alpha x+nfrac{pi}{2}right)}.label{ref17}
end{align}

Пример 4.

Найти (f^{(n)}(x)), если:

(f(x)=sin^{3}x);
(f(x)=displaystyle frac{1}{x^{2}-3x+2}).

Решение.

Из равенства (sin^{3} x=3sin x-4sin^3 x) следует, что (sin^{3} x=displaystyle frac{3}{4}sin x-displaystyle frac{1}{4}sin3x). Применяя формулы eqref{ref8} и eqref{ref17}, получаем
$$
(sin^{3}х)^{(n)}=frac{3}{4}sin left(x+nfrac{pi}{2}right)-frac{3^{n}}{4}sin left(3x+nfrac{pi}{2}right).nonumber
$$
Так как (displaystyle frac{1}{x^{2}-3x+2}=frac{1}{x-2}-frac{1}{x-1}), то, применяя формулу eqref{ref13}, получаем
$$
left(frac{1}{x^{2}-3x+2}right)^{(n)}=(-1)^{n}n!left(frac{1}{(x-2)^{n+1}}-frac{1}{(x-1)^{n+1}}right).quadblacktrianglenonumber
$$

Формула Лейбница.

Теорема.

Если функции (u) и (v) имеют в точке (x) производные n-го порядка, то функция (uv) также имеет в точке (x) производную n-го порядка, причем
$$
(uv)^{(n)}=uv^{(n)}+C_{n}^{1}u^{(1)}v^{(n-1)}+C_{n}^{2}u^{(2)}v^{(n-2)}+ldots+C_{n}^{n-1}u^{(n-1)}v^{(1)}+u^{(n)}v,label{ref18}
$$
где (C_{n}^{k}=displaystyle frac{n(n-1)cdots(n-(k-1))}{k!},; 1leq kleq n).

Формулу eqref{ref18} называют формулой Лейбница и записывают в виде
$$
(uv)^{(n)}=sum_{k=0}^{n}C_{n}^{k}u^{(k)}v^{(n-k)},label{ref19}
$$
где (u^{(0)}=u, v^{(0)}=v, C_{n}^{0}=1).

Доказательство.

(circ) Докажем формулу eqref{ref18} методом индукции. При (n=1) эта формула верна, так как
$$
(uv)’=uv’+vu’.nonumber
$$
Пусть формула Лейбница верна для производной n-го порядка. Докажем справедливость этой формулы для производной (n+1)-го порядка, предполагая, что существуют (u^{(n+1)}) и (v^{(n+1)}). Так как функции (u) и (v) имеют производные n-го порядка включительно в некоторой окрестности точки (x), то в силу индуктивного предположения равенство eqref{ref19} справедливо в окрестности точки (x). Дифференцируя это равенство и учитывая, что
$$
(u^{(k)}v^{(n-k)})’=u^{(k+1)}v^{(n-k)}+u^{(k)}v^{(n+1-k)},nonumber
$$
получаем
$$
(uv)^{(n+1)}=sum_{k=0}^{n}C_{n}^{k}u^{(k+1)}v^{(n-k)}+sum_{k=0}^{n}C_{n}^{k}u^{(k)}v^{(n+1-k)}.label{ref20}
$$
Преобразуем суммы в правой части равенства eqref{ref20}, выделяя в первой сумме последнее слагаемое, а во второй — первое и сдвигая индекс суммирования в первой сумме на единицу. Получим
$$
sum_{k=0}^{n}C_{n}^{k}u^{(k+1)}v^{(n-k)}=u^{(n+1)}v+sum_{k=1}^{n}C_{n}^{k-1}u^{(k)}v^{(n+1-k)},nonumber
$$
$$
sum_{k=0}^{n}C_{n}^{k}u^{(k)}v^{(n+1-k)}=u^{(n+1)}+sum_{k=1}^{n}C_{n}^{k}u^{(k)}v^{(n+1-k)}.nonumber
$$
Следовательно,
$$
(uv)^{(n+1)}=uv^{(n+1)}+sum_{k=1}^{n}(C_{n}^{k-1}+C_{n}^{k})u^{(k)}v^{(n+1-k)}+u^{(n+1)}v.nonumber
$$
Используя равенство (C_{n}^{k-1}+C_{n}^{k}=C_{n+1}^{k}), получаем
$$
(uv)^{(n+1)}=sum_{k=0}^{n+1}C_{n+1}^{k}u^{(k)}v^{(n+1-k)},nonumber
$$
то есть формула Лейбница справедлива для производных (n+1)-го порядка. (bullet)

Пример 5.

Найти (f^{(n)}(x)) при (n > 2), если:

(f(x)=(x-1)^2sin xsin (x-1));
(f(x)=(1-2x^2)ln (1-3x)^3).

Решение.

Так как (sin xsin (х-1)=displaystyle frac{1}{2}(cos 1-cos(2x-1))) то, применяя формулу Лейбница eqref{ref18}, вторую из формул eqref{ref17} и учитывая, что (((x-1)^{2})^{(k)}=0) при (k > 2), получаем (при (n > 2))
$$
f^{(n)}(x)=-(x-1)^{2}2^{n-1}cosleft(2x-1+frac{npi}{2}right)-n(x-1)2^{n-1}cos left(2x-1+frac{(n-1)pi}{2}right)-n(n-1)2^{n-3}cos left(2x-1+frac{(n-2)pi}{2}right).nonumber
$$
Применяя формулы eqref{ref18} и eqref{ref14}, получаем ((n;>;2))
$$
f^{(n)}(x)=(2x^{2}-1)frac{3^{n+1}(n-1)!}{(1-3x)^n}+4xnfrac{3^{n}(n-2)!}{(1-3x)^{n-1}}+2n(n-1)frac{3^{n-1}(n-3)!}{(1-3x)^{n-2}}. blacktrianglenonumber
$$

Дифференциал n-го порядка.

Пусть функция (y=f(x)) дифференцируема на интервале ((a,b)). Тогда ее дифференциал
$$
dy=f'(x)dxnonumber
$$
в точке (xin(a,b)), который называют также первым дифференциалом функции (f), зависит от двух переменных, а именно от (x) и (dx).

Если дифференциал (dx), совпадающий с приращением (Delta x) независимого переменного (x) не меняется (фиксирован), то дифференциал (dy) является функцией только от (x). Дифференциал этой функции, то есть дифференциал от (f'(x)dx), где (dx) — постоянная величина, называют вторым дифференциалом или дифференциалом второго порядка функции (y=f(x)) в точке (x) и обозначают (d^{2}y) или (d^{2}f). При этом предполагается, что при вычислении дифференциала (d(dy)) (если он существует) приращение (dx) независимого переменного выбрано таким же, как и при вычислении первого дифференциала.

Пусть функция (f) имеет вторую производную в точке (x). Тогда, пользуясь тем, что (dg=g'(x)dx) и (d(Cg)=Cdg), где (C=const), получаем
$$
d^{2}y=d(dy)=d(f'(x)dx)=dxd(f'(x))=dxf″(x)dx=f″(x)dx^{2}.nonumber
$$
Таким образом, при указанных выше условиях второй дифференциал функции (y=f(x)) в точке (x) существует, причем
$$
d^{2}y=f″(x)dx^{2} =y″dx^2,label{ref21}
$$
где
$$
dx^{2}=(dx)^{2}.nonumber
$$
Аналогично, предполагая, что функция (y=f(x)) имеет в точке (x) производную n-го порядка, определим n-й дифференциал (d^{n}y) как дифференциал от (d^{n-1}y), то есть
$$
d^{n}y=d(d^{n-1}y).nonumber
$$
Предполагая, что приращение независимого переменного при вычислении первого и всех последующих дифференциалов выбирается одним и тем же, легко доказать методом индукции формулу
$$
d^{n}y=f^{(n)}(x)dx^{n}.label{ref22}
$$
Из формулы eqref{ref22} следует, что
$$
y^{(n)}=frac{d^{n}y}{dx^n},nonumber
$$
то есть производная (n)-го порядка функции (y=f(x)) равна отношению дифференциала (n)-го порядка этой функции к n-й степени дифференциала независимого переменного.

Из формулы eqref{ref22} следует, что
$$
d^{n}x=0 при n > 1,nonumber
$$
то есть дифференциал n-го порядка независимого переменного при (ngeq 2) равен нулю.

Отметим еще следующие свойства дифференциалов (n)-го порядка в предположении существования (u^{(n)}) и (v^{(n)}).

(d^{n}(Au+Bv)=Ad^{n}u+Bd^{n}v), (A,B) — постоянные;
(d^{n}(uv)=displaystyle sum_{k=0}^{n}C_{n}^{k}d^{k}ud^{n-k}v).

Первое из этих свойств следует из равенств eqref{ref22} и eqref{ref8}, а второе — из равенства eqref{ref22} и формулы eqref{ref19}.

Замечание.

Дифференциал второго порядка, в отличие от первого дифференциала, не обладает свойством инвариантности формы, то есть формула eqref{ref21} не сохраняется при замене (x) на функцию (varphi(t)).
(circ) Действительно, пусть, (x=varphi(t)), тогда (y=f(x)=f(varphi(t))). Если существуют (f″(x)) и (varphi″(t)), то, используя определение дифференциала и правила дифференцирования произведения и сложной функции, получаем
$$
dy=f'(x)dx=f'(varphi(t))varphi'(t)dt,nonumber
$$
откуда
$$
d^{2}y=(f'(varphi(t))varphi'(t))’dt^{2}=f″(varphi(t))(varphi'(t)dt)^{2}+f'(varphi(t))varphi″(t)dt^{2}.nonumber
$$
Так как (varphi'(t)dt=dx,;varphi″(t)dt^{2}=d^{2}x), то
$$
d^{2}y=f″(x)dx^{2}+f'(x)d^{2}x,nonumber
$$
или
$$
d^{2}y=y″dx^{2}+y’d^{2}x.label{ref23}
$$
Из равенств eqref{ref21} и eqref{ref23} следует, что при замене (x) на функцию (varphi(t)) изменяется вид второго дифференциала — в нем появляется слагаемое (y’d^{2}x). Если (x=varphi(t)=at+b), где (a,b) — постоянные, то (d^{2}x=0), и в этом случае вид второго дифференциала не меняется. (bullet)

Источник

Содержание:

Механический смысл второй производной
Вычисления производной любого порядка, формула Лейбница

Если функция $y=f(x)$ имеет производную в каждой точке
$x$ своей области определения, то ее производная
$f^{prime}(x)$ есть функция от
$x$. Функция
$y=f^{prime}(x)$, в свою очередь, может иметь производную, которую
называют производной второго порядка функции $y=f(x)$ (или второй
производной) и обозначают символом $f^{prime prime}(x)$. Таким образом

$f^{prime prime}(x)=frac{mathrm{d}^{2} y}{mathrm{d} x^{2}}=lim _{x rightarrow x_{0}} frac{f^{prime}(x)-f^{prime}left(x_{0}right)}{x-x_{0}}=left(f^{prime}(x)right)^{prime}$

Пример

Задание. Найти вторую производную функции $y(x)=x ln (2 x+3)$

Решение. Для начала найдем первую производную:

$y^{prime}(x)=(x ln (2 x+3))^{prime}=(x)^{prime} cdot ln (2 x+3)+x cdot(ln (2 x+3))^{prime}=$

$=1 cdot ln (2 x+3)+x cdot frac{1}{2 x+3} cdot(2 x+3)^{prime}=ln (2 x+3)+$

$+frac{x}{2 x+3} cdotleft[(2 x)^{prime}+(3)^{prime}right]=ln (2 x+3)+frac{x}{2 x+3} cdotleft[2 cdot(x)^{prime}+0right]=$

$=ln (2 x+3)+frac{x}{2 x+3} cdot 2 cdot 1=ln (2 x+3)+frac{2 x}{2 x+3}$

Для нахождения второй производной продифференцируем выражение для первой производной еще раз:

$y^{prime prime}(x)=left(y^{prime}(x)right)^{prime}=left(ln (2 x+3)+frac{2 x}{2 x+3}right)^{prime}=$

$=(ln (2 x+3))^{prime}+left(frac{2 x}{2 x+3}right)^{prime}=$

$=frac{1}{2 x+3} cdot(2 x+3)^{prime}+frac{(2 x)^{prime} cdot(2 x+3)-2 x cdot(2 x+3)^{prime}}{(2 x+3)^{2}}=$

$=frac{1}{2 x+3}left[(2 x)^{prime}+(3)^{prime}right]+frac{2(x)^{prime} cdot(2 x+3)-2 x cdotleft[(2 x)^{prime}+(3)^{prime}right]}{(2 x+3)^{2}}=$

$=frac{1}{2 x+3}left[2 cdot(x)^{prime}+0right]+frac{2 cdot 1 cdot(2 x+3)-2 x cdotleft[2 cdot(x)^{prime}+0right]}{(2 x+3)^{2}}=$

$=frac{1}{2 x+3} cdot 2 cdot 1+frac{2(2 x+3)-2 x cdot 2 cdot 1}{(2 x+3)^{2}}=$

$=frac{2}{2 x+3}+frac{4 x+6-4 x}{(2 x+3)^{2}}=frac{2}{2 x+3}+frac{6}{(2 x+3)^{2}}=$

$=frac{2(2 x+3)+6}{(2 x+3)^{2}}=frac{4 x+6+6}{(2 x+3)^{2}}=frac{4 x+12}{(2 x+3)^{2}}=frac{4(x+3)}{(2 x+3)^{2}}$

Ответ. $y^{prime prime}(x)=frac{4(x+3)}{(2 x+3)^{2}}$

Производные более высоких порядков определяются аналогично. То есть производная
$n$-го порядка функции
$f(x)$ есть первая производная от производной
$(n-1)$-го порядка этой функции:

$f^{(n)}(x)=frac{mathrm{d}^{n} y}{mathrm{d} x^{n}}=left(f^{(n-1)}(x)right)^{prime}$

Замечание

Число $n$, указывающее порядок производной, заключается в скобки.

Механический смысл второй производной

Теорема

(Механический смысл второй производной)

Если точка движется прямолинейно и задан закон ее движения $s=f(t)$,
то ускорение точки равно второй производной от пути по времени:

$a(t)=s^{prime prime}(t)$

Замечание

Ускорение материального тела равно первой производной от скорости, то есть:

$a(t)=v^{prime}(t)$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Материальная точка движется по закону
$s(t)=2 t^{3}+3 t$, где
$s$ измеряется в метрах, а
$t$ – в секундах. Найти значение
$t$, при котором ускорение точки равно 12.

Решение. Найдем ускорение материальной точки:

$a(t)=s^{prime prime}(t)=left(2 t^{3}+3 tright)^{prime prime}=left(left(2 t^{3}+3 tright)^{prime}right)^{prime}=left(left(2 t^{3}right)^{prime}+(3 t)^{prime}right)^{prime}=$

$=left(2 cdot 3 t^{2}+3 cdot 1right)^{prime}=left(6 t^{2}+3right)^{prime}=left(6 t^{2}right)^{prime}+(3)^{prime}=$

$=6 cdotleft(t^{2}right)^{prime}+0=6 cdot 2 t=12 t$

Искомое время $t$ найдем из уравнения:

$a(t)=12 Rightarrow 12 t=12 Rightarrow t=1 mathrm{c}$

Ответ. $t=1 c$

Вычисления производной любого порядка, формула Лейбница

Для вычисления производной любого порядка от произведения двух функций, минуя последовательное применение
формулы вычисления производной от произведения двух функций, применяется формула Лейбница:

$(u v)^{(n)}=u^{(n)} v+C_{n}^{1} u^{(n-1)} v^{prime}+C_{n}^{2} u^{(n-2)} v^{prime prime}+ldots+C_{n}^{n-1} u^{prime} v^{(n-1)}+u v^{(n)}$

где $C_{n}^{k}=frac{n !}{k !(n-k) !}$,
$n !=1 cdot 2 cdot ldots cdot n$ – факториал
натурального числа
$n$.

Пример

Задание. Найти $y^{(4)}(x)$, если
$y(x)=e^{4 x} sin 3 x$

Решение. Так как заданная функция представляет собой произведение двух функций
$u(x)=e^{4 x}$,
$v(x)=sin 3 x$, то для нахождения производной четвертого
порядка целесообразно будет применить формулу Лейбница:

$y^{(4)}(x)=left(e^{4 x}right)^{(4)} cdot sin 3 x+C_{4}^{1}left(e^{4 x}right)^{(3)} cdot(sin 3 x)^{prime}+$

$+C_{4}^{2}left(e^{4 x}right)^{prime prime} cdot(sin 3 x)^{prime prime}+C_{4}^{3}left(e^{4 x}right)^{prime} cdot(sin 3 x)^{(3)}+e^{4 x}(sin 3 x)^{(4)}$

Найдем все производные и посчитаем коэффициенты при слагаемых.

1) Посчитаем коэффициенты при слагаемых:

$C_{4}^{1}=frac{4 !}{1 ! cdot(4-1) !}=frac{4 !}{3 !}=frac{3 ! cdot 4}{3 !}=4$

$C_{4}^{2}=frac{4 !}{2 ! cdot(4-2) !}=frac{4 !}{2 ! cdot 2 !}=frac{2 ! cdot 3 cdot 4}{2 ! cdot 2 !}=frac{3 cdot 4}{2}=6$

$C_{4}^{3}=frac{4 !}{3 ! cdot(4-3) !}=frac{4 !}{3 !}=frac{3 ! cdot 4}{3 !}=4$

2) Найдем производные от функции $u(x)$:

$u(x)=e^{4 x}, u^{prime}(x)=left(e^{4 x}right)^{prime}=e^{4 x} cdot(4 x)^{prime}=e^{4 x} cdot 4 cdot(x)^{prime}=4 e^{4 x}$

$u^{prime prime}(x)=left(u^{prime}(x)right)^{prime}=left(4 e^{4 x}right)^{prime}=4 cdotleft(e^{4 x}right)^{prime}=16 e^{4 x}$

$u^{prime prime prime}(x)=left(u^{prime prime}(x)right)^{prime}=left(16 e^{4 x}right)^{prime}=64 e^{4 x}$

$u^{(4)}(x)=left(u^{prime prime prime}(x)right)^{prime}=left(64 e^{4 x}right)^{prime}=256 e^{4 x}$

3) Найдем производные от функции $v(x)$:

$v(x)=sin 3 x, v^{prime}(x)=(sin 3 x)^{prime}=cos 3 x cdot(3 x)^{prime}=3 cos 3 x$

$v^{prime prime}(x)=left(v^{prime}(x)right)^{prime}=(3 cos 3 x)^{prime}=3 cdot(cos 3 x)^{prime}=$

$=3 cdot(-sin 3 x) cdot(3 x)^{prime}=-9 sin 3 x$

$v^{prime prime prime}(x)=left(v^{prime prime}(x)right)^{prime}=-27 cos 3 x, v^{(4)}(x)=left(v^{prime prime prime}(x)right)^{prime}=81 sin 3 x$

Тогда

$y^{(4)}(x)=256 e^{4 x} cdot sin 3 x+4 cdot 64 e^{4 x} cdot 3 cos 3 x+$

$+6 cdot 16 e^{4 x} cdot(-9 sin 3 x)+4 cdot 4 e^{4 x} cdot(-27 cos 3 x)+e^{4 x} 81 sin 3 x=$

$=e^{4 x}(336 cos 3 x-527 sin 3 x)$

Ответ. $y^{(4)}(x)=e^{4 x}(336 cos 3 x-527 sin 3 x)$

Читать дальше: таблица производных высших порядков.

Источник

Производная функции

f(x)

f′(x)

, сама является функцией. Значит, можно найти её производную.

Назовём

f′(x)

производной функции

f(x)

первого порядка.

Производная от производной функции

f(x)

называется производной второго порядка (или второй производной).

Производная от второй производной называется производной третьего порядка (или третьей производной) и т. д.

Производные, начиная со второй, называются производными высших порядков и обозначаются

y′′(иногдаy2),y′′′(иногдаy3),y4,y5…yn…

Иногда используются обозначения

dydx,d2ydx2,d3ydx3…dnydxn…

Ускорение есть вторая производная координаты по времени. В этом состоит механический смысл второй производной.

Производная (n)-го порядка является производной ((n-1)) порядка: yn=yn−1′.

(Сама функция иногда считается производной (0)-го порядка.)

Пример:

y=x5;y′=x5′=5×4;y′′=(y′)′=5×4′=20×3;y3=(y′′)′=(5⋅4×3)′=60×2;y4=(y3)′=(60×2)′=120x;y5=(y4)′=(120x)′=120;y6=y7=y8=…=0.

Источник

Производная F‘(X) функции F(X) сама является функцией аргумента Х, и по отношению к ней также можно ставить вопрос о производной. Производная от первой производной некоторой функции У = F(X) называется Второй производной, или производной второго порядка этой функции. Производная от второй производной называется Третьей производной, или производной третьего порядка. Этот процесс можно продолжить. Производные начиная со второй называются Производными высших порядков. Для их обозначения используют символы: У”, у'”, у(4), у(5), …, у(N) (для второй и третьей производных соответственно еще и У(2) и У(3)) или вместо У пишут F(X): F“(X), F“(х), …, F(N)(X).