Производная неявной функции
Формула
Рассмотрим функцию y(x), которая записывается неявным способом в общем виде $ F(x,y(x)) = 0 $. Производная неявной функции находится двумя способами:
- Дифференцированием обеих частей уравнения
- С помощью использования готовой формулы $ y’ = – frac{F’_x}{F’_y} $
Как найти?
Способ 1
Не требуется приводить функцию к явному виду. Нужно сразу приступать к дифференцированию левой и правой части уравнения по $ x $. Стоит обратить внимание, что производная $ y’ $ вычисляется по правилу дифференцирования сложной функции. Например, $ (y^2)’_x = 2yy’ $. После нахождения производной необходимо выразить $ y’ $ из полученного уравнения и разместить $ y’ $ в левой части.
Способ 2
Можно воспользоваться формулой, в которой используются в числителе и знаменателе частные производные неявной функции $ F(x,y(x)) = 0 $. Для нахождения числителя берем производную по $ x $, а для знаменателя производную по $ y $.
Вторую производную неявной функции можно найти с помощью повторного дифференцирования первой производной неявной функции.
Примеры решений
Рассмотрим практические примеры решений на вычисление производной неявно заданной функции.
| Пример 1 |
|
Найти производную неявной функции $ 3x^2y^2 -5x = 3y – 1 $ |
| Решение |
|
Воспользуемся способом №1. А именно продифференцируем левую и правую часть уравнения: $$ (3x^2y^2 -5x)’_x = (3y – 1)’_x $$ Не забываем при дифференцировании использовать формулу производной произведения функций: $$ (3x^2)’_x y^2 + 3x^2 (y^2)’_x – (5x)’_x = (3y)’_x – (1)’_x $$ $$ 6x y^2 + 3x^2 2yy’ – 5 = 3y’ $$ Далее выражаем y’ из уравнения: $$ 6x y^2 – 5 = 3y’ – 6x^2 yy’ $$ $$ 6x y^2 – 5 = y'(3-6x^2 y) $$ $$ y’ = frac{6x y^2 – 5}{3 – 6x^2y } $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ y’ = frac{6x y^2 – 5}{3 – 6x^2y } $$ |
| Пример 2 |
|
Функция задана неявно, найти производную $ 3x^4 y^5 + e^{7x-4y} -4x^5 -2y^4 = 0 $ |
| Решение |
|
Воспользуемся способом №2. Находим частные производные функции $ F(x,y) = 0 $ Положим $ y $ постоянной и продифференцируем по $ x $: $$ F’_x = 12x^3 y^5 + e^{7x-4y} cdot 7 – 20x^4 $$ $$ F’_x = 12x^3 y^5 + 7e^{7x-4y} – 20x^4 $$ Считаем теперь $ x $ константой и дифференцируем по $ y $: $$ F’_y = 15x^4 y^4 + e^{7x-4y} cdot (-4) – 8y^3 $$ $$ F’_y = 15x^4 y^4 – 4e^{7x-4y} – 8y^3 $$ Подставляем теперь в формулу $ y’ = -frac{F’_x}{F’_y} $ и получаем: $$ y’ = -frac{12x^3 y^5 + 7e^{7x-4y} – 20x^4}{15x^4 y^4 – 4e^{7x-4y} – 8y^3} $$ |
| Ответ |
| $$ y’ = -frac{12x^3 y^5 + 7e^{7x-4y} – 20x^4}{15x^4 y^4 – 4e^{7x-4y} – 8y^3} $$ |
Явные и неявные
В этой статье мы познакомимся с неявными функциями и техникой их дифференцирования. Вспомним для начала, как выглядят функции, заданные явно. Это “обычные” функции вида y=f(x)y=f(x), с которыми вы уже имели дело и умеете вычислять их производные. Запись y=f(x)y=f(x) обозначает, что мы функцию yy смогли выразить (явно представить) через её аргумент xx. З неявными функциями дело обстоит иначе. Здесь мы не можем “перетащить” yy в левую сторону выражения, а все что содержит xx — в правую. Такие функциональные зависимости в общем виде можно записать так:
F(x,y)=0F(x, y)=0
Эта запись означает, что величины xx и yy как-то связанны между собой, но ничего не говорится о том, как yy выражается через xx (и можно ли это вообще сделать). Одну и ту же функцию (но не каждую) можно записать как в явном так и в неявном виде. Например, неявно заданную функцию F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x} можно записать явно: y(x)=−53x2y(x)=-frac{5}{3x^2}. В этом случае нам удалось выразить yy через xx. Или, если:
F(x,y)=x2+y2−1=0F(x, y)=x^2+y^2-1=0
то
y=±1−x2y=pm sqrt{1-x^2}
Здесь функция получилась многозадачной (именно двузначной, отвечающей двум знакам), но это не страшно. Мы все-равно представили yy как выражение зависящее от xx. В правой стороне у нас присутствует только xx.
Но существуют случаи, когда этого сделать нельзя. Можно навести множество примеров таких функций. Например:
F(x,y)=ylnx+eyy2F(x, y)=yln x+e^yy^2
Ну попробуйте выразить отсюда yy через xx. То есть запишите эту функцию в виде y=f(x)y=f(x). Вот вам и пример неявной заданной функции. Ещё пример:
F(x,y)=xsinx+ysiny−12F(x, y)=xsin x+ysin y-12
Здесь, мы хотя и не можем выразить yy через xx, но мы все-равно можем считать yy функцией от аргумента xx. Так как каждому значению xx будут соответствовать какие-то значения yy.
Естественно, возникает вопрос о дифференцировании подобных функций. Вы уже понимаете, что эта операция очень важна, и было бы тяжело поверить, что математики ничего не придумали на этот счет.
Дифференцирование неявно заданных функций
Оказывается, что для того чтобы посчитать производную от yy по xx нам не обязательно решать уравнение:
F(x,y)=0F(x, y)=0
Теоретически можно доказать (пользуюсь определением производной, производя предельный переход и т. д.), что:
dydx=−∂F(x,y)∂x∂F(x,y)∂yfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}
Обозначение ∂partial обозначает частную производную. Мы здесь имеем дело с двумя переменными xx и yy и берем производные от функции F(x,y)F(x, y) по этим величинам. Так, выражение:
∂F(x,y)∂xfrac{partial F(x, y)}{partial x}
говорит, что берется производная от F(x,y)F(x, y) по xx, при этом величина yy считается постоянной. Следует обратить внимание на знак “минус” перед дробью, а также на то, что мы не можем сократить числитель и знаменатель на ∂F(x,y)partial F(x, y), так как производные берутся по разным величинам. Вооружившись этой главной формулой вычисления производных от неявных функций, перейдем к разбору нескольких примеров.
Примеры
F(x,y)=x2+y2−1F(x, y)=x^2+y^2-1
∂F(x,y)∂x=2x, ∂F(x,y)∂y=2yfrac{partial F(x, y)}{partial x}=2x, frac{partial F(x, y)}{partial y}=2y
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−2x2y=−xyfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{2x}{2y}=-frac{x}{y}
F(x,y)=xsinx+ysiny−12F(x, y)=xsin x+ysin y-12
∂F(x,y)∂x=sinx+xcosx, ∂F(x,y)∂y=siny+ycosyfrac{partial F(x, y)}{partial x}=sin x+x cos x, frac{partial F(x, y)}{partial y}=sin y+y cos y
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−sinx+xcosxsiny+ycosyfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{sin x+xcos x}{sin y+ycos y}
- F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x}
∂F(x,y)∂x=3y−5×2, ∂F(x,y)∂y=3xfrac{partial F(x, y)}{partial x}=3y-frac{5}{x^2}, frac{partial F(x, y)}{partial y}=3x
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−3y−5x23x=−3yx2−53x3frac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{3y-frac{5}{x^2}}{3x}=-frac{3yx^2-5}{3x^3}
Но здесь мы можем выразить yy через xx явно:
y=−53x2y=-frac{5}{3x^2}
Подставим это выражение в формулу для производной выше:
dydx=103x3frac{dy}{dx}=frac{10}{3x^3}
А теперь поступим так, как будто нам с самого начала была известна явная зависимость y=f(x)y=f(x). То есть продифференцируем функцию y(x)=−53x2y(x)=-frac{5}{3x^2} по xx:
dydx=ddx(−53×2)=−53(−2)1×3=103x3frac{dy}{dx}=frac{d}{dx}Big(-frac{5}{3x^2}Big)=-frac{5}{3}(-2)frac{1}{x^3}=frac{10}{3x^3}
Получили то же самое. Значит мы все сделали правильно.
Определение
Если независимая переменная $x$ и функция
$y$ связаны уравнением вида
$F(x,y)=0$, которое не разрешено относительно
$y$, то функция
$y$ называется неявной функцией переменной
$x$.
Пример
$$x^{2} sin y+x y-1=0$$
Всякую явно заданную функцию $y=f(x)$ можно записать в
неявном виде $y-f(x)=0$. Обратно сделать не всегда возможно.
Несмотря на то, что уравнение $F(x,y)=0$ не разрешимо
относительно $y$, оказывается возможным найти производную
от $y$ по
$x$. В этом случае необходимо
продифференцировать обе
части заданного уравнения, рассматривая функцию $y$ как
функцию от $x$, а затем из полученного уравнения найти
производную $y^{prime}$.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти вторую производную
$y^{prime prime}$ неявной функции
$x^2+xy^2=1$.
Решение. Продифференцируем левую и правую часть заданного равенства, при этом помним, что
$y$ является функцией переменной
$x$, поэтому производную от нее будем брать
как производную от сложной функции. В итоге получаем:
$$left(x^{2}+x y^{2}right)^{prime}=(1)^{prime}$$
$$left(x^{2}right)^{prime}+left(x y^{2}right)^{prime}=0$$
$$2 x+(x)^{prime} cdot y^{2}+x cdotleft(y^{2}right)^{prime}=0$$
$$2 x+1 cdot y^{2}+x cdot 2 y cdot y^{prime}=0 Rightarrow 2 x+y^{2}+2 x y cdot y^{prime}=0$$
Из полученного равенства выражаем $y^{prime}$:
$$2 x y cdot y^{prime}=-left(2 x+y^{2}right) Rightarrow y^{prime}=-frac{2 x+y^{2}}{2 x y}$$
Для нахождения второй производной продифференцируем равенство
$2 x+y^{2}+2 x y cdot y^{prime}=0$ еще раз:
$$begin{array}{c}
left(2 x+y^{2}+2 x y cdot y^{prime}right)^{prime}=(0)^{prime} \
(2 x)^{prime}+left(y^{2}right)^{prime}+left(2 x y cdot y^{prime}right)^{prime}=0 \
2(x)^{prime}+2 y cdot y^{prime}+2left(x y cdot y^{prime}right)^{prime}=0
end{array}$$
Подставив вместо $y^{prime}$ найденное выше выражение, получаем:
$$begin{array}{l}
2 cdot 1+2 yleft(-frac{2 x+y^{2}}{2 x y}right)+2left[(x y)^{prime} cdot y^{prime}+x y cdotleft(y^{prime}right)^{prime}right]=0 \
2-frac{2 x+y^{2}}{x}+2left[left{(x)^{prime} cdot y+x cdot(y)^{prime}right} cdot y^{prime}+x y cdot y^{prime prime}right]=0 \
frac{2 x-2 x-y^{2}}{x}+2left[left{1 cdot y+x cdot y^{prime}right} cdot y^{prime}+x y cdot y^{prime prime}right]=0 \
-frac{y^{2}}{x}+2left[left(y-frac{2 x^{2}+x y^{2}}{2 x y}right) cdotleft(-frac{2 x+y^{2}}{2 x y}right)+x y cdot y^{prime prime}right]=0 \
-frac{y^{2}}{x}+2left[frac{2 x y^{2}-2 x^{2}-x y^{2}}{2 x y} cdotleft(-frac{2 x+y^{2}}{2 x y}right)+x y cdot y^{prime prime}right]=0
end{array}$$
После упрощения получаем:
$$frac{4 x^{2}-3 y^{4}}{2 x y^{2}}+2 x y cdot y^{prime prime}=0$$
Из полученного равенства выражаем вторую производную $$y^{prime prime}(x)$$:
$$y^{prime prime}(x)=frac{3 y^{4}-4 x^{2}}{4 x^{2} y^{3}}$$
Ответ. $y^{prime prime}(x)=frac{3 y^{4}-4 x^{2}}{4 x^{2} y^{3}}$
Читать дальше: производная функции, заданной параметрически.
Производная неявной функции
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение
Если функция вида $y=y(x)$ задана уравнением $F(x;y(x)) = 0$, то функция является неявно заданной.
Для нахождения неявной функции необходимо выполнить следующие действия:
- Продифференцировать обе части уравнения по х.
- Поскольку $у$ — дифференцируемая функция, для ее нахождения используется правило вычисления производной сложной функции.
- В правой части уравнения должно получится значение 0.
Примечание
Это значит перенести все слева направо и привести к уравнению вида $F(x;y(x)) = 0$.
- Решить полученное уравнение относительно $y'(x)$.
Пример 1
Найти производную неявной функции.
[2x^{3} y-4y=3x]
Решение.
- Приведем функцию к виду $F(x;y(x)) = 0$, для чего необходимо перенести все влево и приравнять к 0.
- Продифференцируем полученное равенство
- По свойству линейности:
- Первое слагаемое — сложная функция
- Решаем уравнение относительно $y’$
[2x^{3} y-4y-3x=0]
[left(2x^{3} y-4y-3xright){{‘} } =0’]
[2left(x^{3} yright){{‘} } -4y’-3x’=0′]
[2left(x^{3} yright){{‘} } -4y’-3x’=0′]
[2cdot 3x^{2} y’-4y’-3=0]
[y'(6x^{2} -4)=3]
[y’=frac{3}{6x^{2} -4} ]
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример 2
Найти вторую производную неявной функции.
[x^{3} -xy^{2} =2]
Решение.
- Приведем функцию к виду $F(x;y(x)) = 0$
- Продифференцируем полученное равенство
- По свойству линейности:
- Второе слагаемое — сложная функция
- Выразим $y’$
- Продифференцируем полученное выражение повторно
- Упростим
- Заменим $y’$ полученным выше выражением
- Приведем выражение к общему знаменателю и упростим
[x^{3} -xy^{2} -2=0]
[left(x^{3} -xy^{2} -2right){{‘} } =0’]
[x^{3} {{‘} } -left(xy^{2} right){{‘} } -2’=0’]
[3x^{2} -left(x’y^{2} +xy^{2} {{‘} } right)=0]
[3x^{2} -y^{2} -2xycdot y{{‘} } =0]
[y{{‘} } =frac{y^{2} -3x^{2} }{2xy} ]
[3left(x^{2} right){{‘} } -left(y^{2} right){{‘} } +2left(xycdot y{{‘} } right){{‘} } =0]
[6x-2ycdot y{{‘} } +2left(xy’cdot y{{‘} } +xycdot y{{‘} } {{‘} } right)=0]
[6x-2ycdot y{{‘} } +2left(left(x’y+xy’right)cdot y{{‘} } +xycdot y{{‘} } {{‘} } right)=0]
[6x-2ycdot y{{‘} } +2left(left(y+xy’right)cdot y{{‘} } +xycdot y{{‘} } {{‘} } right)=0]
[6x-2ycdot y{{‘} } +2left(yy{{‘} } +xy’y+xycdot y{{‘} } {{‘} } right)=0]
[6x-2ycdot frac{3x^{2} -y^{2} -2}{2xy} +2left(yfrac{3x^{2} -y^{2} -2}{2xy} +xyfrac{3x^{2} -y^{2} -2}{2xy} +xycdot y{{‘} } {{‘} } right)=0]
[6x-frac{3x^{2} -y^{2} -2}{x} +2left(frac{3x^{2} -y^{2} -2}{2x} +frac{3x^{2} -y^{2} -2}{2} +xycdot y{{‘} } {{‘} } right)=0]
[6x-frac{6x^{2} -2y^{2} -4}{2x} +2left(frac{3x^{2} -y^{2} -2}{2x} +frac{3x^{3} -xy^{2} -2x}{2x} +frac{2x^{2} ycdot y{{‘} } {{‘} } }{2x} right)=0]
[6x-frac{6x^{2} -2y^{2} -4}{2x} +left(frac{6x^{2} -2y^{2} -4+6x^{3} -2xy^{2} -4x+4x^{2} ycdot y{{‘} } {{‘} } }{2x} right)=0]
[frac{-6x^{2} -2y^{2} -4+6x^{2} -2y^{2} -4+6x^{3} -2xy^{2} -4x+4x^{2} ycdot y{{‘} } {{‘} } }{2x} =6x]
[-4y^{2} -8+6x^{3} -2xy^{2} -8x+4x^{2} ycdot y{{‘} } {{‘} } =6x]
[y{{‘} } {{‘} } =frac{14x+4y^{2} +8-6x^{3} +2xy^{2} }{4x^{2} y} ]
«Производная неявной функции» 👇
Пример 3
Найти вторую производную неявной функции.
[log _{4} left(frac{4x^{2} }{y} right)=4]
Решение.
- Приведем функцию к виду $F(x;y(x)) = 0$
- Продифференцируем полученное равенство
- Упростим
- Выразим $y’$
[log _{4} left(frac{4x^{2} }{y} right)-4=0]
[left(log _{4} left(frac{4x^{2} }{y} right)right){{‘} } -4’=0]
[frac{1}{frac{4x^{2} }{y} ln 4} cdot left(frac{4x^{2} }{y} right){{‘} } =0]
[frac{y}{4x^{2} ln 4} cdot frac{8xy-4x^{2} y’}{y^{2} } =0]
[frac{8xy-4x^{2} y’}{4yx^{2} ln 4} =0]
[frac{8xy}{4yx^{2} ln 4} -frac{4x^{2} y’}{4yx^{2} ln 4} =0]
[frac{4x^{2} y’}{4yx^{2} ln 4} =frac{8xy}{4yx^{2} ln 4} ]
[y’=frac{8xy4yx^{2} ln 4}{4x^{2} 4yx^{2} ln 4} ]
[y’=frac{2y}{x} ]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 11.12.2022
Производная функции, заданной неявно.
Производная параметрически заданной функции
В данной статье мы рассмотрим еще два типовых задания, которые часто встречаются в контрольных работах по высшей математике. Для того чтобы успешно освоить материал, необходимо уметь находить производные хотя бы на среднем уровне. Научиться находить производные практически с нуля можно на двух базовых уроках Как найти производную? Примеры решений и Производная сложной функции. Если с навыками дифференцирования всё в порядке, тогда поехали.
Производная функции, заданной неявно
Или короче – производная неявной функции. Что такое неявная функция? Давайте сначала вспомним само определение функции одной переменной:
Функция одной переменной 
– это правило, по которому каждому значению независимой переменной 
соответствует одно и только одно значение функции 
.
|
Переменная |
называется независимой переменной или |
|
аргументом. |
|
|
Переменная |
называется зависимой переменной или функцией. |
До сих пор мы рассматривали функции, заданные в явном виде. Что
это значит? Устроим разбор полётов на конкретных примерах.
Рассмотрим функцию 
Мы видим, что слева у нас одинокий «игрек», а справа – только «иксы». То есть, функция 
в явном виде выражена через независимую переменную 
.
Рассмотрим другую функцию: 
Здесь переменные 
и 
расположены «вперемешку». Причем
никакими способами невозможно выразить «игрек» только через «икс». Что это за способы? Перенос слагаемых из части в часть со сменой знака, вынесение за скобки, перекидывание множителей по правилу пропорции и др. Перепишите равенство
и попробуйте выразить «игрек» в явном виде: 
. Можно крутить-вертеть уравнение часами, но у вас этого не получится.
Разрешите познакомить: 
– пример неявной функции.
В курсе математического анализа доказано, что неявная функция существует (однако не всегда), у неё есть график (точно так же, как и у «нормальной» функции). У неявной функции точно так же существует первая производная, вторая производная и т.д. Как говорится, все права секс-меньшинств соблюдены.
И на этом уроке мы научимся находить производную от функции, заданной неявно. Это не так сложно! Все правила дифференцирования, таблица производных элементарных функций остаются в силе. Разница в одном своеобразном моменте, который мы рассмотрим прямо сейчас.
Да, и сообщу хорошую новость – рассмотренные ниже задания выполняются по довольно жесткому и чёткому алгоритму без камня
перед тремя дорожками. Пример 1
Найти производную от функции, заданной неявно
1)На первом этапе навешиваем штрихи на обе части:
2)Используем правила линейности производной (первые два правила урока Как найти производную? Примеры решений):
3)Непосредственное дифференцирование.
Как дифференцировать 
и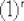 
совершенно понятно. Что делать там, где под штрихами есть «игреки»?
– просто до безобразия, производная от функции равна её производной: 
.
Как дифференцировать 
Здесь у нас сложная функция. Почему? Вроде бы под синусом всего
одна буква «игрек». Но, дело в том, что всего одна буква «игрек» –
САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ (см. определение в начале урока). Таким образом, синус – внешняя функция, 
– внутренняя функция. Используем правило дифференцирования сложной функции 
:
Произведение дифференцируем по обычному правилу 
:
Обратите внимание, что 
– тоже сложная функция, любой
«игрек с наворотами» – сложная функция:
Само оформление решения должно выглядеть примерно так:
Если есть скобки, то раскрываем их:
4)В левой части собираем слагаемые, в которых есть «игрек» со штрихом. В правую часть – переносим всё остальное:
5)В левой части выносим производную 
за скобки:
6)И по правилу пропорции сбрасываем эти скобки в знаменатель правой части:
Производная найдена. Готово.
Интересно отметить, что в неявном виде можно переписать любую функцию. Например, функцию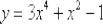 
можно переписать так: 
. И дифференцировать её по только что рассмотренному алгоритму. На самом деле фразы «функция, заданная в неявном виде» и «неявная функция» отличаются одним смысловым нюансом. Фраза «функция, заданная в неявном виде» более общая и корректная, 
– эта функция задана в неявном виде, но здесь можно выразить «игрек» и представить функцию в явном виде.
Под фразой «неявная функция» понимают «классическую» неявную функцию, когда «игрек» выразить нельзя.
Второй способ решения
Внимание! Со вторым способом можно ознакомиться только в том случае, если Вы умеете уверенно находить частные производные. Начинающие изучать математический анализ и чайники, пожалуйста, не читайте и пропустите этот пункт, иначе в голове будет полная каша.
Найдем производную неявной функции 
вторым способом.
Переносим все слагаемые в левую часть:
И рассматриваем функцию двух переменных:
Тогда нашу производную можно найти по формуле 
Найдем частные производные:
Таким образом:
Второй способ решения позволяет выполнить проверку. Но оформлять им чистовой вариант задания нежелательно, поскольку частные производные осваивают позже, и студент, изучающий тему «Производная функции одной переменной», знать частные
производные как бы еще не должен. Рассмотрим еще несколько примеров. Пример 2
Найти производную от функции, заданной неявно
Навешиваем штрихи на обе части:
Используем правила линейности:
Находим производные:
Раскрываем все скобки:
Переносим все слагаемые с 
в левую часть, остальные – в правую часть:
В левой части выносим 
за скобку:
Окончательный ответ:
Пример 3
Найти производную от функции, заданной неявно 
Полное решение и образец оформления в конце урока.
Не редкость, когда после дифференцирования возникают дроби. В таких случаях от дробей нужно избавляться. Рассмотрим еще два примера.
Пример 4
Найти производную от функции, заданной неявно 
Заключаем обе части под штрихи и используем правило линейности:
Дифференцируем, используя правило дифференцирования сложной функции 
и правило дифференцирования частного
:
Раскрываем скобки:
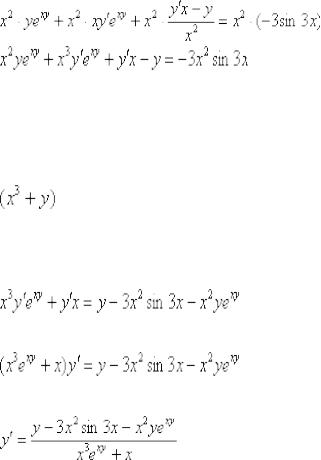
Теперь нам нужно избавиться от дроби. Это можно сделать и позже, но рациональнее сделать сразу же. В знаменателе дроби находится 
. Умножаем каждое слагаемое каждой части на 
. Если подробно, то выглядеть это будет так:
Иногда после дифференцирования появляется 2-3 дроби. Если бы у нас была еще одна дробь, например, 
, то операцию нужно было бы повторить – умножить каждое слагаемое каждой части на
Далее алгоритм работает стандартно, после того, как все скобки раскрыты, все дроби устранены, слагаемые, где есть «игрек штрих» собираем в левой части, а в правую часть переносим всё остальное:
В левой части выносим 
за скобку:
Окончательный ответ:
Пример 5
Найти производную от функции, заданной неявно 
Это пример для самостоятельного решения. Единственное, в нём, перед тем как избавиться от дроби, предварительно нужно будет
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
