Как найти производную обобщенной функции

1. Введение.

   Начать изучение
   

2. Пространство основных функций.

   Начать изучение
   

3. Пространство обобщенных функций.

   Начать изучение
   

4. Сходимость в пространстве обобщенных функций.

   Начать изучение
   

5. Умножение обобщенной функции на бесконечно дифференцируемую функцию.

   Начать изучение
   

6. Производная обобщенной функции.

   Начать изучение
   

7. Операция сдвига аргумента для обобщенных функций.

   Начать изучение
   

Введение.

В физике постоянно пользуются такими идеализированными понятиями, как материальные точки, точечные заряды, магнитные диполи и т. д. На самом деле сосредоточенных в точке масс или зарядов не существует. Когда говорят о материальной точке массы 1, то это идеализированная модель шара достаточно малого радиуса (varepsilon) и массы 1. Если в пространстве нет других масс, то плотность материи в пространстве будет распределена по следующему закону:
$$
delta_{varepsilon}(x) = left{
begin{array}{ll}
displaystylefrac{1}{4pivarepsilon^{3}/3}, & |x| leq varepsilon,\
0, & |x| > varepsilon,
end{array} right.label{ref1}
$$
где (x in boldsymbol{R}^{3}). Заметим, что
$$
intlimits_{boldsymbol{R}^{3}} delta_{varepsilon}(x) dx = 1.label{ref2}
$$
Если устремить (varepsilon) к +0, то из eqref{ref1} получим, что предельная плотность (delta(x)) имеет вид
$$
delta(x) = left{
begin{array}{ll}
+infty, & x = 0,\
0, & x neq 0.
end{array} right.label{ref3}
$$

Зная плотность eqref{ref3}, нельзя по ней восстановить массу при помощи интегрирования, так как функция eqref{ref3} не интегрируема ни по Риману, ни в несобственном смысле.

Чтобы обойти это затруднение, рассмотрим вместо поточечного предела функций (delta_{varepsilon}(x)) при (varepsilon rightarrow +0) так называемый “слабый предел”.

Будем (delta_{varepsilon}(x)) рассматривать как линейный функционал над линейным пространством непрерывных в (boldsymbol{R}^{3}) функций, ставящий в соответствие каждой непрерывной в (boldsymbol{R}^{3}) функции (varphi(x)) число
$$
(delta_{varepsilon}, varphi) = intlimits_{boldsymbol{R}^{3}} delta_{varepsilon}(x) varphi(x) dx = intlimits_{|x| leq varepsilon} frac{varphi(x) dx}{4pivarepsilon^{3}/3}.nonumber
$$
Применяя теорему о среднем, получаем, что
$$
lim_{varepsilon rightarrow +0} (delta_{varepsilon}, varphi) = lim_{varepsilon rightarrow +0} varphi(tilde{x}_{varepsilon}) = varphi(0) = (delta, varphi),label{ref4}
$$
где (delta) есть линейный функционал, ставящий в соответствие непрерывной функции число (varphi(0)).

Если для любой непрерывной функции выполнено равенство eqref{ref4}, то говорят, что линейный функционал (delta) есть слабый предел линейных функционалов (delta_{varepsilon}) при (varepsilon rightarrow +0).

При таком подходе по плотности легко восстановить массу точки. Она равна
$$
lim_{varepsilon rightarrow +0} intlimits_{boldsymbol{R}^{3}} delta_{varepsilon}(x) dx = lim_{varepsilon rightarrow +0} (delta_{varepsilon}, 1) = (delta, 1) = 1.nonumber
$$
Функционал eqref{ref4} называют (delta)-функцией Дирака.

Перейдем теперь к более строгому и систематическому изложению так называемых распределений или обобщенных функций.

---

Пространство основных функций.

Пространство непрерывных функций слишком широко для того, чтобы, используя его, можно было построить содержательную теорию обобщенных функций. Удобно рассматривать некоторые специальные подпространства. Для простоты ограничимся функциями одной переменной.

Будем рассматривать комплекснозначные функции, определенные на (boldsymbol{R}). Носителем функции (varphi(x)) назовем замыкание множества тех (x), где (varphi(x) neq 0). Если носитель функции есть ограниченное множество, то функция (varphi(x)) называется финитной (она обращается в нуль вне некоторого отрезка). Пусть (mathcal{D}) есть множество финитных и бесконечно дифференцируемых на (boldsymbol{R}) функций. Очевидно, что (mathcal{D}) есть линейное пространство. Введем в этом пространстве сходимость.

---

Пространство обобщенных функций.

Множество всех линейных непрерывных функционалов будем обозначать через (mathcal{D’}). Множество (mathcal{D’}) будет линейным пространством, если естественным образом определить операцию сложения непрерывных линейных функционалов и операцию умножения непрерывных линейных функционалов на комплексные числа. Если (alpha, beta in boldsymbol{C}), (f_{1}, f_{2} in mathcal{D’}), то по определению (alpha f_{1} + beta f_{2}) есть непрерывный линейный функционал, действующий на основные функции (varphi in mathcal{D}) по следующему правилу:
$$
(alpha f_{1} + beta f_{2}, varphi) = alpha(f_{1}, varphi) + beta(f_{2}, varphi).label{ref6}
$$

Нетрудно показать, что определение корректно, то есть что функционал (alpha f_{1} + beta f_{2}), определяемый равенством eqref{ref6}, действительно линеен и непрерывен.

В (mathcal{D’}) выделяют класс регулярных функционалов. Если функция (f(x)) абсолютно интегрируема на любом конечном отрезке (локально интегрируема), то она порождает функционал
$$
(f, varphi) = intlimits_{-infty}^{+infty} f(x)varphi(x) dx.label{ref7}
$$

Линейные непрерывные функционалы, не являющиеся регулярными, будем называть сингулярными.

Пространство (mathcal{D’}) называют пространством обобщенных функций, а элементы этого пространства — обобщенными функциями.

---

Сходимость в пространстве обобщенных функций.

Вместо последовательности функционалов (f_{n} in mathcal{D’}) иногда рассматривают семейство функционалов ({f_{varepsilon}}), зависящих от параметра (varepsilon). В этом случае запись
$$
f_{varepsilon} xrightarrow{mathcal{D’}} f mbox{при} varepsilon rightarrow +0
$$
означает, что (displaystylelim_{varepsilon rightarrow +0}(f_{varepsilon}, varphi) = (f, varphi)) для любой функции (varphi in mathcal{D}). В частности, запись
$$
f_{varepsilon} rightarrow delta mbox{при} varepsilon rightarrow +0nonumber
$$
означает, что
$$
lim_{varepsilon rightarrow +0}(f_{varepsilon}, varphi) = (delta, varphi) = varphi(0) mbox{для любой} varphi in mathcal{D}.label{ref13}
$$

---

Умножение обобщенной функции на бесконечно дифференцируемую функцию.

Введем операцию умножения обобщенной функции на бесконечно дифференцируемую функцию (psi(x)).

Определение корректно, поскольку (psivarphi in mathcal{D}).

По определению обобщенная функция (f) равна нулю на интервале ((a, b)), если для любой функции (varphi in mathcal{D}), носитель которой лежит в ((a, b)), выполнено равенство ((f, varphi) = 0). Так, (delta)-функция равна нулю на любом интервале ((a, b)), не содержащем точку (x = 0). Две обобщенные функции (f_{1}) и (f_{2}) называются равными на интервале ((a, b)), если (f_{1}-f_{2} = 0) на ((a, b)). В частности, (f_{1}) и (f_{2}) равны на (boldsymbol{R}), если их значения совпадают на любой основной функции (varphi in mathcal{D}).

---

Производная обобщенной функции.

Пусть (f(x)) — непрерывно дифференцируемая на (boldsymbol{R}) функция; тогда функция (f'(x)) порождает регулярный функционал
$$
(f’, varphi) = intlimits_{-infty}^{+infty} f'(x)varphi(x) dx, varphi in mathcal{D}.
$$
Интегрируя по частям, получаем, пользуясь тем, что (varphi = 0) вне некоторого отрезка ([-A, A]), следующее равенство:
$$
(f’, varphi) = intlimits_{-infty}^{+infty} f'(x)varphi(x) dx =\= left.f(x)varphi(x)right|_{-infty}^{+infty}-intlimits_{-infty}^{+infty} f(x)varphi'(x) dx =-intlimits_{-infty}^{+infty} f(x)varphi'(x) dx.nonumber
$$
Итак, в рассматриваемом случае
$$
(f’, varphi) = -(f, varphi’), varphi in mathcal{D}.label{ref19}
$$
Равенство eqref{ref19} лежит в основе определения производной обобщенной функции.

Производные высших порядков определяются для обобщенных функций по индукции:
$$
f^{(k)} = (f^{(k-1)})’, k = 2, 3, ldotsnonumber
$$

Легко проверить, что для любой функции (varphi in mathcal{D}) выполнено равенство
$$
(f^{(k)}, varphi) = (-1)^{k}(f, varphi^{(k)}).nonumber
$$

Таким образом, обобщенные функции имеют производные всех порядков.

---

Операция сдвига аргумента для обобщенных функций.

Пусть (f(x)) есть локально интегрируемая на (boldsymbol{R}) функция. Для нее определена операция сдвига аргумента (T_{h}), а именно (T_{h}f(x) = f(x-h)). Если (varphi in mathcal{D}) то
$$
(T_{h}f, varphi) = intlimits_{-infty}^{+infty} f(x-h)varphi(x) dx = intlimits_{-infty}^{+infty} f(x)varphi(x + h) dx = (f, T_{-h}varphi).label{ref21}
$$

Хотя значение обобщенной функции в точке не определено, но для нее можно формально ввести операцию сдвига аргумента по аналогии с формулой eqref{ref21}:
$$
(T_{h}f, varphi) = (f, T_{-h}varphi), varphi in mathcal{D}.label{ref22}
$$

Если (delta(x)) есть (delta)-функция, то (T_{h}delta) обычно обозначают через (delta(x-h)). Тогда для любой функции (varphi in mathcal{D})
$$
(delta(x-h), varphi(x)) = (delta(x), varphi(x + h)) = varphi(h).nonumber
$$

Лекция 6

Дифференцирование
обобщённой функции

В отличие от обычных
функций, которые не всегда имеют
производные (в обычном смысле), обобщённые
функции имеют производные всех порядков,
которые являются также обобщенными
функциями. Если
функция

непрерывна и обладает непрерывной
производной, то можно построить функционал

(26)

Интегрируя по
частям и учитывая, что функция

обращается в нуль
вне некоторого интервала [a,
b],
получим

(27)

Это равенство и
кладётся в основу общего определения
производной
обобщённой функции.

Пусть f
– произвольный
линейный непрерывный функционал на
основном пространстве K.
Тогда,
функционал g,
заданный формулой

(28)

называется
производной от функционала f
и обозначается

или

(29)

Учитывая (26) и (27)
имеем

(30)

Легко убедится,
что функционал g
также является линейным, непрерывным
функционалом на пространстве K.

Легко проверить,
что выполняются обычные правила
дифференцирования, а именно:

– Производная суммы
равна сумме производных

(
f₁
+ f₂
) ^/
= f₁^/
+ f₂^/
(31)

– Постоянный
множитель выносится за знак производной

(
a
f₁)
^/
= a
f ^/,
a
– const (32)

– Произведение
бесконечно дифференцируемой функции
a(x)
на обобщённую
функцию f
:

(a(x)
f
) ^/=
a
^/(x)
f
+ a
f
^/
(33)

Действительно,
мы имеем:

Для нескольких
независимых переменных:

Определим для
каждой обобщённой функции f
её частные
производные по каждому из независимых
переменных

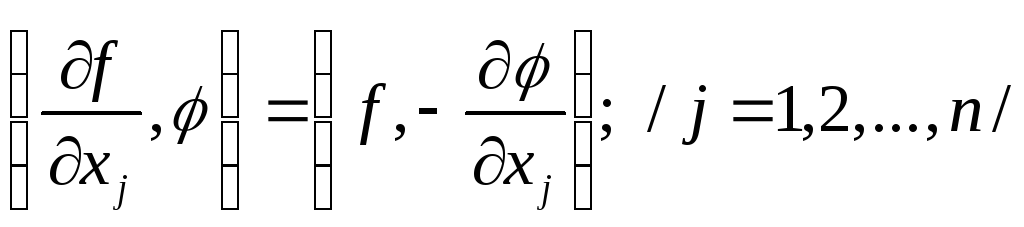
(34)

Поскольку, результат
дифференцирования обобщённой функции
есть снова обобщённая функция, можно
определить производную любого порядка

и т.д.

Т.о. все обобщённые
функции бесконечно дифференцируемы.

Рассмотрим примеры
для случая
функции одной независимой переменной.

Пример 1.
Рассмотрим функцию Хевисайда

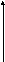
Отвечающий ей
функционал обозначим также
.
Согласно формуле (28) функционал

действует на основную функцию

так:

(35)

/ по определению
“хорошей” или “основной” функции /

Таким образом, в
силу определения дельта функции (5)

(36)

Следующая производная

и т.д.

Для смещённой
дельта функции из (36) получим

(37)

П
ример
2
Пусть f
(x)
– кусочно-непрерывная функция с
кусочно-непрерывной производной f
^/(x),
в точках

разрывы I
рода со «скачками» h₁,
h₂,
… ,

Производная f
^/(x)
определена всюду кроме конечного числа
точек. Найдём производную от функционала
f
, соответствующего функции f(x).

Введём функцию:

(38)

Очевидно, что она
всюду непрерывна и имеет производную
f
^/(x)
всюду, кроме конечного числа точек. Как
показано ранее (см.(28)), функционал f
^/
соответствует функции f
^/(x),
если функции f(x)
и
f
^/(x)
непрерывны. Тогда, из равенства (38),
дифференцируя его, получим

Откуда

(39)

Т.е. если f(x)
кусочно-непрерывная функция с
кусочно-непрерывной производной, то
при дифференцировании, каждая точка
разрыва I
рода функции f(x)
со «скачком» h_k
добавляет
в выражение производной слагаемое
.

Разрывы
обобщённых функций ведут к дельта
функциям в производных.

Пример 3
Найти
производную обобщённой функции
.

Здесь мы и встречаемся
с необходимостью регуляризации
расходящегося интеграла.

Вставка:
Регуляризация расходящегося интеграла.

Пусть f(x)
– функция, локально интегрируемая
всюду, кроме т. x₀,
в которой имеется неинтегрируемая
особенность (например,

на оси). Тогда, интеграл

(40),

где

– основная функция, вообще говоря,
расходится. Но
он сходится,
если

равна нулю в окрестности т. x₀.
Если можно доопределить, возникающий
при этом функционал, который на основные
функции действует по формуле (40), то
такой функционал f
называется
регуляризацией расходящегося интеграла
(40) (или
регуляризацией функции f(x)).

Так, для

, можно положить:

с любыми a
> 0 и b
> 0.

Продолжение
Примера 3

Запишем

Как известно,
полученный предел называется главным
значением
по Коши оси
.
Мы его будем обозначать
.
Соответствующую обобщённую функцию мы
будем обозначать 1/x,
тогда
.
Функционал 1/x
не регулярный, но совпадает с функцией
1/x
всюду, кроме x
= 0.

Пример 4.
Найдём производную от логарифма
комплексной функции (это также обобщённая
функция):
;
определяемой равенством

если
,
где
,
а
,
то

Тогда

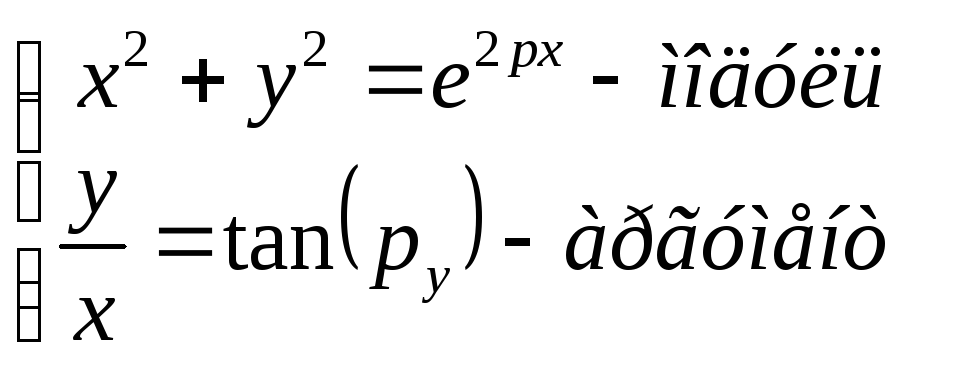
Пояснение1:

Можно записать

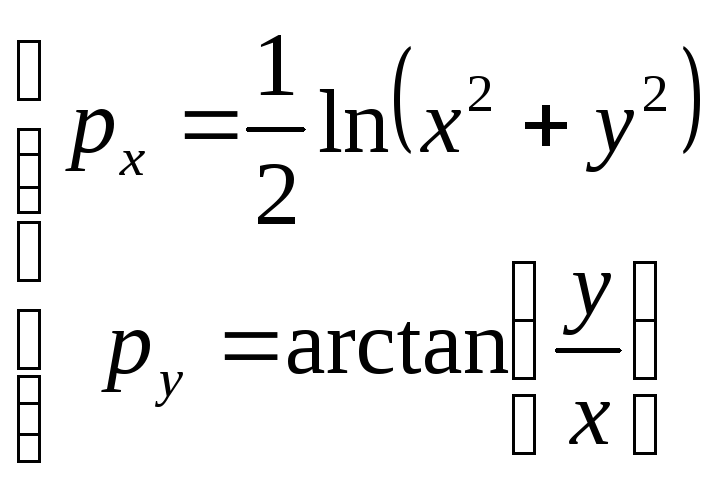
Модуль комплексного
числа

Переходим к пределу,
при

п

ричём

;

–
по модулю всегда ограничено и стремится
к пределу при

Т.е.

имеет скачок величиной
.

Перепишем:

при

переходя к пределу, видим, что

.

Т.к.

и учитывая, что
,
получим
.
Тогда
,

поэтому

Т.е. ещё раз
заметим, что надо внимательно следить
за разрывами. Они ведут к дельта функциям.

Пояснение 2:

Исходя из:

и при

Значит:

или

Пояснение 3.

укручается и
становится ступенькой. В пределе – это
функция Хевисайда, только перевёрнутая.
При x
замена на (-x)
мы получим Хевисайд:

.

Пример 5.
Для случая
нескольких независимых переменных.

Для непрерывных
функций f(x)
с
кусочно-непрерывными частными
производными, дифференцирование
соответствующих регулярных функционалов,
приводит снова к регулярным функционалам.

Найдем в трехмерном
пространстве результат применения
оператора Лапласа

к регулярному функционалу, определенному
функцией
,
где

Функция

гармоническая в любой области, не
содержащей начала координат, так, что
выражение
,
при
,
обращается в нуль (в обычном смысле).

Покажем это. Запишем
оператор Лапласа

тогда

;

проделав аналогично
для других переменных, имеем

Итак,

во всех точках, кроме
.
В окрестности этой точки надо действовать
аккуратно с помощью функционала.
Рассматривая оператор Лапласа в
пространстве обобщенных функций, находим

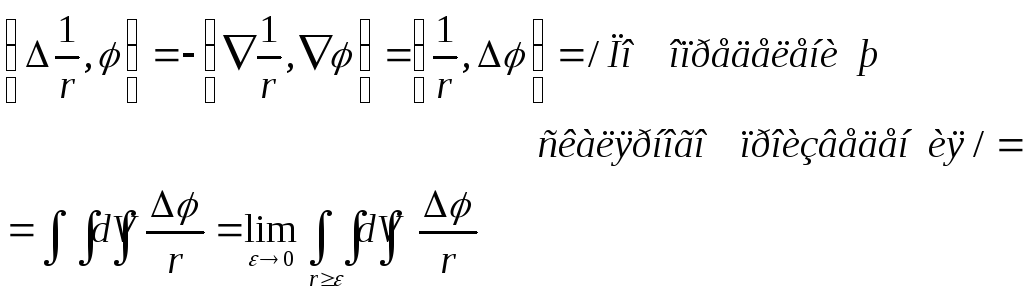
Теперь, по формуле
Грина для шарового слоя (

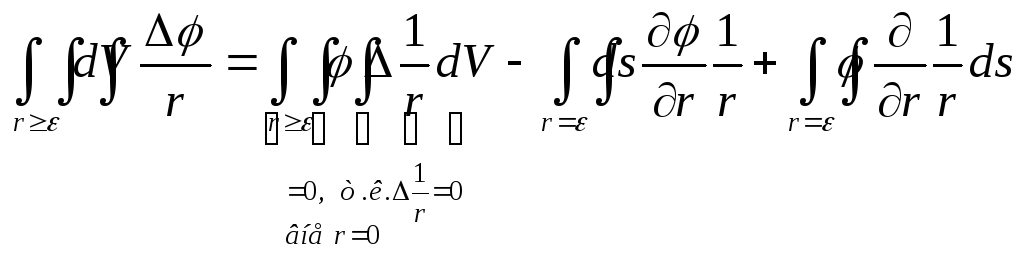
dS
– есть элемент сферы

Пояснение:
формула
Грина в общем случае

Теперь простые
оценки

/

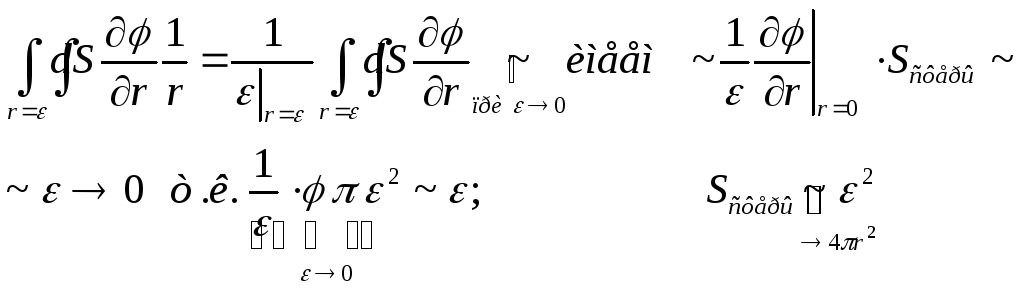
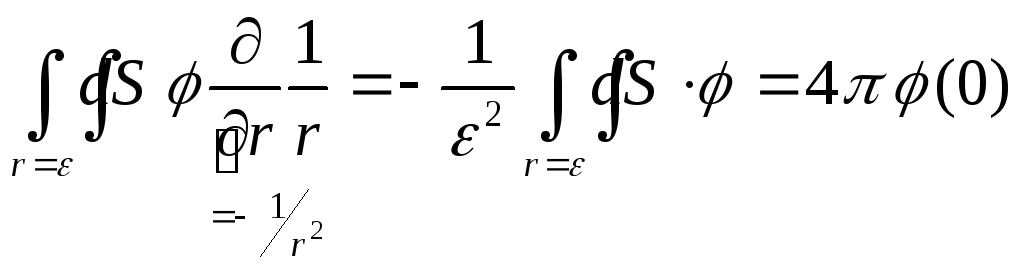
И тогда

т.е. через функционалы

Но отсюда вытекает,
что

т.е. вторая
производная в трехмерном пространстве
равна дельта-функии.

Аналогично, в
двумерном пространстве

Пояснение :

где a
настолько велико, что вне шара

функция

тождественно равна нулю.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Продолжаем разговор об обобщенных функциях. В первой части обсудили идею их введения. Давайте кратко вспомним, в чем там дело.

Дело в следующем. Часто в одной точке функцию не определить как следует, и нужды нет. Пример — скорость в виде |t|. Ускорение в нуле не определено (хотя можно что-то придумать), но оно и не нужно, строго говоря. Нам достаточно способа исследовать функцию в окрестности точки. Для этого надо умножить ее на единицу в окрестности точки и на нуль вне ее, и взять интеграл.

А тогда нам и не нужно определение функции как правила, задающего точкам (пусть не всем) значения в них. Достаточно, если мы можем вычислять такие “интегралы” — выбрать пробную функцию и по ней указать, что получится.

Правда, чтобы увязать концы с концами, пробные функции полагаем гладкими, а не кусочно-постоянными, но это техника.

Собственно, как определить мгновенную скорость в точке по данным наблюдений? Брать путь, пройденный за малое время, ну и смотреть, что получится. А путь — это скорость, умноженная на время. Ускорение тоже можно оценить, но умножать надо уже не на интервал времени, а на линейную функцию — но это техника.

Итак, обобщенная функция — это линейное правило, сопоставляющее пробной функции φ (гладкой и равной нулю вне некоторого отрезка) число. Для обычных функций f это интеграл ∫f(x)φ(x)dx по всей числовой прямой.

Как для обобщенной функции f определить производную f’?

Это такое правило: сопоставим функции φ то число, которое сопоставляет сама обобщенная функция f функции -φ’.

Для обычных дифференцируемых функций это совпадает с обычной производной, потому что интегрирование по частям:

∫f'(x)φ(x)dx = -∫f(x)φ'(x)dx,

интеграл по всей прямой, а терминальные слагаемые исчезают — ведь φ(x) равна нудю вне некоторого отрезка!

Аналогично задаются старшие производные. Например, вторая производная f” — это правило, которое сопоставляет функции φ то число, которое сама f сопоставляет функции φ”.

Итак, производные у обобщенной функции есть все и всегда. Причем обычные функции, которые являются (не все) обобщенными, тоже обладают всеми производными в указанном смысле. Что приятно.

Например, функция “модуль”, f(x)=|x|, непрерывна, но не дифференцируема в нуле. В нуле производной в обычном смысле нет. В других точках она есть, конечно. Обобщенная производная есть — это функция знака, равная -1 для отрицательных и +1 для положительных значений. Разумеется, она совпадает с обычной производной там, где та определена. Значения в нуле нет, но оно для обобщенных функций роли не играет. Вторая производная модуля, она же первая для функции знака, это удвоенная дельта. Легко проверить, и это интересно сделать самостоятельно.

У дельты тоже есть производная, это диполь. И так далее.

Если импульс ударный, это сила, которая является дельтой по времени: до момента силы нет, после тоже, но за нулевое время передан ненулевой импульс. Пусть будет удвоенная дельта. Ускорение две дельты, тогда скорость — функция знака, “до” шарик катился туда, “после” — обратно. Путь шарика — функция модуля, он непрерывен: сначала расстояние до стенки убывает, потом — растет.

Есть теорема, что любая обобщенная функция есть производная некоторого порядка некоторой непрерывной (с оговорками).

Теперь ряды. Про ряды Фурье будет заметка, а пока скажу лишь, что ряд Фурье — это разложение функции на некотором отрезке по синусам sin(nx) и косинусам cos(nx). Как на рисунке. При этом коэффициенты получаются интегралами от соответствующего синуса или косинуса и самой функции.

Но синусы и косинусы можно считать пробными (за пределами отрезка мы их гладко загоним в нуль — это техника), и тогда коэффициенты Фурье легко получаются для обобщенных функций тоже. Для них можно записать разложение в ряд, и ряд будет сходиться как обобщенный, и к той функции, что его породила.

Например, дельта, которая описана правилом φ(0), дает для всех синусов нулевой коэффициент, а для косинусов — один и тот же для всех.

На рисунке — несколько сумм, дающих представление о сходимости к дельте.

Как известно, коэффициенты Фурье для обычной функции стремятся к нулю, и чем быстрее, тем функция более гладкая. У дельты, как видите, они к нулю не стремятся. У ее производной — уже растут как n. То есть дельта “хуже” любой нормальной функции, а диполь хуже дельты. При этом коэффициенты Фурье обобщенных функций не могут расти быстрее степени n. Извините. Это объясняет стрелу времени в диффузии.

Кто не хочет переходить по ссылке: Краевую задачу для уравнения диффузии можно решить (с оговорками) через ряды Фурье для любых начальных данных, хоть даже и обобщенной функции; а вот в обратном времени — нет, “начальное” распределение должно быть особенным — по сути, тем, на чем остановилась диффузия в прямом времени.

Про применение обобщенных функций, на простых примерах — будет третья часть.

До встречи.

Путеводитель по каналу

1

13.02.2021.

Лекция
№3.

Часть
I.

Дифференцирование
обобщенных функций.

Обобщённые функции обладают рядом удобных свойств. Например,
при надлежащем обобщении понятия производной, любая обобщённая функция
оказывается бесконечно дифференцируемой, сходящиеся ряды из обобщённых функций
можно почленно дифференцировать бесконечное число раз.

Пусть f C ^pRⁿ.
Тогда при всех ,  

 p,
и D
справедлива формула интегрирования по частям

D
f ,^ 
 
D f^

x
x dx   1
^ 
f  x D
^x
dx    
1 ^  f ,D^.

Это равенство мы и примем за определение
(обобщённой) производной D^
f обобщённой функции f D^:

                                                      D^ f ,_ 1^f
,D^_,
D.
                (13)

Проверим, что D^ f D^. Действительно,
поскольку f D^, то функционал D^ f ,
определяемый правой частью равенства (13), линейный:

D^ f ,_ 1^f
,D^(1)^( f ,D^D^)

 1^f
,D^_ 1^f
,D^__D^ f ,__D^ f ,_
и непрерывный:

D^ f ,_k 1^f
,D^_k0,   k ,

так
как если _k 0,   k  в D ,
то D^_k  0,   k   в D .
В частности, при f 
равенство (13) принимает вид D^,_  1^D^_0,
D.

Обозначим D^ f x
классическую производную (там, где она существует). Из определения обобщённой
производной вытекает, что если обобщённая функция f C ^pG,
то

D^f D^f x
,  xG,  
 p.

Справедливы следующие
свойства операции дифференцирования обобщённых функций.

a)                      
Операция дифференцирования D^ линейна и
непрерывна из D^ в D^:

                                                  D^f
 gD^ f  D^g,      f
,gD^;

D^ f_k  0,  k   в D^, если f_k
 0,
k   в D^.

Докажем непрерывность.
По определению производной при всех D имеем

D^f_k ,_  1^f_k
,D^_0, k ,

что и означает, что D^ f_k  0, k   в D^. Линейность
доказывается аналогично.

В частности, если _x
– «шапочка», то

D^_x D^x,
 0 в D^.

b)                     
Любая обобщённая функция бесконечно дифференцируема.

Действительно,
если f D^{, то} ^x^f_i D^; в свою очередь
^
_^xf_i
^_D^ _x
_{j } и т.д.

c)                      
Результат дифференцирования не зависит от порядка
дифференцирования:

D^ f  D^D^ f  D^D^ f ,

так как

D
f , 1f
,D 1f
,DD

 1^D^ f ,D^_D^D^ f ,_
и

Df,1f,D1f,DD

1^D^f,D^_D^D^f ,_
для всех D.

d)                     
Если f D^ и aC^( Rⁿ ),
то справедлива формула Лейбница для дифференцирования произведения af .
Например:

(af
) a
f  f  a  .

                                                                               x₁          x₁                 x₁

Действительно, если  – любая
основная функция, то

 (af
)                                  a  a          a

  x₁ ,  af ,x₁    f ,a x₁    f , x₁      x₁    f , x₁   

 f ,^x^a₁^^^x^f₁ ,a^^^x^a₁ f ,^^a ^x^f₁ ,^^^x^a₁ f ,^

      f      a        


a x1  x1 f , .

e)                      
Если обобщённая функция f 0, xG, то и D^ f  0,

supp
D^ f

supp f .

В самом деле, если DG,
то D^DG,
а потому

D^f ,_  1^f
,D^_0, DG,

что и означает D^ f  0, xG.



f)                       
Если ряд u_k x
 Sx,
составленный из локально интегрируемых

k1

функций u_k ( x ),
сходится равномерно на каждом компакте, то его можно почленно дифференцировать
любое число раз, и полученные ряды будут сходиться в D^.

Действительно, поскольку при любом R  0

_px R

                                                       S
_p x u_k
x
^_
Sx, p
,

k1

то S _p  S,   p  в D^. Но тогда, по
свойству непрерывности операции дифференцирования,

p

                                                            D^S _p  D^u_k  D^S,       p
  в D^,

k1

что и требовалось доказать.

Отсюда, в частности, вытекает: если

                                                                      c_k
 A
k ^m 
b,                                                 (14)



то тригонометрический ряд c_ke^ikx
сходится в D^R.

k

Действительно, в силу (14) ряд

                                                                            c0 xm2 ^
         ck         eikx

                                                                       m
 2! kikm2

сходится равномерно в R. Следовательно, ряд,
представляющий его производ-



ную порядка m 
2, сходится в D^R
и совпадает с рядом c_ke^ikx .

k

Часть
II.

Примеры
производных различных обобщённых функций.

Рассмотрим примеры, связанные с
дифференцированием обобщённых функций в D^R.

1.            
Пусть  – функция Хевисайда:

_x_
_1,
x  0,
_0,
x  0.

Найдём производную -функции по определению:



, ,  xdx
 x^₀^ 0 ,.

0

Значит, xx.

2.            
Пусть функция f x
такова, что f C¹x
 x₀
и f C¹x
 x₀.
Покажем, что

                                 f  
f x h_f x₀
x
 x₀
,
                         (15)

где h_f x₀

– скачок функции f x
в точке x₀ :

h_f x₀
 f x₀
 0 f x₀
 0.
Действительно, если DR,
то

                                                                                                ^x0                                                          


f , 
f ,   f xxdx
  
f xxdx
 
f xxdx


                                                                                                                                       x₀

      u  f x           du
 f
x^dx_x0₀                        ^x₀

  f
xx^
 
f xxdx
 dv
xdx
v x_

                                ^                                                                                                                                          

 f xx_x0_0  
f xxdx
 
f xxdx
 f
x₀
 0x₀


                                                 x₀                                                           


f x₀  0x₀
 
f x₀  0 f x₀
 0x₀
 
f xxdx



h_f
x₀
x
 x₀
,x 
f x,x

 h_f
x₀
x
 x₀
 
f x,x.

3.             
Пусть функция f x
имеет не более чем счётное множество изолированных точек разрыва первого рода x_k
,
а её классическая производная  f x
– кусочно-непрерывная функция на R. Тогда формула (15)
естественно обобщается:

                        f  
f x h_f
x_k
x
 x_k
.
                          (16)

k

Применим формулу (16) к
нахождению обобщённой производной периодической функции

1              
x

                                    f₀
x         ,  x0;2; f₀
x
 2 f₀ x:

2              
2

                                                                                                                         1       

f₀x
f₀x ^h_f
2kx
 2k  _2
 _k^x
 2k.
                                                                                                                 (17)

_k_Z

Мы видим, таким образом,
что обобщённые и классические производные, вообще говоря, не совпадают!

4.             
Докажем формулу

21k
ikx        k
x
 2k.
        (18) e 


Для этого разложим 2-периодическую
функцию

x                          2
x  x

                                       ^
f₀ tdt
 ₂  _4, x0;2, f
x
 2 f x

₀

в равномерно сходящийся ряд Фурье:

1

e

                        0^x f0 tdt
6
 2
k^^
k12           ikx
.

k0

По свойству f) операции дифференцирования этот ряд можно
почленно дифференцировать в D^
любое число раз. Дифференцируя его дважды и учитывая

(17), получим

f₀21 kx2k₂1_
k^e_ikx ,

k0

1 
ikx 
x
 2k.
откуда имеем e
 

                                         2k               k

Отметим, что левая часть равенства (18) есть ряд Фурье 2
– периодиче-



ской обобщённой функции x
 2k.

k

5. Покажем, что общее решение уравнения
xmu  0 в DR задаётся формулой	(19)
v1 u  ckkx,	(20)

k0

где c_k – произвольные постоянные.

Поскольку при всех D
и k 0,1^,K, m  1

xmk,k,xm 1k ,xmk 1k xmk 0 ,

                                                                                                                x_0

то

x^m_^kx 0, k  0, 1,K, m  1, и,
следовательно, обобщённая функция (20) удовлетворяет уравнению (19).

Докажем, что формула (20) даёт общее решение в D^R
этого уравнения. Пусть x
– основная функция, равная 1 в окрестности точки x  0 (такая
функция существует по лемме 1). Тогда любая функция  из D
представляется в виде

                        xxm1kk!0
xk  xmx,
            (21)

k0

где

                                                                   1
                  m1

x xm xxk_0kk!0
xk  .

Функция D,
так как она финитна и бесконечно дифференцируема; бесконечная
дифференцируемость её в точке x 
0 следует из формулы Тейлора

            x N kk!0
km O
x N1 ,

                                                                    x      

km

справедливой в некоторой окрестности (где 1) точки
0 при всех N 
m .

Следовательно,
если uD^ – решение
уравнения (19), то, в силу (21),

u, _u,x^mk^01k_k_!0
xk _
 u,xmx m1kk!0u,xxk 

                                                                                                 k0

                                  m1                                           m1                               m1   k,, где

 xmu,  1k ckk0 ck k,  ck

                                  k0                                            k0                                k0                    

^{ 1}^k
u,
c_k  x^k
.
И так как для любой функции D выполнено равенство k!

u, ^_
^m^1c_k^k,_^_,
то общее решение уравнения (19) в классе обобщённых

                     k0                     

m1

функций – это функция u  c_k^k
.

k0

Заметим, что в классе локально
интегрируемых функций уравнение (19) имеет единственное решение u  0 .

6. Проверим, что функция EttZt,
где Zt есть
решение однородного дифференциального уравнения

LZ  Z^m
 a₁tZ^m1 K
a_mtZ
 0
, удовлетворяющее условиям

Z0 Z0K
Z^m20 0, Z^m10 1,
удовлетворяет уравнению LEt.

Действительно, пользуясь формулой (15), получаем

EttZt,K,E^m1ttZ^m1t,

E^mtttZ^mt,

откуда

LE tLZ
tt,

что и утверждалось.

Рассмотрим примеры, связанные с
дифференцированием обобщённых функций в D^Rⁿ,
n  2.

7. Обобщением
функции x
является двойной слой на поверхности.

Пусть S – кусочно-гладкая двусторонняя
поверхность, ⁿr – нормаль к S и x

– непрерывная функция, заданная на S . Введём
обобщённую функцию



nr    S
        ,  xnrxdS, D.  rS  S  n Очевидно, что  rS D ,         supp  nrS   S .  n	(22)


    
,
действующую по правилу

Обобщённая функция  nr_S 
называется двойным слоем на поверхности S _

с плотностью x,
ориентированным по нормали ⁿr . 8. Пусть

x 2

                                         Ex,t t
n e
4a2t .                                                  (23)

2a
t


Докажем, что 

                                     ^E  a²ΔE x,t.
                                                   (24)

t

Функция Ex,t
локально интегрируема в R^n1, поскольку E  0, t  0 ; E  0, t  0 и при
t  0

                                                                                                              n        1           2

          Ex,tdx
 2a
^t      dx
 ^i_1 _ei di  1.               (25)

Если t 
0 , то EC^, а потому

E  x 2  nE,

t 4a2t 2 2t

                                                                 

                          xi             2a2t x2Ei2   4ax4i2t 2  2a12t E,
E a2                                           x 2 n  x 2	n 0 .	(26)
 ΔE 2 2  E 2 2  E

E
xi E,

           t                           4a t 2t 4a t 2t

                                                                                      

Пусть ^DR^n1.
Учитывая равенство (26), получаем

Et
 a2ΔE,  E, a2Δ  
nEx,tt
 a2Δdxdt 

                                t                    0 R                    

                                                  ^
a Δ                   

 lim

_Ex,t_       2  dxdt  lim Ex,x,dx


0 n  _t  0Rn ε R

         
                                 

 
 E  a2ΔEdxdt lim Ex,x,0dx


         
Rn t                          0 Rn

lim0 En x,x,x,0dx lim0 En x,x,0dx, R           R так как, в силу (25), Ex,x,x,0dx KEx,dx  K. RnRn Докажем теперь соотношение	(27)
Ex,t n x, t 0 в DRn .	(28)

4a²t2

Действительно, пусть xD.
Тогда, учитывая, что

_Ex,tx0dx
                           K
_n 
 4ra22t r ndr 

e

                                                                 4a²t           4a²t2 ⁰                                  

        2Kn         ta ^eu2undu  Ct ,

          n           

                2             0

n

где _n – площадь
поверхности единичной сферы в Rⁿ (_n  S1ds ^2_ n²_ ),


2 
в силу (25), получаем при t 0
соотношение (28):

Ex,t,_Ex,txdx0_Ex,tdx                   

_Ex,tx0dx0,.

Формула (24) следует из соотношений (27)
и (28). Заметим, что предельное соотношение (28) справедливо и для ограниченных
функций, непрерывных в точке 0 .

9. Пусть x  x_1
и E₁x,t ¹ _at
 x
.
2a

          Докажем, что 2Et 1  a2 2E21 x,t.
                                          (29)

                                                       2                 x

Функция
E₁x,t
локально интегрируема в R² и обращается в нуль вне
замыкания множества Г^
x,t
t 0,
x  at
(множество Г^
называют будущим световым конусом). Пусть xD,
тогда

 2E1 a2 2E21 ,  E1 ,2t2  a2 x22   E1x,t 2t2  a2 x22 dxdt 

         

 t
2                 x          

                                                                                                                                    x 

           1  2          a
         

 2a 
x t 2 dtdx  2
0 ^atat x2 2 dxdt   21a 
_xt, a _dx
_

a

                                                                                                                       x 

2  

 21 ₀tat,t
 a xat,tdt   21 0
ddtat,tdt
 21
0
ddtat,tdt


0,00,00,0,,

что и доказывает равенство (29).

Часть
III.

Прямое
произведение обобщённых функций.

Пусть f x
и gy –
локально интегрируемые функции в пространствах

Rⁿи R^m
соответственно. Функция f xgy
также будет локально интегрируемой в R^nm.
Она определяет регулярную обобщённую функцию, действующую на основные функции x,
yDR^nm
по формулам

fxgy,
fxgyx,ydxdy                                 ₍₃₀₎


fx^gyx,y^dydxfx,gy,x,y,

gy
fx,gy
fxx,ydxdy                                _(30′)

gy^
fxx,y^dxdygy,fx,x,y.

Эти равенства выражают теорему
Фубини о совпадении повторных интегралов с кратным. Равенство (30) мы и примем
за определение прямого произведения f x gy
обобщённых функций f xD^Rⁿ
и gyD^R^m:

        
f x gy, 
f x,gy,x,y,
_DR^nm.
     (31)

Покажем, что определение корректно, т.е.
что правая часть равенства (31) определяет линейный непрерывный функционал на DR^nm .

Рассмотрим следующую лемму (без доказательства). Лемма
5. Для любых gD^R^m
и DR^nm 
функция

x gy,x,
y
принадлежит DRⁿ
,
причем при всех 

                                                      D^x gy,D^_xx,y.
                       (32)

Далее, если _k 0, k  в DR^nm ,
то 

_k x gy,_k x,y0, k  в _DRⁿ
.

Вернемся к определению прямого произведения. Согласно лемме 5
x gy,x,yDRⁿ
для всех _DR^nm.
Следовательно, правая часть (31) равная  f ,,
имеет смысл для любых обобщённых функций f и g и
определяет функционал на DR^nm .
Далее, из линейности функционалов f и g следует
линейность этого функционала.

Докажем, что построенный функционал
непрерывен на DR^nm .
Пусть _k 0,  k   в DR^nm .
Тогда по лемме 5

gy,_k x,y0, k  в _DRⁿ
,

а потому, в силу непрерывности функционала f
на DRⁿ
,

f x,gy,_k x,y0, k , что и обозначает
непрерывность линейного функционала, стоящего в правой части равенства (31).

Таким образом,
функционал f x gyD^R^nm,
т. е. является обобщённой функцией.

Рассмотрим свойства прямого произведения.

а) Коммутативность прямого произведения.

Пусть даны обобщённые функции f D^Rⁿ
и gD^R^m.
Наряду с прямым произведением f x gy,
в соответствии с формулой (30′) определяется прямое произведение gy f x:

         gy f x, gy,f
x,x,y,
_ДR^nm
      (31′)

Оказывается, что

                               f
x gx gy f x,
                                          (33)

т. е. операция прямого произведения коммутативна. 

Действительно на основных функциях ДR^nm
вида

N

              x,y u_l
xv_l
y,
u_l _ДRⁿ
,  v_l _ДR^m

            (34)

l1

равенство (33) вытекает из определений (31) и (31′):

                                                 N                           N


f x gy, _
f ,u_l g,v_l
_
 
f ,u_l g,v_l 

                                                 l1                         l1

                                                                                                ^N                        

 _
g,v_l 
f ,u_l _  gy f x,.

                                                                                               l1                      

Чтобы распространить (33) на любые
основные функции, рассмотрим лемму о том, что множество основных функций вида
(34) плотно в^ДR^nm.

Лемма 6. Для любой функции ДR^nm
существует последовательность основных функций _k x,y,   
kN
 вида (34), сходящаяся к  в _ДRnm.

ПустьДR^nm.
В силу леммы 6 существует последовательность _n
основных функций вида (45), сходящаяся к  в ^ДR^nm.
Пользуясь непрерывностью на ДR^nm
функционалов f xgy
и gy f x
и равенством

(33) на функциях вида (34), получим равенство (33) и в общем
случае:

f
x gy, limf
x gy,_k limgy f x,_k gy f x,.

                                                       k                                                 k

b)   Операция
прямого произведения f x gy
линейна и непрерывна отно-

сительно f (из D^Rⁿ

в D^R^nm )
и относительно g (из D^Rⁿ

в D^R^nm ),
т.е.

f₁xf₂
x gyf₁x gyf₂
x gy,

f₁,
f₂ D^Rⁿ,
gD^R^m;

f_k
x gy0, k  в D^R^nm ,
если f_k 0,
k  в D^Rⁿ
.

Докажем непрерывность. Пусть ДR^nm.
По лемме 5

x gy,x,yДRⁿ
.
Поэтому, пользуясь определением (31) прямого произведения, получаем

f_k
x gy, f_k
x,gy,x,y f_k
,0, k , что и требовалось
доказать.

c)    Ассоциативность
прямого произведения.

Если f D^Rⁿ,
gD^R^m
и hD^R^k,
то

f
xgy hz f
x gy hz.

Действительно, если _ДR^nmk,
то

f xgy hz, f
x,gy hz, f
x,gy,hz,  f
x gy,hz, f
x gy hz,.

d)   Дифференцирование
прямого произведения.

D^_x f
x gy D^ f x gy.

В самом деле, если _ДR^nm,
то

D^_x f
x gy,_  1^f
x gy,D^_x

  1^gy,f
x,D^_xx,y gy,D^_x f
x,_     D^ f x gy,_.

e)    Умножение
прямого произведения.

Если aC^Rⁿ
,
то axf
x gy axf
x gy.

Действительно, если _ДR^nm,
то 

axf
x gy, 
f x gy,a 
f x,gy,axx,y  
f x,axgy,x,y axf
x,gy,x,y  axf
x gy,.

f)     Сдвиг
прямого произведения.

f
 gx
 h,
y f x
 h gy.

В самом деле, если _ДR^nm,
то 


f 
gx  h, y, 
f x gy,x
 h,
y gy,
f x,x
 h,
y

 gy,
f x  h,x,
y 
f x  h gy,.

g)   Говорят, что
обобщённая функция вида f x1y
не зависит от y . Она

действует по правилу: если ДR^nm,
то

f
x1y, f
x^,x,ydy 1y f x, f
x,x,ydy.

Таким образом, получено равенство 

f
x^,x,y^dy f
x,x,ydy,

справедливое для всех f D^Rⁿ
и _ДR^nm.

Рассмотрим некоторые примеры обобщённых функций в D^R²
.

1. Обобщённую функцию _at
 x
из D^R²

определим равенством

_at
 x
tat
 xtat
 x,

где обобщённые функции tat
 x
и tat
 x
есть результаты линейных замен переменных  t,  at  x в ,
т.е.

 at  x x  a

tat
 x,x,t , a,

                                                                t          t 




,, a, , a,  a,d x
 a


0

 a1
^0 x, ax
_dx;

 at  x x  a

tat
 x,x,t ,a,

                                                                t          t 




,,a, ,a, a,d x
 a


0

        1       x

 a
0  x,a
dx
.

Значит,

_at
 x
,x,t tat
 x,x,t tat
 x,x,t a1 0
 x dx  1  x,ax dx  a1  x, ax dx 

   x, a      a 0      



                                                                              

  a,d a,d a, a,d.

        0                                         0                                    0

Мы получили, что at
 x
,x,t a1
_ x, ax dx
или



_at  x ,x,t at,t at,tdt
.

0

2.
Найдём частные производные функции _at
 x.
Пусть ДR²,
тогда

^ ^t
at
 x
,x,t^
 ^at
 x
,
^tx,t^
 ^2at
 x
_tx,tdxdt


_{                                                                   R}

                                

                                         
     x



^_ _tx,tdt_dx
 ^_
x^, _{a }_dx
 a^at
 x
,x,t

                
a                        


a_at
 x
,x,t.



Таким образом, at
 x
 aat
 x
.

t

^^x
_at
 x
,x,t^  ^_at
 x
,^xx,t^  _R2_at
 x
_x x,tdxdt
 

          ^at                                                                                                                                   

  
_
_x x,tdx_dt
 at,t at,tdt
  at,tdt
 at,tdt


            0 at                                0                                                                     0                                     0


tat
 x,x,t tat
 x,x,t  tat
 xat
 x,x,t.



_{Таким образом,} _at
 x
tat
 xat
 x.

x