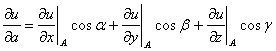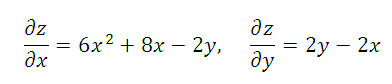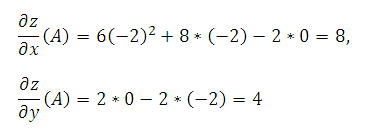Градиент функции
Градиент — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины u. Другими словами, направление градиента есть направление наибыстрейшего возрастания функции.
Назначение сервиса. Онлайн калькулятор используется для нахождения градиента функции нескольких переменных. (см. пример) При этом решаются следующие задачи:
- нахождение частных производных функции, запись формулы градиента, вычисление наибольшой скорости возрастания функции в указанной точке;
- вычисление градиента в точке A, нахождение производной в точке A по направлению вектора a;
- нахождение полного дифференциала функции.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Решение со всеми исходными формулами сохраняется в формате Word.
Полный дифференциал для функции двух переменных: 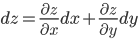
Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=dxf(x,y,z)dx+dyf(x,y,z)dy+dzf(x,y,z)dz
Алгоритм нахождения градиента
- Вычисление частных производных по формуле:
- Вычисление частных производных в точке A.
- Нахождение направляющих углов вектора a.
- Вычисление производной в точке A по направлению вектора a по формуле;
- Наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Производная функции по направлению
Как найти?
Постановка задачи
Найти производную функции $ u(x,y,z) $ в точке $ M (x_1,y_1,z_1) $ по направлению вектора $ overline{l} = (l_x,l_y,l_z) $
План решения
Если для функции $ u(x,y,z) $ существует производная в точке $ M(x_1,y_1,z_1) $, то значит в этой точке существует производная по любому направлению $ overline{l} $ и находится по формуле:
$$ frac{partial u}{partial l} = frac{partial u}{partial x} bigg |_M cdot cos alpha + frac{partial u}{partial y} bigg |_M cdot cos beta + frac{partial u}{partial z} bigg |_M cdot cos gamma $$
- Находим частные производные первого порядка:
$$ frac{partial u}{partial x}; frac{partial u}{partial y}; frac{partial u}{partial z} $$ - Вычисляем полученные производные в точке $ M(x_1,y_1,z_1) $:
$$ frac{partial u}{partial x} bigg |_{M(x_1,y_1,z_1)}; frac{partial u}{partial y} bigg |_{M(x_1,y_1,z_1)}; frac{partial u}{partial z} bigg |_{M(x_1,y_1,z_1)} $$ - Получаем направляющие косинусы по формулам:
$$ cos alpha = frac{l_x}{|overline{l}|}; cos beta = frac{l_y}{|overline{l}|}; cos gamma = frac{l_z}{|overline{l}|} $$ - Подставляем все полученные данные в формулу и записываем ответ
Примеры решений
| Пример 1 |
| Найти производную функции $ u = x+ln(z^2+y^2) $ в точке $ M (2,1,1) $ по направлению вектора $ overline{l} = (-2,1,-1) $ |
| Решение |
|
Находим частные производные первого порядка и вычисляем их начение в точке $ M $: $$ frac{partial u}{partial x} = 1; frac{partial u}{partial x} bigg |_{M(2,1,1)} = 1 $$ $$ frac{partial u}{partial y} = frac{2y}{z^2+y^2}; frac{partial u}{partial y} bigg |_{M(2,1,1)}=1 $$ $$ frac{partial u}{partial z} = frac{2z}{z^2+y^2}; frac{partial u}{partial z} bigg |_{M(2,1,1)} = 1 $$ Вычисляем направляющие косинусы: $$ cos alpha = frac{-2}{sqrt{(-2)^2+1^2+(-1)^2}} = frac{-2}{sqrt{6}} $$ $$ cos beta = frac{1}{sqrt{(-2)^2+1^2+(-1)^2}} = frac{1}{sqrt{6}} $$ $$ cos gamma = frac{-1}{sqrt{(-2)^2+1^2+(-1)^2}} = – frac{1}{sqrt{6}} $$ Подставляем полученные частные производные в точке $ M $ и направляющие косинусы в формулу: $$ frac{partial u}{partial l} = 1 cdot (-frac{2}{sqrt{6}}) + 1 cdot frac{1}{sqrt{6}} + 1 cdot (-frac{1}{sqrt{6}}) = -frac{2}{sqrt{6}} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ frac{partial u}{partial l} = -frac{2}{sqrt{6}} $$ |
| Пример 2 |
| Найти производную $ u = xy – frac{x}{z} $ в точке $ M(-4,3,-1) $ по направлению вектора $ overline{l} = (5,1,-1) $ |
| Решение |
|
Берем частные производные первого порядка от функции в точке $ M(-4,3,-1) $: $$ frac{partial u}{partial x} = y – frac{1}{z}; frac{partial u}{partial x} bigg |_{M(-4,3,-1)} = 4 $$ $$ frac{partial u}{partial y} = x; frac{partial u}{partial y} bigg |_{M(-4,3,-1)} = -4 $$ $$ frac{partial u}{partial z} = frac{x}{z^2}; frac{partial u}{partial z} bigg |_{M(-4,3,-1)} = -4 $$ Вычисляем направляющие косинусы: $$ cos alpha = frac{5}{sqrt{5^2+1^2+(-1)^2}} = frac{5}{sqrt{27}} $$ $$ cos beta = frac{1}{sqrt{5^2+1^2+(-1)^2}} = frac{1}{sqrt{27}} $$ $$ cos gamma = frac{-1}{sqrt{5^2+1^2+(-1)^2}} = frac{-1}{sqrt{27}} $$ По формуле производной по направлению получаем ответ: $$ frac{partial u}{partial l} = 4 cdot frac{5}{sqrt{27}} + (-4) cdot frac{1}{sqrt{27}} + (-4) cdot frac{-1}{sqrt{27}} = frac{20}{sqrt{27}} $$ |
| Ответ |
| $$ frac{partial u}{partial l} = frac{20}{sqrt{27}} $$ |
Формула производной по направлению
а) Дана функция z=z(x,y) , направляющий вектор l и точка А. Найти производную по направлению в точке.
Решение.Формула производной по направлению:
1) Находим частные производные:
2) Находим значение частных производных в точке A(-2; 0):
Частные производные можно найти с помощью калькулятора частные производные.
3) Находим направляющие косинусы:
Направляющие косинусы, т.е. координаты нормированного (единичного) вектора можно найти с помощью калькулятора нормировки вектора.
4) Полученные значения частных производных и направляющих косинусов подставляем в формулу производной по направлению, получаем:
Следующий пример.
б) Дана функция z=z(x,y) , точка А и точка N.
Найти производную в точке A по направлению точки N.
Решение. Выполнение первых двух пунктов решения совпадает с примером 1, поэтому начинаем с пункта 3.
3) Находим координаты направляющего вектора l:
4) Находим направляющие косинусы:
5) Полученные значения частных производных и направляющих косинусов подставляем в формулу производной по направлению, получаем:
Второй способ найти производную функции по направлению см. градиент функции.
Калькулятор для нахождения производной функции в точке по направлению вектора.
Найдите производную функции `z=x^2y+ln(xy)`в точке `M(1;1)` по направлению вектора `vecl=(4;3)`
Пример ввода функции:
`z=x^2y+ln(xy)` `M(1;1)` `vecl=(4;3)` -> `z`=x**2*y+ln(x*y) ->`M_x`=1 ->`M_y`=1 ->`vecl_x`=4 ->`vecl_y`=3
`z=x^3y+ln(x^3y)` `M(-1;-2)` `vecl=(-3;4)` -> `z`=x**3*y+ln(x**3*y) ->`M_x`=-1 ->`M_y`=-2 ->`vecl_x`=-3 ->`vecl_y`=4
`z=xy^3+ln(xy^3)` `M(1;1)` `vecl=(-3;-4)` -> `z`=x*y**3+ln(x*y**3) ->`M_x`=1 ->`M_y`=1 ->`vecl_x`=-3 ->`vecl_y`=-4
`z=x^2y+ln(x^2y^3)` `M(1;1)` `vecl=(-3;4)` -> `z`=x**2*y+ln(x**2*y**3) ->`M_x`=1 ->`M_y`=1 ->`vecl_x`=-3 ->`vecl_y`=4
`z=xy^2+ln(x+y)` `M(2;-1)` `vecl=(-3;4)` -> `z`=x*y**2+ln(x+y) ->`M_x`=2 ->`M_y`=-1 ->`vecl_x`=-3 ->`vecl_y`=4
Для решения задач необходима регистрация
Градиент функции и производная по направлению вектора
Краткая теория
Градиентом называется вектор, направление которого указывает направление максимально быстрого возрастания функции f(x). Нахождение этой векторной величины связано с определением частных производных функции. Производная по направлению это скалярная величина и показывает скорость изменения функции при движении вдоль направления, заданного некоторым вектором.
Пример решения задачи
Задача
Даны функция
, точка
и вектор
. Найти:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Нахождение градиента функции
1) Найдем градиент
функции в точке
:
Искомый градиент:
Нахождение производной по направлению вектора
2) Найдем производную
в направлении вектора
:
где
-угол,
образованный вектором и осью
Искомая производная в
точке
: