Пусть
функция
дифференцируема в некотором интервале.
Тогда её производная
,
вообще говоря, зависит отх
, то есть
является функцией от х.
Следовательно, по отношению к ней снова
можно ставить вопрос о существовании
производной.
Определение.
Производная
от первой производной называется
производной
второго порядка или второй производной
и обозначается символом
или
,
то есть
.
Пример
1. Найти
вторую производную от функции
.
Решение. Найдем
первую производную функции:
.
Находим вторую
производную как производную первой
производной:
.
Определение.
Производная
от второй производной называется
производной третьего порядка или третьей
производной и обозначается символом
или
.
Определение.
Производной
n-ого
порядка функции
называется
первая производная от производной
(n-1)-го
порядка данной функции и обозначается
символом
или
:
.
Определение.
Производные
порядка выше первого называются
высшими
производными.
Пример
2. Найти
производную четвертого порядка функции
.
Решение. Находим
последовательно первую, вторую, третью
и четвертую производные:
,
,
,
.
Пример
3.Найти
производную n-ого
порядка для функции
(k–const).
Решение. Имеем:
,
,
,
.
Пример
4. Найти
производную n-ого
порядка для функции
.
Решение. Имеем:
,
,
,
,
.
Замечание.
Аналогично можно получить формулу n-ой
производной функции
:
.
Пример
5. Найти
производную n-ого
порядка для степенной функции
, где
и
– любое вещественное число.
Решение.
Дифференцируя последовательно, получим:
,
,
,
.
В
частном случае, когда
,
гдеm
– натуральное число, получим:
,
при
.
Замечание.
При строгом выводе формулы для производной
n-ого
порядка следует применять метод
математической индукции.
Вторая
производная параметрически заданной
функции
Если
функция задана параметрически уравнениями
,
то для нахождения производной второго
порядка нужно продифференцировать
выражение для её первой производной,
как сложной функции независимой
переменной.
Так
как
,
то
,
и с учетом того,
что
,
получим
,
то есть
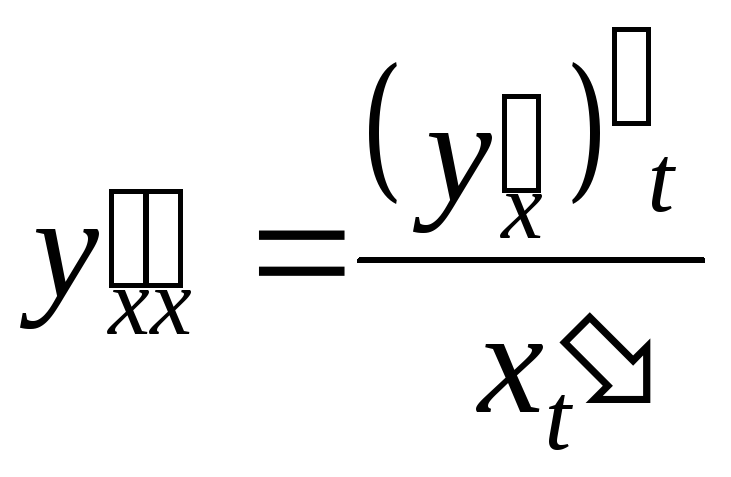
Аналогично можно найти третью
производную
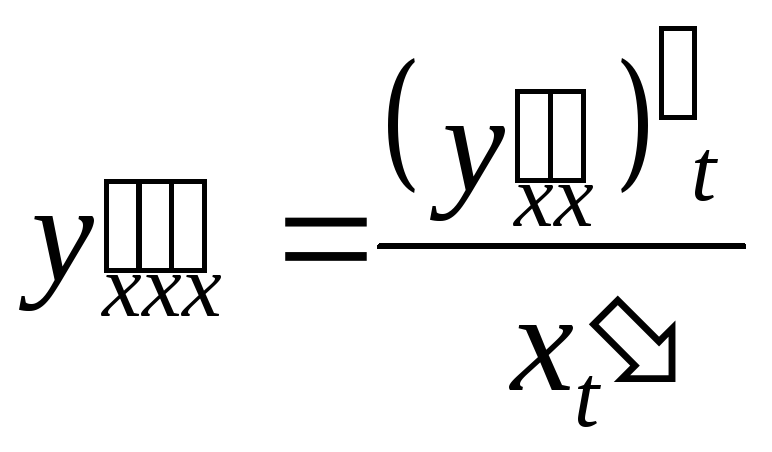
Пример
7. Найти
вторую производную параметрически
заданной функции
,
.
Решение.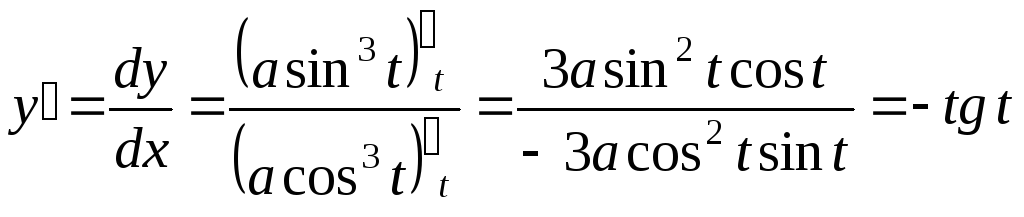
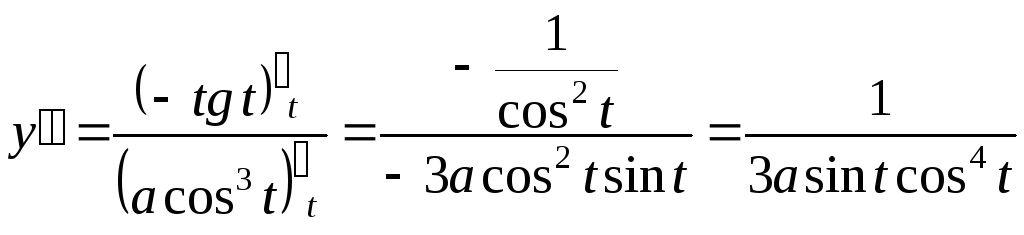
Формула Лейбница
Для
нахождения производной n-ого
порядка от произведения двух функций
большое практическое значение имеет
формула Лейбница.
Пусть
u
и
v
– некоторые
функции от переменной х,
имеющие производные любого порядка и
y=uv.
Выразим n-ую
производную
через производные функцийu
и
v.
Имеем последовательно
,
,
.
Легко подметить
аналогию между выражениями для второй
и третьей производных и разложением
бинома Ньютона соответственно во второй
и третьей степенях, но вместо показателей
степени стоят числа, определяющие
порядок производной, а сами функции
можно рассматривать как «производные
нулевого порядка». Учитывая это, получим
формулу Лейбница:
. (2)
Эту формулу
можно доказать методом математической
индукции.
Пример.
Найти пятую
производную функции
.
Решение.
Положим
и
.
Найдем,
,
,
,
;
.
Подставляя эти выражения в формулу
Лейбница при,
получим
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Под понятием производные различных порядков обычно понимаются производные первого или высших порядков.
Дифференцирование производной первого порядка [F^{prime}(x)] позволит вычислить производную от производной — именуемую производной второго порядка. Далее назовем определение производной.
Производная производной второго порядка именуется производной третьего порядка, в этой связи производная n-го
порядка определяется как производная от производной n-1го порядка.
Производная функции второго порядка обозначается записью [y^{prime prime}] или [F^{prime prime}(x)]. Дифференцировка функции [n] раз приводит к получению производной вида [f n(x)].
Дифференцирование второго порядка
Производные в математике всегда находятся по определенной формуле. Итак, формула дифференцирования второго порядка записывается следующим образом:
[f^{prime prime}(x)=frac{d^{2} y}{d x^{2}}=lim _{x rightarrow x_{0}}=frac{f^{prime}(x)-f^{prime}left(x_{0}right)}{x-x_{0}}=left(f^{prime}(x)right)^{prime}]
В случае, если степень меньше, чем порядок производной, производная n-го порядка будет равна нулю.
Таблица с формулами производных высших порядков
Формулы для нахождения производных высших порядков наиболее удобно представить в виде таблицы формул производных:
| Функция | Формула нахождения |
| [left(x^{p}right)^{(n)}] | [left(x^{p}right)^{(n)}=p(p-1)(p-1) ldots(p-n+1) x^{p-n}] |
| [left(a^{k x+b}right)^{(n)}] | [left(a^{k x+b}right)^{(n)}=k^{n} a^{k x+b} 1 n^{n} a] |
| [left(e^{k x+b}right)^{(n)}] | [left(e^{k x+b}right)^{(n)}=k^{n} e^{k x+b}] |
| [(sin a x)^{(n)}] | [(sin a x)^{(n)}=a^{n} sin left(a x+frac{п n}{2}right)] |
| [(cos a x)^{(n)}] | [(sin a x)^{(n)}=a^{n} cos left(a x+frac{п n}{2}right)] |
| [left((a x+b)^{p}right)^{n}] | [left((a x+b)^{p}right)^{n}=a^{n} p(p-1)(p-2) ldots(p-n+1)(a x+b)^{n-1}] |
| [left(log _{a}|x|right)^{(n)}] | [left(log _{a}|x|right)^{(n)}=frac{(-1)^{n-1}(n-1) !}{x^{n} ln a}] |
| [(ln |x|)^{n}] | [left(log _{a}|x|right)^{(n)}=frac{(-1)^{n-1}(n-1) !}{x^{n}}] |
| [(a u(x)+beta gamma(x))^{n}] | [(a u(x)+beta gamma(x))^{n}=a u^{n}(x)+beta^{n} gamma(x)] |
Нет времени решать самому?
Наши эксперты помогут!
Примеры нахождения производных
Примеры
Пример 1
Как найти производную первого порядка функции по формуле произведения:
[|f(x) cdot g(x)|^{prime}=f(x)^{prime} cdot g(x)+f(x) cdot g(x)^{prime}\y^{prime}=[x cdot ln (2
x+1)]^{prime}=x^{prime} cdot ln (2 x+1)+x cdot(ln (2 x+1))^{prime}\=1 cdot ln (2 x+1)+x cdot(ln
(2 x+1))^{prime}=y^{prime}\=ln (2 x+1)+x cdot(ln (2 x+1))^{prime}\=ln (2 x+1)+x frac{1}{2 x+1}
cdot(2 x+1)^{prime}=ln (2 x+1)+2 x cdot frac{1}{2 x+1}\=ln (2 x+1)+frac{2 x}{2 x+1}]
Как найти производную второго порядка в данном выражении:
[y^{prime prime}=left(ln (2 x+1)+frac{2 x}{2 x+1}right)^{prime}=ln (2 x+1)^{prime}+left(frac{2
x}{2 x+1}right)^{prime}\=left(frac{1}{2 x+1}right) cdot(2 x+1)^{prime}+frac{2 x^{prime} cdot(2
x+1)-2 x cdot(2 x+1)^{prime}}{(2 x+1)^{2}}\=y^{prime prime}=frac{2}{2 x+1}+frac{2(2 x+1)-2 x cdot
2}{(2 x+1)^{2}}=frac{2}{2 x+1}+frac{2((2 x+1)-2 x)}{(2 x+1)^{2}}\=frac{2}{2 x+1}+frac{2}{(2
x+1)^{2}}]
Упростим полученное решение:
[y^{prime prime}=frac{2(2 x+1)}{(2 x+1)^{2}}+frac{2}{(2 x+1)^{2}}=frac{2(2 x+1)+2}{(2 x+1)^{2}}=frac{4
x+4}{(2 x+1)^{2}}]
Пример 2
Задача на нахождение производной различных порядков на примере производной четвертого порядка:
[y=x^{5}-x^{4}+3 x^{3}]
Решение:
[y^{prime}=left(x^{5}-x^{4}+3 x^{3}right)^{prime}=5 x^{4}-4 x^{3}+3 cdot 3 x^{2}=5 x^{4}-4 x^{3}+9
x^{2}\y^{prime prime}=left(5 x^{4}-4 x^{3}+9 x^{2}right)^{prime}=20 x^{3}-12 x^{2}+18 x\y^{prime
prime prime}=left(20 x^{3}-12 x^{2}+18 xright)^{prime}=60 x^{2}-24 x+18\y^{4}=left(60 x^{2}-24
x+18right)^{prime}=120 x-24]
Пример 3
Нахождение производной различных порядков от функций на следующем частном примере:
[y=frac{x^{2}+5 x^{3}}{18}]
Ответ: решение не является сложным и не потребует онлайн-калькулятора. Наибольшая степень одной из переменных
равна 3, что меньше степени производной. Следовательно, производная четвертого порядка равна 0.
Пример 4
Необходимо найти производную 13 порядка для [y=sin x]
Решение: найдем производную первого порядка (и затем 2-4 порядков)
[y^{prime}=sin ^{prime} x=cos x=sin left(x+frac{pi}{2}right)\y^{prime prime}=cos ^{prime}
x=-sin x=sin left(x+2 frac{pi}{2}right)\y^{prime prime prime}=-sin ^{prime} x=-cos x=sin
left(x+3 frac{pi}{2}right)\y^{(4)}=-cos ^{prime} x=sin x=sin left(x+4 frac{pi}{2}right)]
Следовательно:
[y^{(n)} sin left(x+frac{n cdot pi}{2}right), n in N]
Итоговый результат:
[y^{(13)}=sin left(x+frac{13 cdot pi}{2}right)=cos x]
Пример 5
Подсчитайте производную четвертой степени функции [x^{8}]
Решение:
Используем формулу нахождения производной высшего порядка
[left(x^{p}right)^{(n)}=p(p-1)(p-1) ldots(p-n+1) x^{p-n}]
Учтем, что p=8, n=4
[left(x^{8}right)^{(4)}=8(8-1)(8-2)(8-4+1) x^{8-4}=8 cdot 7 cdot 6 cdot 5 cdot x^{4}=1680 x^{4}\left(x^{8}right)^{(4)}=1680 x^{4}]
Пример 6
Подсчитайте производную функции [y=2^{x}-operatorname{arctg} x].
Решение:
[y^{prime}=left(2^{x}-operatorname{arctg} xright)^{prime}=left(2^{x}right)^{prime}-(operatorname{arctg} x)^{prime}]
Используем формулы для обратной и тригонометрической функции [y^{prime}=2^{x} ln 2-frac{1}{1+x^{2}}]
Ответ: [y^{prime}=2^{x} ln 2-frac{1}{1+x^{2}}]
Производная функции
f(x)
,
f′(x)
, сама является функцией. Значит, можно найти её производную.
Назовём
f′(x)
производной функции
f(x)
первого порядка.
Производная от производной функции
f(x)
называется производной второго порядка (или второй производной).
Производная от второй производной называется производной третьего порядка (или третьей производной) и т. д.
Производные, начиная со второй, называются производными высших порядков и обозначаются
y′′(иногдаy2),y′′′(иногдаy3),y4,y5…yn…
Иногда используются обозначения
dydx,d2ydx2,d3ydx3…dnydxn…
Ускорение есть вторая производная координаты по времени. В этом состоит механический смысл второй производной.
Производная (n)-го порядка является производной ((n-1)) порядка: yn=yn−1′.
(Сама функция иногда считается производной (0)-го порядка.)
Пример:
y=x5;y′=x5′=5×4;y′′=(y′)′=5×4′=20×3;y3=(y′′)′=(5⋅4×3)′=60×2;y4=(y3)′=(60×2)′=120x;y5=(y4)′=(120x)′=120;y6=y7=y8=…=0.

