Как найти производную от 1 lnx

Как найти производную от 1 lnx

<<ArteR>>



Знаток

(457),
закрыт



5 лет назад

Лучший ответ

Romnet

Мыслитель

(7924)


11 лет назад

Используем формулы (c/v)’ = – cv’/v^2 и (lnx)’ = 1/x
(1/lnx)’ = – (lnx)’ / ln^2(x) = – 1 / (x * ln^2(x))

PS: c – любое число, константа. v – какая-нибудь функция.

Остальные ответы

Похожие вопросы

Источник

bold{mathrm{Basic}} bold{alphabetagamma} bold{mathrm{ABGamma}} bold{sincos} bold{gedivrightarrow} bold{overline{x}spacemathbb{C}forall} bold{sumspaceintspaceproduct} bold{begin{pmatrix}square&square\square&squareend{pmatrix}} bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx}
ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square}
left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec
alpha beta gamma delta zeta eta theta iota kappa lambda mu
nu xi pi rho sigma tau upsilon phi chi psi omega
A B Gamma Delta E Z H Theta K Lambda M
N Xi Pi P Sigma T Upsilon Phi X Psi Omega
sin cos tan cot sec csc sinh cosh tanh coth sech
arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech
begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge
(square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil
overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset
vee wedge neg oplus cap cup square^{c} subset subsete superset supersete
int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod
lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x}
(2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5)
(1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1)
mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить}
arcsin sin sqrt{square} 7 8 9 div
arccos cos ln 4 5 6 times
arctan tan log 1 2 3 –
pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

  • frac{d}{dx}(frac{3x+9}{2-x})

  • frac{d^2}{dx^2}(frac{3x+9}{2-x})

  • (sin^2(theta))”

  • производное:от:f(x)=3-4x^2,::x=5

  • неявная:производная:frac{dy}{dx},:(x-y)^2=x+y-1

  • frac{partial}{partial ypartial x}(sin (x^2y^2))

  • frac{partial }{partial x}(sin (x^2y^2))

  • Показать больше

Описание

Поэтапное дифференцирование функций

derivative-calculator

frac{d}{dx}left(frac{1}{lnx}right)

ru

Блог-сообщения, имеющие отношение к Symbolab

  • High School Math Solutions – Derivative Calculator, the Chain Rule

    In the previous posts we covered the basic derivative rules, trigonometric functions, logarithms and exponents…

    Read More

    • Введите Задачу

    Сохранить в блокнот!

    Войти

    Источник

    Найдем производную функции f(x)=ln⁡xf(x)= ln x и приведем некоторые ее свойства и практические примеры использования.

    Производная функции f(x)= ln x

    Как известно, производной функции f(x)f(x), определенной в точке x0x_0 и в некотором интервале, содержащем x0x_0, называют предел следующего вида:

    f′(x0)=dfdx∣x=x0=lim⁡Δx→0f(x0+Δx)−f(x0)Δxf^{‘}(x_0)=dfrac{df}{dx}Bigr|_{x=x_0}=limlimits_{Delta x to 0}dfrac{ f(x_0+ Delta x)-f(x_0 )}{ Delta x}

    если только такой предел существует.

    Таким образом, для вычисления производной функции f(x)f(x) необходимо последовательно:

    1. Записать выражение для приращения функции:

    Δf(x0)=f(x0+Δx)−f(x0)Delta f(x_0 )=f(x_0+Delta x)-f(x_0 )

    1. Упростить, по возможности, дробь

    Δf(x0)Δx=f(x0+Δx)−f(x0)Δxdfrac {Delta f(x_0)}{Delta x}=dfrac {f(x_0+Delta x)-f(x_0)}{Delta x}

    1. Вычислить предел дроби при Δx→0Delta x to 0 и записать полученное выражение для производной.

    Применим этот алгоритм к вычислению производной натурального логарифма:

    1. Записываем приращение функции:

    Δf(x0)=f(x0+Δx)−f(x0)=ln⁡(x0+Δx)−ln⁡x0=ln⁡x0+Δxx0Delta f(x_0)= f(x_0+Delta x)-f(x_0)= ln (x_0+Delta x)-ln {x_0}=ln dfrac { x_0+Delta x }{ x_0}

    1. Получаем дробь:

    Δf(x0)Δx=1Δx⋅ln⁡x0+Δxx0=ln⁡(1+Δxx0)1Δx=1x0ln⁡(1+1×0/Δx)x0Δxdfrac {Delta f(x_0)}{Delta x}= dfrac {1}{Delta x} cdot ln {dfrac {x_0+Delta x }{ x_0}}=ln {Bigl( 1+dfrac {Delta x }{ x_0} Bigr)}^ {dfrac {1}{Delta x}}=dfrac {1}{x_0} ln {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}

    1. Вычисляем производную:

    f′(x0)=lim⁡Δx→0(1x0ln⁡(1+1×0/Δx)x0Δx)=1×0⋅lim⁡Δx→0ln⁡(1+1×0/Δx)x0Δx=1×0⋅ln⁡lim⁡Δx→0(1+1×0/Δx)x0Δxf'(x_0 )=limlimits_{Delta x to 0} Bigl( dfrac {1}{ x_0} ln {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}Bigr) =dfrac {1}{ x_0} cdot limlimits_{Delta x to 0} ln {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}=dfrac {1}{ x_0} cdot ln limlimits_{Delta x to 0} {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}

    Для вычисления предела

    lim⁡Δx→0(1+1×0/Δx)x0Δxlimlimits_{Delta x to 0} {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}

    обозначим:

    x0Δx=ndfrac {x_0}{ Delta x }=n

    Учитывая, что n→∞ntoinfty при условии, что Δx→0Delta x to 0, получаем:

    lim⁡Δx→0(1+1×0/Δx)x0Δx=lim⁡n→∞(1+1n)nlimlimits_{Delta x to 0} {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}=limlimits_{ntoinfty } {Bigl( 1+dfrac {1 }{n} Bigr)}^{ n}

    Полученный предел является одним из представлений экспоненты, числа e≈2,71828e≈2, 71828 (число Непера или число Эйлера):

    e=lim⁡n→∞(1+1n)ne=limlimits_{ntoinfty } {Bigl( 1+dfrac {1 }{n} Bigr)}^{ n}

    Тогда, искомая производная равна:

    f′(x0)=1×0⋅ln⁡lim⁡Δx→0(1+1×0/Δx)x0Δx=1×0⋅ln⁡e=1x0f'(x_0) =dfrac {1}{ x_0} cdot ln limlimits_{Delta x to 0} {Bigl( 1+dfrac {1 }{ x_0 / Delta x } Bigr)}^{ dfrac {x_0}{Delta x}}=dfrac {1}{ x_0}cdot ln e=dfrac {1}{ x_0}

    Таким образом:

    f′(x)=(ln⁡x)′=1xf'(x)=(ln x) ‘=dfrac {1}{ x}

    Некоторые свойства и практические примеры

    1. Приведем правило для нахождения производной обратной функции.

    Пусть дана функция y=f(x)y=f(x), в которой переменная x является аргументом. Полагая теперь аргументом переменную y, получим функцию в виде x=g(y)x=g(y).

    Очевидно, что f(g(y))=yf(g(y))=y или f(g(x))=xf(g(x))=x. Такую функцию g(x)g(x) называют обратной для f(x)f(x). Производную обратной функции можно найти по правилу:

    yx′=dydx=1dxdy=1xy′y_x’=dfrac {dy}{dx}=dfrac {1}{dfrac {dx}{dy}}=dfrac {1}{x_y’}

    Пример 1

    Используя правило для обратной функции найти производную функции f(x)=ln⁡x.f(x)= ln{x}.

    Решение

    Заметим, что обратной для логарифмической функции ln⁡xln{x} является показательная функция exe^x. Действительно:

    f(g(x))=ln⁡ex=xf(g(x)) = ln {e^x} = x

    Воспользуемся далее формулой для производной экспоненты:

    (ex)′=ex(e^{x})^{‘}=e^{x}

    Получаем:

    yx′=(ln⁡x)′=1(ey)y′=1ey=1eln⁡x=1xy_x’ = (ln {x})’ = dfrac {1}{(e^{y})^{‘}_y}= dfrac {1}{e^y}= dfrac {1}{e^{ln x}}= dfrac {1}{x}

    Как и следовало ожидать, результат совпадает с полученным ранее.

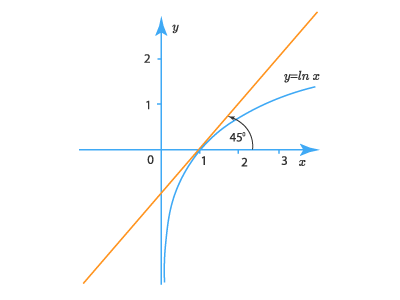
    1. Угол наклона αalpha касательной к графику функции y=ln⁡xy= ln {x} в точке x=x0x=x_0 определяется соотношением:

    tg⁡α=y′(x0)=1x0tg alpha =y^{‘} (x_0 )= dfrac {1}{x_0}

    Здесь угол αalpha это угол между касательной и осью OxOx отсчитываемый от положительного направления OxOx против часовой стрелки.

    Производная функции f(x)=ln⁡xf(x)= ln {x} в точке x0=1x_0=1 равна 11:

    f′(x0)=(ln⁡x)x0=1′=11=1f’ (x_0 ) = (ln {x})_{x_0=1}^{‘}=dfrac {1}{1}=1

    Это означает, что касательная к графику в точке M(1;0),(x0=1,y0=ln⁡1=0)M(1;0), (x_0=1, y_0=ln {1} = 0) составляют с осью OxOx угол 45°(tg⁡45°=1)45° (tg {45°}=1)

    Производная натурального логарифма.png

    1. Производная сложной функции y=ln⁡g(x)y=ln {g(x)} согласно правил дифференцирования, равна:

    y′=g′(x)1g(x)y’=g'(x) dfrac {1}{g(x)}

    1. Производная сложной функции y=u(v)y=u(v), где v=ln⁡xv= ln {x} равна:

    y′=uv′⋅v′=uv′⋅1xy’=u’_v cdot v’=u’_v cdot dfrac {1}{x}

    Пример 2

    Найти производную функции f(x)=ln⁡(x2+2x)f(x)=ln {(x^2+2x)}

    Решение

    f′(x)=(ln⁡(x2+2x))′=(x2+2x)′⋅1×2+2x=2x+2×2+2xf'(x)=(ln {(x^2+2x)})’=(x^2+2x)’ cdot dfrac {1}{x^2+2x}=dfrac {2x+2}{x^2+2x}

    Пример 3

    Найти производную функции

    f(x)=sin⁡(ln⁡2x)f(x)= sin {(ln {2x})}

    Решение

    Полагаем ln⁡2x=vln {2x}=v

    Тогда:

    f′(x)=(sin⁡v)v′⋅v′=cos⁡v⋅(ln⁡2x)′=cos⁡(ln⁡2x)⋅(2x)′⋅12x=cos⁡(ln⁡2x)xf'(x)=(sin {v})’_v cdot v’ = cos {v} cdot (ln {2x})’ =cos{(ln {2x})} cdot (2x)’ cdot dfrac {1} {2x} = dfrac {cos(ln{2x})} {x}

    Тест по теме «Производная натурального логарифма»

    Источник

    Содержание:

    • Формула
    • Примеры вычисления производной натурального логарифма

    Формула

    $$(ln x)^{prime}=frac{1}{x}$$

    Производная от натурального логарифма равна единице, деленной на $x$ .

    Натуральный логарифм, $ln x$ – это логарифм, в основании которого
    находится число $e$ .

    Заметим, что эту формулу можно получить из формулы производной для логарифма
    $log_{alpha} x$ по произвольному основанию, учитывая тот факт,
    что основание натурального логарифма есть число $e$ :

    $$(ln x)^{prime}=left(log _{e} xright)^{prime}=frac{1}{x ln e}=frac{1}{x}$$

    Здесь было применено свойство логарифма: $log_{alpha} alpha=1$

    Если под натуральным логарифмом находится сложная функция $u=u(x)$,
    то производная исходной функции будет равна:

    $$(ln u)^{prime}=frac{1}{u} cdot u^{prime}$$

    Примеры вычисления производной натурального логарифма

    Пример

    Задание. Найти производную функции $y(x)=frac{ln x}{3}$

    Решение. Искомая производная

    $$y^{prime}(x)=left(frac{ln x}{3}right)^{prime}$$

    По свойствам производной константу выносим за знак производной и находим производную натурального логарифма по формуле:

    $$y^{prime}(x)=frac{1}{3} cdot(ln x)^{prime}=frac{1}{3} cdot frac{1}{x}=frac{1}{3 x}$$

    Ответ. $y^{prime}(x)=frac{1}{3 x}$

    236

    проверенных автора готовы помочь в написании работы любой сложности

    Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

    Пример

    Задание. Вычислить производную функции $y(x)=ln 3 x$

    Решение. Искомая производная:

    $$y^{prime}(x)=(ln 3 x)^{prime}$$

    Так как подлогарифмическая функция является сложной, то при нахождении берем вначале
    производную логарифма и умножаем ее на производную подлогарифмической функции. Таким образом, будем иметь:

    $$y^{prime}(x)=frac{1}{3 x} cdot(3 x)^{prime}$$

    Константу выносим за знак производной, а производная от
    $x$ равна единице:

    $$y^{prime}(x)=frac{1}{3 x} cdot 3 cdot(x)^{prime}=frac{1}{x} cdot 1=frac{1}{x}$$

    Ответ. $y^{prime}(x)=frac{1}{x}$

    Читать дальше: производная экспоненциальной функции (e^x)’.

    Источник

    Производная натурального логарифма

    Определение
    Производная натурального логарифма равна отношению единицы и выражения, стоящего под знаком самого логарифма: $$ (ln x)’ = frac{1}{x} $$

    Данная формула выводится из формулы производной логарифма с основанием $ a = e $:

    $$ (ln x)’=(log_e x)’=frac{1}{xln e}=frac{1}{x} $$

    Примеры решений

    Пример 1
    Найти производную натурального логарифма во второй степени: $$ y(x) = ln^2 x $$
    Решение

    Чему равна производная натурального логаримфа известно из определения. Но в данном случае есть степень, поэтому функция сложная. Берем производную степенной функции по правилу: $ (x^p)’ = px^{p-1} $, а затем умножаем на производную логарифма:

    $$ y'(x) = (ln^2 x)’ = 2ln x cdot (ln x)’ = 2ln x cdot frac{1}{x} = frac{2ln x}{x} $$

    Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
    Ответ
    $$ y'(x) = frac{2ln x}{x} $$
    Пример 2

    Найти производную натурального логарифма сложной функции:

    $$ y(x) = ln cos x $$
    Решение

    Логарифм косинуса представляет собой сложную функцию. Поэтому сначала берем производную от натурального логарифма, а затем производную от косинуса по правилу: $ (cos x)’ = -sin x $

    $$ y'(x) = (ln cos x)’ = frac{1}{cos x} cdot (cos x)’ = frac{-sin x}{cos x} = -tg x $$
    Ответ
    $$ y'(x) = -tg x $$
    Источник

    Добавить комментарий