Как найти производную от напряжения

Резисторы параллельно

Интегрирующая цепь RC

Рассмотрим электрическую цепь из резистора сопротивлением R и конденсатора ёмкостью C, представленную на рисунке.

Элементы R и C соединены последовательно, значит, ток в их цепи можно выразить, исходя из производной напряжения заряда конденсатора dQ/dt = C(dU/dt) и закона Ома U/R. Напряжение на выводах резистора обозначим U_R.
Тогда будет иметь место равенство:

Проинтегрируем последнее выражение . Интеграл левой части уравнения будет равен U out + Const . Перенесём постоянную составляющую Const в правую часть с тем же знаком.
В правой части постоянную времени RC вынесем за знак интеграла:

В итоге получилось, что выходное напряжение U out прямо-пропорционально интегралу напряжения на выводах резистора, следовательно, и входному току I in.
Постоянная составляющая Const не зависит от номиналов элементов цепи.

Чтобы обеспечить прямую пропорциональную зависимость выходного напряжения U out от интеграла входного U in, необходима пропорциональность входного напряжения от входного тока.

Нелинейное соотношение U in/I in во входной цепи вызвано тем, что заряд и разряд конденсатора происходит по экспоненте e -t/τ , которая наиболее нелинейна при t/τ ≥ 1, то есть, когда значение t соизмеримо или больше τ.
Здесь t — время заряда или разряда конденсатора в пределах периода.
τ = RC — постоянная времени — произведение величин R и C.
Если взять номиналы RC цепи, когда τ будет значительно больше t, тогда начальный участок экспоненты для короткого периода (относительно τ) может быть достаточно линейным, что обеспечит необходимую пропорциональность между входным напряжением и током.

Для простой цепи RC постоянную времени обычно берут на 1-2 порядка больше периода переменного входного сигнала, тогда основная и значительная часть входного напряжения будет падать на выводах резистора, обеспечивая в достаточной степени линейную зависимость U in/I in ≈ R.
В таком случае выходное напряжение U out будет с допустимой погрешностью пропорционально интегралу входного U in.
Чем больше величины номиналов RC, тем меньше переменная составляющая на выходе, тем более точной будет кривая функции.

В большинстве случаев, переменная составляющая интеграла не требуется при использовании таких цепей, нужна только постоянная Const, тогда номиналы RC можно выбирать по возможности большими, но с учётом входного сопротивления следующего каскада.

В качестве примера, сигнал с генератора — положительный меандр 1V периодом 2 mS подадим на вход простой интегрирующей цепи RC с номиналами:
R = 10 kOhm, С = 1 uF. Тогда τ = RC = 10 mS.

В данном случае постоянная времени лишь в пять раз больше времени периода, но визуально интегрирование прослеживается в достаточной степени точно.
График показывает, что выходное напряжение на уровне постоянной составляющей 0.5в будет треугольной формы, потому как участки, не меняющиеся во времени, для интеграла будут константой (обозначим её a), а интеграл константы будет линейной функцией. ∫adx = ax + Const. Величина константы a определит тангенса угла наклона линейной функции.

Проинтегрируем синусоиду, получим косинус с обратным знаком ∫sinxdx = -cosx + Const.
В данном случае постоянная составляющая Const = 0.

Если подать на вход сигнал треугольной формы, на выходе будет синусоидальное напряжение.
Интеграл линейного участка функции — парабола. В простейшем варианте ∫xdx = x 2 /2 + Const.
Знак множителя определит направление параболы.

Недостаток простейшей цепочки в том, что переменная составляющая на выходе получается очень маленькой относительно входного напряжения.

Рассмотрим в качестве интегратора Операционный Усилитель (ОУ) по схеме, показанной на рисунке.

С учётом бесконечно большого сопротивления ОУ и правила Кирхгофа здесь будет справедливо равенство:

Напряжение на входах идеального ОУ здесь равно нулю, тогда на выводах конденсатора U_C = U out = — U in .
Следовательно, U out определится, исходя из тока общей цепи.

При номиналах элементов RC, когда τ = 1 Sec, выходное переменное напряжение будет равно по значению интегралу входного. Но, противоположно по знаку. Идеальный интегратор-инвертор при идеальных элементах схемы.

Дифференцирующая цепь RC

Рассмотрим дифференциатор с применением Операционного Усилителя.

Идеальный ОУ здесь обеспечит равенство токов I_R = — I_C по правилу Кирхгофа.
Напряжение на входах ОУ равно нулю, следовательно, выходное напряжение U out = U_R = — U in = — U_C .
Исходя из производной заряда конденсатора, закона Ома и равенства значений токов в конденсаторе и резисторе, запишем выражение:

Отсюда видим, что выходное напряжение U out пропорционально производной заряда конденсатора dU in /dt , как скорости изменения входного напряжения.

При величине постоянной времени RC, равной единице, выходное напряжение будет равно по значению производной входного напряжения, но противоположно по знаку. Следовательно, рассмотренная схема дифференцирует и инвертирует входной сигнал.

Производная константы равна нулю, поэтому постоянная составляющая при дифференцировании на выходе будет отсутствовать.

В качестве примера, подадим на вход дифференциатора сигнал треугольной формы. На выходе получим прямоугольный сигнал.
Производная линейного участка функции будет константой, знак и величина которой определится наклоном линейной функции.

Для простейшей дифференцирующей цепочки RC из двух элементов используем пропорциональную зависимость выходного напряжения от производной напряжения на выводах конденсатора.

Если взять номиналы элементов RC, чтобы постоянная времени была на 1-2 порядка меньше длины периода, тогда отношение приращения входного напряжения к приращению времени в пределах периода может определять скорость изменения входного напряжения в определённой степени точно. В идеале это приращение должно стремиться к нулю. В таком случае основная часть входного напряжения будет падать на выводах конденсатора, а выходное будет составлять незначительную часть от входного, поэтому для вычислений производной такие схемы практически не используются.

Наиболее часто дифференцирующие и интегрирующие цепи RC применяют для изменения длины импульса в логических и цифровых устройствах.
В таких случаях номиналы RC рассчитывают по экспоненте e -t/ RC исходя из длины импульса в периоде и требуемых изменений.
Например, ниже на рисунке показано, что длина импульса T i на выходе интегрирующей цепочки увеличится на время 3τ. Это время разряда конденсатора до 5% амплитудного значения.

На выходе дифференцирующей цепи амплитудное напряжение после подачи импульса появляется мгновенно, так как на выводах разряженного конденсатора оно равно нулю.
Далее следует процесс заряда и напряжение на выводах резистора убывает. За время 3τ оно уменьшится до 5% амплитудного значения.

Здесь 5% — величина показательная. В практических расчётах этот порог определится входными параметрами применяемых логических элементов.

Замечания и предложения принимаются и приветствуются!

Производная — напряжение

Производная напряжения стабилизирует автоматическую систему регулирования возбуждения прежде всего при холостом ходе генератора. [1]

Производная напряжения по плотности тока ( дифференциальное сопротивление) по-разному зависит от плотности тока при разных режимах работы ТЭ. [3]

Определяются также две конвективные производные и вращательная производная напряжения . [4]

Сигналы отклонения напряжения генератора от заданного значения и производная напряжения формируются в блоке напряжения ВН. Для повышения быстродействия регулятора в нем используется двухканальная схема измерения отклонения напряжения генератора от заданного значения. Быстродействующий канал построен на измерении отклонения амплитудного значения напряжения, а инерционный — отклонения среднего значения трехфазного напряжения от того же значения. Синхронное измерение отклонения амплитудного значения осуществляется отдельно для каждой фазы напряжения генератора, а результаты суммируются. При этом с целью исключения влияния высших гармонических в кривой напряжения измеряется интеграл разности между амплитудой напряжения и заданной величиной за период. [5]

At / ( отклонение напряжения) и U ( производная напряжения ), выход которых пропорционален указанным величинам. [7]

Этот элемент воздействует на регулятор / так, что если производная напряжения электрофильтра положительна, оно монотонно повышается. Если производная отрицательна — режим вблизи пробоя, происходит снижение напряжения. [8]

Напряжение на конденсаторе пропорционально интегралу от тока, а значит, ток есть производная напряжения . S приведены оба способа дифференцирования. Напряжение, предназначенное для питания последующей цепи, получается на небольшом сопротивлении, включенном последовательно с конденсатором. В обоих случаях работа схем усложняется за счет присутствия сопротивления. [10]

Компенсатор, показанный на рис. 60, г, позволяет увеличить точность компенсации остаточного тока за счет того, что в ней вторая производная напряжения , пропорциональная остаточному току, аппроксимируется линейно изменяющимся во времени напряжением, что ближе отвечает поведению компенсируемой величины остаточного тока. При использовании такого компенсатора в принципе увеличивается точность компенсации остаточного тока за счет более точного учета зависимости второй производной выходного напряжения компенсатора. [11]

Устройства АОСН непосредственно контролируют снижение напряжения с учетом его длительности. Для повышения быстроты действия может использоваться производная напряжения . В тех случаях, когда не обеспечивается достаточная эффективность при контроле напряжения в месте установки устройства, можно применять более сложные устройства с фиксацией повреждений в разных точках энергосистем и телепередачей сигналов. [12]

ИПН — измерительный преобразователь напряжения, ФПН — формирователь сигнала производной напряжения, ИПЧ — измерительный преобразователь частоты, ФПЧ — формирователь сигнала производной частоты, ИПАТ — измерительный преобразователь активного тока, ИПРТ — то же реактивного тока, РТВ — регулятор тока возбуждения, И11ТВ — измерительный преобразователь тока возбуждения, ИПНС — то же напряжения сети, Т — таймер, Пр — процессор, ОЗУ — оперативное запоминающее устройство, ПЗУ — постоянное запоминающее устройство, И1 — интерфейсный блок, М — мультиплексор, БУА — блок управления п адресации, К — коммутатор, МОИ — модуль обмена информации, АЦП — аналого-цифровой преобразователь, ДАЛ — га: фро-аналоговый преобразователь, У СО — устройство связи с объектом. МУ — модуль укно-женпя — МВДИ — модули ввода и вывода дискретной информации, II — пульт регулятора, ПИУ — прибор пндпкащш универсальный, HP — клавишный регистр, U — напряжение, V — производная напряжения , / и / — частота п ее производная, / а п If — активный п реактивный токи генератора; if — ток возбуждении, с7с — напряжение сети. [14]

В моменты времени t и t2 ( рис. 1.6, б) восстанавливающаяся прочность равна напряжению дуги, и первая производная напряжения по времени равна нулю. Действительно, прочность промежутка равна напряжению дуги, когда подводимая к дуге и отводимая от нее мощности становятся равными друг другу. В это время производная напряжения дуги ид по времени t должна быть равной нулю. [15]

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.
СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ.

Электромагнитные колебания — взаимосвязанные колебания электрического и магнитного полей.

Электромагнитные колебания появляются в различных электрических цепях. При этом колеблются величина заряда, напряжение, сила тока, напряженность электрического поля, индукция магнитного поля и другие электродинамические величины.

Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.

Это затухающие колебания, так как сообщенная системе энергия расходуется на нагревание и другие процессы.

Вынужденные электромагнитные колебания — незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.

Электромагнитные колебания описываются теми же законами, что и механические, хотя физическая природа этих колебаний совершенно различна.

Электрические колебания — частный случай электромагнитных, когда рассматривают колебания только электрических величин. В этом случае говорят о переменных токе, напряжении, мощности и т.д.

Колебательный контур — электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R.

Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует).

Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k

величины, характеризующие состояние системы:

величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .

ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ

Можно показать, что уравнение свободных колебаний для зарядаq = q(t) конденсатора в контуре имеет вид

где q» — вторая производная заряда по времени. Величина

является циклической частотой. Такими же уравнениями описываются колебания тока, напряжения и других электрических и магнитных величин.

Одним из решений уравнения (1) является гармоническая функция

Период колебаний в контуре дается формулой (Томсона):

Величина φ = ώt + φ , стоящая под знаком синуса или косинуса, является фазой колебания.

Фаза определяет состояние колеблющейся системы в любой момент времени t.

Ток в цепи равен производной заряда по времени, его можно выразить

Чтобы нагляднее выразить сдвиг фаз, перейдем от косинуса к синусу

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

1. Гармоническая ЭДС возникает, например, в рамке, которая вращается с постоянной угловой скоростью в однородном магнитном поле с индукцией В. Магнитный поток Ф , пронизывающий рамку с площадью S ,

где- угол между нормалью к рамке и вектором магнитной индукции .

По закону электромагнитной индукции Фарадея ЭДС индукции равна

где — скорость изменения потока магнитной индукции.

Гармонически изменяющийся магнитный поток вызывает синусоидальную ЭДС индукции

где — амплитудное значение ЭДС индукции.

2. Если к контуру подключить источник внешней гармонической ЭДС

то в нем возникнут вынужденные колебания, происходящие с циклической частотой ώ, совпадающей с частотой источника.

При этом вынужденные колебания совершают заряд q, разность потенциалов u , сила тока i и другие физические величины. Это незатухающие колебания, так как к контуру подводится энергия от источника, которая компенсирует потери. Гармонически изменяющиеся в цепи ток, напряжение и другие величины называют переменными. Они, очевидно, изменяются по величине и направлению. Токи и напряжения, изменяющиеся только по величине, называют пульсирующими.

В промышленных цепях переменного тока России принята частота 50 Гц.

Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени. Необходимо использовать среднюю за период мощность — отношение суммарной энергии W, поступающей в цепь за период, к величине периода:

Поэтому количество теплоты, выделится за время Т:

Действующее значение I силы переменного тока равно силе такого постоянного тока, который за время, равное периоду T, выделяет такое же количество теплоты, что и переменный ток:

Отсюда действующее значение тока

Аналогично действующее значение напряжения

Трансформатор — устройство, увеличивающее или уменьшающее напряжение в несколько раз практически без потерь энергии.

Трансформатор состоит из стального сердечника, собранного из отдельных пластин, на котором крепятся две катушки с проволочными обмотками. Первичная обмотка подключается к источнику переменного напряжения, а к вторичной присоединяют устройства, потребляющие электроэнергию.

называют коэффициентом трансформации. Для понижающего трансформатора К > 1, для повышающего

Пример. Заряд на пластинах конденсатора колебательного контура изменяется с течением времени в соответствии с уравнением . Найдите период и частоту колебаний в контуре,циклическую частоту, амплитуду колебаний заряда и амплитуду колебаний силы тока. Запишите уравнение , выражающее зависимость силы тока от времени.

Из уравнения следует, что . Период определим по формуле циклической частоты

Зависимость силы тока от времени имеет вид:

Ответ: заряд совершает колебания с периодом 0,02 с и частотой 50 Гц, которой соответствует циклическая частота 100 рад/с, амплитуда колебаний силы тока равна 510 3 А, ток изменяется по закону:

i=-5000 sin100t

Источник

Таким образом, при достаточно общих
предположениях, хорошо выполняющихся
на практике, электродвижущую силу
(э.д.с.), переменное напряжение и ток,
можно представить в виде произведения
случайной амплитуды Um(t)
и гармонической функции случайной фазы
Ψ (t).

Как известно, такое представление
электрических величин требует наложения
определенных ограничений на сомножители,
которые в общем случае нельзя выбирать
произвольно. Для устранения неоднозначности
наиболее целесообразно использовать
представление переменного напряжения
в электрической цепи в комплексном
аналитическом виде:

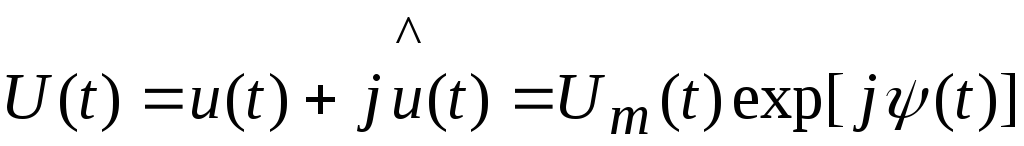; (2.4)

где
; (2.5)

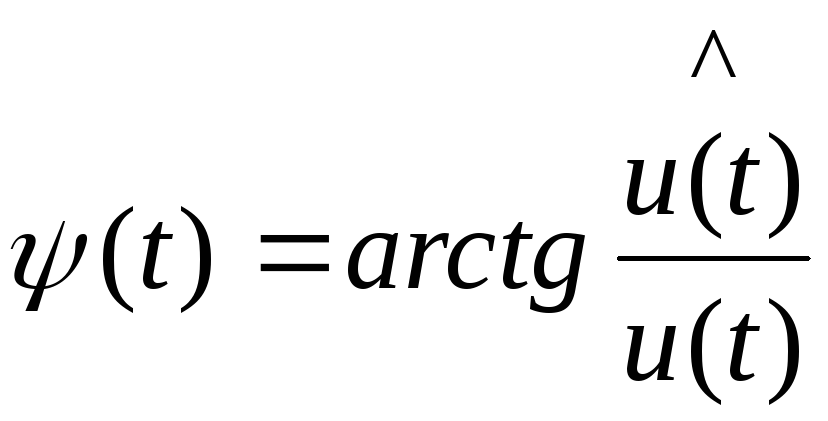, (2.6)

u(t)
‑ реальное напряжение в электрической
цепи;

-дополняющая
компонента, связанная с u(t)
преобразованием Гильберта:

(2.7)

(2.8)

При этом выражение для реального
напряжения может быть представлено в
виде:

(2.9)

Такое
представление переменного (в общем
случае случайного) напряжения u(t)
имеет следующие преимущества:

а) амплитуда и фаза напряжения связаны
между собой единственным образом, что
исключает неоднозначность;

б) комплексный спектр напряжения
U()отличен
от нуля только при положительных,
причем спектры напряженийu(t)исовпадают по форме и отличаются только
масштабным множителем, т.е. спектр
комплексного напряжения в этом случае
имеет ту же структуру, что и спектр
исходного реального напряженияu(t);

в) представление переменного напряжения
в комплексном виде (2.9) может быть
применимо как к быстро, так и к медленно
изменяющимся напряжениям в электрических
и электронных цепях,

В тех случаях, когда зависимость
напряжения от времени u(t)характеризуется быстрым изменением со
средней круговой частотойср=2fср,
можно считать, что за время, равное по
крайней мере нескольким периодам,
амплитуда и фаза остаются практически
неизменными.

Выражение для комплексного аналитического
представления переменного флуктуирующего
напряжения может быть записано в виде:

(2.10)

или

(2.11)

где

–
комплексная огибающая узкополосного
случайного процесса:

(2.12)

–
средняя круговая частота, определяемая
выражением:

(2.13)

где
-дисперсия
флуктуаций напряжения, квадрат которой
определяется из выражения:

(2.14)

– энергетический спектр напряжения,
определяющийся выра­жением:

(2.15)

2.3.2. Учет флуктуаций амплитуды и фазы при выполнении операций диференцирования и интегрирования

Флуктуации амплитуды и фазы напряжения
и тока в электрической цепи необ­ходимо
учитывать при выполнении операций
дифференцирования и ин­тегрирования.
Пусть, например,

(2.16)

В случае, когда
или,
т.е. амплитуда и фаза постоянны, первая
производная имеет вид:

(2.17)

Собственно n-ая производная равна

(2.18)

Из
рассмотрения выражений (2.17) и (2.18) видно,
что операция дифференцирования
эквивалентна умножению исходного
выражения ( 2.16) на «j».

Аналогично оказывается, что операция
интегрирования эквивалентна делению
выражения (2.16.) на «j».
Соотношения (2.17), (2.18) положены в основе
широко применяемого символического
метода расчета электрических цепей

При
анализе или синтезе реальных электрических
и электронных цепей с учетом флуктуаций
амплитуды и фазы напряжения производную
по времени от выражения (2.I6.)
необходимо представлять в следующем
виде:

(2.19)

Соответственно
n-ая производная по аналогии
с (2.19) принимает вид:

(2.20)

Как следует из выражений (2.19) и(2.20),
оператор « j« , используемый при символическом
методе, следует везде заменить на
оператор:

. (2.21.)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #