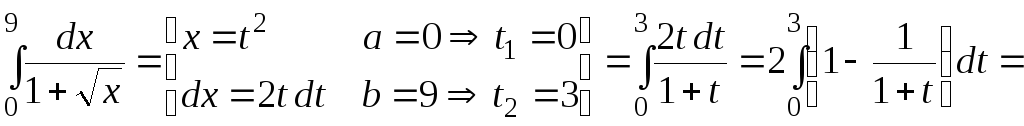Определенный интеграл с переменным верхним пределом
До сих пор мы рассматривали определенный
интеграл с постоянными пределами
интегрирования
и
.
Если оставить постоянным нижний предел
интегрирования
,
а верхний
изменять так, чтобы
,
то величина интеграла будет изменяться.
Интеграл вида
называется определенным интегралом с
переменным верхним пределом и является
функцией верхнего предела
.
Здесь для удобства переменная
интегрирования обозначена буквой
,
а верхний предел интегрирования —
буквой
.
С геометрической точки зрения, функция
в случае
0
представляет собой площадь заштрихованной
на рисунке криволинейной трапеции.
Найдем производную от
по
,
т. е. производную определенного
интеграла по верхнему пределу.
Теорема. Производная определенного
интеграла от непрерывной функции
no его переменному
верхнему пределу существует и равна
подынтегральной функции, в которой
вместо переменной интегрирования
подставлено значение верхнего
предела:

Доказательство. Возьмем любую точку
и придадим ей приращение
так, чтобы
.
Тогда
.
Используя аддитивность определенного
интеграла, имеем
.
Применяя теорему о среднем, получаем
,
где
.
По определению производной, учитывая,
что функция непрерывна, получим:
.
⊠
Из теоремы следует, что определенный
интеграл с переменным верхним пределом
является первообразной для подынтегральной
функции
на отрезке
.
,
т. е. установлена связь между
неопределенным и определенным
интегралами.
Так как интеграл
существует для любого значения
,то
данная теорема является одновременно
и теоремой о существовании первообразной
у каждой непрерывной функции
.
Этой первообразной может быть
определенный интеграл с переменным
верхним пределом.
Формула Ньютона-Лейбница
Теорема. Значение определенного
интеграла на отрезке
от непрерывной функции
равно разности значений любой ее
первообразной, вычисленной при
и
:
.
Доказательство. Пусть функция
,
непрерывная на отрезке
,
следовательно, она имеет на этом отрезке
первообразную, например
.
Пусть
— любая другая первообразная функция
на том же отрезке
.
Так как первообразные
и
отличаются друг от друга постоянным
слагаемым, то имеет место равенство
,
,
.
Подставляя в это равенство значение
,
получим
.
Полагая
и обозначая переменную интегрирования
через
,
получаем основную формулу интегрального
исчисления:
.
которая называется формулой Ньютона —
Лейбница.
⊠
Формула Ньютона — Лейбница позволяет
избавиться от вычисления определенных
интегралов как пределов интегральных
сумм, и задача вычисления определенного
интеграла сводится к задаче вычисления
неопределенного интеграла.
Основные методы
вычисления определенного интеграла
Вычисление простейших интегралов с
помощью формулы Ньютона — Лейбница.
Если
— одна из первообразных непрерывной
на
функции
,
то справедлива формула Ньютона —
Лейбница
Эта формула позволяет свести вычисление
определенного интеграла к вычислению
неопределенного.
Пример. Вычислить
.
Решение.
.
Замена переменной (подстановка) в
определенном интеграле.
Этот метод, как и в случае неопределенного
интеграла, позволяет упростить вычисления,
т. е. привести подынтегральное выражение
к соответствующей табличной форме.
Применение замены переменной в
определенном интеграле базируется на
следующей теореме.
Теорема. Если функция
непрерывна на отрезке
,
а функция
непрерывно дифференцируема на отрезке
,
причем
,
то справедлива формула замены переменной
в определенном интеграле:

Доказательство. Пусть выполняются
условия теоремы и
— первообразная для функции
на отрезке
. По формуле Ньютона — Лейбница
⊠
Отметим, что при вычислении интеграла
методом замены переменной одновременно
с преобразованием подынтегрального
выражения изменяются соответственно
и пределы интегрирования.
Пример. Вычислить
.
Решение.
Интегрирование по частям в определенном
интеграле. Пусть
и
— дифференцируемые на отрезке
функции переменной
.
Тогда
.
Проинтегрируем обе части последнего
равенства на отрезке
По формуле Ньютона — Лейбница
.
Следовательно,
Эта формула называется формулой
интегрирования по частям в определенном
интеграле.
Пример. Вычислить
.
Решение. Применим формулу интегрирования
по частям в определенном интеграле
.
Вычисление
площадей плоских фигур
в прямоугольной
системе координат
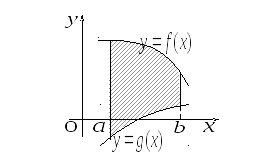
Из геометрического смысла определенного
интеграла следует, что если
r0
,
то площадь криволинейной трапеции,
ограниченной кривой
,
осью
и прямыми
,
может быть вычислена по формуле
.
Если
0
,
то
.
Если подынтегральная функция
конечное число раз меняет знак на
отрезке
,
то площадь заштрихованной на
рисунке фигуры
равна алгебраической сумме площадей
соответствующих криволинейных трапеций,
лежащих над осью
(со знаком « + ») и под этой осью (со
знаком « — »).
Для того чтобы получить общую площадь
заштрихованной отрезок интегрирования
надо разбить на частичные отрезки,
на которых функция
сохраняет знак, то есть

Если надо вычислить площадь фигуры,
ограниченной линиями
,
,
то эту площадь рассматривают как разность
площадей двух криволинейных трапеций
и
.
В этом случае
,
если
.
В случае, когда разность
не сохраняет знак на отрезке
,
этот отрезок разбивают на частичные
отрезки, на каждом из которых функция
сохраняет знак.
Пример. Определить площадь фигуры,
ограниченной кривыми
,
,
.
Решение. Решив систему уравнений
найдем точки
,
пересечения параболы
и прямой
.
Следовательно,
(кв.ед.)
Вычисление
площадей плоских фигур
в полярной
системе координат
Пусть требуется вычислить площадь
фигуры, ограниченной линией
,
заданной в полярной системе координат
уравнением
,
.
За базовую фигуру в полярной системе
координат принимается криволинейный
сектор — фигура, ограниченная линией
и радиусами-векторами
,
.
При этом криволинейный сектор будем
считать правильной фигурой, т. е. такой,
что любой луч
,
,
исходящий из полюса
,
пересекает линию
не более, чем в одной точке. Будем также
предполагать, что функция
непрерывна на отрезке
.
Для вычисления площади криволинейного
сектора
применим алгоритм составления
интегральной суммы с последующим
предельным переходом к определенному
интегралу.
1. Разобьем отрезок
на
частичных отрезков точками
.
Обозначим
,
.
Проведем лучи
,
.
Тогда криволинейный сектор
разобьется на
частичных криволинейных секторов.
2. На каждом частичном отрезке
,
выберем произвольным образом точку
и найдем значения функции
в этих точках:
.
3. Предположим, что на каждом из частичных
отрезков
функция
постоянна и совпадает со значением
.
Тогда каждый частичный криволинейный
сектор можно заменить круговым сектором
с радиусом
и центральным углом
.
Площадь такого кругового сектора
вычисляется по формуле
.
Тогда
. (1)
Приближенное равенство тем точнее, чем
меньше частичные отрезки, т. е. чем больше
.
4. За точное значение площади S
криволинейного сектора
можно принять предел интегральной суммы
(1) при
.
.
Таким образом, площадь криволинейного
сектора вычисляется по формуле
.
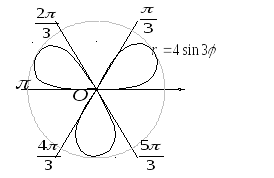
Пример. Вычислить площадь фигуры,
ограниченной
,
0.
Решение. Найдем область определения
данной функции.
0
0
0
,
при
,
при
,
при
,
при
,
На интервале от 0 до
функция
определена на трех участках. Изобразим
график функции на рисунке.
Так как функция периодическая, то
Несобственные
интегралы
Несобственные интегралы являются
обобщением определенных интегралов в
случаях бесконечных промежутков
интегрирования и неограниченных функций.
Несобственные
интегралы с бесконечными
пределами
интегрирования (первого рода)
Пусть функция
непрерывна на промежутке
. Тогда она будет непрерывной на любом
конечном отрезке
,
.
Для функции
,
непрерывной на
,
существует определенный интеграл
,
зависящий от верхнего предела
интегрирования. Этот интеграл определяет
некоторую величину, например площадь
криволинейной трапеции, ограниченной
графиком функции
0,
прямыми
и осью
. Будем неограниченно увеличивать
верхний предел интегрирования (+).
При этом возможны два случая: либо
при
+
имеет предел, либо не имеет.
Определение. Несобственным интегралом
с бесконечным верхним пределом
интегрирования от непрерывной функции
на промежутке
+)называется
предел
при
+:
(1)
Аналогично определяется несобственный
интеграл с бесконечным нижним пределом
интегрирования от непрерывной функции
на промежутке (–:
(2)
Если пределы в правых частях формул (1)
и (2) существуют и конечны, то соответствующие
несобственные интегралы называются
сходящимися, если пределы не существуют
или бесконечны,— то расходящимися.
Несобственный интеграл с двумя
бесконечными пределами интегрирования
от непрерывной функции
на промежутке ]–;+[,
обозначаемый
,
предварительно представляют в виде
,
Тогда по определению
(3)
причем этот несобственный интеграл
называется сходящимся, если оба предела
существуют. Если хотя бы один из пределов
не существует или бесконечен, то
несобственный интеграл
называется расходящимся.
Интегралы (1) — (3)называются также
несобственными интегралами первого
рода.
С геометрической точки зрения сходящийся
несобственный интеграл
означает, что фигура, ограниченная
кривой
0,
прямыми
,
у = 0 и бесконечно вытянутая в направлении
оси
,
имеет конечную площадь
.
Аналогичная геометрическая интерпретация
имеет место для сходящихся несобственных
интегралов (2) и (3).
Пример. Исследовать на сходимость
интеграл
.
Решение.
.
Итак интеграл
сходится и определяет площадь
бесконечной криволинейной трапеции,
изображенной на рисунке.
Пример. Исследовать на сходимость
интеграл
Решение.
–.
т. е. данный интеграл расходится. а
площадь S бесконечной
криволинейной трапеции, изображенной
на рисунке не ограничена.
Критерии сходимости несобственных
интегралов первого рода
Приведем без доказательства три теоремы,
с помощью которых можно исследовать
вопрос о сходимости некоторых несобственных
интегралов первого рода.
Теорема. (признак сравнения). Если
на промежутке [;+[
определены две неотрицательные функции
и
,
интегрируемые на каждом конечном отрезке
,
причем 0
для
[
;+[,
то из сходимости интеграла
следует сходимость интеграла,
а из расходимости интеграла
следует
расходимость интеграла
.
Теорема (предельный признак сравнения).
Если на промежутке [;+¥[
определены две положительные функции
и
,
интегрируемые на любом конечном отрезке
, и существует конечный предел
,
то несобственные интегралы
и
сходятся или расходятся одновременно.
Теорема. Если на промежутке
[;+¥[функция
меняет знак и несобственный интеграл
сходится, то сходится также и
.
Отметим, что несобственный интеграл
называют абсолютно сходящимся, если
сходится интеграл
.
Несобственные
интегралы от
неограниченных
функций (второго рода).
Определение. Несобственным интегралом
от функции
,
непрерывной на промежутке
и имеющей бесконечный разрыв в точке
,
или несобственным интегралом второго
рода называется предел интеграла
при
:
. (4)
Аналогично если функция
имеет бесконечный разрыв в точке
,
то полагают
. (5)
Если же функция
имеет разрыв второго рода в некоторой
внутренней точке отрезка
,
то, пользуясь свойством аддитивности
определенного интеграла, данный интеграл
представляют в виде суммы двух
интегралов:
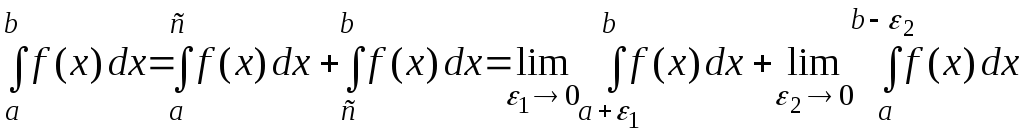
Если пределы в правых частях формул (4)
— (6) существуют и конечны, то
соответствующие несобственные интегралы
от разрывной функции в точках
,
и
называются сходящимися, в противном
случае — расходящимися.
С геометрической точки зрения сходящийся
несобственный интеграл второго рода
означает, что фигура, ограниченная
кривой
0,
прямыми
,
и бесконечно вытянутая в направлении
оси
имеет конечную площадь
.
Пример. Исследовать на сходимость
несобственный интеграл.
Решение. При
и при
подынтегральная функция имеет бесконечный
разрыв, следовательно
Итак, несобственный интеграл сходится
и определяет площадь
бесконечной криволинейной трапеции,
изображенной на рисунке.
Пример. Исследовать на сходимость
несобственный интеграл
.
Решение. При
подынтегральная функция имеет бесконечный
разрыв, следовательно
является несобственным интегралом
второго рода, тогда по определению
+.
т. е. несобственный интеграл расходится.
Геометрически это означает, что площадь
криволинейной трапеции, изображенной
на рисунке, не ограничена.
У этого термина существуют и другие значения, см. Список объектов, названных в честь Лейбница.
У этого термина существуют и другие значения, см. Формула Лейбница.
Формулой Лейбница в интегральном исчислении называется правило дифференцирования под знаком интеграла, зависящего от параметра, пределы которого зависят от переменной дифференцирования. Формула названа в честь немецкого математика Готфрида Лейбница.
Формулировка[править | править код]
Пусть функция 

![[alpha ,;beta ]times [c,;d]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a709a367d611a56931e6346fc1fcde7c1c6f8a7a)
![[alpha ,;beta ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/46ea054a4d5d2df49501fdad2dfa370a8134b340)


![[c,;d]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8eef5081f39687e139249c6f243c160e4e1dc80)


![[c,;d]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8eef5081f39687e139249c6f243c160e4e1dc80)
Литература[править | править код]
- Ильин В. А., Садовничий В. А., Сендов Бл. Х. Математический анализ. Ч.1. — 2-е изд., перераб. — М.: Изд-во МГУ, 1985. — 662 с.
|
|
Это статья-заготовка по математике. Помогите Википедии, дополнив эту статью, как и любую другую. |
Интеграл с переменным верхним пределом. Вычисление определенных интегралов
разделов
от теории до практики
примеров
Примеры решения задач
видео
Примеры решения задач
-
Интеграл с переменным верхним пределом.
Начать изучение
-
Непрерывность интеграла.
Начать изучение
-
Дифференцируемость интеграла.
Начать изучение
-
Существование первообразной у непрерывной функции.
Начать изучение
-
Вычисление определенных интегралов.
Начать изучение
-
Формула Ньютона Лейбница.
Начать изучение
-
Замена переменного.
Начать изучение
-
Интегрирование по частям.
Начать изучение
-
Простейшие дифференциальные уравнения.
Начать изучение
-
Дифференциальные уравнения первого порядка.
Начать изучение
-
Дифференциальные уравнения второго порядка.
Начать изучение
Интеграл с переменным верхним пределом.
Определение.
Если функция (f) интегрируема на отрезке ([a, b]), то для любого (x in [a, b]) существует интеграл
$$
F(x) = intlimits_a^x f(t) dt.label{ref1}
$$
который называется интегралом с переменным верхним пределом.
Непрерывность интеграла.
Теорема 1.
Если функция (f) интегрируема на отрезке ([a, b]), то функция (F(x)) непрерывна на этом отрезке.
Доказательство.
(circ) Пусть (x in [a, b]) и (x + Delta x in [a, b]). Докажем, что
$$
Delta F = F(x + Delta x)- F(x) rightarrow 0 mbox{при} Delta x rightarrow 0.nonumber
$$
В силу свойств интеграла
$$
Delta F = intlimits_a^{x + Delta x} f(t) dt- intlimits_a^x f(t) dt = intlimits_x^{x + Delta x} f(t) dt.label{ref2}
$$
Так как функция (f) интегрируема на отрезке ([a, b]), то она ограничена, то есть
$$
exists M > 0: forall x in [a, b] rightarrow |f(x)| leq M.label{ref3}
$$
Согласно правилу оценки интеграла из eqref{ref2} и eqref{ref3} следует, что
$$
|Delta F| leq left|intlimits_x^{x + Delta x} f(t) dtright| leq M |Delta x|,nonumber
$$
откуда получаем: (Delta F rightarrow 0) при (Delta x rightarrow 0), то есть функция (F) непрерывна в точке (x). Поскольку (x) — произвольная точка отрезка ([a, b]), то функция (F) непрерывна на отрезке ([a, b]). (bullet)
Дифференцируемость интеграла.
Теорема 2.
Если функция (f) интегрируема на отрезке ([a, b]) и непрерывна в точке (x_{0} in [a, b]), то функция (F(x) = displaystyleintlimits_a^x f(t) dt) дифференцируема в точке (x_{0}), причем
$$
F'(x_{0}) = f(x_{0}).label{ref4}
$$
Доказательство.
(circ) Пусть (Delta x neq 0) и (x_{0} + Delta x in [a, b]); тогда при (x = x_{0}) справедливо равенство eqref{ref2}. Докажем, что
$$
sigma = frac{Delta F}{Delta x}- f(x_{0}) rightarrow 0 mbox{при} Delta x rightarrow 0.label{ref5}
$$
Преобразуем (sigma), пользуясь тем, что (displaystyleintlimits_{x_{0}}^{x_{0} + Delta x} dt = Delta x) ( пример здесь). В силу свойств интеграла
$$
sigma = frac{1}{Delta x} intlimits_{x_{0}}^{x_{0} + Delta x} f(t) dt- frac{f(x_{0})}{Delta x} intlimits_{x_{0}}^{x_{0} + Delta x} dt = frac{1}{Delta x} intlimits_{x_{0}}^{x_{0} + Delta x} (f(t)- f(x_{0})) dt,nonumber
$$
откуда
$$
|sigma| = frac{1}{|Delta x|} left|intlimits_{x_{0}}^{x_{0} + Delta x} |f(t)- f(x_{0})| dtright|.label{ref6}
$$
По условию функция (f) непрерывна в точке (x_{0}), то есть для любого (varepsilon > 0) существует число (delta = delta(varepsilon) > 0) такое, что для всех (t in U_{delta}(x_{0})) выполняется неравенство
$$
|f(t)- f(x_{0})| < varepsilon,label{ref7}
$$
где (U_{delta} = {t: |t- x_{0}| < delta}). Пусть (|Delta x| < delta); тогда (|t- x_{0}| leq |Delta x| < delta), так как (t in l), где (l) — отрезок с концами (x_{0}) и (x_{0} + Delta x). Поэтому для всех (Delta x) таких, что (|Delta x| < delta), выполняется неравенство eqref{ref7}. Но тогда из eqref{ref6} следует, что (|sigma| < displaystylefrac{1}{|Delta x|} varepsilon |Delta x| = varepsilon). Таким образом, для любого (varepsilon > 0) найдется число (delta > 0) такое, что для всех (Delta x), удовлетворяющих условию (0 < |Delta x| < delta), выполняется неравенство (displaystyleleft|frac{Delta F}{Delta x}- f(x_{0})right| < varepsilon), то есть выполняется условие eqref{ref5}. Это означает, что справедливо равенство eqref{ref4}. (bullet)
Замечание 1.
Если (x_{0} = a), то равенство eqref{ref4} записывается в виде (F_{+}'(a) = f(a)), а если (x_{0} = b), то в виде (F_{-}'(b) = f(b)).
Существование первообразной у непрерывной функции.
Теорема 3.
Если функция (f) непрерывна на отрезке ([a, b]), то она имеет первообразную на этом отрезке, причем первообразной для функции (f) является интеграл с переменным верхним пределом eqref{ref1}, и поэтому
$$
int f(x) dx = intlimits_a^x f(t) dt + C.label{ref8}
$$
где (C) — произвольная постоянная.
Доказательство.
(circ) Пусть (x) — произвольная точка отрезка ([a, b]). По теореме 2 функция (F(x)), определяемая формулой eqref{ref1}, имеет в точке (x) производную, равную (f(x)), то есть
$$
F'(x) = frac{d}{dx}left(intlimits_a^x f(t) dtright) = f(x).label{ref9}
$$
Согласно определению первообразной функция (F(x)) является первообразной для функции (f(x)) на отрезке ([a, b]), и поэтому справедливо равенство eqref{ref8}. (bullet)
Замечание 2.
Согласно теореме 3 (формула eqref{ref9}) операция интегрирования непрерывной функции с переменным верхним пределом является обратной к операции дифференцирования. Утверждение о том, что производная интеграла с переменным верхним пределом от непрерывной функции равна значению подынтегральной функции при значении аргумента, равном верхнему пределу интеграла, является важнейшим фактом курса математического анализа.
Следствие.
Из теоремы 3 и теоремы о двух первообразных функциях следует, что всякая первообразная (Phi(x)) для функции (f), непрерывной на отрезке ([a, b]), имеет вид
$$
Phi(x) = intlimits_a^x f(t) dt + C, a leq x leq b,label{ref10}
$$
где (C) — постоянная.
Вычисление определенных интегралов.
Формула Ньютона Лейбница.
Теорема 4.
Если функция (f(x)) непрерывна на отрезке ([a, b]) и если (Phi(x)) — какая-нибудь первообразная для (f(x)) на этом отрезке, то справедлива формула Ньютона Лейбница
$$
intlimits_a^b f(x) dx = Phi (b)- Phi (a),label{ref11}
$$
Доказательство.
(circ) Согласно следствию из теоремы 3 существует число (C) такое, что справедливо равенство eqref{ref10}. Подставляя в формулу eqref{ref10} (x = a) и учитывая, что (displaystyleintlimits_a^a f(t) dt = 0), получаем (C = Phi (a)). Поэтому равенство eqref{ref10} можно записать в виде
$$
Phi(x) = intlimits_a^x f(t) dt + Phi (a).label{ref12}
$$
Равенство eqref{ref12} выполняется при любых значениях (x in [a, b]) и, в частности, при (x = b), то есть
$$
Phi(b) = intlimits_a^b f(t) dt + Phi (a),nonumber
$$
откуда следует формула eqref{ref11}, так как величина определенного интеграла не зависит от того, какой буквой обозначается независимое переменное в интеграле. (bullet)
Замечание 3.
Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления и часто записывают в виде
$$
left.intlimits_a^b f(x) dx = Phi(x)right|_{a}^{b}.nonumber
$$
Пример 1.
Доказать, что для любых (m in N, n in N) справедливы равенства:
- $$
intlimits_{- pi}^{pi} sin mx cos nx dx = 0.label{ref13}
$$ - $$
intlimits_{- pi}^{pi} sin^{2} mx dx = intlimits_{- pi}^{pi} cos^{2} nx dx = pi.label{ref14}
$$
Решение.
- (triangle) Воспользовавшись формулой (sin alpha cos beta = displaystylefrac{1}{2}(sin(alpha + beta) + sin (alpha- beta))), получаем
$$
J = intlimits_{- pi}^{pi} sin mx cos nx dx = frac{1}{2} intlimits_{- pi}^{pi} sin (m + n)x dx + frac{1}{2} intlimits_{- pi}^{pi} sin (m- n)x dx.nonumber
$$Если (m neq n), то
$$
J = left.frac{1}{2(m + n)}cos(m + n)xright|_{- pi}^{pi} + left.frac{1}{2(m- n)}cos(m- n)xright|_{- pi}^{pi} = 0,nonumber
$$
так как (cos pi k = (- 1)^{k}) для любого (k in Z). Если (m = n), то
$$
J = frac{1}{2} intlimits_{- pi}^{pi} sin 2nx dx = 0nonumber
$$
для любого (n in mathbb{N}). Таким образом, равенство eqref{ref13} справедливо при любых (m, n in mathbb{N}). - Применяя формулы (sin^{2} alpha = displaystylefrac{1- cos 2 alpha}{2}) и (cos^{2} alpha = displaystylefrac{1 + cos 2 alpha}{2}) и учитывая, что (displaystyleintlimits_{- pi}^{pi} cos 2nx dx = 0) при любом (n in N), a (displaystyleintlimits_{- pi}^{pi} dx = 2pi), получаем равенство eqref{ref14}. (blacktriangle)
Замечание 4.
Определенный интеграл можно использовать для эффективного вычисления предела последовательности, если ее можно рассматривать как последовательность интегральных сумм некоторой интегрируемой функции.
Пример 2.
Найти с помощью интеграла (displaystylelim_{n rightarrow infty} S_{n}), если:
- (S_{n} = displaystylefrac{1^{alpha} + 2^{alpha} + ldots + n^{alpha}}{n^{alpha + 1}}, alpha > 0).
- (S_{n} = displaystylefrac{1}{n + 1} + frac{1}{n + 2} + ldots + frac{1}{2n}).
Решение.
- (triangle) Запишем (S_{n}) в виде (S_{n} = displaystylefrac{1}{n}sum_{k=1}^{n}left(frac{k}{n}right)^{alpha}) и заметим, что (S_{n}) — интегральная сумма для функции (f(x)=x^{alpha}) на отрезке [0,1], соответствующая разбиению (T) этого отрезка на отрезки (Delta_{k} = displaystyleleft[frac{k- 1}{n}, frac{k}{n}right], k = overline{1, n}), каждый из которых имеет длину (displaystylefrac{1}{n}); в качестве точки (xi_{k} in Delta_{k}) берется конец отрезка (Delta_{k}), то есть (xi_{k} = displaystylefrac{k}{n}). Так как (l(T) = displaystylefrac{1}{n} rightarrow 0) при (n rightarrow infty), а функция (x^{alpha}) непрерывна на отрезке ([0,1]), то существует
$$
lim_{n rightarrow infty} S_{n} = intlimits_0^1 x^{alpha} dx = left.frac{x^{alpha + 1}}{alpha + 1}right|_{0}^{1} = frac{1}{alpha + 1}.nonumber
$$ - Так как (S_{n} =displaystylefrac{1}{n}sum_{substack{k=1}}^{substack{n}}frac{1}{1 + k/n})- интегральная сумма для функции (displaystylefrac{1}{1 + x}) на отрезке ([0,1]), то
$$
lim_{n rightarrow infty} S_{n} = intlimits_0^1 frac{dx}{1 + x}=left.ln{(1+x)}right|_{0}^{1} = ln 2. blacktrianglenonumber
$$
Пример 3.
Доказать, что если функция (f) непрерывна на (R), а функции (varphi) и (psi) дифференцируемы на (R), то
$$
frac{d}{dx} left(intlimits_{varphi (x)}^{psi (x)} f(t) dtright) = psi^{‘}(x)f(psi(x))- varphi^{‘}(x)f(varphi(x)).label{ref15}
$$
Решение.
(triangle) Пусть (F) — первообразная для функции (f); тогда по формуле Ньютона-Лейбница находим
$$
intlimits_{varphi (x)}^{psi (x)} f(t) dt = F(t)|_{t = varphi(x)}^{t = psi(x)} = F(psi(x))- F(varphi(x)),nonumber
$$
откуда, используя правило дифференцирования сложной функции и равенство (F^{‘}(t) = f(t)), получаем формулу eqref{ref15}. (blacktriangle)
Замена переменного.
Теорема 5.
Пусть функция (f(x)) непрерывна на интервале ((a_{0}, b_{0})) а функция (varphi(t)) имеет непрерывную производную на интервале ((alpha_{0}, beta_{0})), причем (varphi(t) in (a_{0}, b_{0})) при всех (t in (alpha_{0}, beta_{0})).
Тогда если (alpha in (alpha_{0}, beta_{0})), (beta in (alpha_{0}, beta_{0})), (a = varphi(alpha)), (b = varphi(beta)), тo справедлива формула замены переменного в определенном интеграле
$$
intlimits_a^b f(x) dx = intlimits_{alpha}^{beta} f(varphi(t))varphi^{‘}(t) dt.label{ref16}
$$
Доказательство.
(circ) Так как (a in (a_{0}, b_{0})), (b in (a_{0}, b_{0})), а функция (f(x)) непрерывна на интервале ((a_{0}, b_{0})), то по формуле Ньютона-Лейбница находим
$$
intlimits_a^b f(x) dx = Phi(b)- Phi(a).label{ref17}
$$
где (Phi^{‘}(x) = f(x)) для всех (x in (a_{0}, b_{0})).
Функция (Phi(varphi(t))) является первообразной для функции, стоящей под знаком интеграла в правой части формулы eqref{ref16}, так как
$$
frac{d}{dt}(Phi(varphi(t)) = Phi'(varphi(t))varphi'(t) = f(varphi(t))varphi^{‘}(t).nonumber
$$
Применяя к функции (f(varphi(t))varphi^{‘}(t)) формулу Ньютона-Лейбница и учитывая, что (varphi(alpha) = a, varphi(beta) = b), получаем
$$
intlimits_{alpha}^{beta} f(varphi(t))varphi'(t) dt = Phi(varphi(beta))- Phi(varphi(alpha)) = Phi(b)- Phi(a).label{ref18}
$$
Из равенств eqref{ref17} и eqref{ref18} следует формула eqref{ref16}. (bullet)
Замечание 5.
При условиях теоремы 5 формула eqref{ref16} справедлива как при (alpha leq beta), так и при (alpha > beta).
Формула eqref{ref16} остается в силе и в случае, когда функции (f) и (varphi) заданы соответственно на отрезках ([a, b]) и ([alpha, beta]), причем множество значений функции (varphi) содержится в отрезке ([a, b]), где (a = varphi(alpha), b = varphi(beta)). В этом случае под производными сложной функции (Phi(varphi(t))) и концах отрезка ([alpha, beta]) понимаются соответствующие односторонние производные.
Пример 4.
Вычислить (J = displaystyleintlimits_0^R sqrt{R^{2}- x^{2}} dx).
Решение.
(Delta) Полагая (x = R sin t), где (displaystyle 0 leq t leq frac{pi}{2}), получаем (sqrt{R^{2}- x^{2}} = R cos t, dx = R cos t dt). По формуле eqref{ref16} находим
$$
J = R^{2} intlimits_0^{pi/2} cos^{2}t dt = frac{pi R^{2}}{4}. blacktrianglenonumber
$$
Пример 5.
Пусть функция (f) непрерывна на отрезке ([-a, a]). Доказать, что:
- если (f) — нечетная функция, то
$$
intlimits_{-a}^a f(x) dx = 0; nonumber
$$ - если (f) — четная функция, то
$$
intlimits_{-a}^a f(x) dx = 2 intlimits_0^a f(x) dx.label{ref19}
$$
Решение.
- (triangle) Если (f) — нечетная функция, то есть (f(-x) =- f(x)) для всех (x in [-a, a]), то, полагая (x = -t) и используя формулу eqref{ref16}, получаем
$$
intlimits_{-a}^0 f(x) dx =- intlimits_{-a}^0 f(-t) dt = intlimits_0^a (-f(t)) dt =- intlimits_0^a f(x) dx,nonumber
$$
откуда следует, что
$$
intlimits_{-a}^a f(x) dx = intlimits_{-a}^0 f(x) dx + intlimits_0^a f(x) dx = 0.nonumber
$$ - Если (f) — четная функция, то (displaystyleintlimits_{-a}^0 f(x) dx = intlimits_0^a f(x) dx), откуда следует равенство eqref{ref19}. (blacktriangle)
Пример 6.
Доказать, что если (f) — непрерывная на (R) периодическая с периодом (T) функция, то для любого (a in R) справедливо равенство
$$
intlimits_a^{a + T} f(x) dx = intlimits_0^T f(x) dx.label{ref20}
$$
Решение.
(triangle) Используя свойства интеграла, запишем равенство
$$
intlimits_a^{a + T} f(x) dx = intlimits_a^0 f(x) dx + intlimits_0^T f(x) dx + intlimits_T^{a + T} f(x) dx.label{ref21}
$$
Полагая (x = t + T) и учитывая, что функция (f) определена на (R) и (f(t + T) = f(t)) для всех (t in R) в силу периодичности функции (f), получаем
$$
intlimits_T^{a + T} f(x) dx = intlimits_0^a f(t + T) dt = intlimits_0^a f(t) dt = -intlimits_a^0 f(x) dx.label{ref22}
$$
Из равенств eqref{ref21} и eqref{ref22} следует формула eqref{ref20}. (blacktriangle)
Пример 7.
Вычислить (J = displaystyleintlimits_{-pi/2}^{5pi/2} sin^{5} x cos^{8} x dx).
Решение.
(triangle) Так как подынтегральная функция является периодической с периодом (2pi) и нечетной, то, используя примеры 5 и 6, получаем
$$
J = intlimits_{-pi}^{pi} sin^{5} x cos^{8} x dx=0. blacktrianglenonumber
$$
Интегрирование по частям.
Теорема 6.
Если функции (u(x)) и (v(x)) имеют на отрезке ([a, b]) непрерывные производные, то справедлива формула интегрирования по частям
$$
intlimits_a^b uv’ dx = (uv)|_{a}^{b}- intlimits_a^b vu’dxlabel{ref23}
$$
Доказательство.
(circ) Интегрируя на отрезке ([a, b]) тождество
$$
uv’ = (uv)’- u’v,nonumber
$$
где (uv’, (uv)’, u’v) — непрерывные функции, получаем
$$
intlimits_a^b uv’ dx = intlimits_a^b (uv)’ dx- intlimits_a^b u’v dx.label{ref24}
$$
По формуле Ньютона Лейбница находим
$$
intlimits_a^b (uv)’ dx = (uv)|_{a}^{b} = u(b)v(b)- u(a)v(a).nonumber
$$
Поэтому равенство eqref{ref24} можно записать в виде eqref{ref23}. (bullet)
Замечание 6.
Учитывая, что (v’ dx = dv, u’ dx = du), формулу eqref{ref23} иногда записывают в виде
$$
intlimits_a^b u dv = (uv)|_{a}^{b}- intlimits_a^b v du.nonumber
$$
Пример 8.
Вычислить (J = displaystyleintlimits_1^2 x ln x dx).
Решение.
(triangle) Применяя формулу eqref{ref23}, где (u = ln x, v = displaystylefrac{x^{2}}{2}), получаем
$$
J = left.left(frac{x^{2}}{2} ln xright)right|_{1}^{2}- intlimits_1^2 frac{x^{2}}{2} frac{1}{x} dx = 2 ln 2- frac{1}{2} intlimits_1^2 x dx,nonumber
$$
то есть
$$
J = 2 ln 2- frac{3}{4}. blacktrianglenonumber
$$
Простейшие дифференциальные уравнения.
Дифференциальные уравнения первого порядка.
Задачу о нахождении первообразной для непрерывной на интервале ((a, b)) функции (f(x)) можно сформулировать так: найти функцию (y(x)), которая на интервале ((a, b)) является решением уравнения
$$
y'(x) = f(x).label{ref25}
$$
Уравнение такого вида является обыкновенным дифференциальным уравнением первого порядка. Все решения уравнения eqref{ref25} можно записать в виде
$$
y(x) = intlimits_{x_{0}}^x f(t) dt + C,label{ref26}
$$
где (x_{0} in (a, b), C) — произвольная постоянная.
Чтобы выделить единственное решение уравнения eqref{ref25}, достаточно задать значение функции (y(x)) в какой-либо точке, например в точке (x_{0}). Если (y(x_{0}) = y_{0}), то из формулы eqref{ref26} получаем
$$
y(x) = y_{0} + intlimits_{x_{0}}^x f(t) dt.nonumber
$$
В приложениях часто встречаются дифференциальные уравнения первого порядка, имеющие вид
$$
y'(x) = ky(x),label{ref27}
$$
где (k) — постоянная. Уравнением eqref{ref27} описывается, например, закон размножения бактерий, так как скорость роста числа бактерий пропорциональна их количеству.
Решениями уравнения eqref{ref27} являются функции (y = C e^{kx}), где (C) — произвольная постоянная. Можно показать, что других решений уравнение eqref{ref27} не имеет. Если известно, что (y(x_{0}) = y_{0}), то (C = y_{0}), и поэтому
$$
y=y_0 e^{k(x-x_0)}.nonumber
$$
Дифференциальные уравнения второго порядка.
Рассмотрим уравнение
$$
y″(x) + omega^{2}y(x) = 0,label{ref28}
$$
где (omega) — некоторое положительное число. Уравнение eqref{ref28} называют уравнением гармонических колебаний.
Легко проверить, что функции (cos omega x) и (sin omega x) являются решениями уравнения eqref{ref28}. Отсюда следует, что функции вида
$$
y = C_{1} cos omega x + C_{2} sin omega x,label{ref29}
$$
где (C_{1}) и (C_{2}) — произвольные постоянные, удовлетворяют уравнению eqref{ref28}. Можно показать, что других решений уравнение eqref{ref28} не имеет. Если известно значение функции (y(x)) и значение ее производной при (x = x_{0}) (начальные условия), то есть заданы числа (y_{0} = y(x_{0})) и (tilde{y}_{0} = y'(x_{0})), то этими условиями определяется единственное решение уравнения eqref{ref28}. Например, если(y(0) = 0, y'(0) = 1), то из формулы eqref{ref29} находим (C_{1} = 0, C_{2} = displaystylefrac{1}{omega}), и поэтому (y = displaystylefrac{1}{omega} sin omega x).
Обратимся к уравнению
$$
y″(x)- omega^{2}y(x) = 0,label{ref30}
$$
где (omega > 0). Его решениями, как нетрудно проверить, являются функции (e^{omega x}) и (e^{- omega x}), и поэтому функции вида
$$
y = C_{1}e^{omega x} + C_{2}e^{- omega x},label{ref31}
$$
где (C_{1}) и (C_{2}) — произвольные постоянные, также удовлетворяют уравнению eqref{ref30}.
Можно показать, что других решений уравнение eqref{ref30} не имеет. Если заданы числа (y_{0} = y(x_{0})) и (tilde{y}_{0} = y'(x_{0})), то из формулы eqref{ref31} найдем (C_{1}) и (C_{2}) и тем самым определим единственное решение уравнения eqref{ref30}. Например, если известно, что (y(0) = 1, y'(0) = 0), то (C_{1} + C_{2} = 1, omega C_{1}- omega C_{2} = 0), откуда (C_{1} = C_{2} = displaystylefrac{1}{2}) и поэтому (y = displaystylefrac{1}{2} (e^{omega x}- e^{- omega x} = operatorname{ch} omega x)).