Как найти производную произведения трех множителей, приведите пожалуйста какой нить пример
неопознанный чел
Ученик
(17),
закрыт
12 лет назад
Дополнен 12 лет назад
спасибо большое
Лучший ответ
Юрик
Высший разум
(117860)
12 лет назад
Вот.
(u•v•w)’=(u•v)’•w+u•v•w’= u‘•v•w + u•v‘•w +u•v•w’
[x•(x+1)•(x+2)]’= (x+1)•(x+2)+x•(x+2)+x•(x+1)=
=x²+x+2x+2+x²+2x+x²+x=3x²+6x+2.
Остальные ответы
Анатолий Назаров
Ученик
(107)
1 год назад
y=x*e^x*sinx обозначим t=x*e^x тогда у=t*sinx y’=t’*sinx+(sinx)’*t=t’*sinx+cosx*x*e^x t’=1*e^x+x*e^x=(1+x)*e^x
y’=(1+x)*e^x*sinx+cosx*x*e^x
Похожие вопросы
Содержание:
- 1 Таблица производных простых функций
- 2 Правила дифференцирования
- 3 Пошаговые примеры — как найти производную
- 4 Найти производные самостоятельно, а затем посмотреть решения
-
-
- 4.0.0.1 Ещё больше домашних заданий на нахождение производных
-
-
- 5 Продолжаем искать производные вместе
-
-
- 5.0.0.1 Ещё больше домашних заданий на нахождение производных
-
-
- 6 Примеры решений
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную, надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
 .
.
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
 .
.
Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
 .
.
Пример 2. Найти производную функции
 .
.
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200. ), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто |  |
| 2. Производная независимой переменной. Чаще всего “икса”. Всегда равна единице. Это тоже важно запомнить надолго |  |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. |  |
| 4. Производная переменной в степени -1 |  |
| 5. Производная квадратного корня |  |
| 6. Производная синуса |  |
| 7. Производная косинуса |  |
| 8. Производная тангенса |  |
| 9. Производная котангенса |  |
| 10. Производная арксинуса |  |
| 11. Производная арккосинуса |  |
| 12. Производная арктангенса |  |
| 13. Производная арккотангенса |  |
| 14. Производная натурального логарифма |  |
| 15. Производная логарифмической функции |  |
| 16. Производная экспоненты |  |
| 17. Производная показательной функции |  |
Правила дифференцирования
Правило 1. Если функции

дифференцируемы в некоторой точке  , то в той же точке дифференцируемы и функции
, то в той же точке дифференцируемы и функции


т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.

Правило 2. Если функции


дифференцируемы в некоторой точке  , то в то же точке дифференцируемо и их произведение
, то в то же точке дифференцируемо и их произведение


т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной:

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:

Правило 3. Если функции


дифференцируемы в некоторой точке  и
и  , то в этой точке дифференцируемо и их частное u/v , причём
, то в этой точке дифференцируемо и их частное u/v , причём

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье “Производная произведения и частного функций”.
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u‘v , в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде  , то следуйте на занятие “Производная суммы дробей со степенями и корнями”.
, то следуйте на занятие “Производная суммы дробей со степенями и корнями”.
Если же перед Вами задача вроде  , то Вам на занятие “Производные простых тригонометрических функций”.
, то Вам на занятие “Производные простых тригонометрических функций”.
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
 .
.
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:


Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:

А проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например,  , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями”.
, то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями”.
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде  , то Вам на урок “Производные простых тригонометрических функций”.
, то Вам на урок “Производные простых тригонометрических функций”.
Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на  :
:

Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Найти производные самостоятельно, а затем посмотреть решения
Пример 7. Найти производную функции
 .
.
Пример 8. Найти производную функции
 .
.
Пример 9. Найти производную функции
 , где a и b — константы.
, где a и b — константы.
Пример 10. Найти производную функции
 .
.
Пример 11. Найти производную функции
 .
.
Ещё больше домашних заданий на нахождение производных
Продолжаем искать производные вместе
Пример 12. Найти производную функции
 .
.
Решение. Применяя правила вычисления производной алгебраической суммы функций, вынесения постоянного множителя за знак производной и формулу производной степени (в таблице производных — под номером 3), получим
 .
.
Пример 13. Найти производную функции

Решение. Применим правило дифференцирования произведения, а затем найдём производные сомножителей, так же, как в предыдущей задаче, пользуясь формулой 3 из таблицы производных. Тогда получим

Пример 14. Найти производную функции

Решение. Как и в примерах 4 и 6, применим правило дифференцирования частного:

Теперь вычислим производные в числителе и перед нами уже требуемый результат:

Пример 15.Найти производную функции

Шаг1. Применяем правило дифференцирования суммы:

Шаг2. Найдём производную первого слагаемого. Это табличная производная квадратного корня (в таблице производных — номер 5):

Шаг3. В частном знаменатель — также корень, только не квадратный. Поэтому преобразуем этот корень в степень:

и далее дифференцируем частное, не забывая, что число 2 в первом слагаемом числителя — это константа, производная которой равна нулю, и, следовательно всё первое слагаемое равно нулю:

Корень из константы, как не трудно догадаться, является также константой, а производная константы, как мы знаем из таблицы производных, равна нулю:
 ,
,
а производная, требуемая в условии задачи:

Ещё больше домашних заданий на нахождение производных
Напоминаем, что чуть более сложные примеры на производную произведения и частного — в статьях “Производная произведения и частного функций” и “Производная суммы дробей со степенями и корнями”.
Также настоятельно рекомендуем изучить производную сложной функции.
После предварительной артподготовки будут менее страшны примеры, с 3-4-5 вложениями функций. Возможно, следующие два примера покажутся некоторым сложными, но если их понять (кто-то и помучается), то почти всё остальное в дифференциальном исчислении будет казаться детской шуткой.
Найти производную функции 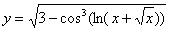
Как уже отмечалось, при нахождении производной сложной функции, прежде всего, необходимо правильно РАЗОБРАТЬСЯ во вложениях. В тех случаях, когда есть сомнения, напоминаю полезный приём: берем подопытное значение «икс», например,  и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
1) Сначала нам нужно вычислить выражение  , значит, сумма
, значит, сумма  – самое глубокое вложение.
– самое глубокое вложение.
2) Затем необходимо вычислить логарифм: 
3) Далее косинус: 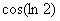
4) Потом косинус возвести в куб: 
5) На пятом шагу разность: 
6) И, наконец, самая внешняя функция – это квадратный корень: 
Формула дифференцирования сложной функции  применятся в обратном порядке, от самой внешней функции, до самой внутренней. Решаем:
применятся в обратном порядке, от самой внешней функции, до самой внутренней. Решаем:

Вроде без ошибок:
1) Берем производную от квадратного корня.
2) Берем производную от разности, используя правило 
3) Производная тройки равна нулю. Во втором слагаемом берем производную от степени (куба).
4) Берем производную от косинуса.
5) Берем производную от логарифма.
6) И, наконец, берем производную от самого глубокого вложения  .
.
Может показаться слишком трудно, но это еще не самый зверский пример. Возьмите, например, сборник Кузнецова и вы оцените всю прелесть и простоту разобранной производной. Я заметил, что похожую штуку любят давать на экзамене, чтобы проверить, понимает студент, как находить производную сложной функции, или не понимает.
Следующий пример для самостоятельного решения.
Найти производную функции 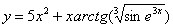
Подсказка: Сначала применяем правила линейности и правило дифференцирования произведения
Полное решение и ответ в конце урока.
Настало время перейти к чему-нибудь более компактному и симпатичному.
Не редка ситуация, когда в примере дано произведение не двух, а трёх функций. Как найти производную от произведения трёх множителей?
Найти производную функции 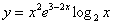
Сначала смотрим, а нельзя ли произведение трех функций превратить в произведение двух функций? Например, если бы у нас в произведении было два многочлена, то можно было бы раскрыть скобки. Но в рассматриваемом примере все функции разные: степень, экспонента и логарифм.
В таких случаях необходимо последовательно применить правило дифференцирования произведения  два раза
два раза
Фокус состоит в том, что за «у» мы обозначим произведение двух функций:  , а за «вэ» – логарифм:
, а за «вэ» – логарифм:  . Почему так можно сделать? А разве
. Почему так можно сделать? А разве  – это не произведение двух множителей и правило не работает?! Ничего сложного нет:
– это не произведение двух множителей и правило не работает?! Ничего сложного нет:

Теперь осталось второй раз применить правило  к скобке
к скобке 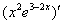 :
:

Можно еще поизвращаться и вынести что-нибудь за скобки, но в данном случае ответ лучше оставить именно в таком виде – легче будет проверять.
Рассмотренный пример можно решить вторым способом:

Оба способа решения абсолютно равноценны.
Найти производную функции 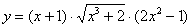
Это пример для самостоятельного решения, в образце он решен первым способом.
Рассмотрим аналогичные примеры с дробями.
Найти производную функции 
Здесь можно пойти несколькими путями:

или так: 
Но решение запишется более компактно, если в первую очередь использовать правило дифференцирования частного  , приняв за
, приняв за  весь числитель:
весь числитель:

В принципе, пример решён, и если его оставить в таком виде, то это не будет ошибкой. Но при наличии времени всегда желательно проверить на черновике, а нельзя ли ответ упростить?
Приведём выражение числителя к общему знаменателю и избавимся от трёхэтажности дроби:

Минус дополнительных упрощений состоит в том, что есть риск допустить ошибку уже не при нахождении производной, а при банальных школьных преобразованиях. С другой стороны, преподаватели нередко бракуют задание и просят «довести до ума» производную.
Более простой пример для самостоятельного решения:
Найти производную функции 
Продолжаем осваивать приёмы нахождения производной, и сейчас мы рассмотрим типовой случай, когда для дифференцирования предложен «страшный» логарифм
Найти производную функции 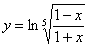
Тут можно пойти длинным путём, используя правило дифференцирования сложной функции:

Но первый же шаг сразу повергает в уныние – предстоит взять неприятную производную от дробной степени 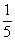 , а потом ещё и от дроби
, а потом ещё и от дроби 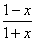 .
.
Поэтому перед тем как брать производную от «навороченного» логарифма, его предварительно упрощают, используя известные школьные свойства:

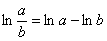
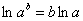
! Если под рукой есть тетрадь с практикой, перепишите эти формулы прямо туда. Если тетради нет, перерисуйте их на листочек, поскольку оставшиеся примеры урока буду вращаться вокруг этих формул.
Само решение можно оформить примерно так:
Преобразуем функцию: 
Находим производную: 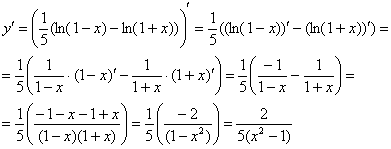
Предварительное преобразование самой функции значительно упростило решение. Таким образом, когда для дифференцирования предложен подобный логарифм, то его всегда целесообразно «развалить».
А сейчас пара несложных примеров для самостоятельного решения:
Найти производную функции 
Найти производную функции 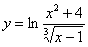
Все преобразования и ответы в конце урока.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9123 —  | 7290 —
| 7290 —  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Производная произведения равна произведению производной первого множителя на второй множитель плюс произведение первого множителя на производную второго множителя:
Следует отметить, что не в коем случае производная произведения функций НЕ РАВНА произведению производных каждого множителя!
Примеры решений
Находим производные от каждого из множителей. Для множителя $ x $ производная будет равна: $$ (x)’=1 $$
Для второй функции $ ln x $ производная находится по формуле для логарифма и равна:
В целом пользуясь формулой производной произведения записыаем ответ:
$$ y’=(xln x)’=(x)’ln x + x(ln x)’=ln x + xcdot frac<1> = ln x + 1 $$
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
| Пример 1 |
| Найти производную произведения двух функций $ y = xln x $ |
| Решение |
| Ответ |
| $$ y’=ln x + 1 $$ |
Производная первой функции равна: $$ (x^2)’=2x $$
Производная второй функции равна: $$ (e^<3x>)’=e^<3x>cdot (3x)’=e^ <3x>cdot 3 = 3e^ <3x>$$
Используя правило получаем:
Выносим экспоненты за скобки для упрощенной записи ответа:
| Пример 2 |
| Найти производную функции $ y = x^2e^ <3x>$ |
| Решение |
|
0 / 0 / 0 Регистрация: 16.12.2011 Сообщений: 30 |
|
|
1 |
|
Производная произведения трех функций27.08.2015, 17:27. Показов 45032. Ответов 3
Доброго времени суток! Подскажите, пожалуйста, чему равна производная произведения трех функций? Спасибо.
0 |
|
26 / 24 / 6 Регистрация: 15.08.2015 Сообщений: 165 Записей в блоге: 4 |
|
|
27.08.2015, 17:33 |
2 |
|
Решение(u•v•w)’=(u•v)’•w+u•v•w’= u‘•v•w + u•v‘•w +u•v•w’
2 |
|
0 / 0 / 0 Регистрация: 16.12.2011 Сообщений: 30 |
|
|
27.08.2015, 17:40 [ТС] |
3 |
|
Спасибо!
0 |
|
Диссидент
27465 / 17154 / 3780 Регистрация: 24.12.2010 Сообщений: 38,635 |
|
|
01.09.2015, 22:04 |
4 |
|
чему равна производная произведения трех функций? Формулу легко получить, учитывая что u*v*w = (u*v)*w
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
01.09.2015, 22:04 |
|
Помогаю со студенческими работами здесь
Вычислить значение квадратного корня из произведения трех переменных переменных! Помогите решить! Представить n!=1*2*3*.*n в виде произведения трёх последовательных целых чисел Составить программу определения произведения трех наименьших из 4 чисел X, Y, Z, T Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 4 |
2
Основные правила дифференцирования
Правило
1. Если
функции
дифференцируемы
в некоторой точке ,
то в той же точке дифференцируемы и
функции
причём
(5)
т.е.
производная алгебраической суммы
функций равна алгебраической сумме
производных этих функций.
Следствие. Если
две дифференцируемые функции отличаются
на постоянное слагаемое, то их производные
равны, т.е.
(6)
Правило
2. Если
функции
и
дифференцируемы
в некоторой точке ,
то в то же точке дифференцируемо и их
произведение
причём
(7)
т.е.
производная произведения двух функций
равна сумме произведений каждой из этих
функций на производную другой.
Следствие
1. Постоянный
множитель можно выносить за знак
производной:
(8)
Следствие
2. Производная
произведения нескольких дифференцируемых
функций равна сумме произведений
производной каждого из сомножителей
на все остальные.
Например,
для трёх множителей имеем:
(9)
Правило
3. Если
функции
и
дифференцируемы
в некоторой точке и , то
в этой точке дифференцируемо и их
частное u/v
, причём
(10)
т.е.
производная частного двух функций равна
дроби, числитель которой есть разность
произведений знаменателя на производную
числителя и числителя на производную
знаменателя, а знаменатель есть квадрат
прежнего числителя.
Пример
4. Найти
производную функции
Решение.
Применяя правила (5) и (8) и формулу (4)
дифференцирования степенной функции
получим
Пример
5. Найти
Найти
производную функции
Решение.
Применим правило (7) дифференцирования
произведения, а затем найдём производные
сомножителей так же, как в примере 4.
Тогда получим
Пример
6. Найти
производную функции
Решение.
Применим правило (10) дифференцирования
частного:
Затем,
так же как и выше, вычислим производные
в числителе. Имеем
|
Логарифмическим
Теперь Отсюда |
|
Пример |
|
Вычислить
Применяем |
|
Пример |
|
Найти
Прологарифмируем |
|
Пример |
|
Вычислить
Возьмем Теперь |
|
Пример |
|
Продифференцировать .
Сначала Дифференцируя Следовательно, |
3.6: Цепное правило — Mathematics LibreTexts
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2495
- Гилберт Странг и Эдвин «Джед» Герман
- OpenStax
Цели обучения
- Укажите цепное правило для композиции двух функций.
- Примените цепное правило вместе с степенным правилом.
- Правильно применяйте цепное правило и правило произведения/частного в сочетании, когда оба необходимы.
 2+1} ). В этом разделе мы изучаем правило нахождения производной композиции двух или более функций.
2+1} ). В этом разделе мы изучаем правило нахождения производной композиции двух или более функций.
Получение цепного правила
Когда у нас есть функция, представляющая собой композицию двух или более функций, мы можем использовать все методы, которые мы уже изучили, чтобы дифференцировать ее. Однако использование всех этих методов для разбиения функции на более простые части, которые мы можем различать, может оказаться громоздким. Вместо этого мы используем цепное правило , которое гласит, что производная составной функции — это производная внешней функции, вычисляемой как внутренняя функция, умноженная на производную внутренней функции. 93)).
Теперь, когда мы вывели частный случай цепного правила, мы сформулируем общий случай, а затем применим его в общей форме к другим составным функциям. Неформальное доказательство приведено в конце раздела.
Правило: Цепное правило
Пусть (f) и (g) — функции. Для всех (x) в области определения (g), для которых (g) дифференцируемо в (x) и (f) дифференцируемо в (g(x)), производная сложной функции
[h(x)=(f∘g)(x)=fbig(g(x)big) nonumber ]
определяется как
[h'(x)=f’big(g(x)big)cdot g'(x).
 nonumber ]
nonumber ] Альтернативно, если (y) является функцией (u), а (u) является функцией (x), то
[dfrac{dy} {dx}=dfrac{dy}{du}⋅dfrac{du}{dx}. nonumber ]
Стратегия решения проблем: применение цепного правила
- Чтобы дифференцировать (h(x)=fbig(g(x)big)), начнем с определения (f(x) ) и (g(x)).
- Найдите (f'(x)) и оцените его в (g(x)), чтобы получить (f’big(g(x)big)).
- Найти (g'(x).)
- Напишите (h'(x)=f’big(g(x)big)⋅g'(x).)
Примечание : Применяя цепное правило к композиции из двух или более функций, имейте в виду, что мы работаем от внешней функции внутрь. Также полезно помнить, что производная от композиции двух функций может считаться состоящим из двух частей; производная композиции трех функций состоит из трех частей; и так далее. Также помните, что мы никогда не оцениваем производную по производной. 93) в точке (x=−2).
- Подсказка
-
Используйте предыдущий пример в качестве руководства.

- Ответить
-
(у=-48х-88)
Комбинирование цепного правила с другими правилами
Теперь, когда мы можем комбинировать цепное правило и правило степени, мы рассмотрим, как комбинировать цепное правило с другими изученными нами правилами. В частности, мы можем использовать его с формулами для производных тригонометрических функций или с правилом произведения.
Пример (PageIndex{4}): использование цепного правила для общей функции косинуса
Найдите производную (h(x)=cosbig(g(x)big).)
Решение
Подумайте о (h(x)=cosbig(g(x)big)) как (fbig(g(x)big)), где (f (х)=cos х). Поскольку (f'(x)=-sin x), мы имеем (f’big(g(x)big)=-sinbig(g(x)big)). Затем делаем следующий расчет.
[begin{align*} h'(x)&=f’big(g(x)big)cdot g'(x) & & text{Применить правило цепочки.} \[ 4 пт] 95+2x).)
Упражнение (PageIndex{3})
Найдите производную (h(x)=sin(7x+2).
 )
) - Подсказка
-
Сначала примените цепное правило к (h(x)=sinbig(g(x)big)), а затем используйте (g(x)=7x+2).
- Ответить
-
(h'(x)=7cos(7x+2))
Здесь мы приводим список формул производных, которые можно получить, применяя цепное правило в сочетании с формулами производных тригонометрических функций. Их выводы аналогичны тем, которые использовались в приведенных выше примерах. Для удобства формулы также даны в обозначениях Лейбница, которые некоторым учащимся легче запомнить. (Мы обсудим цепное правило с использованием обозначений Лейбница в конце этого раздела.) Нет абсолютной необходимости запоминать их как отдельные формулы, поскольку все они являются приложениями цепного правила к ранее выученным формулам.
Использование цепного правила с тригонометрическими функциями
Для всех значений (x), для которых определена производная,
Композиции трех или более функций
Теперь мы можем комбинировать цепное правило с другими правилами для дифференцирования функций, но когда мы дифференцируем состав трех или более функций, нам нужно применять цепное правило более одного раза. Если мы посмотрим на эту ситуацию в общих чертах, мы можем сгенерировать формулу, но нам не нужно ее запоминать, так как мы можем просто применить цепное правило несколько раз.
В общих чертах сначала пускаем
[k(x)=hBig(fbig(g(x)big)Big).nonumber ]
Тогда, применяя цепное правило, мы получаем
[k'( x)=dfrac{d}{dx}Big(hbig(fbig(g(x)big)big)Big)=h’Big(fbig(g(x) big)Big)⋅dfrac{d}{dx}Big(fbig(g(x)big)Big).nonumber ]
Снова применяя цепное правило, получаем
[ k'(x)=h’Big(fbig(g(x)big)Big)cdot f’big(g(x)big)cdot g'(x).nonumber ]
Правило: цепное правило для композиции трех функций
Для всех значений (х), при которых функция дифференцируема, если
(k(x)=hBig(fbig(g(x)big)Big),)
затем
(k'(x)=h’Big(f big(g(x)big)Big)cdot f’big(g(x)big)cdot g'(x).
 )
) Другими словами, мы применяем цепное правило дважды.
Обратите внимание, что производная от композиции трех функций состоит из трех частей. (Аналогичным образом производная композиции четырех функций состоит из четырех частей и т. д.) Кроме того, помните, , мы всегда можем работать снаружи внутрь, беря по одной производной за раз. 93))
Пример (PageIndex{9}): Использование цепного правила в задаче о скорости
Частица движется вдоль координатной оси. Его положение в момент времени t определяется выражением (s(t)=sin(2t)+cos(3t)). Какова скорость частицы в момент времени (t=dfrac{π}{6})?
Решение
Чтобы найти (v(t)), скорость частицы в момент времени (t), мы должны продифференцировать (s(t)). Таким образом,
[v(t)=s'(t)=2cos(2t)−3sin(3t).nonumber ]
Доказательство цепного правила
На этом этапе мы представляем очень неформальное доказательство цепного правила.
 Ради простоты мы игнорируем некоторые вопросы: например, мы предполагаем, что (g(x)≠g(a)) для (x≠a) в некотором открытом интервале, содержащем (a). Начнем с применения предельного определения производной к функции (h(x)), чтобы получить (h'(a)):
Ради простоты мы игнорируем некоторые вопросы: например, мы предполагаем, что (g(x)≠g(a)) для (x≠a) в некотором открытом интервале, содержащем (a). Начнем с применения предельного определения производной к функции (h(x)), чтобы получить (h'(a)): [h'(a)=lim_{x→a} dfrac{fbig(g(x)big)−fbig(g(a)big)}{x−a}. nonumber ]
Переписывая, получаем
[h'(a)=lim_{x→a}dfrac{fbig(g(x)big)−fbig(g(a) big)}{g(x)−g(a)}⋅dfrac{g(x)−g(a)}{x−a}. номер]
Хотя ясно, что
[lim_{x→a}dfrac{g(x)−g(a)}{x−a}=g'(a), nonumber ]
it не очевидно, что
[lim_{x→a}dfrac{fbig(g(x)big)−fbig(g(a)big)}{g(x)−g( а)}=f’большой(г(а)большой). nonumber ]
Чтобы убедиться, что это так, вспомним сначала, что, поскольку (g) дифференцируема в (a), (g) также непрерывно в (a.). Таким образом,
[lim_{x→a}g(x)=g(a). nonumber ]
Затем сделайте замену (y=g(x)) и (b=g(a)) и используйте замену переменных в пределе, чтобы получить
[lim_{x→a}dfrac{fbig(g(x)big)−f big(g(a) big)}{g(x)−g(a)}= lim_{y→b}dfrac{f(y)−f(b)}{y−b}=f'(b)=f’big(g(a)big).
 nonumber ]
nonumber ] Наконец,
[h'(a)=lim_{x→a}dfrac{fbig(g(x)big)−fbig(g(a)big )}{g(x)−g(a)}⋅dfrac{g(x)−g(a)}{x−a}=f’big(g(a)big)cdot g'( а). nonumber ]
□
Пример (PageIndex{10}): Использование цепного правила с функциональными значениями
Пусть (h(x)=fbig(g(x)big). ) Если (g(1)=4,g'(1)=3) и (f'(4)=7), найти (h'(1).)
Решение
Используйте цепное правило, затем подставьте.
[ begin{align*} h'(1)&=f’big(g(1)big)cdot g'(1) & & text{Применить правило цепочки.} \[ 4pt]
&=f'(4)⋅3 & &text{Подстановка}; г(1)=4 ;текст{и};г'(1)=3. \[4pt]
&=7⋅3 & &text{Подстановка}; f'(4)=7. \[4pt]
&=21 & &text{Упростить.} end{align*} nonumber ]Упражнение (PageIndex{6})
Дано (h(x)=f (г(х))). Если (g(2)=-3,g'(2)=4,) и (f'(-3)=7), найди (h'(2)).
- Подсказка
-
Следуйте примеру (PageIndex{10}).

- Ответить
-
28
Цепное правило с использованием обозначений Лейбница
Как и в случае с другими производными, которые мы видели, мы можем выразить цепное правило с помощью обозначений Лейбница. Это обозначение цепного правила широко используется в физических приложениях.
Для (h(x)=f(g(x)),) пусть (u=g(x)) и (y=h(x)=f(u).) Таким образом,
[h'(x)=dfrac{dy}{dx}nonumber ]
[f'(g(x))=f'(u)=dfrac{dy}{du} nonumber ]
и
[g'(x)=dfrac{du}{dx}.nonumber ]
Следовательно,
[dfrac{dy}{dx}=h'(x )=f’big(g(x)big)cdot g'(x)=dfrac{dy}{du}⋅dfrac{du}{dx}.nonumber ]
Правило: Цепное правило Используя обозначения Лейбница
Если (y) является функцией (u), а (u) является функцией (x), то
[dfrac{dy}{dx} =dfrac{dy}{du}⋅dfrac{du}{dx}. номер] 93).)
Ключевые понятия
- Цепное правило позволяет различать композиции из двух или более функций.
 {n−1}cdot g'(x))
{n−1}cdot g'(x))
Глоссарий
- Цепная линейка
- цепное правило определяет производную составной функции как производную от внешней функции, вычисленную как внутреннюю функцию, умноженную на производную от внутренней функции
Эта страница под названием 3.6: The Chain Rule распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Странгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
-
- Теги
-
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- цепная линейка
- источник@https://openstax.
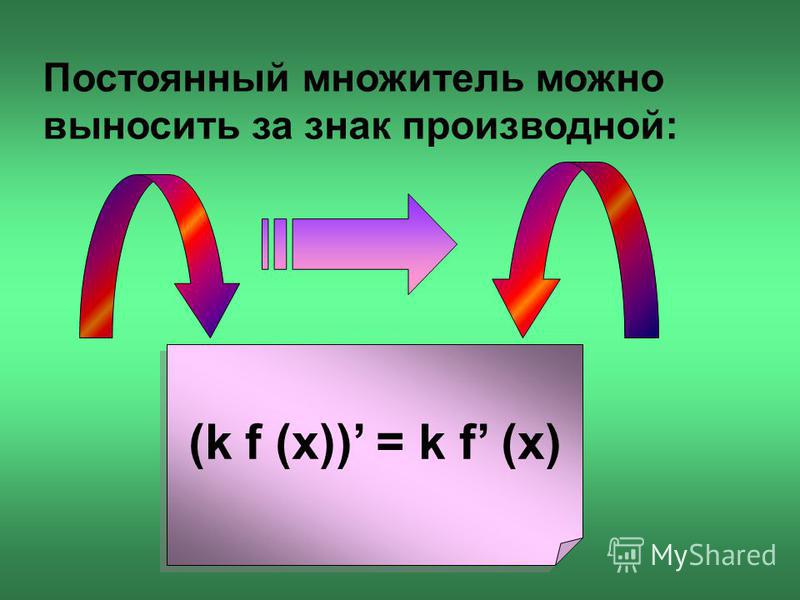
(dfrac{d}{dx}Big(sin(g( x))Big)=cos(g(x))cdot g'(x)) (dfrac{d}{dx}Big(sin uBig)=cos ucdotdfrac{du}{dx}) (dfrac{d}{dx}Big(cos(g(x))Big)=-sin(g(x))cdotg'(x)) (dfrac{d}{dx}Big(cos uBig)=-sin ucdotdfrac{du}{dx}) 92ucdotdfrac{du}{dx}) (dfrac{d}{dx}Big(text{sec}(g(x))Big)=text{sec}(g(x))tan(g(x)) cdot g'(x)) (dfrac{d}{dx}Big(text{sec},uBig)=text{sec},utan ucdotdfrac{du}{dx}) (dfrac{d}{dx}Big(text{csc}(g(x))Big)=-text{csc}(g(x))cot(g(x) )cdot g'(x)) (dfrac{d}{dx}Big(text{csc},uBig)=-text{csc},ucot u cdotdfrac{du}{dx}.  )
) 94})
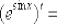 ,
, 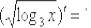 ,
, 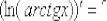 ,
,
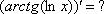 ,
, 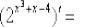 ,
, 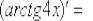 ,
,
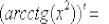 ,
, 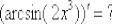 ,
, 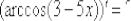 Ответы в конце урока
Ответы в конце урока
Сложные производные
После предварительной артподготовки будут менее страшны примеры, с 3-4-5 вложениями функций. Возможно, следующие два примера покажутся некоторым сложными, но если их понять (кто-то и помучается), то почти всё остальное в дифференциальном исчислении будет казаться детской шуткой.
Пример 2
Найти производную функции 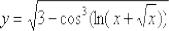
Как уже отмечалось, при нахождении производной сложной функции, прежде всего, необходимо правильно РАЗОБРАТЬСЯ во вложениях. В тех случаях, когда есть сомнения, напоминаю полезный приём:
берем подопытное значение «икс», например, 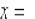 и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
1)Сначала нам нужно вычислить выражение 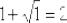 , значит, сумма
, значит, сумма  – самое глубокое вложение.
– самое глубокое вложение.
2)Затем необходимо вычислить логарифм: 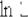
3)Далее косинус: 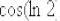

4)Потом косинус возвести в куб: 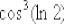
5)На пятом шагу разность: 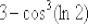
6)И, наконец, самая внешняя функция – это квадратный корень:
Формула дифференцирования сложной функции 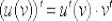 применятся в обратном порядке, от самой внешней функции, до самой внутренней. Решаем:
применятся в обратном порядке, от самой внешней функции, до самой внутренней. Решаем:
Вроде без ошибок….
(1)Берем производную от квадратного корня.
(2)Берем производную от разности, используя правило
(3)Производная тройки равна нулю. Во втором слагаемом берем производную от степени (куба).
(4)Берем производную от косинуса.
(5)Берем производную от логарифма.
(6)И, наконец, берем производную от самого глубокого вложения
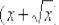 .
.
Может показаться слишком трудно, но это еще не самый зверский пример. Возьмите, например, сборник Кузнецова и вы оцените всю прелесть и простоту разобранной производной. Я заметил, что похожую штуку любят давать на экзамене, чтобы проверить, понимает студент, как находить производную сложной функции, или не понимает.
Следующий пример для самостоятельного решения.
Пример 3
Найти производную функции 
Подсказка: Сначала применяем правила линейности и правило дифференцирования произведения
Полное решение и ответ в конце урока.
Настало время перейти к чему-нибудь более компактному и симпатичному.
Не редка ситуация, когда в примере дано произведение не двух, а трёх функций. Как найти производную от произведения трёх множителей?
Пример 4
Найти производную функции 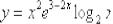
Сначала смотрим, а нельзя ли произведение трех функций превратить в произведение двух функций? Например, если бы у нас в произведении было два многочлена, то можно было бы раскрыть скобки. Но в рассматриваемом примере все функции разные: степень,
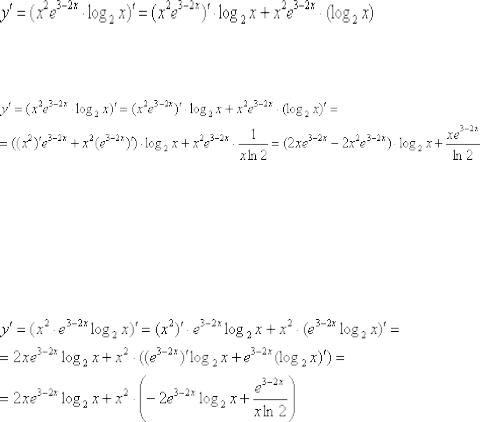
экспонента и логарифм.
В таких случаях необходимо последовательно применить правило дифференцирования произведения 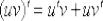 два раза
два раза
Фокус состоит в том, что за «у» мы обозначим произведение двух функций: 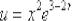 , а за «вэ» – логарифм:
, а за «вэ» – логарифм: 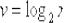 . Почему так можно сделать? А разве
. Почему так можно сделать? А разве 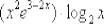 – это не произведение двух множителей и правило не работает?! Ничего сложного нет:
– это не произведение двух множителей и правило не работает?! Ничего сложного нет:
Теперь осталось второй раз применить правило 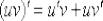 к скобке
к скобке 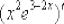 :
:
Можно еще поизвращаться и вынести что-нибудь за скобки, но в данном случае ответ лучше оставить именно в таком виде – легче будет проверять.
Готово.
Рассмотренный пример можно решить вторым способом:
Оба способа решения абсолютно равноценны. Пример 5
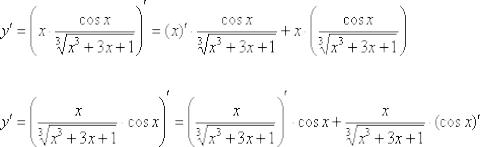
Найти производную функции 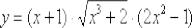
Это пример для самостоятельного решения, в образце он решен первым способом.
Рассмотрим аналогичные примеры с дробями. Пример 6
Найти производную функции 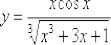 Здесь можно пойти несколькими путями:
Здесь можно пойти несколькими путями:
или так:
Но решение запишется более компактно, если в первую очередь использовать правило дифференцирования частного 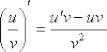 , приняв за
, приняв за 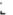 весь числитель:
весь числитель:

В принципе, пример решён, и если его оставить в таком виде, то это не будет ошибкой. Но при наличии времени всегда желательно проверить на черновике, а нельзя ли ответ упростить? Приведём выражение числителя к общему знаменателю и избавимся от трёхэтажности дроби:
Минус дополнительных упрощений состоит в том, что есть риск допустить ошибку уже не при нахождении производной, а при банальных школьных преобразованиях. С другой стороны, преподаватели нередко бракуют задание и просят «довести до ума» производную.
Более простой пример для самостоятельного решения:

Пример 7
Найти производную функции 
Продолжаем осваивать приёмы нахождения производной, и сейчас мы рассмотрим типовой случай, когда для дифференцирования предложен «страшный» логарифм
Пример 8
Найти производную функции 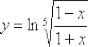
Тут можно пойти длинным путём, используя правило дифференцирования сложной функции:
Но первый же шаг сразу повергает в уныние – предстоит взять неприятную производную от дробной степени 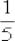 , а потом ещё и от
, а потом ещё и от
дроби 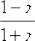 .
.
Поэтому перед тем как брать производную от «навороченного» логарифма, его предварительно упрощают, используя известные школьные свойства:
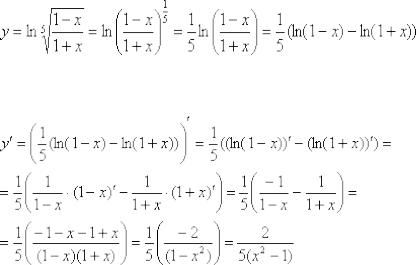
! Если под рукой есть тетрадь с практикой, перепишите эти формулы прямо туда. Если тетради нет, перерисуйте их на листочек, поскольку оставшиеся примеры урока буду вращаться вокруг этих формул.
Само решение можно оформить примерно так:
Преобразуем функцию:
Находим производную:
Предварительное преобразование самой функции значительно упростило решение. Таким образом, когда для дифференцирования предложен подобный логарифм, то его всегда целесообразно «развалить».
А сейчас пара несложных примеров для самостоятельного решения: Пример 9
Найти производную функции 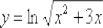 Пример 10
Пример 10
Найти производную функции 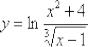
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

 Сообщение было отмечено Димидиум как решение
Сообщение было отмечено Димидиум как решение



