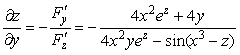как решить эти примеры с частными производными?заранее спасибо за подсказки))
матильда
Ученик
(213),
закрыт
14 лет назад
найти частные производные dz/du, dz/dv, если z=x^2ln^2 (y^2-x^2), где y=sinu+sinv , x=sinu-sinv ? замена х и у здесь не подходит, как-то по другому…
2) найти частную производную d^3Z/dxdy^2, если z=sin(xy) огромное человеческое спасибо.)
Дополнен 15 лет назад
ОБалдеть…0.о
НИКОЛАЙ. огромное спасибо!! опять выручили))))

|
дz |
= 2xy; |
дz |
= 2; |
||||
|
дx |
дx P |
||||||
|
дz |
= x2 ; |
дz |
|||||
|
= 1. |
|||||||
|
дy |
|||||||
|
дy P |
Следовательно, grad z=2i+j (рис. 10).
Производные и дифференциалы высших порядков
1°. Частные производные высших порядков. Частными производными второго порядка
функции z=f(х,у) называются частные Производные от ее частных производных первого порядка.
Для производных второго порядка употребляются обозначения
|
д2 z |
= f ”xx ( x, y ); |
||
|
дx2 |
|||
|
д2 z |
= f ”xx ( x, y ). |
||
|
дxдy |
|||
Аналогично определяются и обозначаются частные производные порядка выше второго.
Если частные производные, подлежащие вычислению, непрерывны, то результат многократного дифференцирования не зависит от порядка дифференцирования.
Пример. Найти частные производные второго порядка от функции z = arctg xy .
Решение. Найдем сначала частные производные первого порядка:
|
дz |
= |
1 |
1 |
= |
y |
, |
||||||||||||||||||||||||||||||||||||||||
|
дx |
1 |
+ |
x2 |
y |
x2 |
+ y2 |
||||||||||||||||||||||||||||||||||||||||
|
y2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
дz |
1 |
x |
x |
|||||||||||||||||||||||||||||||||||||||||||
|
= |
− |
= − |
. |
|||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||
|
дy |
x |
y |
x |
+ y |
||||||||||||||||||||||||||||||||||||||||||
|
1 |
+ |
|||||||||||||||||||||||||||||||||||||||||||||
|
y2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
Теперь дифференцируем вторично: |
||||||||||||||||||||||||||||||||||||||||||||||
|
д2 z |
= |
д |
y |
= − |
2xy |
, |
||||||||||||||||||||||||||||||||||||||||
|
дx2 |
дx |
x2 + y2 |
(x2 + y2 )2 |
|||||||||||||||||||||||||||||||||||||||||||
|
д2 z |
д |
x |
2xy |
|||||||||||||||||||||||||||||||||||||||||||
|
= |
− |
= |
. |
|||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
(x |
2 |
2 2 |
|||||||||||||||||||||||||||||||||||||||||
|
дy |
x |
+ y |
+ y |
|||||||||||||||||||||||||||||||||||||||||||
|
дy |
) |
(x2 − y2 ) |
||||||||||||||||||||||||||||||||||||||||||||
|
д2 z |
= |
д |
y |
= |
1(x2 |
+ y2 )− |
2y y |
= |
||||||||||||||||||||||||||||||||||||||
|
. |
||||||||||||||||||||||||||||||||||||||||||||||
|
дxдy |
дy |
x2 + y2 |
(x2 + y2 )2 |
(x2 + y2 )2 |
|
Заметим, что так называемую «смешанную» частную производную можно найти и иначе, а |
||||||||||||||||||||||||||
|
д2 z |
д2 z |
д |
x |
1 |
(x2 + y2 )− 2x x |
(x2 − y2 ) |
||||||||||||||||||||
|
именно: |
= |
= |
− |
= − |
= |
. |
||||||||||||||||||||
|
2 |
(x |
2 |
2 |
2 |
(x |
2 |
2 |
2 |
||||||||||||||||||
|
x |
+ y |
2 |
+ y |
+ y |
||||||||||||||||||||||
|
дxдy дyдx дx |
) |
) |
2°. Дифференциалы высших порядков. Дифференциалом второго порядка функции z=f(х, у)
называется дифференциал от дифференциала (первого порядка) этой функции d²z=d(dz). Аналогично определяются дифференциалы функции г порядка выше второго, например:
d³z=d(d²z) и, вообще, d n z = d (d n−1z).
68

Если z=f(х,у), где х и y — независимые переменные, то дифференциал 2-го порядка функции г вычисляется по формуле
|
d 2 z = |
д2 z dx2 |
+ 2 |
д2 z |
dxdy + |
д2 z dy2 . |
(1) |
|
|
дxдy |
|||||||
|
дx2 |
дy2 |
Вообще, справедлива символическая формула
|
д |
д |
n |
||||
|
d n z = dx |
+ dy |
z , |
||||
|
дx |
||||||
|
дy |
которая формально развертывается по биномиальному закону.
Если z=f(х,у), где аргументы х и у суть функции одного или нескольких независимых переменных, то
|
d |
2 |
z = |
д2 z |
dx |
2 |
+ 2 |
д2 z |
dxdy + |
д2 z |
dy |
2 |
+ |
дz |
d |
2 |
x + |
дz |
d |
2 |
y .(2) |
|
дx2 |
дxдy |
дy2 |
дx |
дy |
||||||||||||||||
Если х и у — независимые переменные, d²x=0, d²y=0 и формула (2) становится тождественной формуле (1).
Пример. Найти полные дифференциалы 1-го и 2-го порядков функции z = 2x2 − 3xy − y2 .
|
Решение. 1-й способ. Имеем: |
дz |
= 4x − 3y, |
дz |
− 3x − 2y . |
|||||||||||||||||
|
дx |
дy |
||||||||||||||||||||
|
Поэтому |
dz = |
дz |
dx + |
дz |
dy = (4x − 3y)dx − (3x + 2y)dy . |
||||||||||||||||
|
дx |
дy |
||||||||||||||||||||
|
Далее, d |
2 |
z = |
д2 z |
dx |
2 |
+ 2 |
д2 z |
дxdy + |
д2 z |
dy |
2 |
= |
4dx |
2 |
− 6дxdy − 2dy |
2 |
. |
||||
|
дx2 |
дxдy |
дy2 |
|||||||||||||||||||
2-й способ. Дифференцированием находим:
dz = 4xdx − 3(ydx + xdy) − 2ydy = (4x − 3y)dx − (3x + 2y)dy .
Дифференцируя ещё раз и помня, что dx и dy не зависят от х и у, получим: d 2 z = (4dx − 3dy)dx − (3dx + 2dy)dy = 4dx2 − 6dxdy − 2dy2 .
Интегрирование полных дифференциалов
1°. Условие полного дифференциала. Для того чтобы выражение Р(х,у)dx+Q(х,у)dу, где функции P(х,y) и Q(х,у) непрерывны в односвязной области D вместе со своими частными производными первого порядка, представляло собой в области D полный дифференциал
некоторой функции u(х,у), необходимо и достаточно выполнение условия ддQx ≡ ддPy .
Пример. Убедится в том, что выражение (2x+y)dx+(x+2y)dy=du= ддux dx = ддuy dy , где u —
искомая функция.
По условию ддux = 2x + y , следовательно, u = ∫(2x + y)dx = x2 + xy + ϕ (y) .
Но, с другой стороны, ддuy = x + ϕ ‘(y) = x + 2y , откуда ϕ ‘(y) = 2y ,ϕ (y) = y2 + C и
u = x2 + xy + y2 + C .
Окончательно, (2x + y)dx + (x + 2y)dx = d (x2 + xy + y2 + C).
69

2º. Случай трех переменных. Аналогично выражение P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz, где
P(x,y,z)dx, Q(x,y,z)dy, R(x,y,z)dz — непрерывные, вместе со своими частными производными 1-го порядка, функции переменных х, у и z, тогда и только тогда представляет собой полный дифференциал некоторой функции u(х,у,z), когда выполнены условия
ддQx ≡ ддPy , ддRy ≡ ддQz , ддPz ≡ ддRx .
Пример. Убедится в том, что выражение (3x2 + 3y −1)dx + (z2 + 3x)dy + (2yz + 1)dz есть полный дифференциал некоторой функции, и найти эту функцию.
Решение. Здесь P=3x²+3y-1, Q=z²+3x, R=2yz+1. Устанавливаем, что
ддQx = ддPy = 3, ддRy = ддQz = 2z, ддPz = ддRx = 0
и, следовательно, (3x2 + 3y −1)dx + (z2 + 3x)dy + (2yz + 1)dz = du = ддux dx + ддuy dy + ддuz dz , где u
— искомая функция.
Имеем: ддux = 3x2 + 3y −1, значит u = ∫(3x2 + 3y −1)dx = x2 + 3xy − x + ϕ (y, z) .
С другой стороны,
ддuy = 3x + ддϕy = z2 + 3x, ддuz = ддϕz = 2yz + 1,
откуда ддϕy = z2 и ддϕz = 2yz + 1. Задача сводится к отысканию функции двух переменных
ϕ (у,z), частные производные которой известны и выполнено условие полного дифференциала. Находим ϕ :
ϕ (y, z) = ∫z2dy = yz2 +ψ (z)
ддϕz = 2yz +ψ ‘(z) = 2yz + 1, ψ ‘(z) = 1,ψ (z) = z + C,
т. е. ϕ (y, z) = yz2 + z + C . Окончательно, u=x²+3xy-x+yz²+z+C.
Дифференцирование неявных функций
1°. Случай одной независимой переменной. Если уравнение f(х,у) =0, где f(х,у) — дифференцируемая функция переменных х и у, определяет у как функцию от х, то производная этой неявно заданной функции при условии, что f‘y(х, у)≠0, может быть найдена по формуле
|
dy |
= − |
fx ‘(x, y) |
. |
(1) |
|||||
|
dx |
f y ‘(x, y) |
||||||||
|
Производные высших порядков находятся последовательным дифференцированием |
|||||||||
|
формулы (1). |
|||||||||
|
Пример. Найти |
dy |
и |
d 2 y |
, если (x²+y²)³-3(x²+y²)+1=0. |
|||||
|
dx |
dx2 |
||||||||
|
70 |
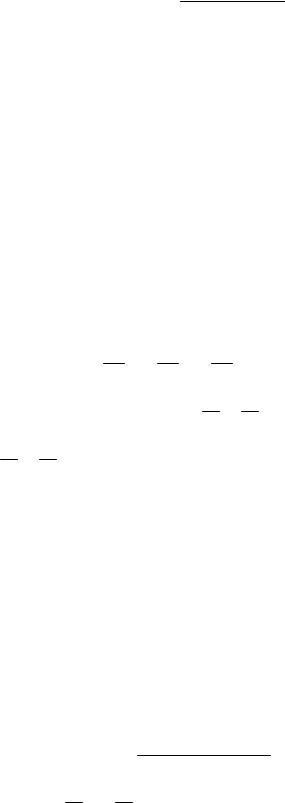
Решение. Обозначая левую часть данного уравнения через f(х,y) найдем частные производные
f’x(x,y)=3(x²+y²)²·2x-3·2x=6x[(x²+y²)-1], f’y(x,y)=3(x²+y²)²·2y-3·2y=6y[(x²+y²)-1].
Отсюда, применяя формулу (1), получим:
|
dy |
fx ‘(x, y) |
6x[(x2 + y2 )2 −1] |
x |
|||
|
= − |
= − |
6y[(x2 + y2 )2 −1]= − |
. |
|||
|
dx |
f y ‘(x, y) |
y |
Чтобы найти вторую производную, продифференцируем по х найденную первую производную, учитывай при этом, что у есть функция х:
|
dy |
x |
|||||||||||||||
|
d 2 y |
d |
x |
y − x |
− |
y2 + x2 |
|||||||||||
|
1 y − x dx |
y |
|||||||||||||||
|
= |
− |
= − |
= − |
= − |
. |
|||||||||||
|
dx2 |
y2 |
y2 |
y2 |
|||||||||||||
|
dx |
y |
2°. Случай нескольких независимых переменных. Аналогично, если уравнение F(х, у, z)=0, где F(х, у, z) — дифференцируемая функция переменных х, у и z, определяет z как функцию независимых переменных х и у и Fz(x, у, z)≠0, то частные производные этой неявно заданной функции, вообще говоря, могут быть найдены по формулам
|
дz |
F ‘(x,y,z) |
дz |
Fy‘(x,y,z) |
|||||
|
= − |
x |
, |
= − |
(2) |
||||
|
дx |
Fz‘(x,y,z) |
дy |
||||||
|
Fz‘(x,y,z) . |
Другой способ нахождения производных функции z следующий: дифференцируя уравнение
F(х, у, z) = 0, получим:
ддFx dx + ддFy dy + ддFz dz = 0.
Отсюда можно определить dz, а следовательно, ддxz и ддyz .
Пример. Найти ддxz и ддyz , если x² – 2y²+3z² – yz+y=0.
Решение.
1-й способ. Обозначая левую часть данного уравнения через F(х, у, z), найдем частные производные F’x(x,y,z)=2x, F’y(x,y,z)=-4y-z+1, F’z(x,y,z)=6z-y.
Применив формулы (2), получим:
|
дz |
= − |
Fx‘ ( x, y,z ) |
= − |
2x |
; |
||||||
|
дx |
F ‘ ( x, y,z ) |
6 z − y |
|||||||||
|
z |
|||||||||||
|
дz |
− |
Fy‘ ( x, y,z ) |
= − |
1 − 4 y − z |
. |
||||||
|
дy |
F ‘ ( x, y,z ) |
6 z − y |
|||||||||
|
z |
2-й способ. Дифференцируя данное уравнение, получим:
2х dx-4y dy+6z dz-y dz-z dy+dy=0
Отсюда определяем dz, т. е. полный дифференциал неявной функции:
dz = 2xdx + (1− 4y − z)dy . y − 6z
Сравнивая с формулой dz = ддxz dx + ддyz dy , видим, что
71

|
дz |
= |
2x |
, |
дz |
= |
1− 4y − z |
. |
|
y − 6z |
дy |
||||||
|
дx |
y − 6z |
3°. Система неявных функций. Если система двух уравнений
F(x, y,u.v)= 0,G(x, y,u.v)= 0,
определяет u и v как функции переменных х и у и якобиан
|
D( F ,G ) |
дF |
дF |
|||||
|
= |
дu |
дv |
≠ 0 , |
||||
|
D( u,v ) |
|||||||
|
дG |
дG |
||||||
|
дu |
дv |
то дифференциалы этих функций (а следовательно, и их частные производные) могут быть найдены из системы уравнений
|
dx + |
∂F |
dy + |
∂F |
du + |
∂F |
dv = 0, |
|
|
∂y |
∂u |
∂v |
(3) |
||||
|
dx + |
∂G |
dy + |
∂G |
du + |
∂G |
||
|
dv = 0. |
|||||||
|
∂y |
∂u |
∂v |
Пример: Уравнения u+v=x+y, xu+yv=1 определяют u и v как функции х и у; найти
ддux , ддuy , ддvx , ддvy .
Решение. 1-й способ. Дифференцируя оба уравнения по х, получим:
|
дu |
+ |
дv |
= 1, |
||||||||||||||
|
дx |
дx |
||||||||||||||||
|
u + x |
дu |
+ y |
дv |
= 0, |
|||||||||||||
|
дx |
|||||||||||||||||
|
дx |
|||||||||||||||||
|
отсюда |
|||||||||||||||||
|
дu |
= − |
u + y |
, |
дv |
= |
u + x |
. |
||||||||||
|
дx |
x − y |
дx |
|||||||||||||||
|
x − y |
Аналогичным образом найдем:
|
дu |
= − |
u + y |
, |
дv |
= |
u + x |
. |
|
дy |
x − y |
дy |
|||||
|
x − y |
2-й способ. Дифференцированием находим два уравнения, связывающие дифференциалы всех четырех переменных: du+dv=dx+dy, x du+u dx+y dv+v dy=0.
Решив эту систему относительно дифференциалов du и dv, получим:
|
du = − |
( u + y )dx + ( v + y )dy |
, |
dv = |
( u + x )dx + ( v + x )dy |
. |
||||||||||||||
|
x − y |
x − y |
||||||||||||||||||
|
Отсюда |
|||||||||||||||||||
|
дu |
= − |
u + y |
, |
дu |
= − |
u + x |
, |
||||||||||||
|
дx |
x − y |
дy |
x − y |
||||||||||||||||
|
дu |
= |
u + y |
, |
дu |
= |
u + x |
. |
||||||||||||
|
дx |
|||||||||||||||||||
|
x − y |
дy |
x − y |
4°. Параметрическое задание функции. Если функция г переменных х и у задана параметрически уравнениями x=x(u,v), y=y(u,v), z=z(u,v) и
72

|
D(x, y) |
дx |
дx |
|||||
|
= |
дu |
дv |
≠ 0 |
, |
|||
|
D(u,v) |
дy |
дy |
|||||
|
дu |
дv |
то дифференциал этой функции может быть найден из системы уравнений
|
∂x |
du + |
∂x |
dv, |
|||
|
dx = |
||||||
|
∂u |
∂v |
|||||
|
∂y |
∂y |
|||||
|
du + |
dv, |
|||||
|
dy = |
(4) |
|||||
|
∂u |
∂v |
|||||
|
dz = |
∂z |
du + ∂z dv. |
||||
|
∂u |
∂v |
|||||
Зная дифференциал dz=p dx+q dy, находим частные производные ддxz = p и ддyz = q .
Пример. Функция z аргументов х и у задана уравнениями x=u+v, y=u²+v², z=u²+v² (u≠v).
Найти ддxz и ддyz .
Решение. 1-й способ. Дифференцированием находим три уравнения, связывающие дифференциалы всех пяти переменных:
dx = du + dv,dy = 2udu + 2vdv,
dz = 3u2du + 3v2dv.
Из первых двух уравнений определим du и dv:
|
du = |
2vdx + dy |
, |
dv = |
dy + 2udx |
. |
|
2( v − u ) |
|||||
|
2( v − u ) |
Подставим в третье уравнение найденные значения du и dv:
|
dz = 3u2 2vdx − dy |
+ 3v2 dy − 2udx = 6uv(u − v)dx + 3(v2 − u2 )dy |
= −3uvdx + |
3 (u + v)dy . |
|||||||||||||||||||||||||||||||
|
2(v − u) |
2(v − u) |
2(v − u) |
2 |
|||||||||||||||||||||||||||||||
|
Отсюда |
||||||||||||||||||||||||||||||||||
|
дz |
= −3uv, |
дz |
= |
3 |
(u + v) . |
|||||||||||||||||||||||||||||
|
дx |
дy |
2 |
||||||||||||||||||||||||||||||||
|
2-й способ. Из третьего данного уравнения можно найти: |
||||||||||||||||||||||||||||||||||
|
дz |
= |
3u |
2 |
дu |
+ 3v |
2 |
дv |
; |
дz |
= |
3u |
2 |
дu |
+ 3v |
2 |
дv |
(5) |
|||||||||||||||||
|
дx |
дx |
дx |
дy |
дy |
дy |
|||||||||||||||||||||||||||||
|
Продифференцируем первые два уравнения сначала по х, затем по у: |
||||||||||||||||||||||||||||||||||
|
1 = |
∂u |
+ |
∂v |
, 0 = |
∂u |
+ |
∂v |
, |
||||||||||||||||||||||||||
|
∂x |
∂y |
∂y |
∂y |
|||||||||||||||||||||||||||||||
|
∂u |
∂v |
∂u |
∂v . |
|||||||||||||||||||||||||||||||
|
0 = 2u |
+ 2v |
, 1 = 2u |
+ 2v |
|||||||||||||||||||||||||||||||
|
∂x |
∂x |
∂y |
∂y |
|||||||||||||||||||||||||||||||
Из первой системы найдем:
Из второй системы найдем:
Подставляя выражения ддxz
|
дu |
= |
v |
дv |
= |
u |
. |
||||||||
|
дx |
v − u, дx |
u − v |
||||||||||||
|
дu |
= |
1 |
, |
дv |
= |
1 |
. |
|||||||
|
дy |
2( u − v ) |
дy |
2( u − v ) |
|||||||||||
и ддyz в формулу (5), получим:
73
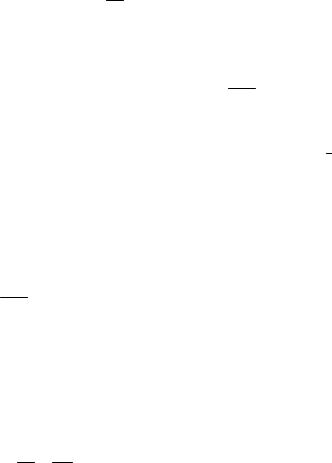
|
дz |
= 3u2 |
v |
+ 3v |
2 |
u |
= −3uv, |
|||||||
|
дx |
v − u |
u − v |
|||||||||||
|
дz |
= 3u2 |
1 |
+ |
3v2 |
1 |
= |
3 |
( u + v ). |
|||||
|
дy |
2(v − u) |
2(u − v) |
2 |
Замена переменных
При замене переменных в дифференциальных выражениях входящие в них производные следует выразить через другие производные по правилам дифференцирования сложной функции.
1°. Замена переменных в выражениях, содержащих обыкновенные производные.
|
Пример. Преобразовать уравнение |
|||||||||
|
x2 |
d 2 y |
+ 2x |
dy |
+ |
a2 |
y = 0 , |
|||
|
dx2 |
dx |
x2 |
|||||||
|
полагая |
x = |
1 |
. |
||||||
|
t |
Решение. Выразим производные от у по х через производные от у по t. Имеем:
|
dy |
dy |
dy |
|||||||||
|
= |
dt |
= |
dt |
||||||||
|
dx |
dx |
1 |
|||||||||
|
dt |
− |
||||||||||
|
t2 |
|||||||||||
|
d dy |
|||||||||||
|
dy |
|||||||||||
|
dt dt |
|||||||||||
|
= − |
2t |
||||||||||
|
dx |
dt |
dt
= −t2 dydt ,
|
d |
2 |
y |
|||
|
+ t2 |
(− t2 )= 2t2 |
||||
|
dt2 |
|||||
+ t2 d 2 2y . dt
Подставляя найденные выражения производных в данное уравнение и заменяя х через 1t ,
получим:
|
1 |
2 |
dy |
2 d 2 y |
1 |
2 |
dy |
2 |
2 |
||||||||||||||||
|
t |
2t |
+ t |
+ 2 |
− t |
+ a |
t |
y = 0 |
|||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||
|
t |
dt |
dt |
t |
|||||||||||||||||||||
|
dt |
или
d 2 2y + a2 y = 0 . dt
|
Пример. Преобразовать уравнение |
||||||||
|
d 2 y |
dy 2 |
dy |
||||||
|
x |
+ |
− |
= 0, |
|||||
|
dx2 |
dx |
dx |
приняв за аргумент у, а за функцию х.
Решение. Выразим производные от у по х через производные от х по у.
dydx = dx1 ; dy
74

d 2 x dy2
d 2 y dx2
|
d 2 x |
||||||
|
d |
1 dy |
= − |
dy2 |
|||
|
dy |
dx |
dx |
dx 2 |
|||
|
dy |
dy |
1 dx dy
= − dx 2 .dy
Подставив эти выражения производных в данное уравнение, будем иметь:
|
d 2 x |
|||||||||||||||||||||||||||||||||
|
dy2 |
1 |
1 |
|||||||||||||||||||||||||||||||
|
x − |
+ |
− |
= 0 , |
||||||||||||||||||||||||||||||
|
dx |
2 |
dx |
2 |
dx |
|||||||||||||||||||||||||||||
|
dy |
|||||||||||||||||||||||||||||||||
|
dy |
dy |
||||||||||||||||||||||||||||||||
|
или, окончательно, |
|||||||||||||||||||||||||||||||||
|
d 2 x |
dx |
2 |
|||||||||||||||||||||||||||||||
|
x |
−1+ |
= 0 . |
|||||||||||||||||||||||||||||||
|
dy2 |
|||||||||||||||||||||||||||||||||
|
dy |
|||||||||||||||||||||||||||||||||
|
Пример. Преобразовать уравнение |
|||||||||||||||||||||||||||||||||
|
dy |
= |
x + y |
, |
||||||||||||||||||||||||||||||
|
dx |
x − y |
||||||||||||||||||||||||||||||||
|
перейдя к полярным координатам |
|||||||||||||||||||||||||||||||||
|
x=r cosφ, y=r cosφ. |
(1) |
||||||||||||||||||||||||||||||||
|
Решение. Рассматривая r как функцию φ, из формул (1) получим: |
|||||||||||||||||||||||||||||||||
|
dх = соsφ dr – r sinφ dφ, dy=sinφ+r cosφ dφ, |
|||||||||||||||||||||||||||||||||
|
отсюда |
|||||||||||||||||||||||||||||||||
|
sinϕ |
dr |
+ r cosϕ |
|||||||||||||||||||||||||||||||
|
dy |
= |
sinϕdr + rcosϕdϕ |
= |
dϕ |
|||||||||||||||||||||||||||||
|
. |
|||||||||||||||||||||||||||||||||
|
dx |
cosϕdr − r sinϕdϕ |
cosϕ |
dr |
− r sinϕ |
|||||||||||||||||||||||||||||
|
dϕ |
|||||||||||||||||||||||||||||||||
|
Подставляя в данное уравнение выражения для х, у и |
dy |
, будем иметь: |
|||||||||||||||||||||||||||||||
|
dx |
|||||||||||||||||||||||||||||||||
|
sinϕ |
dr |
+ r cosϕ |
|||||||||||||||||||||||||||||||
|
dϕ |
= |
sinϕdr + rcosϕdϕ |
, |
||||||||||||||||||||||||||||||
|
dr |
|||||||||||||||||||||||||||||||||
|
cosϕ |
− r sinϕ |
cosϕdr − r sinϕdϕ |
|||||||||||||||||||||||||||||||
|
dϕ |
|||||||||||||||||||||||||||||||||
или, после упрощений, ddrϕ = r .
2°. Замена переменных в выражениях, содержащих частные производные. Пример. Уравнение колебаний струны
|
д2u |
= a2 |
д2u |
(a ≠ 0) |
|
|
дt2 |
дx2 |
|||
преобразовать к новым независимым переменным α иβ , где α = x − αt , β = x + αt .
Решение. Выразим частные производные от u по х и y через частные производные от u по α иβ . Применяя формулы дифференцирования сложной функции
ддut = ддαu ддαt + ддβu ддβt , ддux = ддαu ддαx + ддβu ддβx ,
получим:
75

|
дu |
дu |
дu |
|||||||||
|
= |
(−α ) + |
α |
= α |
||||||||
|
дα |
дβ |
дβ |
|||||||||
|
= |
дu |
1+ |
дu |
1 = |
дu |
+ |
дu |
. |
|||
|
дα |
дβ |
дα |
|||||||||
|
дβ |
Дифференцируем вторично, применяя те же формулы:
|
д2u |
д |
дu |
д |
дu |
дα |
д |
дu |
дβ |
|||||||||||||||||||
|
= |
= |
+ |
= |
||||||||||||||||||||||||
|
дt2 |
дt |
дt |
дβ |
дt |
|||||||||||||||||||||||
|
дt |
дα |
дt |
дt |
||||||||||||||||||||||||
|
д2u |
д2u |
д2u |
д2u |
||||||||||||||||||||||||
|
= α |
− |
( −α ) + |
α |
− |
α = |
||||||||||||||||||||||
|
дα |
2 |
2 |
|||||||||||||||||||||||||
|
дαдβ |
дβ |
дαдβ |
|
д2u |
д2u |
д2u |
|||||||||||||||||||||||||||||||||||
|
= α 2 |
− 2 |
+ |
; |
||||||||||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||||||||
|
дαдβ |
дβ |
||||||||||||||||||||||||||||||||||||
|
дα |
|||||||||||||||||||||||||||||||||||||
|
д2u |
д |
дu |
д |
дu дα |
д |
дu |
дβ |
||||||||||||||||||||||||||||||
|
= |
= |
+ |
= |
||||||||||||||||||||||||||||||||||
|
дx2 |
дx |
дx |
дβ |
дx |
дx |
||||||||||||||||||||||||||||||||
|
дx |
дα |
дx |
|||||||||||||||||||||||||||||||||||
|
д2u |
д2u |
д2u |
д2u |
||||||||||||||||||||||||||||||||||
|
= |
+ |
1 + |
+ |
1 |
= |
||||||||||||||||||||||||||||||||
|
2 |
дαдβ |
дβ |
2 |
||||||||||||||||||||||||||||||||||
|
дα |
дαдβ |
||||||||||||||||||||||||||||||||||||
|
= |
д2u |
+ 2 |
д2u |
+ |
д2u |
. |
|||||||||||||||||||||||||||||||
|
дα 2 |
дαдβ |
дβ 2 |
|||||||||||||||||||||||||||||||||||
Подставив в данное уравнение, будем иметь:
|
2 |
д2u |
д2u |
д2u |
2 |
д2u |
д2u |
д2u |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
α |
− 2 |
+ |
= α |
+ 2 |
+ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дα |
дαдβ |
дβ |
дα |
дαдβ |
дβ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
или |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
д2u |
= 0. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дαдβ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример. Преобразовать уравнение |
x2 |
дz |
+ y2 |
дz |
= z2 , приняв за новые независимые |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дx |
дy |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
переменные u=х, v = |
1 |
− |
1 |
и за новую функцию |
w = |
1 |
− |
1 |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
y |
z |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение. Выразим частные производные |
дz |
и |
дz |
через частные производные |
дw |
и |
дw |
. Для |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дx |
дy |
дv |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дu |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
этого продифференцируем данные соотношения между старыми и новыми переменными |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
du = dx, dv = |
dx |
− |
dy |
, |
dw = |
dx |
− |
dz |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
x2 |
y2 |
x2 |
z2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
С другой стороны, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дw = |
дw |
du + |
дw |
dv . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дu |
дv |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Поэтому |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дw |
du + |
дw |
dv = |
dx |
− |
dz |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дu |
дv |
z2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
или |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дw |
dx + |
дw dx |
− |
dy |
dx |
− |
dz |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дu |
дv |
y2 |
= |
x2 |
z2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
2 |
Отсюда
76
Помогаю со студенческими работами здесь

Представить двойной интеграл int int f(x,y)dxdy в виде повторного интеграла с внешним…
Получить производную нужно
На фото, помогите мужики, правда надо )
Нужно вычислить символьно производную и интеграл
Вычислить символьно производную и интеграл:

Здравствуйте) помогите пожалуйста!
По какой формуле нужно наити производную?
sqrt{x}

Здравствуйте. помогите пожалуйста решить задачку,
y=ln(x+4),Нужно составить производную n ого…
Нужно вычислить производную из абсолютно случайного выражения
люди помогите написать программу для вычисления производной, а то в школе совсем уже забили ими,…
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму:
Явные и неявные
В этой статье мы познакомимся с неявными функциями и техникой их дифференцирования. Вспомним для начала, как выглядят функции, заданные явно. Это “обычные” функции вида y=f(x)y=f(x), с которыми вы уже имели дело и умеете вычислять их производные. Запись y=f(x)y=f(x) обозначает, что мы функцию yy смогли выразить (явно представить) через её аргумент xx. З неявными функциями дело обстоит иначе. Здесь мы не можем “перетащить” yy в левую сторону выражения, а все что содержит xx — в правую. Такие функциональные зависимости в общем виде можно записать так:
F(x,y)=0F(x, y)=0
Эта запись означает, что величины xx и yy как-то связанны между собой, но ничего не говорится о том, как yy выражается через xx (и можно ли это вообще сделать). Одну и ту же функцию (но не каждую) можно записать как в явном так и в неявном виде. Например, неявно заданную функцию F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x} можно записать явно: y(x)=−53x2y(x)=-frac{5}{3x^2}. В этом случае нам удалось выразить yy через xx. Или, если:
F(x,y)=x2+y2−1=0F(x, y)=x^2+y^2-1=0
то
y=±1−x2y=pm sqrt{1-x^2}
Здесь функция получилась многозадачной (именно двузначной, отвечающей двум знакам), но это не страшно. Мы все-равно представили yy как выражение зависящее от xx. В правой стороне у нас присутствует только xx.
Но существуют случаи, когда этого сделать нельзя. Можно навести множество примеров таких функций. Например:
F(x,y)=ylnx+eyy2F(x, y)=yln x+e^yy^2
Ну попробуйте выразить отсюда yy через xx. То есть запишите эту функцию в виде y=f(x)y=f(x). Вот вам и пример неявной заданной функции. Ещё пример:
F(x,y)=xsinx+ysiny−12F(x, y)=xsin x+ysin y-12
Здесь, мы хотя и не можем выразить yy через xx, но мы все-равно можем считать yy функцией от аргумента xx. Так как каждому значению xx будут соответствовать какие-то значения yy.
Естественно, возникает вопрос о дифференцировании подобных функций. Вы уже понимаете, что эта операция очень важна, и было бы тяжело поверить, что математики ничего не придумали на этот счет.
Дифференцирование неявно заданных функций
Оказывается, что для того чтобы посчитать производную от yy по xx нам не обязательно решать уравнение:
F(x,y)=0F(x, y)=0
Теоретически можно доказать (пользуюсь определением производной, производя предельный переход и т. д.), что:
dydx=−∂F(x,y)∂x∂F(x,y)∂yfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}
Обозначение ∂partial обозначает частную производную. Мы здесь имеем дело с двумя переменными xx и yy и берем производные от функции F(x,y)F(x, y) по этим величинам. Так, выражение:
∂F(x,y)∂xfrac{partial F(x, y)}{partial x}
говорит, что берется производная от F(x,y)F(x, y) по xx, при этом величина yy считается постоянной. Следует обратить внимание на знак “минус” перед дробью, а также на то, что мы не можем сократить числитель и знаменатель на ∂F(x,y)partial F(x, y), так как производные берутся по разным величинам. Вооружившись этой главной формулой вычисления производных от неявных функций, перейдем к разбору нескольких примеров.
Примеры
F(x,y)=x2+y2−1F(x, y)=x^2+y^2-1
∂F(x,y)∂x=2x, ∂F(x,y)∂y=2yfrac{partial F(x, y)}{partial x}=2x, frac{partial F(x, y)}{partial y}=2y
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−2x2y=−xyfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{2x}{2y}=-frac{x}{y}
F(x,y)=xsinx+ysiny−12F(x, y)=xsin x+ysin y-12
∂F(x,y)∂x=sinx+xcosx, ∂F(x,y)∂y=siny+ycosyfrac{partial F(x, y)}{partial x}=sin x+x cos x, frac{partial F(x, y)}{partial y}=sin y+y cos y
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−sinx+xcosxsiny+ycosyfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{sin x+xcos x}{sin y+ycos y}
- F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x}
∂F(x,y)∂x=3y−5×2, ∂F(x,y)∂y=3xfrac{partial F(x, y)}{partial x}=3y-frac{5}{x^2}, frac{partial F(x, y)}{partial y}=3x
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−3y−5x23x=−3yx2−53x3frac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{3y-frac{5}{x^2}}{3x}=-frac{3yx^2-5}{3x^3}
Но здесь мы можем выразить yy через xx явно:
y=−53x2y=-frac{5}{3x^2}
Подставим это выражение в формулу для производной выше:
dydx=103x3frac{dy}{dx}=frac{10}{3x^3}
А теперь поступим так, как будто нам с самого начала была известна явная зависимость y=f(x)y=f(x). То есть продифференцируем функцию y(x)=−53x2y(x)=-frac{5}{3x^2} по xx:
dydx=ddx(−53×2)=−53(−2)1×3=103x3frac{dy}{dx}=frac{d}{dx}Big(-frac{5}{3x^2}Big)=-frac{5}{3}(-2)frac{1}{x^3}=frac{10}{3x^3}
Получили то же самое. Значит мы все сделали правильно.
Примеры нахождения частных производных
Задача 2. Найти частные производные ,
и
, если переменные x, y, и z связаны равенством 4x2 y ez – cos(x3 – z) + 2y2 + 3x = 0.
Решение находим с помощью калькулятора.
Для F(x, y, z) = 4x2 y ez – cos(x3 – z) + 2y2 + 3x получаем:
F’x= (4x2 yez – cos(x3 – z) + 2y2 + 3x)’x = [считаем y и z постоянными] =
= 8x y ez + sin( x3 – z)3x2 + 3 = 8x y ez + 3x2 sin( x3 – z) + 3;
F’y= (4x2 y ez – cos(x3 – z) + 2y2 + 3x)’y = [считаем x и z постоянными] =
= 4x2 ez + 4y;
F’z = (4x2 y ez – cos(x3 – z) + 2y2 + 3x)’z = [считаем x и y постоянными] =
= 4x2 y ez – sin (x3 – z).
По формулам находим частные производные:
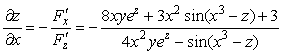
и по формуле (3) получаем: 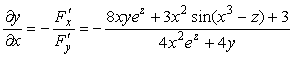
Ответы: 

Задание. Найти частные производные функции z в точке A(-1;0).
z = ln(x2+y2)+y/x
Решение.
Находим частные производные:
Задание №2. Найти частные производные 1-го и 2-го порядка.
z = x3 + 3x2y – sin(xy)
Скачать решение
Задача 1. Дана функция z = f(x,y). Требуется:
1) найти частные производные dz/dx и dz/dy;
2) найти полный дифференциал dz;
3) показать, что для данной функции справедливо равенство: d2z/dxdy = d2z/dydx.
Пример 1. Показать, что функция удовлетворяет уравнению
.
Решение.
Найдем частные производные и
.


Подставим их в уравнение
Получим тождество. Следовательно, функция z удовлетворяет данному уравнению.
Пример 2. Дана функция и две точки A(4;2 )и B(4.03;1.96). Требуется: 1) вычислить значение функции в точке В;
2) вычислить приближенное значение функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом;
3) оценить в процентах относительную погрешность, возникшую при замене приращения функции ее дифференциалом.
Решение.
1.
2.
Итак, z0=5, z≈z0+df(A); 
Найдем .

;


f(4.03;1.96)=≈5+0.8·0.03+1.2·(-0.04)=5.072.

.
Перейти к онлайн решению своей задачи
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).