Как найти производную по направлению скалярного поля – Сайт, где вы сможете решить свои вопросы

Предположим,
что в каждой точке М
некоторой области D
задано
значение
скалярной
величины
,
т. е. такой
величины, которая полностью
характеризуется
своим числовым значением. Например, это
может быть температура точек неравномерно
нагретого тела, плотность распределения
электрических зарядов, потенциал
электрического поля и т. д. При этом
называют скалярной функцией точки и
записывают.

ОПРЕДЕЛЕНИЕ. Если
в области D
задана скалярная функция точки
,
то говорят, что в этой области задано
скалярное поле.

Если
скалярное поле отнесено к системе
координат
,
то задание точкиМ
равносильно
заданию ее координат
.

Поверхностью
уровня
скалярного поля называют геометрическое
место точек, в которых функция
принимает постоянное значение, т. е.,
в зависимости от физического смысла
поля они могут называться изотермическими,
изобарическими и т. п.

Важной
характеристикой скалярного поля является
скорость изменения поля в заданном
направлении.

Пусть
задано скалярное поле, т. е. задана
функция
.
Возьмем точкуи некоторое направление,
определяемое направляющими косинусами.
При перемещении в данном направлении
точкив точкуфункцияполучает приращение

которое
называют приращением функции в данном
направлении. Величину перемещения точки
обозначим через,
тогда можно записать, что

ОПРЕДЕЛЕНИЕ. Производной
функции
в направленииназывают предел отношения приращения
функции в этом направлении к величине
перемещения при условии, что перемещение
стремится к нулю

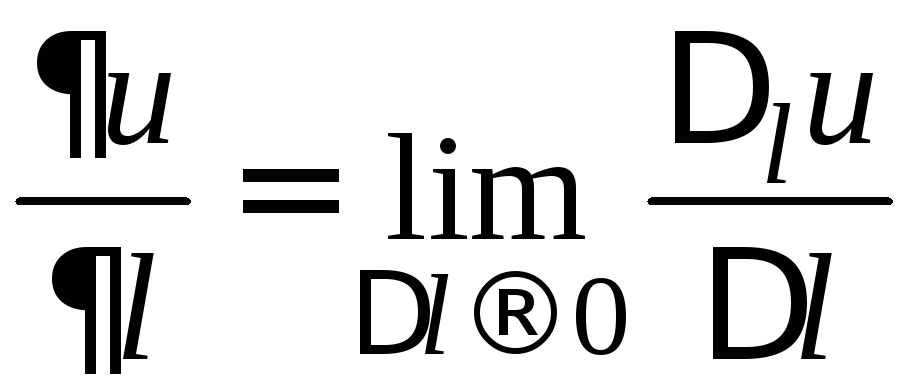Вычислить
производную по направлению можно,
используя следующую теорему:

ТЕОРЕМА. Если
функция
дифференцируема, то ее производнаяпо любому направлениюсуществует и равна

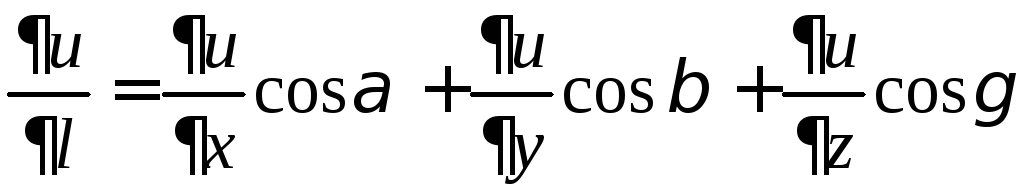где
–
направляющие косинусы направления.

ПРИМЕР. Найти
производную функции
в точкепо направлению, идущему от точкик точке.

РЕШЕНИЕ

Найдем
единичный вектор e,
соответствующий направлению
:

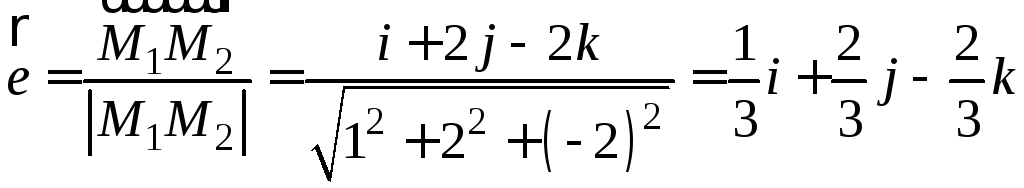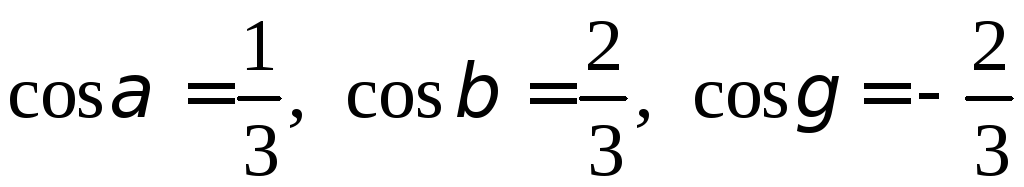Частные
производные функции
равны:

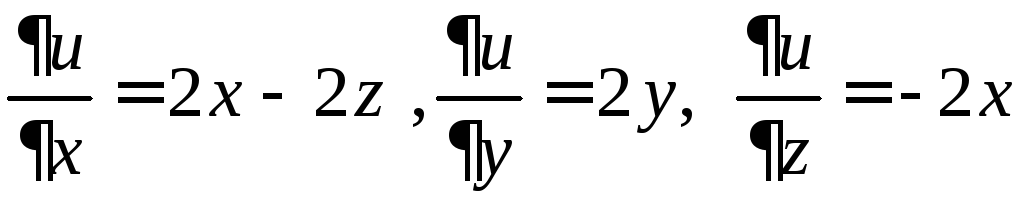Вычислим
частные производные в точке
и найдем производную по направлению из
равенства

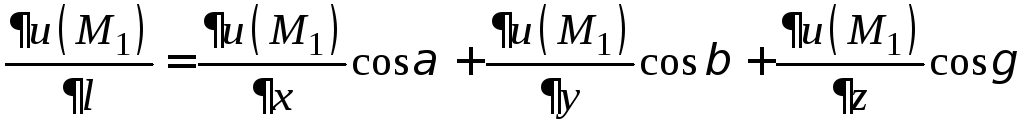получим
.

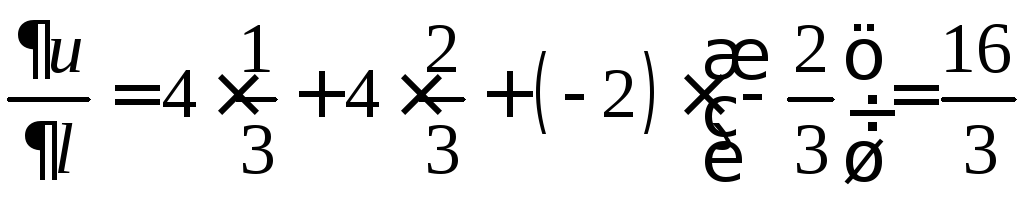ОПРЕДЕЛЕНИЕ. Градиентом
функции
называют вектор, проекциями которого
служат значения частных производных
этой функции, т. е.

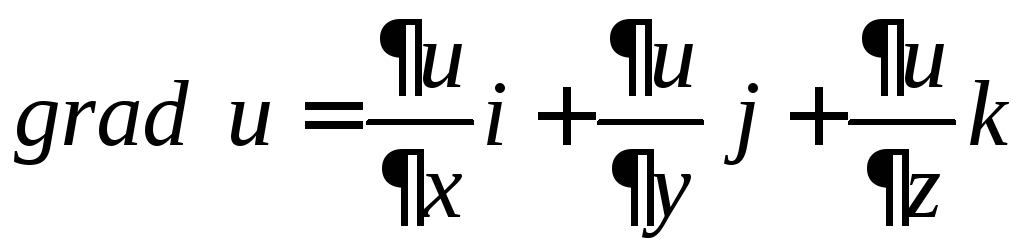Используя
определение градиента, формулу производной
по направлению можно записать в виде:

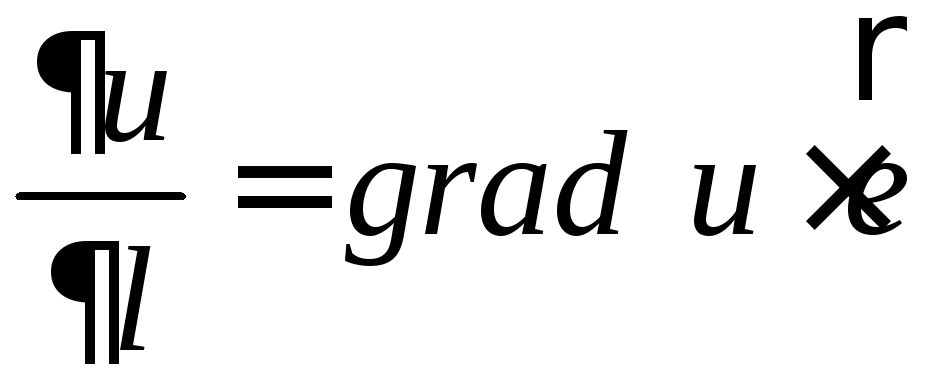где
– единичный вектор направления.

Меняя
направление
,
мы будем получать различные значения
производной,
причем наибольшее значение наблюдается,
когда направлениесовпадает с вектором.
Таким образом,определяет направление, в котором
скорость возрастания функции
является
наибольшей.

Градиент
скалярного поля в данной точке по
величине и направлению равен максимальной
скорости изменения поля в данной точке.

ПРИМЕР. Дано
скалярное поле
.
Составить уравнение линии уровня.
Вычислить с помощью градиента производную
скалярного поля в точке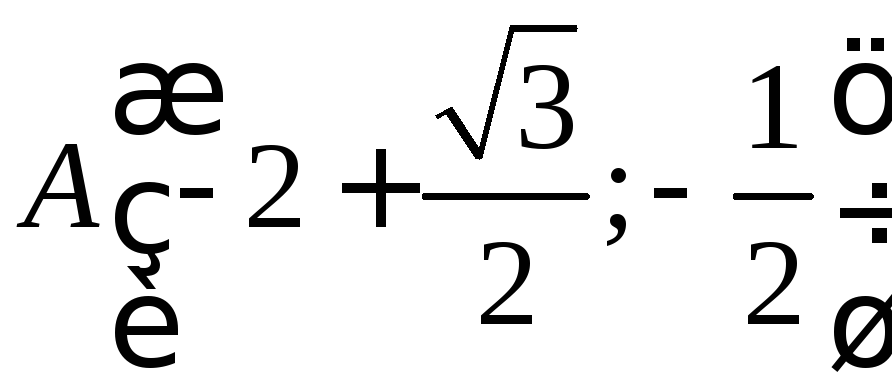по направлению вектора.
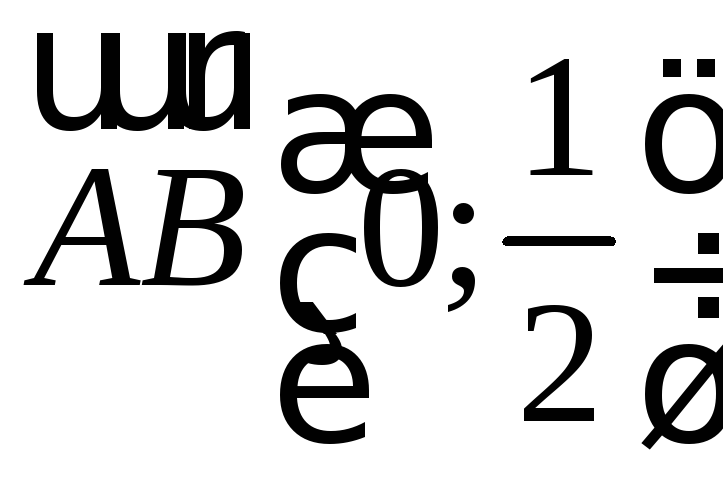Найти наибольшую скорость изменения
скалярного поля в точке.

РЕШЕНИЕ

Поверхностью
уровня (линией уровня) данного скалярного
поля является окружность с центром в
точке
,
радиуса 1:

,
.

Градиент
функции равен: .

Найдём
единичный вектор направления
:,
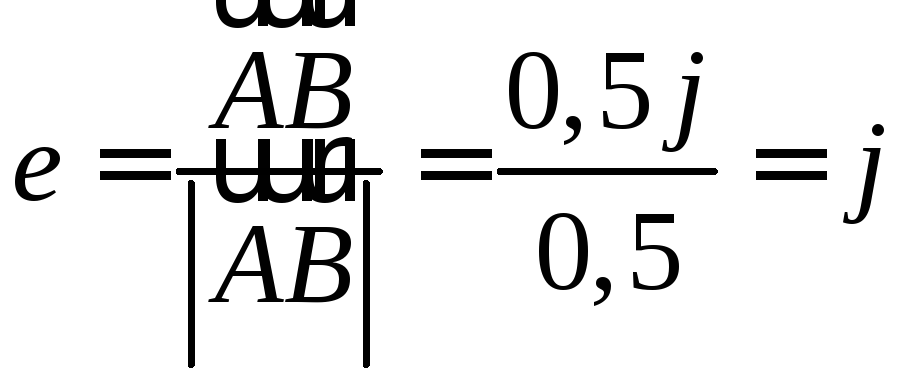а затем производную скалярного поляпо направлениюв точке:

,
.

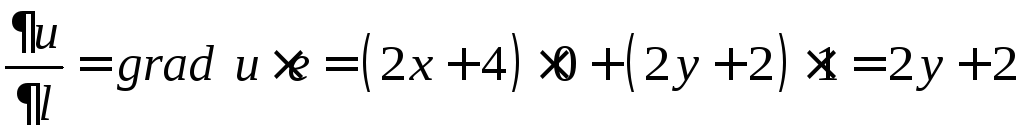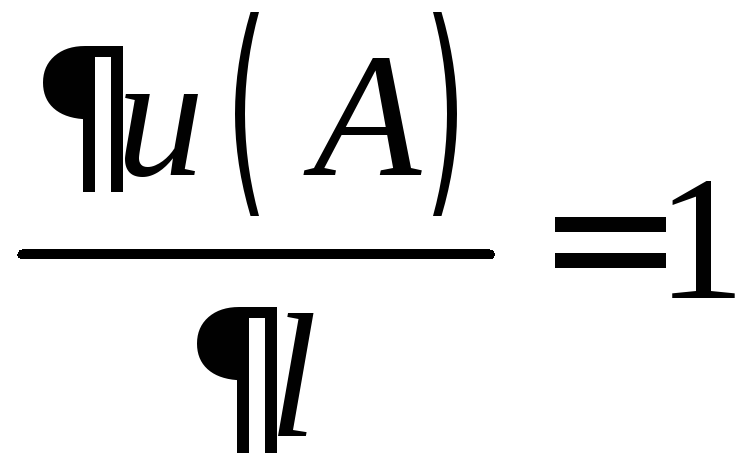Так
как
,
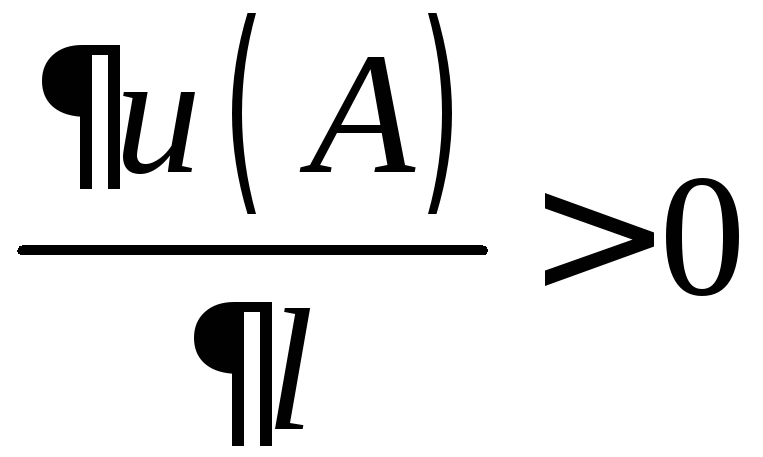то данное скалярное поле возрастает по
направлению векторасо скоростью равной 1.

Теперь
найдём производную по направлению
:

,
.

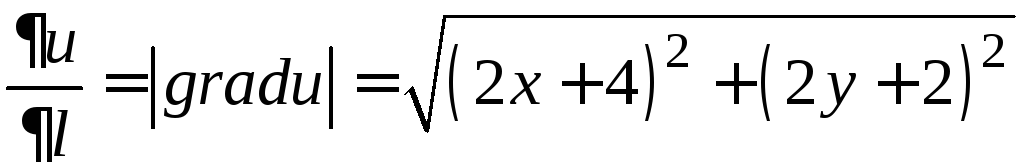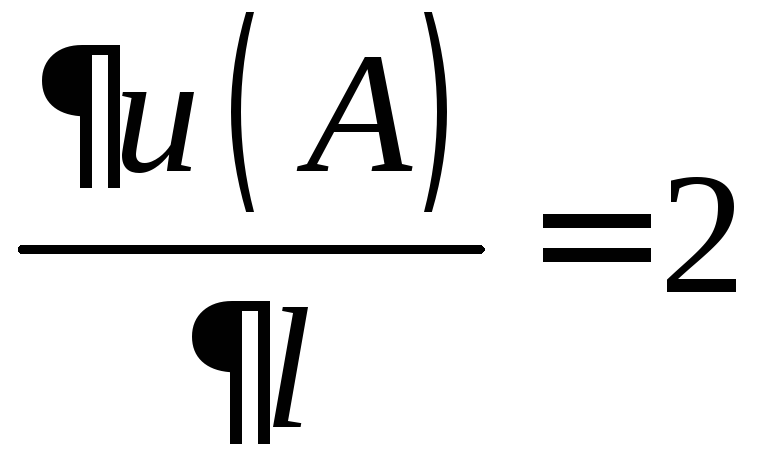Наибольшая
скорость возрастания скалярного поля
в точке
равна 2.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Производная по направлению

Для характеристики скорости изменения поля 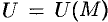Производная по направлению скалярного поля в заданном направлении введем понятие «производной по направлению».

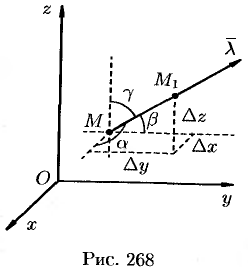
Возьмем в пространстве, где задано поле 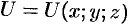Производная по направлению скалярного поля , некоторую точку 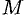и найдем скорость изменения функций при движении точки 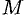в произвольном направлении 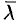. Пусть вектор 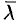имеет начало в точке 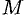Производная по направлению скалярного поля и направляющие косинусы .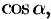

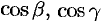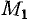Приращение функции Производная по направлению скалярного поля , возникающее при переходе от точки к некоторой точке в направлении вектора 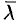определяется как

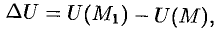
Производная по направлению скалярного поля

или

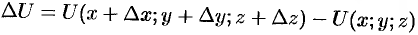
Производная по направлению скалярного поля

(см. рис. 268). Тогда

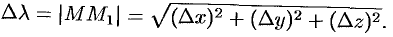
Производная по направлению скалярного поля

Производной от функции 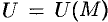Производная по направлению скалярного поля в точке 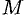по направлению 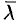называется предел

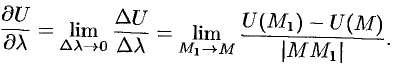
Производная по направлению 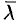скалярного поля

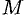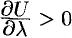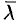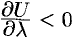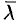Производная по направлению Производная по направлению скалярного поля и характеризует скорость изменения функции (поля) в точке по этому направлению. Если , то функция возрастает в направлении Производная по направлению скалярного поля , если , то функция в направлении убывает. Кроме того, величина 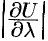представляет собой мгновенную скорость изменения функции Производная по направлению скалярного поля в направлении 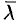в точке 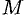: чем больше 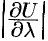, тем быстрее изменяется функция . В этом состоит физический смысл производной по направлению.

Выведем формулу для вычисления производной по направлению, считая, что функция 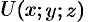Производная по направлению скалярного поля дифференцируема в точке 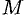. Тогда ее полное приращение в этой точке 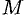можно записать так:

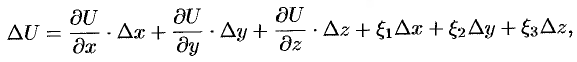
Производная по направлению скалярного поля

где 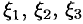Производная по направлению скалярного поля — бесконечно малые функции при 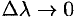(см. п. 44.3).

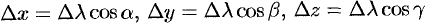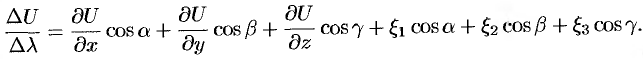
Поскольку Производная по направлению скалярного поля , то

Производная по направлению скалярного поля

Переходя к пределу при 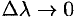Производная по направлению скалярного поля , получим формулу для вычисления производной по направлению:

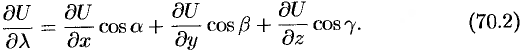
Производная по направлению скалярного поля

В случае плоского поля 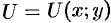Производная по направлению скалярного поля имеем: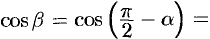 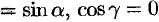. Формула (70.2) принимает вид:

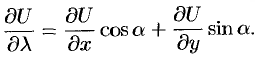
Производная по направлению скалярного поля

Замечание. Понятие производной по направлению является обобщением понятия частных производных 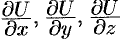Производная по направлению скалярного поля . Их можно рассматривать как производные от функции 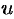по направлению координатных осей , и . Так, если направление 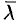совпадает с положительным направлением оси Производная по направлению скалярного поля , то, положив в формуле (70.2) 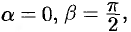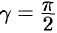, получим .

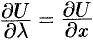Пример №70.1.

Найти производную функции 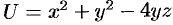Производная по направлению скалярного поля в точке 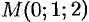в направлении от этой точки к точке .

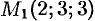Решение:

Находим вектор 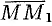Производная по направлению скалярного поля и его направляющие косинусы:

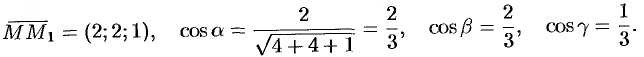
Производная по направлению скалярного поля

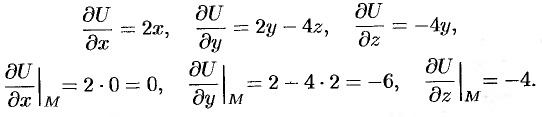
Находим частные производные функции и вычисляем их значения в точке Производная по направлению скалярного поля :

Производная по направлению скалярного поля

Следовательно, по формуле (70.2) имеем:

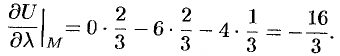
Производн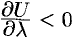ая по направлению скалярного поля

Поскольку Производная по направлению скалярного поля , то заданная функция в данном направлении убывает.

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Источник

Конев В.В. Скалярные и векторные поля

Производная скалярного поля по направлению вектора

Пусть функция

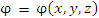описывает некоторое скалярное поле. Выберем произвольную точку

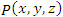и сместимся из нее на малый вектор

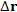в близко расположенную точку

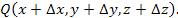При этом значение функции

изменяется на величину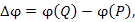

При обсуждении градиента скалярного
поля

было показано, что разность 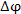можно представить в виде скалярного произведения градиента и вектора смещения :

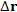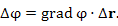
Разделим обе части этого равенства на величину вектора смещения. (Заметим, что отношение вектора смещения к его величине представляет собой единичный вектор 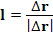в направлении 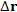.) Далее выполним предельный переход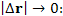

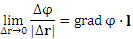Предел в левой части вышеприведенного равенства называется производной скалярного поля по направлению вектора l и записывается в виде

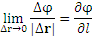Таким образом, производная функции по заданному направлению равна скалярному произведению градиента функции на единичный вектор этого направления:

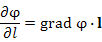Поскольку вектор 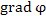направлен с сторону наиболее быстрого возрастания функции , а его величина равна скорости изменения в этом направлении, то проекция градиента поля на произвольное направление равна быстроте изменения функции в таком направлении.


Следовательно, производная функции по направлению вектора l представляет собой скорость изменения в этом направлении.


Заметим, что понятие производной функции по направлению вектора является обобщением понятия частной производной функции. Например, частную производную 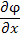   можно интерпретировать как производную функции по направлению вектора i, т.е. вдоль положительного направления оси 0x.

Используя
свойство скалярного произведения векторов,

формулу для производной скалярного поля по направлению вектора можно представить в координатной форме записи:

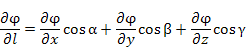Здесь 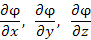– координаты вектора 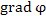; α, β и γ – углы, образованные вектором l с положительными направлениями координатных осей; направляющие косинусы cos α, cos β и cos γ являются координатами единичного вектора l .

Источник

Линейной формойОтносительно вектораНазывают скалярное произведе

Ние вектораНа некоторый векторНе зависящий от-радиус-

Вектор точки– вектор, соединяющий точки

Скалярное полеНазывается дифференцируемым в точкеИз области

Если приращение поляВ этой точке можно представить в виде

(29.3)

Где– расстояние между точками

Градиентом дифференцируемого в точкеСкалярного поля называют векторИз (29.3). Обозначение:

Если поле дифференцируемо в каждой точке области, то оно дифференцируемо в. В этом случае

При заданной декартовой системе координат

Свойства градиента:

Если– базис в ортогональной криволинейной системе координат

, то

Где– параметры Ламе, определенные формулой

(29.6)

В цилиндрической системе координат в сферической системе координат

Дифференциалом скалярного поляНазывают скалярное произведение

Пусть _ – единичный вектор, указывающий направлениеВ точкеОбласти– произвольная точка, отличная отИ такая, что вектор коллинеарен вектору

Предел– расстояние между

ТочкамиI, если он существует, называют производной поляВ точ

КеПо направлениюИ обозначают символом

Где

ИЛИ

Если е имеет направление, то

Пример 29.3. Найти величину и направление градиента скалярного поля В точке

Находим частные производные функции к их значения в точке:

По формуле (29.4) получаем

Величину градиента находим по формуле (29.5):

Пример 29.4. Найти производную поляВ точке

По направлению вектора iОбразующего с координатными осями острые углы Установить характер изменения поля в данном направлении. Частные производные функцииВ точкеИмеют значения: